Protonation and water exchange kinetics in sandwich polyoxometalates

Abstract

Density functional theory is used to explore the locus and consequences of protonation in [Zn₄(HO)₂(PW₉O₃₄)₂]¹⁰⁻. The results are used to explain recent observations regarding the contrasting pH effects on the water-ligand exchange in [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ and [Co₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻, and the general effect of protonation on solvent exchange in metal oxides is discussed.

---

Introduction

Polyoxometalates are discrete metal oxide clusters of V, Nb, Ta, Mo and W in their respective highest oxidation states, and exhibit a large structural diversity.^1,2 This diversity is mirrored by the broad range of chemistries that this class of molecules demonstrates. In addition to being attractive as oxidative and reductive catalysts due to the absence of easily degradable organic moieties, polyoxometalates make interesting models for the study of geochemically relevant reactions, as many polyoxometalates are nanometre-sized and resemble mineral fragments and surface features in terms of size and functional groups.^3–5

Polyoxometalates can also be used as ligands to immobilise mineral-like fragments of other metal oxide classes. The Wells–Dawson polyoxometalates [M₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ (1) and [M₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ (2) – where M is Mn(II),⁶ Fe(III),⁷ Co(II),^8,9 Ni(II),⁶ Cu(II) or^8,9 Zn(II),^8,9– contain a birnessite-like sheet of M–O units sandwiched between two polyoxometalate ligands, and with aquo-ligands bound to the outer M sites. This arrangement offers a rare opportunity to probe the chemistry of small ligands, such as water, bound to mineral-like surfaces using solution phase methods. In particular, there is a limited amount of data on ligand exchange on metal oxide centres surrounded only by other metal oxide centres, where the system is a discrete cluster with a well-defined structure.

Reports that [Co₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ was capable of catalysing the oxidation of water¹⁰ stimulated an interest in the interaction of water with this type of ion, leading to the simultaneous study by two groups of the water-exchange kinetics of [Co₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻,¹¹ and [Co₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻,^11,12 using Swift–Connick formalism.^13,14 While the systems exhibit a two-proton protonation event with a pK_a of ca. 4.2,¹¹ the rates of exchange were found to be pH-independent. The location of protonation was suggested to be on the polyoxometalate ligand, in particular as the pK_a of the aquo-ligand is likely to be considerably higher than the determined pK_a. This is, however, in contrast to earlier work, where the locus of protonation was assigned to the aquo ligand,¹⁵ but consistent with assignments based on molecular electrostatic potentials.¹⁶

Sharma et al. determined the rates of aquo-ligand exchange on the structurally similar [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ ion, also using Swift–Connick formalism.¹⁷ In contrast with the behaviour of the Co(II)-derivative, the rate of ligand exchange on the Mn(II)-derivative shows profound dependence on the pH. Here, the rate of exchange increases by a factor of 15 as the pH is lowered from 6.0 to 3.5. Yet, this molecule too exhibits a two-proton protonation event with a pK_a of ca. 4.4, which is very similar to the determined pK_a of the Co(II) cluster, and is likely to be associated with the same protonation locus.

While these Wells–Dawson molecules are of interest in themselves, the issue of protonation of metal oxide materials – both as discrete clusters and extended mineral and catalyst surfaces – is of much broader importance. Being able to predict loci of protonation and the effect of protonation is thus of considerable interest. In addition, the surface charge density of [M₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ is ca −0.2 C m⁻², which is comparable with that of common minerals, and makes these polyoxometalate clusters particularly interesting targets.

Here we attempt to computationally determine the loci of protonation in Wells–Dawson complexes, explain the difference in pH dependence of rates of aquo-ligand exchange between the Co(II) and Mn(II) derivatives, and tie these conclusions to more general observations of aquo-ligand exchanges in metal oxide materials.

Results and discussion

Computations using density functional theory (DFT) at the PBE0¹⁸/def2-svp¹⁹ and PBE0/def2-tzvp levels of theory together with implicit solvation through the polarizable continuum model²⁰ as implemented in G16²¹ were focused on the zinc(II)-containing molecule [Zn₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ over the paramagnetic target molecules [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻, [Co₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ and [Co₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ owing to the difficulty in accurate modelling paramagnetic systems by DFT, and the smaller size of the [PW₉O₃₄]⁹⁻ ligand, while still having essentially the same structure in the proximity of the M₄ plane. Unless otherwise specified, results reported in the text were obtained at PBE0/def2-tzvp with PCM to approximate solvation in water. Partial charges were computed as natural atomic charges from Natural Bond Order analysis,²² or using the Mesler–Singh–Kollman scheme using UFF radii,²³ or Breneman's modified CHelp scheme using radii of 1.39 and 1.80 Å for Zn and W,²⁴ respectively, or the Hu, Lu and Yan charge-fitting method.²⁵ Additional tabulated energies, optimised structures etc. are provided in the ESI.†

Exploration of protonation loci thus focused on [Zn₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ due to its small size and diamagnetic nature. Protonation of all oxygen sites was explored (see Fig. 1) and each site was protonated symmetrically by two protons to reproduce the experimental observation of protonation in these molecules being a two-proton protonation event, and the corresponding structure was optimised. The relative energies and Zn–OH₂ bond distances for the protonated molecules, and the partial charges for the corresponding oxygen sites in the unprotonated molecule, are tabulated in Table 1.

Fig. 1 Structure of [M₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ with the different protonation sites labelled.

Table 1 Energies, bond distances, and partial charges using different partition methods in H₂[Zn₄(H₂O)₂(PW₉O₃4)₂]⁸⁻ as a function of protonation site

Entry	Site	Δε (kcal mol^−1)	d(M–OH2) (Å)	NBO^a (a.u.)	MKUFF^b (a.u.)	CHelpG^c (a.u.)	HLYGAt^d (a.u.)
Geometries optimised at pbe0/def2-tzvp with PCM (water). The d(M–OH2) in the non-protonated form is 2.236 Å. Partial charges were calculated for the unprotonated molecule at pbe0/def2-tzvp.a Natural atomic charges from Natural Bond Order analysis.^22b The Mesler–Singh–Kollman scheme, using UFF radii.^23c Breneman's modified CHelp scheme, using radii of 1.39 and 1.80 Å for Zn and W, respectively.^24d The Hu, Lu, and Yang charge fitting method using G09 standard atom densities.^25
1	A (μ2)	22.038	2.207	−0.8962	−0.8249	−0.8623	−0.7099
2	B (μ2)	20.798	2.199	−0.9154	−0.8872	−0.8608	−0.7214
3	C (μ2)	19.601	2.199	−0.9041	−0.8214	−0.8384	−0.7307
4	D (μ2)	17.639	2.202	−0.9121	−0.8391	−0.8253	−0.7342
5	E (μ2)	16.933	2.200	−0.9145	−0.8684	−0.8235	−0.7276
6	F (μ2)	16.457	2.193	−0.9119	−0.8654	−0.8414	−0.7254
7	G (μ2)	18.579	2.199	−0.9117	−0.9102	−0.8475	−0.7810
8	H (μ2)	16.735	2.205	−0.9025	−0.8440	−0.8818	−0.7296
9	I (μ2)	0.007	2.183	−0.9603	−0.9449	−0.9021	−0.8769
10	J (μ2)	0	2.190	−0.9611	−0.9238	−0.9428	−0.7954
11	K (μ3)	13.45	2.202	−1.1089	−0.9283	−0.9950	−0.9731
12	L (μ2)	20.83	2.193	−0.9177	−0.8560	−0.8593	−0.7460
13	M (η)	40.908	2.197	−0.7537	−0.7113	−0.7519	−0.6610
14	N (η)	46.815	2.202	−0.7887	−0.7025	−0.7447	−0.6628
15	O (η)	41.19	2.202	−0.7528	−0.7067	−0.7517	−0.6531
16	P (η)	50.725	2.209	−0.7387	−0.6770	−0.7230	−0.6295
17	Q (η)	49.693	2.207	−0.7419	−0.6843	−0.7155	−0.6378

---

The relative energies of the protonated isomers at PBE0/def2-tzvp were found to vary by ca. 51 kcal mol⁻¹ between the lowest and highest energy sites. The computations reveal the preferred loci of protonation as being the μ₂-sites I and J, which are the only two sites that bridge one Zn and one W atom. These sites differ only by ca. 7 cal mol⁻¹ in energy, with J being the lower energy site. Site K, which is a μ₃ site connecting two Zn atoms and one W atom, lies higher in energy by ca. 13 kcal, which is lower than the μ₂ W–O–W sites in the molecule, which typically lie 17–22 kcal mol⁻¹ above the J site in energy. The terminal sites range from 41–51 kcal mol⁻¹ above the J site in energy. While the accuracy and precision of the computational approach is likely to be fairly low, given the poly-anionic nature of the molecule and not accounting for specific solvent interactions such as hydrogen bonding or ion pairing in the computations, these energy differences are large enough to be significant. The loci I and J are thus likely to be the most important sites of protonation. This is consistent with general experimental observations of polyoxometalates, in that μ₂ oxygen sites protonate preferentially over terminal (η) oxygen sites.

The computed relative energies and bond distances depend to varying extents on the choice of basis set. For bridging (μ₂ and μ₃) sites, both PBE0/def2-svp and PBE0/def2-tzvp give very relative energies that are typically higher by ca. 2 kcal mol⁻¹ when the smaller basis set it used, whereas the relative energies for the terminal sites differ by 4–5 kcal mol⁻¹ (Fig. 2). In spite of these difference, either level of theory locates the correct locus of protonation, which opens up the possibility for the investigation of larger complexes.

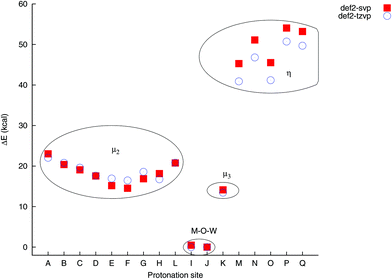Fig. 2 Comparison of relative isomer energies as a function of protonation site and basis set. The energies are only noticeably basis-set dependent for the η-O sites.

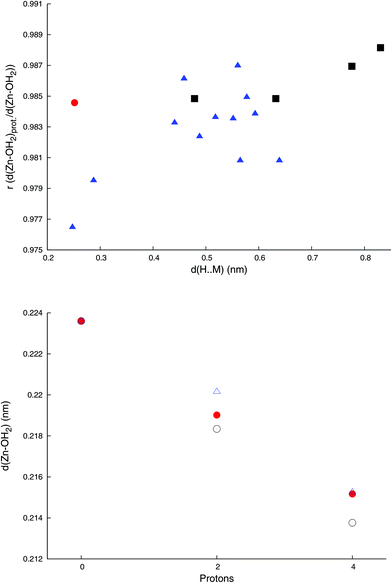
Simultaneous protonation by two protons reduces the surface charge from ca −0.2 C m⁻² by ca. 0.04 C m⁻², and – apart from a larger general contraction caused by the change in charge – leads to a contraction of the Zn–OH₂ bond (Fig. 3), which scales moderately with the distance between the Zn–OH₂ bond and the locus of protonation.

Fig. 3 Top: M–OH₂ distances as a function of H⁺⋯M distance in [Zn₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻. μ₃-O: empty circle, μ₂-O: filled circles, η-O: filled squares. Bottom: Zn–OH₂ distance as a function of the number of protons at positions I (empty circles), J (filled circles) and K (empty triangles). All computations were done at the PBE0/def2-tzvp level with implicit solvation (PCM).

While PBE0/def2-tzvp predicts longer bond distances than PBE0/def2-svp for Zn–OH₂ in the protonated complexes, both methods predict similar fractional Zn–OH₂ bond distances relative to the unprotonated complexes. Thus, either level of theory captures the same general effect of protonation (see ESI, Fig. S2†), with PBE0/def2-tzvp predicting somewhat larger protonation-induced relative contractions in Zn–OH₂ bond distances than PBE0/def2-svp (0.985–0.990). While in this study we have been able to do all the computations at the PBE0/def2-tzvp level of theory, it would thus be justifiable to explore larger systems using PBE0/def2-svp with similar qualitative results.

Protonation at the identified loci, sites I and J, causes the contraction of the Zn–OH₂ bond from 2.236 Å to 2.183 Å (site I) and 2.190 Å (site J). Adding a further two protons, so that all I or J sites are protonated, causes the Zn–OH₂ bond to further contract (Fig. 3) to 2.138 and 2.152 Å, respectively. The energy difference between these two states is ca. 0.2 kcal, which is likely less than the precision of the computational method.

The correlation between relative energies of the protonated isomers and computed partial charges of the different oxygen sites using a few different schemes was also explored at both pbe0/def2-svp and pbe0/def2-tzvp. As expected from the large difference in isomer energies corresponding to protonation of η and μ₂ oxygen sites, and these two groups differing substantially in terms of partial charges, the different partial charges schemes correlate quite well with the computed energies (Fig. 4 (top)). However, at pbe0/def2-svp all investigated schemes predict that the most negative oxygen site is site K, which is not the energetically most favoured site of protonation (see ESI, Fig. S3†). This discrepancy seems to be a general phenomenon, where e.g. NBO charges for the [Nb₁0O₂₈]⁶⁻ ion indicates that the most electronegative oxygen site is a μ₃-O atom,²⁶ whereas energetic calculations reveal the locus of protonation to lie elsewhere.³

Fig. 4 Top: Comparison of partial charges from different methods, with relative energies of H₂[Zn₄(H₂O)₂(PW₉O₃4)₂]⁸⁻ protonated in different loci. All partial charges methods indicate that site K (μ₃) has the most negative partial charge. Bottom: Molecular electrostatic potential surface of [Zn₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻. The colour vs. potential range is from −0.84 (red) to −0.65 (blue). All computations were done at PBE0/def2-tzvp with PCM.

The partial charges computed by in particular MKUFF and HLYGAt are, however, basis set dependent, and decrease with increasing basis set size, whereas the NBO charges vary very little. Intriguingly, at pbe0/def2-tzvp MKUFF gives a more negative partial charge for the I-site than the K-site. Apart from not being helpful in identifying sites I and J as the loci of protonation, this basis set dependence further suggests that these partial charges partitioning methods are not reliable in determining the locus of protonation in metal oxide clusters.

The molecular electrostatic potential (MEP) map (Fig. 4 (bottom)) also identifies the W–O–Zn oxygen sites as having the most negative potential, and appears to indicate that sites I and J have more negative potential than K, which is in accordance with the energetic computations. However, identifying the exact locus based on the MEP map can be challenging, and in itself provides primarily a qualitative view, although it suggests a computationally less demanding approach to gaining an appreciation for where protonation may occur. The chief advantage of the MEP approach is then that it succeeds in separating sites I and J from the other μ₂ sites, but it fails to conclusively identify sites I and J over site K as the protonation loci.

The protonation state of the ions in this study at a given pH is not known as only the change in state is measured through titrimetry, it is likely that they are unprotonated above pH 7 given the pK_as of ditungstic acid, which are ca. 3.5 and 4.6, respectively.²⁷ The protonation event that is identified through titration, based on its pK_a thus probably corresponds to that of addition of two protons to the unprotonated ion, and the likely locus is either site I or J. It is also possible that the protonated system consists of a Boltzmann distributed range of species where sites I and J are protonated to different extents – the precision of the calculations here are not sufficient to rule this in or out.

As part of a study on the rates of aquo-ligand exchange in monomeric coordination complexes of Co(II) and Mn(II), Acharya et al. compared M–OH₂ (M = Mn(II), Co(II)) distances with literature data for rates of water exchange.²⁸ While rates of exchange for Co(II) and seven-coordinate Mn(II) complexes do not correlate strongly, or at all, with the M–OH₂ bond distance, there is a strong correlation for six-coordinate Mn(II) complexes (Fig. 5). Similarly, rates of exchange were found to correlate with the number of 1,10-phenanthroline or 2,2′-bipyridyl ligands in Mn(II) complexes, but not in Co(II) complexes.

Fig. 5 Rates of water exchange vs. M–OH₂ distances for Mn(II), Fe(III), Co(II) and Ni(II). See Acharya et al.²⁸, Balogh et al.²⁹ and ESI† for data and references.

In light of the observed rate vs. bond-distance dependence in Mn(II) complexes in the literature, and lack thereof in Co(II) complexes, it is not surprising that a process that leads to M–OH₂ bond contraction, such as protonation, then affects [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ different to [Co₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻, although it in itself does not explain the underlying mechanism. It does, however, already suggest an approach to predicting which Wells–Dawson derivatives will exhibit weak vs. strong pH-dependent rates of exchange. The lack of correlation for hepta-coordinate Mn(II) further supports the mechanism being interchange associative for the hexa-coordinate Mn(II), in line with the general view.³⁰ Likewise, the lack of strong correlation for Co(II) is consistent with the interchange pathway generally accepted for this ion. What is important to note, however, is that although these models were developed for monomeric complexes, they are often assumed to be applicable to more complex systems, but it is rarely possible to conclusively confirm this.

Based exclusively on the agreement of the rate behaviours of the polyoxometalates in this study, with those of monomeric complexes in the literature involving the same Mn(II) and Co(II) centres, we suggest that the aquo-ligand exchange in the Mn(II) polyoxometalate follows an interchange associative pathway and that it follows an interchange dissociative pathway for Co(II).

The microscopic view of the reaction mechanisms in the present case is not clear, however. In the case of a suggested interchange associative mechanism for [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻, the Mn(II) is situated in a fairly rigid site where such a mechanism is would have been less anticipated. However, the computed protonation-induced bond distance change for the Zn(II) complex, −0.05 Å, suggests a ca. ten-fold rate increase when compared with the plot for Mn(II) complexes (Fig. 5), which is in good agreement with the observed ca. 15-fold rate increase. Similar plots for octahedral Ni(II) and Fe(III) complexes from the literature suggests that Fe(III) will show a significant decrease in rates of exchange with pH and decreasing bond distance, whereas the behaviour of Ni(II) is more difficult to predict. We do not want to speculate on the exact mechanism of the Co(II) polyoxometalate, other than to state that while it appears counter-intuitive that a shortening of the bond-distance of an exchanging ligand should not affect the rate of exchange, the literature data is quite conclusive in demonstrating the lack of correlation between Co(II)–OH₂ bond distances and rates of aquo-ligand exchange.

Conclusions

Prompted by the lack of pH-dependence of the rate of exchange of the aquo-ligand in [Co₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ and the strong pH dependence of the same type of exchange in [Mn₄(H₂O)₂(P₂W₁₅O₅₆)₂]¹⁶⁻ – in spite of their similar protonation profile – we have located the sites of protonation in a nanometre-sized sandwich polyoxometalate using energetic computations. Alternative approaches to locating protonation sites have also been investigated, but only direct computation of the relative energies of the different protonated isomers appears to be reliable. The loci of protonation were found to be sites I and J, which are two Zn–O–W oxygen sites.

Protonation induces a contraction of the Zn–OH₂ bond distance which scales directly with increased protonation of sites I and J, as well as moderately with the distance between the Zn–OH₂ zinc atom and the site of protonation, although the change in charge of the molecule is responsible for the majority of contraction effect.

A literature comparison between crystallographically determined bond distances and rates of aquo-ligand exchange in a series of complexes revealed that the rate of aquo-ligand exchange in monomeric Mn(II) complexes, which undergo interchange associative exchange, is bond distance dependent, whereas it is not for monomeric Co(II) complexes, which undergo interchange dissociative exchange. Because the observed increase in the rate of exchange of the Mn(II) polyoxometalate correlates well with that which would be caused by the computed Zn–OH₂ shortening, and because the rates of exchange in the Co(II) polyoxometalates is not affected by the expected change in bond distance, we suggest that this implies that the mechanisms of aquo-ligand exchange in the polyoxometalates in this study may be the same as for the monomeric Co(II) and Mn(II) complexes.

Finally, we here show through protonation of a wide range of sites in the [Zn₄(H₂O)₂(PW₉O₃₄)₂]¹⁰⁻ ion that the metal–aquo-ligand bond contraction depends on the distance between the protonation sites and the metal–aquo ligand even when that distance exceeds 0.75 Å (Fig. 3), which has significant implications for the modelling and understanding of extended surfaces such as minerals. Fragments used either computationally or conceptually must thus be large enough to capture the essential chemistry, or key aspects of the mechanism, such as protonation, may be overlooked.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is dedicated to the memory of the late Professor Leone Spiccia. MPB and CAO acknowledge generous support from the Kempe Foundation (JCK-1719). Computational resources were in provided by the High Performance Computing Center North (HPC2N) via grant SNIC 2018/3-253.

References

1. Y.-F. Song and R. Tsunashima, Chem. Soc. Rev., 2012, 41, 7384–7402.
2. S.-S. Wang and G.-Y. Yang, Chem. Rev., 2015, 115, 4893–4962.
3. J. R. Rustad and W. H. Casey, Nat. Mater., 2012, 11, 223–226.
4. W. H. Casey, Environ. Chem., 2015, 12, 1–19.
5. W. H. Casey and J. R. Rustad, New J. Chem., 2016, 40, 898–905.
6. C. J. Gomez-Garcia, J. J. Borras-Almenar, E. Coronado and L. Ouahab, Inorg. Chem., 1994, 33, 4016–4022.
7. X. Zhang, Q. Chen, D. C. Duncan, C. F. Campana and C. L. Hill, Inorg. Chem., 1997, 36, 4208–4215.
8. R. G. Finke and M. W. Droege, Inorg. Chem., 1983, 22, 1006–1008.
9. R. G. Finke, M. W. Droege and P. J. Domaille, Inorg. Chem., 1987, 26, 3886–3896.
10. Q. Yin, J. M. Tan, C. Besson, Y. V. Geletii, D. G. Musaev, A. E. Kuznetsov, Z. Luo, K. I. Hardcastle and C. L. Hill, Science, 2010, 328, 342–345.
11. C. A. Ohlin, S. J. Harley, J. G. McAlpin, R. K. Hockin, B. Q. Mercado, R. L. Johnson, E. M. Villa, M. K. Fidler, M. M. Olmstead, L. Spiccia, R. D. Britt and W. H. Casey, Chem. – Eur. J., 2011, 17, 4408–4417.
12. D. Lieb, A. Zahl, E. F. Wilson, C. Streb, L. C. Nye, K. Meyer and I. Ivanovi-Burmazovi, Inorg. Chem., 2011, 50, 9053–9058.
13. T. J. Swift and R. E. Connick, J. Chem. Phys., 1962, 37, 307–320.
14. T. J. Swift and R. E. Connick, J. Chem. Phys., 1964, 41, 2553–2554.
15. L. Ruhlmann, L. Nadjo, J. Canny, R. Contant and R. Thouvenot, Eur. J. Inorg. Chem., 2002, 2002, 975–986.
16. S. Romo, J. A. Fernández, J. M. Maestre, B. Keita, L. Nadjo, C. de Graaf and J. M. Poblet, Inorg. Chem., 2007, 46, 4022–4027.
17. R. Sharma, J. Zhang and C. A. Ohlin, Dalton Trans., 2015, 44, 19068–19071.
18. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6159.
19. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
20. J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3093.
21. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision B.01, Gaussian Inc., Wallingford CT, 2016.
22. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, C. R. Landis and F. Weinhold, NBO 6.0, http://nbo6.chem.wisc.edu/.
23. B. H. Besler, K. M. Merz and P. A. Kollman, J. Comput. Chem., 1990, 11, 431–439.
24. C. M. Breneman and K. B. Wiberg, J. Comput. Chem., 1990, 11, 361–373.
25. H. Hu, Z. Lu and W. Yang, J. Chem. Theory Comput., 2007, 3, 1004–1013.
26. S. Hayashi, S. Yamazoe, K. Koyasu and T. Tsukuda, RSC Adv., 2016, 6, 16239–16242.
27. G. Schwarzenbach, G. Geier and J. Littler, Helv. Chim. Acta, 1962, 45, 2601–2612.
28. S. S. Acharya, B. Winther-Jensen, L. Spiccia and C. A. Ohlin, Aust. J. Chem., 2017, 70, 751–754.
29. E. Balogh, A. M. Todea, A. Müller and W. H. Casey, inorg. Chem., 2007, 46, 7087–7092.
30. Y. Ducommun, K. E. Newman and A. E. Merbach, Inorg. Chem., 1980, 19, 3696–3703.

---

Footnote

† Electronic supplementary information (ESI) available: Optimised structures, computed energies, partial charges and molecular electrostatic surface. See DOI: 10.1039/C8DT02342E

---