Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Fine-tuning polyoxometalate non-linear optical chromophores: a molecular electronic “Goldilocks” effect†
Ahmed
Al-Yasari
ae,
Philip
Spence
 a,
Hani
El Moll
a,
Nick
Van Steerteghem
b,
Peter N.
Horton
c,
Bruce S.
Brunschwig
a,
Hani
El Moll
a,
Nick
Van Steerteghem
b,
Peter N.
Horton
c,
Bruce S.
Brunschwig
 d,
Koen
Clays
b and
John
Fielden
d,
Koen
Clays
b and
John
Fielden
 *a
*a
aSchool of Chemistry, University of East Anglia, Norwich, NR4 7TJ, UK. E-mail: John.Fielden@uea.ac.uk
bDepartment of Chemistry, University of Leuven, Celestijnenlaan 200D, B-3001 Leuven, Belgium
cUK National Crystallography Service, School of Chemistry, University of Southampton, Southampton, SO17 1BJ, UK
dBeckman Institute, MC 139-74, California Institute of Technology, 1200 East California Blvd, Pasadena, CA 91125, USA
eCollege of Pharmacy, University of Kerbala, Kerbala, Iraq
First published on 27th June 2018
Abstract
A new aryl-imido polyoxometalate non-linear optical chromophore (POMophore) with a diphenylamino donor group attains the highest βzzz, 0 value (196 × 10−30 esu by Hyper-Rayleigh Scattering, HRS), and best transparency/non-linearity trade off yet for such materials. Stark spectroscopic and DFT investigation of this compound, plus NMe2 and carbazole analogues, show that its high performance results from a combination of strongly dipolar electronic transitions, and strong electronic communication across the π-system.
The chemistry of covalent polyoxometalate (POM) “hybrid” compounds has advanced rapidly in recent years. Organic groups can be connected to many of the common POM cluster anions, and an increasing range of post-synthetic modifications enable incorporation of POMs into complex organic architectures.1 However, study of the physical properties,2 and associated applications3 of these structures is still in its infancy. Relatively little is known about the interaction between the POM and organic subunit, and indeed in most systems electronic communication between them appears to be weak.
With strong electronic communication between an acceptor (e.g. a POM) and more electron rich moieties, many useful optical and photophysical properties can emerge – such as non-linear optical (NLO) effects. NLO materials are used to manipulate laser light, and the tunable properties and strong, fast responses associated with molecular donor–acceptor systems (vs. traditional extended inorganic solids) is critical to development of advanced applications in telecommunications, optical/electro-optical computing and imaging.4 We recently showed that the strong POM-organic communication in donor-functionalized arylimido-Lindqvist ([Mo6O19]2−) anions results in promising 2nd order NLO (laser frequency doubling) properties.5 Specifically, these POM acceptors combined with short (phenyl) π-bridges give rise to a better combination of transparency and 2nd order NLO activity than planar, dipolar organic systems. Thus, they may help overcome the challenge of obtaining materials that have high NLO coefficients (β), while avoiding problems for efficiency and stability that result from reabsorption of second harmonic (SH) light. As yet though, absolute β-values for these POMophores fall far short of records and extension of the organic π-system – a classic means of increasing β – has been seen to sacrifice any advantage over purely organic (nitro) analogues.5b
Herein, we investigate the effect of using the weaker, but more conjugated donor groups carbazole (cbz) and diphenylamino (NPh2) on the behaviour of extended POMophores. We find that, of the donor groups tested so far, NPh2 is the best adapted for use in POMophores – producing the highest β0 and best transparency/non-linearity trade-off. This results from a combination of stronger electronic communication, and strong, relatively high energy electronic transitions that maintain a highly dipolar nature.
The synthetic approach to 1 to 3 (Fig. 1) centres on the DCC-mediated coupling of anilines with [NBu4]2[Mo6O19].1c,5 For both 1 and 2, we found the most expeditious route was to first synthesize the precursor diphenylamino and cbz functionalized ligands, before reaction with hexamolybdate. The synthesis of 3 was previously published.5b Notably, both 1 and 2 (most of all 2) are more vulnerable to hydrolysis than 3 and other previously studied arylimido-POMs (a-POMs), and require careful handling. As there is no difference in steric protection of the imido-bond, this observation implies a difference in electronic structure that increases its reactivity. UV-vis spectra (Table 1, Fig. S1 in ESI†) show that compared to 3, these compounds both show blue shifts in Emax of the intra-hybrid charge transfer (IHCT5b) band, consistent with their weaker electron donors. However, they also absorb more strongly across the range from 300 to 400 nm, likely a result of stronger π-conjugation. Despite the weaker donors, the reduction potentials of the {Mo6} unit in 1 and 2 are at a similar potential to that of 3 (Table 1), suggesting that communication between the POM and NMe2 donor is weaker than with NPh2 or cbz.
| λ max/nma (ε, 103 M−1 cm−1) | E max (eV) | Assignment | E 1/2 vs. Ag/AgCl/Vb (ΔE/mV) | |
|---|---|---|---|---|
| a Concentrations ca. 10−5 M in MeCN. b Solutions ca. 10−3 M in analyte and 0.1 M in [NBu4][BF4] at a glassy carbon working electrode with a scan rate of 100 mV s−1. Ferrocene internal reference E1/2 = 0.46 V, ΔEp = 80 mV. Data for 3 are from ref. 5b. | ||||
| 1 | 227 (70.4) | 5.28 | O → Mo and π → π* | −0.503 (64) |
| 292 (48.4) | 4.25 | O → Mo and π → π* | ||
| 327 (31.3) | 3.78 | O → Mo and π → π* | ||
| 341 (33.7) | 3.63 | O → Mo and π → π* | ||
| 385 (43.4) | 3.20 | IHCT | ||
| 2 | 292 (41.2) | 4.28 | O → Mo and π → π* | −0.503 (64) |
| 327 (36.2) | 3.74 | O → Mo and π → π* | ||
| 414 (45.3) | 2.98 | IHCT | ||
| 3 | 248 (36.2) | 5.02 | O → Mo and π → π* | −0.498 (61) |
| 292 (44.5) | 4.24 | O → Mo and π → π* | ||
| 421 (41.2) | 2.94 | IHCT | ||
HRS-determined β-values for 1 to 3 are shown in Table 2. For 1, the higher value obtained at 1100 nm is likely more accurate, as at 1064 nm the analysis was complicated by a need to deconvolute HRS and fluoresence signal. Even so, both resonance corrected static β-values (β0) for 1 are substantially lower than that of 3, commensurate with the lower donor strength. For 2, β0 is around 40% higher than for 3, and combined with its lower λmax, this makes it the best performing POMophore described to date. Compound 2 is also the first extended POMophore that clearly outperforms comparable purely organic systems, as shown by an intrinsic β value that breaks through empirical performance limits (defined by intrinsic β vs. λmax) defined by Kuzyk for planar, dipolar organics (Fig. 2).7 Although POM electrons are not included in the N used to calculate intrinsic β, this analysis clearly shows that the POM must influence the NLO properties of the organic system. Moreover, the POM is broadly analogous to the aryl remote acceptor in N-aryl stilbazolium chromophores – the electrons of this aryl group are not included in N for these systems, and yet N-aryl stilbazoliums do not exceed the apparent limit in Fig. 2.7b
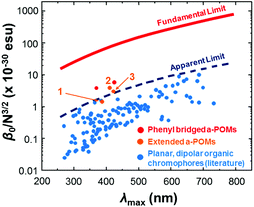 | ||
| Fig. 2 Intrinsic β vs. λmax for 1, 2 and 3vs. short (phenyl bridged) POMophores,5 and planar, dipolar organic chromophores.7 Compound 2 is the first POMophore to clearly breach Kuzyk's apparent limit for the performance of planar, dipolar organic chromophores. | ||
| λ max (nm) | β zzz , 1064a | β 0, 1064 | β zzz , 1100a | β 0, 1100 |
β
0/N3/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
|
|---|---|---|---|---|---|---|
| (10−30 esu) | ||||||
| a β zzz calculated assuming a single dominant tensor component, measured using 1064 or 1100 nm fundamental laser beams. The quoted units (esu) can be converted into SI units (C3 m3 J−2) by dividing by a factor of 2.693 × 1020. b Non-resonant, static β estimated from βzzz using the two state model.6 Data for 3 are from ref. 5b. c N = number of π-electrons in bridge.7 | ||||||
| 1 | 388 | 150 ± 36 | 62 ± 15 | 190 ± 28 | 82 ± 12 | 1.57 |
| 2 | 415 | 590 ± 20 | 196 ± 7 | — | — | 3.75 |
| 3 | 421 | 440 ± 55 | 139 ± 17 | — | — | 2.65 |
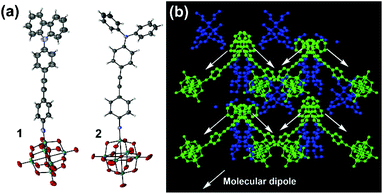
Thus, it appears that the POM contributes more to the NLO properties of 2, than it does to those of 3, leading to a reversal of the trend seen for structurally analogous systems with the NO2 acceptor,8 where NMe2 outperforms NPh2 with both alkyne and alkene bridges. This suggests that the POM acceptor must alter the electronic structure of the organic donor and bridge, and since NPh2 is a weaker donor than NMe2, it must increase β by influencing charge separation and communication across the bridge. Indeed, the X-ray crystal structures of both 1 and 2vs. 3 (Fig. 3, see ESI† for full details) are consistent with stronger conjugation. Whereas that of 3 shows a ca. 86° twist between the planes of the two phenyl rings,5b in 2 this is only ca. 22°, and in 1 19°. Moreover, the imido (acceptor) ring in 2 shows a shortening of the ortho-to-meta C–C bonds (mean distance 1.36(2) Å vs. 1.42(2) Å for ortho/meta-to-para), suggesting a significant contribution from a quinoidal resonance form. This is not present in the imido ring of 3, while in 1 disorder and application of various restraints precludes such in depth analysis. However, it should be noted the weak rotational barrier of unhindered phenylacetylenes (ca. 1 kcal mol−1)9 means that these differences will not persist in solution. The X-ray structure of 2 also reveals that it is the first POMophore to crystallize in a non-centrosymmetric space group (Pna21), with polar packing of chromophore dipoles. These are oriented at ca. 90° to one another, giving the structure net polarity (Fig. 4b) and making it a potential bulk NLO material. Instability resulting from large solvent occupied void spaces has prevented further investigation of this, but the result suggests that adding steric bulk to the organic system may be one way to counteract the influence of the POM in the crystallization process and encourage formation of polar materials.
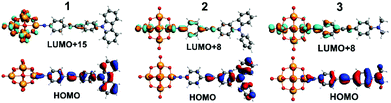 | ||
| Fig. 4 TDF-DFT calculated HOMOs for 1 to 3 (bottom) and most important acceptor orbitals LUMO+x (in terms of oscillator strength (top)). | ||
Evidence that differences in electronic structure between 1, 2 and 3 persist in glasses and solution is provided by a combination of Stark spectroscopy (see ESI† for details), and DFT calculations. In Stark, the low temperature (77 K) electronic absorption spectra in butyronitrile have a similar overall form to the room temperature spectra in MeCN, but all three compounds show substantial red shifts in the low-energy IHCT band (16 to 35 nm). This can be an indicator of dipolar electronic transitions.10 The Stark-derived Σβ0 values for the series (Table 3, see ESI† for details of fitting and extraction of charge transfer parameters) follow a similar trend to HRS β0, although measurement and fitting uncertainties are large and in all cases values are larger than HRS β0 – a common observation in prior work.5b,7,11 Similar to 3, the fit of the main low energy peak in 2 consists of three Gaussians, each at slightly higher energy than those of 3. Dipole moment changes Δμ and charge transfer distances r associated with these peaks in 2 and 3 are within experimental error of one another (though consistently slightly higher for 2), as are most other measured parameters. However, an additional peak in 2 requires a 4th Gaussian for an adequate fit, and while its transition is less dipolar in nature (lower Δμ values) it shows strong electronic coupling (higher Hab) and a high value of μ12 means that it contributes significantly to Σβ0. In 1, the four Gaussian components have less dipolar character their counterparts in 1 and 3, and generally electronic coupling is stronger than in either 2 or 3. The overall picture suggests that 2 hits a sweet spot where transitions are just as dipolar than those of 3, yet electronic communication across the diphenylacetylene bridge is strong.
| λ max (nm) | E max (eV) | Amp (norm) | Fwhh (eV) | f os | μ 12 (D) | Δμ12d (D) | Δμabe (D) | r 12 (Å) | r ab (Å) | H ab (103 cm−1) |
c
b
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) i i |
β 0 (10−30 esu) | Σβ0k (10−30 esu) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| a In butyronitrile at 77 K; observed absorption maxima with maxima for Gaussian fitting functions in brackets. Data in all subsequent columns relate to fitted curves. b Obtained from (4.6 × 10−9 M cm2) εmax× fw1/2 where εmax is the maximal molar extinction coefficient and fw1/2 is the full width at half height (in cm−1). c Calculated using eqn (2), ESI. d Calculated from fintΔμ12 using fint = 1.33. e Calculated from eqn (1), ESI. f Delocalized electron-transfer distance calculated from Δμ12/e. g Effective (localized) electron-transfer distance calculated from Δμab/e. h Calculated from eqn (3), ESI. i Calculated from eqn (4), ESI. j Calculated from eqn (5), ESI. k Sum of the β0 vales from each individual Gaussian function, to 2 s.f. Estimated errors are ca. ±20% on β0, μ12 and Δμ12, ±30% on Δμab, Hab and ±50% cb2 and are further discussed in the ESI. | ||||||||||||||
| 1 | 404 (433) | 3.07 (2.86) | 0.13 | 0.16 | 0.06 | 2.4 | 12.5 | 13.4 | 2.6 | 2.8 | 4.2 | 0.97 | 11 | 180 |
| (405) | (3.06) | 0.56 | 0.44 | 0.82 | 8.4 | 17.7 | 24.4 | 3.7 | 5.1 | 8.5 | 0.87 | 155 | ||
| (366) | (3.39) | 0.16 | 0.28 | 0.16 | 3.6 | 9.1 | 11.6 | 1.9 | 2.4 | 8.4 | 0.90 | 12 | ||
| (342) | (3.62) | 0.15 | 0.28 | 0.16 | 3.4 | — | — | — | — | — | — | 0 | ||
| 2 | 444 (475) | 2.79 (2.61) | 0.22 | 0.18 | 0.13 | 3.6 | 22.5 | 23.7 | 4.7 | 4.9 | 3.2 | 0.98 | 51 | 350 |
| (451) | (2.75) | 0.29 | 0.28 | 0.28 | 5.2 | 24.2 | 26.3 | 5.0 | 5.5 | 4.4 | 0.96 | 101 | ||
| (425) | (2.92) | 0.30 | 0.42 | 0.46 | 6.4 | 25.0 | 28.1 | 5.2 | 5.9 | 5.4 | 0.94 | 142 | ||
| (355) | (3.50) | 0.20 | 0.55 | 0.51 | 6.2 | 15.8 | 20.0 | 3.3 | 4.2 | 8.7 | 0.90 | 57 | ||
| 3 | 456 (482) | 2.72 (2.57) | 0.30 | 0.20 | 0.16 | 4.0 | 21.6 | 23.1 | 4.5 | 4.8 | 3.7 | 0.97 | 64 | 280 |
| (456) | (2.72) | 0.41 | 0.28 | 0.34 | 5.7 | 23.3 | 26.0 | 4.9 | 5.4 | 4.9 | 0.95 | 121 | ||
| (426) | (2.91) | 0.29 | 0.35 | 0.31 | 5.3 | 24.6 | 26.8 | 5.1 | 5.6 | 4.7 | 0.96 | 96 | ||
TD-DFT calculations of the electronic spectra and β values of 1 to 3 in acetonitrile solvent have been performed using the ADF program, with the SAOP functional and TZ2P basis set. Previously,5b we showed that a solvent forcefield is necessary for these calculations to reflect experimental trends, although the β-values computed were much larger (up to 30×) than those observed experimentally. The methods used here are an incremental improvement on those previously published. Values are closer to experiment, but still high (reflecting low computed transition energies, see ESI†), and the trend is an excellent match for Stark and HRS findings. βzzz, 0 of 960 (1), 1300 (3) and 2160 × 10−30 (2) are obtained, and normalising all three techniques to 2 as 100% (Table S2†) makes it clear just how good the agreement in trend is between experiment and theory. A qualitative interpretation of the TD-DFT-computed orbital-to-orbital transitions is thus justified, and reveals two key differences between 2 and 3. Firstly, the HOMO level of 2 is concentrated on the NPh2 group and immediately appended aryl ring (Fig. 4), whereas in 3 it spreads across the entire organic system – as does the HOMO−1 for both systems. This may increase the dipole moment change associated with strong, low energy transitions to the LUMO+6 and LUMO+8, which spread across POM and imido-ring, and is reflected in the very slightly higher Δμ values found for 2 by Stark (although they are within experimental error of those for 3). Secondly, 3 has a weak transition from an imido-phenyl based HOMO−5, to a POM-based LUMO+7, at a high computed energy (3.39 eV, Table S5 and Fig. S7†). In 2, a similar transition is observed from the HOMO−9 to LUMO+1 (Table S4 and Fig. S6†), but the calculated energy is 0.7 eV lower and calculated fos nearly 3× higher – possibly due to involvement of the alkyne bridge. This seems consistent with the fourth Gaussian peak used to fit the Stark spectrum of 2, which has both moderately high Hab and Δμ, and appears responsible for most of the β enhancement vs.3. In compound 1, the HOMO and HOMO−1 (Fig. 4 and S5†) are both distributed across the entire organic fragment, similar to 3, but in addition the imido-phenyl based HOMO−3 also spreads across the alkyne to the donor ring (Fig. S5†). This strengthened conjugation across the bridge means that the most important acceptor orbitals (LUMO+8, +15 and +18, Fig. 4 and S5†) also spread onto the donor phenyl ring, as well as POM and phenylimido groups, and transitions to entirely POM-based orbitals are very weak compared to both of the other POMophores (Table S3–S5 and Fig. S5–S7†). This change in electronic structure and the nature of the transitions is entirely consistent with the smaller dipole moment changes and stronger electronic coupling found for this compound by Stark spectroscopy.
In conclusion, we have synthesised the highest performance, POM-based molecular 2nd order NLO chromophore known to date, and crystallised it in a polar space group indicating a potential path to bulk materials. A combined spectroscopic and computational approach has revealed that its high β0 and high visible transparency result from a moderate-strength conjugated donor group that increases electronic communication (vs. alkylamino donors) without sacrificing charge separation. These findings are relevant not only to molecular design of new POM-based NLO chromophores, but also to systems for light energy conversion by charge separation. Moreover, the near-identical trends in β between computation and experiment, and the qualitative consistency of the computed transitions and Stark measurements, suggests our TD-DFT approach is a valid tool to help understand these systems, although much further work is needed to improve its quantitative accuracy.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the UK EPSRC National Mass Spectrometry Facility for MS. This work was supported by: the Iraqi Government (HCED scholarship to AAY), Royal Society of Chemistry, EPSRC (EP/M00452X/1) and Fonds voor Wetenschappelijk Onderzoek-Vlaanderen (FWO-V, PhD fellowship for NVS). BSB acknowledges support from the Beckman Institute of the California Institute of Technology. Stark data were collected and analysed at the Molecular Materials Resource Center of the Beckman Institute of the California Institute of Technology.In addition to the supplementary information and deposited cif files, data can be accessed by contacting the corresponding author.
Notes and references
- (a) A. Dolbecq, E. Dumas, C. R. Mayer and P. Mialane, Chem. Rev., 2010, 110, 6009 CrossRef PubMed; (b) A. Proust, B. Matt, R. Villanneau, G. Guillemot, P. Gouzerh and G. Izzet, Chem. Soc. Rev., 2012, 41, 7605 RSC; (c) J. Zhang, F. Xiao, J. Hao and Y. Wei, Dalton Trans., 2012, 41, 3599 RSC; (d) S. Chakraborty, A. Keighley, V. Dusevich, Y. Wang and Z. Peng, Chem. Mater., 2010, 22, 3995 CrossRef; (e) K. Kastner, A. J. Kibler, E. Karjalainen, J. A. Fernandes, V. Sans and G. N. Newton, J. Mater. Chem. A, 2017, 5, 11577 RSC.
- (a) K. J. Elliott, A. Harriman, L. Le Pleux, Y. Pellegrin, E. Blart, C. R. Mayer and F. A. Odobel, Phys. Chem. Chem. Phys., 2009, 11, 8767 RSC; (b) B. Matt, X. Xiang, A. L. Kaledin, N. Han, J. Moussa, H. Amouri, S. Alves, C. L. Hill, T. Lian, D. G. Musaev, G. Izzet and A. Proust, Chem. Sci., 2013, 4, 1737 RSC; (c) S. Fujimoto, J. M. Cameron, R.-J. Wei, K. Kastner, D. Robinson, V. Sans, G. N. Newton and H. Oshio, Inorg. Chem., 2017, 56, 12169 CrossRef PubMed.
- (a) M. Bonchio, M. Carraro, G. Scorrano and A. Bagno, Adv. Synth. Catal., 2004, 346, 648 CrossRef; (b) B. Matt, J. Fize, J. Moussa, H. Amouri, A. Pereira, V. Artero, G. Izzet and A. Proust, Energy Environ. Sci., 2013, 6, 1504 RSC; (c) M. Lu, B. Xie, J. Kang, F.-C. Chen, Y. Yang and Z. Peng, Chem. Mater., 2005, 17, 402 CrossRef; (d) H. El Moll, F. A. Black, C. J. Wood, A. Al-Yasari, A. R. Marri, I. V. Sazanovich, E. A. Gibson and J. Fielden, Phys. Chem. Chem. Phys., 2017, 19, 18831 RSC.
- (a) Nonlinear Optics of Organic Molecules and Polymers, ed. H. S. Nalwa and S. Miyata, CRC Press, Boca Raton, FL, 1997 Search PubMed; (b) S. R. Marder, Chem. Commun., 2006, 131 RSC; (c) M. G. Kuzyk, J. Mater. Chem., 2009, 19, 7444 RSC.
- (a) A. Al-Yasari, N. Van Steerteghem, H. El Moll, K. Clays and J. Fielden, Dalton Trans., 2016, 45, 2818 RSC; (b) A. Al-Yasari, N. Van Steerteghem, H. Kearns, H. El Moll, K. Faulds, J. A. Wright, B. S. Brunschwig, K. Clays and J. Fielden, Inorg. Chem., 2017, 17, 10181 CrossRef PubMed.
- (a) J. L. Oudar and D. S. Chemla, J. Chem. Phys., 1977, 66, 2664 CrossRef; (b) J. L. Oudar, J. Chem. Phys., 1977, 67, 446 CrossRef.
- (a) K. Tripathy, J. Pérez Moreno, M. G. Kuzyk, B. J. Coe, K. Clays and A. M. Kelley, J. Chem. Phys., 2004, 121, 7932 CrossRef PubMed; (b) K. Clays and B. J. Coe, Chem. Mater., 2003, 15, 642 CrossRef.
- C. R. Moylan, R. J. Tweig, V. Y. Lee, S. A. Swanson, K. M. Betterton and R. D. Miller, J. Am. Chem. Soc., 1993, 115, 12599 CrossRef.
- S. M. LeCours, S. G. DiMagno and M. J. Therien, J. Am. Chem. Soc., 1996, 118, 11854 CrossRef.
- P. Suppan and C. Tsiamis, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 1553 RSC.
- (a) B. J. Coe, J. A. Harris, K. Clays, A. Persoons, A. Wostyn and B. S. Brunschwig, Chem. Commun., 2001, 1548 RSC; (b) B. J. Coe, J. Fielden, S. P. Foxon, M. Helliwell, B. S. Brunschwig, I. Asselberghs, K. Clays, J. Olesiak, K. Matczyszyn and M. Samoc, J. Phys. Chem. A, 2010, 114, 12028 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Synthetic and other experimental/computational details, CIF files. CCDC 1837358 and 1837405. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt01491d |
| This journal is © The Royal Society of Chemistry 2018 |