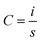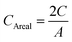Extending lead-free hybrid photovoltaic materials to new structures: thiazolium, aminothiazolium and imidazolium iodobismuthates

Abstract

We report on the synthesis, crystal structures, optoelectronic properties and solar cell device studies of three novel organic–inorganic iodobismuthates – [C₃H₄NS]₃[Bi₂I₉] ([TH]₃[Bi₂I₉]), [C₃H₄N₂]₃[Bi₂I₉] ([IM]₃[Bi₂I₉]) and [C₃H₅N₂S][BiI₄] ([AT][BiI₄]) as lead-free light harvesters. [TH]₃[Bi₂I₉] and [IM]₃[Bi₂I₉] show zero-dimensional structures, whereas a one-dimensional edge-sharing chain structure of BiI₆-octahedra was observed in [AT][BiI₄], with interchain short I⋯I contacts also giving rise to the possibility of three-dimensional charge transport ability. Accordingly, greater energy dispersion in the band structure of [AT][BiI₄] can be observed, and less contribution from the organic moities at the conduction band minimum in [AT][BiI₄] than [TH]₃[Bi₂I₉] have been confirmed by density functional theory calculations. Moreover, bandgap values are redshifted from 2.08 eV for [TH]₃[Bi₂I₉] and 2.00 eV for [IM]₃[Bi₂I₉] to 1.78 eV for [AT][BiI₄], determined by UV-Vis reflectance spectroscopy. Power conversion efficiency of 0.47% has been achieved by using ([AT][BiI₄]) as the light absorber in a hole-conductor-free, fully printable solar cell, with relatively good reproducibility. We also note the observation of a capacitance effect for the first time in a photovoltaic device with bismuth-based solar absorber, which may be related to the mesoporous carbon counter-electrode.

---

Introduction

Photovoltaic (PV) devices based on hybrid lead halide perovskite materials have been extensively studied with merits including low cost,¹ high absorption coefficient,² small exciton binding energy,^3,4 long charge carrier diffusion length,^5,6 and commercial scalability.^7,8 In the last few years, the power conversion efficiency (PCE) of lead perovskite solar cells soared from 3.9% (ref. 9) in 2013 to over 22% today,¹⁰ as well as much increased stability under humidity and oxygen.^11–14 In addition, lead-halide perovskites have also been studied in other devices including capacitors,¹⁵ batteries¹⁶ and the integration of a solar cell and supercapacitor.¹⁷ However, one intrinsic limitation of these perovskite materials is the toxicity of lead, which raises environmental and health concerns and thus hinders future large-scale implementation.^18,19 Recently, studies on lead-free metal–halide PV materials have attracted lots of attention. Moving upwards from Pb in the periodic table, tin-perovskites including CH₃NH₃SnX₃ (X = Cl, Br, I) and Cs₃SnX₃ (X = Br, I) have been studied, with more than 6% PCE achieved in a solar cell.^20–24 However, their future applications are limited because of their extreme sensitivity to air, owing to the fast oxidation from Sn²⁺ to the more stable Sn⁴⁺. Shifting to the right of Pb is the element bismuth, which is the least toxic heavy metal and also adopts a 6S² electronic configuration in the common Bi(III) state, analogous to Pb(II). Photovoltaic effects of bismuth-halide materials as light harvesters have been confirmed, with much increased stability compared to lead-based absorbers.^25–27 Great diversity among the anionic structures of iodobismuthates can be found. Among them, zero-dimensional (0D) [Bi₂I₉]³⁻ complexes have been extensively studied as potential PV materials,^28–30 with organic [CH₃NH₃]⁺ and inorganic cations Cs⁺. However, with the notable exceptions of Cs₃Bi₂I₉ (which exceeds 1.09% PCE³⁰) and high-vacuum deposition of [CH₃NH₃][Bi₂I₉] (with 1.64% PCE³¹), PCEs are normally reported around 0.2–0.3% for such 0D materials.^32,33 One possible reason for this is that the iodobismuthates are built from discrete Bi/I binuclear anions with low structural and electronic dimensionality, which leads to limited charge carrier transport.³⁴ Attempts to increase the dimensionality have been made by investigating A₂MBiX₆ (M = Ag, K, Na, etc.) bismuth-based double perovskite materials.^35–40 Devices based on this structural type have reached efficiencies of more than 2% so far.³⁵ However, theoretical studies prove that the Ag(I) and Bi(III) combination leads to indirect wide bandgap materials, suggesting the double-perovskite motif may be limited for PV applications.³⁷ An extended inorganic iodobismuthate network can be achieved by adopting 1D chain structures, including [BiI₄⁻]_n and [BiI₅²⁻]_n.^41,42 In our own work, solar cells with 1D iodobismuthates as light absorbers have achieved 0.90% using organic–inorganic [C₅H₆N][BiI₄].⁴³ Recently, inorganic silver bismuth iodide materials have shown promise as solar absorbers, with PCE of 4.3% achieved by Ag₃BiI₆, which belongs to the rudorffite family.⁴⁴ In addition, low dimensional [CH₃NH₃][Bi₂I₉] shows promise as a capacitor material,⁴⁵ with much higher capacitance achieved compared with the capacitor employing 3D lead-halide perovskite.¹⁵

In this work, 0D organic–inorganic bismuth-halide materials thiazolium bismuth iodide [TH]₃[Bi₂I₉], imidazolium bismuth iodide [IM]₃[Bi₂I₉] and 1D 2-aminothiazolium bismuth iodide [AT][BiI₄] have been synthesised and studied as crystalline materials, as thin-films, and in solar cell devices. Involvement of bismuth 6p orbitals and iodide 5p orbitals of [AT][BiI₄] in the conduction band minimum has been computationally proven, with higher dispersions at the band edges. More interestingly, the bandgap value of [AT][BiI₄] has redshifted to 1.78 eV compared to [TH]₃[Bi₂I₉], and we also observe increased thermostability of the materials when presented as thin-films. Cost effective solar cells with a carbon counter electrode and fabricated with [AT][BiI₄] as the light absorber have led to PCE of 0.47%, with good reproducibility. Interestingly, an unexpected capacitance effect has also been observed in the device, which opens up the possibility to consider [AT][BiI₄] as a lead-free candidate in solar energy conversion/storage integration devices. In this study, we demonstrate the crucial role of the cationic entity in determining the characteristics of these new materials.

Results and discussion

Crystal structures and intermolecular interactions

[TH]₃[Bi₂I₉] and [AT][BiI₄] were both crystalized in the orthorhombic crystal system with space group Pbcm and Pbca. The main crystallographic data of both compounds are shown in Table 1, with more detailed information on bond angles and bond distances available in Tables S1–S4.† The crystal structure of [IM]₃[Bi₂I₉] has been previously reported by Węcławik et al.,⁴⁶ and adopts an isomorphous structure to [TH]₃[Bi₂I₉]. As indicated earlier, hybrid iodobismuthate compounds featuring [Bi₂I₉]³⁻ and [BiI₄]⁻ motifs can be commonly found in the literature. For both [TH]₃[Bi₂I₉] and [AT][BiI₄], The Bi–I distances observed here show no significant difference to other studies.^47,48

Table 1 Crystallographic data for [TH]₃[Bi₂I₉] (C₉H₁₂Bi₂I₉N₃S₃) and [AT][BiI₄] (C₃H₅BiI₄N₂S)

Formula	C9H12Bi2I9N3S3	C3H5BiI4N2S
D calc/g cm^−3	3.598	4.064
μ/mm^−1	18.937	22.546
Formula weight	1818.46	819.77
Crystal system	Orthorhombic	Orthorhombic
Space group	Pbcm	Pbca
a/Å	9.8257(2)	18.5429(4)
b/Å	14.6666(3)	7.53048(19)
c/Å	23.2957(4)	19.1421(6)
V/Å^3	3357.13(11)	2672.94
Wavelength/Å	0.71073	0.71073
wR2(all data)	0.1159	0.0803
wR2	0.1151	0.0770
R 1 (all data)	0.0609	0.0499
R 1	0.0590	0.0412

---

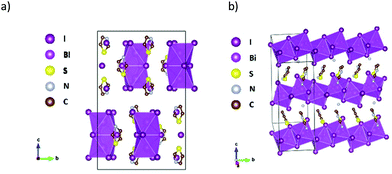
In [TH]₃[Bi₂I₉], one of the thiazolium cations and the [Bi₂I₉]³⁻ unit lie on a crystallographic mirror plane. In the case of the disordered thiazolium ring, the nitrogen and sulfur atoms are interchangeable by substitutional disorder. Fig. 1a shows the schematic picture of the major part (occupancy factors > 0.66) of the disordered crystal. Similarly, highly disordered imidazolium cations were found in both high temperature and low temperature crystal phases of [IM]₃[Bi₂I₉], with a high temperature phase of hexagonalP63/mmc and low temperature space group of orthorhombic Cmcm space group. In the unit cell of [TH]₃[Bi₂I₉], two BiI₃ fragments are linked by three iodine atoms to form the binuclear anionic units, with hydrogen bonding interactions to the neighbouring thiazolium rings (Fig. S1†). The Bi–I (bridging) distances range from 3.2354(12) Å to 3.2758(12) Å, which are longer than that of terminal Bi–I, ranging from 2.9585(12) Å to 2.9624(12) Å. This slight distortion probably originates from the repulsion of bismuth atoms in the binuclear species. The packing of the thiazolium rings is shown in Fig. S2,† where the ring plane forms layers parallel to (1 2 0) and (−1 2 0) lattice planes. In both [TH]₃[Bi₂I₉] and [IM]₃[Bi₂I₉], only hydrogen bonding interactions of (H)–C⋯I and (H)–N⋯I can be seen between the organic and inorganic entities, with no I⋯I contacts between the anionic units, which implies little intermolecular interactions exist that might lead to extended electronic delocalisation in the crystal lattice.

Fig. 1 Schematic diagram of the major part of the disordered [TH]₃[Bi₂I₉] (a) and [AT][BiI₄] (b) unit cell. The unit cell boundary is marked with dark lines, and bismuth iodide octahedra are shown in magenta. Hydrogen atoms are omitted for clarity.

One-dimensional [BiI]₄⁻ anionic chains propagate along the b-axis in [AT][BiI₄], with aminothiazolium cationic rings arranged in between the edge-sharing BiI₆ chains (Fig. 1b). The Bi–I bond lengths range from 2.9219(5) Å to 3.2648(5) Å, with shorter bond lengths for terminal Bi–I than bridging ones. The angles for Bi–I(bridging)–Bi range from 92.314(14)° to 93.046(14)°, while I(terminal)–Bi–I(bridging) range from 85.297(15)° to 97.347(17)°. Such structural distortion of [BiI₆]³⁻ octahedra originates from the repulsion between the heavy bismuth atoms in two adjacent [BiI₆]³⁻ building blocks. Intermolecular interactions can be observed when viewing along different axis in the crystal lattice of [AT][BiI₄], where the atomic distance is less than the sum of their van der Waals radii (Fig. 2). Short I⋯I contacts between two adjacent [BiI]₄⁻ anionic chains can been seen along the a-axis, which enables the possibility of interchain charge delocalisation. In addition, short S⋯I and (H)N⋯I contacts between organic entities and inorganic frameworks are also seen in the b- and c-axis directions. Weak π–π stacking interactions brought by aminothiazolium rings can be found in the crystal structure, with the centroid distance of 3.839 Å and the vector-normal angle less than 20°.⁵⁰ Therefore, the one-dimensional [BiI]₄⁻ anionic chains in the crystal structure of [AT][BiI₄] facilitate the charge transport ability along that direction, and other short contacts built up by van der Waals interactions help to promote higher dimensionality charge carrier mobility. This is similar to what we observed in our previous work on [pyridinium][BiI₄].⁴³ However, by introducing S and –NH₃⁺ in the cation, more involvement for the intermolecular interactions from the organic moieties can be seen, specifically short S⋯I and (H)N⋯I contacts. Thus the cationic thiazolium ring in [TH]₃[Bi₂I₉], increases the dimensionality of the crystal structure, which together with the increased intermolecular interactions potentially leads to higher dimensionality of the charge carrier transport network.

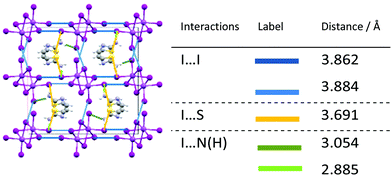Fig. 2 Left: b-Axis view of [AT][BiI₄] unit cell with interchain interactions highlighted in blue (I⋯I), yellow (I⋯S) and green (I⋯N(H)). Right: List of short contacts in [AT][BiI₄] unit cell below the sum of the van der Waals radii (3.96 Å for I⋯I, 3.78 Å for I⋯S, and 3.18 Å for I⋯N(H)).⁴⁹

Electronic band structure and density of states

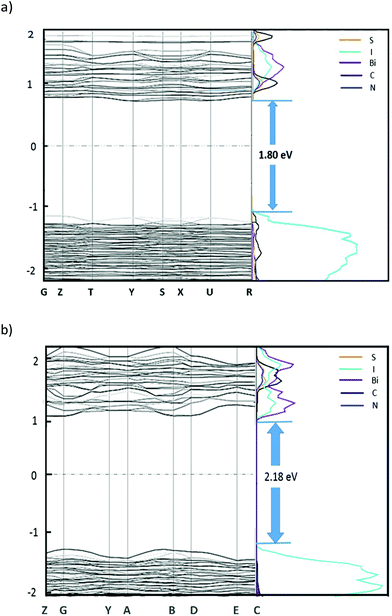
Density functional theory (DFT) calculations were carried out for both [TH]₃[Bi₂I₉] and [AT][BiI₄] using CASTEP 16.11 ⁵¹ to investigate the electronic band structure along the high symmetry k-points in the first Brillion zone, utilising the PBE functional and the Tkatchenko and Scheffler (TS) method to account for van der Waals (dispersion) interactions. The atomic coordinates for both compounds were taken from the crystal structure, while only the major part (occupancy factors > 0.6) of the disordered [TH]₃[Bi₂I₉] crystal structure was considered for the calculation. For each crystal structure, full optimisation of atomic positions and unit cell parameters were undertaken prior to obtaining density of states (DOS) plots which were subsequently broken down to partial DOS plots, to permit observation of contributions from different elements to the electronic bands (Fig. 3).

Fig. 3 Electronic band structures and projected density of states (bismuth 6p orbital: purple; iodine 5p orbital: cyan; sulfur 3p orbital: yellow; carbon 2p orbital: black; nitrogen 2p orbital: navy) for [TH]₃[Bi₂I₉] (a) and [AT][BiI₄] (b). The Fermi level was set at 0 eV.

Direct bandgaps for both materials were calculated, with the value of 1.80 eV at the middle of K-points Y (−0.5, 0.0, 0.0) and S (−0.5, 0.5, 0.0) for [TH]₃[Bi₂I₉], and 2.18 eV at B (0.5, 0.0, 0.0) for [AT][BiI₄]. For both compounds, the main contribution to the valence band maximum (VBM) is from the iodine 5p states, with slightly higher band dispersion noted for [AT][BiI₄], especially along the 1D [BiI₄]⁻ chain direction (G–Y and A–B). This band broadening effect is mostly attributed to the polar Bi (6p)–I (5p) σ-bonding interactions. The noticeable dispersion along Z–G corresponds to the inter-chain direction in the crystal structure, which is mainly attributed to the short I⋯I contacts that exist in between the parallel [BiI₄]⁻ chains. Compared with [TH]₃[Bi₂I₉], whose conduction band minimum (CBM) has mixed contributions of organic entities together with Bi 6p states, little contribution to the CBM from the organic cations can be seen in [AT][BiI₄]. The dominant role played by the inorganic entities at the CBM of [AT][BiI₄] appear to be the σ* antibonding interactions of Bi 6p with iodine 5p states which give rise to band broadening. The generally flat band structure of [TH]₃[Bi₂I₉], indicates a limited ability in this material for charge carrier transport. This is ubiquitous among 0D bismuth-halide complexes as the low structural dimensionality inhibits the charge carriers mobilities and hence less electronic dispersion is observed.³⁴ Note band structure computation was not carried out for [IM]₃[Bi₂I₉] as similar results to [TH]₃[Bi₂I₉] were expected.

Structural, optical and electrochemical studies on thin films

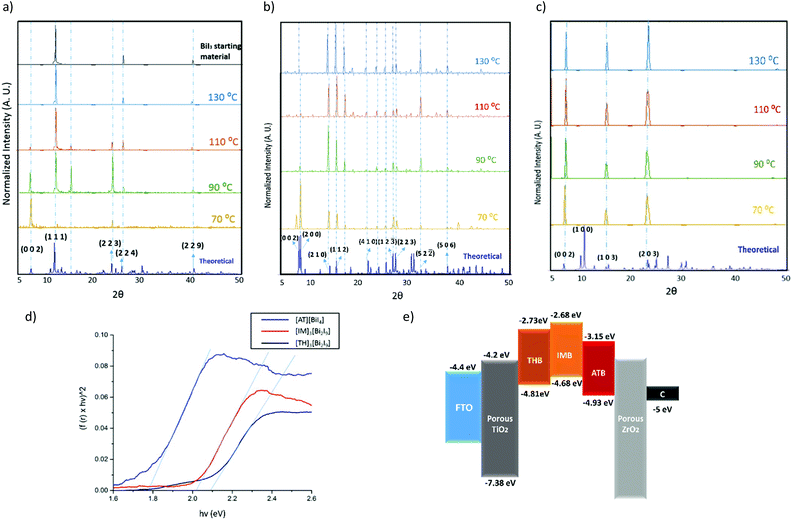
We have studied the three title compounds as thin films, prepared by spin-coating on quartz, to explore their structural properties in the solid state. Different temperatures were chosen for annealing after spin-coating, from 70 °C to 130 °C. All three title materials show good consistency with the simulated powder XRD pattern from single-crystal data (Fig. 4a–c), with some preferred orientation evident as thin films. Preferred orientation on the (0 0 2) plane for both [TH]₃[Bi₂I₉] and [IM]₃[Bi₂I₉] can be observed as thin films, which corresponds to the plane composed of terminal iodine atoms in the [Bi₂I₉]³⁻ binuclear unit. It is worth noting that [TH]₃[Bi₂I₉] decomposed back to the starting material BiI₃ after annealing at temperatures higher than 110 °C, with the characteristic (0 0 2) plane disappearing as the annealing temperature increased. Higher thermal stability can be observed for both [AT][BiI₄] and [IM]₃[Bi₂I₉], although the intensity of the characteristic (0 0 2) and (2 0 0) planes in [AT][BiI₄] become gradually weaker. These planes are built up by the propagating [BiI₄]⁻ chains at the unit cell boundaries (Fig. S3†) and we assume that higher temperatures lead to less structural coherence of the Bi–I anionic chains. No obvious structural changes occur after two weeks exposure to air in the dark, indicating high stability of all three compounds (Fig. S4†).

Fig. 4 Powder XRD patterns on thin films of [TH]₃[Bi₂I₉] (a), [AT][BiI₄] (b) and [IM]₃[Bi₂I₉] (c) annealed at different temperatures comparing to the theoretical patterns predicted from the single-crystal XRD (blue). (d) Tauc plots from diffuse reflectance measurements. (e) Energy level diagram including other components in the solar cell. Energies are expressed in electron volts, reference to the electron energy in vacuum.

Diffuse reflectance measurements were carried out for the three materials as powders scratched off from thin films, to estimate their optical bandgaps by converting their reflectance spectra into Tauc plots (Fig. 4d). A direct band gap value of 2.08 eV was determined for [TH]₃[Bi₂I₉] annealed at 70 °C, while much lower band gap values were observed for thin films annealed at higher temperatures, in line with decomposition into BiI₃ when the annealing temperature was higher than 70 °C (Fig. S5a†). A direct band gap value of 1.78 eV was determined for [AT][BiI₄] and 2.00 eV for [IM]₃[Bi₂I₉], with no substantial change under increased annealing temperatures (Fig. S5b and c†). We note that some inconsistency in comparing these with the calculated bandgap values. This is attributed to limitations in DFT calculations in accurate determination of bandgap values.⁵² It is worth noting that [AT][BiI₄] shows good crystallinity as a thin film, with around 8 μm × 10 μm crystal grains under higher annealing temperatures (Fig. S5c and S6†).

The materials were then spin-coated on conducting glass and used as working electrodes in cyclic voltammetry measurements, in order to study their electrochemical properties. The ionization energy (IE) and electron affinity (EA) for both compounds were estimated using the method by Crespilho et al.,⁵³ based on the experimentally-measured redox potential. Irreversible oxidation and reduction processes were observed for all materials, and some dissolution of both thin films occurred within minutes. The estimated energy levels are summarized in Table 2, with the energy level diagram in Fig. 4e. Note that the VBM has been pushed to a lower energy level by adding the –NH₃⁺ group on the thiazolium ring, which potentially facilitates the hole injection into the carbon counter electrode.

Table 2 Summary of electrochemical oxidation onset potential (E′_ox), electrochemical oxidation potential (E_ox), ionization energy (IE), optical-determined energy band gap (E_g) and estimated electron affinity energy (E_A) values for [TH]₃[Bi₂I₉], [IM]₃[Bi₂I₉] and [AT][BiI₄]. The relationship between oxidation potential onset and Ag/AgCl electrode is shown in the equation E_ox = E′_ox + E_Ag/AgCl ≈ E′_ox + E_vac + 4.4 (ref. 53)

Compounds	E′ox (V vs. Ag/AgCl)	E ox (V vs. vacuum)	IE (eV)	E g (eV)	EA (eV)
[TH]3[Bi2I9]	0.41	4.81	−4.81	2.08	−2.73
[AT][BiI4]	0.52	4.92	−4.92	1.78	−3.15
[IM]3[Bi2I9]	0.28	4.68	−4.68	2.00	−2.68

---

Device studies

The photovoltaic performance of [AT][BiI₄] was tested in solar cell devices, as it is the most promising material among the three title compounds due to its suitable bandgap value, relatively larger band energy dispersion and better energy level alignment. The solar cell devices in this study are based on FTO/(TiO2/ZrO2/carbon)/perovskite structure, with solution-processable photovoltaic material infiltrated through the triple-layer mesoscopic scaffold (Fig. 5a). This type of solar cell is printable and cost effective, as carbon is used as the counter electrode while no hole-transporting materials or noble metals were employed. The J–V curve thus obtained when [AT][BiI₄] acts as a light harvester is shown in Fig. 5b. Further studies on the device suggest that the device shows capacitance characteristics, analogous with capacitors formed by common carbon/electrolyte capacitor components in the cell structure. When the bias voltage was applied, the device was charged instantly under the initial potential, followed by charged current release in addition to the photo-generated current (I_p). To further confirm this, we carried out controlled experiments in the dark, and a slightly lower device current was observed. The difference in device performance with/without illumination shows the actual photocurrent I_p from the device (Fig. 5b). Avoiding capacitance effects by scanning forwards from zero volts shows the photovoltaic performance of [AT][BiI₄] is 0.47%, with open-circuit voltage (Voc) = 0.37 V, short-circuit current density (Jsc) = 3.29 mA cm⁻², fill factor (FF) = 0.39. The incident photon-to-current efficiency (IPCE) measurement is shown in Fig. 5c, with most of the yield originating from the ultraviolet to violet spectrum. The integration of the IPCE curve is somewhat lower that the current density of the best solar cell device, but this has been observed before for PSCs based on this type of structure.⁵⁴ From the stabilized current measurements, a drop of current can be seen over time (Fig. S7†). No oxidation/reduction reactions of [AT][BiI₄] were detected during the cyclic voltammetry of the devices (Fig. S8†), and the comparison of short-circuit current tests of the device before/after J–V test is shown in Fig. S9,† which indicated that a significant charge has been stored during the reverse J–V scan. We speculate that the origins of the capacitance effect in the device relate to the mesoporous carbon electrode and the presence of potentially mobile protons in the aminothiazolium. The aminothiazolium counterion has both a protonated and an unprotonated nitrogen atom, which may provide possibilities for proton migration to and from the TiO₂ layer. Further device studies on photo-generated energy storage were carried out, and a discharging process under short-circuit conditions of about 5 seconds was observed after light soaking (Fig. 5d). Looking into the cyclic voltammetry of the solar cell device, we estimate the capacitance of the device to be 0.12 mF, with areal capacitance of 0.075 mF cm⁻². Thus this report is the first instance of the capacitance effect in a solar cell using a bismuth-based light absorber, which may prove a useful future direction for study of lead-free solar cell/capacitor devices for solar energy generation and storage.

Fig. 5 (a) Schematic cross section picture of a triple-layer mesoscopic solar cell infiltrated with [AT][BiI₄] precursor solution. (b) J–V curve of a [AT][BiI₄] solar cell under light condition, reverse scan (black), under dark condition, reverse scan (red) and under light condition, forward scan (blue). The large hysteresis indicates the charging process when voltage was applied in the beginning of a reverse scan. (c) IPCE measurement of a [AT][BiI₄] solar cell. (d) Short-circuit current test of a [AT][BiI₄] solar cell after 1 min light soaking for capacitance measurements.

Conclusions

Three organic–inorganic iodobismuthates were synthesised, characterised and studied as potential lead-free solar absorbers. All the compounds contain organic cations with heterocyclic 5-membered rings, with different inorganic frameworks from 0D for [TH]₃[Bi₂I₉] and [IM]₃[Bi₂I₉] to 1D [AT][BiI₄]. Direct band gap values around 2.05 eV were determined for both 0D materials while 1.78 eV was determined for the 1D material. Additionally, the conduction band minimum (CBM) value of [AT][BiI₄] has been shifted to lower value, which enables better energy level match with TiO₂ for electron injection purpose. Computational studies suggest that more involvement of organic entities in the conduction band minimum can be found for [TH]₃[Bi₂I₉], while major contributions of Bi 6p and I 5p antibonding interactions were found for [AT][BiI₄]. Both [IM]₃[Bi₂I₉] and [AT][BiI₄] showed better thermostability than [TH]₃[Bi₂I₉]. Device studies with [AT][BiI₄] as a solar absorber shows 0.47% efficiency (forward scan), with unusual capacitive effects during the reverse scan, likely caused by proton migration between the aminothiazolium cationic entities and the TiO₂ layer. This points towards the possibility that devices with a carbon counter electrode and [AT][BiI₄] as a light harvester have potential as lead-free solar energy generator and storage devices.

Experimental methods

Materials

All the following chemicals were brought from Sigma-Aldrich and used as received unless stated otherwise: bismuth(III) iodide (powder, 99%), thiazole (97%), aminothiazole (≥98.0%), hydriodic acid (55%), water (distilled), dimethylformamide (≥99.0%), dimethylsulfoxide (≥99.0%) and ethanol (analytical grade). ¹H NMR was carried out in deuterated oxide (D₂O) for thiazloium iodide and 2-aminothiazolium iodide on a Bruker Advance Pro500 spectrometer and referenced externally to SiMe₄.

Thin-films formation

The precursor solutions of 1 M [TH]₃[Bi₂I₉]/[IM]₃[Bi₂I₉]/[AT][BiI₄] were made by mixing 3 : 2/3 : 2/1 : 1 molar ratio of thiazolium iodide/imidazolium iodide/aminothiazolium iodide with bismuth iodide in a mixture of DMF : DMSO = 7 : 3 solvent, followed by stirring at room temperature overnight. Spin-coating was performed using a Laurell WS-6505-6NPP-LITE spin coater, with FTO glass slides sonicatedly cleaned in soap/deionized water/ethanol as substrates. The substrate was then carefully deposited by 50 μL of solution, and the spin-coating process was carried out at 2000 rpm for 1 min, followed by annealing on a hotplate from 70 °C to 130 °C for 20 minutes.

Single crystal X-ray diffraction

Dark red plate-shaped crystals of [TH]₃[Bi₂I₉] ([AT][BiI₄]) were obtained by solvent layering of bismuth iodide ethanol solution and thiazolium iodide (aminothiazolium iodide) water solution. A suitable sized single crystal was mounted on a MITIGEN holder in Paratone oil. X-ray diffraction data were collected using a Rigaku Oxford Diffraction SuperNova diffractometer equipped with an Oxford Cryosystems Cryostream 700+ low-temperature device, operating at T = 250.0 K for [TH]₃[Bi₂I₉] and 110 K for [AT][BiI₄]. The model was refined with version 2014/7 of ShelXL (Sheldrick, 2015) using least squares minimisation. Data were measured using ω scans of 0.5° per frame for 20.0 s using MoK_α radiation (micro-focus sealed X-ray tube, 50 kV, 0.8 mA).

Computational methods

Density functional theory (DFT) based computational studies were carried out to study the electronic band structure of [TH]₃[Bi₂I₉] and [AT][BiI₄], using the CASTEP 16.11 computational package⁵¹ utilized with the PBE functional⁵⁵ and the TS dispersion correction scheme.⁵⁶ The geometry coordinates of each crystal structure were obtained from their single crystal XRD results and generated from VESTA software.⁵⁷ ‘On-the-fly’ pseudopotentials were used for the calculations, which were generated directly from the CASTEP package. A series of single-point energy calculations have been carried out to identify suitable cut-off energies (E_cut) for plane wave basis sets (dE_tot/dE_cut ≤ 0.003 eV per atom), with E_cut = 450 eV for [TH]₃[Bi₂I₉] and E_cut = 400 eV for [AT][BiI₄]. Unit cell parameters were set to fixed at experimental values and optimized structures were considered to have achieved once the convergence criteria (maximum change in system energy 2.0 × 10⁻⁵ eV per atom, maximum force 0.05 eV Å⁻¹, and maximum root-mean square (RMS) atomic displacement 0.002 Å) were reached. Monkhorst–Pack grids was used for Brillouin zone sampling, with separation between k-points was less than 0.08 Å⁻¹. Electronic band structure plots of [TH]₃[Bi₂I₉] and [AT][BiI₄] were then calculated based on k-vectors linking high symmetry points, and also via selected k-points corresponding to strong intermolecular interactions. Density of States plot (DOS) and partial DOS plots for each crystal structure were generated by OptaDOS,⁵⁸ which permits the contributions from different elements to be ascertained.

UV-Vis diffuse reflectance

Diffuse reflectance measurements were carried out for a spin-coated thin film and powders of each compound, on a Jasco V-670 spectrophotometer with SpectaManager software. The measurements were performed at room temperature in the range of 250–850 nm. The Kubelka–Munk function was used to analyse the data collected from diffuse reflectance measurements, and values of direct band gap of each compound were constructed by Tauc plots. The validity of assumptions on allowed direct lowest energy transitions was considered together with the result from DFT calculations.

Materials characterization

Diffuse reflectance measurements were carried out using a Jasco V-670 spectrophotometer with SpectaManager software, with the wavelength of 250–850 nm. The diffuse reflectance data were analysed by Kubelka–Munk function, and the values of direct band gap of each compound were estimated by Tauc plots. A direct band gap was considered as this was consistent with the DFT calculations.

Cyclic voltammetry for material studies were carried out in N₂-degassed dichloromethane, dissolving 3 M N(C₄H₉)₄BF₄ as electrolyte. A three-electrode cell with an Autolab Type III potentiostat was used, and the results were further analysed on GPES electrochemical software. Spin-coated compounds on FTO conducting glasses were used as working electrodes; Pt was used as counter electrode; Ag/AgCl was used as reference electrode. A scan rate of 50 mV s⁻¹ was used for every redox process, with the correction from ferrocenium/ferrocene (Fc⁺/Fc) internal standard, taken to be at 0.63 V against NHE.⁵⁹

Device fabrications

Fluorine doped tin oxide (FTO) glass was firstly etched to form two detached electrodes (Fig. 5a) through laser before being cleaned subsequently with detergents, deionized water and ethanol in an ultrasonic cleaner. The titanium diisopropoxide bis(acetyl acetonate) solution dissolved in isopropanol was sprayed on the surface of FTO at 450 °C to form a compact layer of titanium dioxide (TiO₂). Mesoporous layers of TiO₂, ZrO₂ and carbon were then deposited layer by layer by screen printing method. The TiO₂ layer was sintered at 500 °C for 40 minutes, and the ZrO₂ and carbon layers were sintered at 400 °C for 40 minutes. Detailed information can be found in the previous report. Finally, 2.5 μl of the precursor solution was infiltrated into the triple layer cell, followed by a covered annealing at 60 °C for 40 minutes.

Device characterisation

Photocurrent density versus voltage characteristics of solar cell devices were characterised by Keithley Model 2400 digital sourcemeter with Newport solar simulator (model 91192). An irradiance of 100 mW cm⁻² was calibrated by the standard reference cell (Newport Oriel PV reference cell, model 91150 V) prior to the measurements. A black mask with a circular aperture (0.07 cm²) was used to cover the active area of the device. The J–V testing was performed with both reverse and forward scan directions at 250 mV s⁻¹ (sweep delay time of 100 ms).

Cyclic voltammetry (CV) test for solar cell devices was measured with a ZAHNER Zennium Electrochemical Workstation in the dark condition and the sweep rate was 100 mV s⁻¹. The stabilized current were tested under a bias voltage of 0.27 V with the same sourcemeter and solar simulator. No preconditioning protocol was used before the characterization. The IPCE spectra were measured using a 150 W xenon lamp (Oriel) fitted with a monochromator (Cornerstone 74004) as a monochromatic light source. Calibration with the Oriel Si detector was carried out before IPCE measurements. The cell capacitance was calculated from the CV measurement of the device, according to the equation below

where ‘i’ is the average of cathodic current and ‘s’ is the scan rate for the measurement.

The areal capacitance was calculated according to the equation

where ‘A’ is the electrode area.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors thank the University of Edinburgh for financial support and access to high performance computing resources (via the ECDF), along with the EaSTCHEM Research Computing facility for access to software. Y. Hu and H. W. Han acknowledge financial support from the National Natural Science Foundation of China (21702069, 91733301, 91433203, 61474049), the Ministry of Science and Technology of China (863, 2015AA034601), and the China Postdoctoral Science Foundation (2016M600588). We thank School of Chemistry in the University of St Andrews for performing the SEM measurement, with the help from Dr Julia Payne. We also thank Dr Philipp J. Altmann and Dr Kai Wang for their suggestions on crystal structure determination.

Notes and references

1. H. J. Snaith, J. Phys. Chem. Lett., 2013, 4, 3623–3630.
2. S. De Wolf, J. Holovsky, S. J. Moon, P. Löper, B. Niesen, M. Ledinsky, F. J. Haug, J. H. Yum and C. Ballif, J. Phys. Chem. Lett., 2014, 5, 1035–1039.
3. A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T. W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582–587.
4. W. J. Yin, T. Shi and Y. Yan, Adv. Mater., 2014, 26, 4653–4658.
5. Y. Li, W. Yan, Y. Li, W. Wang, Z. Bian, L. Xiao and S. Wang, Sci. Rep., 2015, 1–22.
6. S. D. Stranks, G. E. Eperon, G. Grancini, C. Menelaou, M. J. P. Alcocer, T. Leijtens, L. M. Herz, A. Petrozza and H. J. Snaith, Science, 2013, 342, 341–344.
7. N.-G. Park, M. Grätzel, T. Miyasaka, K. Zhu and K. Emery, Nat. Energy, 2016, 1, 16152.
8. L. K. Ono, N.-G. Park, K. Zhu, W. Huang and Y. Qi, ACS Energy Lett., 2017, 1749–1751.
9. T. M. Akihiro Kojima, K. Teshima and Y. Shirai, J. Am. Chem. Soc., 2009, 131, 6050–6051.
10. W. S. Yang, B. W. Park, E. H. Jung, N. J. Jeon, Y. C. Kim, D. U. Lee, S. S. Shin, J. Seo, E. K. Kim, J. H. Noh and S. Il Seok, Science, 2017, 356, 1376–1379.
11. D. Wang, M. Wright, N. K. Elumalai and A. Uddin, Sol. Energy Mater. Sol. Cells, 2016, 147, 255–275.
12. X. Zhu, D. Yang, R. Yang, B. Yang, Z. Yang, X. Ren, J. Zhang, J. Niu, J. Feng and S. (Frank) Liu, Nanoscale, 2017, 9, 12316–12323.
13. M. Lira-Cantú, Nat. Energy, 2017, 2, 17115.
14. X. Qin, Z. Zhao, Y. Wang, J. Wu, Q. Jiang and J. You, J. Semicond., 2017, 38, 011002.
15. S. Zhou, L. Li, H. Yu, J. Chen, C. P. Wong and N. Zhao, Adv. Electron. Mater., 2016, 2, 1–8.
16. N. Vicente and G. Garcia-Belmonte, J. Phys. Chem. Lett., 2017, 8, 1371–1374.
17. Z. Liu, Y. Zhong, B. Sun, X. Liu, J. Han, T. Shi, Z. Tang and G. Liao, ACS Appl. Mater. Interfaces, 2017, 9, 22361–22368.
18. B. Hailegnaw, S. Kirmayer, E. Edri, G. Hodes and D. Cahen, J. Phys. Chem. Lett., 2015, 6, 1543–1547.
19. A. Babayigit, A. Ethirajan, M. Muller and B. Conings, Nat. Mater., 2016, 15, 247–251.
20. W. Liao, D. Zhao, Y. Yu, C. R. Grice, C. Wang, A. J. Cimaroli, P. Schulz, W. Meng, K. Zhu, R. G. Xiong and Y. Yan, Adv. Mater., 2016, 28, 9333–9340.
21. M. H. Kumar, S. Dharani, W. L. Leong, P. P. Boix, R. R. Prabhakar, T. Baikie, C. Shi, H. Ding, R. Ramesh, M. Asta, M. Graetzel, S. G. Mhaisalkar and N. Mathews, Adv. Mater., 2014, 26, 7122–7127.
22. L. Serrano-Lujan, N. Espinosa, T. T. Larsen-Olsen, J. Abad, A. Urbina and F. C. Krebs, Adv. Energy Mater., 2015, 5, 1501119.
23. F. Hao, C. C. Stoumpos, D. H. Cao, R. P. H. Chang and M. G. Kanatzidis, Nat. Photonics, 2014, 8, 489–494.
24. N. K. Noel, S. D. Stranks, A. Abate, C. Wehrenfennig, S. Guarnera, A.-A. Haghighirad, A. Sadhanala, G. E. Eperon, S. K. Pathak, M. B. Johnston, A. Petrozza, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 3061–3068.
25. P. V. Kamat, J. Bisquert and J. Buriak, ACS Energy Lett., 2017, 2, 904–905.
26. Z. Shi, J. Guo, Y. Chen, Q. Li, Y. Pan, H. Zhang, Y. Xia and W. Huang, Adv. Mater., 2017, 29, 1605005.
27. F. Giustino and H. J. Snaith, ACS Energy Lett., 2016, 1, 1233–1240.
28. M. Pazoki, M. B. Johansson, H. Zhu, P. Broqvist, T. Edvinsson, G. Boschloo and E. M. J. Johansson, J. Phys. Chem. C, 2016, 120, 29039–29046.
29. M. B. Johansson, H. Zhu and E. M. J. Johansson, J. Phys. Chem. Lett., 2016, 7, 3467–3471.
30. B. W. Park, B. Philippe, X. Zhang, H. Rensmo, G. Boschloo and E. M. J. Johansson, Adv. Mater., 2015, 27, 6806–6813.
31. Z. Zhang, X. Li, X. Xia, Z. Wang, Z. Huang, B. Lei and Y. Gao, J. Phys. Chem. Lett., 2017, 8(17), 4300–4307.
32. T. Singh, A. Kulkarni, M. Ikegami and T. Miyasaka, ACS Appl. Mater. Interfaces, 2016, 8(23), 14542–14547.
33. A. Kulkarni, T. Singh, M. Ikegami and T. Miyasaka, RSC Adv., 2017, 7, 9456–9460.
34. Z. Xiao, W. Meng, J. Wang, D. B. Mitzi and Y. Yan, Mater. Horiz., 2017, 4, 206–216.
35. E. Greul, M. L. Petrus, A. Binek, P. Docampo and T. Bein, J. Mater. Chem. A, 2017, 5, 19972–19981.
36. A. H. Slavney, L. Leppert, D. Bartesaghi, A. Gold-Parker, M. F. Toney, T. J. Savenije, J. B. Neaton and H. I. Karunadasa, J. Am. Chem. Soc., 2017, 139, 5015–5018.
37. C. N. Savory, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2016, 1, 949–955.
38. E. T. McClure, M. R. Ball, W. Windl and P. M. Woodward, Chem. Mater., 2016, 28, 1348–1354.
39. G. Volonakis, M. R. Filip, A. A. Haghighirad, N. Sakai, B. Wenger, H. J. Snaith and F. Giustino, J. Phys. Chem. Lett., 2016, 7, 1254–1259.
40. A. H. Slavney, T. Hu, A. M. Lindenberg and H. I. Karunadasa, J. Am. Chem. Soc., 2016, 138, 2138–2141.
41. A. J. Lehner, D. H. Fabini, H. A. Evans, C. Hébert, S. R. Smock, J. Hu, H. Wang, J. W. Zwanziger, M. L. Chabinyc and R. Seshadri, Chem. Mater., 2015, 27, 7137–7148.
42. N. Louvain, N. Mercier and F. Boucher, Inorg. Chem., 2009, 48, 879–888.
43. T. Li, Y. Hu, C. Morrison, W. Wu, H. Han and N. Robertson, Sustainable Energy Fuels, 2017, 1–9.
44. I. Turkevych, S. Kazaoui, E. Ito, T. Urano, K. Yamada, H. Tomiyasu, H. Yamagishi, M. Kondo and S. Aramaki, ChemSusChem, 2017, 10, 3754–3759.
45. J. K. Pious, M. L. Lekshmi, C. Muthu, R. B. Rakhi and V. C. Nair, ACS Omega, 2017, 2, 5798–5802.
46. M. Węcławik, A. Gągor, R. Jakubas, A. Piecha-Bisiorek, W. Medycki, J. Baran, P. Zieliński and M. Gałązka, Inorg. Chem. Front., 2016, 3, 1306–1316.
47. S. A. Adonin, M. N. Sokolov and V. P. Fedin, Coord. Chem. Rev., 2016, 312, 1–21.
48. L. M. Wu, X. T. Wu and L. Chen, Coord. Chem. Rev., 2009, 253, 2787–2804.
49. C. E. Housecroft and A. G. Sharpe, Inorganic Chemistry, Pearson, Cambridge, 2012.
50. C. Janiak, J. Chem. Soc., Dalton Trans., 2000, 3885–3896.
51. S. J. Clark, M. D. Segall, C. J. Pickard, P. J. Hasnip, M. I. J. Probert, K. Refson and M. C. Payne, Z. Kristallogr., 2005, 220, 567–570.
52. A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Phys. Rev. B, 1996, 53, 3764–3774.
53. F. N. Crespilho, V. Zucolotto, J. R. Siqueira, A. J. F. Carvalho, F. C. Nart and O. N. Oliveira, Int. J. Electrochem. Sci., 2006, 1, 151–159.
54. Y. Hu, Z. Zhang, A. Mei, Y. Jiang, X. Hou, Q. Wang and K. Du, Adv. Mater., 2018, 1705786, 1–7.
55. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
56. A. Tkatchenko and M. Scheffler, Phys. Rev. Lett., 2009, 102, 073005.
57. K. Momma and F. Izumi, J. Appl. Crystallogr., 2014, 1–2.
58. A. J. Morris, R. J. Nicholls, C. J. Pickard and J. R. Yates, Comput. Phys. Commun., 2014, 185, 1477–1485.
59. V. V. Pavlishchuk and A. W. Addison, Inorg. Chim. Acta, 2000, 298, 97–102.

---

Footnotes

† Electronic supplementary information (ESI) available: Crystallographic data, short contacts, certain Miller indices planes, powder XRD, thin-film Tauc plots, stabilised current measurement, cyclic voltammetry and short-circuit current. CCDC 1536017 and 1561659. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/c8dt00864g

‡ These authors contributed equally to this work.

---