Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Boron-phil and boron-phob structure units in novel borides Ni3Zn2B and Ni2ZnB: experiment and first principles calculations†
F.
Failamani‡
 a,
R.
Podloucky
b,
J.
Bursik
a,
R.
Podloucky
b,
J.
Bursik
 c,
G.
Rogl
ade,
H.
Michor
c,
G.
Rogl
ade,
H.
Michor
 d,
H.
Müller
d,
E.
Bauer
de,
G.
Giester
f and
P.
Rogl
d,
H.
Müller
d,
E.
Bauer
de,
G.
Giester
f and
P.
Rogl
 *ae
*ae
aInstitute of Materials Chemistry and Research, University of Vienna, Währingerstraße 42, A-1090 Vienna, Austria. E-mail: peter.franz.rogl@univie.ac.at
bInstitute of Physical Chemistry, University of Vienna, Sensengasse 4, A-1090 Vienna, Austria
cInstitute of Physics of Materials, Academy of Sciences of the Czech Republic, Žižkova 22, 61662 Brno, Czech Republic
dInstitute of Solid State Physics, TU Wien, Wiedner Hauptstraße 8-10, A-1040 Vienna, Austria
eChristian Doppler Laboratory for Thermoelectricity, Vienna, Austria
fInstitute of Mineralogy and Crystallography, University of Vienna, Althanstraße 14, A-1090 Vienna, Austria
First published on 22nd January 2018
Abstract
The crystal structures of two novel borides in the Ni–Zn–B system, τ5-Ni3Zn2B and τ6-Ni2ZnB, were determined by single crystal X-ray diffraction (XRSC) in combination with selected area electron diffraction in a transmission electron microscope (SAED-TEM) and electron probe microanalysis (EPMA). Both compounds crystallize in unique structure types (space group C2/m, a = 1.68942(8) nm, b = 0.26332(1) nm, c = 0.61904(3) nm, β = 111.164(2)°, RF = 0.0219 for Ni3Zn2B, and space group C2/m, a = 0.95296(7) nm, b = 0.28371(2) nm, c = 0.59989(1) nm, β = 93.009(4)°, RF = 0.0163 for Ni2ZnB). Both compounds have similar building blocks: two triangular prisms centered by boron atoms are arranged along the c-axis separated by Zn layers, which form empty octahedra connecting the boron centered polyhedra. Consistent with the (Ni+Zn)/B ratio, isolated boron atoms are found in τ5-Ni3Zn2B, while B–B pairs exist in τ6-Ni2ZnB. The crystal structure of Ni2ZnB is closely related to that of τ4-Ni3ZnB2, i.e. Ni2ZnB can be formed by removing the nearly planar nickel layer in Ni3ZnB2 and shifting the origin of the unit cell to the center of the B–B pair. The electrical resistivity and specific heat of τ5-Ni3Zn2B reveal the metallic behavior of this compound with an anomaly at low temperature, possibly arising from a Kondo-type interaction. Further analysis on the lattice contribution of the specific heat reveals similarity with τ4-Ni3ZnB2 with some indications of lattice softening in τ5-Ni3Zn2B, which could be related to the increasing metal content and the absence of B–B bonding in τ5-Ni3Zn2B. For the newly found phases, τ5-Ni3Zn2B and τ6-Ni2ZnB as well as for τ3-Ni21Zn2B20 and τ4-Ni3ZnB2 density functional theory (DFT) calculations were performed by means of the Vienna Ab initio Simulation Package (VASP). Total energies and forces were minimized in order to determine the fully relaxed structural parameters, which agree very well with experiment. Energies of formations in the range of −25.2 to −26.9 kJ mol−1 were calculated and bulk moduli in the range of 179.7 to 248.9 GPa were derived showing hardening by increasing the B concentration. Charge transfer is discussed in terms of Bader charges resulting in electronic transfer from Zn to the system and electronic charge gain by B. Ni charge contributions vary significantly with crystallographic position depending on B located in the neighbourhood. The electronic structure is presented in terms of densities of states, band structures and contour plots revealing Ni–B and Ni–Zn bonding features.
1. Introduction
Additions of Zn in novel Ni–B–Zn coatings on steels (used in the automotive, aerospace, petrochemical, textile and electronics industries) were found to significantly improve crystallinity, mechanical properties, and corrosion resistance.1,2 Little, however, is known how crystalline Ni–Zn-borides might influence long term stability. Although the first investigation of the Ni–Zn–B system in 1962 by Stadelmaier3 provided an isothermal section at 800 °C and a liquidus projection in the Ni-rich part, only the crystal structure of the τ-phase Ni20Zn3B6 has since been studied carefully by several groups,3–6 whilst the crystal structure of the other three compounds remained unknown: ψ-Ni57Zn13B30, χ-Ni45Zn30B25, and φ-Ni49Zn31B20. With the increasing interest in Ni–B–Zn coatings on steels, our group (for details see the papers by Malik et al.7–9) has recently reinvestigated the system and identified six ternary compounds: the crystal structures were solved for Ni12ZnB8−x (labeled as τ2, probably to be identified as ψ-Ni57Zn13B30 of Stadelmaier3) as well as for Ni21Zn2B20 (labeled as τ3, new structure type) and Ni3ZnB2 (labeled as τ4, new structure type).7 The crystal structures of two further compounds are still unknown: Ni48Zn32B20 (in at%, labeled as τ5,8 likely similar to the φ-phase of ref. 3), and Ni47Zn23B30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 (in at%, labeled as τ6, likely similar to the χ-phase of ref. 3). Moreover, a detailed study on the homogeneity region of the τ-phase (labeled as τ1) was also presented,8 which showed both Ni/Zn and Zn/B4 atom substitutions. Physical properties have been investigated so far only for the compounds, τ3-Ni21Zn2B20 and τ4-Ni3ZnB2, both revealing metallic and paramagnetic behavior.9
8 (in at%, labeled as τ6, likely similar to the χ-phase of ref. 3). Moreover, a detailed study on the homogeneity region of the τ-phase (labeled as τ1) was also presented,8 which showed both Ni/Zn and Zn/B4 atom substitutions. Physical properties have been investigated so far only for the compounds, τ3-Ni21Zn2B20 and τ4-Ni3ZnB2, both revealing metallic and paramagnetic behavior.9
In this paper, we aim to complete the previous work by: (i) solving the crystal structures of τ5 and τ6 from single crystal X-ray analyses backed by SAED-TEM, (ii) elucidating the electronic structure and chemical bonding by DFT calculations, (iii) defining the physical properties of τ5 and τ6, and accordingly (iv) revising the isothermal section at 800 °C.
Besides phase stability issues, the combination of transition metal elements and main group metals in intermetallic-like borides reveals an interesting combination of structural units which are composed of transition metal boride slabs (“boron-phil” part), that are connected by bonds between the transition element and the main group metal (“boron-phob” part).10–12 It is worth mentioning that due to the electron deficiency of boron in most cases, only electropositive elements such as rare earth metals can form the so called “higher borides” with three-dimensional boron frameworks.13–18 In this work, we have particularly focused on the four ternary borides (τ3, τ4, τ5, and τ6) which all adhere to the isopleth extending from NiB to NiZn. As bonding defines the physical properties, the DFT studies accompanying the experiment will provide thermodynamic and elastic stability and elucidate the underlying electronic structure in terms of charge transfer, density of states, band structures and charge density distribution.
2. Experimental methods
2.1. Sample preparation and characterisation techniques
For sample preparation, the following materials were used: nickel rods, foils, or wires, zinc filings (all metals from Alfa Aesar, D with 99.9 mass% purity), and crystalline boron pieces (Alfa Aesar, D, 99.5 mass% B). Zn filings were prepared mechanically from zinc, which was purified by heating Zn granules in an evacuated quartz ampoule at 800 °C. Due to the volatility of Zn and in order to reach equilibrium at the desired temperature, the sample preparation was conducted in two steps. First, NixB (x ≤ 3) master alloys were prepared by arc-melting of nickel pieces/foils and boron pieces under a Ti-gettered Ar atmosphere. The powdered NixB master alloys were subsequently mixed with Zn filings and compacted in a steel die without lubricant. For samples with compositions close to the Ni–Zn binary system, finely cut Ni wires (Φ = 0.25 mm,![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ≤ 3 mm) were used in addition to Ni3B powder and Zn filings. The pellets were placed inside protective Al2O3 crucibles and sealed inside separate quartz tubes under ∼250 mbar of Ar.
≤ 3 mm) were used in addition to Ni3B powder and Zn filings. The pellets were placed inside protective Al2O3 crucibles and sealed inside separate quartz tubes under ∼250 mbar of Ar.
Heat treatments were performed in a resistance furnace at 875 and 900 °C for a week, with an intermediate holding at 500 °C overnight. After the first heat treatment, samples were quenched in cold water, re-powdered in a tungsten carbide mortar, compacted, sealed, and heat treated in the same way as described above. Single phase samples for physical properties measurements were prepared as indicated above. Additionally, sintering processes were performed by hotpressing the pre-compacted powder pellets in alumina powder inside a graphite die at 850 °C for 30 minutes. After removing the residual alumina powder on the sample's surface, they were cut into bars with dimensions of ∼10 × 2 × 1 mm3 with a low speed diamond saw.
X-ray powder diffraction patterns were collected after every heat treatment on a Guinier-Huber G670 image plate recording system with monochromatic CuKα1 radiation. Microstructures and compositions were examined by light optical microscopy (LOM) and scanning electron microscopy (SEM) on a Zeiss Supra 55 VP equipped with an EDX detector. The compositions of each phase were obtained by averaging several point measurements (on grains larger than at least 5 μm) and area measurements for the solid and the solidified liquid phase, respectively. Due to the difficult identification of B spectral lines, only the Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio could be measured reliably with SEM-EDX, while the boron content determinations rely solely on the single crystal refinements, or from estimation based on the weight percent measurement in EDX.
Zn ratio could be measured reliably with SEM-EDX, while the boron content determinations rely solely on the single crystal refinements, or from estimation based on the weight percent measurement in EDX.
Due to the ductile nature of the metal rich borides, mechanical isolation and fragmentation significantly deformed the single crystal specimens, making them unsuitable for single crystal data collection. Consequently, the single crystal specimens were separated from the flux via acid leaching (details on the system inherent flux are given in section 3.1.). Hot diluted HCl solution was used for τ5, while a cold mixture of concentrated HCl and HNO3 was used for τ6. In the latter, the leaching process was first performed by immersing the sample in cold concentrated HCl. After the sample's surface was passivated, drop-wise concentrated HNO3 was added while stirring the mixture until a violent reaction was observed. The reaction was stopped immediately by diluting the mixture with distilled water. In both cases, the single crystal specimens were filtered and washed several times with distilled water. Needle-shaped crystals (length/cross section ratio <3) were mounted on glass capillaries and inspected on an AXS D8-GADDS to ensure high crystal quality, lattice parameters, and crystal symmetry.
Single crystal data collections were performed at room temperature on a Bruker APEXII diffractometer equipped with a CCD area detector and an Incoatec Microfocus Source IμS (30 W, multilayer mirror, Mo-Kα; λ = 0.071069 nm; detector distance of 3 cm; full sphere; 2° < 2θ < 70°). Orientation matrices and unit cell parameters were derived using the Bruker APEXII software suite.19 Besides the general treatment of absorption effects using the multi-scan technique (SADABS; redundancy of integrated reflections >8), no additional absorption corrections were performed because of the rather irregular cross-section (mainly due to the attack of the acid) and practically small dimensions of the investigated specimens. The structures were solved by direct methods using program SIR-9220 and refined with the SHELXL-9721 program within the WinGX package.22 The crystal structure data were subsequently standardized with program STRUCTURE-TIDY.23
For TEM investigation, a Philips CM12 STEM transmission electron microscope (TEM) operated at 120 kV with an EDAX EDX analyser was employed to get information about the crystal symmetry and lattice parameters of selected phases. The samples for the TEM study were prepared in the form of thin lamellae (lateral dimensions about 10 × 7 μm2) using a focused ion beam (FIB) technique in a TESCAN LYRA 3 XMU FEG/SEM × FIB scanning electron microscope.
Electrical resistivity measurement was performed on a bar shaped polycrystalline sample by a standard four probe AC bridge technique in a homemade equipment from 2 to 300 K. Contacts were made by spot welding thin gold wires (d = 100 μm) on the sample's surface. For better mechanical stability, the spot welded contacts were coated with silver epoxy. Specific heat was measured in a Quantum Design PPMS in the same temperature range as the electrical resistivity measurement.
Hardness was measured with two different pieces of equipment, a microhardness tester, AD Paar MHT-4, mounted on a Zeiss Axioplan optical microscope employing a load of 1 N, applying a rate of 0.1 N s−1 and a loading time of 10 s (referred to as HV0.1, “static”). For all these indentations the hardness is 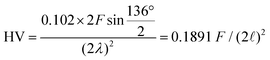 with the diagonal length 2
with the diagonal length 2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) of the indent and F as the indentation load in N. To get reliable results, about 10 different impressions for each grain and phase were applied. The second equipment, a microindenter MHT4 with a Zeiss microscope, provided the hardness (further on referred to as “dynamic”) and in parallel the Young's modulus, E. A load of 1 N and a rate of 0.1 N s−1 were used. For the evaluation of Young's modulus from indentation experiments, the Poisson's number, ν, must be available, which in our case was inferred from a RUS measurement of the closely related compound τ4-Ni3ZnB2 (ν = 0.29(1); see ref. 9). The polycrystalline bulk modulus B and the shear modulus G are then obtained from the quasi-isotropic relations:
of the indent and F as the indentation load in N. To get reliable results, about 10 different impressions for each grain and phase were applied. The second equipment, a microindenter MHT4 with a Zeiss microscope, provided the hardness (further on referred to as “dynamic”) and in parallel the Young's modulus, E. A load of 1 N and a rate of 0.1 N s−1 were used. For the evaluation of Young's modulus from indentation experiments, the Poisson's number, ν, must be available, which in our case was inferred from a RUS measurement of the closely related compound τ4-Ni3ZnB2 (ν = 0.29(1); see ref. 9). The polycrystalline bulk modulus B and the shear modulus G are then obtained from the quasi-isotropic relations: 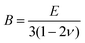 ,
, 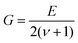 . It should be noted that prior to hardness measurements, the samples were polished with a 0.3 μm aluminum oxide paste to produce an optical finish. A capacitance dilatometer24 served to acquire thermal expansion coefficients in the temperature range of 4.2 to 300 K.
. It should be noted that prior to hardness measurements, the samples were polished with a 0.3 μm aluminum oxide paste to produce an optical finish. A capacitance dilatometer24 served to acquire thermal expansion coefficients in the temperature range of 4.2 to 300 K.
2.2. DFT calculations
The density functional theory (DFT) calculations for the Ni–Zn–B compounds were performed by means of the plane-wave based Vienna ab initio simulation package (VASP)25,26 making use of the pseudopotential construction according to the projector-augmented-wave method.27 For the Ni pseudopotential, the 16 valence states 3p6 and 3d10 were considered, whereas for Zn, the 12 valence states 3d10 and 4s2 and for B, the 3 valence states 2s2 and 2p1 were taken into account. For the exchange–correlation functional, the generalized gradient approximation according to Perdew et al.28 was chosen. The VASP calculations were done with high precision according to the energy cutoff of 600 eV. For k space integration, the Gaussian smearing method with a value for σ of 0.1 eV was applied. Regular k space grids of (10 × 10 × 3), (7 × 22 × 8), (4 × 24 × 11), and (7 × 23 × 1) k-points for the τ3, τ4, τ5, and τ6 phases were constructed according to the parameter KSPACING = 0.1 in the INCAR file of VASP. For all the calculations, all structural parameters such as lattice parameters and atomic positions are fully relaxed by minimizing atomic forces and total energy. The k space integration for deriving the density of states (DOS) was made by applying the linear tetrahedron integration29 for the k-point grids mentioned above.The enthalphy of formation at T = 0 K and zero pressure per mol atoms, ΔHf, was derived for each compound from differences of total DFT energies per unit cell,
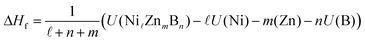 | (1) |
![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ZnmBn) represents the total energy of the compound and U(X), X = Ni, Zn, B, the total energies of the respective elemental ground state phases. The radii for calculating the local DOS were RNi = 1.058, RZn = 1.270, and RB = 0.905 Å. Atomic volumes and charges were computed by analyzing charge densities in terms of the quantum theory of atoms in molecules according to Bader et al.30–33 His method utilizes the gradient of the density searching for surfaces of zero flux. The definition of charge transfer Δqion, as it appears in the paper, is the difference of the self-consistent Bader charge minus the Bader charge of the superposed free atom charge densities. By that, there is no need to fall back to any ad-hoc assumptions based on free atoms or ions. More details are given in ref. 34.
ZnmBn) represents the total energy of the compound and U(X), X = Ni, Zn, B, the total energies of the respective elemental ground state phases. The radii for calculating the local DOS were RNi = 1.058, RZn = 1.270, and RB = 0.905 Å. Atomic volumes and charges were computed by analyzing charge densities in terms of the quantum theory of atoms in molecules according to Bader et al.30–33 His method utilizes the gradient of the density searching for surfaces of zero flux. The definition of charge transfer Δqion, as it appears in the paper, is the difference of the self-consistent Bader charge minus the Bader charge of the superposed free atom charge densities. By that, there is no need to fall back to any ad-hoc assumptions based on free atoms or ions. More details are given in ref. 34.
3. Results and discussion
3.1. Formation, stability and crystal growth of τ5 and τ6 phases
During the investigation of the ternary Ni–Zn–B system by Malik et al.,8 attempts to grow single crystals of τ5 and τ6 were unsuccessful due to the intergrowth of phases and a hair-like morphology inside the grains. Moreover, strong adhesion of eutectic regions to the τ5 and τ6 grains made it difficult to isolate proper crystals. Based on these facts in the present investigation we revised the strategy for the single crystal growth and used isothermal annealing followed by quenching. Indeed, samples with a nominal composition of Ni47Zn22B31 (in at%) annealed at 900 °C (Fig. 1a) showed large crystallites of τ4 surrounded by a thin layer of τ6. Comparing this microstructure with the microstructure presented by Malik et al.8 at 880 °C suggests that τ6 is formed via a peritectic-like reaction from τ4 at 890 ± 10 °C. Details on the phase compositions of samples prepared for the single crystal growth are given in Table I of the ESI.† Accordingly, a temperature of 875 °C was chosen for the single crystal growth based on the existence of the binary Ni–Zn eutectic![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ↔ NiZn-ht + Ni2Zn11 at 875 °C,35 which provides the liquid phase for the single crystal growth.
↔ NiZn-ht + Ni2Zn11 at 875 °C,35 which provides the liquid phase for the single crystal growth.
 | ||
| Fig. 1 Selected micrographs of Ni–Zn–B alloys annealed at 900 °C (a) Ni47Zn22B31; annealed at 875 °C: (b) Ni40Zn50B10, (c) Ni35Zn55B10, (d) Ni56Zn44B10, (e) Ni42Zn44B14, and (f) Ni50Zn30B20. For the detailed phase composition see Table I of the ESI.† | ||
Selected micrographs in Fig. 1b–f document the attempts to grow the single crystals of τ5 and τ6. The single crystals obtained in this investigation are grown from equilibrium with the Zn-rich eutectic with a Ni/Zn ratio of 39.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 60.8 (∼Ni36.0Zn56B8.0 at%), and were selected from samples with the compositions of Ni40Zn50B10 (Fig. 1b) and Ni42Zn44B14 (Fig. 1e) for τ5 and τ6, respectively.
60.8 (∼Ni36.0Zn56B8.0 at%), and were selected from samples with the compositions of Ni40Zn50B10 (Fig. 1b) and Ni42Zn44B14 (Fig. 1e) for τ5 and τ6, respectively.
3.2. Structure analyses
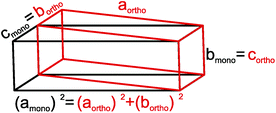 | ||
| Fig. 2 Relationship between the body centered orthorhombic (red) and C-centered monoclinic (black) unit cells of τ5-Ni3Zn2B. | ||
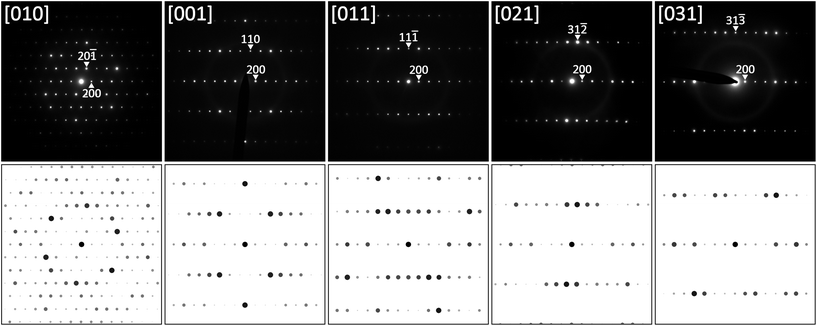
Using this relationship, TEM SAED patterns obtained at various sample tilts were re-indexed on the basis of the C-centered monoclinic cell. Fig. 3 shows several examples together with simulated SAED patterns using software JEMS.36,37 It should be emphasized that all diffraction patterns were completely indexed on the monoclinic cell without any signs for superstructure formation.
The crystal structure of τ5 was successfully solved with direct methods in the lowest symmetry i.e. in the C-centered monoclinic space group C2, yielding five crystallographic metal positions and one boron position, all in general Wyckoff site 4i (x,y,z). Due to the small difference in the ordinal number and consequently only a small difference in the X-ray scattering power, nickel and zinc atom positions were assigned (i) from crystal chemical considerations (taking into account the small affinity of Zn towards boron), and the larger atom size of Zn with respect to Ni (CN12 radii: RNi = 0.1246 nm; RZn = 0.1394 nm; see ref. 38) supported also by (ii) atom displacement parameters (ADPs).
The initial refinement in the space group C2 settled quickly at a reasonable RF2 value of 0.035 with residual electron density of less than ±3.6 e Å−3. The analysis of a missing symmetry employing program PLATON39 suggested the addition of a mirror plane perpendicular to the two-fold rotation axis, which consequently results in an inversion symmetry. The structure was subsequently transformed and refined in the centrosymmetric space group C2/m. The final refinement with anisotropic ADPs for metal atoms and isotropic ADPs for boron converged to a low residual factor of RF2 = 0.0219 and a residual electron density less than ±1.33 e Å−3. The detailed and standardized crystallographic data of τ5 are presented in Table 1. Interatomic distances are listed in Table II of the ESI.† Refinement of boron occupancy results in only a slight deviation from full site occupancy. Thus, the structure refinement yields a fully ordered structure with three Ni sites, two Zn sites and one B site, all in position 4i (x,0,y), which corresponds to a Wyckoff sequence of 12,i6. Search for isotypic compounds in Pearson's Crystal Data,40 based on the lattice parameter and the Wyckoff sequence, gave no result: this suggests that τ5-Ni3Zn2B is a new structure type. A Rietveld refinement (see Fig. I of the ESI†) of the X-ray powder pattern from the sample of which the τ5 single crystals were selected (Ni40Zn50B10 in at%) confirmed the structure solution.
| Parameter/compound | τ5-Ni3Zn2B | τ6-Ni2ZnB |
|---|---|---|
Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio, EPMA/refinement Zn ratio, EPMA/refinement |
62.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5/60 37.5/60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40 40 |
68.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31.5/66.7 31.5/66.7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 33.3 33.3 |
| Refinement composition (at%) | Ni50.0Zn33.3B16.7 | Ni50.0Zn25.0B25.0 |
| Structure type | Own type | Own type |
| 2θ range (°) | 5.171 ≤ 2θ ≤ 72.558 | 6.802 ≤ 2θ ≤ 72.620 |
| a(SC)/a(XPD-Si standard) (nm) | 1.68942(8)/1.6934(2); DFT [1.696467] | 0.95296(7)/0.9549(6); DFT [0.954008] |
| b(SC)/b(XPD-Si standard) (nm) | 0.26332(1)/0.26448(1); DFT [0.263834] | 0.28371(2)/0.28466(3); DFT [0.28435] |
| c(SC)/c(XPD-Si standard) (nm) | 0.61904(3)/0.62152(3); DFT [0.619690] | 0.59989(1)/0.6006(3); DFT [0.601324] |
| β(SC)/β(XPD-Si standard) (°) | 111.164(2)/111.170(4); DFT [111.344] | 93.009(4)/93.01(5); DFT [92.996] |
| Reflections in refinement | 703 ≥ 4σ(Fo) of 723 | 427≥ 4σ(Fo) of 446 |
| Number of variables | 35 | 23 |
| R F 2 = ∑|Fo2 − Fc2|/∑Fo2 | 0.0219 | 0.0162 |
| wR2 | 0.0533 | 0.0335 |
| R Int | 0.0426 | 0.0253 |
| GOF | 1.232 | 1.243 |
| Extinction (Zachariasen) | 0.0182(8) | 0.0175(8) |
| M1 in 4i (x,0,z); occ. | x = 0.07909(2); z = 0.10781(5); 1.00(—) Ni1 | x = 0.45925(3); z = 0.19908(4); 1.00(—) Ni1 |
| [DFT: x; z] | x = 0.079453; z = 0.110651 | x = 0.460496; z = 0.196963 |
| U 11; U22; U33; U23 = U12 = 0; U13 | 0.0017(1); 0.0061(2); 0.0037(2); 0.0007(1) | 0.0045(1); 0.0056(1); 0.0056(1); 0.0004(1) |
| M2 in 4i (x,0,z); occ. | x = 0.11705(2); z = 0.56127(5); 1.00(—) Ni2 | x = 0.72930(3); z = 0.16342(4); 1.00(—) Ni2 |
| [DFT: x; z] | x = 0.116902; z = 0.559792 | x = 0.728978; z = 0.163505 |
| U 11; U22; U33; U23 = U12 = 0; U13 | 0.0033(1); 0.0056(2); 0.0046(1); 0.0008(1) | 0.0038(1); 0.0060(1); 0.0045(1); 0.0005(1) |
| M3 in 4i (x,0,z); occ. | x = 0.24022(2); z = 0.32068(5); 1.00(—) Ni3 | x = 0.13083(3); z = 0.46672(4); 1.00(—) Zn |
| [DFT: x; z] | x = 0.239784; z = 0.320496 | x = 0.130741; z = 0.467678 |
| U 11; U22; U33; U23 = U12 = 0; U13 | 0.0019(1); 0.0065(2); 0.0032(1); 0.0005(1) | 0.0066(1); 0.0081(1); 0.0051(1); 0.0002(1) |
| M4 in 4i (x,0,z); occ. | x = 0.32445(2); z = 0.05714(5); 1.00(—) Zn1 | x = 0.0931(2); z = 0.0515(4); 1.00(—) B |
| [DFT: x; z] | x = 0.324597; z = 0.058113 | x = 0.094038; z = 0.049909 |
| U 11; U22; U33; U23 = U12 = 0; U13 | 0.0038(1); 0.0075(2); 0.0047(1); 0.0017(1) | U iso = 0.0066(4) |
| M5 in 4i (x,0,z); occ. | x = 0.48766(2); z = 0.27981(5); 1.00(—) Zn2 | — |
| [DFT: x; z] | x = 0.487293; z = 0.279410 | |
| U 11; U22; U33; U23 = U12 = 0; U13 | 0.0035(1); 0.0071(2); 0.0051(1); 0.0016(1) | |
| M6 in 4i (x,0,z); occ. | x = 0.3476(2); z = 0.6437(5); 1.00(—) B | — |
| [DFT: x; z] | x = 0.346310; z = 0.640957 | |
| U 11; U22; U33; U23 = U12 = 0; U13 | U iso = 0.0068(4) | |
| Residual electron density; max; min in (electron per nm3) × 103 | 1.33; −1.24 | 1.03; −0.76 |
The Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio obtained from single crystal refinement (60
Zn ratio obtained from single crystal refinement (60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 40) deviates only slightly from the EPMA ratio of 62.5
40) deviates only slightly from the EPMA ratio of 62.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 37.5. From the Ni–Zn–B isothermal section at 800 °C, τ5 exhibits a small homogeneity range from Ni
37.5. From the Ni–Zn–B isothermal section at 800 °C, τ5 exhibits a small homogeneity range from Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio 60.6
Zn ratio 60.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 39.4 to 63.8
39.4 to 63.8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 36.2 at a constant boron concentration, which is also preserved up to 875 °C. Zinc is known to have poor affinity to boron in many intermetallic compounds, i.e. Zn–B contacts (<0.24 nm) are rarely found in the literature.40 Therefore, the deviation from the stoichiometric ratio could be explained by a minor nickel substitution on one or both Zn sites. As mentioned above, due to the similarity between nickel and zinc, as well as the small amount of the substitution, crystallographic quantification of the disorder cannot be carried out reliably based on X-ray intensity data. The increasing nickel content, however, results in a practically linear decrease of the unit cell volume, consistent with Vegard's law as shown in Fig. II of the ESI.†
36.2 at a constant boron concentration, which is also preserved up to 875 °C. Zinc is known to have poor affinity to boron in many intermetallic compounds, i.e. Zn–B contacts (<0.24 nm) are rarely found in the literature.40 Therefore, the deviation from the stoichiometric ratio could be explained by a minor nickel substitution on one or both Zn sites. As mentioned above, due to the similarity between nickel and zinc, as well as the small amount of the substitution, crystallographic quantification of the disorder cannot be carried out reliably based on X-ray intensity data. The increasing nickel content, however, results in a practically linear decrease of the unit cell volume, consistent with Vegard's law as shown in Fig. II of the ESI.†
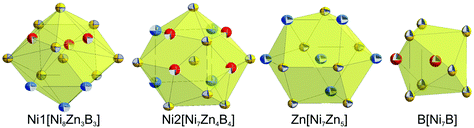
Although nickel and zinc atoms have the same coordination number of 13 and 12, respectively (see Fig. 4), the environment of the three nickel atoms, Ni1, Ni2, and Ni3, differ one to the other: a monocapped distorted cuboctahedron, a monocapped elongated pentagonal bipyramid/tricapped pentagonal prism, and a distorted pseudo Frank–Kasper polyhedron. In contrast to the nickel atoms, both Zn atoms have the same coordination number and the coordination polyhedron, which takes the form of a distorted anti-cuboctahedron. Whilst the Zn1 atom is coordinated by 7 nickel atoms and 5 Zn atoms with Ni–Zn distances less than 0.26 nm, the distorted anti-cuboctahedron around the Zn2 atom consists of 8 nickel atoms and 4 Zn atoms with some longer Ni–Zn distances (>0.26 nm). The boron atom in this compound is surrounded by 7 nickel atoms, which form a monocapped triangular (trigonal) prism.
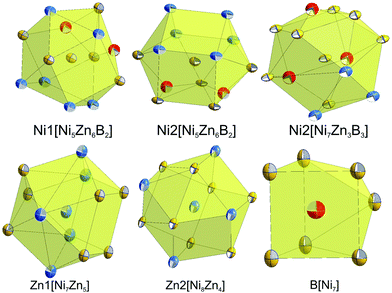 | ||
| Fig. 4 Coordination polyhedra of atom sites in τ5-Ni3Zn2B. Atoms are presented with ADPs from single crystal refinement: Ni (gold), Zn (blue), and B (red). | ||
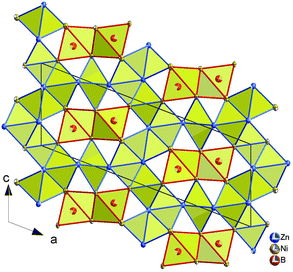
The crystal structure of τ5-Ni3Zn2B is shown in Fig. 5. It can be viewed as an arrangement of two edge sharing monocapped trigonal prisms formed by boron and nickel atoms (B[Ni7]) along the c-axis, separated by corrugated rectangular sheets of Zn. Along the b-axis, infinite columns of face sharing trigonal prisms are formed with a shift of ½b between adjacent columns. Such an arrangement of boron polyhedra in τ5 is based on the Re3B-type, where infinite boron polyhedra are connected along the c-axis, forming layers of edge sharing bi-capped trigonal metal prisms along the b-axis separated by empty metal octahedra. On the other hand, stacking the boron polyhedra in the direction of the a-axis results in similar infinite columns of face sharing trigonal prisms with a shift of ½a between the columns. A similar edge sharing arrangement can also be found in Ni3B (Fe3C-type) along the b-axis. In this case, however, additional edge sharing polyhedra via one of the trigonal prism edges are observed forming a zigzag-like arrangement of the capped triangular prisms, also connecting the two layers of edge sharing trigonal prisms. It is interesting to mention here that in the binary Ni–B system, Ni3B crystallizes in the Fe3C-type instead of the Re3B-type, whereas the layer of empty octahedra can be considered to be related to the CsCl(ht)/CuTi(rt)-type NiZn phase in the binary Ni–Zn system.40
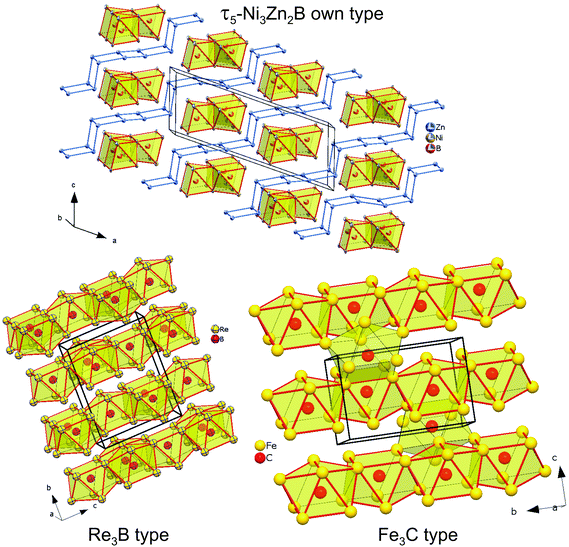 | ||
| Fig. 5 The crystal structure of τ5-Ni3Zn2B (top), Re3B (bottom-left), and Fe3C (bottom-right). Atoms in τ5 are presented with ADPs from single crystal refinement: Ni (gold), Zn (blue), and B (red). | ||
The structure of τ5 can be formed by cleaving the infinite edge sharing capped trigonal prisms in the Re3B structure by a corrugated rectangular zinc sheet, which also fills the space between the layers of edge sharing capped trigonal prisms. The insertion of a Zn sheet also results in the formation of some edge and face sharing empty octahedra Ni2Zn4 formed by nickel from the boron polyhedra and the zinc sheet (see Fig. 6). The building block arrangement of τ5 is analogous to that in the neighboring compounds τ4-Ni3ZnB2 and τ6-Ni2ZnB (see the next section).
The possibility of small interstitial atoms X (X = C, N, and O) residing inside the octahedra is ruled out due to its rather small cavity size, i.e. the shortest distances between the center of the octahedra to the nearest Ni/Zn atoms are less than 0.186 nm (for details see Table III of the ESI†). Such a distance would be within the range of Ni–X contacts in the Ni–X binaries (0.175–0.196 nm), but too short for Zn–X contacts in binary Zn–X compounds (>0.195 nm).40 Consequently, partial filling of the octahedral void(s) would create split positions of the Zn atoms, like those in V5Sb4C1−x.41 Moreover, the low value of RF2 and the residual electron density of the single crystal refinement documents that there is practically no electron density at or near the center of the octahedra.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) αtriclinic, bmonoclinic = ctriclinic, cmonoclinic = atriclinic, βmonoclinic = γtriclinic (see Fig. 7).
αtriclinic, bmonoclinic = ctriclinic, cmonoclinic = atriclinic, βmonoclinic = γtriclinic (see Fig. 7).
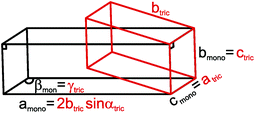 | ||
| Fig. 7 Relationship between the triclinic (red) and C-centered monoclinic (black) unit cells of τ6-Ni2ZnB. | ||
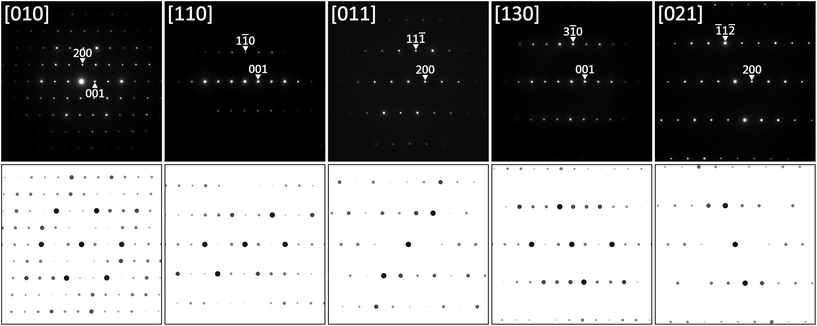
Based on the X-ray single crystal data, TEM SAED patterns could be re-indexed using the proper C-centered monoclinic unit cell, as shown on several examples in Fig. 8 together with simulated patterns. Also in this case, all diffraction patterns were completely indexed on the monoclinic cell without any signs for superstructure formation.
The analysis of the systematic extinctions in the X-ray single crystal diffraction pattern suggested C2/m as the space group with the highest symmetry possible. Structural solution employing direct methods in this space group was straightforward and resulted in three metal and one boron positions, all in site 4i (x,0,y). Refinement of the structure quickly converged to a low RF2 value of 0.0162 with residual electron density less than ±1.03 e Å−3. The final formula from the refinement Ni2ZnB indicates a fully ordered structure. The Ni![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zn ratio from EPMA (68.5
Zn ratio from EPMA (68.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 31.5), however, indicates a small substitution of zinc by nickel. Since there is only one Zn site in the structure, a fixed amount (5.5%) of nickel based on EPMA was introduced into the Zn site. Refinement with this configuration insignificantly lowered the RF2 and the residual electron density to 0.0160 and ±1.01 e Å−3, respectively. The detailed results of the single crystal refinement are presented in Table 1. The single crystal structure solution was further confirmed by Rietveld refinement of the alloy Ni42Zn44B14 from which the single crystals were obtained (see Fig. IV of the ESI†).
31.5), however, indicates a small substitution of zinc by nickel. Since there is only one Zn site in the structure, a fixed amount (5.5%) of nickel based on EPMA was introduced into the Zn site. Refinement with this configuration insignificantly lowered the RF2 and the residual electron density to 0.0160 and ±1.01 e Å−3, respectively. The detailed results of the single crystal refinement are presented in Table 1. The single crystal structure solution was further confirmed by Rietveld refinement of the alloy Ni42Zn44B14 from which the single crystals were obtained (see Fig. IV of the ESI†).
Table IV of the ESI† lists all the interatomic distances in τ6-Ni2ZnB, which comply with the sum of atomic radii. The coordination polyhedra obtained from program DIDO9542 are presented in Fig. 9. The atomic environment around Ni1 and Ni2 is in the form of distorted 14- and 15-vertex Frank–Kasper polyhedra, respectively. In these coordination polyhedra, several long Ni–Ni distances (0.27 < dNi–Ni < 0.285 nm) are observed. Despite their rather long interatomic distances, these nickel atoms are included in the coordination polyhedra due to a significant area contribution to the Dirichlet domain. In contrast, the B atom that resides inside the coordination sphere of the Zn atom is excluded from the coordination polyhedron due to the same reason described in the case of τ5, and thus the coordination polyhedron around the Zn atom takes the form of an anti-cuboctahedron, similar to that in τ5. As a consequence of the lower M/B ratio of 3 in τ6, direct B–B contacts (dB–B = 0.1850 nm) in the form of boron pairs are observed,34 with the B–B distance being somewhat longer than the sum of covalent radii. The triangular prism around the boron atoms in τ6 is capped by boron and nickel atoms. In general, all coordination polyhedra in τ6 look almost exactly the same as those in τ4-Ni3ZnB2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7 if the Zn–B contacts are omitted.
7 if the Zn–B contacts are omitted.
 | ||
| Fig. 9 Coordination polyhedra of τ6-Ni2ZnB. Atoms are presented with ADPs from single crystal refinement: Ni (gold), Zn (blue), and B (red). | ||
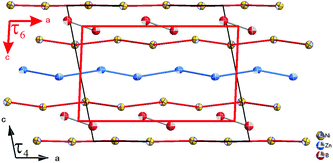
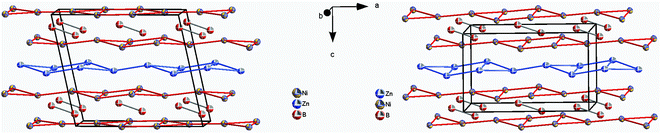
The similarity in the unit cell, and the coordination polyhedra in τ4-Ni3ZnB2 and τ6-Ni2ZnB, suggests that these two compounds are closely related. τ4 can be considered as a √2 superstructure of τ6, particularly c(τ4) = √2c(τ6) (see Fig. 10). τ4-Ni3ZnB2 is the compound with the higher boron content M/B = 2 and shows an arrangement of two stacked layers of AlB2-type units, which form 4-membered zigzag B-chains along the c-axis, similar to those in the Dy3Ni2 structure. The AlB2 double layers in τ4 are separated by a block of edge sharing distorted octahedra formed by nickel and zinc. Alternatively, the structure of τ4 can be considered as an arrangement of boron pairs and slightly puckered metal layers of Ni at z ∼ ¼, Zn at z ∼ ½, and a nearly planar Ni layer at z ∼ 0 along the c-axis (see Fig. 11). The boron pairs, which form the 4 membered zigzag boron chains, are formed by B1 and B2 atoms, and they are located between two nickel layers. A similar arrangement is found in τ6. In this case, however, as the result of its lower boron content (M/B = 3), one AlB2 layer is missing. Consequently, the 4-membered zigzag B-chain is now replaced by a B–B pair. The missing AlB2 layer is also reflected in the shorter c-axis of τ6 compared to that of τ4. The same arrangement of five edge sharing distorted octahedra formed by nickel and zinc, which connect the AlB2 layers, is also found in τ6. An alternative representation of the τ6 structure is presented in Fig. 11. One can see an identical arrangement of metal layers and boron pairs along the c-axis. The planar nickel layer at z ∼ 0, however, is missing, while the slightly puckered nickel and zinc layers are still present in the same sequence. The possibility of filling the octahedral voids in τ4 and τ6 by small atoms (carbon, nitrogen, and oxygen) is excluded based on the same arguments described in the case of τ5 (for details see also Table V of the ESI†).
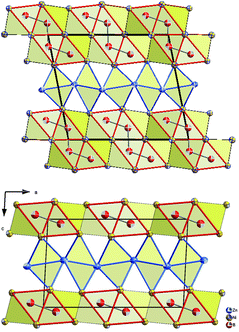 | ||
| Fig. 10 Projection of τ4 (top) and τ6 (bottom) on the a–c plane. Atoms are presented with ADPs from single crystal refinement: Ni (gold), Zn (blue), and B (red). | ||
 | ||
| Fig. 11 Arrangement of metal layers and boron pairs in τ4-Ni3ZnB2 (left) and τ6-Ni2ZnB (right). Atoms are presented with ADPs from single crystal refinement: Ni (gold), Zn (blue), and B (red). | ||
In contrast to those in τ4, the boron pairs in τ6 are formed between boron atoms of the same crystallographic site. This is a consequence of the inversion symmetry operating on the B atom, i.e. the center of the boron pairs lies exactly on the inversion center. Due to its larger lattice parameters together with the different choice of the origin of the unit cell, the center of gravity of the boron pairs in τ4 is further away from the inversion center. From the projection of τ4 along the b-axis in Fig. 12, one can clearly see the unit cell of τ6 within τ4, which can be considered as the result of the removal of the planar nickel layer at z ∼ 0 and shifting the origin of the unit cell to the center of the boron pairs.
Finally, the comparison of the crystal structures of τ4, τ5, and τ6 reveals similar building block arrangements, i.e. boron polyhedra separated by a Zn layer or connected by empty octahedra. The main difference is that the Zn layer in τ5 is corrugated, which can be considered as the result of shifting the rectangular sheet of Zn in the c direction. Furthermore, due to the higher M/B ratio in τ5, B–B contacts are not observed, while compounds with a lower M/B ratio show B–B contacts in the form of a 4-membered zigzag chain (τ4) and pairs (τ6).
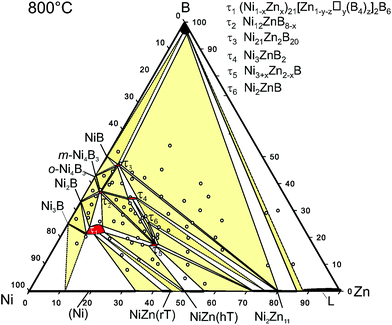 | ||
| Fig. 13 Isothermal section of Ni–Zn–B at 800 °C, revised from the original, presented by Malik et al.8 Sample positions refer to open circles. | ||
3.3. DFT calculations
Discussing charge transfer (see Fig. 14; for details see Tables VI to IX of the ESI†), it is generally observed that B gains an electronic charge, whereas Zn is becoming a positive ion. In the Zn-poor τ3-phase, Ni also donates an electronic charge in an appreciable amount to B, and the more B-neighbours Ni has, the more positive it gets ranging up to 0.38q (in units of the proton charge) for Ni2. There are, however, also the Ni4 and Ni5 positions with a rather small loss of the electronic charge. Zn delivers an appreciable amount of electronic charge resulting in Δqion = 0.38q. As compared to the other three phases, the positive charge of Zn is about 0.12 to 0.14q larger. Concerning the charges of B for the different phases, their variations ranging from −0.41 to −0.34q are substantially smaller than those for Zn. However, when only the Zn rich phases τ4, τ5, and τ6 are considered, the positive charge of Zn is rather constant varying from Δqion = 0.24 to 0.26q. For Ni, there are much larger differences in the charge ranging from even negative values for the τ5 phase to neutral and a positive charge of 0.34q for Ni3 in the τ4 phase.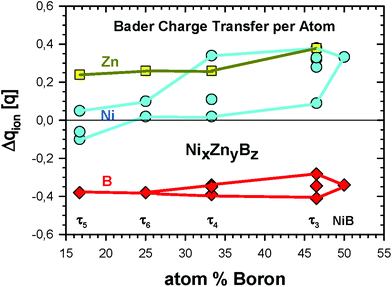 | ||
| Fig. 14 Bader charge transfer Δqion (in units of the proton charge q) for the ternary Ni–Zn–B compounds. Details of transfer quantities per crystallographic site can be found in Tables VI to IX of the ESI.† | ||
The changes of the Bader volume for Zn and B clearly correspond to the ionic charges, namely the negative ionic charge means a larger atomic volume and vice versa. For Ni, the volume changes fluctuate more significantly. For some Ni positions, one even finds an increased volume for a positive ion, as for example for τ4 and τ6.
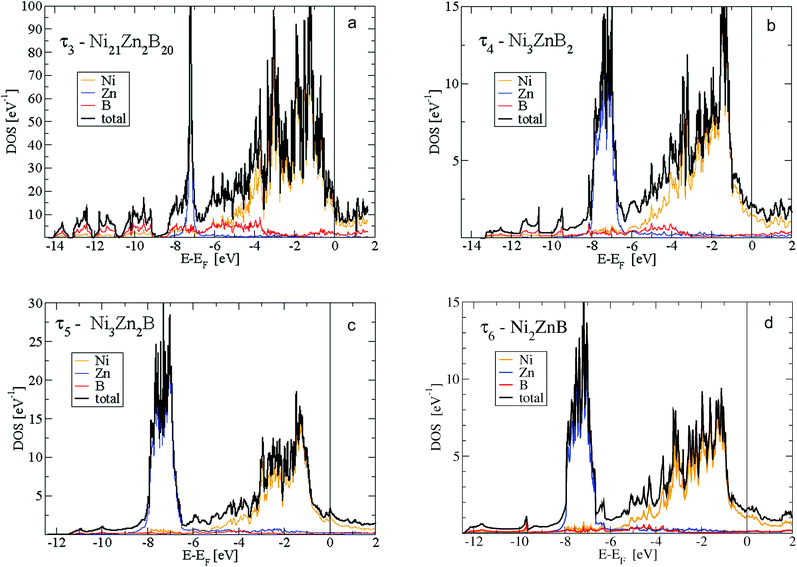
Fig. 15 shows the density of states (DOS) of the 4 phases τ3 to τ6. In addition, for the newly found τ5 and τ6 phases, the s- and p-like DOS for B and Zn are presented in Fig. 16. The main features are very similar. Below −8 eV, the DOS is of predominantly B-s character with a small mixing of Ni d-like states. For the B-rich τ3 and τ4 phases, the DOS starts at about 1 eV lower in energy at −14.5 eV. Peculiar DOS features appear in this energy range which indicate localised interactions of B-s states with neighbouring Ni d-like states. In particular for the τ3 phase 4 well separated peaks with a height of about 10 eV−1 are discernible. The splitting of the DOS is due to the different crystallographic positions of B and Ni atoms.
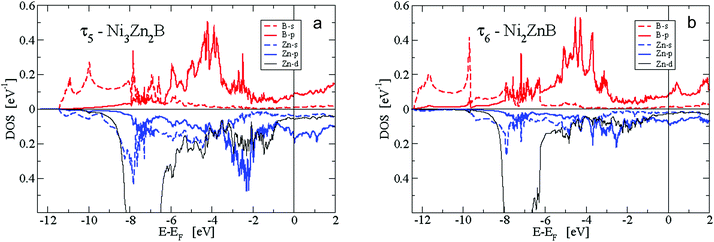
The second predominant DOS feature is a large peak at about −7.5 eV below EF with a width of approximately 1.5 eV for the τ4, τ5 and τ6 phases. This peak, which is very narrow for the Zn-poor τ3-phase, is due to the rather localised d-like states of Zn. It should be noted that the Zn-d states have to be taken into account as valence states for a high-quality DFT calculation in order to derive reliable total energies, relaxed structural parameters and elastic properties. At the lower edge of the Zn peak, Fig. 16 shows B-s states with hybridisation patterns similar to the Zn s- and p-like DOS, which presumably are mediated by Ni states since Zn is not neighbouring B.
Between −6.5 and −5 eV, there are features of a substantially smaller but increasing DOS. In particular, B-p states arise due to hybridization with Ni-d states. Fig. 16 reveals the rising of the B p-like DOS. Above −5 eV, clearly, Ni-d states start to become important and are strongly dominant in the energy region up to a sharp dropdown at −1 eV. In this energy region, B-p states strongly hybridize with Ni-d states. Noticeably in Fig. 16a for the τ5-phase, there occurs a distinct splitting of B-p states with peaks at about −4 and −2.5 eV. The splitting of the B-p states correlates with the splitting of the Ni-d states. The B-p peak at −2.5 eV coincides with a remarkable peak of Zn-p character. The steep decrease of the Ni d-like and total DOS at −1 eV is followed by small values with a still significant Ni-d character. The admixture of B and Zn states is now rather small. Interestingly, for the τ5-phase the Fermi energy is located at a small peak of the DOS which is of predominantly Ni-d character. Because of this peak, the τ5-phase might be prone to the formation of defects (vacancies and/or anti-sites) which could shift the Fermi energy up or down, where the DOS is smaller. In fact, the experimental stoichiometry as discussed above finds small deviations from the ideal stoichiometry, for which, however, the DFT calculations were made. The values of the DOS at the Fermi energy and the corresponding specific heat constant γ as presented in Table 2 clearly indicate metallic behaviour for all phases. The values per atom are rather small and increase with increasing Zn concentration.
| Compound | DOS/f.u. | γ/f.u. | γ/atom |
|---|---|---|---|
| τ3-Ni21Zn2B20 | 12.89 | 30.38 | 0.71 |
| τ4-Ni3ZnB2 | 2.15 | 5.07 | 0.84 |
| τ6-Ni2ZnB | 1.56 | 3.68 | 0.92 |
| τ5-Ni3Zn2B | 3.13 | 7.38 | 1.23 |
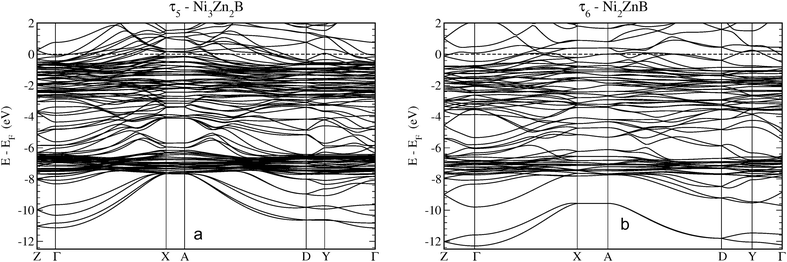
Fig. 17 shows the electronic bands for the τ5 and τ6 phases along high symmetry directions of the monoclinic cell. The features as discussed in the DOS are clearly visible. At the lowest energy region, one finds bands with s-like parabolic dispersions from Γ to X, which are split off in energy by about 1 eV. The Zn d-states are clearly visible at about −7 eV represented by rather flat bands of the localised character. Above the Zn-d peak until about −3 eV, the bands are less densely distributed until Ni-d states become predominant as indicated by rather flat bands. Interactions with mostly B-p states broaden the energy region of the Ni-d states sizeably. Finally, dispersive bands cross the Fermi energy indicating the metallic character of the compounds. More details are presented in a close-up around EF in Fig. IV of the ESI.†
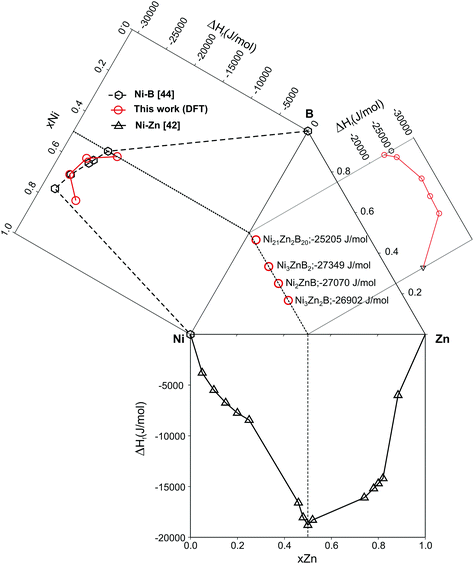
Table 3 summarizes DFT data on the enthalphy of formation at T = 0 K and zero pressure per mol atoms, ΔHf, which were derived for each compound from differences of the total DFT energies per unit cell (according to eqn (1)). Data are plotted in Fig. 18 as a function of the B-content within the isopleth NiZn to NiB of the Ni–Zn–B phase diagram. From the DFT derived energies of formation, it is found that τ6-Ni2ZnB (ΔHf = −27.07 kJ mol−1) would thermodynamically not be stable at T = 0 by 0.06 kJ mol−1 when compared with the neighbouring phases τ5-Ni3Zn2B (ΔHf = −26.90 kJ mol−1) and τ4-Ni3ZnB2 (ΔHf = −27.35 kJ mol−1). It is possible that deviations of experimental samples from ideal stoichiometry might be responsible for the experimentally observed stability because of mixing entropy. Also vibrational entropies might stabilize the τ6-phase. The DFT data document the relative stability of the ternary with respect to the binary compounds.43–45 The present calculation for the Ni-borides (see in our forthcoming paper) reveals slightly lower heat of formations for the end members Ni3B and NiB in relation to the thermodynamically derived values from recent CALPHAD assessments.44,45
| Compound | Boron, at% | ΔHf, kJ mol−1 | B, GPa |
|---|---|---|---|
| τ5-Ni3Zn2B | 16.7 | −26.90 | 184.2 |
| τ6-Ni2ZnB | 25.0 | −27.07 | 179.7 |
| τ4-Ni3ZnB2 | 33.3 | −27.35 | 223.7 |
| τ3-Ni21Zn2B20 | 46.5 | −25.20 | 248.9 |
The bulk moduli (listed in Table 3) increase with increasing boron concentrations (from B = 179.7 for τ6-Ni2ZnB to B = 248.9 GPa for the B-rich τ3-Ni21Zn2B20 phase), in accordance with the increase of the rigid B–B bonds.
Fig. 19a illustrates the (positive) electron density in the τ5-Ni3Zn2B phase in a plane containing Ni, Zn and B atoms orientated perpendicular to the b axis. Strikingly, triangular/tetrahedral patterns corresponding to Ni3–B units appear in the density. The B atom placed above the plane causes broad circular features around the Ni atoms in the plane, which widely overlap in between the Ni atoms. B in the plane is surrounded by a triangular shaped density distribution which is caused by bonding features towards the three Ni atoms below the plane of the slice. A small bridge of density is built from Zn to its neighbouring Ni atoms indicating weak bonding.
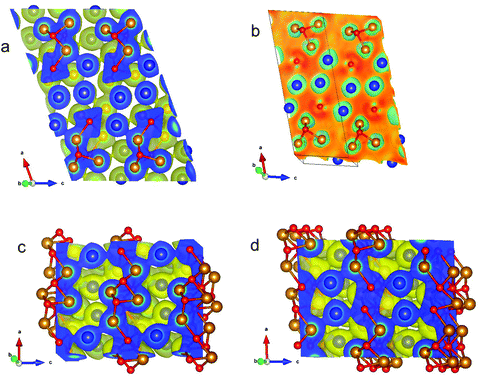 | ||
| Fig. 19 (a) Self-consistent electron density for monoclinic τ5-Ni3Zn2B perpendicular to the b axis in a plane containing Ni and Zn atoms. The electron density is positive. (b) Difference of self-consistent minus superposed free atom electron density for monoclinic τ5-Ni3Zn2B in the same plane as in (a). (c) Self-consistent electron density for orthorhombic τ6-Ni2ZnB perpendicular to the b axis in a plane with Ni and Zn atoms. (d) Self-consistent electron density for orthorhombic τ6-Ni2ZnB perpendicular to the b axis in planes with B atoms. For the self-consistent electron density images, yellow enveloping surface refers to a constant value of the electron density of 0.04 Å−3. Relative colouring for the slice reaches from 0.04 (blue) to 4.60 Å−3 (red). For all images, compass referring to the crystal axes is shown in the left corner. Colouring of atoms: Ni gold, Zn blue, and B red. Graphic produced by VESTA.46 | ||
Fig. 19b shows the difference of self-consistent minus superposed free atom electron densities illustrating the gain and loss in density after bonding occurs (i.e. after solving Schrödinger's equation by means of DFT). Clearly, the density gain between the in-plain B and Ni atoms is visualized. Somewhat smaller is the gain in between the in-plane Ni atoms below B out-of-plane. Green rings around Ni and Zn atoms correspond to a density loss. Fig. V of the ESI† shows the same contours as Fig. 19b but with rotated axes. Here, the empty regions (regions of negative difference charge density), from which charge was transferred, are directly visible as they surround Ni and Zn atoms. The two different types of B, namely in- and out-of-plane, are now distinguishable. In Fig. 19c for the density of the τ6-Ni2ZnB phase, similar features as for τ5-Ni3Zn2B are observed: broad overlapping circles for the Ni atoms situated below the sticking out B atoms. Now Ni–Zn–Ni density bridges appear indicating that Zn prefers Ni neighbours. In Fig. 19d, striking features occur for one atomic plane above the plane as shown in Fig. 19c. Now, the plane contains Ni, Zn and nearest neighbour B atoms. A σ-type bonding pattern between the B atoms with a distance of 0.186 nm is seen which is accompanied by Ni–B bonding features. Again, Ni–Zn bridges appear in the contour plot.
4. Physical properties
In this study, only τ5 could be obtained in the single phase and the dense form, therefore only the physical properties of τ5 will be presented. Attempts to prepare τ6 resulted in multiphase samples containing τ4, τ5, and τ6, possibly due to the uncontrolled evaporation of Zn during hot pressing that shifted the overall composition to the narrow three-phase field τ4-τ5-τ6.4.1. Electrical resistivity
The electrical resistivity of τ5 is shown in Fig. 20. The absolute resistivity value at room temperature (∼20 μΩ cm) is rather low, and the residual resistivity ratio of 3.2 evidences a rather good sample quality. As expected from the DOS (see section 3.3.), the electrical resistivity of τ5 shows a metallic behavior from room temperature to ∼40 K. Below 40 K, a resistivity minimum is observed, followed by a slight increase down to 2 K. The low temperature upturn is well described by a simple logarithmic temperature dependence (see the inset in Fig. 20), indicating the presence of a Kondo type interaction. The non-stoichiometry in τ5 could be responsible for the existence of a small amount of uncompensated Ni spins, which act as magnetic impurities in an otherwise non-magnetic host. The EDX measurement of this sample shows a slightly higher Ni content, x = 0.03 for Ni3+xZn2−xB. Similarly, an upturn is also observed in the specific heat (see the next section). Above 40 K, the electrical resistivity behavior could be well described by the Bloch–Grüneisen model (ρBG), accounting for the electron–phonon scattering. The total electrical resistivity of τ5 can be expressed as a combination of the aforementioned scattering processes and the residual resistivity (ρ0) arising from static defects and impurities: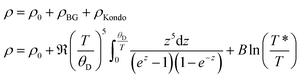 | (2) |
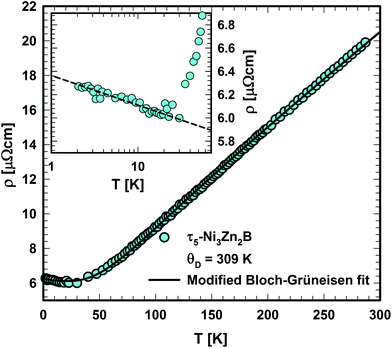 | ||
| Fig. 20 Temperature dependent electrical resistivity of τ5-Ni3Zn2B. The inset shows the low temperature resistivity upturn in the logarithmic temperature scale. | ||
A least squares fit based on eqn (2) results in a Debye temperature of ΘD = 309 K, practically similar to that of 310 K for τ4.9 The Debye temperature is significantly smaller than the value obtained from the specific heat data, which could be related to the assumptions used in the model.
4.2. Specific heat
Fig. 21 shows the specific heat of τ5 from room temperature down to 2 K. An anomaly is observed below 5 K. By excluding the upturn, a Sommerfeld coefficient γ = 10.7 mJ mol−1 K−2 and a β coefficient of 0.1732 mJ mol−1 K−4 could be extracted from a least-squares fit based on the equation in Fig. 21. The latter corresponds to a Debye temperature of 407 K, a value lower than that of the related compound τ4 (ΘD = 510 K), suggesting a lattice softening in this compound due to the absence of B–B contacts. A slightly higher value of the Sommerfeld coefficient in τ5 compared to that in τ4 is consistent with the slightly higher DOS at the Fermi level in τ5. A comparison of the Sommerfeld coefficient extracted from the DFT calculation of the density of states of τ5 (3.13 states per eV per f.u.; γband = 7.38 mJ mol−1 K−2; see Table 2) with the experimental value γexp. = 10.7 mJ mol−1 K−2 gives a hint on the electron–phonon enhancement factor λ = 0.45 (from the relationship γexp. = (1 + λ)γband). A similar enhancement factor of 0.38 is also found in τ4 (γexp. = 7 mJ mol−1 K−2,9γband = 5.07 mJ mol−1 K−2).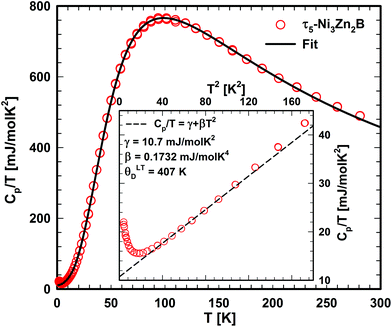 | ||
| Fig. 21 Temperature dependent specific heat of τ5. The solid line represents the fit based on eqn (3). The inset (as Cp/T vs. T2) shows the low temperature upturn. | ||
A more detailed description of the lattice contribution to the specific heat is possible in terms of the Debye and Einstein model, i.e.:
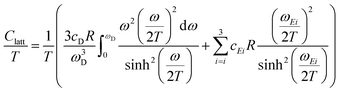 | (3) |
An analysis based on eqn (3) requires the usage of, at least, three Einstein modes to account for the experimental data. Here six atoms in the formula unit are represented by 18 phonon branches, which consist of 3 acoustic branches accounted for by the Debye model and 15 optical branches distributed over three Einstein modes. Least-squares fits to the experimental data, with an addition of the electronic contribution, result in a Debye contribution with a frequency of 218 K and the spectral weight of 3. The Einstein contribution consists of three frequencies, 149, 275 and 601 K with the corresponding spectral weights of 1, 10 and 4, respectively. In order to compare with the Debye temperature obtained from the low temperature T3 coefficient β yielding 407 K, the Debye frequency obtained from the fit with eqn (3) must be multiplied by 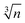 (n is the number of atoms in the formula unit) yielding 396 K, which is in reasonably close agreement.
(n is the number of atoms in the formula unit) yielding 396 K, which is in reasonably close agreement.
Comparing the result with that of τ4,9 it is evident that the phonon frequencies in τ5 are smaller compared to those in τ4 (ωD = 269 K, ωE1 = 191 K, ωE2 = 348 K and ωE3 = 714 K), possibly as the result of the increasing metal content and consequently, the absence of B–B bonding in τ5. Similar to τ4,9 the spectral weight of the high frequency mode corresponds well with the boron stoichiometry. The absence of B–B bonds could also be indicated by softening of the highest frequency Einstein mode compared to that of τ4 where B–B bonds in the form of 4-membered zigzag B chains are observed.
4.3. Thermal expansion
The temperature dependent thermal expansion of τ5 is shown in Fig. 22. At a first glance, the thermal expansion behaves like ordinary metals, showing only a weak temperature dependence for T < 50 K, followed by an almost linear dependency at a higher temperature.47 From the linear behaviour at temperatures between 200 to 300 K, a linear thermal expansion coefficient (CTE) of 15.1 × 10−6 K−1 was obtained, a value that is substantially larger than that of τ4 (10.4 × 10−6 K−1). This relationship is backed by the heat capacity data, where the difference in Debye and Einstein temperatures hint to substantial differences of the lattice stiffness, when τ5 is compared with τ4.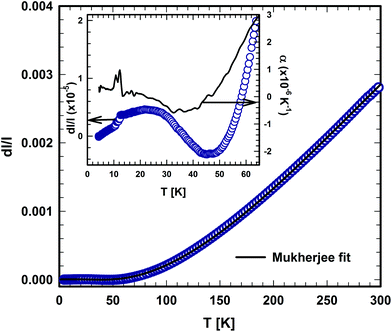 | ||
| Fig. 22 Temperature dependent thermal expansion of τ5-Ni3Zn2B. The solid lines represent the fit based on the model of Mukherjee.52 | ||
A careful inspection of the low temperature part (below 70 K) of the thermal expansion data reveals some anomalies (see the inset in Fig. 22), in which the coefficient of thermal expansion α shows negative values between ∼25 and 45 K. Moreover, a kink in the length change (d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /
/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ), which is associated with a jump in the CTE at around 10 K, is also observed. The origin of those anomalies is still unknown and further detailed investigations are required to reveal the origin of these anomalies. However, in the absence of distinct magnetic contributions, the negative thermal expansion of τ5, from about 20 to 50 K, is presumably associated with transverse vibrational modes (“guitar string vibrations”) which cause negative acoustic branches in the Grüneisen tensor (for further details, see ref. 48 and 49). Non-magnetic materials known so far for their negative expansion contain Si, GaAs, CuCl, Rb-halides, ZrMo3O8 or ZrW3O8 (see for instance ref. 48–51).
), which is associated with a jump in the CTE at around 10 K, is also observed. The origin of those anomalies is still unknown and further detailed investigations are required to reveal the origin of these anomalies. However, in the absence of distinct magnetic contributions, the negative thermal expansion of τ5, from about 20 to 50 K, is presumably associated with transverse vibrational modes (“guitar string vibrations”) which cause negative acoustic branches in the Grüneisen tensor (for further details, see ref. 48 and 49). Non-magnetic materials known so far for their negative expansion contain Si, GaAs, CuCl, Rb-halides, ZrMo3O8 or ZrW3O8 (see for instance ref. 48–51).
An analysis of the temperature dependence of the thermal expansion (d![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) /
/![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) ), based on the semi-classical model developed by Mukherjee,52 allows us to extract the Debye and Einstein temperatures of τ5. The range of the Debye temperatures was constrained in the fitting process based on the value obtained from the specific heat, while the other parameters were allowed to vary freely. Debye and Einstein temperatures of 410 K and 111 K were obtained from the fit, respectively. The Einstein temperatures obtained from the thermal expansion fit are somewhat lower than those obtained from the specific heat data, suggesting the existence of a low lying optical mode. A similar situation was also encountered in τ4, where a low Einstein temperature of 151 K was obtained from the thermal expansion data, which is smaller than those obtained from specific heat data.
), based on the semi-classical model developed by Mukherjee,52 allows us to extract the Debye and Einstein temperatures of τ5. The range of the Debye temperatures was constrained in the fitting process based on the value obtained from the specific heat, while the other parameters were allowed to vary freely. Debye and Einstein temperatures of 410 K and 111 K were obtained from the fit, respectively. The Einstein temperatures obtained from the thermal expansion fit are somewhat lower than those obtained from the specific heat data, suggesting the existence of a low lying optical mode. A similar situation was also encountered in τ4, where a low Einstein temperature of 151 K was obtained from the thermal expansion data, which is smaller than those obtained from specific heat data.
4.4. Hardness
Due to a well-polished surface, the Vickers hardness indentations could easily be placed inside of the grains of the as-cast samples and 2![[small script l]](https://www.rsc.org/images/entities/i_char_e146.gif) could be measured correctly (see Fig. VI of the ESI†). For the grains of τ5-Ni3Zn2B, the static HV0.1 = 432 ± 13, whereas for the grains of τ6-Ni2ZnB, the static hardness is slightly higher with HV0.1 = 470 ± 14. Hardness measurements were also performed on the hot-pressed samples. For hot-pressed τ5-Ni3Zn2B HV0.1 = 468 ± 19 and for the hot-pressed τ6-Ni2ZnB HV0.1 = 475 ± 19. Both values are slightly larger than for individual grains. Dynamic hardness data are usually smaller than the static ones as they are evaluated directly during the impression, whereas in case of the static hardness, the impression can “shrink” after the load is withdrawn. The surface of the hot-pressed samples had very small pores, but big enough that the microindenter MHT4 was not applicable. For the grains of τ5, the dynamic hardness HV0.1 = 288, of τ6 HV = 325.
could be measured correctly (see Fig. VI of the ESI†). For the grains of τ5-Ni3Zn2B, the static HV0.1 = 432 ± 13, whereas for the grains of τ6-Ni2ZnB, the static hardness is slightly higher with HV0.1 = 470 ± 14. Hardness measurements were also performed on the hot-pressed samples. For hot-pressed τ5-Ni3Zn2B HV0.1 = 468 ± 19 and for the hot-pressed τ6-Ni2ZnB HV0.1 = 475 ± 19. Both values are slightly larger than for individual grains. Dynamic hardness data are usually smaller than the static ones as they are evaluated directly during the impression, whereas in case of the static hardness, the impression can “shrink” after the load is withdrawn. The surface of the hot-pressed samples had very small pores, but big enough that the microindenter MHT4 was not applicable. For the grains of τ5, the dynamic hardness HV0.1 = 288, of τ6 HV = 325.
Using a Poisson number ν = 0.29(1), as obtained from the RUS measurement of the closely related compound τ4-Ni3ZnB2,9 elastic moduli can be evaluated. In case of τ5, E = 163, B = 136, and G = 63; for τ6, E = 99, B = 60, and G = 40 (all values given in GPa). Considering the softer nature of both τ5 and τ6, these values compare well with those of τ4-Ni3ZnB2 where HV = 500, E = 199 GPa, B = 158 GPa and G = 77 GPa.9 The data for the bulk moduli show good agreement with the DFT calculation (see Table 3).
From the measured elastic moduli, average sound velocity, and thus the Debye temperatures, were calculated by Anderson's equation.53 For τ5, a Debye temperature of 418 K was obtained, which agrees well with the value obtained from other measurements. For τ6, a smaller Debye temperature of 342 K was derived.
5. Conclusions
The crystal structures of the hitherto two unknown phases in the Ni–Zn–B system, τ5-Ni3Zn2B and τ6-Ni2ZnB, have been elucidated from a combination of X-ray single crystal study, selected area electron diffraction, and electron probe microanalysis. Both compounds crystallize in new structure types and have a similar building block construction: the crystal structures are characterized by the arrangement of Zn layers/empty octahedra, separating the boron centered polyhedra. The B–B interactions agree well with the M/B ratio described in the literature, where isolated boron atoms and B–B pairs are found in τ5-Ni3Zn2B and τ6-Ni2ZnB, respectively. The arrangement of boron polyhedra in τ5-Ni3Zn2B is related to that in Re3B, whereas AlB2 fragments are found in the τ6-Ni2ZnB structure. The crystal structures of the neighboring compounds are closely related: τ4-Ni3ZnB2 can be considered as a √2c superstructure of Ni2ZnB and can be derived by inserting Ni layers and shifting the origin of the unit cell. The boron concentrations of Ni3Zn2B and Ni2ZnB obtained from the single crystal studies allow us to revise the Ni–Zn–B isothermal section at 800 °C, particularly the phase composition of τ5-Ni3Zn2B and τ6-Ni2ZnB. τ5-Ni3Zn2B shows metallic-type electrical resistivity over a wide temperature range with a Kondo type behavior at low temperature, possibly due to some uncompensated Ni-spins distributed in a non-magnetic-metallic host. Specific heat and hardness measurements of τ5-Ni3Zn2B confirm the softer nature of this compound due to the high metal content and the absence of B–B bonding as indicated by the lower hardness, and Debye and Einstein temperatures compared to those of τ4-Ni3ZnB2.DFT calculations resulted in a very good agreement with the experimental structure data. The ground state total energies and forces were minimized for deriving the ab initio structural parameters. Hitherto unknown energies of formation were evaluated revealing a small instability of the τ6-Ni2ZnB phase. Bulk moduli were determined from volume dependent total energies showing a distinct increase for B-rich compounds reaching 248.9 GPa for the τ3-Ni21Zn2B20 compound. Charge transfer was defined in terms of differences of the so-called Bader charge purely based on the densities of the compounds. As an effect of bonding, B accumulates charge whereas Zn delivers charge to the system. Ni reacts in a more complicated way by varying its charge transfer depending on the local arrangement of B atoms. The analysis of the underlying electronic structure reveals Ni–B bonding characteristic for trigonal geometrical arrangements and short B–B distances. Zn prefers Ni as neighbours as expressed by the bonding features of the corresponding density.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
F. Failamani is thankful for the support from the Austrian Federal Ministry of Science and Research (BMWF) under an Ernst Mach ASEA UNINET fellowship. DFT calculations were performed on the Vienna Scientific Cluster VSC3. The authors acknowledge the kind support of Dipl. Ing. Patrick Heinrich (TU Wien) in collecting the specific heat data.References
- R. A. Shakoor, R. Kahraman, U. S. Waware, Y. Wang and W. Gao, Int. J. Electrochem. Sci., 2014, 9, 5520–5536 Search PubMed.
- T. Sakai, Y. Kamimoto and R. Ichino, Jpn. J. Appl. Phys., 2015, 55, 01AA24 CrossRef.
- H. H. Stadelmaier, J.-D. Schöbel and L. T. Jordan, Metall, 1962, 16, 752–754 CAS.
- H. H. Stadelmaier and T. S. Yun, Z. Metallkd., 1962, 53, 754–756 CAS.
- H. H. Stadelmaier, R. A. Draughn and G. Hofer, Z. Metallkd., 1963, 54, 640–645 CAS.
- D. Kotzott, M. Ade and H. Hillebrecht, J. Solid State Chem., 2010, 183, 2281–2289 CrossRef CAS.
- Z. P. Malik, O. Sologub, A. Grytsiv, G. Giester and P. F. Rogl, Inorg. Chem., 2011, 50, 7669–7675 CrossRef CAS PubMed.
- Z. Malik, A. Grytsiv, P. Rogl, G. Giester and J. Bursik, J. Solid State Chem., 2013, 198, 150–161 CrossRef CAS.
- Z. Malik, A. Grytsiv, H. Michor, G. Rogl, S. Puchegger, H. Müller, M. Kriegisch, E. Bauer, C. Eisenmenger-Sittner and P. Rogl, J. Alloys Compd., 2013, 550, 302–307 CrossRef CAS.
- P. Rogl, in Inorganic Reactions and Methods: Formation of Bonds to Group-I, -II, and -IIIB Elements, ed. J. J. Zuckerman and A. P. Hagen, John Wiley & Sons, Inc., 1991, vol. 13, pp. 85–167 Search PubMed.
- P. Rogl and H. Nowotny, J. Less-Common Met., 1978, 61, 39–45 CrossRef CAS.
- G. Akopov, M. T. Yeung and R. B. Kaner, Adv. Mater., 2017, 29, 1604506 CrossRef PubMed.
- G. A. Slack, C. I. Hejna, M. Garbauskas and J. S. Kasper, J. Solid State Chem., 1988, 76, 64–86 CrossRef CAS.
- S. Andersson and T. Lundström, J. Solid State Chem., 1970, 2, 603–611 CrossRef CAS.
- Z. Malik, O. Sologub, G. Giester and P. Rogl, J. Alloys Compd., 2013, 561, 276–283 CrossRef CAS.
- O. Sologub, L. Salamakha, B. Stöger, Y. Michiue and T. Mori, Acta Mater., 2017, 122, 378–385 CrossRef CAS.
- T. Mori, in Handbook on the Physics and Chemistry of Rare Earths, ed. K. A. Gschneidner, J.-C. Bünzli and V. Pecharsky, North-Holland, 2008, vol. 38, pp. 105–173 Search PubMed.
- O. Sologub, L. P. Salamakha, H. Michor, E. Bauer, B. Stöger and P. F. Rogl, J. Alloys Compd., 2016, 675, 99–103 CrossRef CAS.
- APEX2 Software Suite, Bruker AXS Inc., Madison, Wisconsin, USA, 2005 Search PubMed.
- A. Altomare, G. Cascarano, C. Giacovazzo, A. Guagliardi, M. C. Burla, G. Polidori and M. Camalli, J. Appl. Crystallogr., 1994, 27, 435–435 Search PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Crystallogr., 2008, 64, 112–122 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- L. M. Gelato and E. Parthé, J. Appl. Crystallogr., 1987, 20, 139–143 CrossRef.
- M. Rotter, H. Müller, E. Gratz, M. Doerr and M. Loewenhaupt, Rev. Sci. Instrum., 1998, 69, 2742–2746 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter, 1996, 54, 11169–11186 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter, 1999, 59, 1758–1775 CrossRef CAS.
- P. Blöchl, Phys. Rev. B: Condens. Matter, 1994, 50, 17953–17979 CrossRef.
- J. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. Methfessel and A. T. Paxton, Phys. Rev. B: Condens. Matter, 1989, 40, 3616–3621 CrossRef CAS.
- R. F. W. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, USA, 1990 Search PubMed.
- R. F. W. Bader, in Encyclopedia of Computational Chemistry, John Wiley & Sons, Ltd, 2002 Search PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- P. F. Rogl, R. Podloucky, H. Noël and G. Giester, Acta Mater., 2018, 144, 484–495 CrossRef CAS.
- Pauling File Binary Edition, Version 1.0, Release 2002/1, ASM International, Materials Park, OH, USA, 2002 Search PubMed.
- P. Stadelmann, JEMS: Java Electron Microscopy Software, Switzerland, 2017 Search PubMed.
- P. A. Stadelmann, Ultramicroscopy, 1987, 21, 131–145 CrossRef CAS.
- E. Teatum, K. Gschneidner and J. Waber, LA-2345, US Department of Commerce, Washington, DC, 1960 Search PubMed.
- A. L. Spek, J. Appl. Crystallogr., 2003, 36, 7–13 CrossRef CAS.
- P. Villars and K. Cenzual, Pearson's Crystal Data–Crystal Structure Database for Inorganic Compounds, release 2014/15, ASM International, Materials Park, OH, USA, 2014 Search PubMed.
- F. Failamani, P. Broz, D. Macciò, S. Puchegger, H. Müller, L. Salamakha, H. Michor, A. Grytsiv, A. Saccone, E. Bauer, G. Giester and P. Rogl, Intermetallics, 2015, 65, 94–110 CrossRef CAS.
- E. Koch and W. Fischer, Z. Kristallogr. - Cryst. Mater., 1996, 211, 251–253 CAS.
- N. Ahmad and J. N. Pratt, Thermochim. Acta, 1981, 45, 139–151 CrossRef CAS.
- W.-H. Sun, Y. Du, Y. Kong, H.-H. Xu, W. Xiong and S.-H. Liu, Int. J. Mater. Res., 2009, 100, 59–67 CrossRef CAS.
- G. Cacciamani, P. Riani and F. Valenza, Calphad, 2011, 35, 601–619 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. H. K. Barron and G. K. White, Heat Capacity and Thermal Expansion at Low Temperatures, Springer US, USA, 1st edn, 1999 Search PubMed.
- H. Ibach, Phys. Status Solidi B, 1969, 31, 625–634 CrossRef CAS.
- R. Moser, Ph.D. Thesis, University of Vienna, 2016.
- K. Wang and R. R. Reeber, Appl. Phys. Lett., 2000, 76(16), 2203–2204 CrossRef CAS.
- J. S. O. Evans, J. Chem. Soc., Dalton Trans., 1999, 3317–3326 RSC.
- G. D. Mukherjee, C. Bansal and A. Chatterjee, Phys. Rev. Lett., 1996, 76, 1876–1879 CrossRef CAS PubMed.
- O. L. Anderson, J. Phys. Chem. Solids, 1963, 24, 909–917 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c7dt04769j |
| ‡ Current address: National Institute for Materials Science, International Center for Material Nanoarchitectonics (MANA), Namiki 1-1, Tsukuba, 305-0044, Japan. |
| This journal is © The Royal Society of Chemistry 2018 |