Rise of A-site columnar-ordered A₂A′A′′B₄O₁₂ quadruple perovskites with intrinsic triple order

Abstract

A-site-ordered AA′₃B₄O₁₂ quadruple perovskites (with twelve-fold coordinated A and square-planar coordinated A′ sites) were discovered in 1967. Since then, there have been considerable research efforts to synthesize and characterize new members of such perovskites. These efforts have led to the discoveries of many interesting physical and chemical properties, such as inter-site charge transfer and disproportionation, giant dielectric constant, multiferroic properties, reentrant structural transitions and high catalytic activity. The first member of A-site columnar-ordered A₂A′A′′B₄O₁₂ quadruple perovskites (with ten-fold coordinated A, square-planar coordinated A′ and tetrahedrally coordinated A′′ sites), CaFeTi₂O₆, was discovered in 1995, and for 19 years it was the only representative of this family. In the last few years, A₂A′A′′B₄O₁₂ perovskites have experienced rapid growth. Herein, we present a brief overview of the recent developments in this field and highlight an under-investigated status and great potential of A₂A′A′′B₄O₁₂, which can be prepared mainly at high pressure and high temperature. The presence of the A′′ site gives an additional degree of freedom in designing such perovskites. The A₂A′A′′B₄O₁₂ perovskites are discussed in comparison with well-known AA′₃B₄O₁₂ perovskites.

---

Alexei A. Belik

Alexei Belik graduated from the Department of Materials Science of Moscow State University (MSU), Russia, in 1997 and received his PhD in inorganic chemistry at MSU in 1999. He did his first postdoc (2000–2002) at the National Institute for Materials Science (NIMS), Japan, under the supervision of Prof. Fujio Izumi and his second postdoc (2002–2004) at the Institute for Chemical Research, Kyoto University, under the supervision of Profs. Mikio Takano and Masaki Azuma. In 2004, he joined the NIMS again as an independent scientist under the ICYS program. In 2006, he took a permanent position at the NIMS. He was an MANA independent scientist for 9 years.

---

Introduction

ABO₃ compounds crystallize in a number of structure types [e.g., perovskites, LiNbO₃, corundum, ilmenite, hexagonal BaMnO₃-type structures (2H, 4H, 6H, 15R and so on), hexagonal LuMnO₃-type, pyroxenes, rare earth sesquioxide structures (A, B and C (bixbyite)), AlFeO₃, KSbO₃, PbReO₃, CaIrO₃ and others] depending on the relative size of the A and B cations and on the nature of cations.¹ The perovskite-type structure is one of the most important and adaptive structures in inorganic chemistry, and it has the largest number of representatives.^2–4 It is built from a framework of corner-shared BO₆ octahedra that form cavities, which are filled with A cations. The ideal perovskite structure is cubic (space group Pm3̄m) with a_p ≈ 3.8 Å. However, the cubic structure is rarely realized at room temperature because of the mismatch among the sizes of A, B and O. The mismatch, which is usually described by the Goldschmidt tolerance factor,⁵ leads to different distortions. Distortions can be considered as tilts of rigid BO₆ octahedra in a first approximation. And tilts, in turn, are described by using the Glazer tilt system and B–O–B bond angles.⁶ There are basically 15 tilt systems in ABO₃ perovskites.⁴ In simple ABO₃ perovskites, the B–O–B tilt angles are within the range of 140–180°.

A special class of the perovskite family is formed for the a⁺a⁺a⁺ tilt system with very large B–O–B tilt angles of about 140–145° (space group of the parent structure is Im3̄).^7,8 It is the so-called A-site-ordered quadruple perovskites, AA′₃B₄O₁₂, which have a twelve-fold coordinated A site and a square-planar coordinated A′ site. The A′ site is typically occupied by Jahn–Teller cations [such as, Cu²⁺ and Mn³⁺] or other cations which allow a square-planar coordination: Cu³⁺,⁸ Fe²⁺,^9,10 Co²⁺,¹¹ Pd²⁺,¹² Pb⁴⁺ (ref. 13) and Mn²⁺ (ref. 14), and most of the AA′₃B₄O₁₂ compounds need high pressure (HP) and high temperature (HT) for their preparation. The AA′₃B₄O₁₂ quadruple perovskite subfamily of the perovskite family has also numerous representatives with A = Na⁺, Mn²⁺, Cd²⁺, Ca²⁺, Sr²⁺, Pb²⁺, R³⁺ (R = rare earths), Ce⁴⁺, Bi³⁺ and Th⁴⁺, and B = Mn³⁺, Mn⁴⁺, Fe³⁺, Cr³⁺, Al³⁺, Ti⁴⁺, V⁴⁺, Ge⁴⁺, Sn⁴⁺, Ru⁴⁺, Ir⁴⁺, Ta⁵⁺, Nb⁵⁺, Sb⁵⁺ and others.⁷ This subfamily was discovered in 1967 in CaCu₃Ti₄O₁₂ during Cu²⁺ doping of CaTiO₃.¹⁵ Since then, there have been considerable research efforts to synthesize and characterize new members of such quadruple perovskites. These efforts have led to the discoveries of many interesting physical and chemical properties, for example, giant dielectric constant,⁷ inter-site charge transfer and disproportionation,⁸ multiferroic properties, reentrant structural transitions,¹⁶ and high catalytic activity.¹⁷

Another special class of the perovskite family can be formed with the a⁺a⁺c⁻ tilt system and with very large B–O–B tilt angles of about 140–150° (space group of the parent structure is P4₂/nmc).^3,4 In such a case, compounds with the A₂A′A′′B₄O₁₂ stoichiometry are formed. Therefore, they can also be called A-site-ordered quadruple perovskites, where A′ is the site with a square-planar coordination and A′′ is the site with a tetrahedral coordination. To distinguish them from AA′₃B₄O₁₂, we suggest calling them A-site columnar-ordered¹⁸ quadruple perovskites. The first representative of this subfamily, CaFeTi₂O₆, was discovered just in 1995.^9,19,20 CaFeTi₂O₆ was the only representative of such quadruple perovskites for 19 years, and this distortion of perovskites was considered to be highly exotic and rare.^3,4 Only in 2014 was another representative reported, CaMnTi₂O₆.²¹ In the last few years, A₂A′A′′B₄O₁₂ quadruple perovskites have experienced rapid growth.^18,22–24 The purpose of this frontier article is to highlight their under-investigated status and great potential and to attract attention of the perovskite and high-pressure communities. The A₂A′A′′B₄O₁₂ quadruple perovskites are compared with the AA′₃B₄O₁₂ ones.

Crystal structure descriptions

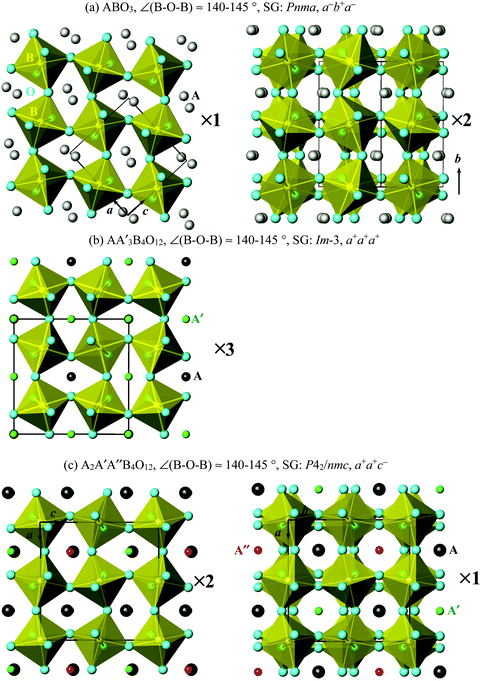
Simple ABO₃ perovskites can have, and AA′₃B₄O₁₂ and A₂A′A′′B₄O₁₂ quadruple perovskites have very strong tilts of the BO₆ octahedral sublattice with the B–O–B bond angles reaching 140–145°. In simple ABO₃ perovskites, such strong tilts are realized in compounds with quite small A cations, for example, A = Sc and In.^25,26 The ABO₃ perovskites with such strong tilts usually have GdFeO₃-related distortions²⁶ with the (ideal) space group Pnma (√2a_p × 2a_p × √2a_p) and the tilt system of a⁻b⁺a⁻, which means that BO₆ octahedra are rotated in one direction (in-phase) along the b axis and in opposite directions (out-of-phase) along the a and c axes (in cubic axes of the original Pm3̄m cell) (Fig. 1a). The AA′₃B₄O₁₂ quadruple perovskites have a 2a_p × 2a_p × 2a_p cell and the a⁺a⁺a⁺ tilt system, which means that BO₆ octahedra are rotated in one direction along all three crystallographic directions (Fig. 1b). The A₂A′A′′B₄O₁₂ quadruple perovskites have a 2a_p × 2a_p × 2a_p cell and the a⁺a⁺c⁻ tilt system, which means that BO₆ octahedra are rotated in one direction along the a and b axes and in opposite directions along the c axis (Fig. 1c). Therefore, on considering the B sublattice, all three perovskites are very similar to each other and differ from each other by a number of the in-phase (very strong) tilts of the BO₆ octahedra.

Fig. 1 Connections of BO₆ octahedra along different directions in (a) ABO₃ simple perovskites, (b) AA′₃B₄O₁₂ quadruple perovskites and (c) A₂A′A′′B₄O₁₂ quadruple perovskites, emphasizing different tilt systems. A, A′ and A′′ sites are shown by spheres. SG: space group.

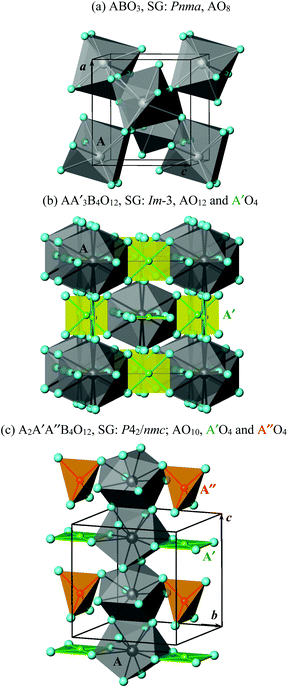
The different numbers of the in-phase BO₆ tilts (determined, of course, primarily by the stoichiometry) create different numbers and types of cavities for A cations (Fig. 2). There is one type of cavity in the case of ABO₃, and the coordination number is reduced from twelve (in the ideal cubic ABO₃) to eight. The AO₈ polyhedra are connected by edges to form a three-dimensional (3D) network (Fig. 2a).

Fig. 2 Fragments of structures with polyhedra for the A, A′ and A′′ sites in (a) ABO₃ simple perovskites, (b) AA′₃B₄O₁₂ quadruple perovskites and (c) A₂A′A′′B₄O₁₂ quadruple perovskites. B atoms are omitted for clarity. SG: space group.

There are two types of cavities in the case of AA′₃B₄O₁₂ with a ratio of 1 : 3. The A site keeps a twelve-fold coordination as in the ideal cubic ABO₃, and the A′ site has four very short A′–O bond lengths, four much longer A′–O bond lengths, and four very long A′–O bond lengths (in total, still twelve). The four very short A′–O bond lengths form a square-planar coordination. The AO₁₂ polyhedra are isolated from each other. The A′O₄ squares are also isolated from each other (Fig. 2b), and they are oriented in such a way that they are orthogonal to each other, but they are 3D-connected through the longer A′–O bond lengths. The AO₁₂ and A′O₄ polyhedra are 3D-connected through edges.

There are three types of cavities in the case of A₂A′A′′B₄O₁₂ with a ratio of 2 : 1 : 1. Therefore, such perovskites have intrinsic triple A-site ordering. The A site has a ten-fold coordination (plus two very long bond lengths), and both A′ and A′′ sites have four very short A′–O and A′′–O bond lengths with similar values of 1.9–2.1 Å, four much longer bond lengths, and four very long bond lengths (in total, still twelve). The four very short A′–O bond lengths form a square-planar coordination. However, the four very short A′′–O bond lengths form a tetrahedral coordination (Fig. 2c). Therefore, the A′ and A′′ sites have fundamentally different coordination environments, and they should be distinguished even though they have similar bond lengths. The AO₁₀ polyhedra are connected through edges and form chains (columns) along the c axis. The A′O₄ squares and A′′O₄ tetrahedra are separated from each other, but they are connected through the longer A′–O bonds to form chains (columns) along the c axis. Because of the existence of the –AO₁₀–AO₁₀– columns and the –A′O₄₊₄–A′′O₄– columns (or columns consisting of isolated A′O₄ and A′′O₄ units), A₂A′A′′B₄O₁₂ perovskites can be called A-site columnar-ordered perovskites. Connections of the AO₁₀ and A′O₄ polyhedra through edges, the AO₁₀ and A′′O₄ polyhedra through corners and the –AO₁₀–AO₁₀– columns through corners create a 3D network. Tetrahedral coordination is usually not realized in oxygen-stoichiometric ABO₃ perovskites; only the removal of oxygen in ordered manners creates tetrahedral sites.⁴ The A₂A′A′′B₄O₁₂ perovskites are oxygen-stoichiometric perovskites with tetrahedral sites.

Known examples and expected compositions of A₂A′A′′B₄O₁₂

The number of reported A₂A′A′′B₄O₁₂ perovskites is so limited at the moment that they all can be simply listed here (for example, in the chronological order of discovery and in the short formulae): CaFeTi₂O₆ (space group P4₂/nmc),^{9,10,19,20,27} CaMnTi₂O₆ (space group P4₂mc),^21,28,29 RMnMnSbO₆ (R = La, Pr, Nd and Sm) (space group P4₂/n),²² RMnGaTiO₆ (R = Sm and Gd) (space group P4₂/nmc),¹⁸ RMnMn₂O₆≡RMn₃O₆ (R = Gd–Tm and Y) (space group Pmmn),²³ CaMnFeReO₆,²⁴ CaMnMnReO₆ ²⁴ and Ca₂CuMnFe₂Re₂O₁₂ (space group P4₂/n).²⁴ We recently prepared R³⁺₂Mn³⁺Mn²⁺[Mn³⁺₃Ti⁴⁺]_BO₁₂ (space group P4₂/nmc), R³⁺₂Mn²⁺Mn²⁺[Mn³⁺₂Ti⁴⁺₂]_BO₁₂ (space group P4₂/nmc), R³⁺₂Mn³⁺Ga³⁺[Mn³⁺₄]_BO₁₂ (space group P4₂/nmc) and R³⁺₂Cu²⁺Mn²⁺[Mn³⁺₂]_B1[Mn⁴⁺₂]_B2O₁₂ (space group Pmmn), where []_B means the presence of one B site and []_B1[]_B2 means a B-site order.³⁰ (We note that it was not possible to precisely determine the degree of Cu²⁺ and Mn²⁺ ordering and Mn³⁺ and Ga³⁺ ordering in the last two compounds with X-ray powder diffraction).

Because of the similarities in the B sublattice (Fig. 1), it is expected that the B site of A₂A′A′′B₄O₁₂ can be occupied by most of the B-type cations for perovskites and their different combinations (a list of examples is given in the second paragraph of Introduction).

The A sites in all three families retain large environments with some variations in the coordination numbers. Therefore, it is expected that the A site of A₂A′A′′B₄O₁₂ can be occupied by many typical A cations for perovskites (a list of examples is given in the second paragraph of Introduction). Despite the twelve-fold coordination of the A site in AA′₃B₄O₁₂, we are not aware of any such perovskites with A = Ba²⁺. This fact shows that strong and almost fixed tilts of the BO₆ octahedra put limits on the possible A–O bond lengths. It is well illustrated by the crystal structures of AMn₇O₁₂ with A = Cd, Ca, Sr and Pb,^31,32 where the A–O bond lengths are almost the same in all these compounds (l(A–O) ∼ 2.6–2.7 Å) independent of the size of A cations. With high enough pressure, small cations can be forced into the A site resulting in rattling (e.g., in CuCu₃V₄O₁₂),³³ while too large cations (e.g., A = Ba) cannot. In A₂A′A′′B₄O₁₂, the A-site coordination number and A–O bond lengths (l(A–O) ∼ 2.3–2.5 Å (×6) and l(A–O) ∼ 2.7 Å (×4)) are further reduced in comparison with AA′₃B₄O₁₂. This fact can put additional limits on the size of A-type cations that can be forced into the A site. All rare-earth elements (except Ce and Pm) and Ca²⁺ were found so far at the A site of A₂A′A′′B₄O₁₂. The size of Na⁺ is close to those of Ca²⁺ and La³⁺;³⁴ therefore, we can also expect such compounds with A = Na⁺. We also emphasize that depending on compositions at the A′, A′′ and B sites, ranges of stability of A₂A′A′′B₄O₁₂ (A = R = rare-earths) vary from R = La–Sm²² for RMnMnSbO₆ to R = Gd–Tm and Y²³ for RMnMn₂O₆ (in all cases, we always mean the synthesis conditions used; stability ranges can change if the synthesis pressure is increased or other conditions are altered). It means that a number of different rare-earth elements should always be checked when preparing such compounds with different B-site contents. A similar tendency was also observed in AA′₃B₄O₁₂: for example, RMn₃(AlTi₃)O₁₂ is formed for R = La–Sm, but not for R = Gd–Lu;¹⁴ RMn₇O₁₂ is formed for R = La–Er and Y, but not for R = Tm–Lu.²³ On the other hand, RCu₃Mn₄O₁₂ can be prepared for all R at a relatively low pressure of 2 GPa.³⁵

The A′O₄ sites of AA′₃B₄O₁₂ and A₂A′A′′B₄O₁₂ are identical. Therefore, it is expected that they can be occupied by the same cations. They are listed and highlighted by bold letters in Table 1, which also gives some other cations with a possible square-planar coordination. We note that there are reports about the presence of Li⁺ (e.g., in (Li_1.333Cu_1.333)Ta₄O₁₂)³⁶ and very small amounts of Fe³⁺ and Ti⁴⁺ at the A′ site of AA′₃B₄O₁₂.^37,38 Mn³⁺, Cu²⁺, Fe²⁺ and Mn²⁺ were found so far in the A′ site of A₂A′A′′B₄O₁₂ quadruple perovskites.

Table 1 A list of some cations (in the order of increasing radius) that can have a square-planar oxygen coordination environment³⁹ and their ionic radii

Cation	Radius (Å)	Cation	Radius (Å)
Radii are taken from ref. 34 (for the square-planar (SQ) coordination if available) except for Mn^3+ and Cu^3+ (rSQ(Mn^3+/Cu^3+) = l(Mn/Cu–O) − r(O^2−), where l(Mn–O) = 1.91 Å and l(Cu–O) = 1.88 Å are the average Mn–O and Cu–O bond distances in AMn^3+3B4O12 and ACu^3+3B4O12 quadruple perovskites (taking the four shortest Mn/Cu–O bonds) and r(O^2−) = 1.4 Å). Cations marked by bold letters (Cu^3+, Mn^3+, Cu^2+, Co^2+, Fe^2+, Pd^2+, Pb^4+ and Mn^2+) were found in the A′ site of AA′3B4O12 quadruple perovskites; note that Li^+ (together with Cu^2+)^36 and very small amounts of Ti^4+ and Fe^3+ were also reported.^37,38 Mn^3+, Cu^2+, Fe^2+ and Mn^2+ were found so far in the A′ site of A2A′A′′B4O12 quadruple perovskites. LS: low-spin.
Cu ^3+	≈0.48	Fe ^2+	0.64
Ni^2+(LS)	0.49	Pd ^2+	0.64
Mn ^3+	≈0.51	Pb ^4+	0.65
Cu ^2+	0.57	Mn ^2+	0.66
Co ^2+	0.58	Ag^3+	0.67
Pt^2+	0.60	Au^3+	0.68
		Cr^2+	Not available

---

The A′′O₄ tetrahedral site is unique in A₂A′A′′B₄O₁₂. Table 2 gives a list of some cations that can have a tetrahedral coordination environment and their ionic radii.³⁴ Cu²⁺, Fe²⁺ and Mn²⁺ were found so far in the A′′ site of A₂A′A′′B₄O₁₂ and they probably accidentally overlap with cations found at the A′ site (Fig. 3). The charge and size of Co²⁺, Mg²⁺ and Zn²⁺, for example, are close to those of Cu²⁺, Fe²⁺ and Mn²⁺, but they should preferably occupy the tetrahedral A′′ site instead of the square-planar A′ site.³⁹ On the other hand, however, all cations shown in Table 2 can have an octahedral coordination, and some of them (e.g., Ni²⁺, Sn⁴⁺ and Ti⁴⁺) show a very strong preference for such an environment.³⁹ Therefore, strong competitions with the octahedral B sites or the formation of other phases where such cations have an octahedral coordination are possible. One strategy to force them into the A′′ site is to use cations at the B sites with an even stronger preference for octahedral environments (similar to NiCr₂O₄ and CuCr₂O₄ spinels). We can expect that with high enough pressure during the synthesis some elements from Table 2 (in addition to Cu²⁺, Fe²⁺ and Mn²⁺) can be stabilized at the A′′ site. For example, 5 GPa was enough to stabilize Fe²⁺ in the square-planar A′ site of CaFe₃Ti₄O₁₂, while more than 12 GPa was required to prepare CaFeTi₂O₆ with Fe²⁺ in both the square-planar A′ and tetrahedral A′′ sites.⁹

Fig. 3 A schematic figure with some cations that can have a tetrahedral coordination and a square-planar coordination in oxides and their overlap.³⁹ Bold letters show cations found at the A′ site of AA′₃B₄O₁₂. Cu²⁺, Fe²⁺ and Mn²⁺ (underlined) were found so far in the A′′ site of A₂A′A′′B₄O₁₂ quadruple perovskites.

Table 2 A list of some cations (in the order of increasing radius) that can have a tetrahedral oxygen coordination environment³⁹ and their ionic radii

Cation	Radius (Å)	Cation	Radius (Å)
Radii are taken from ref. 34. Cations marked by bold letters (Cu^2+, Fe^2+ and Mn^2+) were found so far in the A′′ site of A2A′A′′B4O12 quadruple perovskites. HS: high-spin.
Ge^4+	0.39	Cu ^2+	0.57
Al^3+	0.39	Co^2+(HS)	0.58
Ti^4+	0.42	Li^+	0.59
Ga^3+	0.47	Zn^2+	0.60
Fe^3+	0.49	Fe ^2+ (HS)	0.63
Ni^2+	0.55	Pb^4+	0.65
Sn^4+	0.55	Mn ^2+ (HS)	0.66
Mg^2+	0.57	Cd^2+	0.78
		Co^3+	Not available

---

An attempt to prove the above concept (about the location of different elements at the A′ and A′′ sites) was made as shown in ref. 24 by the synthesis of Ca₂CuMnFe₂Re₂O₁₂ aiming at Cu²⁺ at the A′ site and Mn²⁺ at the A′′ site. We synthesized R₂CuMnMn₄O₁₂. We also tried to insert Ga³⁺ and prepared R₂MnGaMn₄O₁₂ (space group P4₂/nmc).³⁰ We emphasize that because Mn³⁺ can disproportionate during the synthesis as found in RMnMn₂O₆ = [R³⁺₂]_A[Mn³⁺]_A′[Mn²⁺]_A′′[Mn³⁺₂]_B1[Mn³⁺Mn⁴⁺]_B2O₁₂,²³ any cation/charge distributions are possible between [R³⁺₂]_A[Mn³⁺]_A′[Ga³⁺]_A′′[Mn³⁺₄]_BO₁₂ with Ga³⁺ at the A′′ site and [R³⁺₂]_A[Mn³⁺]_A′[Mn²⁺]_A′′[Mn³⁺₂Mn⁴⁺Ga³⁺]_BO₁₂ with Ga³⁺ at the B site (assuming³⁹ that the A′′ site cannot be occupied by Mn³⁺ and Mn⁴⁺). Our structural analysis with X-ray powder diffraction data gave evidence that the cation distribution is more close to the former case (A′′–O bond lengths of 1.89 Å were more consistent with Ga–O bond lengths). However, a precise model can only be determined with neutron diffraction, and this method is an essential tool to study cation distributions in A₂A′A′′B₄O₁₂.

The presence of the A′′ site gives an additional degree of freedom in A₂A′A′′B₄O₁₂, and the number of elements that can have a tetrahedral environment is larger than that with a square-planar environment (Fig. 3). Therefore, it is expected that A₂A′A′′B₄O₁₂ perovskites should be numerous and versatile.

Known distortions

The parent structure of AA′₃B₄O₁₂ has the space group Im3̄ (no. 204). All distortions from the direct group–subgroup relations are experimentally realized (except for the same Im3̄ symmetry with 6a_p × 6a_p × 6a_p) (Fig. 4). These distortions are exemplified in CaCu₃Ti₄O₁₂ (the parent structure),^15,40 CaCu₃Ga₂Sb₂O₁₂,⁴¹ Ce_0.5Cu₃Ti₄O₁₂,⁴² (Li_1.333Cu_1.333)Nb₄O₁₂,³⁶ CaCu₃Fe₄O₁₂,^8,38 A²⁺Mn₇O₁₂ (A = Cd, Ca, Sr and Pb)^31,32 and BiCu_0.2Mn_6.8O₁₂.¹⁶ Most of these distortions are temperature-driven, that is, they are observed on cooling for a particular composition, and there exists a high-temperature parent modification. However, there are a few composition-driven distortions, that is, they are determined by a particular composition and take place during the synthesis.^41,42 The I23 distortion in (Li_1.333Cu_1.333)Nb₄O₁₂ could be temperature-driven (caused by Nb displacements), but no evidence (no phase transitions to the parent structure) was reported;³⁶ this is why we call it composition-driven. There are a number of temperature-driven distortions that cannot be described by the direct group–subgroup paths, for example, in LaMn₇O₁₂ (Im3̄ ⇒ (Immm) ⇒ I2/m),⁴³ NaMn₇O₁₂ (Im3̄ ⇒ (Immm) ⇒ (I2/m) ⇒ C2/m)^44,45 and BiMn₇O₁₂ (Im3̄ ⇒ (Immm) ⇒ I2/m ⇒ Im ⇒ I1),⁴⁶ and there is one such composition-driven distortion in Cu_2+xTa₄O₁₂ (Im3̄ ⇒ (Pm3̄) ⇒ Pmmm),⁴⁷ where space groups in parentheses give group–subgroup links. Despite a large number of AA′₃B₄O₁₂-type compounds, proper polar distortions are realized only in one case of BiMn₇O₁₂ due to the effects of the lone electron pair of Bi³⁺.⁴⁶ But the ferroelectricity of BiMn₇O₁₂ has not been demonstrated yet.

Fig. 4 A schematic diagram of all direct group–subgroup distortions and other known distortions of the parent structure of AA′₃B₄O₁₂ quadruple perovskites (space group Im3̄). Direct group–subgroup distortions are shown by solid arrows; other distortions are shown by dashed arrows. Examples of known distortions are given. Types of A- and B-site orders or number of distinct sites are highlighted. All distortions keep the 2a_p × 2a_p × 2a_p cell except R3̄, P3̄, R3̄(00γ)0 and C2/m. T: a temperature-driven distortion, C: a composition-driven distortion, NC: non-centrosymmetric, NP: non-polar.

The parent structure of A₂A′A′′B₄O₁₂ has the space group P4₂/nmc (no. 137). There are seven distortions from the direct group–subgroup relations (except for the same P4₂/nmc symmetry with 2a_p × 2a_p × 6a_p and 6a_p × 6a_p × 2a_p) (Fig. 5). Three of them have already been found experimentally. Surprisingly, a temperature-driven proper polar distortion takes place in CaMnTi₂O₆ without any effects of lone electron pairs.²¹ This is a quite promising fact in comparison with the AA′₃B₄O₁₂ family. Rock-salt B-site (space group P4₂/n)^22,24 and layered B-site (space group Pmmn)²³ orders have already been realized in A₂A′A′′B₄O₁₂. The reported P4₂/n distortion is composition-driven. The Pmmn distortion in RMnMn₂O₆ could be temperature-driven, but no evidence (no phase transitions to the parent structure) was found so far; this is why we call it composition-driven. It is interesting that the Pmmn model has potential for an additional 1 : 1 rock-salt A-site order (that is, it has two independent A sites: A1 and A2), which might be realized, for example, in a hypothetical compound [Ca²⁺]_A1[Dy³⁺]_A2[Mn³⁺]_A′[Mn²⁺]_A′′[Mn³⁺₂]_B1[Mn⁴⁺₂]_B2O₁₂ (it is just given to illustrate compositional design principles). The polar P4₂mc distortion has potential for an additional 1 : 1 columnar A-site order: [Na⁺]_A1[Nd³⁺]_A2[Mn²⁺]_A′[Mn²⁺]_A′′[Ti⁴⁺₄]_BO₁₂ (a hypothetical compound to illustrate compositional design principles). A1–O and A2–O distances in the Pmmn (e.g., RMnMn₂O₆) and P4₂mc (e.g., CaMnTi₂O₆) models are different; therefore, there might be driving forces for the ordering of cations with different oxidation states and sizes. The rock-salt A-site ordering is rare in ABO₃;^3,4 however, the ordering would not be direct in the Pmmn model because the A sublattice is ‘diluted’ by A′ and A′′.

Fig. 5 A schematic diagram of all direct group–subgroup distortions of the parent structure of A₂A′A′′B₄O₁₂ quadruple perovskites (space group P4₂/nmc). Examples of known distortions are given. Types of A- and B-site orders or number of distinct sites are highlighted. All distortions keep the 2a_p × 2a_p × 2a_p cell except Ccca. T: a temperature-driven distortion, C: a composition-driven distortion, NC: non-centrosymmetric, NP: non-polar.

Physical and chemical properties of A₂A′A′′B₄O₁₂

As already mentioned, CaMnTi₂O₆ crystallizes in a polar space group. This compound shows a structural phase transition from P4₂mc to the parent P4₂/nmc structure at 630 K. The phase transition is accompanied by sharp dielectric constant anomalies and the loss of second-harmonic generation signals. Moreover, a room-temperature ferroelectric P–E hysteresis loop was demonstrated.²¹ These results proved that CaMnTi₂O₆ is ferroelectric at a ferroelectric Curie temperature of 630 K. The shifts of Mn²⁺ cations at the A′ site from the square-planar plane and Ti⁴⁺ cations from the center of the TiO₆ octahedra are responsible for the polar distortion.^21,29 Polarization was calculated to be about 0.3 C m⁻², and a highly tunable semiconducting energy band gap was predicted in CaMnTi₂O₆.²⁹ The P4₂mc-to-P4₂/nmc ferroelectric transition was also found at room temperature at about 7 GPa.²⁸

Without the assistance from the B sublattice, the interaction among magnetic cations at the A′ and A′′ sites is usually very weak (at least, among Mn²⁺): CaMnTi₂O₆ has the Néel temperature (T_A,N) of about 10 K,²¹ while SmMnGaTiO₆ was reported to order at T_A,N = 3 K, and no ordering was found in GdMnGaTiO₆.¹⁸ In the case of SmMnGaTiO₆ and GdMnGaTiO₆, even small disordering of Ga³⁺ and Mn²⁺ between the A′′ and B sites could suppress a long-range magnetic ordering. On the other hand, magnetic interactions through Ti⁴⁺ could be enhanced in CaMnTi₂O₆ resulting in higher T_N similar to a higher magnetic transition temperature in CaCu₃Ti₄O₁₂ in comparison with CaCu₃Ge₄O₁₂ and CaCu₃Sn₄O₁₂.³ No cooperative long-range magnetic order of the parent compound, CaFeTi₂O₆, was found down to 4.2 K.²⁷

The presence of magnetic cations at the B sites significantly enriched magnetic behaviours. First, the ordering temperature of Mn²⁺ at the A′ and A′′ sites can reach T_A,N = 70 K in CaMnFeReO₆ ²⁴ and T_A,C = 100 K in CaMnMnReO₆.²⁴ Second, the magnetic ordering of Mn²⁺ at the A′ and A′′ sites can be either antiferromagnetic (T_A,N in CaMnFeReO₆)²⁴ or ferromagnetic (T_A,C in CaMnMnReO₆ ²⁴ and T_C = 76 K in NdMnMnSbO₆).²² Magnetic cations at the B sublattice can order first as in CaMnMnReO₆ at T_B,C = 120 K (a ferrimagnetic structure),²⁴ can order first with much higher temperatures as in CaMnFeReO₆ at T_B,C = 500 K and in Ca₂CuMnFe₂Re₂O₁₂ at T_B,C = 560 K (a ferrimagnetic structure of Fe³⁺ and Re⁵⁺)²⁴ or can order at the same temperature with the A′ and A′′ sites as in NdMnMnSbO₆.²² There is a spin reorientation transition in NdMnMnSbO₆ at 42 K driven by order of the Nd moments.²² RMnMn₂O₆ compounds also show complex magnetic behaviours at several transition temperatures (two or three magnetic transitions depending of R and stoichiometry);²³ but magnetic structures have not been investigated yet. The maximum magnetic transition temperature is about 80 K in RMnMn₂O₆,²³ but it jumps to about 180 K in R₂CuMnMn₄O₁₂ after Cu²⁺ doping.³⁰ This jump could be caused by the increase of the Mn⁴⁺ concentration at one of the B sites from [Mn³⁺₂]_B1[Mn³⁺Mn⁴⁺]_B2 to [Mn³⁺₂]_B1[Mn⁴⁺₂]_B2. Most of the R₂CuMnMn₄O₁₂ compounds exhibit three magnetic transitions (e.g., at 15, 145 and 180 K for R = Tm).³⁰ Significant magnetoresistance was found in CaMnFeReO₆ and magnetoresistance switching was observed in Ca₂CuMnFe₂Re₂O₁₂.²⁴ Therefore, A₂A′A′′B₄O₁₂ perovskites show complex magnetic properties.

It was found that RMnMn₂O₆ (≡RMn₃O₆) compounds are prone to non-stoichiometry, R_1−δMn₃O_6−1.5δ, with δ = −(0.059–0.071) for R = Gd, δ = 0 for R = Dy, δ = 0.05–0.1 for R = Ho and Y, and δ = 0.12 for R = Er and Tm, and their magnetic properties are highly sensitive to the δ values.²³ The real rare-earth cation deficiency was formed in the case of Er_0.88Mn₃O_5.82 and Tm_0.88Mn₃O_5.82; and the cation distribution can be written as [Tm³⁺_1.76]_A[Mn³⁺]_A′[Mn²⁺]_A′′[Mn³⁺₂]_B1[Mn³⁺Mn⁴⁺]_B2O_12−δ.³⁰ However, the manganese deficiency in GdMn_3−yO_6−1.5y is realized through the doping of a small amount of Gd into the tetrahedral A′′ site: [Gd³⁺₂]_A[Mn³⁺]_A′[Mn²⁺_0.86Gd³⁺_0.14]_A′′[Mn³⁺₂]_B1[Mn^3.43+₂]_B2O₁₂.³⁰ The location of rare-earth elements at tetrahedral sites is very unusual.³⁹ RMnMn₂O₆ compounds were prepared from R₂O₃ and Mn³⁺₂O₃.²³ However, during the synthesis at HP and HT, charge disproportionation takes place because Mn can enter the A′′ site only in the oxidation state of +2.

Neutron diffraction showed that Fe³⁺ cations occupy the A′ site (8%) and the A′′ site (16%) in CaMnFeReO₆.²⁴ This fact shows that Fe³⁺ can in principle be at the tetrahedral A′′ site (Fig. 3). The location of a very small amount of Fe³⁺ cations at the square-planar A′ site was also observed in AA′₃B₄O₁₂ by Mössbauer spectroscopy, but the concentration never reaches a few percent.³⁸ A very small antisite disorder at the B sites was found in CaMnFeReO₆ (3% Fe/Re) and CaMnMnReO₆ (4% Mn/Re); CaMnMnReO₆ also had about 5% of Mn at the Ca site,²⁴ and small amounts of Mn were found at the Nd and Sb sites of NdMnMnSbO₆.²²

Different atoms (e.g., Cu²⁺ and Mn²⁺) that can occupy both tetrahedral and square-planar sites (Fig. 3) order poorly between the A′ and A′′ sites as found by neutron diffraction in the case of Ca₂CuMnFe₂Re₂O₁₂ (60% Cu and 40% Mn at A′ and 23–36% Cu and 64–77% Mn at A′′);²⁴ and the degree of ordering can depend on synthesis conditions.²⁴ On the other hand, different charge orderings take place (at the A′ and A′′ sites and/or at the B site) for the same atom; examples with Mn known so far are: RMnMn₂O₆, R₂MnMn[Mn₃Ti]_BO₁₂ and R₂CuMnMn₄O₁₂. Mn²⁺ and Mn³⁺ at the A′ site can be distinguished by Mn–O bond lengths: l(Mn²⁺–O) ∼ 2.1 Å and l(Mn³⁺–O) ∼ 1.91 Å. Other good candidates for such same-atom charge-ordered scenarios are Cu, Co and Fe (Fig. 3). Another interesting observation is that when the B site is solely occupied by Mn with the average oxidation state higher than +3, there seems to be a tendency for a layered B-site ordering with the appearance of one layer consisting of highly distorted (by the Jahn–Teller effect) Mn³⁺O₆ octahedra.

Very few compositions of AA′₃B₄O₁₂ can be prepared at ambient pressure (for example, (Li_1.333Cu_1.333)Nb₄O₁₂,³⁶ Cu_2+xTa₄O₁₂,⁴⁷ CaMn₇O₁₂ and CaCu₃Ti₄O₁₂).³ The majority of AA′₃B₄O₁₂ requires HP and HT synthesis conditions. All known A₂A′A′′B₄O₁₂ require HP and HT conditions. They were prepared at 12 GPa–1670 K for CaFeTi₂O₆,²⁰ 7 GPa–1470 K for CaMnTi₂O₆,²¹ 10 GPa–1470 K for RMnMnSbO₆,²² 6 GPa–1370 K for RMnGaTiO₆,¹⁸ 6 GPa–1670 K for RMnMn₂O₆,²³ and 10 GPa–1670 K for CaMnFeReO₆ (and others).²⁴

The symmetry of A₂A′A′′B₄O₁₂ under synthesis conditions is crucial for the realization of ordering of different cations between the A′ and A′′ sites. In general, three situations are possible for compounds with the A₂A′A′′B₄O₁₂ stoichiometry. First, the structure can have one crystallographic A site (e.g., with the maximum symmetry of Pm3̄m and a_p × a_p × a_p). In this case, we will probably have GdFeO₃-type structures (simple ABO₃ perovskites) with random distribution of all A cations at one site after quenching and pressure release.²² Second, the structure can have two crystallographic A sites with the 1 : 1 ratio (e.g., with P4/mmm symmetry and √2a_p × √2a_p × a_p considered in ref. 29). In this case, it is difficult to expect noticeable ordering of different cations between the A′ and A′′ sites. Third, the structure can have three A sites with the 2 : 1 : 1 ratio (e.g., with I4/mmm symmetry and 2a_p × 2a_p × 2a_p). In this case, the ordering of different cations between the A′ and A′′ sites can be realized. If the second case takes place (for some compositions), a modification of synthesis conditions could help to increase the ordering. In most cases, samples are quenched after the synthesis, but slow cooling could drive (partial) ordering. We are not aware of any in situ HP and HT studies of either AA′₃B₄O₁₂ or A₂A′A′′B₄O₁₂.

Some arguments in favor of the terminology

The AA′₃B₄O₁₂ and A₂A′A′′B₄O₁₂ quadruple perovskites have many common structural features (Fig. 1 and 2). The parent structures of both families have the doubled lattice parameter along all three crystallographic directions, 2a_p × 2a_p × 2a_p, in comparison with a simple ABO₃ perovskite with a_p ≈ 3.8 Å resulting in eight ABO₃ formula units in their unit cell. The simplest composition with integer numbers can be written as AA′₃B₄O₁₂ (Z = 2), corresponding to four ABO₃ units. This is why such perovskites are called quadruple. This formula reflects the presence of the A and A′ cations with quite different coordination environments with the 1 : 3 ratio. Because 1 and 3 are odd numbers (and A and A′ are quite different cations), this formula is retained in the majority of cases. However, there are very few exceptions when A′ = A (for example, CuCu₃V₄O₁₂ and MnMn₃Mn₄O₁₂).^33,48 For such cases, the formula can be reduced to simple ABO₃ (Z = 8). However, this formal formula reduction does not eliminate the structural features of such perovskites – they still belong to the A-site-ordered quadruple perovskite family. Note that perovskites and perovskite-related compounds with the 1 : 3 B-site ordering can also be referred to as (B-site-ordered) quadruple perovskites.^49,50 By analogy, the simplest composition with integer numbers can be written as A₂A′A′′B₄O₁₂ (Z = 2), which reflects quite different coordination environments for the A, A′ and A′′ sites with the 2 : 1 : 1 ratio. The A₂A′A′′B₄O₁₂ formula corresponds to quadruple perovskites. It turns out that A′′ = A′ in many cases for perovskites reported so far, and the formula can be reduced to the double perovskite one, AA′B₂O₆. However, this formal formula reduction does not reflect the structural features of such perovskites, which still belong to the A-site columnar-ordered quadruple perovskite family, A₂A′A′′B₄O₁₂. Ca₂CuMnFe₂Re₂O₁₂,²⁴ R₂CuMnMn₂Mn₂O₁₂ (or R₂CuMn₅O₁₂)³⁰ and R₂MnGaMn₄O₁₂ (or R₂GaMn₅O₁₂)³⁰ already require the quadruple formula to write them in integer numbers.

Conclusion

A-site columnar-ordered A₂A′A′′B₄O₁₂ quadruple perovskites are in the incipient stage of research. They can be considered as an extended and more complex version of the A-site-ordered AA′₃B₄O₁₂ quadruple perovskites (with twelve-fold coordinated A and square-planar coordinated A′ sites) because A₂A′A′′B₄O₁₂ has ten-fold coordinated A and square-planar coordinated A′ sites plus an additional tetrahedrally coordinated A′′ site. This A′′ site gives an additional degree of freedom in A₂A′A′′B₄O₁₂ because the number of elements that can have a tetrahedral environment is larger than that with a square-planar environment. The A₂A′A′′B₄O₁₂ perovskites are the only oxygen-stoichiometric perovskites with tetrahedral sites. This article highlights great potential of A₂A′A′′B₄O₁₂ and gives some design principles.

Note added in proof

After this paper was accepted, the synthesis of ferroelectric Ca_2−xMn_xTi₂O₆ (x = 0.6) by a spark plasma sintering method was reported.⁵¹

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by JSPS KAKENHI Grant Numbers JP15K14133 and JP16H04501 and JSPS Bilateral Open Partnership Joint Research Projects. We thank Mr L. Zhang (NIMS), Dr Y. Matsushita (NIMS) and Dr K. Yamaura (NIMS) for their help with unpublished experimental data mentioned in this article and Profs. E. V. Antipov (Moscow State University) and I. A. Presniakov (Moscow State University) for discussion.

References

1. D. M. Giaquinta and H.-C. zur Loye, Chem. Mater., 1994, 6, 365–372.
2. R. H. Mitchell, Perovskites: Modern and Ancient, Almaz Press, Thunder Bay, Ontario, Canada, 2002.
3. G. King and P. M. Woodward, J. Mater. Chem., 2010, 20, 5785–5796.
4. A. M. Abakumov, A. A. Tsirlin and E. V. Antipov, Transition-Metal Perovskites, in Comprehensive Inorganic Chemistry II (Second Edition): From Elements to Applications, ed. J. Reedijk and K. R. Poeppelmeier, Elsevier, Amsterdam, 2013, vol. 2, pp. 1–40.
5. V. M. Goldschmidt, Naturwissenschaften, 1926, 14, 477–485.
6. A. M. Glazer, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1975, 31, 756–762.
7. A. N. Vasil'ev and O. S. Volkova, Low Temp. Phys., 2007, 33, 895–914.
8. I. Yamada, J. Ceram. Soc. Jpn., 2014, 122, 846–851.
9. K. Leinenweber, J. Linton, A. Navrotsky, Y. Fei and J. B. Parise, Phys. Chem. Miner., 1995, 22, 251–258.
10. J. Linton, A. Navrotsky and Y. Fei, Phys. Chem. Miner., 1998, 25, 591–596.
11. S. V. Ovsyannikov, Y. G. Zainulin, N. I. Kadyrova, A. P. Tyutyunnik, A. S. Semenova, D. Kasinathan, A. A. Tsirlin, N. Miyajima and A. E. Karkin, Inorg. Chem., 2013, 52, 11703–11710.
12. K. Shiro, I. Yamada, N. Ikeda, K. Ohgushi, M. Mizumaki, R. Takahashi, N. Nishiyama, T. Inoue and T. Irifune, Inorg. Chem., 2013, 52, 1604–1609.
13. Y. Sakai, et al. , J. Am. Chem. Soc., 2017, 139, 4574–4581.
14. G. Shimura, Y. Shirako, K. Niwa and M. Hasegawa, J. Solid State Chem., 2016, 242, 55–62.
15. A. Deschanvres, B. Raveau and F. Tollemer, Bull. Soc. Chim. Fr., 1967, 4077–4078.
16. A. A. Belik, Y. Matsushita and D. D. Khalyavin, Angew. Chem., Int. Ed., 2017, 56, 10423–10427.
17. I. Yamada, Sci. Technol. Adv. Mater., 2017, 18, 541–548.
18. G. Shimura, K. Niwa, Y. Shirako and M. Hasegawa, Eur. J. Inorg. Chem., 2017, 835–839.
19. K. Leinenweber and J. Parise, J. Solid State Chem., 1995, 114, 277–281.
20. N. Yao, A. Navrotsky and K. Leinenweber, J. Solid State Chem., 1996, 123, 73–82.
21. A. Aimi, D. Mori, K. Hiraki, T. Takahashi, Y. J. Shan, Y. Shirako, J. S. Zhou and Y. Inaguma, Chem. Mater., 2014, 26, 2601–2608.
22. E. Solana-Madruga, A. M. Arevalo-Lopez, A. J. Dos Santos-Garcia, E. Urones-Garrote, D. Avila-Brande, R. Saez-Puche and J. P. Attfield, Angew. Chem., Int. Ed., 2016, 55, 9340–9344.
23. L. Zhang, Y. Matsushita, K. Yamaura and A. A. Belik, Inorg. Chem., 2017, 56, 5210–5218.
24. G. M. McNally, A. M. Arévalo-López, P. Kearins, F. Orlandi, P. Manuel and J. P. Attfield, Chem. Mater., 2017, 29, 8870–8874.
25. A. A. Belik, Y. Matsushita, M. Tanaka and E. Takayama-Muromachi, Chem. Mater., 2012, 24, 2197–2203.
26. A. A. Belik and W. Yi, J. Phys.: Condens. Matter, 2014, 26, 163201.
27. (a) W. M. Reiff, K. Leinenweber and J. Parise, Mater. Res. Soc. Symp. Proc., 1997, 453, 387–392; (b) H. Li, S. Liu, L. Chen, C. Li and Z. Wang, Physica E, 2015, 69, 133–137.
28. J. Ruiz-Fuertes, T. Bernert, D. Zimmer, N. Schrodt, M. Koch-Muller, B. Winkler, L. Bayarjargal, C. Popescu, S. MacLeod and K. Glazyrin, Phys. Rev. B, 2017, 96, 094101.
29. G. Y. Gou, N. Charles, J. Shi and J. M. Rondinelli, Inorg. Chem., 2017, 56, 11854–11861.
30. L. Zhang, Y. Matsushita, K. Yamaura and A. A. Belik, unpublished results.
31. Y. S. Glazkova, N. Terada, Y. Matsushita, Y. Katsuya, M. Tanaka, A. V. Sobolev, I. A. Presniakov and A. A. Belik, Inorg. Chem., 2015, 54, 9081–9091.
32. A. A. Belik, Y. S. Glazkova, Y. Katsuya, M. Tanaka, A. V. Sobolev and I. A. Presniakov, J. Phys. Chem. C, 2016, 120, 8278–8288.
33. Y. Akizuki, I. Yamada, K. Fujita, K. Taga, T. Kawakami, M. Mizumaki and K. Tanaka, Angew. Chem., Int. Ed., 2015, 54, 10870–10874.
34. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
35. J. Sanchez-Benitez, J. A. Alonso, M. J. Martinez-Lope, A. de Andres and M. T. Fernandez-Diaz, Inorg. Chem., 2010, 49, 5679–5685.
36. M. Sato and Y. Hama, J. Mater. Chem., 1993, 3, 233–236.
37. J. Li, M. A. Subramanian, H. D. Rosenfeld, C. Y. Jones, B. H. Toby and A. W. Sleight, Chem. Mater., 2004, 16, 5223–5225.
38. I. Yamada, M. Murakami, N. Hayashi and S. Mori, Inorg. Chem., 2016, 55, 1715–1719.
39. D. Waroquiers, X. Gonze, G.-M. Rignanese, C. Welker-Nieuwoudt, F. Rosowski, M. Göbel, S. Schenk, P. Degelmann, R. André, R. Glaum and G. Hautier, Chem. Mater., 2017, 29, 8346–8360.
40. M. A. Subramanian, D. Li, N. Duan, B. A. Reisner and A. W. Sleight, J. Solid State Chem., 2000, 151, 323–325.
41. S.-H. Byeon, M. W. Lufaso, J. B. Parise, P. M. Woodward and T. Hansen, Chem. Mater., 2003, 15, 3798–3804.
42. T. Saito, R. Yamada, C. Ritter, M. S. Senn, J. P. Attfield and Y. Shimakawa, Inorg. Chem., 2014, 53, 1578–1584.
43. H. Okamoto, M. Karppinen, H. Yamauchi and H. Fjellvag, Solid State Sci., 2009, 11, 1211–1215.
44. S. V. Streltsov and D. I. Khomskii, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 201115.
45. A. Prodi, A. Daoud-Aladine, F. Gozzo, B. Schmitt, O. Lebedev, G. van Tendeloo, E. Gilioli, F. Bolzoni, H. Aruga-Katori, H. Takagi, M. Marezio and A. Gauzzi, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 180101.
46. A. A. Belik, Y. Matsushita, Y. Kumagai, Y. Katsuya, M. Tanaka, S. Yu. Stefanovich, B. I. Lazoryak, F. Oba and K. Yamaura, Inorg. Chem., 2017, 56, 12272–12281.
47. S. G. Ebbinghaus, Prog. Solid State Chem., 2007, 35, 421–431.
48. S. V. Ovsyannikov, A. M. Abakumov, A. A. Tsirlin, W. Schnelle, R. Egoavil, J. Verbeeck, G. Van Tendeloo, K. V. Glazyrin, M. Hanfland and L. Dubrovinsky, Angew. Chem., Int. Ed., 2013, 52, 1494–1498.
49. M. A. Subramanian, J. Solid State Chem., 1994, 111, 134–140.
50. Y. Shimoda, Y. Doi, M. Wakeshima and Y. Hinatsu, J. Solid State Chem., 2010, 183, 1962–1969.
51. Z. Y. Li, et al. , J. Am. Chem. Soc., 2018 DOI:10.1021/jacs.7b11219.

---