Open Access Article
Open Access ArticleEffect of linear and non-linear pseudohalides on the structural and magnetic properties of Co(II) hexacoordinate single-molecule magnets†
L.
Váhovská
ab,
S.
Vitushkina
c,
I.
Potočňák
b,
Z.
Trávníček
 d and
R.
Herchel
d and
R.
Herchel
 *d
*d
aP. J. Šafarik University in Košice, Department of Inorganic Chemistry, Institute of Chemistry, Moyzesova 11, Košice, Slovakia
bUniversity of Veterinary Medicine and Pharmacy in Košice, Department of Chemistry, Biochemistry and Biophysics, Institute of Biochemistry, Komenského 73, Košice, Slovakia
cV.N. Karazin Kharkov National University, Faculty of Chemistry, Department of Applied Chemistry, Svobody sq. 4, Kharkov, Ukraine
dDepartment of Inorganic Chemistry, Regional Centre of Advanced Technologies and Materials, Faculty of Science, Palacký University, 17. listopadu 12, Olomouc, Czech Republic. E-mail: radovan.herchel@upol.cz
First published on 19th December 2017
Abstract
A series of mononuclear hexacoordinate Co(II) complexes with the 4-amino-3,5-bis(2-pyridyl)-1,2,4-triazole (abpt) ligand and various linear and non-linear pseudohalides, such as NCSe (selenocyanate), N{C(CN)2}2 (1,1,3,3-tetracyano-2-azapropenide, tcap), NO2C(CN)2 (nitrodicyanomethanide, nodcm), C(CN){C(CN)2}2 (1,1,2,3,3-pentacyanopropenide, pcp), NO2NCN (nitrocyanamide, nca), and ONC(CN)2 (nitrosodicyanomethanide, ndcm), was prepared. X-ray analyses revealed the formation of the complexes with the general compositions [Co(abpt)2(solv)2]X2 (solv = H2O and X = tcap (1), solv = H2O and X = nodcm (2), solv = CH3OH and X = pcp (3)) or [Co(abpt)2(X)2] (X = nca (4), X = NCSe (5), X = ndcm (6)). The impact of axial co-ligands (solv or X) on the magnetic properties was investigated experimentally by measuring temperature- and field-dependent static (DC) and dynamic magnetic (AC) data as well as theoretically using the CASSCF/NEVPT2, AILFT, and AOM methods. Large magnetic anisotropy was found for all complexes 1–6 and was treated either by the spin Hamiltonian or with the Hamiltonian including the orbital angular momentum. Furthermore, the AC susceptibility measurements confirmed the slow relaxation of the magnetization in a non-zero static magnetic field, thus these complexes can be classified as field-induced single-molecule magnets with an estimated energy barrier Ueff up to 100 K.
Introduction
The mononuclear cobalt(II) coordination compounds have attracted a lot of interest since the discovery of so-called single-ion magnets (SIMs),1 which form a subclass of the large family of single-molecule magnets (SMMs) having only one paramagnetic metal ion within the complex unit. The characteristic feature of SMMs is slow relaxation of the magnetization and magnetic hysteresis at low temperatures originating at the molecular level.2,3 Thus, these molecular nanomagnets are fascinating molecular materials due to their auspicious application potential in, for example, information storage, quantum computing, and spintronics.4The magnetic bistability of SMMs is due to the existence of the energy barrier (U) acting against the spin momentum reversal. In the case of 3d-metal complexes, U is usually related to the zero-field splitting (ZFS)5 of the ground spin state as U = |D|S2 for an integer and U = |D|(S2 − 1/4) for a non-integer spin value S, where D is the axial ZFS parameter defined within the spin Hamiltonian formalism. The advantage of SIMs is that the magnetic anisotropy of mononuclear complexes can be tuned by the rational design of the ligand field strength of the utilized ligands and their coordination geometry around the central atom.6 This contrasts with polynuclear SMMs, in which it is hard to predict the ground state properties due to variation of the exchange coupling among metal atoms and their overall contributions to the magnetic anisotropy. Furthermore, it was shown that increasing the number of metal atoms in polynuclear compounds does not explicitly lead to an increase of U due to the mutual relation between S and D.7 To date, many SIMs have been reported for 3d-metals with various coordination numbers and geometries, e.g. Fe(I8/II9/III10), Ni(I11/II12), Cu(II),13 or Mn(III).14 The history of mononuclear Co(II) compounds exhibiting slow relaxation of magnetization started in 2011,15 and was followed by further reports on SMM behavior in tetra-,16 penta-,17 hexa-,18 hepta-,19 or octa-coordinate20 mononuclear Co(II) coordination compounds.
In the case of hexacoordinate Co(II) complexes, two limiting geometries can be distinguished, either an ideal octahedron or trigonal prism, both possessing an orbitally degenerate ground state, i.e. either 4T1g for Oh or 4E for D3h. This can lead to a huge magnetic anisotropy and hence large U. However, until now, the slow relaxation of magnetization in a zero static magnetic field has only been reported for geometries close to D3h.21,22 In the case of (pseudo)octahedral complexes, the deviation from the ideal geometry to D4h symmetry can lead again to the orbitally degenerate ground state 4Eg for an elongated tetragonal bipyramid or to the 4A2g ground state for a compressed tetragonal bipyramid. Such geometrical changes accompanied by variation in the ligand field strength and donor atoms’ properties can result in easy-axis/easy-plane magnetic anisotropy or even in triaxial magnetic anisotropy. This richness of conceivable magnetic behavior is inspiring for a deeper study of hexacoordinate Co(II) complexes as candidates for SIMs.
Recently, we have reported on a hexacoordinate [Co(abpt)2(tcm)2] compound (abpt = 4-amino-3,5-bis(2-pyridyl)-1,2,4-triazole, tcm = C(CN)3, tricyanomethanide) behaving as a field-induced SIM with positive axial (D > 0) and large rhombic anisotropy (E/D ≫ 0).23 This motivated us to prepare and study a series of novel mononuclear hexacoordinate Co(II) compounds utilizing the bidentate abpt ligand with other linear and non-linear pseudohalides, such as NCSe (selenocyanate), N{C(CN)2}2 (1,1,3,3-tetracyano-2-azapropenide, tcap), NO2C(CN)2 (nitrodicyanomethanide, nodcm), C(CN){C(CN)2}2 (1,1,2,3,3-pentacyanopropenide, pcp), NO2NCN (nitrocyanamide, nca), and ONC(CN)2 (nitrosodicyanomethanide, ndcm). In this paper, we report their molecular/crystal structures, static and dynamic magnetic properties, and theoretical calculations at the CASSCF/NEVPT2 level, which were employed to better understand their magnetic features.
Results and discussion
Syntheses and characterization
In order to obtain analogous compounds with a similar composition to the [Co(abpt)2(tcm)2] compound described earlier,23 we performed several syntheses with the above-mentioned pseudohalide anions. A stoichiometric reaction between cobalt(II) chloride, abpt, and appropriate non-linear pseudohalide anions in a water–methanol solution gave three ionic mononuclear complexes 1–3 with the general composition [Co(abpt)2(solv)2]X2, where solv = H2O (1 and 2) or CH3OH (3) and X = tcap (1), nodcm (2), and pcp (3), and one molecular complex with the composition [Co(abpt)2(X)2] (X = nca) (4). Thus, the same synthetic procedure led to two different types of octahedral complex, probably due to the different steric hindrance of the respective non-linear pseudohalide anions. Although the bulky anions in 1–3 could not enter the Co(II) coordination sphere and therefore solvent molecules must coordinate, the smaller nca anion in 4 could coordinate as the ligand (Scheme 1). | ||
| Scheme 1 Schematic representations of the synthetic procedures leading to the preparation of 1–6. Ionic complexes are written in red, while molecular complexes are written in blue. | ||
Attempts to prepare analogous [Co(abpt)2(X)2] molecular complexes with NCSe (5) and ndcm anions (6) using the same synthetic procedure as that used in the case of 1–4 were not successful and only powder products were obtained. Elemental analyses indicated the [Co(abpt)2(X)2] (X = NCSe or ndcm) composition, thus we prepared their single crystals using diffusion of the corresponding reactants in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 molar ratio.
1 molar ratio.
The IR spectra of the prepared complexes are quite similar. The presence of the abpt ligand was confirmed by the following characteristic vibrations: ν(N–H) vibrations of the amino group were located in the 3250–3140 cm−1 region; ν(C–H)ar vibrations were found in the 3080–3015 cm−1 region; and ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C)ar and ν(C
C)ar and ν(C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N)ar bands were observed in the 1635–1500 cm−1 and 1500–1400 cm−1 regions, respectively.24 The shifts of those bands to higher wavenumbers with respect to the IR spectrum of free abpt clearly suggest the coordination of the abpt ligand in all of the prepared compounds. The main spectral variations of complexes 1–6 compared to those of free abpt are found in the 408–415 cm−1 (out-of-plane ring deformation) and 604–612 cm−1 (in-plane ring deformation) regions, where absorptions of the pyridine ring of the abpt ligand occur.25 These vibrations in 1–6 are found to be positively shifted, suggesting the coordination of the pyridine nitrogen atom to the metal atom.26 In the spectra of 1–3, bands connected with the vibrations of water or methanol molecules were also observed.
N)ar bands were observed in the 1635–1500 cm−1 and 1500–1400 cm−1 regions, respectively.24 The shifts of those bands to higher wavenumbers with respect to the IR spectrum of free abpt clearly suggest the coordination of the abpt ligand in all of the prepared compounds. The main spectral variations of complexes 1–6 compared to those of free abpt are found in the 408–415 cm−1 (out-of-plane ring deformation) and 604–612 cm−1 (in-plane ring deformation) regions, where absorptions of the pyridine ring of the abpt ligand occur.25 These vibrations in 1–6 are found to be positively shifted, suggesting the coordination of the pyridine nitrogen atom to the metal atom.26 In the spectra of 1–3, bands connected with the vibrations of water or methanol molecules were also observed.
Bands for ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) stretching vibrations from the pseudohalide anions in 1–3, observed in the 2227–2191 cm−1 region, show similar patterns to those for their corresponding free potassium salts K(tcap) for 1, K(nodcm) for 2, and K(pcp) for 3 (2230–2190 cm−1).
N) stretching vibrations from the pseudohalide anions in 1–3, observed in the 2227–2191 cm−1 region, show similar patterns to those for their corresponding free potassium salts K(tcap) for 1, K(nodcm) for 2, and K(pcp) for 3 (2230–2190 cm−1).
Similar wavenumbers and numbers of the absorption bands suggest the presence of uncoordinated polynitrile CN groups as was confirmed by the X-ray structures (vide infra). However, two strong split bands at 2220 and 2002 cm−1 were observed in the spectrum of 2, while only one band at 2210 cm−1 was observed in the spectrum of free K(nodcm). The higher number of bands in the spectrum of 2 indicates a non-equivalence of both terminal cyano groups due to the different number of hydrogen bonds in which both cyano groups are involved. On the other hand, for 4 and 5, only one strong band at 2204 cm−1 and 2083 cm−1 respectively is observed and is significantly shifted to higher wavenumbers compared with the bands observed for the free K(nca) (2188 cm−1) and KNCSe (2064 cm−1), respectively, suggesting coordination of the cyano group to the central atom. Unlike that in the IR spectrum of the free Na(ndcm), the one very strong ν(C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N) stretching vibration is split into two medium peaks around 2218 and 2212 cm−1 in the spectrum of 6. This splitting can be explained by the non-equivalence of the nitrile groups, because only one of them is involved in the intermolecular hydrogen bonding (Fig. S6†).
N) stretching vibration is split into two medium peaks around 2218 and 2212 cm−1 in the spectrum of 6. This splitting can be explained by the non-equivalence of the nitrile groups, because only one of them is involved in the intermolecular hydrogen bonding (Fig. S6†).
Description of structures 1–3
The unit cell parameters and crystal and refinement data for [Co(abpt)2(H2O)2](N{C(CN)2}2)2·2H2O (1), [Co(abpt)2(H2O)2](NO2C(CN)2)2 (2), and [Co(abpt)2(CH3OH)2](C(CN){C(CN)2}2)2 (3) are summarized in Table S1.† In each structure, the asymmetric unit consists of a cobalt atom on an inversion center, one abpt and one water or methanol molecule coordinated to the cobalt, and one uncoordinated pseudohalide anion (Fig. 1). Thus, the Co(II) central atom adopts a CoN4O2 distorted octahedral geometry with four equatorial N atoms from two abpt chelating ligands and two axial O atoms from the coordinated molecules of the solvents. Selected bond lengths and angles for the cobalt coordination sphere are summarized in Table 1 and Table S2.† | ||
| Fig. 1 Molecular structures of 1–3 with displacement ellipsoids (50% probability). [Symmetry codes: (i) 1 − x, 1 − y, 1 − z (1) and (i) 1 − x, 1 − y, −z (2 and 3)]. | ||
| d(Co-Ntr) | d(Co-Npy) | d(Co-Oax/Nax) | Σ | |
|---|---|---|---|---|
a Octahedral distortion calculated as  , where αi stands for 12 cis angles of the coordination polyhedron. , where αi stands for 12 cis angles of the coordination polyhedron.
|
||||
| 1 | 2.081(1) | 2.166(1) | 2.102(1) | 60.0 |
| 2 | 2.112(2) | 2.146(2) | 2.118(2) | 53.2 |
| 3 | 2.058(1) | 2.151(1) | 2.109(1) | 65.4 |
| 4 | 2.086(2) | 2.144(2) | 2.121(2) | 53.2 |
| 5 | 2.086(3) | 2.165(2) | 2.121(3) | 66.3 |
| 6 | 2.104(2) | 2.142(2) | 2.092(1) | 76.4 |
The averaged Co–N bond distances involving the pyridyl groups [Co1–N50 = 2.154(10) Å] are larger than those corresponding to the triazole rings [Co1–N10 = 2.084(27) Å], which is in good agreement with other coordination compounds containing the abpt ligand.27 The axial Co–O bond distances in 1–3 are found in the range of 2.102(1)–2.118(2) Å. The averaged bite angle N10–Co1–N50 (76.88(18)°) strongly differs from 90° as expected for atoms coordinated in the cis position. The abpt ligand is nearly planar with dihedral angles between the triazole and coordinated or uncoordinated rings near to 3.7° and 10.8° on average, respectively. Moreover, the nitrogen atom of the uncoordinated pyridyl ring is projected to the amine group of the triazole ring due to the presence of an intramolecular hydrogen bond, which contributes to the almost planar configuration of the abpt ligand. These facts have been reported in most of the previously described coordination compounds with this ligand.27
The tcap, nodcm, and pcp pseudohalide anions are nearly planar too, with the largest deviation of atoms from the mean planes being 0.048(1) for N2, 0.074(2) for O2, and 0.265(2) Å for atom N5. Due to the presence of the supplementary π-electron systems of the cyano groups in the pseudohalide anions, strong electronic delocalization is observed, as indicated by a number of almost equivalent C–C bond lengths, in the range of 1.433(2)–1.438(2) in 1, 1.407(3)–1.418(3) in 2, and 1.378(3)–1.477(2) Å in 3, which are shorter than typical single C–C bonds (1.54 Å). This delocalization also includes the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds in 1 and 2, which are slightly longer than double C
N bonds in 1 and 2, which are slightly longer than double C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) N bonds (1.27 Å).28 All Ncyanide
N bonds (1.27 Å).28 All Ncyanide![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C distances (1.148(4) Å on average) are close to triple N
C distances (1.148(4) Å on average) are close to triple N![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) C bond distances (1.15 Å) (Table S2†).
C bond distances (1.15 Å) (Table S2†).
The crystal packing is very compact because of short face-to-face distances (Table S5†) and strong O–H⋯N, O–H⋯O, and N–H⋯O intermolecular hydrogen bonds (Table S4†). Due to these hydrogen bonds, a two-dimensional supramolecular layer in the ab plane in 1 (Fig. S1†), a three-dimensional supramolecular network in 2 (Fig. S2†), and a one-dimensional chain parallel to the [0![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) 1] direction in 3 (Fig. S3†) are formed. Moreover, in all the discussed complexes, the amino group of abpt is involved in the intramolecular hydrogen bond linking the uncoordinated pyridyl and triazole rings of abpt. π–π interactions are present between uncoordinated pyridyl rings (containing N60 atoms) of the abpt ligands from the neighboring complexes, with an averaged centroid–centroid distance of 3.79(9) Å. The π–π stacking interactions between the abpt ligands link the 2D hydrogen-bonded layers in 1 and 1D hydrogen-bonded chains in 3 and lead to supramolecular 3D structures, while in 2 π–π stacking interactions contribute to the higher stabilization of the crystal structure.
1] direction in 3 (Fig. S3†) are formed. Moreover, in all the discussed complexes, the amino group of abpt is involved in the intramolecular hydrogen bond linking the uncoordinated pyridyl and triazole rings of abpt. π–π interactions are present between uncoordinated pyridyl rings (containing N60 atoms) of the abpt ligands from the neighboring complexes, with an averaged centroid–centroid distance of 3.79(9) Å. The π–π stacking interactions between the abpt ligands link the 2D hydrogen-bonded layers in 1 and 1D hydrogen-bonded chains in 3 and lead to supramolecular 3D structures, while in 2 π–π stacking interactions contribute to the higher stabilization of the crystal structure.
Description of structures 4–6
The [Co(abpt)2(NO2NCN)2] (4), [Co(abpt)2(NCSe)2] (5), and [Co(abpt)2{ONC(CN)2}2] (6) complexes have a similar structure to that previously described for [Co(abpt)2(tcm)2].23 The molecular structures of 4–6 consist of discrete [Co(abpt)2X2] complexes, where two equivalent chelating abpt ligands stand in the equatorial plane and two equivalent terminal pseudohalide ligands (X) complete the coordination sphere in the trans positions (Fig. 2). Similar trans coordination of the two pseudohalide ligands was observed in the isostructural [M(abpt)2(X)2] complexes with M = Fe (X = NCS,29 NCSe,30 C(CN)3, (NC)2CC(OCH3)C(CN)2, (NC)2CC(OC2H5)C(CN)2,31 N(CN)2,32), M = Ni (X = N3),33 and M = Co (X = NCS).34 Only half of the complex is present in the asymmetric unit of 4–6; the second half is generated by a center of inversion located at the cobalt(II) atom. Each Co(II) atom is in a distorted [CoN6] (4 and 5) or [CoN4O2] (6) octahedral environment; selected bond lengths and bond angles are summarized in Table 1 and Table S3.† | ||
| Fig. 2 Molecular structures of 4–6 with displacement ellipsoids (50% probability). [Symmetry codes: (i) 1 − x, 1 − y, −z (4), (i) −x, −y, −z (5), and 1 − x, −y, 1 − z (6)]. | ||
As in 1–3, the Co–Npyridyl bond distances (Co1–N50 = 2.150(13) Å on average) are longer than those involving the triazole rings (Co1–N10 = 2.092(10) Å on average) and the pseudohalide groups (Co1–X1 = 2.111(17) Å on average, X = N (4 and 5) or O (6)). The deformed octahedral geometry around Co1 in 4–6 is demonstrated mainly by the values of the N10–Co1–N50 bite angles (Table S3†), which strongly differ from the ideal 90° value for cis coordinated atoms. The dihedral angles between the coordinated or uncoordinated pyridyl groups and the triazole ring are very similar to those observed in 1–3 (4.7 and 9.4° on average, respectively).
In the nca anion (4), electronic delocalization is observed as evidenced by the N–N (1.354(3) Å) and C–N (1.325(3) Å) bond lengths, which are shorter than typical N–N (1.47 Å) or C–N (1.43 Å) bond lengths. The geometry and bond lengths and angles in the NCSe (5) and ndcm (6) ligands are very similar to those observed in other coordination complexes involving these ligands35 (Table S3†).
Packing in 4–6 involves face-to-face interactions (Table S5†) and strong intermolecular N–H⋯N and N–H⋯O hydrogen bonds (Table S4†). In 5, only one intermolecular N–H⋯Se hydrogen bond with a hydrogen–acceptor distance of 2.76(5) Å occurs. This value is similar to those observed in other complexes containing NCSe ligands.36
The same interlayer π–π stacking between the coordinated and uncoordinated pyridyl rings from the neighboring complexes occurs in 4–6; the distances between the mean planes in each pair of pyridyl rings range from 3.64 to 3.75 Å. Moreover, the same intramolecular hydrogen bond as that in 1–3, namely N40–HnN⋯N60 (n = 1 in 4 and 2 in 5 and 6), between the non-coordinated pyridyl and triazole rings of abpt is observed too.
In the crystal structure of 4, strong hydrogen bonds lead to the formation of 2D supramolecular layers in the bc plane (Fig. S4†), while π–π stacking interactions contribute to the higher stabilization of these layers. Similarly, in 5, N–H⋯Se hydrogen bonds create layers in the (10![[2 with combining macron]](https://www.rsc.org/images/entities/char_0032_0304.gif) ) plane, which are further stabilized through π–π interactions which occur between the coordinated and uncoordinated pyridyl rings of abpt from neighboring molecules (Fig. S5†). On the other hand, examination of the crystal packing in 6 revealed that this compound had a similar molecular arrangement to that of the [Co(abpt)2(tcm)2] compound23 described earlier: one strong intermolecular N–H⋯N hydrogen bond creates an infinite 1D supramolecular chain running in the [10
) plane, which are further stabilized through π–π interactions which occur between the coordinated and uncoordinated pyridyl rings of abpt from neighboring molecules (Fig. S5†). On the other hand, examination of the crystal packing in 6 revealed that this compound had a similar molecular arrangement to that of the [Co(abpt)2(tcm)2] compound23 described earlier: one strong intermolecular N–H⋯N hydrogen bond creates an infinite 1D supramolecular chain running in the [10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ] direction (Fig. S6†). Individual chains are connected through intermolecular π–π interactions occurring between the centroids of the adjacent coordinated and uncoordinated pyridyl rings (Fig. S6†), thus creating a 3D supramolecular network.
] direction (Fig. S6†). Individual chains are connected through intermolecular π–π interactions occurring between the centroids of the adjacent coordinated and uncoordinated pyridyl rings (Fig. S6†), thus creating a 3D supramolecular network.
Magnetic properties
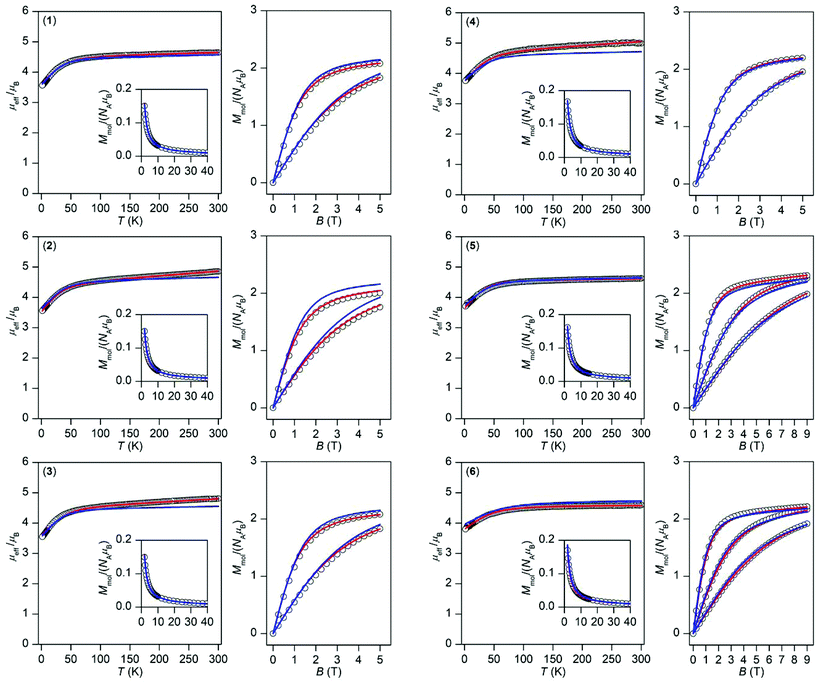 | ||
| Fig. 3 Magnetic data for 1–6 shown as the temperature dependence of the effective magnetic moment and molar magnetization measured at B = 0.1 T and as the isothermal magnetization measured at T = 2, 5, and 10 K. The empty circles represent the experimental data and red solid lines represent the fitted data using eqn (1) or (2) with the parameters listed in Table 1. The blue solid lines represent the calculated data using the CASSCF/NEVPT2 energy levels from CAS(7,10) calculations. | ||
However, the accidental degeneracy of low-lying states cannot be excluded due to variation of the ligand field of the axial co-ligands. Thus, two approaches can be used to describe magnetic properties. The first one is based on the spin Hamiltonian with the zero-field splitting terms defined as:
| Ĥ = D(Ŝz2 − Ŝ2/3) + E(Ŝx2 − Ŝy2) + μBBgŜa | (1) |
The second approach suitable for pseudo-octahedral complexes is based on Griffith’s,40 Lines’,41 and Figgis’42 works, where the orbital angular momentum and spin–orbit coupling is included in the Hamiltonian:
 | (2) |
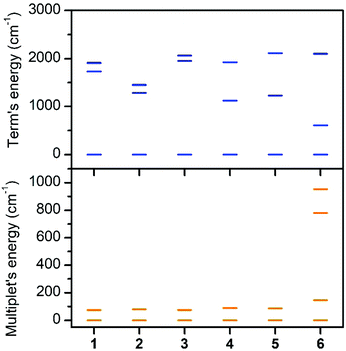
The first excited quartet term is in the range of 1123–1729 cm−1 for 1–5, but in the case of 6 the energy gap is only 609 cm−1. Thus it is obvious that the lowest quartet term is well separated from the excited ones only for 1–5. This is also reflected in the ligand field multiplets calculated after including the spin–orbit coupling, where in the case of 1–5, two lowest Kramers doublets can be described with the ZFS formalism using S = 3/2 (eqn (1)), because the third doublet is well separated from the ground state by an energy difference of 1194–1628 cm−1. However, in the case of 6, the third doublet has an energy of 780 cm−1, therefore the spin Hamiltonian formalism with S = 3/2 is not applicable and the magnetic properties should be analyzed with the L–S Hamiltonian (eqn (2)). The application of the effective Hamiltonian theory for S = 3/2 resulted in the ZFS and g-tensor parameters listed in Table 2. Interestingly, the double-shell effect (CAS(7,5) vs. CAS(7,10)) has only a minor impact on the derived values, which can be deduced by comparing D, E, and the respective g-parameters in Table 2 (e.g. D = 40.0 cm−1 and E/D = 0.303 calculated with CAS(7,5) vs. D = 40.1 cm−1 and E/D = 0.281 calculated with CAS(7,10) for 4). Overall, D is positive and found in a narrow range from 37.0 to 40.1 cm−1 with rhombicity, E/D, spanning the interval 0.065–0.290 for 1–5 and CAS(7,10). Similar analysis applied to 6 resulted in a negative D parameter and one of the g-factors being less than ge, which indirectly confirms that the spin Hamiltonian is not applicable in this case and that these parameters have no physical meaning. Therefore, the CAS(7,10)-CASSCF/NEVPT2 energies of the lowest six Kramers doublets originating from the 4T1g term of 6 were analyzed with the Hamiltonian in eqn (2) and we found these parameters to be: α·λ = −223 cm−1, Δax = −1803 cm−1, and Δrh = −319 cm−1 (Δrh/Δax = 0.176) (Fig. S7†). To validate the ab initio calculations, we employed the calculated CAS(7,10)-CASSCF/NEVPT2 matrices of the spin–orbit coupling (HSOC), the spin momentum (Sx, Sy, Sz), and the orbital momentum (Lx, Ly, Lz) operators to calculate the energy levels for any strength and orientation of the magnetic field by diagonalization of the matrix H defined as:
| H = HSOC + μB(L + geS) | (3) |
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| a The first excited state is relatively close to the ground spin state. b f is a scaling factor used to obtain the best match with the experimental magnetic data. | ||||||
| ZFS and g values based on CASSCF/NEVPT2 calculations with CAS(7,5) | ||||||
| D (cm−1) | 36.6 | 39.8 | 36.8 | 40.0 | 38.2 | −69.7 |
| E/D | 0.123 | 0.089 | 0.113 | 0.303 | 0.312 | 0.258 |
| g x /gy/gz | 2.330/2.464/2.058 | 2.391/2.513/2.083 | 2.316/2.436/2.047 | 2.323/2.546/2.058 | 2.313/2.534/2.057 | 2.230/1.990/2.805 |
| ZFS and g values based on CASSCF/NEVPT2 calculations with CAS(7,10) | ||||||
| D (cm−1) | 37.0 | 39.9 | 36.8 | 40.1 | 38.6 | −66.3 |
| E/D | 0.121 | 0.065 | 0.095 | 0.281 | 0.290 | 0.270 |
| g x /gy/gz | 2.340/2.475/2.055 | 2.410/2.508/2.082 | 2.329/2.435/2.044 | 2.335/2.551/2.058 | 2.326/2.542/2.056 | 2.240/1.991/2.797 |
| U calc. (cm−1) | 75.6 | 80.2 | 74.6 | 89.1 | 86.5 | 146.5 |
| f | 0.986 | 0.971 | 0.999 | 1.010 | 0.991 | 0.950 |
| Analysis of the experimental magnetic data | ||||||
| D (cm−1) | 34.9 | 31.0 | 37.8 | 41.4 | 37.7 | Δ ax = −1345 cm−1 |
| E/D | 0.327 | 0.333 | 0.308 | 0.228 | 0.135 | Δ rh/Δax = 0.174 cm−1 |
| g xy /gz | 2.42/2.00 | 2.36/2.00 | 2.41/2.00 | 2.53/2.00 | 2.46/2.00 | λ = −180 cm−1 |
| χ TIP | 9.1 | 23.9 | 17 | 22 | 5.0 | α = 1.23 |
| U calc. (cm−1) | 80.3 | 71.6 | 85.7 | 89.0 | 77.4 | 108 |
| AILFT and AOM analysis of CASSCF/NEVP2 calculations with CAS(7,5) | ||||||
| B (cm−1) | 1056 | 1055 | 1062 | 1050 | 1051 | 1052 |
| C (cm−1) | 3992 | 3997 | 3956 | 3973 | 3966 | 3985 |
| ξ (cm−1) | 524 | 524 | 524 | 524 | 524 | 524 |
| e trσ/etrπs | 4274/−244 | 3919/−499 | 4658/34 | 4000/−76 | 4042/73 | 3705/−183 |
| e pyσ / e pyπs | 3491/−856 | 3891/−399 | 3728/−711 | 3770/−103 | 3461/−67 | 3864/74 |
| e axσ / e axπ | 2375/992 | 2394/935 | 2693/1064 | 3662/1020 | 3807/991 | 3517/1174 |
This enabled us to calculate the partition function and the integral average of the molar magnetization.23 The great benefit of this procedure is the fact that no restriction of the spin Hamiltonian formalism is applied, thus no ZFS or g-tensor parameters are used. The calculated data are compared to the experimental magnetic data in Fig. 3 and we can conclude that there is good agreement with the low temperature data for all of the compounds; only in the case of 2 is a somewhat larger deviation in the isothermal magnetization found. This shows that a multi-configuration method such as CASSCF/NEVPT2 used here is well-suited for treating the magnetism of Co(II) complexes.
Thus, the outcomes of these calculations were used in fitting the experimental magnetic data of 1–6. Therefore, the spin Hamiltonian model in eqn (1) was used for compounds 1–5, while the L–S Hamiltonian was applied for compound 6. In all cases, the molar magnetization (Mmol) was calculated from the partition function (Z) for a given direction of a magnetic field Ba = B·(sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, sin
φ, sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) φ, cos
φ, cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) as:
θ) as:
 | (4) |
Then, the integral (orientational) average of molar magnetization was calculated
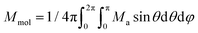 | (5) |
To gain better insight into the relationship between the coordination polyhedron geometry and the magnetic properties, the Mayer bond orders with the CAM-B3LYP DFT functional were also calculated and are plotted in Fig. 5 together with the donor–acceptor bond distances and octahedral distortion parameter Σ. It is evident that the bond orders among the cobalt and nitrogen atoms of the abpt ligand are only slightly varied within 1–6. In the case of the axial ligands, the bond order increases as Co–OH2O ≈ Co–OMeOH < Co–Ondcm < Co–Nnca < Co–NNCSe.
 | ||
| Fig. 5 Bond distances, Mayer bond orders from CAM-B3LYP calculations, and the octahedron distortion parameter Σ. | ||
Moreover, we also used another approach based on the Angular Overlap Model (AOM) to better understand the electronic structure of the reported complexes.46 This ligand field theory classifies ligands as σ-donors, σ-donors and π-donors, and σ-donors and π-acceptors utilizing molecular orbitals between a metal atom and donor atoms. The AOM quantifies the effect of the ligands on the d-orbital splitting with eσ, eπs, and eπc parameters. Here, eσ measures the σ-type molecular overlap and logically always has a positive value due to the formation of donor–acceptor bonds, whereas the π-type molecular overlap can be anisotropic (eπs ≠ eπc) and can adopt positive or negative values for π-donors or π-acceptors. Recently, the ab initio ligand field theory (AILFT) was developed based on CASSCF (CASSCF/NEVPT2) calculations for d-metal coordination compounds and was implemented in ORCA software.47 The AILFT analyses of 1–6 based on CASSCF/NEVPT2 calculations with CAS(7,5) resulted in the Racah parameters (B and C) and ligand field matrix (VLFT) describing the effective ligand field potential acting on the metal d-orbitals. In the next step, we analyzed this VLFT matrix with the AOM using the AOMX program,48 which enabled us to derive the AOM parameters for 1–6. In these calculations, six parameters were varied in total, namely the σ-parameters of the triazole N-donor atoms (etrσ) and pyridine N-donor atoms (epyσ) stemming from the abpt ligand, and eaxσ of the axial O/N donor atoms of the solvent or coordinated pseudohalide ligands. The π-type interactions of the axial donor atoms were considered as isotropic (eaxπs = eaxπc = eaxπ), whereas the π-type interactions of the planar donor atoms of abpt were considered as anisotropic: the in-plane π-interactions were assumed to be negligible (etrπc = epyπc = 0) and the π-type interactions perpendicular to the abpt plane were varied freely (etrπs ≠ epyπs ≠ 0). The results of this analysis are depicted in Fig. 6 and listed in Table 2. The σ-type AOM parameters of 1–6 nicely copy the trend observed from the DFT calculations of the Mayer bond order (Fig. 5). The axial donor atoms Ondcm, NNCSe, and Nnca are stronger σ-donors than OH2O and OMeOH, whereas their π-donor properties are about the same; the maximal value was found for Ondcm in 6. The abpt ligand acts as a strong σ-donor with π-acceptor properties in 1–3, whereas the etrπs and epyπs parameters are close to zero in 4–6. The calculated AOM parameters revealed that the equatorial abpt ligands impose a stronger ligand field than the axially coordinated molecules of the solvents or pseudohalide ligands, which means that this situation resembles the case of the elongated tetragonal bipyramid with the 4Eg ground term. This would imply that the L–S model (eqn (2)) is appropriate for this series, but CASSCF/NEVPT2 calculations showed that this model is suitable only for compound 6. To better understand this phenomenon, the AOM was used, in which two factors were studied: (i) the size of the bite angle of the equatorial bidentate ligand and (ii) the ligand field strength of the axial ligand. The AOMX program was employed using the average values of the AOM parameters found for 1–6 as B = 1054 cm−1, C = 3978 cm−1, and ξ = 524 cm−1, and the equatorial ligands were simulated with eeqσ = 3900 cm−1 and eeqπs = −250 cm−1 with a varying bite angle α = 60–90°. The AOM parameters of the axial ligands were eaxσ = 2000–4000 cm−1 with eaxπ = 1000 cm−1. The energy gap between the two lowest Kramers doublets (Δ1–2) and the energy of the third Kramers doublet (Δ1–3) are visualized in a 2D contour plot in Fig. 7. Evidently, the bite angle α has a dramatic effect on the multiplet levels; a decrease in α led to a decrease in Δ1–2, but on the other hand, to an increase in Δ1–3. Next, the increase in eaxσ resulted in an increase in Δ1–2 and a decrease in Δ1–3 for smaller values of the bite angle. Taking into account the average bite angle for the abpt ligand (α ≈ 76–77°, Tables S2 and S3†), these findings explain why the spin Hamiltonian formalism is applicable for most of the reported compounds (Δ1–3 is larger than 1000 cm−1). Also, this modelling explains why despite the large variation of the axial ligands and their ligand field strength, the ZFS energy gap only varies a little for 1–6. To summarize, this magneto–structural correlation based on AOM theory helped us to better understand the impact of the abpt and various axial co-ligands on the magnetic levels in the reported compounds.
 | ||
| Fig. 6 AOM analysis using the AILFT applied on CASSCF/NEVPT2 calculations with CAS(7,5) for 1–6. The σ-type and π-type AOM parameters are plotted as filled and empty points, respectively. | ||
Dynamic magnetic measurements
The AC susceptibility was measured to study the dynamic magnetic properties of 1–6. We did not find out-of-phase signals in a zero static magnetic field, but upon turning on the magnetic field, the imaginary susceptibility became non-zero for all compounds (Fig. S8–S13†). Then, the AC susceptibility was measured at BDC = 0.1 T and revealed frequency-dependent maxima of the imaginary susceptibility for 1–2 and 4–6, whereas in the case of 3, the signal is frequency-dependent but without maxima (Fig. S14†). This confirms the slow relaxation of the magnetization in 1–6 as a typical feature of SMMs. Moreover, in all the compounds we observed only one relaxation process, which indirectly indicates that cobalt complexes are well-separated in the solid state and there are no efficient exchange pathways to induce other relaxation processes as was reported for other Co(II) SIMs.49 Thus, the experimental data were then analyzed with the one-component Debye's model based on eqn (6):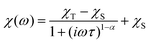 | (6) |
 | ||
| Fig. 8 AC susceptibility data for 1. Top: In-phase χ′ and out-of-phase χ′′ molar susceptibilities at the applied external magnetic field BDC = 0.1 T (solid lines are only guides for the eyes). Middle: Frequency dependence of the in-phase χ′ and out-of-phase χ′′ molar susceptibilities fitted with the one-component Debye's model using eqn (6) (solid lines). Bottom: the Argand (Cole–Cole) plot with solid lines fitted with eqn (6), with on the left side the fit of the resulting relaxation times τ with the Arrhenius law (red line), and the combination of the direct and Orbach processes (blue line) using eqn (7) and the combination of the direct and Raman processes (orange line) using eqn (8). | ||
 | ||
| Fig. 9 AC susceptibility data for 6. Top: In-phase χ′ and out-of-phase χ′′ molar susceptibilities at the applied external magnetic field BDC = 0.1 T (solid lines are only guides for the eyes). Middle: Frequency dependence of the in-phase χ′ and out-of-phase χ′′ molar susceptibilities fitted with the one-component Debye's model using eqn (6) (solid lines). Bottom: The Argand (Cole–Cole) plot with solid lines fitted with eqn (6), with on the left side the fit of the resulting relaxation times τ with the Arrhenius law (red line), and the combination of the direct and Orbach processes (blue line) using eqn (7) and the combination of the direct and Raman processes (orange line) using eqn (8). | ||
| Arrhenius law | Direct and Orbach (eqn (7)) | Direct and Raman (eqn (8)) | Orbach simplified model (eqn (9)) | Raman simplified model (eqn (10)) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| τ 0 (s) | U eff (K) | A (K−1 s−1) | τ 0 (10−6 s) | U eff (K) | A (K−1 s−1) | C (K−n s−1) | n | τ 0 (s) | U eff (K) | C (K−n s−1) | n | |
| a Calculated for f = 1488 Hz. b Calculated for f = 716 Hz. | ||||||||||||
| 1 | 1.04 × 10−7 | 44.1 | 25.2 | 2.60 | 27.4 | 23.1 | 0.0345 | 6.64 | 2.49 × 10−11 | 95.6a | 5.14 × 106 | 13.4a |
| 4.88 × 10−10 | 73.8b | 1.26 × 104 | 10.4b | |||||||||
| 2 | 2.96 × 10−5 | 12.3 | 137 | 29.5 | 14.0 | 99.5 | 9.14 | 3.49 | 3.72 × 10−12 | 104a | 1.48 × 108 | 15.5a |
| 3.51 × 10−10 | 71.8b | 1.84 × 104 | 10.9b | |||||||||
| 3 | — | — | — | — | — | — | — | — | 2.42 × 10−7 | 18.9a | 6.19 × 10−3 | 3.94a |
| 3.11 × 10−7 | 17.1b | 2.09 × 10−3 | 3.35b | |||||||||
| 4 | 2.19 × 10−5 | 12.0 | 459 | 25.9 | 15.6 | 413 | 9.75 | 3.30 | 7.78 × 10−9 | 59.1a | 1.37 × 105 | 11.2a |
| 3.74 × 10−9 | 64.1b | 3.24 × 103 | 9.40b | |||||||||
| 5 | 7.76 × 10−6 | 17.0 | 245 | 25.2 | 12.7 | 82.9 | 65.5 | 2.55 | 3.66 × 10−9 | 67.5a | 1.44 × 104 | 9.83a |
| 1.36 × 10−9 | 74.0b | 1.83 × 104 | 10.0b | |||||||||
| 6 | 1.63 × 10−6 | 28.5 | 131 | 17.1 | 16.4 | 76.1 | 11.4 | 3.32 | 4.4.5 × 10−9 | 68.1a | 4.44 × 102 | 8.08a |
| 1.59 × 10−8 | 57.1b | 4.97 × 101 | 7.06b | |||||||||
As well as the Arrhenius law, we also tried to fit all relaxation times to the combination of the direct (A) and Orbach (τ0 and U) relaxation processes as:
 | (7) |
 | (8) |
Both of these approaches (eqn (7) and (8)) can elucidate the temperature dependence of the relaxation time for 1–2 and 4–6, but are limited only to the AC data having maxima in the Argand diagram, while non-zero out-of-phase AC susceptibility was observed at higher temperatures, which means that such an analysis of thermally activated mechanisms can be biased. Therefore, the AC susceptibility data were also analyzed with a simplified model, which is derived under the assumption that the adiabatic susceptibility is usually approaching zero in single-molecule magnets (χS → 0) for highest temperatures.3a Then the following equation
| ln(χ′′/χ′) = ln(2πfτ0) + Ueff/kT | (9) |
| ln(χ′′/χ′) = ln(2πfC) − nlnT | (10) |
Experimental
Materials and methods
N{C(CN)2}2 (1,1,3,3-tetracyano-2-azapropenide, tcap), NO2C(CN)2 (nitrodicyanomethanide, nodcm), C(CN){C(CN)2}2 (1,1,2,3,3-pentacyanopropenide, pcp), NO2NCN (nitrocyanamide, nca), and ONC(CN)2 (nitrosodicyanomethanide, ndcm) in the form of potassium or sodium salts were synthesized at the Martin Luther University in Halle, Germany. All other chemicals are commercially available and were used without further purification. Elemental analysis of C, H, and N was carried out using a CHNOS Elemental Analyzer vario MICRO (Elementar Analysensysteme GmbH). The infrared spectra of the complexes were recorded on a Nicolet 6700 FT-IR spectrophotometer (Thermo Scientific) equipped with a diamond crystal Smart Orbit™ in the range 4000–400 cm−1. The temperature-dependent (T = 1.9–300 K, B = 0.1 T) and field-dependent (B = 0–5 T, T = 2 or 5 K, or B = 0–9 T, T = 2, 5, or 10 K) magnetization measurements were performed on an MPMS XL-7 SQUID magnetometer (Quantum design Inc., San Diego, CA, USA) or PPMS Dynacool (Quantum design Inc., San Diego, CA, USA). Dynamic magnetic properties were studied by measuring the alternating current (AC) susceptibility on a MPMS XL-7 SQUID magnetometer. The magnetic data were corrected for the diamagnetism of the constituent atoms and for the diamagnetism of the sample holder.Synthesis
Complexes 1–4 were prepared by the same method. A methanol solution (5 mL) of abpt (0.15 mmol, 35.7 mg) was added to a solution of CoCl2 (0.075 mmol, 17.8 mg CoCl2·6H2O) in water (5 mL). The resulting light-yellow solution was mixed with a methanol solution (5 mL) comprising 0.15 mmol of appropriate pseudohalide (27.2 mg tcap, 22.4 mg nodcm, 21.2 mg pcp, or 18.7 mg nca). Yellow powder precipitates of 1–4 were almost immediately formed, filtered off, washed with a small amount of water, and dried in air. The final solutions were allowed to evaporate for a week, giving yellow crystals of 1–4 suitable for X-ray studies, which were filtered off and dried in air.Single crystals of 5 and 6 were obtained at the interfaces of layered systems in large test tubes, with the lower layers comprising an aqueous solution (6 mL) of cobalt(II) nitrate (0.2 mmol, 58.21 mg Co(NO3)2·6H2O) (5) or chloride (47.6 mg CoCl2·6H2O) (6) and NCSe (0.2 mmol, 21.0 mg KNCSe) (5) or ndcm (0.2 mmol, 23.41 mg NaONC(CN)2) (6) and the upper layers comprising an ethanolic solution (5 mL) of abpt (0.2 mmol, 47.65 mg). These layered systems were allowed to stand undisturbed at room temperature. Yellow crystals of 5 and 6 suitable for X-ray analysis were obtained and filtered off after 2 weeks and dried in air.
Crystallography
Diffraction data for 1–6 were collected at 173 K using an Oxford Diffraction Xcalibur2 diffractometer equipped with a Sapphire2 CCD detector using graphite monochromated MoKα radiation (λ = 0.71073 Å). Crysalis CCD was used for data collection while Crysalis RED was used for cell refinement, data reduction, and absorption correction.51 The structures were solved by SUPERFLIP52 and refined against the F2 data using full matrix least squares methods with the program SHELXL-2014.53 Anisotropic thermal parameters were assigned to all non-hydrogen atoms. All aromatic hydrogen atoms of the abpt ligand were inserted in calculated positions appropriate for the data collection temperature (C–H = 0.95 Å) with the isotropic displacement parameters based on the parent C atom, Uiso(H) = 1.2Ueq(C). Hydrogen atoms of the uncoordinated water molecule in 1 and coordinated solvent molecules in 2 and 3, as well as amino-H atoms in all compounds, were found in the difference map and then refined using a riding model. An analysis of the hydrogen bonds was performed using SHELXL-2014, while PLATON54 running under WinGX55 was used to analyze the π–π interactions. DIAMOND56 was used for molecular graphics. The crystal and experimental data are given in Tables S1–S5.†Theoretical methods
The ORCA 4.0 computational package was used for all theoretical calculations.44 The calculations of the ZFS parameters were done using the state-averaged complete active space self-consistent field (SA-CASSCF)57 wave functions complemented by the N-electron valence second-order perturbation theory (NEVPT2)58 using the triple-ζ basis set def2-TZVP59 for all atoms. In the state-averaged approach, all multiplets for a given electron configuration were equally weighted. The ZFS parameters, based on dominant spin–orbit coupling contributions from excited states, were calculated through quasi-degenerate perturbation theory (QDPT),60 in which an approximation to the Breit–Pauli form of the spin–orbit coupling operator (SOMF approximation)61 and the effective Hamiltonian theory62 were utilized. The calculations utilized the RIJCOSX approximation with the auxiliary Coulomb basis def2/JK.63 Increased integration grids (Grid6 and GridX6 in the ORCA convention) and tight SCF convergence criteria were used in all calculations. The Mayer bond orders were calculated with the CAM-B3LYP functional64 and the auxiliary def2/J basis set was also utilized65 together with the RI-JK approximation to exact exchange as implemented in ORCA. The ab initio ligand field theory (AILFT) analysis was done for CAS(7,5) calculations as implemented in ORCA, which resulted in the Racah parameters (B and C), the spin–orbit coupling constant ξ, and the matrix elements of the ligand field matrix VLFT. Subsequently a home-made program was used to fit the AOM parameters using the AOMX software by minimizing the difference of the VLFT matrix elements between ORCA and AOMX. Here, the FORTRAN code PRAXIS was used to find the best solution.66Conclusions
In conclusion, we report on the syntheses and characterization of six Co(II) mononuclear hexacoordinate complexes comprising the bidentate abpt ligand and various co-ligands in axial positions. Several linear and non-linear pseudohalides, such as NCSe (selenocyanate), N{C(CN)2}2 (1,1,3,3-tetracyano-2-azapropenide, tcap), NO2C(CN)2 (nitrodicyanomethanide, nodcm), C(CN){C(CN)2}2 (1,1,2,3,3-pentacyanopropenide, pcp), NO2NCN (nitrocyanamide, nca), and ONC(CN)2 (nitrosodicyanomethanide, ndcm) were employed in the synthesis, but X-ray analysis confirmed only the coordination of the nca, NCSe, and ndcm anions in compounds 4–6, whereas in the rest of the reported compounds 1–3, the solvent molecules (H2O or CH3OH) were incorporated in the first coordination sphere. The magnetic measurements confirmed an S = 3/2 ground spin state with large magnetic anisotropy. The analyses of the experimental magnetic data supported by CASSCF/NEVPT2 calculations were based on either the spin Hamiltonian formalism (compounds 1–5) or on the L–S Hamiltonian (compound 6) and revealed significant energy separations of the lowest Kramers doublets, and thus large magnetic anisotropy. The ground state properties were also rationalized using AILFT together with the AOM, thus explaining the role of a small bite angle of the abpt equatorial ligands and variation of the ligand field strength of the respective axial co-ligands. The measurements of AC susceptibility substantiated the slow relaxation of the magnetization at a small static magnetic field with one relaxation process for all compounds 1–6, thus classifying these substances as field-induced SMMs. The effective spin reversal energy barrier was evaluated by several approaches and a maximal Ueff ≈ 100 K was found for compounds 1 and 2.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was financially supported by the Czech Science Foundation (Grant No. 17-08992S) and the National Program of Sustainability (NPU LO1305) of the Ministry of Education, Youth and Sports of Czech Republic. This work was also supported by the Slovak Research and Development Agency under contract No. APVV-14-0078 and by the project VEGA 1/0598/14.Notes and references
- N. Ishikawa, M. Sugita, T. Ishikawa, S.-y. Koshihara and Y. Kaizu, J. Am. Chem. Soc., 2003, 125, 8694–8695 CrossRef CAS PubMed.
- R. Sessoli, D. Gatteschi, A. Caneschi and M. A. Novak, Nature, 1993, 365, 141–143 CrossRef CAS.
- (a) D. Gatteshi, R. Sessoli and J. Villain, Molecular Nanomagnets, Oxford University Press, New York, 2006 Search PubMed; (b) Single Molecule Magnet and Related Phenomena, in Structure and Bonding, ed. R. Winpenny, Springer, Berlin, 2006, vol. 122 Search PubMed.
- J. S. Miller and D. Gatteschi, Molecule-based magnets themed issue No. 6, Chem. Soc. Rev., 2011, 40, 3065 RSC.
- R. Boča, Coord. Chem. Rev., 2004, 248, 757–815 CrossRef.
- A. K. Bar, C. Pichon and J.-P. Sutter, Coord. Chem. Rev., 2016, 308, 346–380 CrossRef CAS.
- (a) O. Waldmann, Inorg. Chem., 2007, 46, 10035–10037 CrossRef CAS PubMed; (b) F. Neese and D. A. Pantazis, Faraday Discuss., 2011, 148, 229–238 RSC.
- (a) J. M. Zadrozny, D. J. Xiao, J. R. Long, M. Atanasov, F. Neese, F. Grandjean and G. J. Long, Inorg. Chem., 2013, 52, 13123–13131 CrossRef CAS PubMed; (b) J. M. Zadrozny, D. J. Xiao, M. Atanasov, G. J. Long, F. Grandjean, F. Neese and J. R. Long, Nat. Chem., 2013, 5, 577–581 CrossRef CAS PubMed.
- (a) J. M. Zadrozny, M. Atanasov, A. M. Bryan, C.-Y. Lin, B. D. Rekken, P. P. Power, F. Neese and J. R. Long, Chem. Sci., 2013, 4, 125–138 RSC; (b) C. Mathonière, H.-J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083–19086 CrossRef PubMed; (c) X. Feng, C. Mathonière, I.-R. Jeon, M. Rouzières, A. Ozarowski, M. L. Aubrey, M. I. Gonzalez, R. Clérac and J. R. Long, J. Am. Chem. Soc., 2013, 135, 15880–15884 CrossRef CAS PubMed; (d) W. H. Harman, T. D. Harris, D. E. Freedman, H. Fong, A. Chang, J. D. Rinehart, A. Ozarowski, M. T. Sougrati, F. Grandjean, G. J. Long, J. R. Long and C. J. Chang, J. Am. Chem. Soc., 2010, 132, 18115–18126 CrossRef CAS PubMed; (e) D. E. Freedman, W. H. Harman, T. D. Harris, G. J. Long, C. J. Chang and J. R. Long, J. Am. Chem. Soc., 2010, 132, 1224–1225 CrossRef CAS PubMed; (f) D. Weismann, Y. Sun, Y. Lan, G. Wolmershäuser, A. K. Powell and H. Sitzmann, Chem. – Eur. J., 2011, 17, 4700–4704 CrossRef CAS PubMed.
- S. Mossin, B. L. Tran, D. Adhikari, M. Pink, F. W. Heinemann, J. Sutter, R. K. Szilagyi, K. Meyer and D. J. Mindiola, J. Am. Chem. Soc., 2012, 134, 13651–13661 CrossRef CAS PubMed.
- (a) R. C. Poulten, M. J. Page, A. G. Algarra, J. J. Le Roy, I. López, E. Carter, A. Llobet, S. A. Macgregor, M. F. Mahon, D. M. Murphy, M. Murugesu and M. K. Whittlesey, J. Am. Chem. Soc., 2013, 135, 13640–13643 CrossRef CAS PubMed; (b) W. Lin, T. Bodenstein, V. Mereacre, K. Fink and A. Eichhöfer, Inorg. Chem., 2016, 55, 2091–2100 CrossRef CAS PubMed.
- (a) J. Miklovič, D. Valigura, R. Boča and J. Titiš, Dalton Trans., 2015, 44, 12484–12487 RSC; (b) K. E. R. Marriott, L. Bhaskaran, C. Wilson, M. Medarde, S. T. Ochsenbein, S. Hill and M. Murrie, Chem. Sci., 2015, 6, 6823–6828 RSC; (c) D. Lomjanský, J. Moncol’, C. Rajnák, J. Titiš and R. Boča, Chem. Commun., 2017, 53, 6930–6932 RSC.
- R. Boča, C. Rajnák, J. Titiš and D. Valigura, Inorg. Chem., 2017, 56, 1478–1482 CrossRef PubMed.
- (a) R. Ishikawa, R. Miyamoto, H. Nojiri, B. K. Breedlove and M. Yamashita, Inorg. Chem., 2013, 52, 8300–8302 CrossRef CAS PubMed; (b) G. A. Craig, J. J. Marbey, S. Hill, O. Roubeau, S. Parsons and M. Murrie, Inorg. Chem., 2014, 54, 13–15 CrossRef PubMed; (c) J. Vallejo, A. Pascual-Álvarez, J. Cano, I. Castro, M. Julve, F. Lloret, J. Krzystek, G. De Munno, D. Armentano, W. Wernsdorfer, R. Ruiz-García and E. Pardo, Angew. Chem., Int. Ed., 2013, 52, 14075–14079 CrossRef CAS PubMed.
- T. Jurca, A. Farghal, P.-H. Lin, I. Korobkov, M. Murugesu and D. S. Richeson, J. Am. Chem. Soc., 2011, 133, 15814–15817 CrossRef CAS PubMed.
- See e.g.: (a) R. Boča, J. Miklovič and J. Titiš, Inorg. Chem., 2014, 53, 2367–2369 CrossRef PubMed; (b) D.-K. Cao, J.-Q. Feng, M. Ren, Y.-W. Gu, Y. Song and M. D. Ward, Chem. Commun., 2013, 49, 8863–8865 RSC; (c) J. M. Zadrozny, J. Liu, N. A. Piro, C. J. Chang, S. Hill and J. R. Long, Chem. Commun., 2012, 48, 3927–3929 RSC; (d) J. M. Zadrozny and J. R. Long, J. Am. Chem. Soc., 2011, 133, 20732–20734 CrossRef CAS PubMed; (e) M. Idešicová and R. Boča, Inorg. Chim. Acta, 2013, 408, 162–171 CrossRef; (f) M. Idešicová, Ľ. Dlháň, J. Moncoľ, J. Titiš and R. Boča, Polyhedron, 2012, 36, 79–84 CrossRef; (g) M. Idešicová, J. Titiš, J. Krzystek and R. Boča, Inorg. Chem., 2013, 52, 9409–9417 CrossRef PubMed.
- See e.g.: (a) N. Nedelko, A. Kornowicz, I. Justyniak, P. Aleshkevych, D. Prochowicz, P. Krupiński, O. Dorosh, A. Ślawska-Waniewska and J. Lewiński, Inorg. Chem., 2014, 53, 12870–12876 CrossRef CAS PubMed; (b) R. Ruamps, L. J. Batchelor, R. Guillot, G. Zakhia, A.-L. Barra, W. Wernsdorfer, N. Guihery and T. Mallah, Chem. Sci., 2014, 5, 3418–3424 RSC; (c) D. M. Pinero Cruz, D. N. Woodruff, I.-R. Jeon, I. Bhowmick, M. Secu, E. A. Hillard, P. Dechambenoit and R. Clerac, New J. Chem., 2014, 38, 3443–3448 RSC; (d) C. Rajnák, J. Titiš, I. Šalitroš, R. Boča, O. Fuhr and M. Ruben, Polyhedron, 2013, 65, 122–128 CrossRef.
- (a) V. Chandrasekhar, A. Dey, A. J. Mota and E. Colacio, Inorg. Chem., 2013, 52, 4554–4561 CrossRef CAS PubMed; (b) Y.-Y. Zhu, C. Cui, Y.-Q. Zhang, J.-H. Jia, X. Guo, C. Gao, K. Qian, S.-D. Jiang, B.-W. Wang, Z.-M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC; (c) J. Vallejo, I. Castro, R. Ruiz-García, J. Cano, M. Julve, F. Lloret, G. De Munno, W. Wernsdorfer and E. Pardo, J. Am. Chem. Soc., 2012, 134, 15704–15707 CrossRef CAS PubMed.
- (a) X.-C. Huang, C. Zhou, D. Shao and X.-Y. Wang, Inorg. Chem., 2014, 53, 12671–12673 CrossRef CAS PubMed; (b) P. Antal, B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2016, 55, 5957–5972 CrossRef CAS PubMed; (c) B. Drahoš, R. Herchel and Z. Trávníček, Inorg. Chem., 2017, 56, 5076–5088 CrossRef PubMed.
- L. Chen, J. Wang, J.-M. Wei, W. Wernsdorfer, X.-T. Chen, Y.-Q. Zhang, Y. Song and Z.-L. Xue, J. Am. Chem. Soc., 2014, 136, 12213–12216 CrossRef CAS PubMed.
- Y. Y. Zhu, C. Cui, Y. Q. Zhang, J. H. Jia, X. Guo, C. Gao, K. Qian, S. D. Jiang, B. W. Wang, Z. M. Wang and S. Gao, Chem. Sci., 2013, 4, 1802–1806 RSC.
- (a) V. V. Novikov, A. A. Pavlov, Y. V. Nelyubina, M.-E. Boulon, O. A. Varzatskii, Y. Z. Voloshin and R. E. P. Winpenny, J. Am. Chem. Soc., 2015, 137, 9792–9795 CrossRef CAS PubMed; (b) A. A. Pavlov, Y. V. Nelyubina, S. V. Kats, L. V. Penkova, N. N. Efimov, A. O. Dmitrienko, A. V. Vologzhanina, A. S. Belov, Y. Z. Voloshin and V. V. Novikov, J. Phys. Chem. Lett., 2016, 7, 4111–4116 CrossRef CAS PubMed.
- R. Herchel, L. Váhovská, I. Potočňák and Z. Trávníček, Inorg. Chem., 2014, 53, 5896–5898 CrossRef CAS PubMed.
- (a) R. Herchel, Z. Trávníček and R. Zbořil, Inorg. Chem., 2011, 50, 12390–12392 CrossRef CAS PubMed; (b) F. Setifi, C. Charles, S. Houille, F. Thétiot, S. Triki, C. J. Gómez-García and S. Pillet, Polyhedron, 2013, 61, 242–247 CrossRef CAS.
- (a) N. S. Gill, R. H. Nuttall, D. E. Scarfe and D. W. A. Sharp, J. Inorg. Nucl. Chem., 1961, 18, 79–87 CrossRef CAS; (b) R. J. H. Clark and C. S. Williams, Inorg. Chem., 1965, 4, 350–357 CrossRef CAS.
- M. Shakir, S. Parveen, N. Begum and Y. Azim, Polyhedron, 2003, 22, 3181–3186 CrossRef CAS.
- (a) U. García-Couceiro, O. Castillo, J. Cepeda, A. Luque, S. Pérez-Yáñez and P. Román, Inorg. Chim. Acta, 2009, 362, 4212–4218 CrossRef; (b) P. J. Kunkeler, P. J. van Koningsbruggen, J. P. Cornelissen, A. N. van der Horst, A. M. van der Kraan, A. L. Spek, J. G. Haasnoot and J. Reedijk, J. Am. Chem. Soc., 1996, 118, 2190–2197 CrossRef CAS; (c) M. Shakir, S. Parveen, N. Begum and P. Chingsubam, Transition Met. Chem., 2004, 29, 196–199 CrossRef CAS.
- W. L. Jolly, Modern Inorganic Chemistry, McGraw-Hill, Inc., New York, 1991 Search PubMed.
- C.-F. Sheu, S.-M. Chen, S.-C. Wang, G.-H. Lee, Y.-H. Liu and Y. Wang, Chem. Commun., 2009, 7512–7514 RSC.
- N. Moliner, M. C. Muñoz, S. Létard, J.-F. Létard, X. Solans, R. Burriel, M. Castro, O. Kahn and J. A. Real, Inorg. Chim. Acta, 1999, 291, 279–288 CrossRef CAS.
- G. Dupouy, M. Marchivie, S. Triki, J. Sala-Pala, J.-Y. Salaün, C. J. Gómez-García and P. Guionneau, Inorg. Chem., 2008, 47, 8921–8931 CrossRef CAS PubMed.
- N. Moliner, A. B. Gaspar, M. C. Muñoz, V. Niel, J. Cano and J. A. Real, Inorg. Chem., 2001, 40, 3986–3991 CrossRef CAS PubMed.
- M.-L. Tong, C.-G. Hong, L.-L. Zheng, M.-X. Peng, A. Gaita-Arińo and J. M. Clemente Juan, Eur. J. Inorg. Chem., 2007, 2007, 3710–3717 CrossRef.
- M.-X. Peng, C.-G. Hong, C.-K. Tan, J.-C. Chen and M.-L. Tong, J. Chem. Crystallogr., 2006, 36, 703–707 CrossRef CAS.
- I. Potočňák and L. Váhovská, Z. Kristallogr., 2014, 229, 579–586 Search PubMed.
- A. B. Gaspar, M. Carmen Muñoz, N. Moliner, V. Ksenofontov, G. Levchenko, P. Gütlich and J. Antonio Real, Monatsh. Chem., 2003, 134, 285–294 CrossRef CAS.
- R. Boča, Struct. Bonding, 2006, 117, 1–264 CrossRef.
- J. Titiš and R. Boča, Inorg. Chem., 2011, 50, 11838–11845 CrossRef PubMed.
- R. Boča, Theoretical Foundations of Molecular Magnetism, Elsevier, Amsterdam, 1999 Search PubMed.
- J. S. Griffith, The theory of transition metal ions, Cambridge University Press, 1961 Search PubMed.
- M. E. Lines, Phys. Rev., 1963, 131, 546–555 CrossRef CAS.
- B. N. Figgis, M. Gerloch, J. Lewis, F. E. Mabbs and G. A. Webb, J. Chem. Soc. A, 1968, 2086–2093 RSC.
- R. Boča, A Handbook of Magnetochemical Formulae, Elsevier, Amsterdam, 2012 Search PubMed.
- (a) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78 CrossRef CAS; (b) F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1327 CrossRef.
- K. Pierloot, Computational Organometallic Chemistry, ed. T. R. Cundari, Marcel Dekker, Inc., New York, 2001, p. 123 Search PubMed.
- (a) C. Schäffer, Pure Appl. Chem., 1970, 24, 361–392 CrossRef; (b) T. Schönherr, M. Atanasov and H. Adamsky, ed. J. A. McCleverty and T. J. Meyer, Comprehensive Coordination Chemistry II, From Biology to Nanotechnology, Elsevier, 2003, vol. 2, pp. 443–455 Search PubMed; (c) B. N. Figgis and M. A. Hitchman, Ligand Field Theory and Its Applications, Wiley-VCH, New York, 2000 Search PubMed.
- (a) M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 149–220 Search PubMed; (b) S. K. Singh, J. Eng, M. Atanasov and F. Neese, Coord. Chem. Rev., 2017, 344, 2–25 CrossRef CAS.
- P. E. Hoggard, Topics in Current Chemistry, Springer-Verlag, Heinrich Heine Universitat, Berlin, Germany, 1994, vol. 171, pp. 113–141. The AOMX program is maintained by H. Adamsky, Institut fur Theoretische Chemie, Berlin, Germany, Springer-Verlag, Heinrich Heine Universitat, e-mail: E-mail: adamsky@theochem.uni-duesseldorf.de Search PubMed.
- See e.g.: (a) I. Nemec, R. Herchel and Z. Trávníček, Dalton Trans., 2016, 45, 12479–12482 RSC; (b) C. Rajnák, J. Titiš, O. Fuhr, M. Ruben and R. Boča, Inorg. Chem., 2014, 53, 8200–8202 CrossRef PubMed; (c) D. Valigura, C. Rajnak, J. Moncol, J. Titis and R. Boca, Dalton Trans., 2017, 46, 10950–10956 RSC.
- R. L. Carlin, Magnetochemistry, Springer-Verlag, Berlin, 1986 Search PubMed.
- Oxford Diffraction, CrysAlis CCD, CCD Data Collection GUI, Oxford Diffraction Ltd., Oxford, UK, 2007 Search PubMed.
- L. Palatinus and G. J. Chapuis, Appl. Crystallogr., 2007, 40, 786–790 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2017, 71, 3–8 CrossRef PubMed.
- A. L. Spek, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2009, 65, 148–155 CrossRef CAS PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- K. Brandenburg, DIAMOND (Version 3.2i) Crystal Impact GbR, Bonn, Germany, 2009 Search PubMed.
- P. Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194 CrossRef CAS.
- (a) C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305 CrossRef CAS; (b) C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264 CrossRef CAS; (c) C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138–9153 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- D. Ganyushin and F. Neese, J. Chem. Phys., 2006, 125, 024103 CrossRef PubMed.
- F. Neese, J. Chem. Phys., 2005, 122, 034107 CrossRef PubMed.
- R. Maurice, R. Bastardis, C. de Graaf, N. Suaud, T. Mallah and N. Guihéry, J. Chem. Theory Comput., 2009, 5, 2977–2984 CrossRef CAS PubMed.
- F. Weigend, J. Comput. Chem., 2008, 29, 167–175 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- R. Brent, Algorithms for Minimization without Derivatives, Dover, 2002 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Additional X-ray data, magnetic data and analysis, and details of theoretical calculations. CCDC 1583578–1583583. For ESI and crystallographic data in CIF or other electronic format see DOI: 10.1039/C7DT04256F |
| This journal is © The Royal Society of Chemistry 2018 |