The atomic level mechanism of white phosphorous demolition by di-iodine

Abstract

A detailed mechanism of the I₂-induced transformation of white phosphorus into PI₃ emerges from a DFT analysis. This multi-step process implies that at any stage one P–P and two I–I bonds cleavages, associated with the formation of two P–I bonds plus an in situ generated brand new I₂ molecule. Significant electron transfer between the atoms is observed at any step, but the reactions are better defined as concerted rather than redox. Along the steepest descent to the product, no significant barrier is encountered except for the very first P₄ activation, which costs +14.6 kcal mol⁻¹. At the atomic level, one first I₂ molecule, a typical mild oxidant, is first involved in a linear halogen bonding interaction (XB) with one P donor, while its terminal I atom is engaged in an additional XB adduct with a second I₂. Significant electron transfer through the combined diatomics allows the external I atom of the dangling I₃ grouping to convey electrons into the σ* level of one P–P bond with its consequent cleavage. This implies at some point the appearance of a six-membered ring, which alternatively switches its bonding and no-bonding interactions. The final transformation of the P₂I₄ diphosphine into two PI₃ phosphines is enlightening also for the specific role of the I substituents. In fact, it is proved that an organo-diphosphine analogue hardly undergoes the separation of two phosphines, as reported in the literature. This is attributable to the particularly high donor power of the carbo-substituted P atoms, which prevents the concertedness of the reaction but favors charge separation in an unreactive ion pair.

---

Introduction

The interconversion between various allotropes of elemental phosphorus depends on several factors, in particular temperature and pressure but also on the involvement of other chemical species.¹ Our group has devoted much attention towards the molecular white phosphorus, P₄, and its behavior toward transition-metal fragments from both the experimental and theoretical viewpoints.² Such a know-how is also deemed important for interpreting the behavior of other P allotropes such as that of the polymeric red³ and black⁴ phosphorus. In particular, our interest is being presently attracted by the latter, as a precursor of the 2D material, phosphorene, which is obtainable upon exfoliation of the black phosphorus.⁵ As a matter of fact, we are currently involved in a project⁶ aimed at exploring the functionalization of the rugged phosphorene sheets with organic and inorganic species. As in P₄, all the phosphorene sp³ P-atoms are pyramidally connected to the other three equivalent ones, hence a good understanding of the white phosphorus reactivity may offer an interpretational key for studying the behavior of the other allotropes. For instance, it has been reported that phosphorophilic di-iodine molecules contribute to the transformation of red phosphorus into the more ordered black allotrope,⁷ thus suggesting that in this case also some P–P bonds cleave and recombine into a different structure with also containing pyramidal atoms.

In solution, the P₄ molecule is known to be transformed by I₂ into four PI₃ molecules, as summarized by eqn (1):^8,9

P₄ + 6I₂ → 4PI₃ (1)

In spite of relatively small number of atoms involved, no detailed atomic level mechanism of the process has been reported yet. Only a limited number of reaction intermediates have emerged from NMR spectroscopic studies,¹⁰ while more species have remained undisclosed, likely due to their short lifetime. Since modern computational chemistry allows for the detection of even feeble stationary points (including transition states), we present here a reconstruction of the multi-step process of eqn (1) based on a series of sequential energy profiles. In particular, since the diphosphine P₂I₄ is perhaps the best experimentally characterized intermediate in the process,⁹ and possibly the most immediate precursor of PI₃, eqn (1) was split into two sequential parts, such as eqn (2) and (3), respectively:

P₄ + 4I₂ → 2P₂I₄ (2)

P₂I₄ + I₂ → 2PI₃ (3)

As an emblematic step, eqn (3) suggests the inner P–P σ bond cleavage, accompanied by the I–I bond to give two new P–I bonds, thus suggesting a formal 2 + 2 symmetry forbidden reaction. From the orbital viewpoint, this implies the interconversion of σ bonding into σ* MOs or the other way around, with an invariably difficult electron transfer between the levels.¹¹ Another doubt is with respect to the reported method of synthesis for P₂I₄, based on the disproportionation of PI₃.¹² By assuming that eqn (3), in the given form is reverse, there would be again a problem of forbidden symmetry, to the point that one starts doubting on the correct proposition of eqn (3). Also the occurrence of similar problems for some of the steps summarized in eqn (1) cannot be a priori excluded.

With the previous points in mind, an in silico DFT analysis of the whole process was attempted to monitor the mode of electron redistribution and its implications for redox behavior. The latter is more probable for the parallel P₄ + O₂ stepwise process, given the larger electronegativity difference between the atoms. In fact, in the derivatives P₄O₆ and P₄O₁₀ the electrons are preferentially assigned to the oxygen atoms implying that the phosphorus oxidation state evolves from the zero value in P₄ to +3 and +5, respectively.¹³ Such a conclusion appears more questionable for the reactivity of P₄ with I₂, given that the larger electropositivity of the element is closer to that of phosphorus. On the other hand, the participation of I₂ in redox processes is rather general, a previous example studied by us being the oxidation of classic 44e⁻ phosphide bridged Pt₃ clusters to 42e⁻ derivatives with the reduced iodides as terminal ligands.¹⁴

In our computational approach to the P₄ activation, the DFT-D functional was used,¹⁵ since the dispersion forces help detecting particularly feeble adducts, some of which are endergonic and clearly disfavored by entropy. In particular, the latter highlights incipient Halogen Bonding (XB), still far from its canonic formulation emerging in frozen crystal structures,¹⁶ which clearly indicate the occurrence of a major electron density redistribution. In any case, the feeble adducts are fundamental to monitor the energy profile of any given step, characterized by the dynamic evolution of the XB species, which encompasses at some point the features found in the frozen crystal structures and beyond. Accordingly, the calculations were based on the dichloromethane PCM model,¹⁷ in search of consecutive minima and transition states, in order to obtain a complete picture of the progressive electron redistribution at the linear P–I–I assembly and the eventual P–P bond cleavage.

All the steps contributing to eqn (1) seem to imply a concerted process, mainly because of the relatively low basicity of the various P atoms interacting with di-iodine. This point also holds for the allegedly final activation of P₂I₄ to give PI₃ (eqn (3)), but we became somewhat dubious about the result, after reading a recent paper by Cummins and coworkers,¹⁸ who showed how some related organo-substituted diphosphines does not afford any phosphine product with I₂. Eventually, a reasonable explanation of the difference has been found and will be presented toward the end of this paper, while here we anticipate that it most likely depends on the donor power locally available at the atoms of the P–P bond on whether the latter may be cleaved or not.

Other studies in the literature concern the P₄ + I₂ reactivity in the presence of additional co-reactants. For instance, the role of the Ag⁺ cation in the homoleptic silver complex [(P₄)₂Ag]⁺ and others¹⁹ has been summarized in a review article.²⁰ Otherwise, the P₄ activation has been performed in the presence of carbene moieties, which afford partial but incomplete P–P demolition and formation of the P=P double bond.²¹ The latter feature has never been observed by us, excluding such a possibility in our mechanism (vide infra). In other cases, the reaction is promoted by organic radicals²² including a transition metal fragment such as Cp(CO)₂Fe, originating from the homolysis of its dimeric precursor and carrying an unpaired spin at the d⁷ metal.²³ In this regard, other authors have remarked how an unassisted P₄ + I₂ reaction excludes the access to any radical species.²⁴ Also, the calculations corroborated such a result, since our attempts of isolating reaction radical intermediates invariably failed.

A final point concerns the various energy profiles, which emerged from tested analyses of the possible, alternative steps. Most of them occur with evident energy gain and the lack of substantial barriers, with the most important exception of the very first P₄ activation, estimated to be as large as +14.6 kcal mol⁻¹, with an approximate half one later in the process. This implies that the P₄ demolition requires in any case an initial but not excessive activation energy, after which it proceeds rather smoothly to the end.

Experimental section

All the compounds were optimized, within the Gaussian09 program,²⁵ by using the hybrid density functional B97-D.¹⁵ The dispersion forces in the latter are fundamental for allowing some aggregation of the species with consequent definition of the step profiles. All the free energies, derived after the calculations of the vibrational frequencies, refer to a temperature of 298 K. All the calculations were based on the CPCM model¹⁷ for the dichloromethane solvent, most typically used in the various experiments. The basis set 6-31G inclusive of polarization functions was basically used, although as a simplification the Stuttgart/Dresden (SDD) pseudo-potential²⁶ was used for iodine. This appears to be at the origin of some overestimation of the calculated distances vs. the experimentally available ones. The coordinates of the optimized structures and their energetic parameters are reported in the ESI.†

Results and discussion

General aspects of the reactivity between white phosphorus and di-iodine

Eqn (1) is exergonic at −76.4 kcal mol⁻¹, of which −47.4 kcal mol⁻¹ is for the double diphosphine production in eqn (2). The final derivation of the PI₃ product (eqn (3)) affords a further free energy gain of −14.5 kcal mol⁻¹ per P₂I₄ molecule. The computational analysis started with the initial formation of the di-iodine adduct with P₄ and continued with other subsequent derivatives, whose evolution was monitored by a series of relaxed scans of reasonable reaction coordinates. All the encountered key points were then fully optimized, as minima or transition states, thus allowing precise stepwise profiles, based on structural motifs most of which are present in the literature.

To facilitate the reading of the paper, all the steps, detected through the strategy, are anticipated in Fig. 1 and refer to the evolution of the P₄ skeleton, without addressing yet the role of di-iodine molecules to be illustrated case by case. Also, Fig. 1 is subdivided into two main streams, with the left side essentially representing the succession of eqn (2) and (3), while the right side is indicative of possible alternative steps. Cut down to the bone, each step mainly corresponds to a new P–P cleavage, hence it is identified by a progressive Roman number, which is accompanied by an alphabetic character in the case of alternative routes.

Fig. 1 Flowchart showing the computed phosphorus intermediates in the process of eqn (1). The mode of action of the I₂ reactants is similar in the various steps and will be separately illustrated.

The diphosphine cleavage in eqn (3) occurs twice in the left side cascade, but only once in the right side, where some PI₃ product forms at earlier stages, suggesting eqn (4) in place of eqn (2):

P₄ + 5I₂ → P₂I₄ + 2PI₃ (4)

The energy evaluation of the overall eqn (4) shows that the P₂I₄ diphosphine formation is more exergonic than that through eqn (2) (−61.9 vs. −47.4 kcal mol⁻¹), but only for a half amount of the product, since, as expected, the energy balance of the whole process must be the same. The following detailed analyses show that basically any step implies a nucleophilic interaction of an electron pair at P₄ (or one of the fragments derived from its degradation) with I₂ molecule(s). Some behavior difference arises because the P donor power is not constant but varies with local geometry and interconnections. For instance, the original P₄ basicity is the smallest detected, likely due to its strained tetrahedral structure. In any case, however, any incipient P⋯I–I adduct is linear, even suggesting a native Halogen Bonding (XB), which can still be far from its classic equilibrium features, emerging from frozen crystal structures. The latter are generalized with a generic D base (the P lone pair in our case) and a X–Y halogen donor or a X₂ dihalogen, one of which is I₂ itself.¹⁶ The stronger the base, the larger the P–I bonding interaction, while the I⋯I elongation is enhanced with accumulation of the electron density at the most external I atom, closer to an iodide. According to the XB definition,¹⁶ the residual I⋯I interaction is mainly of electrostatic forces, which somehow hide the electron transfer and/or polarization effects occurring to reach the point. On the other hand, the monitoring of the evolution from the initial adduct as well as the underpinning of the ultimate XB scission have been scarcely documented to date. Moreover, the steps for the P₄ reactivity are peculiar not because of the actual heterotypic scission of the terminal iodide at the end of each step, but for the subsequent P–P cleavage associated with the formation of two new P–I bonds. Previously, we have already addressed some other peculiar behavior of XB adducts formed at a metal center upon the I₂ addition to a chloride ligand, which is intriguingly substituted by an in situ formed less electronegative iodide.^27,28 Also in this case, the key information was extracted by the computational monitoring of the system's evolution involving a XB dynamism. The general electronic underpinnings of the latter are briefly summarized in the next section.

Dynamic aspects of the halogen bonding (XB)

In a typical D^δ+–X⋯X^δ− XB interaction (where D is a generic base), the scission of the terminal halide is controlled by the D's donor power. It has been found that the latter is also related to the surrounding crystalline environment, as it has emerged from a number of X-ray structures, with an asymmetric I₃⁻ anion in place of the symmetric expected one.²⁹ This may be seen as a peculiar XB species, where the more distal lateral iodide has for some reason accumulated a larger electron density, hence has a somewhat lower donor power than its trans-axial analogue. Our proposed explanation²⁷ was based on the different interactions of the lateral I₃⁻ atoms with the surrounding cations in the cell. Thus, the more affected I atom is forced a higher accumulation of electron density and behaves as a weaker donor toward the associated I₂ moiety. The extent of the effect varies crystal to crystal, as shown by the various degrees of I₃⁻ asymmetry in different structures. Consequently, the asymmetric I₃⁻ species are like snapshots along the dynamic evolution path of XB. To further clarify the point, we refer to some of our experimental and theoretical analyses^27,28 of generic D⁺–I⋯I⁻ adducts. The larger the D donor power, more electron density is drifted into the I₂ σ* level, which behaves as a unique acceptor because of its relatively low energy. The consequence is that the abstraction of the terminal iodide is progressively easier, especially if facilitated by the presence of a polar solvent. For instance, this occurs in the preparation of organo iodo-compounds from a strong donor such as a carbo-anion and I₂, where the dynamism of the XB intermediate is particularly relevant.³⁰ As mentioned, even a XI₂⁻ mixed trihalide (formally similar to an asymmetric I₃⁻) may undergo a dynamic electron redistribution to the point that a coordinated Cl–I–I⁻ trihalide separates one iodide from the hetero-diatomic I–Cl, which was experimentally detected by Raman spectra.²⁸

To generalize the expected trends of electronic redistribution in a linear XB system, we emphasize the qualitative implications of the generic HOMO in Scheme 1.²⁷ In the latter, the sp hybridization of the central atom depends on the lateral donor power. Only for a fully symmetric triiodide, the central p orbital is uninvolved, with the s orbital alone being equally antibonding, hence repulsive at both sides because of its formal population.³¹ This is consistent with the intrinsic hypervalent character of the symmetric trihalides and more in general XB, because the feature persists upon asymmetrization.

Scheme 1 HOMO of a generic halogen bonded Y–X–D species suggesting the stretching trends.

The control of the relative power of the lateral donors is responsible for the p mixing, which reinforces the bonding of the stronger donor to the central atom. Conversely, a large sp lobe develops toward the opposite weaker donor, which is most likely the terminal halide of the XB system. The latter is affected by bond stretching, if not an actual scission. The fact that the HOMO has larger contributions to the antibonding area, implies a corresponding electron density accumulation, with increasing possibility of the terminal halide scission, especially with the support of an abstractor.

The limiting adducts of an organo-phosphine with di-iodine

The previously indicated trends of XB interactions are experimentally corroborated by the available structures of the 1 : 1 and 1 : 2 adducts of the organo-phosphine PⁱPr₃ with di-iodine.^32,33 Already in PⁱPr₃·I₂ shown in Fig. 2a,³² the I–I distance of 3.38 Å is definitely weakened with respect to the free diatomic of 2.73 Å, while the P–I bond could be considered as single (2.41 Å).

Fig. 2 Experimental structures of PⁱPr₃·I₂ (a) and PⁱPr₃·2I₂ (b) with geometric parameters shown in red italics, while the black ones are those of the corresponding optimized P(CH₃)₃ models.

The mentioned experimental values (in red italics) are satisfactorily reproduced in the DFT optimized model P(CH₃)₃·I₂, shown in black in Fig. 2a.³⁴ Moreover, the distal I atom is found to have a −0.7 charge, consistent with the realistic XB character of the adduct. The structure of the 1 : 2 PⁱPr₃·2I₂ adduct in Fig. 2b ³³ indicates that a second and residually acidic I₂ molecule has the possibility of acting as a real extractor of the first formed iodide, as indicated by the large and non-bonding I⋯I separation of 3.71 Å, attained by the first molecule and the ±0.92 charge separation of the phosphonium and tri-iodide counterions. As a matter of fact, the optimized model best formulates as the ion pair {[P(CH₃)₃I]⁺[I₃]⁻}, although the computed I⋯I and P–I distances and the I₃⁻ asymmetry are somewhat more pronounced than in the experimental data. A better consistency instead is observed for the P–I⋯I angles of 167.1° and 171.1° in the experimental and in silico 1 : 2 species, respectively. The latter deviation from linearity confirms some lost XB character of the first adduct, after the formation of the classic I₃⁻ species. In any case, the computed free energies of the P(CH₃)₃ adducts are consistent with a very high donor power of the organo substituted phosphines. In fact, P(CH₃)₃·I₂ is already exergonic at −23.5 kcal mol⁻¹, while the 1 : 2 adduct gains an additional −7.8 kcal mol⁻¹. In this respect the aggregation of up to three molecules is entropically penalized up to the estimated value of +16.7 kcal mol⁻¹, which is nonetheless overwhelmed by the highly exothermic electron transfer in these species. The entropy seems instead to favor the physical separation of the counterions [PR₃I]⁺ and I₃⁻ by the endergonic amount of −5.6 kcal mol⁻¹. An important conclusion about the phosphine adducts is the occurrence of an actual 1e⁻ redox process independently from the actual separations of the counterions [P(CH₃)₃I]⁺ and I₃⁻ or their combination as an ion pair. Such a picture greatly differs from any of those encountered in the overall P₄ demolition by I₂, because of the limited possibilities of electron transfer with scarcely dative P atoms, such as the I-substituted ones. This point will reappear frequently in the subsequent discussion.

Domino evolution of the P₄ reactivity

Independent of the routes in Fig. 1, the large exergonic balance of the overall process is consistent with its easy experimental occurrence. The possible barriers in various steps have not yet been remarked upon, but they are either small or absent in most cases, except in the very early stages (e.g., steps I or IIa) because of reasons to be clarified. Importantly, the general mode of attack of a P lone pair into I₂ compares with that already illustrated in Fig. 2 relative to the collinear interaction of an organo-phosphine lone pair with a diatomic, with further enhancement of electron transfer upon the addition of a second one. This occurs also in the various steps of the P₄ activation with the basic difference that the less dative P atom transfers a reduced amount of electrons, without preventing the further evolution of the systems in the form of a new P–P bond cleavage. In contrast, the latter event will be shown to be definitely more difficult upon a large shift of the electron density, which leads to an apparently inert ion pair. These aspects, as well as other problems, encountered step by step, will be addressed in the following discussion.

First P–P bond cleavage in P₄

Since no adduct between I₂ and P₄, 1, has ever been experimentally reported or detected, its identification was attempted in silico. To have more chances of identifying such a feeble adduct, the DFT-D functional¹⁵ was adopted, also because the dispersion forces have already enabled us to detect some otherwise metastable metallo-organic initiators of catalytic processes for the transformation of azides.³⁵ Also in this case, an initial minimum of formula P₄·I₂, 1·I₂ (on the left side of Fig. 3) was optimized, although endergonic by as much as +6.2 kcal mol⁻¹. Any lone pair of a P₄ tetrahedron is a potential donor, as shown for instance by its behavior as a η¹ ligand toward a vacant σ metal acceptor. An example is the complex [(np₃)Ni(η¹-P₄)] (where np₃ = N(CH₂CH₂PPh₂)₃),³⁶ first reported by our institute, which was followed by other η¹-P₄ complexes.² Conversely, no structure is available to support the dative interaction of P₄ toward I₂, whose residual acceptor capabilities are given by its σ* level. As a matter of fact, the latter must be higher in energy than any reasonable metal σ hybrid with d character.

Fig. 3 Optimized adducts between P₄ and one or two I₂ molecule(s).

It is evident that in 1·I₂ the dative interaction is still very poor, although its incipient XB character is indicated by the collinearity of the P⋯I and I–I vectors. The lengths of the latter however (3.23 and 2.79 Å, respectively) prove a minimum electron redistribution, which suggested a search for possible alternatives. Thus, by assuming residual basicity for any bent and strained P–P linkage, the species 1·(I₂)_br, in the middle of Fig. 3, was optimized with I₂ in the perpendicular orientation. Also, in this case the diatomic seems minimally perturbed in view of the two large P–I_bridge distances of 3.64 Å. On the other hand, in view of the 0.05 Å P–P elongation and the smaller endergonic balance of +3.9 kcal mol⁻¹, a second diatomic was added to favor the electron withdrawing from P₄, similarly to what happens for the phosphine's bis-adduct of Fig. 2b. As a matter of fact, the new species 1·2I₂, on the right side of Fig. 3, was equally optimized starting from either one of the mono-adducts 1·I₂ or 1·(I₂)_br. An enhanced electron redistribution is indicated by the 0.04 Å stretching of the first added I₂, while its terminal I₁* atom is already forming a quasi-orthogonal I₃ grouping. Also, the 0.03 Å elongation of the P₁–P₂ bridged bond and the average ∼0.15 Å shortening of the P–I_bridge distances are indicative of some activation as well as the almost null free energy cost of the adduct (only +0.7 kcal mol⁻¹). In trying to guess how the species 1·2I₂ may further evolve toward the expected P–P cleavage, we noticed the large spatial freedom of the terminal I₃ grouping. Hence we tested, as a possible reaction coordinate, the shortening of the I₂⋯P₂ distance down to a bonding value. The corresponding relaxed scan from 8.47 to 2.55 Å highlighted a promising profile, since the initial energy loss of only 10 kcal mol⁻¹ later converted to a double size energy gain, all through reasonable chemical species. In fact, the encountered key points could then be fully optimized, affording for step I the precise free energy profile as shown in Fig. 4. Indeed, such a strategy based on relaxed scans and full optimizations allowed us to construct the flowchart of Fig. 1. The process shown in Fig. 4 starts from the left with the separated P₄ and I₂ reactants, which assemble into the adducts 1·(I₂)_br and 1·2I₂ shown in Fig. 3 with a total energy cost of +4.6 kcal mol⁻¹. Another +10.0 kcal mol⁻¹ must be added to reach the transition state (1–2)_TS, whose overall barrier of +14.6 kcal mol⁻¹ is the highest in the overall P₄ demolition process, which hence requires an activation energy to be triggered. Remarkably at (1–2)_TS, the first added I₂ molecule is stretched by 3.45 Å, suggesting that an important electron delocalization has already occurred, as also underlined by the 0.6 Å shortening of the P–I bridging linkages, still almost symmetric. On the other hand, the I₁–I₁* vector is no more perpendicular to P₁–P₂, but reoriented to align with the terminal I₂ atom of the I₃ grouping with the P₁–P₂ linkage (angle of 171°).

Fig. 4 Profile of step I for the first activation of P₄ by two I₂ molecules (free energies in kcal mol⁻¹).

Although at (1–2)_TS the I₂⋯P₂ separation is still as large as 4.20 Å, it seems that some iodine electron density may start transferring to the P₁–P₂ σ* level, as also indicated by the 2.57 Å P₁–P₂ elongation. An effect of this sort for the P–P bond weakening was previously remarked by other authors.³⁷ Also, the vibrations of the unique imaginary frequency for (1–2)_TS is indicative of the intended I₂⋯P₂ bond shortening. Another point worth noting is that the mentioned 3.45 Å elongation of the first added diatomic is still ∼0.3 Å shorter than that of the organo-phosphine aggregate PⁱPr₃·2I₂ shown in Fig. 2b, hence one cannot yet propose an ion pair formulation for it, a point, whose importance will become more evident later.

After (1–2)_TS, the P₁–P₂ bond definitely cleaves, as it emerges from the two subsequent minima, namely the metastable adduct IP₄I·I₂, 2·I₂, and the isolated butterfly 2. Obtaining the former species is exergonic by −20.3 kcal mol⁻¹, while another −2.0 kcal mol⁻¹ is gained on dismantling the residual XB interaction which holds together 2 with the I₂ molecule. The nature of the latter must be emphasized, because it is generated in situ from the two original I₂ molecules, cooperating in the step. Such an event will be repeatedly observed throughout the P₄ demolition, and emphasizes the importance of having I₂ and the associated phosphorous reactant in the 2 : 1 ratio.³⁸

In closing the description of step I, we address the chemical reliability of the butterfly 2 based on the data in the literature and CCDC database.²⁹ From previous NMR investigation of the P₄ + X₂ reaction in CS₂ (X = Cl, Br),^10b the formation of distinct butterfly isomers emerged. In the latter, the two X substituents may point in either opposite direction (as in 2) or both hang over the butterfly's cavity. The former isomer was 4 : 1 more abundant, although information for X = I is definitely less clear in this respect. Also, various structures of the carbo-substituted RP₄R analogues are known in isomeric forms.³⁹ To find possible implications for our system, optimization of the isomer alternative to 2 was found to be +12.2 kcal mol⁻¹ less stable (see Fig. S1†) and moreover the interconversion energy is as high as +35 kcal mol⁻¹. These results suggested continuing the analysis of any possible steps II, exclusively starting from the isomer 2.

First considerations on the plausible concerted mechanism of the P₄ demolition

From the results outlined to date, the following indications emerge:

(i) The P–P cleavage does not exclusively produce only an I-substituted derivative of P₄ but also a brand new I₂ molecule. The latter is indicated as I*–I* to imply its generation from two distinct I–I* diatomics, whose I atoms form the new P–I linkages. Implicitly, step I corresponds to the ter-molecular reaction, shown in eqn (5), which affords two products. By the same token, the ultimate and emblematic diphosphine cleavage in eqn (3), better formulates as eqn (3′), as well as many other intermediate steps:

P₄ + 2I–I* → IP₄I + I*–I* (5)

P₂I₄ + 2I–I* → 2PI₃ + I*–I*. (3′)

Certainly, the continuously reformed I₂ molecules are reutilized in the process, so that overall eqn (1) does not necessarily imply a double number of diatomics (e.g., 12 rather than 6), while it is fundamental that the amount of di-iodine is constantly doubled compared to any P-based reactant.

(ii) The mechanistic study implies that step I and the following ones involve the combination of 3 + 3 bond breakings/makings, in place of the assumed 2 + 2 one.

(iii) The species (1–2)_TS shown in Fig. 4 adumbrates a distorted six-membered P₂I₄ ring (this is the only case also featuring an endocyclic connection, such as the I₁–P₂ one), while somewhat more regular rings will appear in the subsequent steps. Importantly, the sides of the ring convert into two distinct sets 3 + 3 bonds/no-bonds when moving in alternative directions with respect to TS or a point in its proximity (see below). This apparently corroborates the idea of concertedness, implying a significant electron density redistribution between any pair of adjacent connections. With regard to this, it has been already mentioned that the P–P cleavage seems promoted by the σ* population, with the 4e⁻/2c configuration implying initial repulsion, which is eventually mitigated since the bonding and antibonding electron pairs become local and reoriented P lone pairs.

(iv) The concerted mechanism is in particular attributable to the relatively low donor power of the P atoms, such as those of P₄ or its iodine-derivatives. In contrast, the larger donor power of organo-substituted analogues induces, as in the case of the phosphines shown in Fig. 2, a significant charge separation at the I₂ reactant(s), with the resulting ion pair having no further possibility of concerted evolution. The most evident difference between the two situations will emerge, toward the end of this paper, from the behavior of the two differently substituted diphosphines (vide infra).

Second P–P bond cleavage

From the butterfly 2, the P₄ demolition may continue in two possible ways, given that the P–P bond to be cleaved may be either the hinge (step IIa)⁴⁰ or a peripheral one (step IIb). The former is closer to any one of the P₄ precursor, given that its atoms all form P–P bonds, hence one may predict a difficult aggregation with the I₂ molecule(s). As a matter of fact, step IIa encounters some, but not insurmountable, difficulty, which seem to favor the alternative step IIb.

Cleavage of the IP₄I butterfly's hinge (step IIa)

Although the initial aggregate (2·2I₂)_hinge could be reasonably expected to have the P–P edge bridged by I₂, as in 1·2I₂ shown in Fig. 4, the feature is not found in the profile given in Fig. 5, given that only one P atom (P₃) is associated with two I₂ molecules.

Fig. 5 Step IIa for the di-iodine attack on the hinge of the butterfly 2 to give the final puckered four-membered ring 3 (free energies in kcal mol⁻¹).

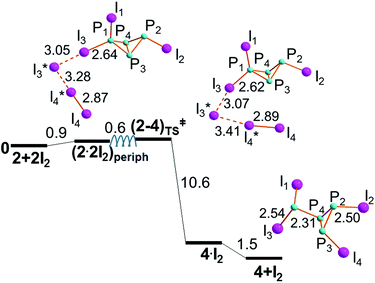
Apparently, the P basicity must be somewhat larger, possibly due to the less strained character of the P–P bond. A more effective interaction is confirmed by the P₃–I₃ and I₃⋯I₃* distances of 2.67 and 3.05 Å, respectively, which are indicative of somewhat more pronounced effects than in any adduct of 1. Moreover, (2·2I₂)_hinge has about half energy cost of +2.2 kcal mol⁻¹. Also, the externally dangling I₃ grouping is again suited for the relaxed scan analysis based on the I₄⋯P₄ shortening. This allowed the optimization of the key points down to the cleavage of the P–P hinge and beyond it. The precise profile features at (2–3)_TS the second significant barrier detected in the whole process. Its +8.4 kcal mol⁻¹ height is about halved with respect to (1–2)_TS, while a significant difference is of the lack of bridge-bonding at the P–P linkage to be cleaved. The first diatomic is instead practically cleaved at 3.90 Å, with the quasi-symmetric terminal I₃ grouping already significantly charged (−0.7). The P₄–P₃ bond is not however significantly stretched (2.37 Å), apparently because the I₄⋯P₄–P₃ angle of 153° is still somewhat bent to limit the electron transfer to the P₄–P₃ σ* level. Most likely, the situations change on the following descent from TS, given that the distance becomes as large as 3.10 Å in the product (PI)₄, 3, with the shape of a puckered four-membered ring. As usual, the product 3 is preceded by an adduct (3·I₂ in Fig. S2†), where the in situ formed I₃*–I₄* diatomic is still slightly interacting. The estimated free energy gains are −17.6 kcal mol⁻¹ at 3·I₂ and −19.6 kcal mol⁻¹ upon separation of the components.

The chemical reliability of the product 3 is corroborated by other analogues in the literature, although without the prove of ad hoc NMR studies.¹⁰ In any case, the stereochemistry of 3 is peculiar for the two pairs of consecutive P–I linkages (not even parallel to each other), which simultaneously point to opposite sides of the ring. No other example of this is instead present in the CCDC,²⁹ which in no case has a P₄ ring with only halogen substituents, but at most two of them in the species P₄I₂(SiR₃)₂.⁴¹ Since other structures feature pairs of trans-diagonal organo-substituents on the same side of the P₄ ring, we computationally tested such a stereochemistry also for (PI)₄. Hence, the corresponding species 3′ in Fig. S3† was compared with that of 3, in order to find out an insignificant energy difference of only <1 kcal mol⁻¹ with a negligible interconversion barrier, as shown by the flat PES near TS. On the other hand, the unique relevance of 3vs. 3′ clearly emerged on analyzing the subsequent step IIIa (see below), which is unique, given that the terminal I₃ rearrangement is highly hindered by the substituents, when starting from 3′.

Cleavage of one peripheral P–P linkage of the IP₄I butterfly (step IIb)

The aggregation of two I₂ molecules is less unhindered at one I-substituted P atom of 2, possibly because the flexibility of the terminal P–I vector confers a larger degree of basicity to the P lone pair. Indeed, the aggregate (2·2I₂)_periph is less endergonic than the (2·2I₂)_hinge one, as it emerges from the comparison of Fig. 5 and 6. Also, the analogue of (2·2I₂)_periph involving the P₂ rather than the P₁ atom has been discarded because the terminal I₃ rearrangement would be hindered by the P₁–I₁ linkage already oriented over the cavity of the butterfly. Hence, step IIb uniquely proceeds as shown in Fig. 6, almost being also barrierless. In fact, a destabilization of only +0.6 kcal mol⁻¹ was estimated by our initial scan, which showed a plateau around (2–4)_TS^‡, which could not be fully optimized. After the latter, our strategy afforded the detailed energy profile given in Fig. 6, still apparently consistent with a concerted mechanism.

Fig. 6 Step IIb for the I₂ attack on one external I-substituted atom of the butterfly 2. The species (2–4)_TS^‡, resulting from a relaxed scan, could not be fully optimized for lying on a flat plateau, indicated by the helical connection (free energies in kcal mol⁻¹).

Although the evolution of the butterfly 2 seems easier through step IIb, step IIa cannot be automatically excluded under the conditions for triggering the P₄ activation, since the barrier, is only half of that already passed in step I. On the other hand, the missing barrier for step IIb seems to imply a subsequent energy gain of only −10.6 kcal mol⁻¹ at the species 4·I₂ (see Fig. S4†), with an additional −1.5 kcal mol⁻¹ gained for the ultimate separation of 4. The latter can be synthetically formulated as I₂P-P₃I₂, to indicate in the right a P₃ ring with three exocyclic bonds, i.e., two equally oriented P–I ones and another P–PI₂ one in opposite directions with respect to the triangle. Again, experimental analogues are known with organo- in place of halogen substituents. Perhaps, the most related species is RClP-P₃ClR with R being a substituted phenyl ring.⁴² In some cases, the two substituents on the same side of the P₃ ring are interconnected by a chain,⁴³ while in 4 two adjacent P–I linkages are not exactly parallel to avoid a close contact.

Third P–P bond cleavage

The cascade of steps through the general mechanism continues from both products of steps IIa and IIb, provided that 3 can be effectively formed in spite of the barriers to be passed. In this case, the left side cascade of Fig. 1, may continue with the opening of the (PI)₄ ring to give the chain P₄I₆, 5, with two terminal PI₂ groupings (step IIIa). Conversely on the right side, the three-membered cycle 4 may follow alternative paths, such as steps IIIb and IIIc, depending on the phosphorus/di-iodine docking mode. In the former case, the three-membered ring (PI)₃, 6, may form together with a dissociating (PI)₃ phosphine 7 or, in the latter, the tripod-like dendrimer P(PI₂)₃, 8, is consequent to the opening of the P₃ cycle at the bond involving the I-substituted P atoms.

Opening of the four-membered ring (PI)₄ (step IIIa)

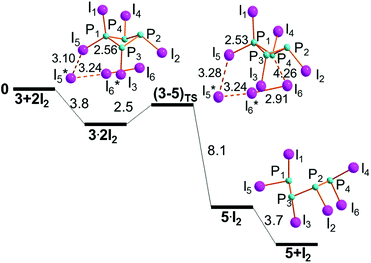
The stereochemistry of the intermediate 3, based on the precursor 2, can in principle afford different adducts of the type 3·2I₂. The one shown on the left side of Fig. 7 does not encounter hindrance problems in the important I₃ grouping rearrangement.

Fig. 7 Step IIIa for transforming 3 into the open chain product 5 (free energies in kcal mol⁻¹).

Remarkably, 3·2I₂ is the first exergonic aggregate encountered in the present P₄ chemistry (−3.8 kcal mol⁻¹), implying that the donor power of the P₁ atom has become larger. This is also corroborated by the more evidently perturbed P₁–I₅ and I₅–I₅* distances of 2.56 and 3.10 Å, respectively. Also in this case, our strategy afforded a reliable energy profile, which includes the low lying transition state (3–5)_TS (+2.5 kcal mol⁻¹). The latter is −1.3 kcal mol⁻¹ more stable than the separated reactants, suggesting an essentially barrierless evolution. The −0.6 charge of the terminal I₃ unit at TS is again consistent with a concerted electron transfer, which determines the cleavage of the P₁–P₄ bond to give the open chain P₄I₆, 5, stabilized by −11.8 kcal mol⁻¹.

As usual, the intermediate 5·I₂ precedes the final mentioned product upon release of the in situ generated I₂ molecule with the exergonic balance of −3.7 kcal mol⁻¹. The still rather closed I₆–P₄–P₁ angle of 135° at (3–5)_TS indicates poor activation of the P₄–P₁ bond, still as short as 2.36 Å. On the other hand, the electron flow to its σ* level becomes possibly on the descent to 5·I₂, once again consistent with the concerted mechanism.

Alternative steps IIIb and IIIc from 4

As the product of step IIb, I₂P-P₃I₂ may aggregate two I₂ molecules in different ways to afford the species (4·2I₂)_a, (4·2I₂)_b and (4·2I₂)_c shown in Fig. 8, whose energy balances are similarly exergonic, namely −2.7, −3.9 and −0.3 kcal mol⁻¹, respectively.

Fig. 8 Optimized structures of the isomeric adducts between I₂P-P₃I₂, 4 and two I₂ molecules.

Both (4·2I₂)_a and (4·2I₂)_b may be almost equivalent precursors of the P₁–P₄ cleavage with separation of the phosphine PI₃, 7, from the cycle (PI)₃, 6. Fig. 9 shows the profile of step IIIb only departing from (4·2I₂)_a. On the other hand, the aggregate (4·2I₂)_b could in principle have the chance of undergoing the triangular P₃ ring opening at either the P₄–P₂ or P₄–P₃ linkage to give the four-membered open chain I₂P-PI-PI-PI₂, 5. The latter process is inhibited by the two P–I vectors departing from the ring, which hinders the I₃ rearrangement. Conversely, the P₂–P₃ side may open up starting from (4·2I₂)_c to afford the dendrimer P(PI₂)₃, 8, as shown by the profile of step IIIc shown in Fig. 10. The mentioned possibilities are here described in some detail.

Fig. 9 Step IIIb for the first cracking of the P₄ skeleton into a PI₃, 7 and the (PI)₃ ring 6 (free energies in kcal mol⁻¹).

Fig. 10 Step IIIc for the opening of the cycle I₂P-P₃I₂, 4, to give the dendrimer P(PI₂)₃, 8 (free energies in kcal mol⁻¹).

Fragmentation of the P₄ skeleton in 4 to give the PI₃ and the ring (PI)₃ (step IIIb)

The cleavage of the P₁–P₃ exocyclic bond in (4·2I₂)_a is monitored as shown in Fig. 9. The encountered +5.3 kcal mol⁻¹ barrier at (4–6)_TS is in actuality as small as +1.4 kcal mol⁻¹ given that the aggregation of the components in (4·2I₂)_a is somewhat exergonic (−3.9 kcal mol⁻¹). This is because of the relatively good basicity of the exocyclic atom P₁, which determines the actual cleavage of the first I₅–I₅* diatomic at TS (separation of 3.96 Å), hence a significant charge delocalization at the terminal I₃ grouping, which is not too asymmetric given the 2.95 and 3.12 Å distances.

The situation is not so dissimilar from that of R₃P·2I₂ shown in Fig. 2b, although it is improper to discuss an ion pair formulation, since the terminal I₆ atom is already at 3.08 Å from the P₄ atom, consistent with the idea of a concerted mechanism at work.

The next intermediate is still an aggregate, namely 6·I₂·7, where the newly formed I₅*–I₆* diatomic holds this time together two distinct molecules. Clearly, there is no direct interaction between the latter as shown by the large P₄⋯P₁ separation of 3.47 Å, but in any case this allows an energy gain of −6.8 kcal mol⁻¹, which almost doubles (another −5.5 kcal mol⁻¹) with the final scission of the three molecular components. In this case, the process seems particularly favored by entropy, whose contribution is evaluated to be about −17 kcal mol⁻¹. The formation of the first of the four expected PI₃ molecules in the overall process is remarkable for preceding that of the diphosphine P₂I₄, until now considered its natural precursor. An early presence of PI₃ could be possibly presumed on the basis of the early NMR data, although not explicitly proved.¹⁰

Opening of the three-membered ring in 4 to give the dendrimer 8 (step IIIc)

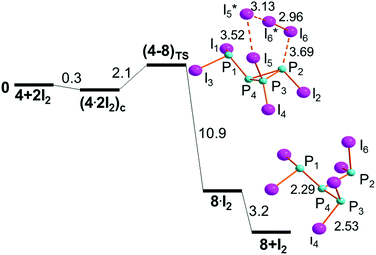
The P₃–P₂ cyclic bond in (4·2I₂)_c does not encounter hindrance problems on its cleavage, because the terminal I₃ grouping occupies the space opposite to the two P–I linkages, as shown in Fig. 10. Being the least stable of the isomers in Fig. 8, (4·2I₂)_c reaches the transition state (4–8)_TS with a cost of only +2.1 kcal mol⁻¹, which is reduced to +1.8 kcal mol⁻¹ with respect to its separated components.

The (4–8)_TS stereochemistry is particularly remarkable for allowing an easy identification of the P₂I₄ six membered ring, which switches the 3 + 3 formed/broken linkages in the ideal concerted nature of the process. In this case, not only the turning TS point is easily reached but also its subsequent descent to the dendrimer 8 seems smooth because of the total energy gain of −14.1 kcal mol⁻¹, of which −3.2 kcal mol⁻¹ is associated with the scission of the intermediate 8·I₂. Again, halogenated species such as 8 have not been structurally characterized, but again the molecular type is supported by related tripodal triphosphanes with organic substituents.⁴⁴

Fourth P–P bond cleavage

In both cascades of Fig. 1, there remain three of the six original P₄ bonds to be cleaved. The precursor on the left side is the open chain P₄I₆, 5, which in principle may be cracked in the middle to give two P₂I₄ diphosphines or allow the scission of a PI₃ phosphine from the chain P₃I₅, 10. On the right side, the fourth P–P cleavage may occur at either the ring (PI)₃, 6, or the dendrimer P(PI₂)₃, 8, which equally afford the chain 10.

Chain-breaking at P₄I₆ (step IVa)

Alternative conformations of 5 are possible as shown by the structure of some organo-substituted P₄ chains in the CCDC.²⁹ In some cases, the chain is overall planar with zig-zag conformation,⁴⁵ while in others it is puckered and similar to a trapezoid, in which one of the cyclic sides has opened up without a major conformational rearrangement.⁴⁶ The latter seems to be the case of compound 5, which derives from the closed cycle 3 without any significant conformational change (see step IIIa in Fig. 7). In other words, the product 5 maintains a chelate shape. This in principle causes some repulsion between the terminal P lone pairs, which is somewhat mitigated by a torsion around the central P₂–P₃ linkage (the corresponding PPPP dihedral angle is 125°). In this manner, the P₄ chain stabilizes, whereas its potential adduct with two I₂ molecules at one lateral P atom encounters major stereochemical problems, which emerge from its attempted optimization. This is clearly indicated by the corresponding species 5·2I₂^‡ (Fig. S5†) with illogical chemical features. For instance, one I atom is found bridging between the two lateral P atoms with an energy cost of about +10 kcal mol⁻¹, hence the species was abandoned as a precursor of the chain breaking. In contrast, the adduct 5·2I₂ involving an inner P atom of 5 has a stabilization energy of −4.4 kcal mol⁻¹ and was used as the starting point of step IVa. For the sake of brevity, the corresponding standard profile is presented in the ESI (Fig. S6†) and highlights the central split of 5 into the two P₂I₄ molecules, 9, through a practically barrierless process and an overall energy gain of −15.3 kcal mol⁻¹. As expected, an intermediate with the in situ formed I₂ molecule, namely 9·I₂·9, precedes the final dissociation of the molecular components, which is exergonic by −4.4 kcal mol⁻¹, likely because of the favourable entropy.

It is worth mentioning at this point an additional feature of 5·2I₂, which has been overlooked until the submission of this paper. Namely, the species is not only the precursor of the diphosphine 9, but it alternatively affords the separation of the phosphine 7 from the shorter chain P₃I₅, 10, whose behavior will be illustrated below. Importantly, this shows an interlink missing until now between the two cascades shown in Fig. 1. Very briefly, the alternative step starting from 5·2I₂, whose detailed profile IVa-bis is shown in Fig. S7,† is also smooth, for having the (5–10)_TS −0.9 kcal mol⁻¹ lower than the reactants and a subsequent free energy gain of −14.1 kcal mol⁻¹. The new results lead to the conclusion that the final product PI₃ is in any case partially attainable even before the achievement of diphosphine 9.

Opening of the three-membered ring 6 in step IVb

On the right side of Fig. 1, the 4^th P–P cleavage may start from the (PI)₃ ring. The observed conformation of the latter with all the I substituents on the same side is somewhat unusual and it is most likely imposed by that of precursor 4 (see step IIIb in Fig. 9). As a matter of fact, the known organo-substituted P₃ analogues have the 2 + 1 distribution of the substituents⁴⁷ and also a calculation for such a (PI)₃ isomer shows a larger stability of −3.9 kcal mol⁻¹. Also, no interconversion of the isomer seems possible in view of a free energy cost >25 kcal mol⁻¹. The computed profile for step IVb shown in Fig. S8† shows that the initial adduct 6·2I₂ leaves large space for the rearrangement of the terminal I₃ grouping and the eventual formation of the open chain P₃I₅, 10. Also, the mechanism is usual with a small barrier of +2.5 kcal mol⁻¹ to be passed at the transition state (6–10)_TS, followed by an overall energy gain of −18.4 kcal mol⁻¹. NMR evidence of P₃I₅ has been provided,⁴⁸ while it is worth mentioning that other similar halogenated chains have been recognized as relevant in the chemistry of small P_n units.^33,44

Alternative generation of the phosphine 7 and the chain 10 from the dendrimer 8 (step IVc)

The pyramidal dendrimer P(PI₂)₃, obtained through step IIIc, can add two di-iodine molecules at either the central P atom, (8·2I₂)_centr, or one of the terminal ones, (8·2I₂)_lat. From both precursors one may expect the analogous P_centr–P_lat bond cleavage but, since (8·2I₂)_centr is more stable by −5.0 kcal mol⁻¹, it was the isomer of choice for step IVc. A new cracking of the P₄ skeleton generates phosphine 7 and the open chain 10, which at this point appears to have various modes of formation. The profile of the step IVc shown in Fig. S9† confirms its unquestionable feasibility, given that (8–10)_TS lies −3.2 kcal mol⁻¹ lower than the separated reactants and the overall exergonic balance is −17.2 kcal mol⁻¹, consistent with the concerted mechanism.

Final P–P cleavages (steps V and VI)

The two last P–P cleavages are equivalent on the left side cascade of Fig. 1 with the generation of four phosphines, 7, from two diphosphines, 9. On the right side, no P₂I₄ molecule has yet formed at the 4^th P–P cleavage, while one-fourth of the PI₃ product is already present (it has alternatively formed through step IIIb or IVc). The amount of phosphine doubles in step V through the cracking of the chain 10, still excluding the mandatory involvement of the diphosphine for its formation. The latter is instead produced with the mentioned 5^th P–P cleavage on the right side, which is in any case based on the cracking of 10, as shown by the subsequent profile.

Cracking in step V of the open chain 10

Irrespective of its formation, the three-membered chain 10 easily undergoes a P–P cleavage under the general mechanism. The profile shown in Fig. S10† assumes that the di-iodine molecule is anchored at the central P atom, although a lateral aggregation should not be dramatically different. The (10–9/7)_TS is again more stable than the separated reactants and from it the splitting of 9 and 7 occurs with an overall energy gain of −14.3 kcal mol⁻¹, of which −4.0 kcal mol⁻¹ is for the final scission of the ter-molecular intermediate 9·I₂·7 shown in Fig. 11, for the particularly favourable entropic contribution.

Fig. 11 Optimized structure of ter-molecular intermediate 9·I₂·7.

The just outlined process prompts an interesting comparison with the inverse, Ag⁺ promoted, combination of PI₃ and P₂I₄ to give the cationic open chain P₃I₆⁺.¹⁹ With the lack of a detailed reaction profile, Scheme 2a suggests how the AgI precipitation may favour the extraction of one iodide from PI₃,³⁵ with the consequent orbital vacancy at the PI₂⁺ grouping being saturated by a P₂I₄ lone pair and the formation of the new P–P bond.

Scheme 2 Comparison of the acidic action of Ag⁺vs. I₂ in the potential formation of the cationic chain P₃I₆⁺.

A similar role could be exerted by the residual I₂ acidity (see Scheme 2b), which could in principle extract an iodide from PI₃ and give I₃⁻, hence the ion pair I₃⁻/P₃I₆⁺. The intermediate 9·I₂·7 shown in Fig. 11 would be the turning point of the reaction, which is energetically penalized in forming the P–P bond, hence excluding the cationic chain P₃I₆⁺ (Fig. S10†).

The ultimate I₂-promoted transformation of the diphosphine P₂I₄ into PI₃ and the inhibition for organo-substituted analogues

The diphosphine's dissociation step to give PI₃ is a ter-molecular process, as it already emerged by the proposal of eqn (3′)vs. eqn (3). The latter implies a 2 + 2 addition, which is a symmetry forbidden reaction,¹¹ because of the inter-crossing of the σ and σ* levels along the pathway and the high energy costs to invert the population. On the other hand, the concept of σ bond metathesis⁴⁹ has been raised for some organometallic compounds of d⁰ elements, with interchanging some coordination bonds associated with the alternative formation/cleavage of metal–element bonds, while the inverse behaviour applies to the associated element–element bonds. Possibly, some relation with eqn (3) may be established because of the electronic equivalence between the P atoms and d⁰ metals, but the point has not been further pursued. Conversely, we continued with the general picture emerging from the various P₄ demolition steps, which is based on the 3 : 3 and not the 2 : 2 ratio of broken/formed bonds. As a matter of fact, P₂I₄ behaves in the known manner toward di-iodine, while other organo-diphosphine analogues do not undergo the P–P cleavage under the action of I₂. We refer in particular to the species P₂(dmb)₂, 11, recently reported by Cummins et al.,¹⁸ where dmb are chains of four carbon atoms, which close two cycles by sharing the same P–P linkage. For the comparative calculations shown in Fig. 12, the realistic model of 11 was preferred to the simpler diphosphine P₂(CH₃)₄ one. A first important difference concerns the initial 1 : 1 adduct 9·I₂vs. 11·I₂. As a matter of fact, an organo-substituted P atom must be a stronger donor, more effectively perturbing the added I₂ molecule, as already noticed for the phosphine adduct PR₃·I₂ in Fig. 2a.⁵⁰ Thus, the I₁₁–I₁₁* elongation in 11·I₂ is definitely larger than in 9·I₂ (3.31 vs. 2.97 Å), while P₁–I₁₁ distance is closer to a single bond (2.53 vs. 2.73 Å). Experimentally, in 11, the two distances are 2.411 and 3.417 Å, respectively. Since no experimental information is available on the aggregate of the organo-diphosphine with two diatomics, we also optimized the species 11·2I₂ and compared it with 9·2I₂. What emerges is the definite cleavage of the first I₂ molecule (I₁₁–I₁₁* = 3.97 Å) and the lost collinearity with the P linearity with the P₁–I₁₁ vector. More remarkable are the free energy changes. While in Fig. 12a, the maximum free energy gain for 9·2I₂ is as usual not large (−2.25 kcal mol⁻¹), the addition of two diatomics to 11 is −28.2 kcal mol⁻¹ (i.e., −19.6 kcal mol⁻¹ and −8.6 kcal mol⁻¹, in the order).

Fig. 12 (a) Final I₂-promoted dissociation of P₂I₄ into two PI₃; and (b) different behavior of the organo-diphosphine 10 with disfavoured P–P cleavage (free energies in kcal mol⁻¹).

Also the terminal and asymmetric I₃⁻ in 11·2I₂ is almost monoanionic (charge = −0.93), the adduct is best formulated as ion pair [11I]⁺[I₃]⁻, whose cation closely resembles the well-known and stable [P₂I₅]⁺ one, which is rather unreactive.⁵¹ It may be deduced at this point that the maximized electron transfer at the species in question is inconsistent with the until now proposed concerted mechanism in these processes. Nonetheless, we continued with our strategy of relaxed scans and subsequent optimizations to evaluate the possible difficulties of the Cummins's system in forming the new I₁₂–P₂ bond and the eventual P₁–P₂ cleavage. As a matter of fact, the profile b in Fig. 12 follows the trends already highlighted in a, although the energies are much different.

Thus, to reach (11–12)_TS the energy cost is +21.0 kcal mol⁻¹vs. the +3.0 kcal mol⁻¹ of (9–7)_TS. While from the latter the generation of distinct PI₃ molecules is as smooth as in all of the previous cases (the energy gains are −9.5 and −5.7 kcal mol⁻¹ at 7·I₂·7 and 2PI₃, respectively), the structure of (11–12)_TS is highly questionable. In fact, this already features broken P₁–P₂ bonds with a separation as large as 3.53 Å, while after the high free energy cost to reach the point, the subsequent energy gains to obtain 12 or its immediate precursor 12·I₂ are as small as −4.2 and −0.5 kcal mol⁻¹, respectively. Likely, our computational strategy has forced the attainment of these minima, which are spontaneously attainable at least through the mechanism proposed in this paper. Incidentally, it is worth mentioning that a compound of type 12 with halogen atoms other than iodine was spectroscopically detected after treating 11 with halogenating reactants other than diatomics, e.g., C₂Cl₆ ¹⁸ or the Grignard species.^18,52 Due to the lack of an X-ray structure, we did not perform any computational analysis.

In closing this section, we mention a final intriguing problem about the reported method of preparation of the diphosphine P₂I₄ upon the disproportionation of PI₃.^12,53 Without deepening any mechanistic aspect of this process, a reductive elimination of I₂ seems unlikely for the same reasons illustrated for the reverse 2 + 2 direct addition implied by eqn (3). Alternatively, the reverse process of Fig. 12a (from right to left) cannot be excluded a priori in spite of the +15 kcal mol⁻¹ barrier to be passed. On the other hand, such an event would not correspond to the actual PI₃ disproportionation but its reaction with an I₂ co-reactant, which is excluded from the environment if not specifically added. Perhaps, other factors may become important as for instance the role played by some specific solvents,⁵³ which we have not explored at this time.

Conclusions and extensions

The computational analysis of the P₄ activation by I₂ to generate the phosphine PI₃ confirms the value of the in silico approach in identifying unclear mechanisms with otherwise unknown intermediates. The overall process, which is exergonic by ∼−76 kcal mol⁻¹, occurs through a sequence of energetically favourable steps, except for an initial barrier of about +15 kcal mol⁻¹. The latter seems due to the still low donor power of the unperturbed white phosphorus, which hardly transfers electron density from its compact and strained structure. After the barrier, a multi-step process is triggered with a repeating concerted action, given the occurrence of 3 + 3 bond breakings/makings in each case. The common feature is a dynamic electron transfer throughout six atoms, cyclically arranged. The process starts with a delocalization of some P electron density through the first formed P–I–I linear unit and continues at the subsequent tri-iodide XB adduct involving a second diatomic. Some electron density ends up to a P–P σ* level with the cleavage of one of the original P₄ sides. The mechanism is evidently ter-molecular at any step with the peculiar reformation of a new di-iodine molecule.

Fig. 1 has already been a useful reference throughout the paper, but provides no energy indication relative to the occurrence of alternative steps. For this, we present the conclusive Fig. 13, outlining the most probable cascade of steps, with the significant barrier, (1–2)_TS, appearing only at the very beginning.

Fig. 13 Favoured cascade of events in the P₄ demolition by I₂, except for the unique initial barrier (1–2)_TS. Half amount of the PI₃ product forms in the earlier stages rather than at the very end.

The analysis indicates a fundamental role played in the attack of I₂ by the P atom donor power. The latter must not be large to trigger a concerted electron transfer without altering the oxidation states of the involved atoms. In fact, an excessive donor power, as in the case of organo-substituted P atoms, determines a major electron transfer and charge separation (ion pair formation), which does not allow concertedness. This point clearly emerged by comparing the P₂I₄ diphosphine with an organo-substituted analogue of the type P₂R₄, which was reported by Cummins and co-workers as being unable to induce P–P cleavage.¹⁸

The present elucidation of the basic intermediates in the P₄ + I₂ process may be relevant for the widely investigated chemistry of phosphorus-based molecules. Moreover, it seems to have a direct impact on our ongoing studies on the functionalization of phosphorene 2D material.⁶ As in P₄, any P atom is pyramidal and directly linked to three equal ones, hence its coordination to an acidic metal center seems plausible, as found for some known P₄ complexes.² As a matter of fact, we have gained some computational evidence, by using the solid state package CRYSTAL,⁵⁴ that the P donor power is rather similar in the two cases, hence a number of metal fragments suitable for phosphorene's coordination in the η¹, η² and η³ modes have been already individuated.⁵⁵ By the same token, the reactivity of phosphorene toward di-iodine molecules could also follow a concerted mechanism in place of a prompt charge separation. On the other hand, a number of disfavouring factors have emerged from our preliminary analyses, such as the reduced freedom of the initial P–I–I and I–I–I pendants of the XB-type to span over the 2D surface and attack a specific σ* level of a P–P to be broken. Possibly, some well tailored modelling is necessary on which we are working now.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The authors acknowledge the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation program (Grant Agreement No. 670173) for funding the project PHOSFUN “Phosphorene functionalization: a new platform for advanced multifunctional materials” through an ERC Advanced Grant. ISCRA-CINECA HP Grants HP10C2QI78 and HP10CFMSCC for the computational resources are also acknowledged.

References

1. (a) D. E. C. Corbridge, The structural Chemistry of Phosphorus, Elsevier, Amsterdam, NL, 1974; (b) F. Bachuber, J. von Appen, R. Dronskowski, P. Schmidt, T. Nilges, A. Pfitzner and R. Weihrich, Angew. Chem., Int. Ed., 2014, 53, 11629–11633.
2. (a) M. Caporali, L. Gonsalvi, A. Rossin and M. Peruzzini, Chem. Rev., 2010, 110, 4178–4235; (b) I. de los Rios, J.-R. Hamon, P. Hamon, C. Lapinte, L. Toupet, A. Romerosa and M. Peruzzini, Angew. Chem., Int. Ed., 2001, 40, 3910–3912; (c) M. Peruzzini, L. Gonsalvi and A. Romerosa, Chem. Soc. Rev., 2005, 34, 1038–1047; (d) P. Barbaro, M. Di Vaira, M. Peruzzini, S. Costantini and P. Stoppioni, Chem. – Eur. J., 2007, 13, 6682–6690; (e) C. Mealli, F. Costanzo, A. Ienco, M. Peruzzini and E. Perez-Carreño, Inorg. Chim. Acta, 1998, 275–276, 366–372.
3. (a) M. E. Schlesinger, Chem. Rev., 2002, 102, 4267–4301; (b) C. C. Stephenson, R. L. Potter, T. G. Maple and J. C. Morrow, J. Chem. Thermodyn., 1969, 1, 59–76.
4. (a) D. Warschauer, J. Appl. Phys., 1963, 34, 1853–1860; (b) A. Brown and S. Rundquist, Acta Crystallogr., 1965, 19, 684–685.
5. (a) H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033–4041; (b) L. Li, Y. Yu, G. J. Ye, Q. Ge, X. Ou, H. Wu, D. Feng, X. H. Chen and Y. Zhang, Nat. Nanotechnol., 2014, 9, 372–377; (c) D. Hanlon, C. Backes, E. Doherty, C. S. Cucinotta, N. C. Berner, C. Boland, K. Lee, A. Harvey, P. Lynch, Z. Gholamvand, S. Zhang, K. Wang, G. Moynihan, A. Pokle, Q. M. Ramasse, N. McEvoy, W. J. Blau, J. Wang, G. Abellan, F. Hauke, A. Hirsch, S. Sanvito, D. D. O'Reagan, G. S. Duesberg, V. Nicolosi and J. N. Coleman, Nat. Commun., 2015, 6(1–11), 8563; (d) M. Serrano-Ruiz, M. Caporali, A. Ienco, V. Piazza, S. Heun and M. Peruzzini, Adv. Mater. Interfaces, 2016, 3(1–8), 1500441.
6. The project PHOSFUN aimed at understanding the basic properties of the phosphorene layers and their applications in the fields of catalysis and nanoelectronics has been financed with an Advanced ERC Grant of the European Commission (see the Acknowledgements).
7. (a) S. Lange, P. Schmidt and T. Nigels, Inorg. Chem., 2007, 46, 4028–4035; (b) Z. Zhang, X. Xin, G. Yan, Q. Li, Y. Yang and T.-L. Ren, Sci. China Mater., 2016, 59, 122–134.
8. F. E. E. Germann and R. N. Traxler, J. Am. Chem. Soc., 1927, 49, 307–312.
9. D. Wyllie, M. Ritchie and E. B. Ludlam, J. Chem. Soc., 1940, 583–587.
10. (a) R. L. Carroll and R. P. Carter, Inorg. Chem., 1967, 6, 401–403; (b) B. W. Tattershall and N. L. Kendall, Polyhedron, 1994, 13, 1517–1521.
11. R. B. Woodward and R. Hoffmann, J. Am. Chem. Soc., 1965, 87, 395–397.
12. I. P. Beletskay, E. I. Tomilenko, N. I. Kamenichnaya, V. I. Staninets, Zh. K. Gorbatenko and N. G. Feshchenko, Khim. Elementoorg. Soedin., 1976, 170.
13. (a) D. J. Heinze, Pure Appl. Chem., 1975, 141–172; (b) N. N. Greenwood and A. Earnshaw, Chemistry of the Elements, 2nd edn, 1997.
14. T. Funaioli, P. Leoni, L. Marchetti, A. Albinati, S. Rizzato, F. Fabrizi de Biani, A. Ienco, G. Manca and C. Mealli, Inorg. Chem., 2013, 52, 4635–4647.
15. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
16. (a) G. R. Desiraju, P. S. Ho, L. Kloo, A. C. Legon, R. Marquardt, P. Metrangolo, P. Politzer, G. Resnati and K. Rissanen, Pure Appl. Chem., 2013, 85, 1711–1713; (b) P. Metrangolo and G. Resnati, Science, 2008, 321, 918–919 and references therein; (c) L. C. Gilday, S. W. Robinson, T. A. Barendt, M. J. Lang, B. R. Mullaney and P. D. Beer, Chem. Rev., 2015, 115, 7118–7195; (d) L. P. Wolters, P. Schyman, M. J. Pavan, W. L. Jorgensen, F. M. Bickelhaupt and S. Kozuch, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 523–546; (e) S. V. Rosokha, C. L. Stern and J. T. Ritzert, Chem. – Eur. J., 2013, 19, 8774–8788.
17. (a) V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001; (b) M. Cossi, N. Rega, G. Scalmani and V. Barone, J. Comput. Chem., 2003, 24, 669–681.
18. I. Knopf, D. Tofan, D. Beetstra, A. Al-Nezari, K. Al-Bahily and C. C. Cummins, Chem. Sci., 2017, 8, 1463–1468.
19. (a) I. Krossing and I. Raabe, Angew. Chem., Int. Ed., 2001, 40, 4406–4408; (b) M. Gonsior, I. Krossing, L. Muller, I. Raabe, M. Jansen and L. van Wullen, Chem. – Eur. J., 2002, 8, 4475–4492.
20. M. H. Holthause and J. J. Weigand, Chem. Soc. Rev., 2014, 43, 6639–6657.
21. (a) J. D. Masuda, W. W. Schoeller, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2007, 46, 7052–7055; (b) J. D. Masuda, W. W. Schoeller, B. Donnadieu and G. Bertrand, J. Am. Chem. Soc., 2007, 129, 14180–14181; (c) O. Back, G. Kuchenbeiser, B. Donnadieu and G. Bertrand, Angew. Chem., Int. Ed., 2009, 48, 5530–5533.
22. B. M. Cossairt and C. Cummins, New J. Chem., 2010, 34, 1533–1536.
23. S. Heinl and M. Scheer, Chem. Sci., 2014, 5, 3221–3225.
24. T. Kennedy and R. S. Sinclair, J. Inorg. Nucl. Chem., 1970, 32, 1125–1133.
25. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2009.
26. M. Dolg, H. Stoll, H. Preuss and R. M. Pitzer, J. Phys. Chem., 1993, 97, 5852–5859.
27. (a) F. Bigoli, P. Deplano, A. Ienco, C. Mealli, M. L. Mercuri, M. A. Pellinghelli, G. Pintus, G. Saba and E. F. Trogu, Inorg. Chem., 1999, 38, 4626–4636; (b) G. Manca, A. Ienco and C. Mealli, Cryst. Growth Des., 2012, 12, 1762–1771.
28. M. E. G. Mosquera, P. Gomez-Sal, L. Diaz, L. M. Aguirre, A. Ienco, G. Manca and C. Mealli, Inorg. Chem., 2016, 55, 283–291.
29. Cambridge Structural Database System, version 5.38, Cambridge Crystallographic Data Centre, Cambridge, UK.
30. M. Schlosser, Organoalkali Chemistry, in Organometallics in Synthesis: Third Manual, John Wiley & Sons, Inc., Hoboken, NJ, 2013, p. 61.
31. The important involvement of the s filled central orbital is not addressed in the widely used Pimentel and Rundle models. (a) C. G. Pimentel, J. Chem. Phys., 1951, 19, 446–448; (b) R. J. Hach and R. E. Rundle, J. Am. Chem. Soc., 1951, 73, 4321–4324.
32. F. Ruthe, P. G. Jones, W.-W. du Mont, P. Deplano and M. L. Mercuri, Z. Anorg. Allg. Chem., 2000, 626, 1105–1111.
33. W. I. Cross, S. M. Godfrey, C. A. McAuliffe, R. G. Pritchard, J. M. Sheffield and G. M. Thompson, J. Chem. Soc., Dalton Trans., 1999, 2795–2798.
34. Calculation performed with the CPCM modeling of the CH₂Cl₂ solvent.
35. G. Manca, E. Gallo, D. Intrieri and C. Mealli, ACS Catal., 2014, 4, 823–832.
36. P. Dapporto, S. Midollini and L. Sacconi, Angew. Chem., Int. Ed., 1979, 18, 469.
37. I. Krossing, J. Chem. Soc., Dalton Trans., 2002, 500–512.
38. I ₂ was instead reported to be often in defect in some of the previous spectroscopic studies of this reactivity, such as the one of ref. 10.
39. (a) R. Fox, R. J. Wright, E. Rivard and P. P. Power, Angew. Chem., Int. Ed., 2005, 44, 7729–7733; (b) J. Bresien, K. Faust, C. Hering-Junghans, J. Rothe, A. Schulz and A. Villinger, Dalton Trans., 2016, 45, 1998–2007.
40. Pairs of the P₄I₂ molecules are not fully equivalent because of the orientation of the two I substituents.
41. A. Lorbach, A. Nadj, S. Tullmann, F. Dornhaus, F. Schödel, I. Sänger, G. Magraf, J. W. Bats, M. Bolte, M. C. Holthausen, M. Wagner and H.-W. Lerner, Inorg. Chem., 2009, 48, 1005–1017.
42. J. Bresien, C. Hering, A. Schulz and A. Villinger, Chem. – Eur. J., 2014, 20, 12607–12615.
43. K.-O. Feldmann and J. J. Weigand, Angew. Chem., Int. Ed., 2012, 51, 7545–7549.
44. (a) G. Fritz, E. Matern, H. Krautscheid, R. Ahlrichs, J. W. Olkowska and J. Pikies, Z. Anorg. Allg. Chem., 1999, 625, 1604–1607; (b) G. Fritz, K. Stoll, W. Hönle and H. G. V. Schnering, Z. Anorg. Allg. Chem., 1986, 544, 127–136; (c) C. Jones, P.-C. Junk and T. C. Williams, J. Chem. Soc., Dalton Trans., 2002, 2417–2418; (d) A. Wisniewska, K. Baranowska, E. Matern and J. Pikies, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2008, 64, 01364.
45. R. Wolf, S. Gomez-Ruiz, J. Reinhold, W. Nohlmann and E. Hey-Hawkins, Inorg. Chem., 2006, 45, 9107–9113.
46. K.-F. Tebbe and R. Frohlich, Z. Naturforsch., B: Chem. Sci., 1982, 37, 534.
47. (a) J. Borm, G. Huttner and O. Orama, J. Organomet. Chem., 1986, 306, 29–38; (b) R. A. Barlett, H. V. Rasika Dias, K. M. Flynn, H. Hope, B. D. Murray, M. M. Olmstead and P. P. Power, J. Am. Chem. Soc., 1987, 109, 5693–5698; (c) N. Tokitoh, A. Tsurusaki and T. Sasamori, Phosphorus, Sulfur Silicon Relat. Elem., 2009, 184, 979–986; (d) A. Baldy and J. Estienne, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 1988, 44, 747–749; (e) N. Burford, C. A. Dyker, M. Lumsden and A. Decken, Angew. Chem., Int. Ed., 2005, 44, 6196–6199.
48. K. B. Dillon and B. Y. Xue, Inorg. Chim. Acta, 2003, 320, 172–173.
49. R. Waterman, Organometallics, 2013, 32, 7249–7263.
50. In the paper of Cummins,¹⁸ it is not specified whether a different ratio between the reactants can alter the system, as it emerged in the case of Fig. 2.
51. M. Gonsior, I. Krossing, L. Muller, I. Raabe, M. Jansen and L. von Wullen, Chem. – Eur. J., 2002, 8, 4475–4492.
52. R. W. Alder, D. D. Ellis, J. K. Hogg, A. Martin, A. G. Orpen and P. N. Taylor, Chem. Commun., 1996, 537–538.
53. A. V. Kirsanov, Zh. K. Gorbatenko and N. G. Feshchenko, Chemistry of Phosphorus Iodides in IUPAC Inorganic Phosphorus Compounds, Prague, 1974, 125–138.
54. R. Dovesi, R. Orlando, A. Erba, C. M. Zicovich-Wilson, B. Civalleri, S. Casassa, L. Maschio, M. Ferrabone, M. De La Pierre, P. D'Arco, Y. Noel, M. Causa, M. Rerat and B. Kirtman, Int. J. Quantum Chem., 2014, 114, 1287–1317.
55. C. Mealli, A. Ienco, M. Peruzzini and G. Manca, manuscript in preparation.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c7dt04034b

---