Open Access Article
Open Access ArticleEffect of Al-distribution on oxygen activation over Cu–CHA†
Lin
Chen
 *a,
Hanne
Falsig
b,
Ton V. W.
Janssens‡
b,
Jonas
Jansson
c,
Magnus
Skoglundh
*a,
Hanne
Falsig
b,
Ton V. W.
Janssens‡
b,
Jonas
Jansson
c,
Magnus
Skoglundh
 d and
Henrik
Grönbeck
d and
Henrik
Grönbeck
 *a
*a
aDepartment of Physics and Competence Centre for Catalysis, Chalmers University of Technology, SE-412 96 Göteborg, Sweden. E-mail: clin@chalmers.se; ghj@chalmers.se
bHaldor Topsoe A/S, Haldor Topsøes Allé 1, 2800 Kgs. Lyngby, Denmark
cVolvo Group Trucks Technology, SE-405 08 Göteborg, Sweden
dDepartment of Chemistry and Chemical Engineering, and Competence Centre for Catalysis, Chalmers University of Technology, SE-412 96 Göteborg, Sweden
First published on 22nd March 2018
Abstract
Cu(NH3)2+-pairs in chabazite (CHA) have been suggested to activate oxygen during low-temperature selective catalytic reduction of nitrogen oxides with ammonia (NH3-SCR). As charge neutrality requires that each Cu-complex is associated with a framework Al, the Al-distribution may affect Cu(NH3)2+-pair formation and subsequent oxygen activation. Here, density functional theory calculations in combination with ab initio molecular dynamics simulations are used to explore Cu(NH3)2+-pair formation and oxygen activation in Cu–CHA. The Al-distribution is found to markedly affect the probability for Cu(NH3)2+-pair formation. Moreover, the molecular dynamics simulations reveal a low-energy reaction path for O2 activation and dissociation. The facile O2 dissociation suggests that Cu-pair formation rather than O2 activation governs the low-temperature NH3-SCR activity. The results indicate that precise synthesis of Cu-exchanged chabazite with respect to Al-distribution may enhance the catalytic activity.
1 Introduction
Binuclear copper sites play an important role in enzymatic reactions as copper containing proteins are known to facilitate a range of zero-, two- or four-electron processes involving oxygen.1–4 The nature of the active binuclear centers has been investigated extensively and characterized as being either coupled or non-coupled, depending on the distance between the metal sites.2 Using model complexes, it has demonstrated that the Cu–Cu distance can be used as a design parameter to stabilize oxygen in different structural and electronic configurations.5,6 Within heterogeneous catalysis, binuclear copper centers have been hypothesized to constitute active sites in ion-exchanged zeolites. One example is single-step conversion of methane to methanol where the reaction has been suggested to proceed over a [Cu–O–Cu]2+ bridge.7,8 Another example is selective catalytic reduction of NOx to N2 with NH3 as a reducing agent (NH3-SCR)9,10 where Cu-exchanged chabazites (Cu–CHA) have emerged as a promising catalyst thanks to good performance over a wide temperature window and high hydrothermal stability.10–13 Synthetic chabazite is a small-pore zeolite which consists of cages with 36 and 12 tetrahedrally coordinated silicon atoms, respectively.14In similarity to many enzymatic reactions, a crucial step in NH3-SCR, is the activation and dissociation of O2.15–20 The understanding of this reaction step is linked to the understanding of the active site under reaction conditions. It has recently been established that Cu+ is solvated by NH3 at temperatures below ∼523 K and that Cu(NH3)2+ is the dominant complex over a wide range of NH3 partial pressures.15–17,21,22 This complex is mobile and weakly bonded to the zeolite framework.23 At higher temperatures, NH3 desorbs and Cu is coordinated directly to the zeolite framework with lost mobility.16,17,22
Density functional theory (DFT) calculations have shown that dissociation of O2 on a pair of Cu-ions is considerably faster than on single Cu ions.16,18,19 Understanding the mobility of Cu(NH3)2+ complexes and Cu-pair formation is, thus, key for the understanding of the low-temperature NH3-SCR activity of Cu–CHA catalysts. As the Cu(NH3)2+ complex is an electronically closed-shell system with weak interactions to other complexes and the zeolite framework, the thermodynamic driving force to form pairs is low. Each complex is instead electrostatically connected to an anionic Si–O(–)–Al site in the zeolite cages. Recent calculations18 have shown that the Cu(NH3)2+ complex has a diffusion radius of about 9 Å from the Si–O(–)–Al site which allows for pair formation with Cu ions located in neighboring cages. The Si/Al ratio in Cu–CHA based NH3-SCR catalysts is commonly in the range 5–20 with a Cu/Al ratio of 0.5.17,24–26 This indicates that each large cage contains at least two Si–O(–)–Al sites and that Cu-pair formation is likely given a 9 Å mobility range. Si–O(–)–Al sites that are not balanced by Cu(NH3)2+ complexes have instead H+ or NH4+ as counter ions and ion-exchange-like processes may further facilitate the Cu(NH3)2+ mobility.23
Oxygen activation and NH3-SCR activity could potentially be enhanced in Cu–CHA if the two Cu(NH3)2+ complexes are stabilized at distances that facilitate adsorption. For metallocomplexes this can be accomplished by ligand design choosing the second coordination shell appropriately.5,6 In the case of Cu–CHA, the analog of the second coordination shell is the zeolite framework and, in particular, the location of the Si–O(–)–Al sites. Thus, the Cu–Cu distance may be steered by the Al-distribution.
In this work, the effect of Al-distribution on oxygen activation on paired Cu(NH3)2+ species in CHA during NH3-SCR conditions is investigated by use of density functional theory calculations in combination with ab initio molecular dynamics simulations. The Al-distribution is found to have a pronounced effect of the pair stability. In addition, the ab initio molecular dynamics simulations uncover a previously overseen, low-energy path for O2 dissociation over Cu(NH3)2+ pairs. The facile oxygen activation and dissociation along this path, which appears to be entropically preferred, suggests that the formation of binuclear copper sites rather than O2 activation governs the low-temperature NH3-SCR activity.
2 Computational methods
Spin-polarised density functional theory (DFT) calculations are performed with the Vienna ab initio simulation package (VASP).27–31 The Kohn–Sham orbitals are expanded with plane waves using an energy cut-off of 480 eV and the interaction between the valence electrons and the cores is described with the plane augmented wave (PAW) method.32,33 The number of valence electrons used in the calculations are 11 for Cu, 4 for Si, 3 for Al, 6 for O, 5 for N and 1 for H. The BEEF-vdW functional34 is used as an approximation to the exchange-correlation functional. This functional includes van der Waals interactions and has previously shown to describe reactions in zeolites satisfactorily.15,35,36Structures are optimized with the conjugate gradient method and geometries are considered to be converged when the electronic energy difference between subsequent steps is smaller than 1 × 10−5 eV and the largest force is smaller than 0.03 eV Å−1. Reaction barriers are calculated by use of the climbing image nudged elastic band (NEB)37,38 technique as implemented in the transition state tools of VASP. Harmonic vibrational frequencies are computed using the finite-difference approach. The identified transition states are confirmed by vibrational analysis with one imaginary frequency towards the product coordinate. The investigated systems are large and the k-point sampling is accordingly restricted to the Γ-point.
To explore the low-energy configurations of Cu(NH3)2+ pairs in CHA, Born–Oppenheimer ab initio molecular dynamics (AIMD) simulations in the NVT ensemble are performed. As for the static calculations, the AIMD is performed with the BEEF-vdW functional. The temperature in the simulation is controlled to be 400 K by a Nosé–Hoover thermostat.39,40 The mass of hydrogen is replaced by the mass of tritium to facilitate the integration of the equations of motion which is done using a time step of 1 fs. The simulations are performed for 6 ps where the first 1 ps is used for equilibration of the system. Properties are extracted from the subsequent 5 ps.
Constrained molecular dynamics is performed at 273 K to obtain the free-energy barriers for oxygen activation over Cu(NH3)2+ pairs. This simulation is performed for 10 ps with a time step of 0.5 fs. Thermodynamic integration of free-energy gradients is performed to calculate the free-energy difference along the reaction path. Assuming that the reaction path can be described via a set of coordinates ξ = {ξk; k = 1,...,r}, the free-energy difference between the initial and final states is calculated according to:
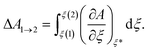 | (1) |
Details for the thermodynamic integration of the free-energy gradients are given in the ESI.†
2.1 Model systems
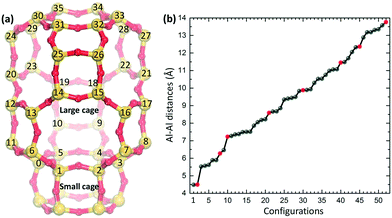
The chabazite structure is modeled using a hexagonal unit cell which includes 36 Si atoms in tetrahedral (T) positions. The optimized cell parameters are a,b = 13.803 Å and c = 15.075 Å. The lattice parameters are kept fixed during the geometry relaxations and molecular dynamics. Chabazite is composed of large and small cages (see Fig. 1(a)), which consists of 36 T and 12 T atoms, respectively. The large cages are constituted by four-, six-, and eight-membered rings, whereas the small cages are made up of four- and six-membered rings. Most experimental data relevant for NH3-SCR are available for CHA materials with a Si/Al ratio between 5 and 20.17,24–26To investigate the effect of Al-distribution, we consider a high Si/Al ratio of 17, which corresponds to two Si–O(–)–Al sites in each unit cell. Cu+ ions in the form of Cu(NH3)2+ complexes are exchanged into the zeolites to preserve charge neutrality. As the Al-sites can be assumed to be evenly distributed in the framework, all feasible configurations with two Si–O(–)–Al in the hexagonal unit cell have been considered. Taking into account the structural symmetry and the Löwenstein's rule (Al–O–Al links are forbidden), we obtain 52 different configurations. The 52 configurations with a site-labeling according to Fig. 1(a) are listed in the ESI.† Here, 8 out of the 52 configurations are selected for detailed analysis (see Table 1 and Fig. 1(b)). The selected configurations have an Al–Al distance ranging from 4.5 to 13.77 Å.
| Conf. | Site labels | Al–Al | Cu–Cu | Al–Cu |
|---|---|---|---|---|
| 1 | 0 + 6 | 4.50 | 3.32 | 5.33, 5.34, 5.39, 5.46 |
| 2 | 0 + 3 | 6.28 | 5.05 | 3.78, 5.37, 8.51, 9.18 |
| 3 | 0 + 20 | 7.24 | 4.70 | 3.96, 4.28, 5.46, 8.33 |
| 4 | 0 + 18 | 8.60 | 5.32 | 3.81, 5.22, 5.95, 9.13 |
| 5 | 0 + 15 | 9.88 | 4.76 | 4.27, 5.28, 6.20, 8.81 |
| 6 | 11 + 26 | 11.46 | 4.91 | 4.27, 5.28, 7.99, 8.54 |
| 7 | 0 + 31 | 12.37 | 5.29 | 3.53, 4.11, 8.64, 8.99 |
| 8 | 11 + 27 | 13.77 | 4.85 | 4.30, 6.32, 8.20, 9.60 |
In order to compare the relative pair formation energy of the considered configurations, the difference in pair formation energy with respect to the stable configuration is calculated as:
| ΔEform = ΔE2Cu@CHA − ΔE2H@CHA | (2) |
3 Results
3.1 Formation of Cu(NH3)2+ pairs
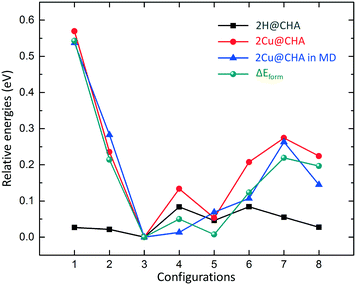
As charge neutrality requires that each Cu ion is balanced by a framework Al atom, the mobility and pair formation of the Cu-complexes depend on the distribution of the Al atoms. Therefore, we investigate the formation of Cu pairs in CHA with different distributions of the Al atoms, using the eight Al–Al configurations presented in Fig. 1 and Table 1. The interactions between the complexes and the framework are non-directional which make the potential energy surface (PES) shallow with many local minima. Molecular dynamics is therefore used to probe the PES and local relaxations are performed from local minima in the potential energies along the simulated trajectories. For non Cu-exchanged CHA, it has been shown that protons balancing Si–O(–)–Al preferably occupy a four-membered ring adjacent to the Al positions.23 Here, we only consider such positions for H+.The results for the stability of pairs and protons are shown in Fig. 2. The Al-distribution has a negligible effect on the stability of the protons given that the relative energies are within 0.1 eV. Regarding the relative formation energies of the Cu(NH3)2+ pairs in CHA, we find a difference in stability of about 0.55 eV for the considered structures. The highest stability is obtained for a structure where the two Al-sites are placed at a distance of 7.24 Å (configuration 3). Configurations with either short or long Al–Al distances result in low stability. The least stable configuration is the one with the shortest Al–Al distance (configuration 1). An intermediate Al–Al distance yields a stability comparable with configuration 3. We conclude that an Al-distribution such as configuration 3 gives a probability for Cu(NH3)2+ pair formation that is considerably higher than, for example, for configuration 1. It should be noted that configuration 2, with two Al3+ in the six-membered ring, has previously been suggested as a favorable configuration41 and used in many computational studies.16,17,23,41 The underlying reason for the difference in stability, is a balance between Coulomb interactions; on one hand between cationic copper sites and on the other hand between Cu+ and anionic Si–O(–)–Al sites. In fact, a simple point charge model with the position of the Al and Cu charges taken from the relaxed structures reproduces the trend in Fig. 2.
To take possible entropic contributions into account, we also calculated the time average of the potential energies along the trajectories. The AIMD results show that, again, configuration 3 has the highest stability and configuration 1 has the lowest stability. The average total potential energy for configuration 2 and 7 is higher than that of configuration 3 by ∼0.3 eV. The configurations with intermediate Al–Al distance (4, 5 and 6) have a similar stability as configuration 3 with an average total potential energy difference within 0.1 eV. The average potential energy for configuration 8 is ∼0.15 eV higher than that of configuration 3. The AIMD results support the static calculations that the stability of the pairs is sensitive to the Al-distribution in CHA. This is important as the activation of oxygen in NH3-SCR involves Cu(NH3)2+ pairs and depends on the mean Cu–Cu distance.
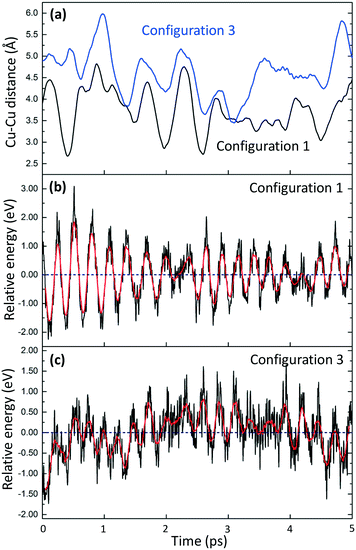
The time evolution of the Cu–Cu distance and potential energy is shown for two cases in Fig. 3. The Cu–Cu distance in configuration 1 ranges from ∼2.7 to ∼4.8 Å. Configuration 3 has a slightly larger range, between ∼3.5 and ∼6 Å. The differences in Cu–Cu distance are in agreement with the lower stability of the Cu(NH3)2+ pairs in the case of configuration 1. The short Cu–Cu distance for configuration 1 indicates a low O2 adsorption energy as the Cu–Cu distance for adsorbed O2 on a pair is about 5 Å. The potential energies of the pairs in configurations 1 and 3 along the AIMD trajectories are reported in Fig. 3(b) and (c). The moving average of the potential energies shows how the stability of the pairs is effected by the Cu–Cu distance. The shorter Cu–Cu distance yields stronger Coulomb repulsion between the pairs, which decreases the stability of the system.
The finding that the Al-distribution affects the formation of Cu-pairs provides an alternative explanation for the observation that not all Cu-ions form pairs and contribute to the low-temperature NH3-SCR activity.18 From this perspective, not all Cu ions are equivalent, as recently proposed,18 and, consequently, a higher propensity of Cu ions in favorable positions will lead to an improved catalytic activity. Our results indicate that the Cu–CHA activity can be improved by controlling the Al-distribution which corresponds to the second coordination shell of the Cu ions.
3.2 A novel path for O2 activation
Following the study of Cu(NH3)2+-pair formation, we have investigated oxygen activation over such pairs with constrained molecular dynamics simulations. This is an extension of previous work16 performed with NEB calculations in the rhombohedral representation of CHA, containing 12 T-sites. The simulations are performed with the two Al3+-sites in the same six-membered ring as this arrangement has been considered in previous studies.16,17,23,41 The Al-loading corresponds to an Si/Al ratio of 5. (The rhombohedral cell is used in these calculations as NEB calculations with the hexagonal cell are computational demanding.) The result is shown in Fig. 4 and reveals a previously overseen path for O2 activation in Cu–CHA. The simulations, which are performed in the singlet-state, show that O2 is initially coordinated to both Cu+-ions in a symmetric manner. A low barrier is found to break this symmetry and coordinate O2 with two bonds to one Cu+ and only one bond to the other complex. In agreement with previous calculations,16,18 the activation is completed with a slightly higher barrier to form the Cu–O2–Cu complex (structure 3 in Fig. 4). The new path appears to be entropically preferred as all performed trajectories have resulted in this path rather than the one previously discussed.16,18 This path involves symmetry breaking in the Cu–O2–Cu complex and has previously been reported for oxygen activation in enzymatic catalysis.5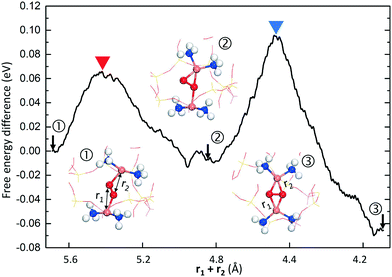 | ||
| Fig. 4 Free energy difference for activation of oxygen over a Cu+ pair in Cu–CHA from constrained molecular dynamics. The numbered structures in the insets are marked by arrows on the trajectory. The constrained MD simulation is performed on the singlet potential energy surface with a local Al–Al structure corresponding to configuration 2 in Table 1. Atom color codes: copper (orange), oxygen (red), nitrogen (blue), hydrogen (white), silicon (yellow), and aluminum (purple). | ||
To further investigate the symmetry-broken path, climbing image NEB calculations are performed, see Fig. 5. The NEB calculations, which are performed spin-polarized, confirm the AIMD simulations. Again, the path can be separated into two steps. The first step has a barrier of 0.34 eV (with an O–O distance of 1.35 Å in the transition state) and results in an activated oxygen molecule with an O–O distance of 1.41 Å. This step includes the spin transition from triplet to singlet. The spin-crossing appears just before the transition state (TS1). (Detailed potential energy surfaces for both the singlet and the triplet state are given in the ESI†). The triplet-singlet excitation energy for O2 adsorbed on the paired complexes is ∼0.2 eV (see ESI†). This is consistent with the fact that the free-energy barrier on the singlet surface is about 0.1 eV, rendering the full barrier to be 0.34 eV. The second step proceeds via a low barrier of 0.14 eV with further elongation of the O2 bond length to 1.48 Å. The barrier along this path is about half of that previously reported.16 The final step for complete dissociation of oxygen into a species with an O–O distance longer than 1.48 Å proceeds according to previous reports16,18 with a free-energy barrier of ∼0.3 eV.
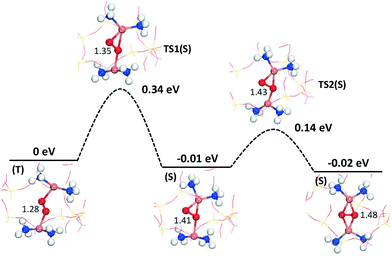 | ||
| Fig. 5 Path for activation of oxygen on the Cu+-pairs in Cu–CHA from CI-NEB calculations. The energies include zero-point corrections. Atom color codes are the same as in Fig. 4. | ||
To assess whether the Si/Al ratio affects the conclusions regarding the activation energy for oxygen, additional AIMD simulations were performed for CHA in the hexagonal unit cell. In this case, the Si/Al ratio is 17. The simulation shows (see ESI†) a free-energy barrier very similar to the result with the lower Si/Al ratio.
4 Conclusions
By use of density functional theory calculations in combination with ab initio molecular dynamics simulations, we have investigated the effect of Al-distribution on oxygen activation on paired Cu(NH3)2+ species in CHA during NH3-SCR conditions. The Al-distribution in the zeolite is found to clearly affect the probability for Cu-pair formation. The difference in pair stability as a function of Al-distribution is found to be as large as 0.55 eV and the Cu-pair formation is most favorable with an intermediate Al–Al distance about 7.5 Å. Having two Al atoms in the six-membered ring, which previously has been postulated to be the favorable location of the Al-sites, turns out to be a configuration with low stability. The dependence on Al-distribution is rationalized by a balance in electrostatic Coulomb interactions. A favorable Al–Al distance provides on one hand a stabilization between Cu+ and the (Si–O(–)–Al) sites in the framework and on the other hand a reduced Cu+–Cu+ repulsion.By performing free-energy simulations of oxygen activation, we have found a new reaction path for O2 activation over Cu(NH3)2+ pairs, with a barrier of 0.35 eV, which is about half of the barrier for the previously discussed reaction paths. The new path has a low structural symmetry and appears to be entropically preferred.
Taking the low activation energy of O2 into consideration suggests that the low-temperature NH3-SCR activity for Cu–CHA is governed by the formation of Cu-pairs rather than by the O2 activation. This indicates that it should be possible to improve the catalytic activity by precise control of the Al-distribution. Our results further stresses the similarity between binuclear copper sites in zeolites and enzymatic catalysis where ligand design has been used to stabilize the desired Cu–Cu distance by appropriate choice of the second coordination shell.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The Competence Centre for Catalysis (KCK) is hosted by Chalmers University of Technology and is financially supported by the Swedish Energy Agency and the member companies AB Volvo, ECAPS AB, Haldor Topsøe A/S, Scania CV AB, Volvo Car Corporation AB, and Wärtsilä Finland Oy. Additional financial support from the Swedish Research Council (2016-05234) and the Chalmers Area of Advance Transport is acknowledged. The calculations have been performed at C3SE (Göteborg) and PDC (Stockholm) through a SNIC grant.References
- C. Elwell, N. Gagnon, B. Neisen, D. Dhar, A. Spaeth, G. Yee and W. Tolman, Chem. Rev., 2017, 117, 2059–2107 CrossRef CAS PubMed.
- E. Solomon, P. Chen, M. Metz, S. Lee and A. Palmer, Angew. Chem., Int. Ed., 2001, 40, 4570–4590 CrossRef CAS PubMed.
- L. Que Jr and W. Tolman, Angew. Chem., Int. Ed., 2002, 41, 1114–1137 CrossRef.
- I. Garcia-Bosch, R. Cowley, D. Díaz, R. Peterson, E. Solomon and K. Karlin, J. Am. Chem. Soc., 2017, 139, 3186–3195 CrossRef CAS PubMed.
- M. Metz and E. Solomon, J. Am. Chem. Soc., 2001, 123, 4938–4950 CrossRef CAS PubMed.
- D. Quist, D. Diaz, J. Liu and K. D. Karlin, J. Biol. Inorg. Chem., 2017, 22, 253–288 CrossRef CAS PubMed.
- C. Hammond, M. M. Forde, M. H. A. Rahim, A. Thetford, Q. He, R. L. Jenkins, N. Dimitratos, J. A. Lopez-Sanchez, N. F. Dummer, D. M. Murphy, A. F. Carley, S. H. Taylor, D. J. Willock, E. E. Stangland, J. Kang, H. Hagen, C. J. Kiely and G. J. Hutchings, Angew. Chem., Int. Ed., 2012, 51, 5129–5133 CrossRef CAS PubMed.
- S. Grundner, W. Luo, M. Sanchez-Sanchez and J. A. Lercher, Chem. Commun., 2016, 52, 2553–2556 RSC.
- A. M. Beale, F. Gao, I. Lezcano-Gonzalez, C. H. Peden and J. Szanyi, Chem. Soc. Rev., 2015, 44, 7371–7405 RSC.
- F. Gao, J. H. Kwak, J. Szanyi and C. H. Peden, Top. Catal., 2013, 56, 1441–1459 CrossRef CAS.
- J. H. Kwak, R. G. Tonkyn, D. H. Kim, J. Szanyi and C. H. Peden, J. Catal., 2010, 275, 187–190 CrossRef CAS.
- S. J. Schmieg, S. H. Oh, C. H. Kim, D. B. Brown, J. H. Lee, C. H. Peden and D. H. Kim, Catal. Today, 2012, 184, 252–261 CrossRef CAS.
- F. Gao, E. D. Walter, E. M. Karp, J. Luo, R. G. Tonkyn, J. H. Kwak, J. Szanyi and C. H. Peden, J. Catal., 2013, 300, 20–29 CrossRef CAS.
- The zeolite SSZ-13 is a silicalite with the same framework as the mineral Chabazite. Here Chabazite is used to denote the framework.
- T. Janssens, H. Falsig, L. Lundegaard, P. Vennestrøm, S. Rasmussen, P. Moses, F. Giordanino, E. Borfecchia, K. Lomachenko, C. Lamberti and S. Bordiga, ACS Catal., 2015, 5, 2832–2845 CrossRef CAS.
- L. Chen, H. Falsig, T. Janssens and H. Grönbeck, J. Catal., 2018, 358, 179–186 CrossRef CAS.
- C. Paolucci, A. Parekh, I. Khurana, J. Di Iorio, H. Li, J. Albarracin Caballero, A. Shih, T. Anggara, W. Delgass, J. Miller and F. Ribeiro, J. Am. Chem. Soc., 2016, 138, 6028–6048 CrossRef CAS PubMed.
- C. Paolucci, I. Khurana, A. Parekh, S. Li, A. Shih, H. Li, J. Di Iorio, J. Albarracin-Caballero, A. Yezerets, J. Miller and W. Delgass, Science, 2017, 357, 898–903 CrossRef CAS PubMed.
- F. Gao, D. Mei, Y. Wang, J. Szanyi and C. Peden, J. Am. Chem. Soc., 2017, 139, 4935–4942 CrossRef CAS PubMed.
- H. Falsig, P. Vennestrøm, P. Moses and T. Janssens, Catal. Today, 2016, 59, 861–865 CrossRef CAS.
- F. Giordanino, E. Borfecchia, K. Lomachenko, A. Lazzarini, G. Agostini, E. Gallo, A. Soldatov, P. Beato, S. Bordiga and C. Lamberti, J. Phys. Chem. Lett., 2014, 5, 1552–1559 CrossRef CAS PubMed.
- K. Lomachenko, E. Borfecchia, C. Negri, G. Berlier, C. Lamberti, P. Beato, H. Falsig and S. Bordiga, J. Am. Chem. Soc., 2016, 138, 12025–12028 CrossRef CAS PubMed.
- L. Chen, J. Jansson, M. Skoglundh and H. Grönbeck, J. Phys. Chem. C, 2016, 120, 29182–29189 CAS.
- A. K. S. Clemens, A. Shishkin, P.-A. Carlsson, M. Skoglundh, Z. M. F. J. Martínez-Casado, O. Balmes and H. Härelind, ACS Catal., 2015, 5, 6209–6218 CrossRef CAS.
- A. Shishkin, H. Kannisto, P. A. Carlsson, H. Härelind and M. Skoglundh, Catal. Sci. Technol., 2014, 4, 3917–3926 CAS.
- E. A. Eilertsen, M. H. Nilsen, R. Wendelbo, U. Olsbye and K. P. Lillerud, Stud. Surf. Sci. Catal., 2008, 174, 265–268 CrossRef.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 13115–13118 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251–14269 CrossRef CAS.
- G. Kresse and J. FurthmÃijller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 64, 11169–11186 CrossRef.
- G. Kresse and J. FurthmÃijller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- We used VASP version 5.4.1.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. Wellendorff, K. T. Lundgaard, A. Møgelhøj, V. Petzold, D. D. Landis, J. K. Nørskov, T. Bligaard and K. W. Jacobsen, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 235149 CrossRef.
- R. Y. Brogaard, P. G. Moses and J. K. Nørskov, Catal. Lett., 2012, 142, 1057–1060 CrossRef CAS.
- R. Y. Brogaard, B. M. Weckhuysen and J. K. Nørskov, J. Catal., 2013, 300, 235–241 CrossRef CAS.
- G. Mills, H. Jónsson and G. K. Schenter, Surf. Sci., 1995, 324, 305–337 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef.
- F. Göltl, R. Bulo, J. Hafner and P. Sautet, J. Phys. Chem. Lett., 2013, 4, 2244–2249 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: Description of Al-distribution, triplet/singlet potential energy curves and additional molecular dynamics simulations. See DOI: 10.1039/c8cy00083b |
| ‡ Present address: Umicore Denmark ApS, Nøjsomhedsvej 20, DK-2800 Kgs. Lyngby, Denmark. |
| This journal is © The Royal Society of Chemistry 2018 |