Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular simulations of self-assembling bio-inspired supramolecular systems and their connection to experiments
Pim W. J. M.
Frederix
 *,
Ilias
Patmanidis
*,
Ilias
Patmanidis
 and
Siewert J.
Marrink
and
Siewert J.
Marrink
 *
*
Groningen Biomolecular Sciences and Biotechnology Institute and Zernike Institute for Advanced Materials, University of Groningen, Groningen, The Netherlands. E-mail: p.w.j.m.frederix@rug.nl; s.j.marrink@rug.nl
First published on 24th April 2018
Abstract
In bionanotechnology, the field of creating functional materials consisting of bio-inspired molecules, the function and shape of a nanostructure only appear through the assembly of many small molecules together. The large number of building blocks required to define a nanostructure combined with the many degrees of freedom in packing small molecules has long precluded molecular simulations, but recent advances in computational hardware as well as software have made classical simulations available to this strongly expanding field. Here, we review the state of the art in simulations of self-assembling bio-inspired supramolecular systems. We will first discuss progress in force fields, simulation protocols and enhanced sampling techniques using recent examples. Secondly, we will focus on efforts to enable the comparison of experimentally accessible observables and computational results. Experimental quantities that can be measured by microscopy, spectroscopy and scattering can be linked to simulation output either directly or indirectly, via quantum mechanical or semi-empirical techniques. Overall, we aim to provide an overview of the various computational approaches to understand not only the molecular architecture of nanostructures, but also the mechanism of their formation.
Introduction
Self-assembly, also known as supramolecular polymerisation, is an extremely common phenomenon in Nature; the formation of membranes, complexation of proteins or even cell–cell interactions all occur through non-covalent interactions. The notion that biomolecular systems can be used to enhance materials design for e.g. medical technology has therefore taken a firm place in chemistry.1 Small bio-inspired molecules, such as lipids or short peptides have received particular attention: they belong to a class of molecules that are easy to synthesize or modify, have a wide chemical diversity and an inherent biocompatibility. Since the first examples and applications in the 1990s,2,3 countless variations of peptides, lipids and combinations thereof, termed peptide amphiphiles (PAs), have been shown to organise themselves into nanostructures with various properties and functions. Commercial applications have been developed in cell culture, medical technology and wound healing, among other fields. Another class of biocompatible materials is that of supramolecular light-harvesting structures, such as dye aggregates that mimic natural photosynthetic systems or can be used in organic photovoltaics.Much of the progress in the field hitherto has been based on trial and error, though slowly but surely researchers are starting to discover the general design principles that govern molecular self-assembly. Finding quantitative (molecular) structure–property relationships (QSPR) in the context of meso–macroscale properties is an exciting endeavour that is still much more in its infancy than QSPR for protein–drug binding, for example. The theory of self-assembly from a thermodynamic point of view is useful to predict self-assembly from knowledge of the partition function landscape underlying the aggregation. This can be successfully applied to well-defined assemblies such as DNA origamis or metal–organic frameworks, as reviewed by Palma, Cecchini and Samorì.4 The main difficulty, however, still lies in the conformational flexibility of small molecules that causes a multidimensional and shallow intermolecular potential energy surface where local disorder is often prominent and entropy and enthalpy continuously interchange.
Experimental techniques lack the spatial resolution to inform on the exact conformation of the individual building blocks. Typically, this means the packing of molecules can only be explained by a combination of many experimental techniques. The sparse nature of the nanostructures in their solvent often precludes common structural determination techniques such as X-ray crystallography or solution-phase NMR. Less information-dense experiments that inform on small parts of the molecular conformations are combined to collect a complete picture of intermolecular interactions. This often involves measurement of light absorption (UV/Vis, infrared (IR) and circular dichroism (CD)) and scattering (dynamic and static light scattering (DLS/SLS), wide or small angle X-ray scattering (WAXS/SAXS), small angle neutron scattering (SANS)). Analysis of these experiments is performed and put besides atomic force or electron micrographs to arrive at a model of molecular interactions.
This approach is limited in three ways: firstly all techniques mentioned above are measuring ensemble averages of molecular conformations. The potentially important disordered component is therefore often neglected and leads to false models of idealized interactions for every molecule. Secondly, interpretation of the raw data occurs via empirical models developed for macromolecular systems. For example, IR absorption and CD of peptides are often compared to models for proteins, which are not generally valid. Finally, the timescale of self-assembly spans nanoseconds to weeks. While macroscale lab experiments can often deal with the upper half of this range, the initial aggregation of molecules is difficult to probe due to both sensitivity and time resolution issues. This precludes obtaining information on the early stages of the mechanism of molecular assembly. This important limitation was also appreciated by the community researching purely biologically relevant peptide or protein aggregation (e.g. amyloidogenic sequences) and it is now understood that the early stages of assembly, also known as the nucleation stage, are crucial for the final outcome and toxicity of biological aggregates.5
One way to overcome these barriers is to use classical molecular simulations. This computational method tracks the motion of individual atoms or molecules over time, thereby negating ensemble averaging and mechanistic limitations. For the last decade simulations have added valuable insights to various self-assembly processes as has recently been reviewed.6–12 However, molecular simulations have often been used as ‘another piece of the puzzle’, working separate from the experimental techniques to qualitatively add to the knowledge about a particular supramolecular polymer. In this review, we attempt to discuss the next step, i.e. using the knowledge built up over this decade to (1) design new self-assembling biomolecular systems using in silico methods and (2) directly validate spectroscopic or scattering results by linking molecular simulation output directly with experimental observables. To achieve this we discuss recent progress in molecular simulations, including enhanced sampling techniques, before proceeding to review specific research that explicitly links the computational and experimental work, both qualitatively or quantitatively via semi-empirical or quantum mechanical calculations. We focus on short peptides, amphipathic dyes, designer PAs and other bioconjugates developed for materials purposes, as summarized in Fig. 1. These molecules give rise to a large variety of morphologies, including nanofibres, tubes and vesicles that function as hydrogels, light-harvesting complexes or drug delivery vehicles, among others. For reviews of computational efforts in combination with experiments on purely biological fragments such as amyloidogenic peptides, lipids, or DNA origami, please consider ref. 13–17.
Molecular simulation techniques
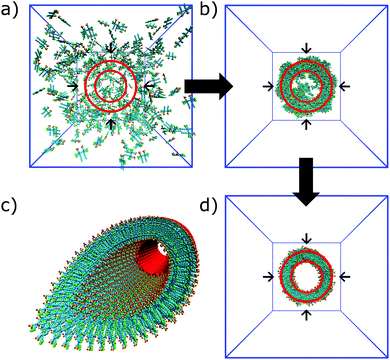
In the process of supramolecular self-assembly individual molecules are coming together via non-covalent interactions. The most widely used simulation technique to study this process is molecular dynamics (MD). In MD, Newton's equations of motion are solved for a system of interacting particles. The interactions are described using classical force field terms which typically contain bonded potentials to model the intra-molecular interactions, and non-bonded potentials (e.g., Lennard-Jones, Coulomb) to model inter-molecular interactions. Solvent may either be represented explicitly or implicitly. In the latter case, stochastic integration techniques, such as Brownian dynamics (BD) and dissipative particle dynamics (DPD) are used. In the case of discontinuous MD (DMD), the equations of motion are solved on a grid for computational speedup. Before running a simulation, a starting structure is generated, either based on a randomized placement of the constituents (e.g., to simulate self-assembly) or by pre-arranging them into the desired morphology (e.g., fibre, vesicle). From the starting configuration, usually some energy minimization and equilibration runs are performed to relax the initial state. Simulated annealing, in which the temperature of the system is temporary increased in a number of cycles, is a popular way to speed up the equilibration phase. Traditionally, MD and related techniques treat all atoms (AA) as interaction centres. To observe formation and equilibration of supramolecular structures, however, all-atom models often prove inadequate. To this end, coarse-grain (CG) force fields, that unite groups of atoms into effective interaction centres, provide a powerful alternative (Fig. 2). A variety of enhanced sampling methods exist to further increase the scope and accuracy of the simulations. Below we give the state-of-the-art of current AA and CG simulations as well as enhanced sampling techniques applied in the field of supramolecular aggregates. Note that when quantum mechanical (QM) effects or covalent bond formation/breakage need to be treated with higher accuracy, ab initio MD protocols could be employed. However, their computational cost has thus far limited them to intramolecular interactions, small molecular aggregates and crystals. For a discussion of the progress using these methods, please consider the review of Li and co-workers.18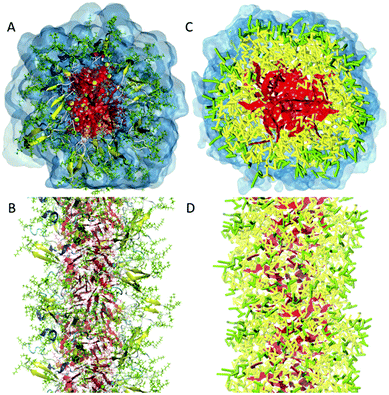 | ||
| Fig. 2 All-atom versus coarse-grain model of a drug-amphiphile filament. The drug-amphiphile consists of a hydrophobic cancer drug camptothecin (CPT) connected to a β-sheet-forming peptide sequence (CGVQIVYKK) via a short linker. (A and B) Top and side views of an all-atom representation of the filament, with CPT shown in red, and peptide residues in green. The β-sheets formed along the length of the filament are shown in yellow. (C and D) CG representation, with CPT also depicted in red, the charged lysine and polar glutamine groups shown in light green, while the other residues shown in yellow. Hydrating water is shown in the top views (A and C) only. Reproduced from ref. 19 with permission from The Royal Society of Chemistry. | ||
All-atom force fields
Force fields with full atomistic detail are the most suitable choice to study the exact conformation of individual building blocks inside a supramolecular aggregate, as they are generally able to accurately capture H-bonding as well as aromatic and charge–charge interactions by representing them via the Coulomb and Lennard-Jones potentials. The force field parameters can be obtained from quantum-mechanical (QM) calculations, together with a variety of experimental data. The ongoing development of AA force fields such as AMBER,20 CHARMM,21,22 OPLS23 and united atom force fields (implicit aliphatic hydrogens) such as GROMOS24,25 has strongly contributed to their popularity in bio-inspired molecular simulations. Solvent-free versions are available for most of these force fields, allowing a significant increase in computational efficiency, in particular for self-assembling systems, at the cost of a reduced accuracy. There seems to be no clear preference of the community which of the atomistic force fields are most suitable for simulating the self-assembly of bio-inspired molecules. Comparative studies are sparse in this context. An exhaustive set of MD simulations on the folding of tetra- and pentapeptides, performed using CHARMM, AMBER, as well as OPLS, showed clear inconsistencies between these force fields.26 A similar observation was made in a study on the dimerization propensity of amino acid side chain residues.27A nice example of the difficulty that simulations at the all-atom level face to obtain equilibrated self-assembled structures is provided by the work of Haverkort et al.41 They performed extensive self-assembly simulations of amphi-pseudoisocyanine, a dye that forms highly ordered, single-walled cylindrical J-aggregates in experiment, see Fig. 3. The simulated structure, although in the correct morphology, contained a high amount of disorder, despite multiple cycles of simulated annealing. Note, however, that the precise level of disorder is not known, as this is difficult to assess experimentally. It is conceivable that the idealized structures often used to illustrate the packing of molecules inside fibres are unrealistic and overly ordered.
 | ||
| Fig. 3 Self-assembly of amphiphilic cyanine dyes into tube structure. The dye molecule is amphi-pseudoisocyanine, a cyanine dye with two hydrophobic tails (CH3 and C18H37). The dye molecules are depicted with the tails purple; the nitrogen atoms are dark blue; the aromatic carbons are pink; the linker between the aromatic rings is light blue; and hydrogens connected to aromatic carbons are white. Perchlorate counterions are shown in green. For the water molecules, oxygen atoms are red and hydrogen atoms are white. Figure adapted with permission from ref. 41. Copyright 2013 American Chemical Society. | ||
Another important target for force field optimization is reproducing crystal packing and melting data. The stacking interactions of aromatic residues in supramolecular polymers, after all, are not too dissimilar from those found in the crystal environment. Adams et al. explicitly considered crystal versus gel packing energetics in the design of efficient gelators.60 In some cases, in particular considering electrostatic interactions between conjugated systems, polarisable models61–66 may be required. Including some electronic degrees of freedom, polarisable models are potentially more accurate, but also more expensive computationally. Applications in the area of supramolecular self-assembly are therefore still lacking. Another important development is that of constant pH models. The pKa of self-assembling molecules is often such that either a fully protonated or a fully deprotonated state is unrealistic. Moreover, the pKa may shift depending on the local environment of the monomer.67 Efficient constant pH algorithms are therefore likely to be of considerable interest.68,69 A second challenge is to improve on tools to streamline the MD workflow. Automated topology builders (CgenFF,70,71 SwissParam,72 LigParGen,73 PRODRG,74 ATB,75 Charmm-GUI,76 H++,77 among others) are playing an increasingly important role in the opportunity to rapidly set-up self-assembly simulations and screen larger groups of input molecules. Extensions to deal with more complex, multi-component systems for a wide range of morphologies are still needed. The third challenge is to extend sampling. At the all-atom level, self-assembly and growth of aggregates is difficult to observe – either formation of a nucleus is required, or one gets easily trapped in disordered aggregates that take a long time to heal. Relaxation of pre-assembled structures is also difficult. The starting structures might thus put a bias to the system, and often this is not known. Continuous improvement of computer hardware, and the ability of most common MD software packages to run efficiently on large numbers of compute nodes including GPUs, alleviates some of this problem, but it is unlikely that AA simulations are capable of dealing with the hierarchy of length and time scale underlying supramolecular self-assembly in the decades to come.
The above caveats also limit the predictive power of AA simulations when searching for new self-assembling systems. For peptide monomers, some MD approaches have resulted in the classification of peptide building blocks towards foldability26 and predicted secondary structure.78,79 However, prediction of the packing of many molecules together in larger nanostructures (dimensions greater than a single foldamer) is not straightforward from recognition motifs. To some extent, AA MD assembly simulations can be used to screen among self-assembly candidates in a high-throughput fashion as demonstrated by Smadbeck et al.34 They developed a hierarchical framework for multimeric assemblies based on computing the interaction potential energy, fold specificity and approximate association affinity of 128 tripeptide sequences, while taking into account experimental constraints and design templates. They discovered multiple new self-assembling systems as verified by experiments. Importantly, Gupta, Adams and Berry were able to predict the gelation behaviour of aromatic peptide conjugates.80 They employed a large experimental training set of both gelling and non-gelling dipeptides with various aromatic capping groups to derive QSPR. They found the most important physicochemical descriptors were the number of rings, predicted molecular aqueous solubility, polar surface area, solvent accessible surface area, A![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P and number of rotatable bonds and were even able to obtain 100% accuracy in their validation set of 9 new molecules in terms of gelation behaviour. MD simulations of assembly could definitely expand the scope of such a method without laborious experiments for every new class of building blocks, but are currently not feasible at the AA level. Two potential solutions are to resort to coarse-grain force fields and to utilize enhanced sampling methods, as will be discussed below.
P and number of rotatable bonds and were even able to obtain 100% accuracy in their validation set of 9 new molecules in terms of gelation behaviour. MD simulations of assembly could definitely expand the scope of such a method without laborious experiments for every new class of building blocks, but are currently not feasible at the AA level. Two potential solutions are to resort to coarse-grain force fields and to utilize enhanced sampling methods, as will be discussed below.
Coarse-grain force fields
As mentioned, self-assembly can take place on various time and length scales. Routine AA MD simulations are currently limited to approximately 106 particles for systems that need to be simulated for 100s of nanoseconds. A cubic system containing pure water would thus be restricted to 22 × 22 × 22 nm3. Some nanostructures may be smaller than this, but in most cases at least one of their dimensions exceeds this limit, especially considering experimental low mM concentrations of monomers. Moreover, structural order often does not converge on nanosecond timescales and the need for longer simulations is omnipresent. Coarse-graining the degrees of freedom of the constituents of the simulation is a popular solution that can extend the use of simulations well beyond these limits.81 However, in particular in the field of supramolecular polymers, it is important to retain the chemical specificity of the building blocks, as it has often been shown that small modifications, such as amino acid mutations, can have a dramatic effect on their self-assembly. Several coarse-grain (CG) force fields have been developed along these lines to study self-assembling systems with chemical specificity.A CG force field that has been used by several research groups for a variety of bio-inspired systems is the Martini force field.82–85 Originally developed to study lipid membranes, the force field has been extended to encompass all major classes of biomolecules as well as other classes of soft matter (polymers) and nanoparticles (e.g., fullerene, carbon nanotubes, gold particles). The non-bonded interactions in the force field are parametrized targeting partitioning free energies of building blocks between water and non-polar solvents, which is also a key concept in the assembly of amphiphiles. This parametrization strategy combined with the inherent versatility and compatibility of the various classes of molecules developed makes the Martini force field particularly attractive to study supramolecular systems. The Martini model relies on a four to one mapping scheme, i.e., four heavy atoms together with associated hydrogen atoms are represented by a CG site (also denoted CG bead). For rings, a higher resolution is used. The interactions between the CG sites are calibrated with respect to experimental thermodynamic data as well as reference AA simulations. Compared to all-atom force fields, the Martini model typically obtains a speed up of three orders of magnitude. In addition, the dynamics of most processes are faster due to an overall reduced friction. This makes the interpretation of time scales somewhat problematic, and typically only provides an order of magnitude estimate of the real dynamics. Another important limitation is the inability of the Martini model to account for secondary structure transitions in longer peptides and proteins, due to the lack of directional hydrogen bonding terms in the force field. Usually the secondary structure is fixed using an elastic network86,87 that can be further optimized with respect to atomistic simulations.88 Other CG force fields that are applied in the field of supramolecular self-assembly are the Shinoda–Devane–Klein (SDK) model,89 which is rather similar in mapping and parameterization strategy to Martini, and the PRIME model,90 a CG protein force field allowing secondary structure changes and making efficient use of discontinuous MD (DMD). In principle, more accurate CG models can be derived based on force matching, iterative Boltzmann (IB) and related procedures.91–95 These approaches aim to capture the higher order correlations of AA reference simulations in effective CG pair potentials. The advantage over generic force fields such as Martini is their higher accuracy, in particular with respect to structural detail. A disadvantage of these models is that they are usually less transferable and require more parameterization effort, plus the need for smaller time steps to integrate the equations of motion, thereby reducing the computational efficiency.
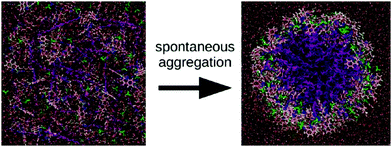
Apart from peptide-based compounds, only few CG studies on other systems have been reported to date. A possible reason is the difficulty to obtain reliable CG models for more complex molecules often involving conjugated ring systems. Exceptions are the CG self-assembly simulations on synthetic constructs from trimaleimide functionalized with peptide linkers and cholesterol, forming nanosponges,109 and of porphyrin/dipeptide mixtures using DPD.110 A recent highlight is the work of Bochicchio and Pavan who parameterized a Martini model for BTA.111 To improve the description of the stacking interactions between the BTA cores, additional charged particles were introduced to mimic hydrogen bonding. The model was further optimized and validated by comparison to all-atom data. Subsequent simulations provide a picture of a stepwise cooperative polymerization mechanism, where initial fast hydrophobic aggregation of the BTA monomers in water is followed by the slower reorganization of these disordered aggregates into ordered directional oligomers. Supramolecular polymer growth then proceeds on a slower time scale. The use of a CG model allowed also for a systematic investigation of the effect of structural variations and temperature on this process. Another example of supramolecular polymer growth is provided in our own lab, based on cyclic macrocycles.112 Using an optimized Martini model, we observe the growth of a macrocycle fibre when individual building blocks are added in solution (Fig. 4). The growth proceeds by adsorption of molecules at the body of the fibre, followed by 1D diffusion along the fibre to reach the tip where the new building blocks attach. This growth process is supported by high-speed AFM experiments.
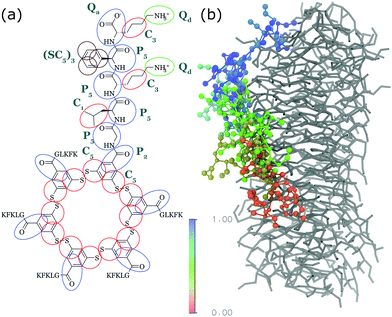 | ||
| Fig. 4 (a) CG Martini mapping of a DCL peptide macrocycle as described in ref. 112. Atoms are grouped into beads as indicated by the circles. Different colours indicate different bead types as labelled. Only one of the 6 arms of the macrocycles is shown explicitly. (b) CG simulation of the growth of a DCL fibre (in grey). A new monomer is added to the solution around the fiber, lands on the side of the fiber at time = 0 μs (red) and diffuses over 1 μs towards the end of the fiber, promoting growth. | ||
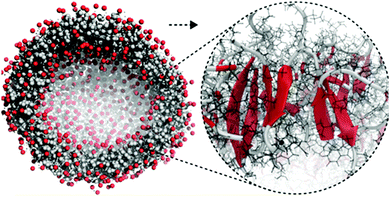 | ||
| Fig. 5 All-atom to coarse-grain backmapping example. CG structure of a self-assembled amphiphilic peptide nanovesicle (left), and zoomed view of the all-atom structure obtained after backmapping (right). In the left image, hydrophilic/hydrophobic residues are coloured red/grey. In the right image, red colour is used to indicate extended secondary structure formation. Figure adapted with permission from Rad-Malekshahi et al.126 Copyright 2015 American Chemical Society. | ||
Enhanced sampling techniques
Whether all-atom, coarse-grained or multiscale models are used, there is often a need for increasing the sampling of conformational space. Capturing supramolecular self-assembly in full requires not only sampling of the many ways individual monomers can pack together, but also sampling the overall morphologies available to hundreds or thousands of monomers as well as sampling of the manifold of kinetic pathways leading from one structure to the other. Several methods exist to increase the effective simulation time of MD simulations, by improving sampling of relevant areas of the assembly path. These methods operate by biasing the potential along a certain reaction coordinate or by effectively lowering energy barriers on the potential energy landscape. Popular methods that are applied in the field of supramolecular self-assembly include replica-exchange MD (REMD),136 meta-dynamics,137,138 steered MD139 and transition path sampling (TPS).140 Examples of these methods are provided below. For a recent review on enhanced sampling techniques, see ref. 141.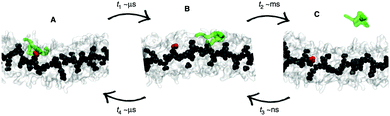 | ||
| Fig. 6 Enhanced sampling with meta-dynamics. Example of BTA fibre growth from Bochicchio et al.151 Starting from a configuration where the activated monomer (green in the snapshots) is stacked onto a hot spot (red) on the fibre surface (A), the monomer does not diffuse directly in water, but tends to diffuse onto the surface of fibre (B) before jumping in the solvent (C). | ||
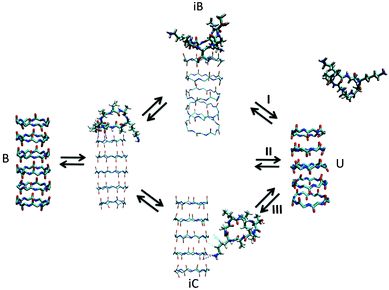 | ||
| Fig. 7 Kinetic pathways obtained with TPS. Example from Brotzakis et al., showing three possible transition mechanisms found from bound (B) to unbound (U) states in the transition path ensemble of tube-forming cyclic peptides. Reproduced from ref. 155 with permission from The Royal Society of Chemistry. | ||
Comparison of simulation and experimental results
Molecular simulations give a unique and often intuitive insight into the dynamics of self-assembled structures by explicitly showing the trajectory of every molecule in the system. Following this line of thought, many research papers have included simulations of the self-assembly process or the dynamics of an assembled structure. However, all too often their interpretation is left to the intuition of the reader and/or author, while knowing the position, velocity and acceleration of every particle in the system allows for quantitative comparisons with reality. The difficulty lies in the discrepancy between what can be measured in a laboratory (macroscale properties, ensemble averages) and what can be directly observed from molecular simulations, i.e. the motion of individual molecules. As the domains of simulations and experiments are converging more can be obtained from direct comparison (nanostructure dimensions and even self-assembly mechanisms), but indirect comparisons through quantum chemical calculations of spectra can be equally useful, especially when optical properties are available from the experiment. In this section, we review advances in both approaches.Direct comparisons of MD results with experiments
A property that shows up in many pre-assembled peptide or PA fibres is spontaneous twisting,175–178 also seen in experimental studies using AFM, TEM and CD spectroscopy. Lai, Rosi and Schatz simulated the formation of chiral nanofibers of a self-assembling gold-binding peptide conjugate, starting from achiral structures using atomistic MD and found the correct handedness and pitch.175 Frederix et al. took a similar approach and identified the handedness and pitch of stacks of peptide macrocycles.54 A still relatively unexplored area is the interaction between fibres. Bundling of fibres is observed in electron micrographs for many systems, but not easily studied due to the large system sizes involved. Initial attempts in this direction can be found in a number of publications.41,179,180 All these results combined suggest that interatomic distances, on both Å and tens of nanometres scale, can reliably be extracted from MD simulations.
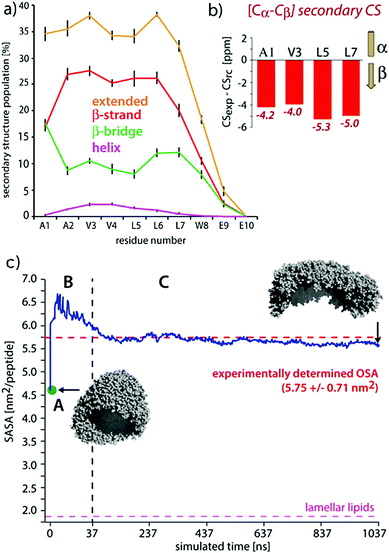 | ||
| Fig. 9 Comparisons of experimental and MD results on a peptide nanocarrier. (a) Residue-specific secondary structure extracted from a 1 μs atomistic simulation of 449 peptides. (b) Residue-specific ssNMR secondary chemical shifts indicating a full-β conformation. (c) Comparison of the occupied surface area (OSA) measured by static light scattering (SLS) and the solvent accessible surface area (SASA) derived from MD simulations. Point A (in green) is the starting system of the atomistic simulation (comprising 2500 SA2 peptides), back-transformed from the CGMD simulation. This system was evolved for 37.5 ns, shown in passage B. In passage C, an assembly of 449 peptides was further evolved for 1 μs. Figure adapted with permission from ref. 126. Copyright 2015 American Chemical Society. | ||
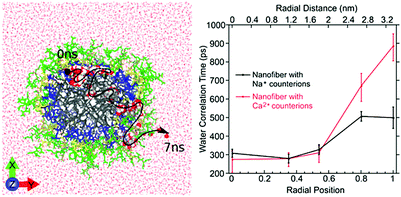 | ||
| Fig. 10 Left: Atomistic simulation snapshot illustrating the trajectory (dashed line) of one water (highlighted) diffusing across the nanofiber in around 7 ns simulation time. Right: Experimentally measured water correlation time as function of the distance from the nanofiber core. Figure reproduced with permission from ref. 45. Copyright 2017 American Chemical Society. | ||
Indirect quantitative comparisons
Density functional theory has been successfully used to determine the vibrational structure of small amphiphiles clusters,110,187 but does not capture long-range coupling and the effect of disorder very well due to its static structure. While DFT-MD has been applied to single or dimers of peptides to resolve the flexibility issue,189 calculating the full electronic structure of a nanostructure of 100s of monomers evolving over time is computationally unattainable. The work of many groups, recently reviewed by Reppert and Tokmakoff.190 has overcome this issue using a mixed quantum-classical approach that uses frequency mapping191–195 and TDC theory196–198 while representing amide groups as environment-dependent coupled oscillators. Experimentally, the groups of, among others, Zanni and Woutersen have studied short various biological fragments of amyloidogenic proteins (e.g.ref. 199 and 200) and shown the power of combining (ultrafast) infrared spectroscopy and calculations for short peptides. The first use specifically for self-assembling designer PA was recently reported by Frederix et al. who studied the self-assembly of self-replicating peptide macrocycles using both experimental techniques and semi-empirical calculations on MD trajectories (see Fig. 11).54 They found excellent agreement between the calculated spectra of a dynamic 1D β-sheet-like fiber and the experimental result. By averaging over many MD frames and saving snapshots with approximately the same frequency as the vibrational period, both the homogeneous and inhomogeneous line broadening of the IR transitions, respectively, are part of the calculation output. This advantage over QM calculations is particularly useful in time-resolved 2D spectra, but also in linear spectra to indicate whether the degree of disorder in the structure is accurately represented by the simulated structure.
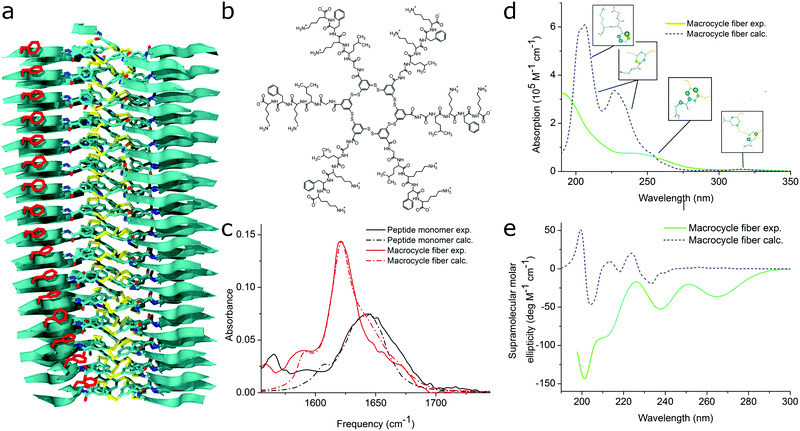 | ||
| Fig. 11 MD simulations and spectral calculations on self-assembled self-replicating peptide macrocycles. (a) Chiral fiber nanostructure from MD simulations. Peptide chains are indicated as ribbons. (b) Macrocycle chemical structure. (c) Experimental and calculated linear infrared spectra of the fiber. (d) Experimental and calculated UV/Vis spectra of the fiber. The location of the transition dipoles for each of the calculated bands are indicated by the insets. (e) Experimental and calculated supramolecular CD spectra of the fiber. Figure adapted from ref. 51. | ||
Other regions in the IR spectrum can also help in interpreting the dynamics of nanostructure as shown by Deshmukh et al. for the water OH stretch region.125 Vibrational spectra of both bulk water and water molecules close to the PA nanofibers were calculated by Fourier transforming of the atomic velocity autocorrelation function obtained from the MD simulation trajectories. This showed much more ordered water molecules in proximity to (especially hydrophilic) PA groups, which was experimentally validated by comparing PA assembly kinetics by IR and CD experiments in H2O and D2O.
Analysis of experimental electronic spectra often occurs on a qualitative level without clear information on the underlying physical principles. This originates from a historic lack of computational power to unravel the electronic structure of large non-covalent aggregates containing a lot of disorder, while the theory on J- and H-aggregates is reasonably well-developed for small complexes. The multitude of vibronic states in supramolecular polymers also complicates matters further because multiple conformations can produce similar spectra when broadened to a large extent by disorder. In order to obtain a quantitative description and information on the molecular arrangement of monomers inside the aggregates, theoretical methods have been employed to model their optical electronic states.201–203 More specifically, exciton Hamiltonians have been used to describe the excitonic states of the system. The basic forms of the Hamiltonians usually include two parameters, one for the molecular electronic excitation and another one for the excitonic coupling of different monomers. Diagonalization of the Hamiltonian operators produces the simulated optical spectra of the aggregates. The electronic coupling and especially the CD signal is often very sensitive to disorder in the molecular packing as theoretically shown by Van Dijk et al. and quantitatively analysed and reviewed by Pescitelli, Di Bari and Berova.204–206 This emphasizes the importance of using MD simulated input structures rather than idealized putative structures. In many cases, the simulated optical spectra present good agreement with the experimental measurements when disorder is taken into account.43,207 Also note that the CD signal calculated by exciton methods typically covers only the supramolecular component of the signal and molecular chirality should be subtracted. However, many studies have demonstrated that the induced CD signal by assembly is generally significantly different or larger than the molecular component, such as for protein secondary structure determination208 and achiral molecules forming helical assemblies.209–212 Alternatively, the molecular CD signal can be extracted from experiments below the critical aggregation concentration or above the critical aggregation temperature.
For self-assembling bio-inspired molecules, electronic structure calculations were recently used to understand the UV/Vis and CD spectra of the self-replicating peptide macrocycles described above (see Fig. 11).54 UV/Vis and CD spectra calculated from MD structures displayed reasonable agreement with experimentally measured spectra, validating the proposed structural models for supramolecular packing. Importantly, the chirality of the nanostructure was appropriately represented by the simulations: both the helical pitch and the handedness (and thus sign of the supramolecular CD signal) were accurately predicted by the combined MD simulations and electronic calculations. Additionally, assignment of the absorption bands to specific chemical moieties in the building block provided crucial information for the assembly mechanism by exploring the behaviour of the bands during T-induced disassembly of the nanofibers.
The calculation of optical properties is of relevance for the structural analysis of self-assembled structures as outlined above, but can also be of inherent significance to the function of the structure. Such is the case in supramolecular light-harvesting structures, such as dye aggregates that mimic natural photosynthetic systems or can be used in organic photovoltaics. A well-studied class of such aggregates is cyanine dyes, which optical properties are determined by the polymethine chromophore (Fig. 1 and 12). Their behaviour in solution and aggregates can be tuned using different substituents such that well-ordered nanostructures are formed as evidenced by cryo-TEM.43,201,213,214 In principle the spontaneous assembly of such systems can be studied using MD simulation, as evidenced by Haverkort et al.41 An amphiphile pseudoisocyanine dye, amphi-PIC, was studied by MD simulations and two types of aggregates, single-walled tubes and ribbons were generated. However, it was found that the final arrangement of the self-assembled structure lacks long-range order. Megow and co-workers therefore studied similar (C8S3) cyanine dyes starting from preformed nanotubes instead of a spontaneously assembled structure. The nanotubes remained stable for approximately 7 ns, although they disintegrated in time afterwards. The simulated absorption spectra for the obtained MD structures resulted in good agreement with the experimentally measured spectra, when the dispersive energy shifts of the molecules in the outer and the inner wall were taken into account in the theoretical models for the optical properties of the nanotubes.44 Similarly satisfying results were obtained from MD structures of other dye aggregates, where theoretical models, experimental measurements and computational studies have been combined together.43,215 These results indicate that the developed systematic procedure for structure prediction of self-organized tubes cyanine dyes is generally valid.
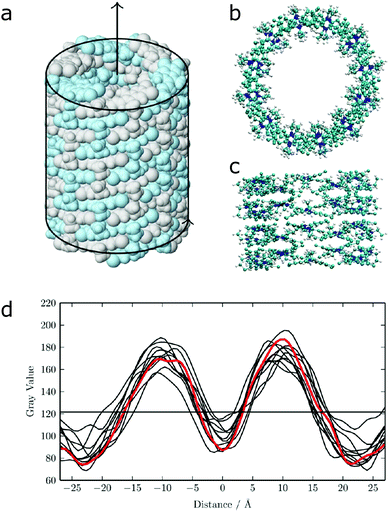 | ||
| Fig. 12 (a) Idealized model for a nanotube structure of TTBC. (b) Top and (c) side view of the tube structure after MD simulations. (d) Comparison of the experimental density profile from cryo-TEM (red) with simulated 2D density profiles from 10 different angles (black lines) of the MD structure. Figure adapted from ref. 43. | ||
Conclusions and outlook
This review discusses the important developments in obtaining insight into the self-assembly of bio-inspired molecular systems using classical MD. On the one hand, advances in force fields and enhanced sampling methods improve the speed and accuracy with which useful information can be obtained from simulations. On the other hand, new experimental techniques and methods to directly relate their results to computational output enhance the synergy between the two traditional realms. To advance our understanding further, we identify several challenges for the field that we expect to accelerate major improvements in the future: the convergence of simulated and experimentally accessible time and length scales, far-from-equilibrium systems, computational model improvement and the rational design of de novo supramolecular systems.Convergence of time and length scales
Self-assembly takes place on both the smallest and largest time and length scales. Simulations are currently the main method to study (the aggregation of) individual molecules, but experimental developments are also going more and more towards single-molecule resolution. Single-molecule spectroscopy has seen great improvements in the last decade, especially in determining the position, structure and dynamics of fluorescent or fluorescently labelled molecules. Microscopy techniques have advanced simultaneously to have better time resolution (e.g. high-speed AFM has sub-second time resolution at a few nm spatial resolution and has in some cases revealed the mechanism of supramolecular polymerization112,216) or better spatial resolution (e.g. super-resolution microscopy has been used to follow both monomer mixing and self-sorting in supramolecular polymers48,217). Another promising technical advance is the development of (nano- and) microfluidics, which has already enabled the detailed study of the anisotropic mechanism of the supramolecular polymerisation of diphenylalanine.218,219 Spatial confinement and control of the chemical potential of building blocks in solution crucially allows for the detection of intermediates in the self-assembly process which are difficult to capture otherwise.With experiments going towards smaller and shorter scales, molecular simulations are going the other direction to meet them in the middle. Both hardware and software developments, together with more accurate coarse-graining techniques are allowing longer simulations of larger systems. Automated parameterisation algorithms, when used with care, can strongly reduce the effort to study new self-assembling systems. Enhanced sampling techniques allow a faster and more complete search of the conformational space available. Naturally, when computational and experimental techniques are able to probe the same molecular processes directly, the confidence in any conclusions deriving from the work is greatly enhanced. For example, some ensemble spectroscopic techniques are being revisited for use in supramolecular chemistry. NMR was long deemed unsuitable for large aggregated structures due to their lack of tumbling in solution, but recently developed protocols for ssNMR have determined the molecular architecture of supramolecular assemblies to almost single-crystal resolution.181,182,220 Technical and theoretical developments in vibrational CD experiments are starting to allow the absolute chirality and organisation of various biomolecular supramolecular architectures to be studied.221 We have not explored calorimetry measurements in this review, but work from the Bouteiller group and others has shown that the thermodynamics of monomer association to a supramolecular polymer can be revealed by isothermal titration or differential scanning calorimetry.222 For the case of BTA, this was combined with MM/MD simulations to get a complete picture of the self-assembly energetics,223 but would ideally be compared to free energy calculations from, for example, umbrella sampling, meta-dynamics or TPS simulations that are more accurate in determining the potential energy landscape.
Steering the pathway: away from equilibrium
The energy landscape of the self-assembly process is, in fact, one of the major subjects of investigation in the supramolecular chemistry field. In an effort to make dynamic, functional and life-like materials, that can self-heal or are responsive, systems need to be able to continuously convert an energy input (e.g. chemical, mechanical) to remain away from thermodynamic equilibrium.224,225 This presents a serious challenge for both experimental and computational studies of self-assembling systems: while it has been shown that supramolecular fibers can represent the thermodynamic minimum,226 in most cases assembled structures represent kinetically trapped states, and the outcome of a self-assembly experiment or simulation therefore depends on the pathway followed.227–230 This implies that a large portion of the multimeric conformational space needs to be sampled to address all possible routes towards a final nanostructure. Techniques like TPS have started to open up this possibility, but require knowledge regarding the start and ending structures, which may not always be available. Recently, experiments and kinetic models have been developed to describe the thermodynamics for short peptide assembly,231 which crucially provides information on kinetic barriers and state equilibria. MD simulations and free energy calculations have great potential to work together with these kinetic equation-based approaches and link these barriers, for example, to actual supramolecular processes. The ultimate challenge would be to control the self-assembly pathways not only globally, but also locally, e.g. using compartmentalisation techniques, laser induced local heating, or stressing and steering with molecular motors. From a theoretical point of view, the aim is to mould the underlying energy landscape in a controlled way in order to bias the propensity of a system to end up in certain states, or to allow or disable certain response directions by adding or removing kinetic barriers. In the end, a non-equilibrium thermodynamic framework is needed to guide simulation efforts in this direction.Computational model improvement
We expect that improvements in the (semi-empirical) quantum mechanical description of supramolecular systems will drive the comparison of simulated and (usually easily accessible) experimental results further. The prediction of IR spectra discussed in the previous section has seen many successes specifically for the amide I band of the spectrum, but an abundancy of self-assembling systems contain other functional groups that are potential markers for structure. Except from brute-force DFT calculations, theory is still lacking to describe vibrational coupling in this case. Electronic calculations are usually more flexible considering functional groups, but the computationally relatively cheap methods that allow using the large number of molecules in an assembly, such as ZINDO/S,232 were developed for and fitted on small organic molecules with mainly single-electron excited states and a small active space, and perhaps should be recalibrated for systems of many molecules with near-degenerate excited states.Finally, we want to note that some of the major successes in describing self-assembly using MD have taken the supramolecular behaviour of the system into account already in the parametrization stage. Indeed, small deviations from reality on the monomer level can be strongly amplified by having hundreds of interacting monomers. For example, some MD force fields suffer from overestimation of protein–protein interactions, because the individual components (amino acids) have been parametrized towards protein stability. This can be solved by including the nature of the assembly, e.g. nucleation–elongation kinetics as a target property. Solutions may include polarisable force fields as discussed above, but can be included as a target in classical MD as well, as shown by Bochicchio and Pavan and our lab.111,112
Toward rational design
In the previous sections we have discussed successes in validating nanostructures proposed based on experiments or even putative structure relying on chemical intuition. However, as the chemical space for bio-inspired nanostructures is enormous, it would be particularly interesting to simplify the effort of discovering new bionanostructures by predictive computational approaches. The rational design of small to medium-sized building blocks that assemble has seen many successes from the field of foldamers,212,233–236 single molecules that fold via non-covalent interactions, often through intramolecular recognition motifs using similar interactions as in the general field of self-assembly (H-bonds, π-stacking etc.). The challenge ahead now is the prediction of the packing of many molecules together in larger nanostructures (dimensions greater than a single foldamer). MD assembly simulations can be used to screen among self-assembly candidates in a high-throughput fashion and one can imagine this approach can be extended to other factors commonly affecting self-assembly, such as pH, and ion nature and concentration.The above considerations point towards a change in mind-set in supramolecular chemistry. It is even argued to abandon the term “self-assembly”, which implies a passive approach, in favour of “non-covalent synthesis”, where the scientist does not only choose a building block to start with, but designs a complete bottom-up route to get from individual components to a functional nanostructure. We conclude that directly applicable input from simulations will prove decisive in speeding up this transformation.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
PF acknowledges support from the Netherlands Organisation for Scientific Research (Veni, 722.015.005). SJM acknowledges funding through an ERC Advanced Grant ‘COMP-MICR-CROW-MEM’. We thank Patrick van der Wel (U. Pittsburgh) and Jannik Nedergaard Pedersen (Aarhus U.) for helpful discussions. We thank Peter Kroon and Guillermo Monreal Santiago (U. Groningen) for help with Fig. 4 and the TOC image.References
- E. Krieg, M. M. C. Bastings, P. Besenius and B. Rybtchinski, Chem. Rev., 2016, 116, 2414–2477 CrossRef CAS PubMed.
- M. R. Ghadiri, J. R. Granja, R. A. Milligan, D. E. McRee and N. Khazanovich, Nature, 1993, 366, 324–327 CrossRef CAS PubMed.
- S. Zhang, T. Holmes, C. Lockshin and A. Rich, Proc. Natl. Acad. Sci. U. S. A., 1993, 90, 3334–3338 CrossRef CAS.
- C.-A. Palma, M. Cecchini and P. Samorì, Chem. Soc. Rev., 2012, 41, 3713–3730 RSC.
- L. Haataja, T. Gurlo, C. J. Huang and P. C. Butler, Endocr. Rev., 2008, 29, 303–316 CrossRef CAS PubMed.
- M. McCullagh, T. Prytkova, S. Tonzani, N. D. Winter and G. C. Schatz, J. Phys. Chem. B, 2008, 112, 10388–10398 CrossRef CAS PubMed.
- N. Thota and J. Jiang, Front. Mater., 2015, 64 Search PubMed.
- T. Tuttle, Isr. J. Chem., 2015, 55, 724–734 CrossRef CAS.
- Q. Cui, R. Hernandez, S. E. Mason, T. Frauenheim, J. A. Pedersen and F. Geiger, J. Phys. Chem. B, 2016, 120, 7297–7306 CrossRef CAS PubMed.
- A. Manandhar, M. Kang, K. Chakraborty, P. K. Tang and S. M. Loverde, Org. Biomol. Chem., 2017, 15, 7993–8005 CAS.
- C. Yuan, S. Li, Q. Zou, Y. Ren and X. Yan, Phys. Chem. Chem. Phys., 2017, 19, 23614–23631 RSC.
- D. Bochicchio and G. M. Pavan, Adv. Phys.: X, 2018, 3, 1436408 Search PubMed.
- J. Nasica-Labouze, P. H. Nguyen, F. Sterpone, O. Berthoumieu, N.-V. Buchete, S. Coté, A. De Simone, A. J. Doig, P. Faller, A. Garcia, A. Laio, M. S. Li, S. Melchionna, N. Mousseau, Y. Mu, A. Paravastu, S. Pasquali, D. J. Rosenman, B. Strodel, B. Tarus, J. H. Viles, T. Zhang, C. Wang and P. Derreumaux, Chem. Rev., 2015, 115, 3518–3563 CrossRef CAS PubMed.
- A. Morriss-Andrews and J.-E. Shea, Annu. Rev. Phys. Chem., 2015, 66, 643–666 CrossRef CAS PubMed.
- L. Nagel-Steger, M. C. Owen and B. Strodel, ChemBioChem, 2016, 17, 657–676 CrossRef CAS PubMed.
- M. Müller, J. Stat. Phys., 2011, 145, 967–1016 CrossRef.
- H. Jabbari, M. Aminpour and C. Montemagno, ACS Comb. Sci., 2015, 17, 535–547 CrossRef CAS PubMed.
- S. Li, W. Li and J. Ma, Acc. Chem. Res., 2014, 47, 2712–2720 CrossRef CAS PubMed.
- M. Kang, H. Cui and S. M. Loverde, Soft Matter, 2017, 13, 7721–7730 RSC.
- R. Salomon-Ferrer, D. A. Case and R. C. Walker, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 198–210 CrossRef CAS.
- A. D. MacKerell, D. Bashford, M. Bellott, R. L. Dunbrack, J. D. Evanseck, M. J. Field, S. Fischer, J. Gao, H. Guo, S. Ha, D. Joseph-McCarthy, L. Kuchnir, K. Kuczera, F. T. K. Lau, C. Mattos, S. Michnick, T. Ngo, D. T. Nguyen, B. Prodhom, W. E. Reiher, B. Roux, M. Schlenkrich, J. C. Smith, R. Stote, J. Straub, M. Watanabe, J. Wiórkiewicz-Kuczera, D. Yin and M. Karplus, J. Phys. Chem. B, 1998, 102, 3586–3616 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. Hatcher, C. Acharya, S. Kundu, S. Zhong, J. Shim, E. Darian, O. Guvench, P. Lopes, I. Vorobyov and A. D. Mackerell, J. Comput. Chem., 2010, 31, 671–690 CAS.
- W. L. Jorgensen and J. Tirado-Rives, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 6665–6670 CrossRef CAS PubMed.
- C. Oostenbrink, A. Villa, A. E. Mark and W. F. Van Gunsteren, J. Comput. Chem., 2004, 25, 1656–1676 CrossRef CAS PubMed.
- M. M. Reif, P. H. Hünenberger and C. Oostenbrink, J. Chem. Theory Comput., 2012, 8, 3705–3723 CrossRef CAS PubMed.
- P. S. Georgoulia and N. M. Glykos, J. Phys. Chem. B, 2013, 117, 5522–5532 CrossRef CAS PubMed.
- D. H. de Jong, X. Periole and S. J. Marrink, J. Chem. Theory Comput., 2012, 8, 1003–1014 CrossRef CAS PubMed.
- K. K. Bejagam, G. Fiorin, M. L. Klein and S. Balasubramanian, J. Phys. Chem. B, 2014, 118, 5218–5228 CrossRef CAS PubMed.
- I. R. Sasselli, R. V. Ulijn and T. Tuttle, Phys. Chem. Chem. Phys., 2016, 18, 4659–4667 RSC.
- R. Chelli, F. L. Gervasio, P. Procacci and V. Schettino, J. Am. Chem. Soc., 2002, 124, 6133–6143 CrossRef CAS PubMed.
- C. A. E. Hauser, R. Deng, A. Mishra, Y. Loo, U. Khoe, F. Zhuang, D. W. Cheong, A. Accardo, M. B. Sullivan, C. Riekel, J. Y. Ying and U. A. Hauser, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 1361–1366 CrossRef CAS PubMed.
- A. Lakshmanan, D. W. Cheong, A. Accardo, E. D. Fabrizio, C. Riekel and C. A. E. Hauser, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 519–524 CrossRef CAS PubMed.
- N. K. Mishra, A. Jain, C. Peter and S. Verma, J. Phys. Chem. B, 2017, 121, 8155–8161 CrossRef CAS PubMed.
- J. Smadbeck, K. H. Chan, G. A. Khoury, B. Xue, R. C. Robinson, C. A. E. Hauser and C. A. Floudas, PLoS Comput. Biol., 2014, 10, e1003718 Search PubMed.
- A. N. Rissanou, E. Georgilis, E. Kasotakis, A. Mitraki and V. Harmandaris, J. Phys. Chem. B, 2013, 117, 3962–3975 CrossRef CAS PubMed.
- M. Kang, P. Zhang, H. Cui and S. M. Loverde, Macromolecules, 2016, 49, 994–1001 CrossRef CAS.
- B. A. Thurston, J. D. Tovar and A. L. Ferguson, Mol. Simul., 2016, 42, 955–975 CrossRef CAS.
- D. Ivnitski, M. Amit, O. Silberbush, Y. Atsmon-Raz, J. Nanda, R. Cohen-Luria, Y. Miller, G. Ashkenasy and N. Ashkenasy, Angew. Chem., Int. Ed., 2016, 55, 9988–9992 CrossRef CAS PubMed.
- M. Garzoni, M. B. Baker, C. M. A. Leenders, I. K. Voets, L. Albertazzi, A. R. A. Palmans, E. W. Meijer and G. M. Pavan, J. Am. Chem. Soc., 2016, 138, 13985–13995 CrossRef CAS PubMed.
- H. Fu, Y. Liu, F. Adrià, X. Shao, W. Cai and C. Chipot, J. Phys. Chem. B, 2014, 118, 11747–11756 CrossRef CAS PubMed.
- F. Haverkort, A. Stradomska, A. H. de Vries and J. Knoester, J. Phys. Chem. B, 2013, 117, 5857–5867 CrossRef CAS PubMed.
- X. Li, F. Buda, H. J. M. de Groot and G. J. A. Sevink, Proc. Natl. Acad. Sci. U. S. A. Search PubMed , submitted.
- C. Friedl, T. Renger, H. v. Berlepsch, K. Ludwig, M. Schmidt am Busch and J. Megow, J. Phys. Chem. C, 2016, 120, 19416–19433 CAS.
- J. Megow, M. I. S. Röhr, M. S. am Busch, T. Renger, R. Mitrić, S. Kirstein, J. P. Rabe and V. May, Phys. Chem. Chem. Phys., 2015, 17, 6741–6747 RSC.
- J. H. Ortony, B. Qiao, C. J. Newcomb, T. J. Keller, L. C. Palmer, E. Deiss-Yehiely, M. Olvera de la Cruz, S. Han and S. I. Stupp, J. Am. Chem. Soc., 2017, 139, 8915–8921 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- A. Iscen and G. C. Schatz, EPL, 2017, 119, 38002 CrossRef.
- M. B. Baker, L. Albertazzi, I. K. Voets, C. M. A. Leenders, A. R. A. Palmans, G. M. Pavan and E. W. Meijer, Nat. Commun., 2015, 6, 6234 CrossRef PubMed.
- O.-S. Lee, S. I. Stupp and G. C. Schatz, J. Am. Chem. Soc., 2011, 133, 3677–3683 CrossRef CAS PubMed.
- Y. Raz, B. Rubinov, M. Matmor, H. Rapaport, G. Ashkenasy and Y. Miller, Chem. Commun., 2013, 49, 6561–6563 RSC.
- A. D. Ozkan, A. B. Tekinay, M. O. Guler and E. D. Tekin, RSC Adv., 2016, 6, 104201 RSC.
- A. L. Boyle, E. H. C. Bromley, G. J. Bartlett, R. B. Sessions, T. H. Sharp, C. L. Williams, P. M. G. Curmi, N. R. Forde, H. Linke and D. N. Woolfson, J. Am. Chem. Soc., 2012, 134, 15457–15467 CrossRef CAS PubMed.
- D. Zanuy, J. Poater, M. Solà, I. W. Hamley and C. Alemán, Phys. Chem. Chem. Phys., 2016, 18, 1265–1278 RSC.
- P. W. J. M. Frederix, J. Idé, Y. Altay, G. Schaeffer, M. Surin, D. Beljonne, A. S. Bondarenko, T. L. C. Jansen, S. Otto and S. J. Marrink, ACS Nano, 2017, 11, 7858–7868 CrossRef CAS PubMed.
- M. Hatip Koc, G. Cinar Ciftci, S. Baday, V. Castelletto, I. W. Hamley and M. O. Guler, Langmuir, 2017, 33, 7947–7956 CrossRef CAS PubMed.
- S. H. Hiew, P. A. Guerette, O. J. Zvarec, M. Phillips, F. Zhou, H. Su, K. Pervushin, B. P. Orner and A. Miserez, Acta Biomater., 2016, 46, 41–54 CrossRef CAS PubMed.
- G. Colherinhas and E. Fileti, J. Phys. Chem. B, 2014, 118, 12215–12222 CrossRef CAS PubMed.
- Z. Yu, A. Erbas, F. Tantakitti, L. C. Palmer, J. A. Jackman, M. Olvera de la Cruz, N.-J. Cho and S. I. Stupp, J. Am. Chem. Soc., 2017, 139, 7823–7830 CrossRef CAS PubMed.
- D. H. de Jong, N. Liguori, T. van den Berg, C. Arnarez, X. Periole and S. J. Marrink, J. Phys. Chem. B, 2015, 119, 7791–7803 CrossRef CAS PubMed.
- D. J. Adams, K. Morris, L. Chen, L. C. Serpell, J. Bacsa and G. M. Day, Soft Matter, 2010, 6, 4144–4156 RSC.
- J. W. Ponder and D. A. Case, Adv. Protein Chem., 2003, 66, 27–85 CrossRef CAS PubMed.
- A. Warshel, M. Kato and A. V. Pisliakov, J. Chem. Theory Comput., 2007, 3, 2034–2045 CrossRef CAS PubMed.
- P. Xu, J. Wang, Y. Xu, H. Chu, J. Liu, M. Zhao, D. Zhang, Y. Mao, B. Li, Y. Ding and G. Li, Adv. Exp. Med. Biol., 2015, 827, 19–32 CrossRef CAS PubMed.
- J. A. Lemkul, B. Roux, D. van der Spoel and A. D. MacKerell, J. Comput. Chem., 2015, 36, 1473–1479 CrossRef CAS PubMed.
- Z. Lin and W. F. van Gunsteren, J. Chem. Theory Comput., 2015, 11, 1983–1986 CrossRef CAS PubMed.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 Search PubMed.
- C. Tang, A. M. Smith, R. F. Collins, R. V. Ulijn and A. Saiani, Langmuir, 2009, 25, 9447–9453 CrossRef CAS PubMed.
- Y. Huang, W. Chen, J. A. Wallace and J. Shen, J. Chem. Theory Comput., 2016, 12, 5411–5421 CrossRef CAS PubMed.
- T. Lazaridis and G. Hummer, J. Chem. Inf. Model., 2017, 57, 2833–2845 CrossRef CAS PubMed.
- K. Vanommeslaeghe and A. D. MacKerell, J. Chem. Inf. Model., 2012, 52, 3144–3154 CrossRef CAS PubMed.
- K. Vanommeslaeghe, E. P. Raman and A. D. MacKerell, J. Chem. Inf. Model., 2012, 52, 3155–3168 CrossRef CAS PubMed.
- V. Zoete, M. A. Cuendet, A. Grosdidier and O. Michielin, J. Comput. Chem., 2011, 32, 2359–2368 CrossRef CAS PubMed.
- L. S. Dodda, I. Cabeza de Vaca, J. Tirado-Rives and W. L. Jorgensen, Nucleic Acids Res., 2017, 45, W331–W336 CrossRef CAS PubMed.
- A. W. Schüttelkopf and D. M. F. van Aalten, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2004, 60, 1355–1363 CrossRef PubMed.
- A. K. Malde, L. Zuo, M. Breeze, M. Stroet, D. Poger, P. C. Nair, C. Oostenbrink and A. E. Mark, J. Chem. Theory Comput., 2011, 7, 4026–4037 CrossRef CAS PubMed.
- S. Jo, T. Kim, V. G. Iyer and W. Im, J. Comput. Chem., 2008, 29, 1859–1865 CrossRef CAS PubMed.
- R. Anandakrishnan, B. Aguilar and A. V. Onufriev, Nucleic Acids Res., 2012, 40, W537–W541 CrossRef CAS PubMed.
- K. Dedachi, T. Shimosato, T. Minezaki and M. Iwaoka, J. Chem., 2013, 2013, 407862 Search PubMed.
- Y. Shen, J. Maupetit, P. Derreumaux and P. Tufféry, J. Chem. Theory Comput., 2014, 10, 4745–4758 CrossRef CAS PubMed.
- J. K. Gupta, D. J. Adams and N. G. Berry, Chem. Sci., 2016, 7, 4713–4719 RSC.
- H. I. Ingólfsson, C. A. Lopez, J. J. Uusitalo, D. H. de Jong, S. M. Gopal, X. Periole and S. J. Marrink, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 225–248 CrossRef PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef CAS PubMed.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef CAS PubMed.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef CAS PubMed.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- X. Periole, M. Cavalli, S.-J. Marrink and M. A. Ceruso, J. Chem. Theory Comput., 2009, 5, 2531–2543 CrossRef CAS PubMed.
- A. B. Poma, M. Cieplak and P. E. Theodorakis, J. Chem. Theory Comput., 2017, 13, 1366–1374 CrossRef CAS PubMed.
- M. Seo, S. Rauscher, R. Pomès and D. P. Tieleman, J. Chem. Theory Comput., 2012, 8, 1774–1785 CrossRef CAS PubMed.
- W. Shinoda, R. DeVane and M. L. Klein, J. Phys. Chem. B, 2010, 114, 6836–6849 CrossRef CAS PubMed.
- M. Cheon, I. Chang and C. K. Hall, Proteins, 2010, 78, 2950–2960 CrossRef CAS PubMed.
- Y. Wang and G. A. Voth, J. Phys. Chem. B, 2010, 114, 8735–8743 CrossRef CAS PubMed.
- A. Villa, N. F. A. van der Vegt and C. Peter, Phys. Chem. Chem. Phys., 2009, 11, 2068 RSC.
- A. Villa, C. Peter and N. F. A. van der Vegt, Phys. Chem. Chem. Phys., 2009, 11, 2077 RSC.
- T. K. Haxton, R. V. Mannige, R. N. Zuckermann and S. Whitelam, J. Chem. Theory Comput., 2015, 11, 303–315 CrossRef CAS.
- S. P. Carmichael and M. S. Shell, J. Phys. Chem. B, 2012, 116, 8383–8393 CrossRef CAS PubMed.
- C. Guo, Y. Luo, R. Zhou and G. Wei, ACS Nano, 2012, 6, 3907–3918 CrossRef CAS PubMed.
- J. Kwon, M. Lee and S. Na, J. Comput. Chem., 2016, 37, 1839–1846 CrossRef CAS PubMed.
- M. Slyngborg and P. Fojan, Phys. Chem. Chem. Phys., 2015, 17, 30023–30036 RSC.
- F. Sun, L. Chen, X. Ding, L. Xu, X. Zhou, P. Wei, J. F. Liang and S.-Z. Luo, J. Phys. Chem. B, 2017, 121, 7421–7430 CrossRef CAS PubMed.
- N. Thota, Y. Ma and J. Jiang, RSC Adv., 2014, 4, 60741–60748 RSC.
- O.-S. Lee, V. Cho and G. C. Schatz, Nano Lett., 2012, 12, 4907–4913 CrossRef CAS PubMed.
- T. Yu and G. C. Schatz, J. Phys. Chem. B, 2013, 117, 14059–14064 CrossRef CAS PubMed.
- G. G. Scott, P. J. McKnight, T. Tuttle and R. V. Ulijn, Adv. Mater., 2016, 28, 1381–1386 CrossRef CAS PubMed.
- P. W. J. M. Frederix, R. V. Ulijn, N. T. Hunt and T. Tuttle, J. Phys. Chem. Lett., 2011, 2, 2380–2384 CrossRef CAS PubMed.
- M. Cheon, I. Chang and C. K. Hall, Biophys. J., 2011, 101, 2493–2501 CrossRef CAS PubMed.
- K. M. Ruff, S. J. Khan and R. V. Pappu, Biophys. J., 2014, 107, 1226–1235 CrossRef CAS PubMed.
- B. Ozgur and M. Sayar, J. Phys. Chem. B, 2016, 120, 10243–10257 CrossRef CAS PubMed.
- J. Kwak, S. Soo Nam, J. Cho, E. Sim and S.-Y. Lee, Phys. Chem. Chem. Phys., 2017, 19, 10274–10281 RSC.
- H. Wang, A. S. Yapa, N. L. Kariyawasam, T. B. Shrestha, M. Kalubowilage, S. O. Wendel, J. Yu, M. Pyle, M. T. Basel, A. P. Malalasekera, Y. Toledo, R. Ortega, P. S. Thapa, H. Huang, S. X. Sun, P. E. Smith, D. L. Troyer and S. H. Bossmann, Nanomedicine, 2017, 13, 2555–2564 CrossRef CAS PubMed.
- K. Liu, Y. Kang, G. Ma, H. Möhwald and X. Yan, Phys. Chem. Chem. Phys., 2016, 18, 16738–16747 RSC.
- D. Bochicchio and G. M. Pavan, ACS Nano, 2017, 11, 1000–1011 CrossRef CAS PubMed.
- P. C. Kroon, J. Ottelé, S. Maity, G. Monreal Santiago, P. W. J. M. Frederix, W. H. Roos, S. J. Marrink and S. Otto, submitted.
- P. W. J. M. Frederix, G. G. Scott, Y. M. Abul-Haija, D. Kalafatovic, C. G. Pappas, N. Javid, N. T. Hunt, R. V. Ulijn and T. Tuttle, Nat. Chem., 2015, 7, 30–37 CrossRef CAS PubMed.
- I. R. Sasselli, I. P. Moreira, R. V. Ulijn and T. Tuttle, Org. Biomol. Chem., 2017, 15, 6541–6547 CAS.
- I. W. Fu, C. B. Markegard, B. K. Chu and H. D. Nguyen, Langmuir, 2014, 30, 7745–7754 CrossRef CAS.
- T. Bereau and K. Kremer, J. Chem. Theory Comput., 2015, 11, 2783–2791 CrossRef CAS PubMed.
- Y. Qi, H. I. Ingólfsson, X. Cheng, J. Lee, S. J. Marrink and W. Im, J. Chem. Theory Comput., 2015, 11, 4486–4494 CrossRef CAS PubMed.
- V. Rühle, C. Junghans, A. Lukyanov, K. Kremer and D. Andrienko, J. Chem. Theory Comput., 2009, 5, 3211–3223 CrossRef PubMed.
- S. Y. Mashayak, M. N. Jochum, K. Koschke, N. R. Aluru, V. Rühle and C. Junghans, PLoS One, 2015, 10, e0131754 CAS.
- A. J. Rzepiela, L. V. Schäfer, N. Goga, H. J. Risselada, A. H. De Vries and S. J. Marrink, J. Comput. Chem., 2010, 31, 1333–1343 CAS.
- P. J. Stansfeld and M. S. P. Sansom, J. Chem. Theory Comput., 2011, 7, 1157–1166 CrossRef CAS.
- P. Brocos, P. Mendoza-Espinosa, R. Castillo, J. Mas-Oliva and Á. Piñeiro, Soft Matter, 2012, 8, 9005–9014 RSC.
- T. A. Wassenaar, K. Pluhackova, R. A. Böckmann, S. J. Marrink and D. P. Tieleman, J. Chem. Theory Comput., 2014, 10, 676–690 CrossRef CAS PubMed.
- R. Pugliese, A. Marchini, G. A. A. Saracino, R. N. Zuckermann and F. Gelain, Nano Res., 2018, 11, 586–602 CrossRef CAS.
- S. A. Deshmukh, L. A. Solomon, G. Kamath, H. C. Fry and S. K. R. S. Sankaranarayanan, Nat. Commun., 2016, 7, 12367 CrossRef CAS PubMed.
- M. Rad-Malekshahi, K. M. Visscher, J. P. G. L. M. Rodrigues, R. de Vries, W. E. Hennink, M. Baldus, A. M. J. J. Bonvin, E. Mastrobattista and M. Weingarth, J. Am. Chem. Soc., 2015, 137, 7775–7784 CrossRef CAS PubMed.
- J. Mondal and A. Yethiraj, J. Chem. Phys., 2012, 136, 84902 CrossRef PubMed.
- P. Kar and M. Feig, J. Chem. Theory Comput., 2017, 13, 5753–5765 CrossRef CAS PubMed.
- A. J. Rzepiela, M. Louhivuori, C. Peter and S. J. Marrink, Phys. Chem. Chem. Phys., 2011, 13, 10437–10448 RSC.
- S. Riniker, A. P. Eichenberger and W. F. van Gunsteren, Eur. Biophys. J., 2012, 41, 647–661 CrossRef CAS PubMed.
- J. Zavadlav, S. Bevc and M. Praprotnik, Eur. Biophys. J., 2017, 46, 821–835 CrossRef CAS PubMed.
- J. Zavadlav, M. N. Melo, S. J. Marrink and M. Praprotnik, J. Chem. Phys., 2014, 140, 54114 CrossRef PubMed.
- J. Zavadlav, R. Podgornik, M. N. Melo, S. J. Marrink and M. Praprotnik, Eur. Phys. J.-Spec. Top., 2016, 225, 1595–1607 CrossRef CAS.
- A. C. Fogarty, R. Potestio and K. Kremer, J. Chem. Phys., 2015, 142, 195101 CrossRef PubMed.
- D. M. Hall, I. R. Bruss, J. R. Barone and G. M. Grason, Nat. Mater., 2016, 15, 727–732 CrossRef CAS PubMed.
- Y. Sugita and Y. Okamoto, Chem. Phys. Lett., 1999, 314, 141–151 CrossRef CAS.
- A. Barducci, M. Bonomi and M. Parrinello, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 826–843 CrossRef CAS.
- L. Sutto, S. Marsili and F. L. Gervasio, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 771–779 CrossRef CAS.
- H. Grubmüller, B. Heymann and P. Tavan, Science, 1996, 271, 997 Search PubMed.
- P. G. Bolhuis, D. Chandler, C. Dellago and P. L. Geissler, Annu. Rev. Phys. Chem., 2002, 53, 291–318 CrossRef CAS PubMed.
- R. C. Bernardi, M. C. R. Melo and K. Schulten, Biochim. Biophys. Acta, Gen. Subj., 2015, 1850, 872–877 CrossRef CAS PubMed.
- X. Mu, K. M. Eckes, M. M. Nguyen, L. J. Suggs and P. Ren, Biomacromolecules, 2012, 13, 3562–3571 CrossRef CAS PubMed.
- S. V. R. Jonnalagadda, E. Ornithopoulou, A. A. Orr, E. Mossou, V. T. Forsyth, E. P. Mitchell, M. W. Bowler, A. Mitraki and P. Tamamis, Mol. Syst. Des. Eng., 2017, 2, 321–335 CAS.
- P. Tamamis, L. Adler-Abramovich, M. Reches, K. Marshall, P. Sikorski, L. Serpell, E. Gazit and G. Archontis, Biophys. J., 2009, 96, 5020–5029 CrossRef CAS PubMed.
- Y. Zhao, L. Deng, J. Wang, H. Xu and J. R. Lu, Langmuir, 2015, 31, 12975–12983 CrossRef CAS PubMed.
- G. Bellesia and J.-E. Shea, Biophys. J., 2009, 96, 875–886 CrossRef CAS PubMed.
- H. H. Arefi and T. Yamamoto, J. Chem. Phys., 2017, 147, 211102 CrossRef PubMed.
- D. J. Smith and M. S. Shell, J. Phys. Chem. B, 2017, 121, 5928–5943 CrossRef CAS PubMed.
- M. Salvalaglio, F. Giberti and M. Parrinello, Acta Crystallogr., Sect. C: Struct, Chem., 2014, 70, 132–136 CrossRef CAS PubMed.
- F. Giberti, M. Salvalaglio and M. Parrinello, IUCrJ, 2015, 2, 256–266 CrossRef CAS PubMed.
- D. Bochicchio, M. Salvalaglio and G. M. Pavan, Nat. Commun., 2017, 8, 147 CrossRef PubMed.
- P. Stock, J. I. Monroe, T. Utzig, D. J. Smith, M. S. Shell and M. Valtiner, ACS Nano, 2017, 11, 2586–2597 CrossRef CAS PubMed.
- T. Yu, O.-S. Lee and G. C. Schatz, J. Phys. Chem. A, 2013, 117, 7453–7460 CrossRef CAS PubMed.
- T. Yu and G. C. Schatz, J. Phys. Chem. B, 2013, 117, 9004–9013 CrossRef CAS PubMed.
- Z. F. Brotzakis, M. Gehre, I. K. Voets and P. G. Bolhuis, Phys. Chem. Chem. Phys., 2017, 19, 19032–19042 RSC.
- J. A. Luiken and P. G. Bolhuis, J. Phys. Chem. B, 2015, 119, 12568–12579 CrossRef CAS PubMed.
- V. Limongelli, M. Bonomi and M. Parrinello, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 6358–6363 CrossRef CAS PubMed.
- M. Lelimousin, V. Limongelli and M. S. P. Sansom, J. Am. Chem. Soc., 2016, 138, 10611–10622 CrossRef CAS PubMed.
- H. J. Risselada, A. E. Mark and S. J. Marrink, J. Phys. Chem. B, 2008, 112, 7438–7447 CrossRef PubMed.
- Q.-Y. Wu, W. Tian and Y. Ma, J. Phys. Chem. B, 2017, 121, 8984–8990 CrossRef CAS PubMed.
- I. Patmanidis, A. S. Bondarenko, T. L. C. Jansen, J. Knoester, A. H. De Vries and S. J. Marrink, submitted.
- M. T. Oakley and R. L. Johnston, J. Chem. Theory Comput., 2014, 10, 1810–1816 CrossRef CAS PubMed.
- N. S. Bieler, T. P. J. Knowles, D. Frenkel and R. Vácha, PLoS Comput. Biol., 2012, 8, e1002692 CAS.
- M. Meli, G. Morra and G. Colombo, Biophys. J., 2008, 94, 4414–4426 CrossRef CAS PubMed.
- U. F. Röhrig, A. Laio, N. Tantalo, M. Parrinello and R. Petronzio, Biophys. J., 2006, 91, 3217–3229 CrossRef PubMed.
- M. Hughes, H. Xu, P. W. J. M. Frederix, A. M. Smith, N. T. Hunt, T. Tuttle, I. A. Kinloch and R. V. Ulijn, Soft Matter, 2011, 7, 10032–10038 RSC.
- A. Bertolani, A. Pizzi, L. Pirrie, L. Gazzera, G. Morra, M. Meli, G. Colombo, A. Genoni, G. Cavallo, G. Terraneo and P. Metrangolo, Chem. – Eur. J., 2017, 23, 2051–2058 CrossRef CAS PubMed.
- C.-A. Palma, P. Samorì and M. Cecchini, J. Am. Chem. Soc., 2010, 132, 17880–17885 CrossRef CAS PubMed.
- K. A. Houton, K. L. Morris, L. Chen, M. Schmidtmann, J. T. A. Jones, L. C. Serpell, G. O. Lloyd and D. J. Adams, Langmuir, 2012, 28, 9797–9806 CrossRef CAS PubMed.
- D. K. Putnam, E. W. Lowe and J. Meiler, Comput. Struct. Biotechnol. J., 2013, 8, e201308006 CrossRef PubMed.
- C. J. Knight and J. S. Hub, Nucleic Acids Res., 2015, 43, W225–W230 CrossRef CAS PubMed.
- J. Cerar, A. Lajovic, A. Jamnik and M. Tomšič, J. Mol. Liq., 2017, 229, 346–357 CrossRef CAS.
- J. Nedergaard Pedersen, P. W. J. M. Frederix, J. Skov Pedersen, S. J. Marrink and D. E. Otzen, ChemBioChem, 2018, 19, 263–271 CrossRef CAS PubMed.
- M. Pereira Oliveira, H.-W. Schmidt and R. Queiroz Albuquerque, Chem. – Eur. J., 2018, 24, 2609–2617 CrossRef CAS PubMed.
- C.-T. Lai, N. L. Rosi and G. C. Schatz, J. Phys. Chem. Lett., 2017, 8, 2170–2174 CrossRef CAS PubMed.
- P. Zhou, L. Deng, Y. Wang, J. R. Lu and H. Xu, J. Colloid Interface Sci., 2016, 464, 219–228 CrossRef CAS PubMed.
- M. Wang, P. Zhou, J. Wang, Y. Zhao, H. Ma, J. R. Lu and H. Xu, J. Am. Chem. Soc., 2017, 139, 4185–4194 CrossRef CAS PubMed.
- X. Periole, T. Huber, A. Bonito-Oliva, K. C. Aberg, P. C. A. van der Wel, T. P. Sakmar and S. J. Marrink, J. Phys. Chem. B, 2017, 122, 1081–1091 CrossRef PubMed.
- K. M. Eckes, X. Mu, M. A. Ruehle, P. Ren and L. J. Suggs, Langmuir, 2014, 30, 5287–5296 CrossRef CAS PubMed.
- Y. Miller, B. Ma and R. Nussinov, J. Phys. Chem. B, 2015, 119, 482–490 CrossRef CAS PubMed.
- K. Nagy-Smith, P. J. Beltramo, E. Moore, R. Tycko, E. M. Furst and J. P. Schneider, ACS Cent. Sci., 2017, 3, 586–597 CrossRef CAS PubMed.
- P. C. A. van der Wel, Solid State Nucl. Magn. Reson., 2017, 88, 1–14 CrossRef CAS PubMed.
- J. H. Ortony, C. J. Newcomb, J. B. Matson, L. C. Palmer, P. E. Doan, B. M. Hoffman and S. I. Stupp, Nat. Mater., 2014, 13, 812 CrossRef CAS PubMed.
- A. Barth and C. Zscherp, Q. Rev. Biophys., 2002, 35, 369–430 CrossRef CAS PubMed.
- M. Grechko and M. T. Zanni, J. Chem. Phys., 2012, 137, 184202 CrossRef PubMed.
- A. M. Woys, A. M. Almeida, L. Wang, C.-C. Chiu, M. McGovern, J. J. de Pablo, J. L. Skinner, S. H. Gellman and M. T. Zanni, J. Am. Chem. Soc., 2012, 134, 19118–19128 CrossRef CAS PubMed.
- S. Fleming, P. W. J. M. Frederix, I. Ramos Sasselli, N. T. Hunt, R. V. Ulijn and T. Tuttle, Langmuir, 2013, 29, 9510–9515 CrossRef CAS PubMed.
- S. Hahn, S.-S. Kim, C. Lee and M. Cho, J. Chem. Phys., 2005, 123, 84905 CrossRef PubMed.
- M.-P. Gaigeot, Phys. Chem. Chem. Phys., 2010, 12, 3336–3359 RSC.
- M. Reppert and A. Tokmakoff, Annu. Rev. Phys. Chem., 2016, 67, 359–386 CrossRef CAS PubMed.
- T. L. C. Jansen, A. G. Dijkstra, T. M. Watson, J. D. Hirst and J. Knoester, J. Chem. Phys., 2006, 125, 44312 CrossRef PubMed.
- J. Kubelka, J. Kim, P. Bour and T. A. Keiderling, Vib. Spectrosc., 2006, 42, 63–73 CrossRef CAS.
- L. Wang, C. T. Middleton, M. T. Zanni and J. L. Skinner, J. Phys. Chem. B, 2011, 115, 3713–3724 CrossRef CAS PubMed.
- M. Reppert and A. Tokmakoff, J. Chem. Phys., 2013, 138, 134116 CrossRef PubMed.
- A. S. Bondarenko and T. L. C. Jansen, J. Chem. Phys., 2015, 142, 212437 CrossRef PubMed.
- S. Krimm and Y. Abe, Proc. Natl. Acad. Sci. U. S. A., 1972, 69, 2788–2792 CrossRef CAS.
- H. Torii and M. Tasumi, J. Raman Spectrosc., 1998, 29, 81–86 CrossRef CAS.
- P. Hamm and S. Woutersen, Bull. Chem. Soc. Jpn., 2002, 75, 985–988 CrossRef CAS.
- S. D. Moran and M. T. Zanni, J. Phys. Chem. Lett., 2014, 5, 1984–1993 CrossRef CAS PubMed.
- S. J. Roeters, A. Iyer, G. Pletikapić, V. Kogan, V. Subramaniam and S. Woutersen, Sci. Rep., 2017, 7, 41051 CrossRef CAS PubMed.
- C. Didraga, A. Pugžlys, P. R. Hania, H. von Berlepsch, K. Duppen and J. Knoester, J. Phys. Chem. B, 2004, 108, 14976–14985 CrossRef CAS.
- F. C. Spano, Annu. Rev. Phys. Chem., 2006, 57, 217–243 CrossRef CAS PubMed.
- F. C. Spano, Acc. Chem. Res., 2010, 43, 429–439 CrossRef CAS PubMed.
- L. van Dijk, P. A. Bobbert and F. C. Spano, J. Phys. Chem. B, 2010, 114, 817–825 CrossRef CAS PubMed.
- G. Pescitelli, L. D. Bari and N. Berova, Chem. Soc. Rev., 2011, 40, 4603–4625 RSC.
- G. Pescitelli, L. D. Bari and N. Berova, Chem. Soc. Rev., 2014, 43, 5211–5233 RSC.
- D. M. Eisele, C. W. Cone, E. A. Bloemsma, S. M. Vlaming, C. G. F. van der Kwaak, R. J. Silbey, M. G. Bawendi, J. Knoester, J. P. Rabe and D. A. V. Bout, Nat. Chem., 2012, 4, 655–662 CrossRef CAS PubMed.
- N. J. Greenfield, Nat. Protoc., 2006, 1, 2876–2890 CrossRef CAS PubMed.
- M. M. J. Smulders, A. P. H. J. Schenning and E. W. Meijer, J. Am. Chem. Soc., 2008, 130, 606–611 CrossRef CAS PubMed.
- E. Schwartz, V. Palermo, C. E. Finlayson, Y.-S. Huang, M. B. J. Otten, A. Liscio, S. Trapani, I. González-Valls, P. Brocorens, J. J. L. M. Cornelissen, K. Peneva, K. Müllen, F. C. Spano, A. Yartsev, S. Westenhoff, R. H. Friend, D. Beljonne, R. J. M. Nolte, P. Samorì and A. E. Rowan, Chem. – Eur. J., 2009, 15, 2536–2547 CrossRef CAS PubMed.
- M. Liu, L. Zhang and T. Wang, Chem. Rev., 2015, 115, 7304–7397 CrossRef CAS PubMed.
- E. Yashima, N. Ousaka, D. Taura, K. Shimomura, T. Ikai and K. Maeda, Chem. Rev., 2016, 116, 13752–13990 CrossRef CAS PubMed.
- H. von Berlepsch and C. Böttcher, J-Aggregates, World Scientific, 2011, pp. 119–153 Search PubMed.
- S. Kirstein, H. von Berlepsch, C. Böttcher, C. Burger, A. Ouart, G. Reck and S. Dähne, ChemPhysChem, 2000, 1, 146–150 CrossRef CAS PubMed.
- E. Cohen, H. Weissman, I. Pinkas, E. Shimoni, P. Rehak, P. Král and B. Rybtchinski, ACS Nano, 2018, 12, 317–326 CrossRef CAS PubMed.
- T. Ando, T. Uchihashi and N. Kodera, Annu. Rev. Biophys., 2013, 42, 393–414 CrossRef CAS PubMed.
- S. Onogi, H. Shigemitsu, T. Yoshii, T. Tanida, M. Ikeda, R. Kubota and I. Hamachi, Nat. Chem., 2016, 8, 743–752 CrossRef CAS PubMed.
- Z. A. Arnon, A. Vitalis, A. Levin, T. C. T. Michaels, A. Caflisch, T. P. J. Knowles, L. Adler-Abramovich and E. Gazit, Nat. Commun., 2016, 7, 13190 CrossRef CAS PubMed.
- T. O. Mason, T. C. T. Michaels, A. Levin, E. Gazit, C. M. Dobson, A. K. Buell and T. P. J. Knowles, J. Am. Chem. Soc., 2016, 138, 9589–9596 CrossRef CAS PubMed.
- A. D. Merg, J. C. Boatz, A. Mandal, G. Zhao, S. Mokashi-Punekar, C. Liu, X. Wang, P. Zhang, P. C. A. van der Wel and N. L. Rosi, J. Am. Chem. Soc., 2016, 138, 13655–13663 CrossRef CAS PubMed.
- D. Kurouski, Anal. Chim. Acta, 2017, 990, 54–66 CrossRef CAS PubMed.
- A. Arnaud and L. Bouteiller, Langmuir, 2004, 20, 6858–6863 CrossRef CAS PubMed.
- A. Desmarchelier, B. G. Alvarenga, X. Caumes, L. Dubreucq, C. Troufflard, M. Tessier, N. Vanthuyne, J. Idé, T. Maistriaux, D. Beljonne, P. Brocorens, R. Lazzaroni, M. Raynal and L. Bouteiller, Soft Matter, 2016, 12, 7824–7838 RSC.
- J. L. England, Nat. Nanotechnol., 2015, 10, 919–923 CrossRef CAS PubMed.
- G. Ashkenasy, T. M. Hermans, S. Otto and A. F. Taylor, Chem. Soc. Rev., 2017, 46, 2543–2554 RSC.
- I. Ramos Sasselli, P. J. Halling, R. V. Ulijn and T. Tuttle, ACS Nano, 2016, 10, 2661–2668 CrossRef CAS PubMed.
- P. A. Korevaar, S. J. George, A. J. Markvoort, M. M. J. Smulders, P. A. J. Hilbers, A. P. H. J. Schenning, T. F. A. D. Greef and E. W. Meijer, Nature, 2012, 481, 492 CrossRef CAS PubMed.
- P. A. Korevaar, C. J. Newcomb, E. W. Meijer and S. I. Stupp, J. Am. Chem. Soc., 2014, 136, 8540–8543 CrossRef CAS PubMed.
- J. Raeburn, A. Z. Cardoso and D. J. Adams, Chem. Soc. Rev., 2013, 42, 5143–5156 RSC.
- M. P. Hendricks, K. Sato, L. C. Palmer and S. I. Stupp, Acc. Chem. Res., 2017, 50, 2440–2448 CrossRef CAS PubMed.
- T. O. Mason, T. C. T. Michaels, A. Levin, C. M. Dobson, E. Gazit, T. P. J. Knowles and A. K. Buell, J. Am. Chem. Soc., 2017, 139, 16134–16142 CrossRef CAS PubMed.
- J. Ridley and M. Zerner, Theor. Chim. Acta, 1973, 32, 111–134 CrossRef CAS.
- D. J. Hill, M. J. Mio, R. B. Prince, T. S. Hughes and J. S. Moore, Chem. Rev., 2001, 101, 3893–4012 CrossRef CAS PubMed.
- S. Hecht and I. Huc, Foldamers: structure, properties, and applications, Wiley-VCH, Weinheim, 2007 Search PubMed.
- J. S. Laursen, J. Engel-Andreasen and C. A. Olsen, Acc. Chem. Res., 2015, 48, 2696–2704 CrossRef CAS PubMed.
- S. H. Yoo and H.-S. Lee, Acc. Chem. Res., 2017, 50, 832–841 CrossRef CAS PubMed.
| This journal is © The Royal Society of Chemistry 2018 |