Multimolecular assemblies on high surface area metal oxides and their role in interfacial energy and electron transfer
Jamie C.
Wang
 a,
Sean P.
Hill
a,
Tristan
Dilbeck
a,
Omotola O.
Ogunsolu
a,
Sean P.
Hill
a,
Tristan
Dilbeck
a,
Omotola O.
Ogunsolu
 b,
Tanmay
Banerjee
b,
Tanmay
Banerjee
 ac and
Kenneth
Hanson
ac and
Kenneth
Hanson
 *ab
*ab
aDepartment of Chemistry and Biochemistry, Florida State University, Tallahassee, Florida 32304, USA. E-mail: hanson@chem.fsu.edu
bMaterials Science and Engineering, Florida State University, Tallahassee, Florida 32306, USA
cMax Planck Institute for Solid State Research, Heisenbergstraße 1, 70569 Stuttgart, Germany
First published on 22nd September 2017
Abstract
High surface area metal oxides offer a unique substrate for the assembly of multiple molecular components at an interface. The choice of molecules, metal oxide, and the nature of the assembly method can have a profound influence on the mechanism, rate, and efficiency of photoinduced energy and electron transfer events at the interface. Owing to their diversity and high level of control, these interfacial assemblies are of interest for numerous applications including solar energy conversion, photoelectrosynthesis, photo-writable memory, and more. Although these assemblies are generated with very different goals in mind, they rely on similar surface binding motifs and molecular structure–property relationships. Therefore, the goal of this review is to summarize the various strategies (i.e. co-deposition, axial coordination, metal ion linkages, electrostatics, host–guest interactions, etc.) for assembling chromophores, hosts, electron donors/acceptors, and insulating co-adsorbent molecules on mesoporous metal oxide substrates. The assembly, synthesis, and characterization, as well as subsequent photoinduced events (i.e. cross-surface energy/electron transfer, interchromophore energy transfer, electron injection, and others) are discussed for the various assembly strategies.
1. Introduction
Photoinduced energy and electron transfer are critical processes in photosynthesis, bioimaging, solar energy conversion, chlorometric/fluorometric sensing, and other applications. Molecular species, as opposed to solid-state materials, are ideal to study/control these phenomena because exquisite synthetic variation of their structures can be used to tune the photo- and electrochemical properties of the chromophores/donors/acceptors.Over the past century, the seminal work of Marcus,1,2 Dexter,3 Förster,4 and others has been key to understanding the thermodynamic and kinetic parameters that dictate intermolecular energy and electron transfer events. The majority of this research has been conducted on molecules dissolved in solution. However, incorporating molecules in media/lattices offers many potential advantages over solutions, including fixed molecular orientations and distances, and the ability to harness and observe kinetic events that are not diffusion limited. The earliest and most notable example of fixed molecular structures of this type is that of natural photosynthetic systems. Through millions of years of evolution these light harvesting assemblies have developed a protein scaffolding to control intermolecular distances and orientations in order to maximize the efficiency of photoinduced energy and electron transfer events.5
Understanding and controlling intermolecular interactions in rigid scaffoldings is crucial for maximizing the efficiency of applications such as artificial solar energy conversion. As a result there is growing interest in generating rigid chromophore–donor/acceptor systems like metal–organic frameworks,6 molecular crystals,7,8 phospholipid bilayers,9,10 derivatized proteins/DNA,11,12 and others. Adhering molecules to a nanocrystalline metal-oxide surface is a particularly appealing strategy because complex, multimolecular structures can be prepared through a simple soaking and self-assembly procedure. Using this strategy, molecules are bound to a photo-/electroactive interface, where intermolecular interactions can be used to perturb electrochemical and photophysical properties of the molecules. Interactions between molecules at the interface can have a profound influence, both positive and negative, on molecule–metal oxide based applications including dye-sensitized solar cells (DSSCs), dye-sensitized photoelectrosynthesis cells (DSPECs), sensing, photo-writable memory, and more. These seemingly disparate applications are the result of similar surface binding motifs and molecular structure–property relationships at the interface.
Despite the increasing popularity and importance of these interfaces there has yet to be a comprehensive review on how multimolecular assemblies on high surface area metal oxides can influence photoinduced energy and electron transfer events at the interface. Therefore, the aims of this review are to (1) compile the current literature for various types of multimolecular interfacial assemblies, (2) summarize their role in energy and electron transfer events, (3) share commonalities between these different types of assemblies/events, (4) describe the plethora of measurement techniques used to characterize these interfaces, and (5) encourage readers to develop new strategies to characterize and harness molecular interactions at interfaces.
1.1 Scope
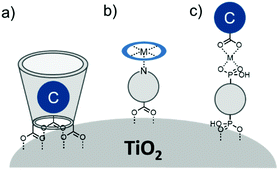
In terms of scope, this review will focus on multimolecular species on high surface area metal oxides and their role in photoinduced events. The discussion has been restricted to high surface area metal oxides because, although planar surfaces are important for a number of applications including electrochemistry,13 sensing,14 and others, high surface area is necessary to achieve sufficient absorption/emission for standard spectroscopic measurements and high absorbance is an essential precursor for efficient solar energy conversion.Multimolecular, in this case, is defined as the adsorption/binding of one or more electrochemically and photophysically distinct small molecules (i.e. not polymers,15 quantum dots,16,17 atomic layer deposited films,18,19etc.) onto the metal oxide surface. The discussion of pre-synthesized assemblies (i.e. dimers, dyads, etc.) will be limited to only a few examples of covalently linked molecules containing electronically distinct molecular moieties. The molecules of interest are categorized as chromophores (C; used interchangeable with dye), hosts, electron donors (D), electron acceptors (A), and “insulating” molecules that are photo- and electrochemically inert under standard measurement conditions for metal oxide interfaces. Catalysts are also an important class of molecules for these types of assemblies, particularly for application in dye-sensitized photoelectrosynthesis cells, but they have been recently reviewed elsewhere and will be omitted from this discussion.20
The review will be partitioned by photophysical process rather than by the method of assembly formation/interaction (e.g. co-deposition, electrostatics, metal ion coordination, etc.). First, in Section 2 we will discuss homochromophoric events like aggregation (Section 2.1), multi-photon/electron generation (Section 2.2), and cross surface energy and electron migration (Section 2.3). Then in Section 3 we cover multi-molecular strategies to control interfacial electron transfer including co-adsorbents (Section 3.1), chromophore–donor/acceptor systems (Section 3.2), and supersensitization (Section 3.3). In Section 4, the co-deposition (Section 4.1), antenna assembly (Section 4.2), and device engineering (Section 4.3) strategies to harness cooperative effects of complementary chromophores will be covered. Finally, supramolecular interactions like host–guest type assemblies will be discussed in Section 5.
The application cited for a majority of these multimolecular films is in dye-sensitized solar cells (DSSCs). Since the characterization and discussion of most of the literature are reported in the context of these devices, a general understanding of DSSCs is necessary to comprehend the entirety of the material reviewed below. Therefore, the next section will contain a brief introduction into the dynamic events, performance metrics, and standard characterization techniques for DSSCs. More comprehensive reviews on DSSCs can be found elsewhere.21
1.2 Dye-sensitized solar cells
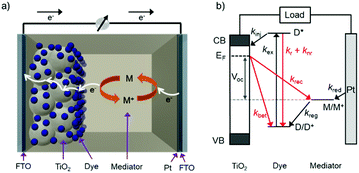
The standard components of a DSSC are depicted in Fig. 1a. In a typical device, transparent conducting substrates are coated with a nanocrystalline semiconducting metal oxide film (typically TiO2) and a regenerative catalyst (typically platinum) as the anode and cathode, respectively. The lack of visible absorption by the large band gap semiconductor is supplemented by functionalizing the metal oxide with a monolayer of one or more types of dye molecules. Between the two electrodes is an electrolyte solution, or polymer, containing an electro-active molecule also known as a redox mediator.22The relative energetics of these components, as well as the dynamic events of a functioning cell under operational conditions, are depicted in Fig. 1b. Photon absorption by the dye molecule (kex) generates an excited state with sufficient potential23 to inject an electron (kinj) into the conduction band of the metal oxide. The now oxidized dye is reduced via electron transfer from the mediator, effectively regenerating the ground state dye (kreg). Concurrently the electron in the metal oxide enters the external circuit to do useful work and then reduces the oxidized mediator at the cathode (kred).22,24,25
In addition to the favorable events described above, there are a number of unfavorable processes that hinder the performance of DSSCs. For example, prior to electron injection, the excited state can decay back to the ground state via radiative (kr) or non-radiative (knr) relaxation.25 Prior to entering the external circuit, the injected electron can transfer to the oxidized dye or mediator via back electron transfer (kBET) and recombination (krec), respectively.22,24
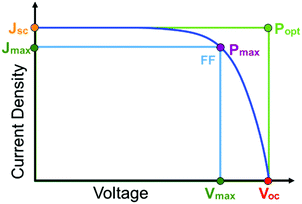
The first and perhaps most important data typically acquired for DSSCs, or any solar cell for that matter, is the current density–voltage (J–V) relationship. For this measurement, the anode and cathode are connected to an electrochemical workstation that sweeps the potential between the electrodes while monitoring the current response both in the dark and under illumination.26 An example J–V curve under irradiation as well as important performance metrics are shown in Fig. 2.
The open circuit voltage (Voc) is the maximum potential difference between the anode and cathode that can be achieved under illumination when no current is flowing through the cell. In a DSSC, the maximum Voc is dependent on the energy difference between the quasi-Fermi level in the semiconducting metal oxide and the potential of the redox mediator in the electrolyte. Since the Fermi level is determined by the electron occupancy in the metal oxide, the Voc is dictated by the ratio between the rate of electrons entering (Ratee−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) in) and exiting (Ratee−
in) and exiting (Ratee−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) out) the metal oxide as described by the modified diode equation (eqn (1))27 where kB is the Boltzmann constant, T is the temperature, and e is the elementary charge.
out) the metal oxide as described by the modified diode equation (eqn (1))27 where kB is the Boltzmann constant, T is the temperature, and e is the elementary charge.
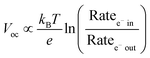 | (1) |
To increase the Voc under a given solar flux, it is necessary to maximize kinj and kreg (Ratee−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) in) while minimizing kBET and krec (Ratee−
in) while minimizing kBET and krec (Ratee−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) out). As noted by Hupp and others,28 every order of magnitude decrease in the rate of loss pathways (kbet and krec) increases the device Voc by ∼59 mV.
out). As noted by Hupp and others,28 every order of magnitude decrease in the rate of loss pathways (kbet and krec) increases the device Voc by ∼59 mV.
J sc, the maximum current flowing while under illumination when there is zero potential, is proportional to the product of several variables including the light harvesting efficiency (LHE(λ)), quantum yields for electron injection (φinj), regeneration (φreg), and the charge collection efficiency (ηcol) as shown in eqn (2).21
| Jsc ∝ LHE(λ)·φinjφregηcol | (2) |
In a DSSC, the light harvesting efficiency, more generally described as absorptance, is the percent of incident photons absorbed by the dye molecules at a given wavelength which is dependent on the metal oxide film thickness as well as the surface coverage and extinction coefficient of the dye molecule.27 The φinj is effectively the ratio between kinj from the excited state of the dye to the sum of all excited state decay pathways (i.e. kinj, knr, kr, etc.) and ηcol is the fraction of electrons injected into the metal oxide that enter the external circuit and are not lost through back electron transfer or recombination. Increasing dye coverage, extinction coefficient, solar spectral overlap, and kinj and decreasing knr, kr, kBET, and krec are all effective strategies for increasing Jsc. A quick note of clarification, for standardization/comparison purposes and to account for the active area of the cell, herein all reported values of Jsc will refer to the short circuit current density (current per area illuminated).
Power conversion efficiency (PCE or η), the primary metric of interest for most solar cell researchers, is the ratio of maximum power output from the device (Pmax) to input power from the light hitting the active material (Pin) and can be calculated using eqn (3).
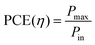 | (3) |
For lab research purposes, an input power of 1 Sun has been standardized to the AM1.5 solar spectrum having an integrated intensity of 100 mW cm−2.21
Since the goal of a DSSC is to generate as much power as possible from solar irradiance, a functioning solar cell is not operating at Voc or Jsc since the power (P = J × V) at these points is zero. Instead, the solar cell is operated under conditions where the product of current (Jmax) and voltage (Vmax) is maximized (Pmax = Jmax × Vmax). An important metric relating Jsc, Voc, and Pmax is the fill factor (FF). The FF (eqn (4)) is a fractional term between 0 and 1 that describes how close an actual cell is behaving relative to an ideal diode with the same Jsc and Voc.
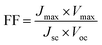 | (4) |
The less than ideal behavior of real DSSCs (FF < 1) is due to shunt resistance (i.e. shorts across the cell) and series resistance (i.e. non-Ohmic contacts between interfaces) that are not infinite and zero, respectively.29
Incident photon-to-current efficiency measurement (IPCE, also known as external quantum efficiency or EQE) is another common characterization technique that effectively measures the photocurrent generation efficiency at a given monochromatic wavelength. If each photon absorbed by the dye(s), regardless of wavelength, has equal probability of generating current, the IPCE spectrum should match the absorptance spectrum.27 A related metric, the absorbed photon-to-current efficiency (APCE, also known as internal quantum efficiency or IQE) is the IPCE divided by the absorptance spectrum. These measurements are particularly useful for quantifying the relative contributions from multi-chromophoric DSSCs.
An additional, but less commonly reported, measurement is electrochemical impedance spectroscopy (EIS). EIS is a relatively complex measurement which will only be briefly mentioned here, but we encourage the reader to learn more about this powerful technique using the references cited here.30,31 During an EIS measurement, photocurrent response is monitored with respect to an applied potential oscillated at a range of frequencies. The phase difference between applied potential and current response is due to the impedance of the materials/interfaces. Fitting the data using an equivalent circuit composed of resistors and capacitors helps determine the electron lifetime and recombination dynamics at interfaces in the DSSC.30,31
There are a number of additional spectroscopic techniques mentioned below that are not necessarily performed on complete devices, but are critical in studying the energy and electron transfer events at the interface.27 For example, time-resolved emission measurements, irradiating a sample with a short pulse of light and monitoring the emission intensity with respect to time after the pulse, are used to quantify the intrinsic radiative and non-radiative decay rates of molecules as well as any additional quenching mechanisms, like energy and electron transfer. Transient absorption spectroscopy (TA) is a pump–probe technique that uses two beams of light, one to excite the sample and the second to monitor changes in absorption spectra over time. This technique is critical for monitoring transient species that are non-emissive, like the cation species formed after electron injection, and the lifetimes of those states. These, and other spectroscopic techniques are often used in conjunction with device measurements to generate a complete understanding of the static and dynamic events dictating the device performance.
2. Chromophore–chromophore interactions
Intermolecular interactions between two chromophores that have the same structures can occur in mediums ranging from solutions to neat solids. Metal oxides are particularly effective at facilitating these chromophore–chromophore interactions due to the close proximity and relatively fixed orientation of dyes bound to the surface. These interactions can facilitate ground state aggregate or excimer formation (Section 2.1), multi-photon/electron processes (Section 2.2), and cross-surface energy and electron transfer (Section 2.3).2.1 Ground and excited state aggregation
Aggregation is the self-association of molecules that occurs when strong van der Waals forces are present between them. In solutions, aggregation is observed typically only at high solute concentrations or when the molecules have low solubility. On metal oxide surfaces the abundance of metal ion binding sites results in close packing and nearly complete monolayer coverage of chromophores. Most chromophores are composed of large aromatic systems that, when fixed in proximity on a surface, can aggregate due to π–π stacking. Aggregation can strongly influence photophysical and electrochemical properties and ultimately improve or hinder device performance.Several possible intermolecular interactions that can occur between chromophores (C) on a metal oxide surface (MO) and are summarized in eqn (5)–(8) with a vertical bar separating independent chromophores.
| MO–C|C → MO–C*|C → MO(e−)–C+|C → MO–C|C | (5) |
| MO–CC → MO–CC* → MO(e−)–CC+ → MO–CC | (6) |
| MO–C|C → MO–CC* → MO(e−)–CC+ → MO–C|C | (7) |
| MO–C|C → MO–C|C* → MO(e−)–CC+ → MO–C|C | (8) |
If molecules are in proximity but do not strongly interact (C|C in eqn (5)), a single chromophore will undergo excitation, electron injection, and BET as described in Section 1.2. During this process the excited state and cation remain localized on a single chromophore. Other molecules that exhibit strong interactions in the ground state will delocalize the absorption event and the resulting excited state will exist across two or more molecules (CC and CC* in eqn (6)). Alternatively, molecules that do not strongly interact in the ground state can, following excitation, form excimer states where the excited state is delocalized across two molecules (CC* in eqn (7)). Then following electron injection and BET, the chromophores dissociate into their independent ground states (C|C).
Although we have depicted a cation dimer (CC+) in eqn (6) and (7), the nature of this post-electron injection state is not well characterized likely due to the difficulty differentiating between transient cation dimers (CC+) and localized cations (C+|C). Along these lines, a fourth possibility (eqn (8)) is that following excitation and electron injection from a single chromophore, a cation dimer is formed with the cation delocalized across two chromophores. We found no reports identifying this species on a metal oxide surface. However, the generation of a stabilized cation dimer may be one strategy to increase the driving force for regeneration by the redox mediator as well as slow BET by pushing the energetics further into the Marcus inverted region.32,33
Ground state aggregation (eqn (6)) is the most commonly reported intermolecular interaction at a metal oxide interface. This is most likely because it can readily be identified, even by visual inspection, due to a shift in absorption features. The two most common types of aggregates are H- and J-type which can readily be described by using Kasha's exciton theory (Fig. 3).34
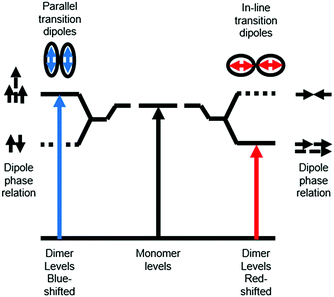 | ||
| Fig. 3 Exciton band energy diagram for molecular aggregates with parallel and in-line transition dipoles. | ||
Chromophore aggregation shifts and broadens the absorption features relative to the monomer due to interaction between transition dipoles of the molecules.35 H-aggregates exhibit face-to-face stacking (parallel) with the out of phase and aligned dipoles resulting in lower and higher energy excited states, respectively. In contrast, J-aggregates are due to head to tail stacking (in-line) with the out of phase dipole alignment increasing the energy and the in phase dipole alignment decreasing the energy of the excited state. Photophysically, because only the aligned dipole transition is allowed, H- and J-aggregation manifests as a hypsochromic and bathochromic shift, respectively, relative to the monomer species.
The first report of aggregation on a high surface area metal oxide surface was by Tributsch in 1969 with pseudocyanine dyes on high roughness ZnO surfaces.36 The ability of these dye aggregates to produce photocurrent was investigated through IPCE and time-resolved photocurrent measurements, with results suggesting photocurrent was produced via direct electron transfer between excited levels in the dye aggregate and the conduction band of the semiconductor.
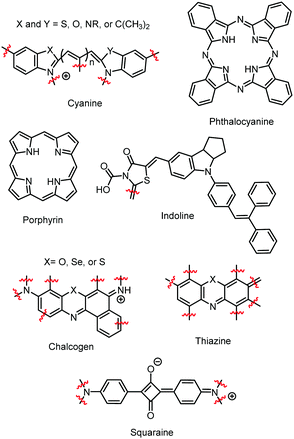
Since these early studies, there have been hundreds of reports of dye aggregation on high surface area metal oxides. The general structure of several classes of dyes that tend to aggregate are shown in Fig. 4 including cyanines,37 indolines,38 porphyrins,39 phthalocyanine,39 chalcogens,40 thiazines,41 and squaraines.42 These complexes all share the characteristics of being relatively planar, large aromatic systems that are susceptible to π–π stacking.
In terms of solar energy conversion, a majority of dye aggregation hinders dye-sensitized device performance.42–48 Low efficiency is often attributed to fast non-radiative decay from the excimer state (MO–CC* → MO–CC) prior to electron injection into the metal oxide (MO–CC* → MO(e−)–CC+). The decreased injection yield reduces the photocurrent and lowers the overall DSSC efficiency.
There are however examples where, by two different mechanisms, dye aggregation can improve the device performance. The first is by acting as an antenna-like species where aggregates absorb higher energy light, transfer that energy to a monomer which can then inject an electron into the metal oxide.49 This is only beneficial when the quantum yield of energy transfer between aggregates and monomers is near unity. The second case involves aggregation induced broadening of absorption transitions and both the monomer and the aggregated state can inject electrons and contribute to photocurrent generation.37,38,41,49–56
For example, Cai and coworkers reported that herring-bone aggregates of cyanine dyes on TiO2 induced both red- and blue-shifted absorption features.50 IPCE measurements indicate that both monomeric and aggregated forms contribute to charge separation and photocurrent generation. A maximum energy conversion efficiency of 2.9% was obtained with a cell whose photocurrent was generated by both the aggregate and monomer.
Recently, using the plant pigment betanin, McHale57 demonstrated a remarkable 2.5 fold increase in power conversion efficiency for a DSSC composed of predominantly aggregated dyes relative to the monomer dominated device. The improvement is attributed to red- and blue-shifted absorption features for the aggregates, Fig. 5. Not only was the IPCE higher, so was the APCE, suggesting that improved photoconversion efficiency is not merely the result of increased light harvesting but is also due to more efficient electron injection from the aggregated dye compared to the monomer. The reported efficiency of 3% is the best yet achieved for a natural dye containing DSSC, which the authors believe can be further increased through changes in electrolyte composition, surface treatment, and other modifications.
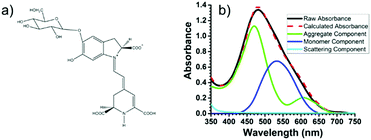 | ||
| Fig. 5 (a) Structure of betanin and (b) spectral deconvolution of the absorption spectrum of betanin on TiO2. Adapted with alterations with permission from ref. 57. Copyright 2016, American Chemical Society. | ||
Although dye aggregation on metal oxide surfaces has become somewhat ubiquitous and sometimes advantageous, systematic studies that couple spectroscopy and photoelectrochemistry to understand the role of aggregates on device performance are relatively limited. Perhaps one of the most extensively studied examples of aggregation at an interface is in cresyl violet dyes.41,53,56
Using TA spectroscopy Liu et al. demonstrate that cresyl violet56 and rhodamine 6G aggregates55 on SnO2 quickly undergo intersystem crossing and are capable of injecting electrons from the triplet excimer state with a rate constant of 2.0 × 108 s−1 and 5.5 × 109 s−1, respectively. Overlaying the IPCE with the absorptance spectra shows that electron injection from the aggregated dye is responsible for photocurrent generation, but the efficiency was still <1%. TA measurements indicate that, due to unfavorable kinetics for regeneration of the oxidized dye by iodide, back electron transfer was highly competitive with photocurrent generation.
Given the sometimes advantageous nature of dye aggregates on metal oxide surfaces, there are some efforts to control aggregate formation. Variations in solvent, dye concentration, and soaking times can be used to manipulate the relative amounts of monomer and aggregate species.57 Treatments of metal oxide film prior to dye loading, such as hydroxylation or salt impregnation, can also influence the formation of aggregates.58
Variations in dye structure can be a powerful tool in manipulating chromophore–chromophore interactions. For example, Mann et al.54 controlled the aggregation of several chalcogenoxanthylium dyes on TiO2 by varying the position of the surface-binding group and the identity of the chalcogen atoms (Fig. 6). The 1-E series of dyes readily formed H-aggregates upon binding to the surface whereas the 2-E series gave amorphous monolayers on the left and right in Fig. 6, respectively. The H-aggregated dyes exhibited broader absorption bands, increased light-harvesting efficiencies, and improved photoelectrochemical performance compared to the dyes which adsorbed in amorphous monolayers. The increased performance is partially attributed to a 2-to-3-fold increase of φinj for the aggregates, relative to the non-aggregated dye.40
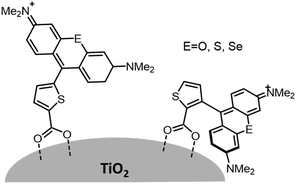 | ||
| Fig. 6 Chemical structure of chalcogenoxanthylium dyes from Mann et al., left 1-E and right 2-E. Adapted with alteration with permission from ref. 54. Copyright 2009, American Chemical Society. | ||
While some aggregates are advantageous, a majority of them are non-productive. Because of this, a number of strategies have been developed to inhibit aggregation including co-adsorption of electro- and photochemically inert molecules like CDCA or CHENO and others listed in Section 3.1 that act as a spacer between chromophores to prevent aggregation.59–68
Unfortunately, due to the limited surface area, co-adsorbents can also decrease the concentration of dyes and reduce total absorption (see Section 3.1.3).69 Alternatively, aggregation can be hindered by synthetically modifying the dye itself such that π–π stacking between molecules is inhibited with bulky ligands63,70–76 or alkyl side chains.75,77–79 Close packing between dyes can also be hindered by engineering dyes with unique shapes that prevent aggregation including H80–82 and starburst shaped molecules.83
While much is known about dye aggregation on high surface area metal oxides, a majority of reports simply note that aggregation is occurring and co-adsorbents are used to inhibit it. To effectively utilize aggregates, more systematic studies are needed in order to understand their influence on electron injection, BET, and ultimately device performance. Complementing spectroscopic, electrochemical, and device measurements with theoretical modeling will no doubt be crucial to this effort. Ab initio modeling of a more than 200 atom system is computationally expensive and therefore theoretical calculations of aggregates on surfaces has been relatively limited.42,57,69,72,73 Only within the last 5–10 years have more in depth studies been used to identify reasons for aggregation and how it affects optical and electronic properties of dyes on metal oxide surfaces.49,70,84–89 Future increases in computational power will allow for prediction of not only the aggregate formation, but also their influence on absorption and subsequent electron transfer events.
2.2 Multi-photon/electron processes
In contrast to the largely non-productive nature of aggregates/excimers discussed in the previous section, over the last 5–10 years there has been an increased interest in using intermolecular interactions on metal oxide surfaces to facilitate productive processes like molecular singlet fission (SF)90 and photon upconversion via triplet–triplet annihilation (TTA-UC).91 Binding SF and TTA-UC molecules to a metal oxide surface is particularly appealing because it can act as a charge separation interface. Additionally, the interface offers a means of controlling the proximity and orientation of molecules which are critical factors dictating the rate and efficiency of these processes. Many of these reports study photophysical events on metal oxides such as nanocrystalline ZrO2, whose relatively high conduction band energy inhibits excited state electron transfer to the substrate.92 More recently, with the goal of solar energy conversion in mind, TiO2 has been employed as the charge separation interface to extract charge from these multiphoton and multielectron processes.In 2015, Johnson and coworkers published the first evidence of SF on a metal oxide surface. In their report the authors physisorbed 1,3-diphenylisobenzofuran, a dye known to undergo SF with 100% efficiency in crystals,103 onto a metal oxide surface (Fig. 7b).104 The introduction of a ZrO2 “insulating layer” of increasing thickness between the dye and TiO2, first decreases (<10 Å) and then increases the photocurrent response (10–15 Å) from the dye. This atypical behavior was rationalized as the ZrO2 layer decreasing the rate of electron injection from the singlet state of the dye to TiO2via tunnelling through the ZrO2 layer. But, with a 10–15 Å insulating layer, they reached a balance where injection from the singlet state (kinjS in Fig. 7a) is sufficiently decreased such that singlet fission (kSF) and electron injection from two long lived triplet states (kinjT) can occur, effectively increasing the photocurrent generated.
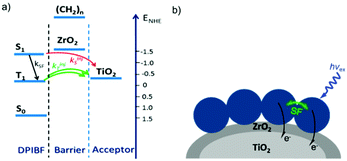 | ||
| Fig. 7 (a) Energy level diagram and interfacial charge transfer events for an isobenzofuran-sensitized metal oxide (kSF = rate of singlet fission, kinjS = rate of singlet injection, kinjT = rate of triplet injection, DPIBF = 1,3-diphenylisobenzofuran). Adapted with alterations with permission from ref. 104. Copyright 2015, American Chemical Society, and (b) a TiO2–ZrO2 core–shell metal oxide functionalized with isobenzofuran undergoing singlet fission (SF) and subsequent electron injection. | ||
Simulations based on TA data and thickness dependent electron injection kinetics are used to support this mechanism but unfortunately the electron injection yields (electrons generated per photons absorbed) were still less than 100%. Similar measurements using a 1,3-diphenylisobenzofuran derivative with a hexoic acid surface-binding functional group were promising but less conclusive. The authors suggest that with other dyes, more rigid surface binding groups, or by manipulating the deposition of a mixture of species on the surface it may be possible to increase the rate and efficiency of SF at an interface and generate a viable SF DSSC. As a side note, it is important to mention that to realize the theoretical efficiency increase to 43%, the SF dye must be supplemented by photocurrent generation from an additional low energy absorbing dye, making multi-chromophoric assembly strategies (Section 4) even more crucial to this endeavour.
TTA-UC was first demonstrated in the mid 1960s,108 but the field largely laid dormant for several decades. A complete rebirth of interest in TTA-UC over the past decade has been fuelled by the development of new, efficient sensitizer molecules, and new strategies for combining TTA molecular pairs.91,109,110 Of particular interest for application in solar energy conversion is the deposition of TTA-UC molecular pairs on metal oxide substrates.
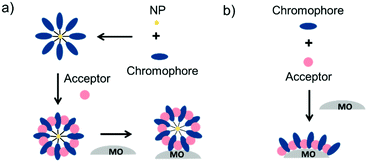
To date, three different strategies have been used to achieve TTA-UC on a metal oxide surface and each are depicted in Fig. 8. The first example was reported by Morandeira and coworkers in 2011, where a green-to-blue TTA-UC efficiency of 6 × 10−4% was achieved by co-adsorbing the sensitizer and acceptor molecules onto a ZrO2 substrate (Fig. 8a).111 Chemically linking the dyes to ZrO2via carboxylate groups resulted in a nearly four-fold increase in the UC efficiency (2 × 10−3%).112
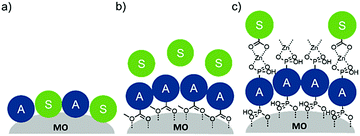 | ||
| Fig. 8 Schematic depiction of (a) co-deposited, (b) solution sensitized, and (c) self-assembled bilayer strategies for facilitating TTA-UC on a metal oxide substrate. | ||
Although the TTA-UC efficiency was relatively low, these reports demonstrated that the close proximity of molecules on a metal oxide could be used to facilitate TET and TTA-UC. The low efficiency can be attributed, at least in part, to co-deposition effectively diluting the acceptor molecule concentration and limiting cross-surface triplet density and energy transfer rates. To remedy this shortcoming, the authors introduced a heterogeneous TTA-UC system with the acceptor molecule bound to the surface and the sensitizer dissolved in solution (Fig. 8b).112 The significant increase in TTA-UC efficiency (0.04%) was attributed to increased acceptor concentration density on the surface. Interestingly, the efficiency limiting process of the heterogeneous scheme was diffusion limited sensitizer-to-acceptor TET and/or non-productive sensitizer–sensitizer TTA.113
Expanding upon this work, Nattestad and coworkers incorporated the heterogeneous TTA-UC scheme into a DSSC. Using TiO2 as the substrate and with the addition of a cobalt based redox mediator into the solution, they observed photocurrent of up to 0.1 μA cm−2 under 560–640 nm illumination at ambient solar intensities.114 Transient absorption and excitation intensity dependent measurements support a TTA-UC photocurrent generation mechanism, making this the first example of an integrated TTA-UC solar cell that directly extracts charge from an upconverted state.
The third strategy, introduced by Hill et al. in 2015, is through self-assembly of molecular multilayers via metal ion linkages (Fig. 8c).115 The multilayer films are formed using a simple, step-wise soaking procedure.116–118 Briefly, a monolayer of acceptor molecules is bound to the metal oxide (ZrO2 or TiO2) via phosphonate groups. Then Zn2+ metal ions are coordinated to a terminal functional phosphonate groups of the acceptor molecules. Finally, a sensitizer layer is bound to the Zn2+ ions via carboxylate groups.
These self-assembled bilayer films are an effective strategy to facilitate TTA-UC emission (QY = 0.23%) and transient photocurrent generation.119 Self-assembled bilayers on TiO2 were incorporated into a DSSC and a sustained photocurrent of 0.009 mA cm−2 was observed under low energy light (485–550 nm) at solar intensities.120 The increased photocurrent relative to the heterogeneous scheme was attributed to having a higher sensitizer concentration.
The incorporation of a second, complementary sensitizer in a trilayer architecture (Fig. 9), increased photocurrent to upwards of 0.074 mA cm−2, while the system reached maximum TTA-UC efficiency below solar intensities (AM1.5, 100 mW cm−2).121 Efforts demonstrated that the choice of redox mediator in these TTA-UC solar cells has a profound influence on their performance with photocurrents as high as 0.158 mA cm−2 under one Sun irradiation with maximum TTA-UC efficiency achieved at excitation intensities well below solar irradiance (0.8 mW cm−2).122 The photocurrent response is particularly notable in that it surpasses the device relevant threshold as outlined by Schmidt and coworkers.123
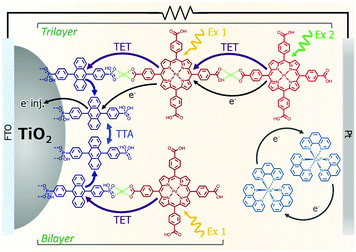 | ||
| Fig. 9 Self-assembled bilayer and trilayer TTA-UC DSSC. Reproduced from ref. 121 with permission from the Royal Society of Chemistry. | ||
Recently, Dilbeck et al. quantified rates of energy and electron transfer in TTA-UC self-assembled bilayer films using a combination of time-resolved emission and TA spectroscopy.124 Although sensitizer–sensitizer TTA can occur and is recognized as a non-productive process with high concentrations of sensitizer in solution, it was found that this process was negligible in the bilayer films presumably due to the limited mobility of the sensitizer in the bilayer architecture. A relatively slow sensitizer to acceptor triplet energy transfer rate limits the energy transfer efficiency and, as a result, the overall TTA-UC efficiency. However, electron injection from the singlet acceptor is ultra-fast and occurs with near unity quantum efficiency. These results indicate that designing new TTA-UC bilayers containing upconversion pairs with increased sensitizer to acceptor energy transfer rates, decreased sensitizer and acceptor non-radiative rates, and increased TTA rates is a key step towards realizing efficient TTA-UC photocurrent generation and improving solar energy conversion efficiencies.
2.3 Cross surface energy and electron migration
In addition to aggregation/excimer formation (Section 2.1) and multi-photon/electron processes (Section 2.2), the densely-packed nature of dyes on metal oxides can effectively facilitate efficient energy and electron transfer events between the same or different dye molecules on the surface. Interest in quantifying the rates of these migration events and increasing our ability to harness them continues to grow because of applications like photon upconversion and photocatalysis that require multiple excited states or the build-up of multiple redox equivalents at a single site at the interface. Below we will discuss the current methodology used to quantify these energy (Section 2.3.1) and electron (Section 2.3.2) transfer events as well as the variables that influence these processes.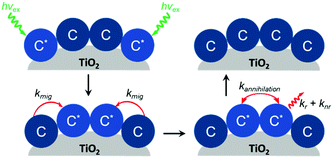 | ||
| Fig. 10 Cross-surface energy transfer and TTA of Ru(deeb)(bpy)22+ on TiO2. Adapted with permission from ref. 125. Copyright 1999 American Chemical Society. | ||
Later in the same year, the Meyer group used a co-sensitization of ruthenium and osmium polypyridyl dyes to directly demonstrate cross-surface energy transfer (Fig. 11).126 In their films, it is energetically favorable for Ru* to transfer energy to the Os dye which effectively acts as an emissive trap. Selective excitation of the Os dye resulted in emission characteristic of the Os complex only. When exciting both Ru and Os dyes equally, in the absence of energy transfer, the Ru emission should be 80 times higher than Os. However, in the co-deposited film, Ru emission was significantly quenched (ΓRu![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ΓOs, 0.3
ΓOs, 0.3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) with near unity efficiency suggesting a Ru to Os energy transfer rate of >108 s−1. Although both inter- and intramolecular energy transfer were well known in solutions127–129 and polymers130–132 of Ru and Os dyes, this was the first time this phenomenon was observed on a metal oxide surface.
1) with near unity efficiency suggesting a Ru to Os energy transfer rate of >108 s−1. Although both inter- and intramolecular energy transfer were well known in solutions127–129 and polymers130–132 of Ru and Os dyes, this was the first time this phenomenon was observed on a metal oxide surface.
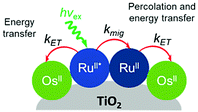 | ||
| Fig. 11 Energy transfer events for a co-deposited film composed of RuII and OsII polypyridyl dyes on a metal oxide surface. Adapted with permission from ref. 133. Copyright 2001 American Chemical Society. | ||
Expanding on this effort, Thomas J. Meyer and coworkers used time-resolved emission in conjunction with Monte Carlo simulations to model cross-surface energy transfer between [Ru(bpy)2(4,4′-(PO3H2)2-bpy)]2+ and [Os(bpy)2(4,4′-(COOH)2-bpy)]2+ on nanocrystalline ZrO2.133 The excited state lifetime of Ru* on ZrO2 was dependent on several factors including the Ru surface coverage, concentration of Os quencher, and monitoring wavelength. Above 70% Ru loading (i.e. above the percolation threshold) Ru*-to-Ru energy migration (kmig ∼ 107 s−1) was followed by Ru*-to-Os energy transfer (ken ∼ 106 s−1). The rate constant for energy transfer was exponentially dependent on the distance between dyes, consistent with a dominant role for a Dexter energy transfer mechanism.
To confirm the proposed mechanism from their previous work, the Gerald J. Meyer group revisited their Ru only and co-deposited Ru and Os TiO2 films using the time-resolved emission and Monte Carlo modelling (MCS) methodology.134 For a fully loaded film, they estimated a rate constant of (30 ns)−1 for isoenergetic Ru* → Ru energy transfer across the nanocrystalline surface. Monte Carlo simulations indicated that due to its relatively long lifetime (τ = 1 μs) a Ru* excited state could transfer energy to any of the ∼800 sensitizers on an ∼20 nm anatase nanoparticle surface.
In 2011, the Gerald J. Meyer group introduced an alternative technique, time-resolved spectroscopic anisotropy, as a means to directly probe cross-surface energy transfer on nanocrystalline metal oxides.135 Briefly, a fraction of the surface bound molecules with the appropriate dipole orientation are excited using plane polarized light and polarized absorption/emission are then monitored both parallel and perpendicular to the incident light. Since the surface bound molecules cannot undergo rotation, any change in the intensity of polarized absorption/emission is indicative of excited state migration across the spherical particle's surface. The anisotropy data for a fully loaded film in conjunction with the Monte Carlo simulation showed a nearest-neighbor hopping rate constant of (120 ns)−1. In contrast to previous co-deposited films, this technique allows researchers to monitor energy migration with a film containing only one dye molecule, mitigating any concerns with the emissive trap inhibiting percolation or disturbing surface packing.
While cross-surface energy transfer is likely a common phenomenon in dye-sensitized devices, it has only been investigated on metal oxide surfaces a handful of times. This is partially due to the difficulty in measuring the isoenergetic energy transfer. However, as shown above, the emergence of the transient anisotropy and time-resolved emission combined with Monte Carlo simulations has made these analyses more straightforward. Understanding the extent to which cross-surface energy transfer occurs will likely become important in maximizing the efficiency of DSSCs and certainly is important when implementing phenomena like triplet–triplet annihilation upconversion on metal oxide surfaces (Section 2.2).
Unlike energy transfer, where emissive species can readily be observed using time-resolved spectroscopy, cross-surface electron transfer is a “dark” event. Transient absorption can be used to monitor electron/hole hopping,135,142–144 but it is much more commonly measured using electrochemical techniques like cyclic voltammetry (CV)145 and chronoabsorptometry (CA).146 For these measurements, the dye functionalized nanocrystalline metal oxide is situated on a planar conductive substrate, usually fluorine doped tin oxide (FTO) coated glass. At sufficiently positive applied potentials, electrons are transferred from the immediately adjacent dyes to the conductive substrate (Fig. 12, top). If the dye surface loading is above the percolation threshold, then electrons diffuse through the molecular monolayer on the nanocrystalline metal oxide surface towards the underlying conductive substrate (Fig. 12, middle), and the process is repeated (Fig. 12, bottom).147
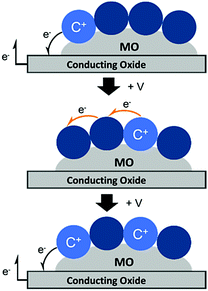 | ||
| Fig. 12 Mechanism of cross-surface electron transfer in a monolayer of dye bound to a MO on a conductive substrate under positive applied potential (+V). | ||
The rate of this charge migration is most commonly quantified using the apparent diffusion coefficient (Dapp) as described in eqn (9) and (10).
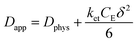 | (9) |
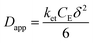 | (10) |
Experimentally, Dapp is typically determined by monitoring the changes in current by CV or, for electrochromic molecules, monitoring changes in absorption with respect to time under applied potential using eqn (11) and (12) respectively:
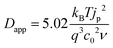 | (11) |
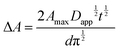 | (12) |
When reporting/interpreting these values, care must be taken in noting the measurement technique since Dapp can vary by up to an order of magnitude for the same film measured by different methods.149–151 A summary of the apparent diffusion coefficients reported for a number of metal oxide bound dyes in various solvents as measured by CV and/or CA are shown in Table 1.
| Entry | Molecule | Γ | Solvent | D app (cm2 s−1) | CA/CV | Ref. |
|---|---|---|---|---|---|---|
| a Sodium(3-(4-(bis(4-methoxyphenyl)amino)phenoxy)propyl)phosphonate. b 1-Ethyl-2-methylimidazolium bis(trifluoromethylsulfonyl)imide. c 5-[[4-[4-(2,2-Diphenylethenyl)phenyl]-1,2,3,3a,4,8b-hexahydrocyclopent[b]indol-7-yl]methylene]-4-oxo-2-thioxo-3-thiazolidineacetic acid. d 2-Cyano-3-[4-[4-(2,2-diphenylethenyl)phenyl]-1,2,3,3a,4,8b-hexahydrocyclopent[b]indol-7-yl]-2-propenoic acid. e 5-[[4-[4-(2,2-Diphenylethenyl)phenyl]-1,2,3,3a,4,8b-hexahydrocyclopent[b]indol-7-yl]methylene]-2-(3-ethyl-4-oxo-2-thioxo-5-thiazolidinylidene)-4-oxo-3-thiazolidineacetic acid. f 5-[[4-[4-(2,2-Diphenylethenyl)phenyl]-1,2,3,3a,4,8b-hexahydrocyclopent[b]indol-7-yl]methylene]-2-(3-octyl-4-oxo-2-thioxo-5-thiazolidinylidene)-4-oxo-3-thiazolidineacetic acid. g (2,2′-Bipyridyl-4,4′-dicarboxylic acid)-bis(2,2′-bipyridyl)ruthenium(II). h Bis(2,2′-bipyridyl-4,4′-dicarboxylic acid)-(2,2′-bipyridyl)ruthenium(II). i Tris(2,2′-bipyridyl-4,4′-dicarboxylic acid)ruthenium(II). j (2,2′-Bipyridyl-4,4′-dimetyhl-dicarboxylic acid)-bis(2,2′-bipyridyl)ruthenium(II). k Bis(2,2′-bipyridyl-4,4′-dimethyl-dicarboxylic acid)-(2,2′-bipyridyl)ruthenium(II). l Tris(2,2′-bipyridyl-4,4′-dimethyl-dicarboxylic acid)ruthenium(II). m cis-Di(thiocyanato)(2,2′-bipyridyl-4,4′-dicarboxylic acid)-(2,2′-bipyridyl-4,4′-tridecyl)ruthenium(II). n cis-Di(thiocyanato)(2,2′-bipyridyl-4,4′-dicarboxylic acid)-(2,2′-bipyridyl-4,4′-bis(vinyltriphenylamine))ruthenium(II). o Bis(isothiocyanato)(4,4′-dicarboxylato-2,2′-bipyridine)(4,4′-dinonyl-2,2′-bipyridine)ruthenium(II). p cis-Di(thiocyanato)-(2,2′-bipyridyl-4,4′-dicarboxylic acid)(4,4′-dimethyl-2,2′-bipyridyl)-ruthenium(II). q Zinc phthalocyanine-tri-tert-butyl-2-carboxylic acid. r Ruthenium phthalocyanine-tri-tert-butyl-2-carboxylic acid. s RuPcA2; see reference for structure. t RuPcA5; see reference for structure. u 4,4′-[(4-[5′-([N-(2,6-Diisopropylphenyl)]-9-perylenyl-3,4-dicarboxyimide)-3,4′-dihexyl-2,2′-bithien-5-yl]phenyl)imino]dibenzoate 4,4′-[(4-[5′-([N-(2,6-diisopropylphenyl)]-9-perylenyl-3,4-dicarboxyimide)-3,4′-dihexyl-2,2′-bithien-5-yl]phenyl)imino]dibenzoate. v cis-Dithiocyanato(4,4′-dicarboxy-2,2′-bipyridine)-(4,4′-dinonyl-2,2′-bipyridyl)Ru(II). w cis-Dithiocyanato(4,4′-dicarboxy-2,2′-bipyridyl)-(4,4′-dimethyl-2,2′-bipyridyl)Ru(II). x cis-Dicyanato(4,4′-dicarboxy-2,2′-bipyridyl)-(4,4′-dimethyl-2,2′-bipyridine)Ru(II). y (4,4′-Dicarboxy-2,2′-bipyridyl)-bis(4,4′-dimethyl-2,2′-bipyridyl)Ru(II). z Bis(4,4′-dicarboxy-2,2′-bipyridyl)-(4,4′-ditridecyl-2,2′-bipyridyl)Ru(II). aa cis-Dithiocyanato-4,4′-bis[p-carboxylic acid]-2,2′:6′,2′′:6′′,2′′′-quaterpyridine Ru(II). ab (2,2′-Bipyridyl-4,4′-dicarboxylic acid)-bis(4,4′-di-tert-butyl-2,2′-bipyridy)ruthenium(II). | ||||||
| 1 | 1a | 3.3 × 10−10 mol cm−2 | Diethylene glycol dimethyl ether | 2.6 × 10−8 | CA | 147 |
| 2 | 1a | 3.3 × 10−10 mol cm−2 | EtMeIm+Tf2N−b | 2.8 × 10−8 | CA | 147 |
| 3 | 1a | 3.3 × 10−10 mol cm−2 | EtMeIm+Tf2N−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4-methyl-2-pentanone (1 4-methyl-2-pentanone (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
5.0 × 10−8 | CA | 147 |
| 4 | 1a | 3.3 × 10−10 mol cm−2 | EtMeIm+Tf2N−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3-methoxypropionitrile (1 3-methoxypropionitrile (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
9.1 × 10−8 | CA | 147 |
| 5 | 1a | 3.3 × 10−10 mol cm−2 | EtMeIm+Tf2N−![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MeCN (1 MeCN (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) 1) |
11 × 10−8 | CA | 147 |
| 6 | D102c | 3.0 × 10−8 mol cm−2 | 0.1 M NBu4PF6/MeCN | ≥5 × 10−9 | CV | 155 |
| 7 | D131d | 4.3 × 10−8 mol cm−2 | 0.1 M NBu4PF6/MeCN | ≥5 × 10−9 | CV | 155 |
| 8 | D149e | 2.0 × 10−8 mol cm−2 | 0.1 M NBu4PF6/MeCN | ≥5 × 10−9 | CV | 155 |
| 9 | D205f | 3.5 × 10−8 mol cm−2 | 0.1 M NBu4PF6/MeCN | ≥5 × 10−9 | CV | 155 |
| 10 | Ru(bpy)2(Ad-tripod-phen)2+ | 3.1 × 10−8 mol cm−2 | 0.1 M TBAPF6/MeCN | ∼10−11 | CA | 157 |
| 11 | Ru(bpy)2(Ad-tripod-bpy)2+ | 3.9 × 10−8 mol cm−2 | 0.1 M TBAPF6/MeCN | ∼10−11 | CA | 157 |
| 12 | Ru(bpy)2(C-tripod-phen)2+ | 4.2 × 10−8 mol cm−2 | 0.1 M TBAPF6/MeCN | ∼10−11 | CA | 157 |
| 13 | Ru(bpy)2(C-tripod-bpy)2+ | 2.0 × 10−8 mol cm−2 | 0.1 M TBAPF6/MeCN | ∼10−11 | CA | 157 |
| 14 | 1g | 2.2 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 13.3 × 10−10 | CA | 146 |
| 15 | 2h | 2.4 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 3.6 × 10−10 | CA | 146 |
| 16 | 3i | 2.4 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 2.7 × 10−10 | CA | 146 |
| 17 | 1cj | 3.7 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 12.1 × 10−10 | CA | 146 |
| 18 | 2ck | 3.7 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 2.9 × 10−10 | CA | 146 |
| 19 | 3cl | 3.7 × 10−8 mol cm−2 | Aqueous 0.1 M HClO4 | 0.6 × 10−10 | CA | 146 |
| 20 | N621m | ∼70% | 0.1 M TBAP/MeCN | 1.2 × 10−9 | CA | 156 |
| 21 | HW456n | ∼60% | 0.1 M TBAP/MeCN | 2.6 × 10−8 | CA | 156 |
| 22 | Z-907o | 1.5 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 2.0 × 10−8 | CV | 145 |
| 23 | N820p | 1.6 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 3.5 × 10−8 | CV | 145 |
| 24 | D131d | 1.5 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 2.8 × 10−8 | CV | 145 |
| 25 | D149e | 1.1 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 27 × 10−8 | CV | 145 |
| 26 | TT-1q | 2.2 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 0.39 × 10−8 | CV | 145 |
| 27 | TT-35r | 7.3 × 10−5 mol cm−3 | 0.1 M TBAP/MeCN | 3.9 × 10−8 | CV | 145 |
| 28 | A2s | 1.2 × 10−4 mol cm−3 | 0.1 M TBAP/MeCN | 1.7 × 10−8 | CV | 145 |
| 29 | A5t | 4.5 × 10−5 mol cm−3 | 0.1 M TBAP/MeCN | 1.3 × 10−8 | CV | 145 |
| 30 | C60-Diels–Alder monocarboxylic acid | 500 mM | 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 EC 50 EC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMC and 1 M lithium imide/MeCN DMC and 1 M lithium imide/MeCN |
6.5 × 10−9 | CV | 153 |
| 31 | Bis(2,2′-bipyridine)(4,4′-diphosphonato-2,2′-bipyridine)ruthenium(II) | 9 × 10−8 mol cm−2 | 0.1 M LiClO4/MeCN | 11 × 10−10 | CA | 138 |
| 32 | [OsII(bpy)2(4,4′-(CO2H)2bpy)](PF6)2 loaded in EtOH | 7 × 10−11 mol cm−2 | 0.1 M TBAH/MeCN | 1.4 × 10−11 | CA | 158 |
| 33 | [OsII(bpy)2(4,4′-(CO2H)2bpy)](PF6)2 loaded in MeCN | 1.1 × 10−10 mol cm−2 | 0.1 M TBAH/MeCN | 1.4 × 10−9 | CA | 158 |
| 34 | PMI-T2-tPAu | 1.5 × 10−10 mol cm−2 | 0.1 M EMITFSI/MeCN | 2.2 × 10−8 | CV | 159 |
| 35 | 1v | — | 0.1 M EMITFSI/MeCN | 4.1 × 10−9 | CV | 149 |
| 36 | 2w | — | 0.1 M EMITFSI/MeCN | 11.4 × 10−9 | CV | 149 |
| 37 | 3x | — | 0.1 M EMITFSI/MeCN | 1.9 × 10−9 | CV | 149 |
| 38 | 5y | — | 0.1 M EMITFSI/MeCN | 0.3 × 10−9 | CV | 149 |
| 39 | 6z | — | 0.1 M EMITFSI/MeCN | 0.02 × 10−9 | CV | 149 |
| 40 | 7aa | — | 0.1 M EMITFSI/MeCN | 0.5 × 10−9 | CV | 149 |
| 41 | bpyg | 1.9 × 10−7 mol cm−2 | 0.1 M LiClO4/MeCN | 2.2 × 10−9 | CA | 151 |
| 42 | bpyg | 1.9 × 10−7 mol cm−2 | 0.1 M LiClO4/MeCN | 1.1 × 10−10 | CV | 151 |
| 43 | dmby | 9.5 × 10−8 mol cm−2 | 0.1 M LiClO4/CH3CN | 5.3 × 10−9 | CA | 151 |
| 44 | dmby | 9.5 × 10−8 mol cm−2 | 0.1 M LiClO4/CH3CN | 3.1 × 10−10 | CV | 151 |
| 45 | dtbab | 7.7 × 10−8 mol cm−2 | 0.1 M LiClO4/CH3CN | 2.4 × 10−10 | CA | 151 |
| 46 | dtbab | 7.7 × 10−8 mol cm−2 | 0.1 M LiClO4/CH3CN | 1.4 × 10−11 | CV | 151 |
As can be seen in Table 1, Dapp can vary by several orders of magnitude from 2.7 × 10−7 cm2 s−1 for D149 on TiO2 in 0.1 M TBAP in acetonitrile at room temperature measured using CV145 to 1.4 × 10−11 for [Ru(4,4′-di-tert-butyl-2,2′-bipyridine)2(dcbH2)](PF6)2 on TiO2 in 0.1 M LiClO4 in acetonitrile at room temperature measured with CV.151 In addition to the dye structure, film porosity, and nanoparticle size,151Dapp is dependent on temperature,152 polarity and pH of the solvent,144,147,153,154 molecular packing and distance between dyes,151,155,156 and, for some dyes, metal ions present in solution.156
For example, in a study by Li et al.160 (Table 1, entries 20 and 21), the percolation dynamics (measured with CA) of a ruthenium complex (N621) are compared with those observed for an analogous dye with an additional triphenyl amine (TPA) donor moiety (HW456), whose structures can be seen in Fig. 13. The increased electronic coupling between the TPA donor moieties made the rate of hole transfer 20 times faster in a monolayer of HW456 compared to a monolayer of N621. With the introduction of mercuric ions into the solvent, hole percolation was quenched for N621 films and enhanced for HW456 due to Hg2+ coordination to the thiocyanate moiety on both dyes. This suggests that the hole percolation pathway is along the overlapped thiocyanate groups for the N621 molecules, whereas in HW456 molecules cation percolation proceeds between intermolecular TPA ligands.
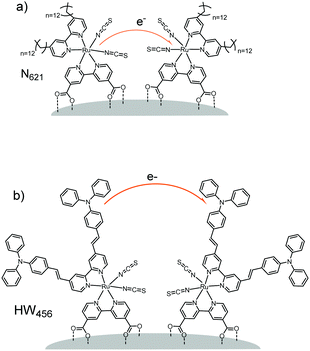 | ||
| Fig. 13 Molecules from Li et al. showing the electron transfer pathways for (a) N621 and (b) HW456.160 | ||
In another systematic study (entries 41–46 in Table 1), DiMarco et al. investigated the self-exchange intermolecular RuIII/II electron transfer for three homologous Ru diimine compounds of the general form [Ru(LL)2(dcbH2)](PF6)2, where LL is 2,2′-bipyridine (bpy), 4,4′-dimethyl-2,2′-bipyridine (dmb), or 4,4′-di-tert-butyl-2,2′-bipyridine (dtb) and dcbH2 is 2,2′-bipyridyl-4,4′-dicarboxylic acid, in order to probe how the electron transfer rate varies as the distance and aliphatic bulk between the Ru centers is increased (bpy < dmb < dtb).151Dapp was determined using both CV and CA and the same trend of dtb < bpy < dmb was found with both techniques, but the value for the latter was an order of magnitude lower than the former. The authors suggest that the large difference in Dapp for these two techniques could lie in the assumption that the semi-infinite diffusion boundary approximation holds true with both techniques.145 That is, the analysis is only valid if the oxidized molecules do not reach the outer edge of the film, an assumption that holds true in CV measurements where only about 5% of the film is oxidized but not necessarily in CA measurements where almost all of the film is oxidized by the end of the measurement.
For molecules where distinct absorption spectral shifts accompany changes in redox state, the rate of electron/hole diffusion through a monolayer film can also be measured using a combination of TA spectroscopy and Monte Carlo simulations. Similar to the experiments described above to determine energy transfer rates (Section 2.3.1) electron migration and site-to-site hopping rates can be determined for single component films using TA anisotropy135 or for a co-deposited film containing the dye of interest and a second molecule that acts as a redox sink.135,142,143 In comparison to electrochemical techniques, spectroscopic determinations of electron migration do not suffer from the boundary limitations described above for Dapp and also, in conjunction with Monte Carlo simulations, allow for the determination of site-to-site electron transfer rates rather than just a bulk diffusion constant.
As an aside, it is worth noting that there have been considerable advances in modeling cross-surface electron transfer processes using ab initio computational methods. More details can be found in the review article recently published by Pastore et al.161
In summary, it is known but perhaps underappreciated that cross-surface electron and hole transfer through dye monolayers on high surface area electrodes can play an important role in emerging dye–semiconductor technologies. Though a powerful experimental approach, Dapp is dependent on numerous variables and can vary by an order of magnitude depending on the measurement/analysis methodology. A combination of TA and MCS may give a more detailed description of the electron hopping events but require additional computational efforts as well as expensive, time consuming, and often difficult spectroscopic measurements. Overall, it is generally safe to suggest that in order to directly compare redox migration events at interfaces with respect to solvent, molecular structure, surface loading, etc., the samples should be measured under the same set of conditions and with the same technique.
3. Interfacial electron transfer
Molecules bound to a metal oxide surface is a geometrically and spatially controllable scaffolding to study and manipulate electron transfer dynamics at interfaces. These electron transfer events can take place between the surface/dye and an electroactive molecule in solution, or between dyes and the surface, and between two molecules on the surface. Regardless of if it occurs in solution or at an interface, electron transfer dynamics can generally be described using Marcus electron transfer theory (eqn (13)).1 The physical parameters that dictate the electron transfer rate (kET) between a donor (D) and acceptor (A) are the Gibbs free energy change (ΔG°), reorganization energy (λ), temperature (T), and electronic coupling between the donor and acceptor molecules (VDA).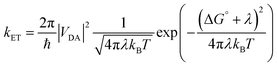 | (13) |
|VDA|2 = |V0|2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−βRDA) exp(−βRDA) | (14) |
The electronic coupling term can loosely be thought of as the height and width of the electron tunneling barrier between the donor and acceptor. As shown in eqn (14), the coupling at a given distance (VDA) is dictated by the coupling at close contact (V0), the attenuation coefficient (η), and perhaps most importantly for the discussion below, the distance (RDA) between D and A. Given that there is an exponential relationship between VDA2 and RDA, and in turn kET, the distance between D and A can have a profound influence on electron transfer rates and ultimately device performance. Therefore, modifications in the molecular structure at the interface can effectively be used to facilitate or hinder electron transfer by decreasing or increasing RDA, respectively.
Below we summarize efforts at manipulating electron transfer events at molecule–metal oxide interfaces using two different types of multimolecular interactions: (1) co-deposition of a dye and an electrochemically inactive “insulator” molecule (Section 3.1), and (2) binding chromophores and donors/acceptors (Section 3.2) to a metal oxide surface. We also discuss how these interactions can be utilized to access unique electron transfer processes like supersensitization (Section 3.3).
3.1 Co-adsorbents
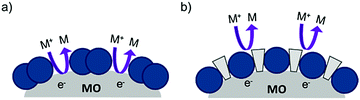 | ||
| Fig. 14 The proposed recombination process at the dye–metal oxide interface in the (a) absence and (b) presence of co-adsorbent molecules. | ||
Under optimized loading conditions, dye molecules form a closely packed, nearly complete monolayer on the metal oxide surface. Despite having high surface loadings there are still exposed portions of TiO2, either in the spaces between molecules or in vacancy defects in the monolayer packing, that are in direct contact with the solvent. These open sites allow for diffusional contact (small RDA) between the oxidized redox mediator and electrons in TiO2 (Fig. 14a) which can result in recombination. The deposition of co-adsorbents in the space between dye molecules not only hinders aggregation, but also effectively inhibits the redox mediator from approaching the surface (large RDA) which slows recombination (Fig. 14b).
In 1978, Miyasaka et al. published one of the earliest reports of using inert co-adsorbents on metal oxide surfaces.172 They demonstrated that, despite having lower dye loading, tin oxide films functionalized with chlorophyll dye and stearic acid as an inert co-adsorbent exhibited both increased photocurrent and photovoltage compared to films with the dye alone. Despite these promising results, the use of inert co-adsorbents in photoelectrochemical cells laid largely dormant until the introduction of high surface area DSSCs by O’Regan and Gratzel in 1991.173 Since then, there has been a sharp increase in use of inert co-adsorbents in DSSCs. A majority of these studies utilize co-adsorbents to prevent dimer/excimer formation in large planar aromatic dyes like porphyrins, coumarins, carbazole, indoline, squaraine and phthalocyanines60,61,63,67,68,174–178 which are susceptible to aggregation through π–π stacking. Most ruthenium polypyridyl dyes, with the exception of black dye,59 do not readily aggregate on the surface and thus co-adsorbents are largely used for slowing recombination at the interface.162–171
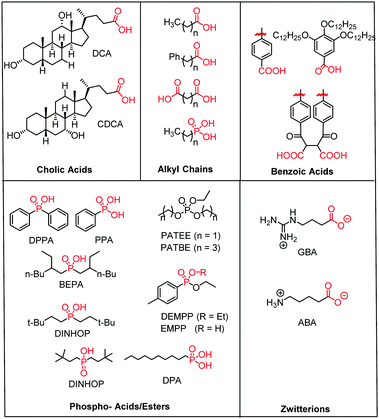 | ||
| Fig. 15 Molecular structure of the most common electro- and photochemically inert co-adsorbents. The surface binding moiety is highlighted in red. | ||
A majority of co-adsorbents are composed of sp3 carbon rings/chains or benzene rings, presumably because they lack absorption in the visible wavelength region, and are electrochemically inactive under operational potentials of dye-sensitized devices. These molecules are typically anchored to the surface via carboxylic acids,61–65 phospho acids,163,167,179–181 or ester groups.171,180,182–184 Both carboxylic and phospho acids bind through covalent linkages.167,182,184,185 In contrast, ester binding is largely assumed to be through hydrogen bonding.180,182 Phosphonic acids are known to have the strongest binding affinity for the surface and thus offer increased DSSC stability,25,167,179–181 however there is currently no definitive evidence that any of these binding groups are superior in terms of device efficiencies.
Of these co-adsorbents, cholic acids, in particular deoxycholic acid (DCA) and chenodeoxycholic acid (CDCA), are by far the most commonly used presumably because (1) their steroidal skeleton offers greater steric bulk compared to alkyl chains, (2) they are commercially available by-products found in the bile of mammals,186 and (3) they have a strong history of significantly improving device performance relative to dye only systems.187
An interesting and distinct type of co-adsorbents are zwitterion molecules.164,169,188 This unique class of molecules allows researchers to tune both the steric and electrostatic properties at the dye interface which directly influences recombination dynamics.
A majority of the co-adsorbents studied to date have relied on commercially available carboxylate and phosphonate functionalized molecules. This is presumably at least partially due to a disconnect between synthetic chemists and researchers studying devices. However, there have been efforts to synthesize novel co-adsorbents with specific design principles in mind.167,168,181,188–190
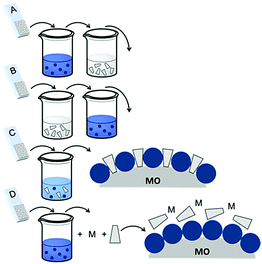 | ||
| Fig. 16 Common loading procedures for dyes (dark blue) and co-adsorbents (gray) on metal oxide substrates (M = mediator). | ||
The final dye/co-adsorbent loading ratio for all four of these strategies is strongly dependent on competitive binding between the two species which is dictated by binding affinities of molecules and concentrations of loading solutions. One common trend, regardless of film preparation strategy, is a decrease in total dye loading in co-adsorbent films, relative to the dye only films, presumably due to limited surface area and competitive desorption. Since the primary goal of these solar cells is to maximize light absorption, special care must be taken to optimize loading conditions to maintain high dye concentrations while still reaping the benefits of co-adsorbent molecules. As far as we can tell, current research efforts rely largely on trial and error to determine the appropriate set of conditions for a given dye/co-adsorbent.61,162,190,196
One of the fundamental limitations hindering the progress in controlling co-adsorbent loading is the difficulty in quantifying surface loading ratios. The lack of absorption and electrochemical signal for the co-adsorbent limits the techniques available to quantify their surface coverage. At least a few reports indicate that co-adsorbent concentrations can be determined using photoelectron spectroscopy (PES),167,185 and scanning tunneling microscopy (STM)197 but have been somewhat limited in their use.
In one study, Marinado et al. used PES measurements to quantify the relative concentration of atoms specific to the dye molecules (e.g. S2p from thiophene) and the co-adsorbents (e.g. P2p from phosphorus binding groups).185 They found that with the same concentration (0.05 mM of co-adsorbent to 0.2 mM D29 dye) of two different co-adsorbents, decylphosphonic acid (DPA) and bis(3,3-dimethyl-butyl)phosphonic acid (DINHOP) (Fig. 15), dye loading was decreased by 53% and 25% respectively. The dye/co-adsorbent ratio also varied between 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3.5 for DPA and 3
3.5 for DPA and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for DINHOP. The authors also investigated CDCA as a co-adsorbent but quantification of surface loading by PES was difficult due to a lack of unique atoms in CDCA. Regardless the authors clearly demonstrate the utility of PES in quantifying co-adsorbent concentrations and that the structure, size, and affinity of the co-adsorbent play important roles in dictating the surface coverages and loading ratios. Additionally, while most researchers only report the concentrations in the loading solutions, this work demonstrates that the dye/co-adsorbent ratio can vary significantly between solution and the surface.
1 for DINHOP. The authors also investigated CDCA as a co-adsorbent but quantification of surface loading by PES was difficult due to a lack of unique atoms in CDCA. Regardless the authors clearly demonstrate the utility of PES in quantifying co-adsorbent concentrations and that the structure, size, and affinity of the co-adsorbent play important roles in dictating the surface coverages and loading ratios. Additionally, while most researchers only report the concentrations in the loading solutions, this work demonstrates that the dye/co-adsorbent ratio can vary significantly between solution and the surface.
| Dye | Co-adsorbent | J sc (mA cm−2) | V oc (mV) | Fill factor | PCE (%) | Ref. | |
|---|---|---|---|---|---|---|---|
| The percent change in the presence of co-adsorbents are noted in parentheses.a 2-Cyano-3-[5-[4-(9-pentyl-9H-carbazol-3-yl)-1,2,3,3a,4,8b-hexahydrocyclopent[b]indol-7-yl]ethenyl-2-thienyl]-2-propenoic acid.b Ruthenium(II) cis-dithiocyanato(4,4′-dicarboxy-2,2′-bipyridine)(1,10-phenanthroline).c 1-[(5-Carboxy-1,3-dihydro-3,3-dimethyl-1-octyl-2H-indol-2-ylidene)methyl]-3-[(1-ethyl-1,3dihydro-3,3-dimethyl-2H-indol-2-ylidene)methyl]-2,4-dihydroxy-cyclobutenediylium.d Zinc(II) 2-carboxy-9(10),16(17),23(24)-tris-[2-(N,N-bis-(9,9-dimethylfluoren-2-yl)-4-aminophenyl)-5,5′-bithiophene]phthalocyanine.e Zinc(II) [10-[2-[10,20-bis[3,5-bis(1,1-dimethylethyl)phenyl]-15-[bis(4-octylphenyl)amino]-porphin-5-yl]ethynyl]-9-anthracenecarboxylato].f Zinc(II) 4,4′-[10,20-bis[4-(dimethylamino)phenyl]-porphine-5,15-diyl]bis-benzoic acid. | |||||||
| C-CAa | DCA | w/o | 14.16 | 628 | 0.66 | 5.87 | 206 |
| w | 18.53 (31%) | 649 (3%) | 0.71 (8%) | 8.49 (45%) | |||
| AR20b | Citric acid | w/o | 9.34 | 610 | 0.485 | 2.8 | 166 |
| w | 14.69 (57%) | 650 (7%) | 0.634 (31%) | 6.1 (118%) | |||
| SQ1c | CDCA | w/o | 8.02 | 509 | 0.69 | 2.82 | 203 |
| w | 10.23 (28%) | 595 (17%) | 0.69 (0%) | 4.23 (50%) | |||
| ZnPc 1d | CDCA | w/o | 3.26 | 503 | 0.68 | 1.11 | 65 |
| w | 5.25 (61%) | 541 (8%) | 0.73 (7%) | 2.07 (86%) | |||
| YD 13e | CDCA | w/o | 4.22 | 631 | 0.71 | 1.89 | 207 |
| w | 6.27 (49%) | 652 (3%) | 0.71 (0%) | 2.9 (53%) | |||
| P2f | CDCA | w/o | 11.1 | 660 | 0.66 | 4.83 | 208 |
| w | 12.4 (12%) | 720 (9%) | 0.68 (3%) | 6.07 (26%) | |||
From device performance alone it is difficult to determine the role of co-adsorbents in preventing aggregation, inhibiting recombination, or other effects because of the intertwined relationship between Jsc and Voc.179,198–201 As discussed in Section 2.1 aggregation can decrease electron injection efficiency due to competitive, fast non-radiative decay from the excimer state. In a device, decreased injection yield will manifest as lower Jsc and lower overall DSSC efficiency.65,175,184,199,202 Co-adsorbents can be used to prevent dye aggregation but interestingly, a majority of concentration dependent studies indicate that with increasing co-adsorbent there is an initial increase in Jsc followed by a decrease.59,177,179,201,203 The initial increase in Jsc is often attributed to an increase in electron injection yield, but it is also important to note that red/blue shifts in the absorption spectrum and changes in extinction coefficient upon co-adsorbent addition may also play a role in influencing the absorption overlap with the solar spectrum.204,205
An eventual decrease in Jsc at high co-adsorbent concentration is due to a decrease in dye loading and a lower light harvesting efficiency of the film. Because of this increase-decrease response curve, optimal device performance and co-adsorbent loading conditions are often determined empirically through concentration dependent studies. In a number of studies, lower Jsc have been obtained at all concentrations of the co-adsorbents. The decreased Jsc and minimal change in the absorption spectra are indicators that the dye molecules do not aggregate on the surface.209,210 For these systems, typically containing ruthenium dyes such as N719, N749 and Z-907,164,169,190,201 co-adsorbents are introduced as a means of slowing recombination and increasing Voc.167,180 Since Voc can be improved by a number of factors including negative conduction band edge shifts,180 higher Jsc, and slower recombination,178 it is important to quantify the role of recombination using techniques like electrochemical impedance spectroscopy (EIS) and transient photovoltage measurements.164,169,190,201 For example, Shen et al. found, via EIS, that a decrease in the number of protons from PPA (2H+) to DPPA (1H+) to PATEE (0H+) was accompanied by an increase in Voc due to a negative shift in the conduction band energy level of TiO2.180 A similar trend was reported by Ren et al. where a 26 mV positive shift and a 33 mV negative shift in conduction band energy was observed for deoxycholic acid (DCA) and sodium deoxycholate, (DCNa) respectively (Fig. 17)184 Neale et al. used infrared transmittance measurements with respect to tetrabutylammonium chenodeoxycholate (TBACDC) loading, to differentiate the role of recombination and conduction band energy shifts on the device Voc.183 Interestingly, the increased Voc in the presence of TBACDC was due to a negative shift in conduction band energy and not to slower recombination. In fact, counter to the expectation shown in Fig. 17, there was a fivefold increase in recombination rate in the presence of co-adsorbent.
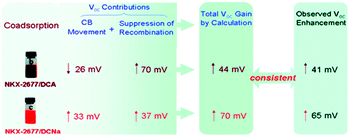 | ||
| Fig. 17 Influence of co-adsorbents on the conduction band energies, recombination rates, and over all Voc. Reprinted with permission from ref. 183. Copyright 2005, American Chemical Society. | ||
3.2 Chromophore–donor/acceptor assemblies
Electron transfer between a chromophore and donor or acceptor molecules has been extensively investigated in solution either as solvated molecules211,212 or with chemically linked chromophore–donor/acceptor assemblies.213–218 These assemblies are particularly appealing because the distance is fixed by the molecular structure and not dictated by the concentration of the solution, random molecular orientations, and diffusion rates. Similar structural control can be achieved at interfaces using several different strategies including covalent linkages (Section 3.2.1), co-deposition (Section 3.2.2), and supramolecular assemblies (Section 3.2.3) of chromophore and donor/acceptor moieties. The metal oxide surface adds an additional variable in that it can also act as an electron acceptor, donor, or insulator.3.2.1.1 Chromophore–donor/acceptor dyads on n-type MO. A majority of these covalent dyad systems contain a donor, rather than acceptor moiety presumably due to their targeted use as TiO2 photoanodes in DSSCs. The typical stepwise events for electron transfer events between donor (D), chromophore (C), and a n-type metal oxide (MO) are summarized in eqn (15)–(19).
| MO–C–D → MO–C*–D | (15) |
| MO–C*–D → MO(e−)–C+–D | (16) |
| MO(e−)–C+–D → MO(e−)–C–D+ | (17) |
| MO(e−)–C–D+ → MO–C–D | (18) |
| MO(e−)–C+–D → MO–C–D | (19) |
In terms of dye-sensitized devices, the primary goal of the MO–C–D architecture is to slow recombination dynamics (eqn (18) and (19)) by reducing the electronic coupling between MO(e−) and the cation species. This is typically achieved through a directional electron transfer cascade where the spatial separation, RDA, in MO(e−)–C–D+ is greater than for MO(e−)–C+. The general design strategy for MO–C–D is to select the components such that the oxidation potential of the donor moiety is more negative, i.e. more easily oxidized, than the chromophore to ensure that electron transfer from C* to MO, and from D to C+, is favorable.
One of the first examples of covalent MO–C–D assemblies was introduced by Gerald J. Meyer and coworkers.224 The complex, Ru(4-(CO2−)-4′-(CO2H)-2,2′-bipyridine)2(4-CH3-4′-CH2-PTZ,-2,2′-bipyridine), is composed of a ruthenium chromophore linked, via methyl spacer, to a phenothiazine (PTZ) donor group. Electron transfer from PTZ to Ru(III) is thermodynamically favorable by ∼360 mV. The charge separated state, TiO2(e−)–RuII–PTZ+ as observed by TA spectroscopy, is generated in less than 30 ns and recombines with a rate constant of 3.6 × 103 s−1. Electron–hole recombination is slowed by a factor of ∼2000 compared to the complex without PTZ (TiO2(e−)–RuIII). When incorporated into a DSSC, there was a 100 mV increase in Voc which was attributed to its slower recombination dynamics relative to the complex without donor.
Since then, a number of MO–C–D systems have been examined (Fig. 18). These complexes are typically composed of a ruthenium polypyridyl chromophore and tri-aryl and/or alkyl amine donor moiety.221,225–229 Presumably, they are selected as the archetypical C and D because of their well understood and well behaved single-electron reversible electrochemistry.230,231 There are several other compounds that utilize zinc porphyrin,221,226,232 copper phenanthroline,233 organic D–π–A,234 and ruthenium pyrazole/pyrrole235 complexes as the chromophore. A majority of reports utilizing C–D molecules on surfaces focus on studying the influence of the donor group on DSSC performance. As reported in the Meyer system described above, they often observe increase in Voc which is attributed to the slowed electron–hole recombination MO(e−)–C–D+. Rarely, but occasionally, this conclusion is supported by TA measurements.227,236–239 As expected from Marcus theory, the MO(e−) to D+ recombination rate decreases exponentially with the distance between the surface and donor group.239 It is interesting to note that for these devices, Jsc was usually either unchanged or decreased upon the addition of the donor group. The decrease in Jsc is often attributed to bulkier donor moieties reducing surface loading, resulting in a lower absorption cross-section in the film.240
A particularly interesting subset of these compounds are those containing multiple donor moieties.233,239–245 Compared to parent molecules without donor groups, these complexes exhibit similar changes in photophysical and device characteristics as the single donor systems (i.e. longer lived charge separation, increased Voc, etc.).246,247 In a relatively unique study, Song et al. made a comparison between Ru(4-(CO2−)-4′-(CO2H)-2,2′-bipyridine)(4-R1-4′-R2-2,2′-pipyridine) (NCS)2 chromophores substituted with one (R1 = CH3, R2 = CH2NCH3Ph) or two (R1, R2 = CH2NCH3Ph) dimethyl aniline donor groups. In DSSCs, the compound with two donor groups had an approximately 5% greater Jsc, Voc and FF with a ∼20% greater overall efficiency compared to the singly substituted complex.246 Later TA measurements suggest improved performance was due to an increased D to C+ electron transfer rate for the double (k = 3.4 × 107 s−1) versus single (k = 2.6 × 107 s−1) donor system.247 These results indicate that although the MO–C–D compounds only undergo single photon-single electron transfer events, the rate/probability of these events increases with more donor moieties.
The above discussion focuses on TiO2–C–D assemblies. Analogous but less studied are the metal oxide–chromophore–acceptor assemblies that are of interest for application in photochromic devices, optical read–write–reset devices, and others. For example, Will et al. synthesized a D–A complex composed of a ruthenium tris-bipyridyl chromophore linked to a methylviologen acceptor group by a methyl spacer.248,249 After loading the complex on TiO2 they were able to demonstrate directional, potential controlled electron transfer (Fig. 19).
 | ||
| Fig. 19 Intramolecular electron transfer of RV on TiO2 with applied bias. Adapted with alterations with permission from ref. 248. Copyright 1998 American Chemical Society. | ||
Under open circuit conditions or a positive applied potential, electron transfer from C* to MO was significantly faster than from C* to A resulting in a 95% electron injection yield. In contrast, under a negative bias, the TiO2 conduction band energy is shifted and the electron injection rate is sufficiently slowed such that 52% of C excited states transfer electrons to the methylviologen moiety. The reduced methylviologen exhibits a color change that effectively demonstrates a MO–C–A assembly can be used as a photo-electrochromic switching material.
3.2.1.2 Chromophore–donor/acceptor dyad on p-type MO. An increasingly popular use of C–A or D–C dyads is for lengthening the charge separation lifetime in the photocathodes of p-type and tandem DSSCs (Section 4.3).250,251 In contrast to the electron accepting nature of n-type materials (i.e. TiO2 and SnO2), p-type semiconductors, like NiO, act as an electron donor, effectively inverting the typical DSSC architecture.
Electron transfer events between A, C, and a p-type metal oxide (pMO) in pMO–C–A assemblies are summarized in eqn (20)–(24).
| pMO–C–A → pMO–C*–A | (20) |
| pMO–C*–A → pMO(h+)–C−–A | (21) |
| pMO(h+)–C−–A → pMO(h+)–C–A− | (22) |
| pMO(h+)–C−–A → pMO–C–A | (23) |
| pMO(h+)–C–A− → pMO–C–A | (24) |
In this scheme, the excited chromophore (eqn (20)) is reduced via electron transfer from the metal oxide, also known as hole injection (eqn (21)). An electron is then transferred from C− to A, affording the pMO(h+)–C–A− charge separated state (eqn (22)). The cation/hole can either diffuse through the pMO and enter the external circuit, or recombine as in eqn (23) or (24) (Fig. 20).
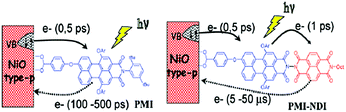 | ||
| Fig. 20 Electron transfer dynamics of PMI and PMI-NDI dyad on NiO. Reprinted with permission ref. 429. Copyright 2009 American Chemical Society. | ||
Odobel and coworkers later generated a squaraine dye–peryleneimide–naphthalenediimide triad.252 In contrast to the dyad, the triad exhibited a charge separation mechanism where excitation of the squaraine was followed by electron transfer to the perylene unit, and then subsequent perylene to naphthalene and NiO to squaraine electron transfer events. In an I−/I3− based p-type DSSC the SQ-PMI-NI triad exhibited a more than three fold higher Jsc but a >30% reduction in Voc relative to the PMI-NI dyad.
Ji et al. also relied on naphthalenediimide as the acceptor unit but with a ruthenium terpyridine complex as the chromophore.253 On NiO the charge separated NiO(+)–C–A− was generated in 1.1 ps but interestingly, the back electron transfer rate was only nominally slower in the dyad (426 ps) than the chromophore only film (371 ps).
An alternative strategy to increase the charge separation lifetime on NiO is by using a donor–chromophore dyad effectively generating a pMO–D–C assembly. Proposed electron transfer events between D, C, and pMO are summarized in eqn (25)–(29).
| pMO–D–C → pMO–D–C* | (25) |
| pMO–D–C* → pMO–D+–C− | (26) |
| pMO–D+–C− → pMO(h+)–D–C− | (27) |
| pMO(h+)–D–C− → pMO–D–C | (28) |
| pMO–D+–C− → pMO–D–C | (29) |
The number of examples of D–C dyads where each component is electronically unique is relatively limited. In 2013, Ji et al. published a dyad that was composed of ruthenium(II) with two 2,2′-bipyridine or 1,10-phenanthroline ligands and one 2-phenylpyridine cyclometallating ligand functionalized with a di(carboxylic acid)-triphenylamine (TPA) surface binding moiety (Fig. 21).254 UV-vis, electrochemistry, DFT calculations, and IPCE measurements indicate that the ruthenium chromophore was largely independent of the TPA group.
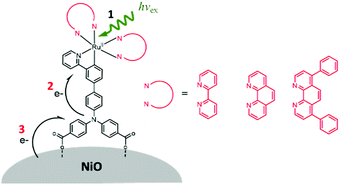 | ||
| Fig. 21 pMO–D–C assembly and proposed electron transfer events by Wu and coworkers. Adapted with alterations with permission from ref. 254. Copyright 2013 American Chemical Society. | ||
In a p-type DSSC, the dyad had a >5-fold increase in Jsc and an order of magnitude higher solar energy conversion efficiency (0.099%) compared to the same dye directly on the NiO surface (0.009%).255 The improved performance is attributed to a longer lived charge separated state, later supported by TA measurements.256 However, it is important to note that while the mechanism proposed in eqn (25)–(29) is feasible, the cation feature for TPA was not observed during TA measurements indicating that it either did not form, or more likely, that reduction of TPA+ by NiO is a faster event.
Odobel257–259 and others260–262 have generated additional dyad-like dyes for use on NiO and in p-type DSSCs, however since the components are linked via acetylene or aromatic bridges, it is not easy to distinguish C–A and D–C from D–π–A systems so they will not be discussed here.
3.2.2.1 Chromophores co-adsorbed with donors. Like the covalent C–D systems described above, the primary goal cited for co-depositing C and D on TiO2 (TiO2–C|D) is to increase the rate of regeneration and inhibit recombination in DSSCs. The observed electron transfer events, in the absence of mediator, can similarly be described using eqn (15)–(19) from Section 3.2.1. However, unlike the numerous reports of covalent C–D systems, reports of co-depositing C and D are largely limited to research efforts by the groups of Fitzmaurice263–265 and Kim.266,267
In 1999, Grätzel and coworkers published a thorough and systematic study comparing the electron transfer rates for a ruthenium(II)bis-terpyridine complex as the chromophore and substituted triphenylamine as the donor in both a covalent and co-deposited films (Fig. 22).227 For the co-deposited film, excitation and electron injection from C (eqn (15) and (16)) was followed by relatively fast (<5 ns) electron transfer from D to C+ (eqn (17)). Interestingly, despite having similar or faster electron transfer rates, the quantum yield for generating the charge separated state was near unity for the covalent dyad (TiO2(e−)–C–D+) but only 60% for the codeposited films (TiO2(e−)–C/D+). The films also exhibit dramatic differences in the lifetime of the charge separated state (eqn (17)) being 3 μs and 30 μs for the co-deposited and covalent systems respectively. The shorter lifetime for the co-deposited film was attributed to the close proximity between TiO2(e−) and D and the well-known distance dependence on electron transfer rate as described in the introduction to this section. Despite this difference, charge recombination is four orders of magnitude slower than D to S+ electron transfer, thus the charge separation yield of TiO2(e−)–C/D+ would still be expected to be near unity. This relatively low yield (60%) was hypothesized to be due to reductive quenching of S* by D (see Section 3.3, eqn (38)) prior to electron injection.
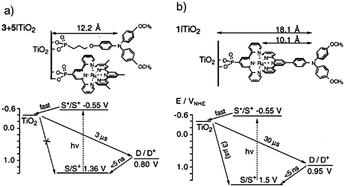 | ||
| Fig. 22 (a) Coadsorbed ruthenium(II) bis-terpyridine complex with 3-(4-(N,N-di-p-anisylamino)phenoxy)-propyl-1-phosphonate donor and (b) covalent dyad structures and their respective electron transfer rates. Reprinted with permission from ref. 227. Copyright 1999 American Chemical Society. | ||
In 2011 Kim and coworkers studied the influence of co-deposition of C and D on DSSC performance (Fig. 23a and d).239 Despite having a lower chromophore loading and decreased absorbance, the DSSC with an anode composed of co-deposited films with 4-[3,6-bis[4-(2-ethylhexyloxy)phenyl]-9H-carbazol-9-yl]benzoic acid (HC-A) as the donor and oligothiophene-containing coumarin (NKX2677) as the chromophore, exhibited an increased Jsc, Voc, and a factor of 1.33 efficiency improvement over the NKX2677 only film. The improvement was attributed to several factors including (1) the co-adsorbent decreasing aggregation/π–π stacking of planar chromophores, (2) slowed charge recombination between injected electrons and the redox mediator,266 (3) at least some photocurrent generation from direct excitation of HC-A at 350 nm, and finally (4) HC-A acting as a hole conductor, effectively reducing the oxidized dyes and relaying holes to the electrolyte. Regarding the latter point, although the driving force for HC-A to NKX2677+ electron transfer is energetically unfavorable (360 mV), oxidized HC-A was observed using TA spectroscopy.
 | ||
| Fig. 23 Molecular structures of co-adsorbent (blue) (a) HC-A1, (b) HC-A′, (c) HC-A′′, and chromophore (black) (d) NKX2677 and (e) FP.239 | ||
In an extension of this work, Kim and coworkers synthesized two additional derivatives of HC-A, HC-A′ and HC-A′′, with varying degrees of π-conjugation (biphenyl and tetramethylbiphenyl) between the carbazole donor group and the surface binding carboxylate group (Fig. 23b and c).267 When co-deposited on TiO2 with a porphyrin based dye, both derivatives were less effective at inhibiting charge recombination compared to the parent dye. The increase in current and voltage, relative to the chromophore only device, was attributed to the increased spectral absorption range, and the decrease of π–π stacking induced aggregation in NKX2677.
In an effort to increase the driving force of D to C+ electron transfer, Kim and coworkers then synthesized two new phenothiazine (PTZ) based donor molecules.268 Using TA spectroscopy they demonstrated that both PTZ donors reduce oxidized dye in ∼100 ns, and exhibit slower BET rate compared to using DCA and HC-A. Despite the slowed recombination and slightly higher photocurrent contribution, devices with PTZ donors had similar performance metrics as the HC-A device.
3.2.2.2 Chromophores co-adsorbed with acceptors. For C|A deposited on TiO2, both A and TiO2 can act as an electron acceptor and thus at least two electron transfer pathways can be envisioned and have been demonstrated. The events depicting excited state electron transfer from C to the metal oxide (eqn (30)–(32)) or the acceptor molecule (eqn (33)–(36)) are given below.
| MO–C|A → MO–C*|A | (30) |
| MO–C*|A → MO(e−)–C+|A | (31) |
| MO(e−)–C+|A → MO–C+|A− | (32) |
| MO–C+|A− → MO–C|A | (33) |
| MO–C*|A → MO–C+|A− | (34) |
| MO–C+|A− → MO(e−)–C+|A | (35) |
| MO(e−)–C+|A → MO–C|A | (36) |
Upon excitation of C (eqn (30)), the electron can transfer directly to the metal oxide surface (eqn (31)), as with a standard DSSC, or to the adjacent acceptor molecule (eqn (34)). In the former case, the electron in the metal oxide can then transfer to a surface bound acceptor (eqn (32)) to generate a surface bound charge separated state (MO–C+|A−). In the latter case the reduced acceptor can transfer an electron to the metal oxide resulting in a MO(e−)–C+|A charge separated state (eqn (35)). Regardless of the nature of the charge separated state, in the absence of an external circuit or sacrificial donor, it will decay back to the original state via charge recombination (eqn (33) and (36)).
One of the earliest examples of C and A codeposited on nanocrystalline TiO2 was reported by Fitzmaurice and coworkers. In their system they chose bis[(4,4′-dicarboxy-2,2′-bipyridine)(4,4′-dimethyl-2,2′-bipyridine)-ruthenium(II)] as the chromophore with a methyl viologen monomer263 or oligomer264 as the acceptor species (Fig. 24a). They observed a long lived (>15 minutes) TiO2–C+|A− charge separated state and proposed a step-wise mechanism proceeding via excitation of C (eqn (30)), electron transfer to the metal oxide (eqn (31)), and then metal oxide mediated electron transfer to the acceptor (eqn (32)). Later experiments, applying a bias to the TiO2, lent support to this mechanism by demonstrating that electrochemically populating the CB of TiO2 resulted in electron transfer from the metal oxide to the acceptor moiety (TiO2(e−)–A → TiO2–A−).265 In a similar TiO2–C|A system, using Ru(bpy)32+ donor and MV2+ acceptor precipitated on TiO2, Zhang et al. used EPR spectroscopy to monitor electron transport through the TiO2 conduction band and further supported a metal oxide mediated charge separation process.269
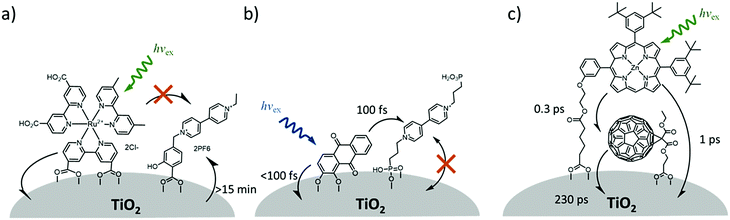 | ||
| Fig. 24 Electron transfer at the interface for co-deposited chromophores and acceptors via three different pathways (a) metal oxide mediated electron transfer from Ru(bpy)3 to MV2+ (ref. 264) (b) alzarin electron transfer to MV2+ (ref. 271) and (c) zinc porphyrin to fullerene electron transfer and direct electron injection to TiO2 (ref. 272). | ||
In later work, Bignozzi and coworkers, using a ruthenium based chromophore and a mixed valence acceptor, established no charge separated state was observed on a ZrO2 substrate due to the lack of both direct C to A electron transfer (eqn (34)) and electron injection into the metal oxide (eqn (31)).270 In contrast, on TiO2, a TiO2–C+|A− state was observed whose lifetime (microseconds) was significantly increased (>40 hours) by depositing PMMA as an oxygen exclusion over layer. The authors concluded that the extremely long lifetime demonstrated that TiO2–C|A films could be used as a self-erasable optical memory device with a lifetime controlled by oxygen diffusion through a polymeric protecting layer.
In contrast to the previous systems, Matylitsky et al. used an electrochemically inert Al2O3 substrate to show that intermolecular electron transfer between an excited alizarin chromophore and methyl viologen acceptor occurred in ∼100 fs (eqn (34)).271 On TiO2 (Fig. 24b), electron injection from C* (eqn (31)) was competitive (occurred in 100 fs) with direct charge separation. Interestingly, TA measurements showed no evidence for TiO2(e−) to acceptor electron transfer (eqn (32)) because recombination dynamics of injected electrons were similar for both TiO2–C and TiO2–C|A films.
Most recently, Stranius et al. utilized this direct C* to A electron transfer mechanism to generate a directional electron transfer cascade from a porphyrin chromophore, to a C60 acceptor, and finally to the TiO2 substrate (Fig. 24c).272 The relatively long surface binding functional group on the porphyrin significantly slowed the recombination event (eqn (36)) and increased the charge separated lifetime to upwards of 20 ms. Presumably this type of TiO2–C|A architecture could be used in a DSSC to decrease recombination (increase Voc) while still maintaining a high electron injection yield (high Jsc).
Through the above work, it is clear that anchoring donor/acceptor moieties onto a semiconductor surfaces is a simple but effective means of manipulating/controlling electron transfer events at an interface. This can be achieved by either introducing an additional charge separation mechanism or facilitating an electron transfer cascade that is not present in the chromophore only systems. The mechanism and rate of these processes is dependent on variables including the energy level of the conduction band, ground and excited state potentials of the chromophore, and redox properties of the donor/acceptor. One under mentioned variable in these studies is D/A loadings which will directly influence electron transfer rates between co-deposited species simply by influencing the distance between D/A and C. As mentioned above with co-adsorbents in Section 3.1, the lack of visible absorption features for the D/A molecules inhibits direct quantification on TiO2. However, desorption/quantification of molecules and then correlation of performance with loading ratios as well as orientation information about the C and D/A species will be a necessary next step in establishing design principles to fully utilize co-deposited donor/acceptor species for applications in membrane design, energy storage, optical memories and photovoltaics.
There are two common approaches for generating porphyrin–fullerene assemblies on metal oxides: (1) pre-assembled structures that are then deposited on a surface, or (2) in situ supramolecular assembly on the surface (Fig. 25).
The first method offers direct control over the C and A/D distances and has been achieved using dendrimers,280–283 peptides oligomers,284,285 dyads,286,287 and polymers.288 The latter method does not require pre-assembly, but instead dissolves both molecular species in solution, and through non-covalent intramolecular interactions, supramolecular assemblies are formed/deposited directly on the surface.289–295
For the most part DSBHJSCs composed of C–A assemblies generate more photocurrent than the sum of devices made with C and A only.284,289,292,296,297 Photocurrent enhancements are attributed to facile charge separation, that is photoinduced electron transfer occurs from the singlet excited state of porphyrin (−0.7 to −1.0 V) to C60 (−0.4 to −0.2 V) which typically occurs within less than 2 ps.297 However, it is difficult to deconvolute other contributing factors such as regeneration/recombination events and additional absorption and photocurrent generation by the fullerene acceptor molecule.280,296
In contrast, Ooyama et al. recently demonstrated that porphyrin dimer–C60 supramolecular assemblies (Fig. 26) can also inhibit device performance.298 In this example, the incorporation of C60 to surface-bound porphyrin dimers (H4–C4–CDPpy(TEO) and H4–Ptz–CPDPy(TEO)) significantly reduced device performance because generation of the charge separated H4–C4–CDPpy(TEO)+–C60− and Ptz–CPDpy(TEO)+–C60− states, and subsequent recombination, were competitive with direct injection from the porphyrin which significantly decreased the Jsc.
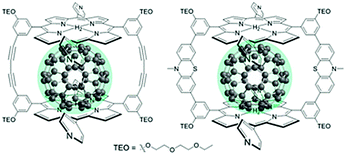 | ||
| Fig. 26 Structure of the Ooyama system (left: H4-C4-CDPpy(TEO), right: H4-Ptz-CPDPy(TEO)). Reprinted from ref. 298 with permission from the Royal Society of Chemistry. | ||
Regardless of specific C and D/A, these supramolecular assemblies share many of the same drawbacks including poor intercalation of large assemblies into pores of the nanocrystalline electrodes299 and limited control over directionality of electron transfer,300 both of which can hinder device performance.
A relatively new, alternative supramolecular strategy, briefly discussed in Section 2.2 and seen again in Sections 4.2 and 5, is to generate self-assembled multilayers via metal ion linkages.115 In contrast to the strategies above, this step-wise assembly procedure generates supramolecular structures from the metal oxide-up in a layer-by-layer fashion. Therefore, it is not limited by diffusion into the pores and the order of molecular deposition can be used to directionally control electron transfer.
Thomas J. Meyer and coworkers recently used this strategy to generate self-assembled trilayers of A–C–D or D–C–A on nanocrystalline indium tin oxide (ITO) electrodes using Zr4+ linking ions (Fig. 27).301 The films effectively behave as molecular analogues of semiconductor p/n junctions where, following excitation of C, a A−–C–D+ or D+–C–A− charge separated state is observed presumably via a stepwise C* to A and D to C+ electron transfer pathway. Under an applied potential of 0 V vs. Ag/AgCl, the films exhibited remarkably slow recombination times of 5.6 s and 26 ms for ITO–D+–C–A− and ITO–A−–C–D+ respectively.
 | ||
| Fig. 27 Layer-by-layer molecular p/n junction assemblies on mesoporous nanoITO electrodes. Reprinted with permission from ref. 301. Copyright 2016 Nature Publishing Group. | ||
In a follow-up to this work Shan et al. generated a D–C bilayer on nanocrystalline NiO for use as photocathodes in DSSCs.302 Upon excitation of the chromophore (NiO–D–C*), the films exhibited vectorial electron transfer away from the surface in a stepwise manner by first generating NiO–D+–C− and then NiO+–D–C− in 15% yield under open circuit conditions. The lifetime of the charge separated state was on the tens of millisecond time scale, several orders of magnitude longer than for C directly on the NiO surface.
More recently, Lim et al. demonstrated a chromophore–donor assembly at TiO2, interface via axial coordination of aluminum–porphyrin with bis(p-anisole)-aminopyridine donor (Fig. 28).303 Electron injection into TiO2 from the surface bound C* followed by electron transfer from D to C+ took place in 0.7 ps and 56 ps, respectively. Interestingly, electron injection is 1 ps faster with the TiO2–C–D assembly compared to reference TiO2–C without the donor.
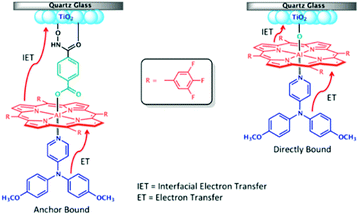 | ||
| Fig. 28 Electron transfer events of TiO2 surface bound aluminum porphyrin axial coordinated to anisolamonipyridine electron donor. Reprinted with permission from ref. 303. Copyright 2017 American Chemical Society. | ||
3.3 Reduced sensitizer injection
In addition to facilitating the formation of long lived charge separated states, co-deposition of chromophores and D/A can result in alternative electron transfer and photocurrent generation mechanisms. One example is reduced sensitizer injection, also known as supersensitization. In a standard dye-sensitized device, photoexcitation is followed by electron injection into the metal oxide and then reduction of subsequently oxidized dye by a donor species (eqn (15)–(17)). In contrast, during supersensitization, the photoexcited dye is first reduced by a donor species, then the reduced dye transfers an electron to the metal oxide (eqn (37) and (38)). Supersensitization increases the theoretical efficiency from 33% to 66% if the electron–hole pair is converted to electric power prior to band edge thermalization.304,305 Spectroscopically these mechanisms can be differentiated by observing the dye cation and anion for excited state and reduced sensitizer injection, respectively.| MO–C|D → MO–C*|D | (37) |
| MO–C*|D → MO–C−|D+ | (38) |
| MO–C−|D+ → MO(e−)–C|D+ | (39) |
| MO(e−)–C|D+ → MO–C|D | (40) |
| MO–C−|D+ → MO–C|D | (41) |
Because the photocurrent generation step, i.e. electron transfer to the metal oxide, is a dark event in reduced sensitizer injection, devices operating by this mechanism are sometimes referred to as a photogalvanic cell, dye-sensitized photogalvanic regenerative solar cell, and/or a photo-galvanic dye-sensitized solar cell (P-DSSC).27 A notable advantage of reduced sensitizer injection is that since the oxidized form of the dye is never generated, oxidatively unstable dyes can still be used. Additionally, the reduced sensitizer typically has more than 200 mV higher potential/driving force for electron transfer to the metal oxide than the excited state dye, thus the name supersensitization. Despite these and other potential advantages, research into supersensitization is somewhat limited compared to standard DSSCs.
While there may be a few earlier examples alluding to a supersenstization mechanism,306 arguably the first definitive demonstration was reported by Nasielski-Hinkens and coworkers in 1985.307 The excited state of the sensitizer molecule, Ru(TAP)3 (TAP = 1,4,5,8-tetraazaphenanthrene) has insufficient driving force for electron injection into the CB of SnO2. However, in the presence of hydroquinone (HQ) donor molecules the dye emission is completely quenched and a photocurrent of 0.3 μA was measured. Stern–Volmer quenching studies suggest that HQ can reduce the excited state of the Ru(TAP)3 with the resulting anion having >600 mV more driving force for electron injection, leading them to attribute the photocurrent to a supersensitization mechanism.
In a system composed of Ru(deeb)(bpy)22+ (deeb = 4,4′-(CO2C2H5)2-2,2′-bipyridine) and phenothiazine (PTZ) as the donor species, Gerald J. Meyer were the first to use TA measurements to monitor reduced sensitizer injection (Fig. 29).308 For solution mixtures, TA measurements clearly demonstrated the reduced dye, Ru(deeb)(bpy)21+, and PTZ cation were quickly generated via reductive quenching. On TiO2, despite the dye lacking the excited state potential to inject into the conduction band (without the addition of Li+ ions),309 the formation of the charge separated PTZ+ and TiO2(e−) state was attributed to reduced sensitizer injection. It is important to note that for the surface bound measurements, no feature of Ru(deppb)(bpy)21+ was directly observed, which was credited to fast (<8 ns) electron transfer from the reduced dye to TiO2.
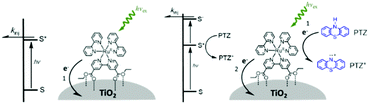 | ||
| Fig. 29 Ru(deep)(bpy)2 direct photoinduced electron injection (left) and with PTZ reduced sensitizer injection mechanism (right). Adapted with permission from ref. 308. Copyright 1999 American Chemical Society. | ||
In a follow up to this work, Ru(deeb)(bpy)22+ and other sensitizers were incorporated into a P-DSSC with TiO2 as the substrate.310 Interestingly, despite >99% excited state quenching of the dyes by PTZ, there is only <5% electron injection efficiency from the reduced dye and minimal photocurrent was observed. One of the rationalizations given for the low injection yield was that the CB of TiO2 (−1.0 V vs. SCE) is not energetically accessible for reduced states of the dye. Presumably, to remedy this shortcoming, devices were then prepared using SnO2 whose conduction band energies are ∼0.5 V lower in energy (i.e. more positive) than TiO2.311 However, the excited state potential of these dyes were sufficient to directly transfer electrons into SnO2 and thus no supersensitization was reported.
Iodide, one of the components of the common I−/I3− based DSSC redox mediator, is also an effective reducing agent for excited chromophores. For example, in 2000 Kamat et al. demonstrated that under an applied bias of 0.15 V vs. Ag/AgCl, C60 clusters deposited on SnO2 with an I−/I3− mediator electrolyte generated photocurrents of up to 0.2 mA cm−2.312 Since the excited state of C60 has insufficient potential to directly inject electrons into SnO2, they attribute the photocurrent generation to electron injection from reduced C60.
Gerald J. Meyer and coworkers observed excited state quenching of Ru(deeb)(bpy)22+* by I− which was tentatively attributed to reductive quenching313 after the formation of π adducts between the dye and iodide ([Ru(deeb)(bpy)2, I]+).314 The reduced sensitizer, Ru(deeb)(bpy)2+, did not inject electrons into TiO2 but rather decayed through a slow recombination with I3−.
Grätzel and coworkers have also observed the reduction of excited state dye by I−.315 Using TA spectroscopy they concluded that approximately 25% of the Ru(2,2′-bipyridyl-4,4′-dicarboxylato)(4,4′-di-nonyl-2′-bipyridyl)(NCS)2 (Z-907) excited states were reductively quenched at high I− concentration. The decay of the Z-907 anion occurred on the millisecond time scale via recombination with I3− but it was unclear why the reduced dye did not inject electrons into TiO2.
A more recent example of supersensitization was reported by Youngblood and coworkers with fullerene and naphthacenequinone sensitizers on TiO2 with solid-state spiro-MeOTAD or I−/I3− in solution as the donors/redox mediators, respectively.316 For a mixture of dye and spiro-MeOTAD, the reduced dye is generated <1 ps after excitation and then recombines on a nanosecond time scale. Upon addition of TiO2, the dye anion decayed significantly faster than the spiro-MeOTAD cation, due to electron transfer from the fullerene anion to TiO2. The close proximity and fast sensitizer reduction in the spiro-MeOTAD device were given as the reason for higher photocurrents than the I−/I3− based device, though the overall performance was still low.
Despite the potential advantages of supersensitization over the traditional excited state electron injection mechanism, an efficient P-DSSC has yet to be demonstrated. From the above reports, it is clear that low injection yields from reduced sensitizers to semiconductors is one of the fundamentally limiting factors responsible for the low photocurrent generation efficiency. Why electron injection yields from the reduced state are so much lower than those from the excited state remains unanswered. Answering this question and subsequently designing new systems with high injection yields will be a crucial step in realizing an efficient P-DSSC.
A majority of studies mentioned in this section involve surface bound dye molecules with donor in solution. However, designing new covalent (Section 3.2.1), co-deposited (Section 3.2.2), or supramolecular (Section 3.2.3) C–D assemblies may be key to realizing efficient supersensitization that is not diffusion limited. At the very least, these assemblies will need to have a C–D pair that can readily undergo reductive electron transfer and a reduced dye with sufficiently negative potentials for electron injection. As an aside, similar oxidative mechanisms could be envisioned for photocathodes composed of dye and acceptor molecules on a p-type semiconductor like NiO but as far as we know that area has been unexplored.
As a final note on this topic, it is important to acknowledge that some currently reported DSSCs could be operating by the supersensitization mechanism, but in the absence of spectroscopic measurements to complement device measurements, the standard electron injection mechanism is assumed.
4. Complementary chromophores
The most commonly published examples of multimolecular assemblies on metal oxide surfaces are those containing two or more chromophores. While these chromophores can be used to quantify cross-surface energy/electron migration (Section 2.3) and other applications (Section 2.2), the primary goal of this effort is to increase broadband light absorption for use in solar energy conversion. In contrast to inorganic crystalline materials, which exhibit broad absorption features (FWHM > 1 eV),317 molecules typically exhibit relatively narrow absorption peaks (FWHM < 0.5 eV). For solar cells containing a single dye molecule, these narrow features, and corresponding absorption gaps, typically result in light transmission losses which leads to decreased photocurrent (lower Jsc) and lower overall device efficiencies.318 In DSSCs, incorporating two or more different chromophores at the metal oxide interface is an increasingly popular and effective strategy to mitigate these losses. The chromophores are typically selected such that the peak of one chromophore fills in the absorption gap of another and vice versa.In terms of interfacial architecture, we have partitioned the multiple chromophore strategies into two primary categories. The first, and by far the most common, is co-deposition of two or more chromophores directly on the metal oxide surface (Section 4.1). The second, is by generating antenna like structures (Section 4.2) where one chromophore is bound to the surface and then, distal to that surface, a second chromophore is attached to the first by either an axial coordination (Section 4.2.1), metal ion linkages (Section 4.2.2), click chemistry (Section 4.2.4), electrostatic interactions (Section 4.2.5), or hydrogen bonding (Section 4.2.6).
4.1 Co-deposition
Co-deposition of complementary chromophores typically entails the chemical linkage of the dye molecule directly to the metal oxide surface, usually via carboxyl (CO2H) or phosphonic acid (PO3H2) functional groups, or to a lesser extent, physisorption. Functionalizing a surface with two or more dyes is readily achieved by either (A) partial loading of one dye followed by soaking in the second dye, (B) a co-loading procedure where the metal oxide film is soaked in a solution containing both dyes, or (C) fully loading of one dye, partial desorption of that dye, followed by soaking in the second dye. Regardless of the loading procedure, the outcome is a distribution of both dye molecules directly bound to the surface as depicted in Fig. 30a.A distinct advantage of co-deposition, as opposed to those described below, is that the chromophores can undergo excitation and electron injection independently of each other. Consequently, the energetic design restrictions remain the same as for a single dye on the surface (i.e. the dye must have sufficient excited state potential for electron injection into the metal oxide and an oxidation potential more positive than the redox mediator for dye regeneration). An additional advantage is that each dye can be synthesized, or purchased, independently with the only rigid structural restriction being that they must contain a surface binding group.
While the co-deposited films do exhibit broadband absorption, one disadvantage is that the absorbance contribution from each chromophore is reduced relative to the fully loaded single sensitizer films, as shown in Fig. 30b. That is, the total dye loading is limited by the available surface area of the metal oxide and, by generating a 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50 co-deposited film of similarly sized dyes, it effectively reduces the absorption contribution of each by half. Absorbance can again be increased by increasing film thickness, but increased thickness can also be a detriment by slowing redox mediator diffusion into the mesoporous films.319 Given that the highest efficiency DSSCs to date utilize co-deposition (vide infra), the advantages of broadband absorption clearly outweigh the absorbance decrease.
50 co-deposited film of similarly sized dyes, it effectively reduces the absorption contribution of each by half. Absorbance can again be increased by increasing film thickness, but increased thickness can also be a detriment by slowing redox mediator diffusion into the mesoporous films.319 Given that the highest efficiency DSSCs to date utilize co-deposition (vide infra), the advantages of broadband absorption clearly outweigh the absorbance decrease.
Over the past two decades, co-deposition of complementary chromophores has significantly increased in popularity.44,50,323–345 The highest efficiency co-deposited DSSCs typically contain a mixture of organic D–π–A dyes,338,346 zinc porphyrins,223,347–350 or ruthenium thiocyanate dyes351–354 with several notable examples depicted in Fig. 31.
The highest efficiency DSSC reported to date, 14.3% PCE published by Kakiage et al. in 2015,346 was achieved by co-depositing ADEKA-1 and LEG4 dyes (Fig. 32). This is a notable accomplishment, not only as the most efficient DSSC to date, but also for being composed of purely organic molecules, with the previous record being 8.14%, using BP-2 and SQ2 dyes.355 Prior to the 14.3% efficient device, the DSSC efficiency record was held by Grätzel and coworkers at 12.3% PCE using a co-deposited film containing a porphyrin dye and an organic dye (YD2-o-C8 and Y123 in Fig. 32b).223 It is notable that efficiencies over 13% were measured at lower light intensities indicating that the device efficiency was limited, in part, by mass transport of the cobalt mediator into the porous metal oxide film. The dye absorption spectral features and device performance metrics for other notable co-deposited DSSCs are summarized in Fig. 31 and Table 3. It is important to note that these are the highest efficiencies reported in literature and are not certified values.
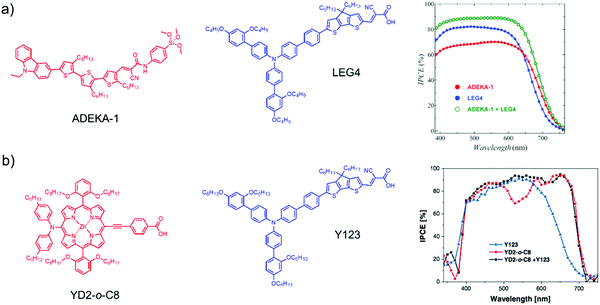 | ||
| Fig. 32 Molecular structure of co-deposited dyes used in the highest efficiency DSSCs (a) ref. 346 adapted with permission from the Royal Society of Chemistry Copyright 2015 and (b) ref. 223. Reprinted with permission from The American Association for the Advancement of Science Copyright 2011. | ||
| Dye | J sc (mA cm−2) | V oc (V) | FF | η (%) | Ref. |
|---|---|---|---|---|---|
| ADEKA-1/LEG4 | 18.27 | 1.014 | 0.77 | 14.3 | 346 |
| Y123 | — | — | — | — | 223 |
| YD-o-C8 | 17.3 | 0.965 | 0.71 | 11.9 | |
| Y123/YD-o-C8 | 17.66 | 0.935 | 0.74 | 12.3 | |
| BD | 20.61 | 0.682 | 0.71 | 10 | 352 |
| D131 | 9.94 | 0.658 | 0.72 | 4.7 | |
| BD/D131 | 23.23 | 0.676 | 0.71 | 11.1 | |
| C1 | 11.21 | 0.780 | 0.65 | 5.7 | 349 |
| XW4 | 16.22 | 0.702 | 0.70 | 7.9 | |
| C1/XW4 | 20.15 | 0.736 | 0.71 | 10.5 | |
| CD4 | 16.52 | 0.734 | 0.74 | 5.8 | 356 |
| YDD6 | 9.66 | 0.671 | 0.72 | 4.7 | |
| YD-o-C8 | 16.6 | 0.758 | 0.71 | 8.8 | |
| CD4/YDD6/YD-o-C8 | 19.28 | 0.753 | 0.72 | 10.4 | |
| LD31 | 20.02 | 0.699 | 0.71 | 9.95 | 348 |
| AN-4 | 8.85 | 0.692 | 0.73 | 4.44 | |
| LD31/AN-4 | 20.27 | 0.704 | 0.72 | 10.3 | |
“we fabricated cells sensitized by [ADEKA-1] and with [carboxy-anchor organic sensitizing dyes which have been reported to have high sensitizing properties] using an electrolyte solution containing an I3/I redox mediator…Among the cells, a significant and the largest improvement in the [IPCE] was observed in the cell photosensitized by [ADEKA-1] with [LEG4].”346
Additionally, often only the best performing cells are reported. As in, only a particular dye and dye loading ratio for the best performing DSSC is published. However, there is likely much insight to be gained through systematic studies on how the dye structure and loading ratios/conditions influence the photophysical and electrochemical properties of the films as well as their performance in devices. Despite the potential importance of these types of studies, the number of reports remains relatively limited.37,347,356–360
In one example, Spitler and coworkers, reported the synthesis and characterization of six different cyanine dye derivatives that were then loaded on TiO2 (Fig. 33).37 Interestingly, time dependent dye loading studies indicate that B1, G6, and R4 initially load as monomers and then form H-aggregates as the surface loading increases. In contrast, G2, G7, and R5, with ethyl substituents on the cyanine core, exhibit the inverse aggregate-to-monomer transition with increased surface loading. Mixtures of these dyes were effective in not only increasing broadband absorption in DSSCs but also in inhibiting dye aggregation resulting in a Jsc increase of 2 mA cm−2 in the mixed B1-G7 DSSC over a comparative N3 control device.
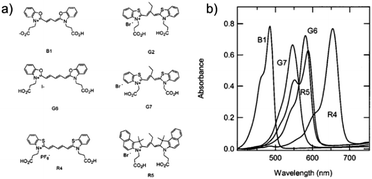 | ||
| Fig. 33 (a) Molecular structure and (b) absorption spectrum of the cyanine dyes used by Splitler and coworkers. Adapted with permission from ref. 37. Copyright 2001 American Chemical Society. | ||
In a similar vein, Delcamp et al. synthesized eight different dyes with structural variation in the π bridges between the squaraine chromophore and the surface anchoring group.359 While a majority of the dyes aggregated at high surface loadings, incorporation of hexyl-substituted cyclopentadithiophene into the bridge disrupted aggregation, and improved device performance was achieved through co-sensitization.
There are several reports where the concentration of porphyrins, squaraines, cyanines, and organic D–π–A dye co-deposited mixtures were systematically varied357,358 and even in one exceptional case, where they studied the influence of dye loading order on device performance.347 The loading ratios can often have a profound impact on the device Jsc and η with a large range of optimum loading ratios from 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1347 to 1
1347 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20356 which is presumably dictated by variables such as the spectral overlap, inhibition of dye aggregation, dye regeneration rates, and others. Unfortunately, while these experiments are useful in maximizing the device performance, the discussion/understanding as to why a particular loading condition is best remains relatively limited.
20356 which is presumably dictated by variables such as the spectral overlap, inhibition of dye aggregation, dye regeneration rates, and others. Unfortunately, while these experiments are useful in maximizing the device performance, the discussion/understanding as to why a particular loading condition is best remains relatively limited.
For example, most manuscripts only report the loading solution concentrations, with few papers352,356 quantifying the amount of each dye absorbed on the surface. Unfortunately, the loading solution concentrations do not provide any information for the actual ratio of chromophores on the surface or their distribution across the surface (i.e. islands vs. homogenous).
A second under reported/studied phenomena is energy and electron transfer events between co-deposited dyes. There are several examples where a dye has insufficient excited state potential to quickly or efficiently inject an electron into TiO2 but can transfer that excited state energy to a second dye that has much higher injection yields.361–363 There are other examples where, after electron injection, the oxidative equivalent is transferred between two different dyes prior to regeneration by the mediator.364 In at least one system, by Hardin, et al., with the appropriate energetics, both intermolecular energy and electron transfer are observed, Fig. 34.365 Computational studies have been applied to co-deposited systems that help to predict energy transfer rates for specific molecular pairs and dyads, which could drive research into these phenomena forward with the benefit of increased charge injection.161,362
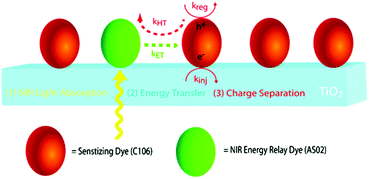 | ||
| Fig. 34 NIR dye attached to a TiO2 surface absorbs NIR photons and uses short-range energy transfer to a sensitizing dye, which is responsible for electron transfer into the TiO2 and hole regeneration with the electrolyte (kreg). Reprinted with permission from ref. 365. Copyright 2011 American Chemical Society. | ||
Given that these events can either improve or hinder device performance, it is clear that steady-state emission, time-resolved emission, and TA measurements could be used to provide fundamental insights into these events and help researchers understand how they influence and can be used to control device performance metrics.
Finally, it is well known that the orientation of dyes relative to the surface can have a profound influence on electron injection yields.366 Similarly, the aggregation and energy/electron transfer events described above are strongly dependent on the orientation of the dyes relative to the surface and to each other. Currently, presumably due to the complexity of the system, there is minimal direct structural information about multiple chromophores at the interface. However, future measurements (NMR, IR, XRD, etc.) or theoretical calculations could be used to correlate the interfacial structure with the rate of these events, and that knowledge could be used to design dyes that exhibit favorable interactions.
4.2 Antenna systems
Molecular antennas are composed of two or more chromophores that are linked via covalent bonds, metal ion coordination, electrostatics, hydrogen bonding, or other interactions.367 These antenna structures have been studied in solution,368 membranes,369 and other motifs but given the topic of this review, we will exclusively focus on chromophore antenna systems on nanocrystalline metal oxide films. This typically entails one chromophore bound to the metal oxide via surface binding groups and then, through various types of interaction, two or more chromophores are linked to the surface bound chromophore.Similar to the co-deposited films from Section 4.1, the primary goal of these assemblies is to increase broadband absorption using complementary absorption features of each chromophore. However, the antenna systems differ from co-deposition in two distinct ways. The first is that, unlike co-deposited films where the chromophores must share surface area which effectively reduces the absorbance of each chromophore by half for a 1 to 1 loaded film, the antenna systems are generated by extending chromophore networks distal from the surface so the absorbance of each type of dye is cumulative. Secondly, in the context of DSSCs, because the antenna molecules are not directly bound to the surface, they must rely on either an energy or electron transfer cascade towards the surface or long distance electron transfer to generate photocurrent.
Some of the earliest chromophores used in DSSCs could be considered antenna systems composed of trinuclear ruthenium complexes with a surface-bound core and two antenna structures coordinated via cyanide ligands.370–372 These complexes, as well as covalent assemblies (i.e. dimers, dyads, etc.) are not electronically distinct molecular moieties and thus will not be discussed here. Instead, below we will focus on antenna systems generated using axial coordination (Section 4.2.1), metal ion linkages (Section 4.2.2), click chemistry (Section 4.2.3), electrostatic interactions (Section 4.2.4), and hydrogen bonding (Section 4.2.5). A schematic depicting these different antenna strategies are shown in Fig. 35.
 | ||
| Fig. 35 Chromophore antenna systems linked via (a) axial coordination, (b) metal ion linkages, (c) click chemistry, (d) electrostatic interactions, and (e) hydrogen bonding. | ||
Later, Panda et al. took an alternative, stepwise approach of first binding a peryleneimide with a terminal pyridyl group to the TiO2 surface and then linking either a zinc porphyrin376 or zinc phthalocyanine377 to the first layer via axial coordination. The antenna systems outperformed their individual components, with increases in Jsc, Voc, and PCE. Supersensitization (Section 3.3) was proposed as the possible photocurrent generation mechanism but no spectroscopic support was provided.
Self-assembled multilayers are formed using a simple, step-wise soaking procedure. For a bilayer film, a monolayer of the first molecule is bound to a high surface area metal oxide. Metal ions are then coordinated to the terminal CO2H or PO3H2 groups of the first molecular layer. Finally, a different molecular layer is bound to the first through the linking metal ions. This approach has been exploited by Lee et al.116,378 and Haga et al.117,379 to functionalize planar gold and silicon surfaces, but was more recently translated to high surface area metal oxide electrodes by Hanson et al.115 The bilayer films were composed of phosphonate derivatized ruthenium polypyridyl complexes linked by ZrIV ions. By tuning the energetics of each dye, they were able to control the direction of energy/electron transfer to or away from the metal oxide surface. The simple and modular nature of the bilayers were illustrated using phosphonated Ru(bpy)3, carboxylated Ru(bpy)3, N719, and ruthenium water oxidation catalysts.
The bilayer strategy was later used to generate an energy and electron transfer cascade DSSC composed of phosphonate derivatives of 1M (p1M) and N3 (Fig. 36), in which the bilayer increased Jsc and Voc compared to each of the dyes alone.380 The multilayer structure was particularly effective at slowing recombination between the electrons in TiO2 and the redox mediator, presumably due to increased steric hindrance of the bilayer. The self-assembled bilayer or trilayer films have subsequently been used to control electron transfer (Section 3.2.3) and facilitate photon upconversion (Section 2.2.2) on a metal oxide substrate.
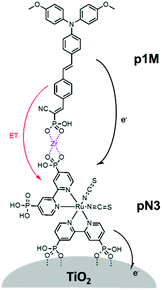 | ||
| Fig. 36 A bilayer assembly composed of pN3 and p1M dyes.380 | ||
The same metal ion coordination chemistry is common in metal organic frameworks (MOFs), and in 2015, within one month of each other, two different strategies emerged for functionalizing nanocrystalline metal oxide substrates with MOFs.381,382
Morris and coworkers used solvothermal reactions to grow a ruthenium polypyridine MOF onto TiO2.382 The MOFs were generated by either (1) heating a mixture of 2,2′-bipyridine-5,5′-dicarboxylic acid, ZrCl4, Ru(bpy)2(2,2′-bipyridine-5,5′-dicarboxylic acid), and a TiO2 film in “one pot”, or (2) growing the 2,2′-bipyridine-5,5′-dicarboxylate-Zr4+ MOF on TiO2 and then incorporating ruthenium via thermal reaction with Ru(bpy)2Cl2. Although the device efficiencies were low (≤0.125%), this work did demonstrate that MOFs can be successfully implemented as an antenna structure in DSSCs (Fig. 37). Time-resolved emission measurements indicate that the triplet excited state can migrate up to 25 nm within the MOF framework, resulting in efficient emission quenching (>90%), presumably due to electron injection into TiO2.
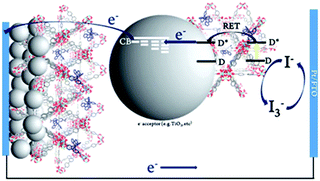 | ||
| Fig. 37 A Ru-MOF sensitized solar cells. Reprinted from ref. 382 with permission from the Royal Society of Chemistry. | ||
Alternatively, Han and coworkers employed the layer-by-layer technique to grow CuII, RuII, and CoII based MOFs.381,383,384 These films were generated by soaking TiO2 films in alternating solutions of metal ions and trimesic, terephthalic, or naphthalenedicarboxylic acids. Powder X-ray diffraction measurements indicate that the MOFs grown via layer-by-layer were structurally the same as those grown by solvothermal methods. One of the key observations of this work was that iodine intercalation or “doping” of the MOFs created cooperative electrical conductivity between the π-electrons from aromatic rings and iodine, shifting the electronic behavior of the MOFs from insulating to conducting. When paired with I−/I3− electrolyte, the Ru-benzene-1,3,5-tricarboxylate MOF gave the best result with a PCE of 1.22% with a 10 layer MOF.384
Click reactions have also been effective at building multi-chromophore antenna structures on planar metal oxide surfaces.390–393 To the best of our knowledge, there is only one example of using click chemistry to directly generate a chromophore antenna structure on nanocrystalline metal oxides. In their report, Unger, Stack, and coworkers first functionalized the TiO2 with a squaraine dye and 4-azidobenzoic acid co-adsorbent.394 The co-adsorbent served two purposes, (1) it prevented H-aggregation of the squaraine dyes (Section 2.1), and (2) it has a terminal azide group that can undergo click chemistry. The co-functionalized TiO2 was then immersed in a solution of copper(I) catalyst and acetylene functionalized organic donor–acceptor dye (Fig. 38b). The two dyes worked cooperatively via efficient (>90%) energy transfer, slowed recombination, and improved overall device performance by 124% relative to a device that did not undergo the click reaction.
Gnichwitz, et al. later used cationic pyridinium dendrimers on ZnO to electrostatically assemble anionic porphyrin molecules on the surface.396 Due to their high energy absorption (<400 nm), the dendrimers had minimal contribution to the photocurrent, and primarily only acted as an assembly scaffold.
D’Souza and coworkers used the complementary absorption features of a surface bound, anionic phthalocyanine, and a cationic porphyrin to generate a panchromatic supramolecular solar cell, Fig. 39.397 After comparing the monolayer and supramolecular assemblies of both the zinc and freebase porphyrin/phthalocyanine, they observed the highest Jsc, Voc, and η with the zinc phthalocyanine/zinc porphyrin assembly, which was attributed to both higher IPCE across a broader wavelength range and slowed recombination at the interface.
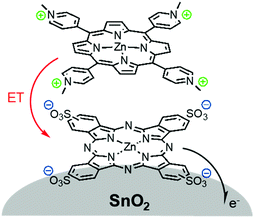 | ||
| Fig. 39 Electrostatically assembled bilayer from D'Souza.397 | ||
In an alternative approach, Kawashima, et al. generated nanoclusters (100–200 nm) composed of anionic C60 and cationic zinc phthalocyanines, which were then electrochemically deposited on the SnO2 surface.398 The IPCE for the clusters was more than 3 times larger than the sum of its parts with measurable photocurrent to nearly 800 nm. The proposed mechanism was charge separation in the cluster followed by electron transfer to the metal oxide, which was indirectly supported by TA measurements of the clusters in suspended solution.
 | ||
| Fig. 40 Hydrogen bonding antenna. Reprinted from ref. 399 with permission from the Royal Society of Chemistry. | ||
This section shows that there are many different non-covalent strategies that can be used to generate antenna structures at metal oxide interfaces. Generally, these assemblies increase the absorption, IPCE, and Jsc compared to the constituent monolayer devices. Additionally, a majority of these films slow recombination dynamics at the MO–dye–mediator interface due to the increased steric hindrance afforded by the supramolecular assembly. While promising, the highest performing DSSCs are still with co-deposited films (Section 4.1) and not assemblies. Given their additive absorption and slowed recombination, there is no reason to believe that an antenna structure with the appropriate dyes and structure could not be as efficient as or better than co-deposited films. However, the energetic and functional group requirements for antenna systems effectively increase the synthetic complexity and the number of steps needed to assemble the film/device. Additional energy and electron transfer events in the assembly introduce new loss pathways, and make it more difficult to characterize the films/mechanism. For example, unlike in the co-deposited films where both dyes are directly adjacent to the surface, the antenna systems require inter-chromophore energy and electron transfer events that are both orientation and distance dependent. Finally, when working with nanocrystalline substrates, there are concerns about the assemblies becoming too large and clogging the pores of the film, which will hinder diffusion of the redox mediators. Regardless of the challenges, there is much left to be learned about the function and assembly of chromophore antennas, not only for application in DSSCs but also in sensors, bio-recognition, catalysis, electroluminescence, and others.
4.3 Device engineering
Up until this point, our discussion has focused on the deposition of two or more molecules in proximity on a metal oxide surface. There are a number of deviations from the standard DSSC architecture that can also be used to effectively harness the complementary absorption features of two dye molecules. For the most part, these strategies can be described as device engineering with a common theme of spatially separating the dye molecules, as schematically summarized in Fig. 41. Spatial separation of dyes offer several advantages over proximity loading. The first is that the dye molecules will not suffer from any possible non-productive intermolecular interactions that can shift absorption spectra, reduce electron injection yields or increase recombination rates. The second is that competitive absorption losses can be mitigated by orienting the high energy absorber first and the low energy absorber second relative to the incident light. Many of these device architectures were reviewed in 2013 by Balasingam et al. and will only be briefly mentioned and updated here.400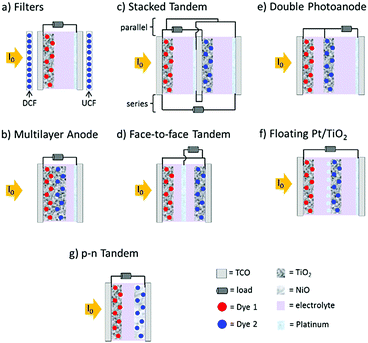 | ||
| Fig. 41 Schematic representation of multiple chromophore containing DSSCs (DCF = down-conversion filter, UCF = up-conversion filter). | ||
The simplest device modification is to incorporate upconversion260,401 or down conversion402,403 filters in front and/or behind the DSSC, respectively (Fig. 41a). These filters are used to hypso- or bathochromically shift the incident light for improved spectral overlap with the absorption of the dye molecule on the metal oxide surface. As opposed to the antenna strategies mentioned in Section 4.2, which rely on non-emissive Dexter or Förster energy transfer, these filters require absorption and then emission from the filter towards the photoactive component of the solar cell. Given that the emission is isotropic, additional design components like reflectors or wave guides are required to efficiently harness the up/down converted light.404
Multilayer anodes are composed of metal oxides, typically TiO2, functionalized with two or more distinct layers of dye molecules as depicted in Fig. 41b. Despite being deposited on the same metal oxide film, the contact between dye one and two only occurs at the interface between the two layers, effectively limiting any possible non-productive interactions. These films have been prepared using several different strategies. One is to utilize slow diffusion rates of a loading/desorption solution to preferentially adsorb/desorb dye on the top of the metal oxide film. The films are then soaked in a second dye to load the remaining surface area.329,354,405–408 Alternative strategies involve pressing,335,409–412 cold spray depositing,413 doctorblading,414,415 or electrophoretic depositing416 a second layer of TiO2 (or Al2O3)417,418 on a TiO2 layer that that is functionalized with dye 1. The second layer is then loaded with dye 2. IPCE measurements of these multilayer devices indicate that photocurrent is generated from both of the dye layers and, when corrected for filter effects, the Jsc is approximately the sum of each layers of the device. The photocurrent is highly sensitive to the thickness of each photoactive layer, as well as the total thickness of the anode.
An alternative multi-chromophore strategy is to incorporate two anodes, sensitized with two different dyes, into a device (Fig. 41c–f). The stacked tandem architecture (Fig. 41c), first introduced by Dürr et al. in 2004,419 is effectively two adjacent DSSCs with two separate electrolyte compartments having a shared transparent substrate. The two DSSCs can be connected in series420–423 or parallel.424 There are also several designs that utilize a single electrolyte compartment, but with the anodes arranged in a face-to-face architecture wired in parallel (Fig. 41d), as well as with a permeable TiO2 (Fig. 41e)425 or TiO2/Pt floating anode (Fig. 41f) wired in parallel and series respectively.426,427 All of these devices are designed such that the incident irradiation is first absorbed by the higher energy dye/anode and the lower energy light is transmitted to the second low energy absorber. As noted above, these multiple anode devices can be connected in either a parallel or series circuit. With the parallel wiring, the Jsc is the sum of the current densities from each component but the Voc is dictated by the lower voltage component. Alternatively for the cells connected in series, the Voc is the sum of the voltages from each anode but current matching of each individual cell is necessary to minimize power losses.421
An alternative tandem strategy, first introduced by Lindquist and coworkers,428 is to replace the photo-passive platinum cathode of a standard DSSC with a photoactive cathode typically composed of a molecular dye on a p-type semiconductor electrode like NiO (Fig. 41g).429 The electrodes are connected in series so the voltage is approximately the sum of the two single electrode devices, but the photocurrent is dominated by the weaker performing electrode. The overall device efficiency was low (0.39%), but this was a crucial proof of concept for a new class of p–n tandem DSSCs. Since the initial report, the device performance has been improved by modifying the dye, the metal oxide electrodes, and electrolyte.430–434 The current record efficiency for a p–n tandem DSSC is held by Bach and coworkers at 1.91%.435 This performance is well below anode-only DSSCs, but there are many opportunities for improvements particularly by slowing down the non-productive recombination processes at the dye–metal oxide interface in the photocathode.429
Regardless of the device architecture shown in Fig. 41, the absorption, charge separation and regeneration events are dictated by the dye–semiconductor interface. As outlined above, there is considerable effort to improve the efficiency of these events using multimolecular interactions on the metal oxide surface. These molecular interactions are often tested in a standard DSSC architecture, but can readily be incorporated into a majority of the device described in Fig. 41. Therefore, our understanding of multimolecular interactions at the interface can be utilized in conjunction with new cell architectures to further increase device performance.
5. Supramolecular interactions
Until this point we have discussed chromophores interacting with themselves (Section 2), donors, acceptors, or insulating co-adsorbents (Section 3), or other chromophores (Section 4) on a nanocrystalline metal oxide substrate. The final category of multimolecular assemblies is comprised of photo- and electro-inactive molecules that are involved in adhering chromophores to the interface. Despite the “inert” nature of these molecules, they can effectively (1) prevent aggregation, (2) slow BET and recombination dynamics, (3) increase photochemical stability, and/or (4) provide a means of adsorbing non-surface binding molecules to the metal oxide surface. These assemblies have been further partitioned into host–guest interactions (Section 5.1), metal–ligand axial coordination (Section 5.2), and self-assembled multilayers (Section 5.3) as depicted in Fig. 42.5.1 Host–guest interactions
Supramolecular host–guest type interactions between molecules in solution have been studied for more than 50 years436,437 with considerable interest in their use as artificial receptor sites and/or drug delivery scaffolds.438 More recently, host–guest interaction has emerged as a strategy to manipulate the surface binding and electron transfer dynamics of dyes on semiconducting interfaces. Work in this area prior to 2011 has been summarized in a perspective by Freitag and Galoppini,439 and thus will only briefly be described here with additional updated references.In these MO–host–guest systems, the host molecules are typically composed of macrocyclic organic molecules with a hydrophobic porous interior and a hydrophilic exterior. Example host structures cyclodextrin (CD), cucur[7]bituril (CB[7]) and octa acid are shown in Fig. 43.
 | ||
| Fig. 43 Structures of host molecules used for host–guest assemblies on nanocrystalline metal oxide films. Reprinted from ref. 439 with permission from the Royal Chemical Society. | ||
On metal oxide surfaces, the guest is typically a dye molecule, electron donor/acceptor with an aromatic core, or ligand that is small enough to insert into the host. These host–guest assemblies on the interface can either be formed in solution and then deposited onto a metal oxide substrate, or the host bound to the surface and then the guest molecule is added.
In 2003, Piotrowiak and coworkers published one of the first examples of a host–guest assembly on TiO2 nanoparticles which was composed of a hemicarceplex host and an azulene dye as the guest.440 This host–guest complex was first generated in solution and then bound to the metal oxide substrate. For both azulene directly bound to the surface and in the assembly (Fig. 44), the quenched emission from azulene was attributed to fast and efficient excited state electron transfer from the dye to the metal oxide substrate. Due to the increased spatial separation between the dye and TiO2, recombination of the charge separated state was three orders of magnitude slower in the host–guest assembly.439,441
 | ||
| Fig. 44 (a) Azulene host–guest assembly and (b) carboxylated azulene on nanocrystalline TiO2. Reprinted from ref. 440 with permission from The Royal Society of Chemistry. | ||
At approximately the same time, Haque et al. were the first to use cyclodextrin, an oligosaccharide derived from starch, as a host for an azobenzene based dye on TiO2 (Fig. 45).442 The host–guest assembly was first synthesized in solution by mixing α-cyclodextrin with diaminoazobenzene in aqueous solution, followed by capping the ends of the guest molecule with relatively large dimethylnaphthylamine groups, sterically inhibiting any reversible release of the dye. For the dye molecule only, there was nominal loading on TiO2. In contrast, monolayer surface coverage was achieved for the host–guest complex, which was attributed to hydrophilic interactions between the TiO2 surface and the OH groups of cyclodextrin, or presumably hydrogen bonding, that is absent in the dye alone. The slowed electron recombination dynamics in the host–guest assembly was due to spatial separation between the dye cation and TiO2 surface.
 | ||
| Fig. 45 Cyclodextrin–azobenzene host–guest assembly. Reprinted from ref. 442 with permission from Wiley-VCH. | ||
Choi et al. used the alternative approach of first depositing cyclodextrin (CD) on a TiO2 surface and then soaking the CD functionalized TiO2 in an organic D–π–A dye (JK-2).443 The surface loading of JK-2 was higher with β-CD (9.78 × 10−8 mol mg−1) than with αCD (7.98 × 10−8 mol mg−1) or γCD (6.97 × 10−8 mol mg−1), whose inner ring diameters are 6.0 Å, 4.7 Å, and 7.5 Å, respectively, but all of which exhibited lower loadings than JK-2 (2.04 × 10−7 mol mg−1) in the absence of CD. Despite the lower loading, DSSCs composed of βCD-(JK-2) assemblies exhibited higher Jsc, Voc, and PCE than the JK-2 only or the JK-2 + DCA co-deposited films. The improved performance was attributed to slowed recombination and increased electron lifetimes in TiO2 for the host–guest film.
Similar efforts using carboxymethyl-β-CD (CMBCD) functionalized TiO2 have been effective in adhering ruthenium(II)444 and iron(II)445 polypyridyl complexes to TiO2. In contrast to CD, CMBCD has surface binding carboxylate groups that presumably increase surface loading and stability of the host molecule. DSSCs using the ruthenium–CMBCD films had increased Voc and, in spite of 9.5 times lower surface coverage, it had comparable Jsc to the dye only devices. Unfortunately, overall device efficiencies were low (<0.3%) due to the low redox potential of their dye (0.48 V vs. SHE) which likely slows regeneration and may increase BET rates.
Using an alternative host with carboxylate groups, Porel et al. demonstrated that coumarin dyes (e.g. C-153, C-480, and C-1) in octa acid hosts can also be used to adhere dyes to the interface.446 The host–guest complexes were first prepared in solution as demonstrated by DOSY NMR experiments. Emission spectra from the assembly on ZrO2 were similar to that observed in solution which suggested that the C-153 molecules were encapsulated and shielded from the local environment in both cases. On TiO2, the assembly was still effective in facilitating excited state electron transfer from the dye to the substrate.
Galoppini and Freitag have demonstrated that host–guest interactions are also an effective means of generating electrochemical cells that are promising for application as electrochromic windows.447 In their films, cucur[7]bituril (CB[7]) and methyl viologen (MV2+) or methyl tolyl viologen (MTV2+) were selected as the host and guest molecules, respectively (Fig. 46a).
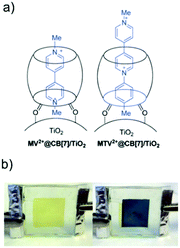 | ||
| Fig. 46 (a) MV2+–CB[7] and MTV2+–CB[7] on TiO2. (Reprinted with permission from ref. 447 Copyright 2010 American Chemical Society) and (b) the electrochromic response of MTV2+–CB[7] on TiO2/FTO before (left) and after (right) an applied bias of −0.8 V vs. SCE (reprinted from ref. 450 with permission from The Royal Society of Chemistry). | ||
There are a few reports of binding carboxylated methylviologen molecules directly to the TiO2 surface448,449 but, as noted by the authors, using the CB[7] host molecule has two distinct advantages: (1) MV2+ and MTV2+ can be adhered to the metal oxide in spite of the lack of surface binding groups, and (2) the host prevents degradation and dimerization of the reduced species.450 When used as an anode in an electrochemical cell under an applied bias of −0.8 V vs. NHE, a strong broad absorption feature with a peak at 600 nm appeared, and was accompanied by a distinctive, yellow to purple, reversible color change as shown in Fig. 46b. Since the applied potential is sufficiently negative, the mechanism is presumably reduction of the TiO2 followed by reduction of MTV2+ at the dye–metal oxide interface, and not via cross surface electron transfer as described in Section 2.2. The color change was reversible for at least 20 switching cycles with minimal degradation.
The final example of a guest–host interaction to be described here was recently reported by Sun and coworkers.451 In their system, a phosphonated ruthenium chromophore covalently lined to a βCD unit was first bound to TiO2. Then upon soaking this film in a ruthenium based catalyst solution, the host–guest assembly was generated by insertion of the phenylpyridine ligand of the catalyst into the cyclodextrin cavity, as depicted in Fig. 47. Based on electrochemical measurements, the ratio of the host chromophore and the guest catalyst was estimated to be around 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. Under a small applied bias, the assemblies were shown to be effective for light driven water oxidation catalysis, albeit at low efficiencies due to competitive recombination. While this example is technically a chromophore–catalyst assembly, which in the introduction we mentioned we would omit from this review, we have included it here because this type of chromophore–host–molecule motif may offer new opportunities in generating chromophore–chromophore and chromophore–D/A type structures.
1. Under a small applied bias, the assemblies were shown to be effective for light driven water oxidation catalysis, albeit at low efficiencies due to competitive recombination. While this example is technically a chromophore–catalyst assembly, which in the introduction we mentioned we would omit from this review, we have included it here because this type of chromophore–host–molecule motif may offer new opportunities in generating chromophore–chromophore and chromophore–D/A type structures.
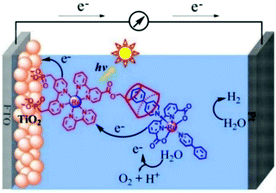 | ||
| Fig. 47 A DSPEC composed of a chromophore–catalyst, host–guest assembly. Reprinted from ref. 451 with permission. Copyright 2016 Wiley-VCH. | ||
5.2 Metal–ligand axial coordination
Metal–ligand axial coordination was briefly mentioned in Section 4.2.1 as a strategy for combining multiple chromophores. This versatile assembly motif is much more commonly used for attaching chromophores to metal oxide surfaces. The most obvious advantage of having a separate axial binding motif as the surface attachment unit is in the simplification of synthesis of the chromophore, but it can also help prevent aggregation. Multi-chromophoric arrays can be constructed in a stepwise, controlled manner, and the orientation of the chromophore relative to the surface can be modulated. Examples of two of the most common strategies for using axial coordination to adhere chromophores to a surface are depicted in Fig. 48. | ||
| Fig. 48 General depiction of (a) chromophore–metal–ligand and (b) metal–ligand axial coordination on metal oxide substrates. | ||
The first involves an anchor–metal–chromophore type of architecture (Fig. 48a) that is generated by binding the nitrogen containing heterocyclic ligand to the metal oxide substrate, followed by treatments with a metal ion and then the chromophore.452–455 The alternative, and more common strategy, is the anchor–chromophore type architecture that is typically generated by dipping a bare metal oxide film in a solution of the axial ligand and then in a solution of the metalloporphyrin or phthalocyanine dye (Fig. 48b).456–460 While a thorough study using the same chromophore but comparing the two aforesaid binding modes is not available, spectroscopic and DSSC data suggest that the anchor–chromophore exhibits better performance than the anchor–metal–chromophore motif presumably due to reduced electronic coupling and slowed electron injection dynamics in the latter.455
In 2009, Brumbach et al. were the first to demonstrate axial ligand coordination of a dye to nanocrystalline TiO2 surfaces.456 For bare or benzoic acid functionalized TiO2, they observed minimal zinc or ruthenium porphyrin dye loading. In contrast, with carboxylated N-heterocycle functionalized TiO2, metallated porphyrin readily adheres to the surface with the amount of surface coverage primarily dictated by the formation constant of axial ligation. The peak splitting of the metal porphyrin Soret band, as well as the lack of nonmetallated porphyrin loading, support an axial–metal binding architecture. Interestingly, with the surface binding motif, phosphonic acid or carboxylic acid, had minimal influence on the dye loading. Axial binding motif was also used to generate mixed chromophore films that exhibited 1.4 times higher efficiencies in DSSCs than individual sensitizers alone.
At about the same time, D’Souza and coworkers employed axial coordination to construct dye–TiO2 electrodes, but with a series of imidazole and pyridine based amines with different basicities as the axial linker.457 As compared to linkers 1–3, higher photocurrents and photovoltages were obtained from DSSCs composed of linker 4 based anodes. The photovoltaic performance using the different linkers follows their metal–ligand binding constants with the dye. The highest device performance (Voc = 0.67 V, Jsc = 1.6 mA cm−2, η = 0.56%) was achieved with the zinc porphyrin–ferrocene dyad 8 and linker 4. The higher performance of 8 was attributed to electron transfer from the ferrocene donor to the oxidized porphyrin, effectively slowing recombination dynamics as described in Section 3.2.1. Electron injection times between 560 and 700 fs indicate there is relatively good electronic coupling between the dye and TiO2 surface.458
D'Souza and coworkers later expanded this axial coordination methodology to zinc porphyrin–oxoporphyrinogen459 (Fig. 49a) and zinc porphyrin–zinc phthalocyanine dyads (ZnP–ZnPc; Fig. 49b).460 For the later system, the higher binding affinity of the imidazole linker to ZnP, was supported using competitive binding/displacement studies of ZnP and ZnPc monomers. The energy and electron transfer dynamics in these chromophore dyad systems were then studied using time-resolved emission/absorption techniques.
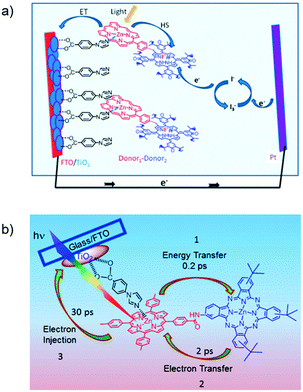 | ||
| Fig. 49 Axial-metal coordinated (a) zinc porphyrin–oxoporphyrinogen (reprinted from ref. 459 by permission of The Royal Society of Chemistry), and (b) zinc porphyrin–zinc phthalocyanine dyads on TiO2. (Reprinted from ref. 460 with permission. Copyright 2012 American Chemical Society.) | ||
Crabtree, Schmuttenmaer, and coworkers did a systematic study varying the anchoring group (carboxylic acid, phosphonic acid, acetylacetone and hydroxamic acid) of the axially ligating pyridine molecule.461 Interestingly, a higher binding constant was obtained with more basic guest molecules such as phenylimidazole compared to pyridine. Minimal dye desorption was observed for any of the linkers, even after soaking in water for several days, which was attributed to the hydrophobicity of the porphyrin dye.
While electron injection rates could not be resolved with transient THz spectroscopy, electron injection efficiencies with carboxylate and hydroxamate linkers were found to be higher than with phosphonate or acetylacetonate linkers. The efficiency of electron injection was later found to correlate with the calculated single molecule conductance of the linkers.462
5.3 Self-assembled multilayers
Self-assembled multilayers via metal ion linkages have already been introduced in Sections 2.2 and 4.2.2 as a means of facilitating triplet–triplet annihilation and generating chromophore–chromophore assemblies, respectively. This strategy is also effective for manipulating electron transfer dynamics at the dye–semiconductor interface.463,464 These films are prepared by stepwise soaking of a metal oxide film in a solution of di-phosphonated bridging molecule, that is photochemically and electrochemically inert under standard conditions, a metal ion, and a carboxylated or phosphonated chromophore as depicted in Fig. 50. Both the nature of the “inert” molecule and the metal ion play a role in the rate, efficiency and mechanism of electron transfer.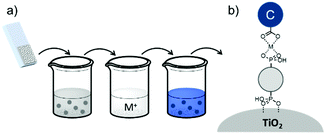 | ||
| Fig. 50 (a) The stepwise loading procedure and (b) a self-assembled bilayer composed of a bridging molecule, metal ion, and chromophore. | ||
In 2015, Wang et al. reported the first example of manipulating electron transfer dynamics in a self-assembled bilayer using a bridging molecule.464 The formation of the bilayer architecture on TiO2 and ZrO2 was supported by ATR-IR and UV-vis measurements. By incrementally increasing the number of benzene rings in the bridging molecule from 1,4-phenylenediphosphonic acid to biphenyl-4,4′-diphosphonic acid to terphenyl-4,4′′-dicarboxylic acid, the authors slowed excited state electron transfer from RuC dye to the TiO2 substrate, as demonstrated by time-resolved emission measurements. The relative efficiency of electron transfer events could even be observed visually (Fig. 51). The exponential decrease in both forward and backward electron transfer rates with respect to the length of the bridging molecule was attributed to the bridge and the ZrIV metal linking ion acting as an electron tunneling barrier between the dye and metal oxide. In DSSCs, using N3 as the dye, increasing the bridge length manifests as an increased lifetime and diffusion length for the electrons in TiO2 as well as an increase in open circuit voltage due to the slowed recombination dynamics.463 However, the overall device performance also decreased with bridge length due to the lower electron injection rate/yield and significant decrease in Jsc.
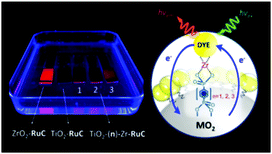 | ||
| Fig. 51 Relative emission quenching in monolayers and self-assembled bilayers on ZrO2 and TiO2. Reprinted with permission from ref. 464. Copyright 2015 American Chemical Society. | ||
While a majority of the self-assembled bilayers are generated using ZrIV and ZnII linking ions, follow up work by the same group demonstrated that that is not always the case. For example, it was shown CuII linking ions significantly quench the excited state of the dye even on ZrO2.465 Despite the near unity quenching of the excited state, electron injection into TiO2 and photocurrent generation did occur in a DSSC suggesting either electron tunneling is competitive with the excited state quenching process or potentially there was a metal ion-mediated hopping mechanism. Copper ions were also shown to slow both back electron transfer and recombination but a mechanism was not reported.
In a follow-up study, investigating a series of metal ions (CdII, CuII, FeII, LaIII, MnII, SnIV, ZrIV and ZnII), excited state quenching and slowed recombination was similarly observed with MnII and FeII.466,467 The nature of the metal ion also had an influence on the photostability of the films with bilayers composed of ZrIV and LaIII ions exhibiting the highest and lowest stability on both TiO2 and ZrO2, respectively. While there is still much to be learned about the role of the bridge and metal ions in these films, it is clear that self-assembled bilayers offer a simple, straightforward, and modular method for manipulating electron transfer dynamics at dye–semiconductor interfaces.
6. Conclusions
Over the past several decades, there has been a sharp rise in interest towards generating multi-molecular assemblies on high surface area metal oxide substrates. The assembly methods are largely based on intermolecular interactions that are well established in solvated systems, but the introduction of a substrate offers new opportunities as well as new challenges for generating, studying, and harnessing these assemblies. Synthetic control of surface binding groups as well as intermolecular interacting moieties of the chromophores, donors/acceptors, and other molecules offers exquisite control over the organic–inorganic interface. A combination of electrochemical as well as steady-state and time-resolved absorption/emission spectroscopic techniques have been crucial in measuring the rate and efficiency of energy and electron transfer events at these assembly–metal oxide interfaces. Key design strategies for improving advantageous while hindering detrimental events in device applications are already emerging.Despite this progress, there is still much to be learned. The compilation of published data indicates a clear need to characterize and report the ratios and surface loadings of the various chromophores, donors/acceptors, and other species in the assemblies. This is particularly challenging for molecules that are photochemically and electrochemically inert under standard measurement conditions, but techniques like NMR and XPS show promise in addressing this shortcoming. Additionally, presumably due to the complexity of the interface and the difficulty of characterizing mesoporous materials, there is a notable lack of structural information about the assemblies at the interface. Theoretical modeling of these many atom systems is increasingly shedding light on the interface, but new developments in experimental characterization techniques for the structure at the interface will have a profound role in establishing structure–property relationships for the assemblies. Regardless of these shortcomings, it is clear that multi-molecular assemblies show great promise for influencing/controlling energy and electron transfer events for a plethora of applications.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This effort was supported in part by the Army Research Office under Grant No. W911NF-14-1-0660 and the National Science Foundation Graduate Research Fellowship under Grant No. DGE-1449440.References
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1965, 43, 679 CrossRef CAS.
- D. L. Dexter, J. Chem. Phys., 1953, 21, 836–850 CrossRef CAS.
- T. Forster, Discuss. Faraday Soc., 1959, 27, 7–17 RSC.
- M. F. Hohmann-Marriott and R. E. Blankenship, Annu. Rev. Plant Biol., 2011, 62, 515–548 CrossRef CAS PubMed.
- H. Miyasaka, Acc. Chem. Res., 2013, 46, 248–257 CrossRef CAS PubMed.
- R. Foster, J. Phys. Chem., 1980, 84, 2135–2141 CrossRef CAS.
- L. Y. Zhu, Y. P. Yi, A. Fonari, N. S. Corbin, V. Coropceanu and J. L. Bredas, J. Phys. Chem. C, 2014, 118, 14150–14156 CAS.
- B. Armitage and D. F. O'Brien, J. Am. Chem. Soc., 1991, 113, 9678–9679 CrossRef CAS.
- K. C. Hwang and D. Mauzerall, Nature, 1993, 361, 138–140 CrossRef CAS PubMed.
- F. D. Lewis, R. L. Letsinger and M. R. Wasielewski, Acc. Chem. Res., 2001, 34, 159–170 CrossRef CAS PubMed.
- E. Galoppini and M. A. Fox, J. Am. Chem. Soc., 1996, 118, 2299–2300 CrossRef CAS.
- M. Tadatsugu, Semicond. Sci. Technol., 2005, 20, S35 CrossRef.
- S. K. Arya, S. Saha, J. E. Ramirez-Vick, V. Gupta, S. Bhansali and S. P. Singh, Anal. Chim. Acta, 2012, 737, 1–21 CrossRef CAS PubMed.
- C.-Y. Hsu, Y.-C. Chen, R. Y.-Y. Lin, K.-C. Ho and J. T. Lin, Phys. Chem. Chem. Phys., 2012, 14, 14099–14109 RSC.
- J. D. Moras, B. Strandberg, D. Suc and K. Wilson, Science, 1996, 271, 933 Search PubMed.
- J. Jasieniak, M. Califano and S. E. Watkins, ACS Nano, 2011, 5, 5888–5902 CrossRef CAS PubMed.
- J. R. Bakke, K. L. Pickrahn, T. P. Brennan and S. F. Bent, Nanoscale, 2011, 3, 3482–3508 RSC.
- M. D. Losego and K. Hanson, Nano Energy, 2013, 2, 1067–1069 CrossRef CAS.
- D. L. Ashford, M. K. Gish, A. K. Vannucci, M. K. Brennaman, J. L. Templeton, J. M. Papanikolas and T. J. Meyer, Chem. Rev., 2015, 115, 13006–13049 CrossRef CAS PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun, L. Kloo and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- J. Albero, P. Atienzar, A. Corma and H. Garcia, Chem. Rec., 2015, 15, 803–828 CrossRef CAS PubMed.
- M. K. Nazeeruddin, R. Humphry-Baker, P. Liska and M. Grätzel, J. Phys. Chem. B, 2003, 107, 8981–8987 CrossRef CAS.
- Z. Zhang, S. M. Zakeeruddin, B. C. O'Regan, R. Humphry-Baker and M. Gratzel, J. Phys. Chem. B, 2005, 109, 21818–21824 CrossRef CAS PubMed.
- V. S. Manthou, E. K. Pefkianakis, P. Falaras and G. C. Vougioukalakis, ChemSusChem, 2015, 8, 588–599 CrossRef CAS PubMed.
- J. A. Christians, J. S. Manser and P. V. Kamat, J. Phys. Chem. Lett., 2015, 6, 852–857 CrossRef CAS PubMed.
- S. Ardo and G. J. Meyer, Chem. Soc. Rev., 2009, 38, 115–164 RSC.
- T. W. Hamann, O. K. Farha and J. T. Hupp, J. Phys. Chem. C, 2008, 112, 19756–19764 CAS.
- F. Fabregat-Santiago, J. Bisquert, E. Palomares, L. Otero, D. Kuang, S. M. Zakeeruddin and M. Grätzel, J. Phys. Chem. C, 2007, 111, 6550–6560 CAS.
- F. Fabregat-Santiago, G. Garcia-Belmonte, I. Mora-Sero and J. Bisquert, Phys. Chem. Chem. Phys., 2011, 13, 9083–9118 RSC.
- F. Fabregat-Santiago, J. Bisquert, G. Garcia-Belmonte, G. Boschloo and A. Hagfeldt, Sol. Energy Mater. Sol. Cells, 2005, 87, 117–131 CrossRef CAS.
- S. G. Yan, J. S. Prieskorn, Y. Kim and J. T. Hupp, J. Phys. Chem. B, 2000, 104, 10871–10877 CrossRef CAS.
- G. B. S. Edward, H. Yonemoto, R. H. Schmeh, S. M. Hubig, B. L. I. R. L. Riley and T. E. Mallouk, J. Am. Chem. Soc., 1994, 116, 4786–4795 CrossRef.
- M. Kasha, H. R. Rawls and M. Ashraf El-Bayoumi, Pure Appl. Chem., 1965, 11, 371 CrossRef CAS.
- N. J. Hestand and F. C. Spano, Acc. Chem. Res., 2017, 50, 341–350 CrossRef CAS PubMed.
- H. Tributsch, Bunsen-Ges. Phys. Chem. Ber., 1969, 73, 582–590 CAS.
- A. Ehret, L. Stuhl and M. T. Spitler, J. Phys. Chem. B, 2001, 105, 9960–9965 CrossRef CAS.
- A. Konno, G. R. A. Kumara, S. Kaneko, B. Onwona-Agyeman and K. Tennakone, Chem. Lett., 2007, 36, 716–717 CrossRef CAS.
- M. V. Martinez-Diaz, G. de la Torre and T. Torres, Chem. Commun., 2010, 46, 7090–7108 RSC.
- K. R. Mulhern, M. R. Detty and D. F. Watson, J. Phys. Chem. C, 2011, 115, 6010–6018 CAS.
- D. Liu and P. V. Kamat, J. Electrochem. Soc., 1995, 142, 835–839 CrossRef CAS.
- T. Maeda, Y. Hamamura, K. Miyanaga, N. Shima, S. Yagi and H. Nakazumi, Org. Lett., 2011, 13, 5994–5997 CrossRef CAS PubMed.
- S. Tatay, S. A. Haque, B. O'Regan, J. R. Durrant, W. J. H. Verhees, J. M. Kroon, A. Vidal-Ferran, P. Gavina and E. Palomares, J. Mater. Chem., 2007, 17, 3037–3044 RSC.
- K. Sayama, S. Tsukagoshi, T. Mori, K. Hara, Y. Ohga, A. Shinpou, Y. Abe, S. Suga and H. Arakawa, Sol. Energy Mater. Sol. Cells, 2003, 80, 47–71 CrossRef CAS.
- A. C. Khazraji, S. Hotchandani, S. Das and P. V. Kamat, J. Phys. Chem. B, 1999, 103, 4693–4700 CrossRef CAS.
- H. Choi, J. K. Lee, K. H. Song, K. Song, S. O. Kang and J. Ko, Tetrahedron, 2007, 63, 1553–1559 CrossRef CAS.
- S. Alex, U. Santhosh and S. Das, J. Photochem. Photobiol., A, 2005, 172, 63–71 CrossRef CAS.
- Z.-S. Wang, Y. Cui, Y. Dan-oh, C. Kasada, A. Shinpo and K. Hara, J. Phys. Chem. C, 2007, 111, 7224–7230 CAS.
- G. Marotta, M. A. Reddy, S. P. Singh, A. Islam, L. Han, F. De Angelis, M. Pastore and M. Chandrasekharam, ACS Appl. Mater. Interfaces, 2013, 5, 9635–9647 CAS.
- M. Guo, P. Diao, Y.-J. Ren, F. Meng, H. Tian and S.-M. Cai, Sol. Energy Mater. Sol. Cells, 2005, 88, 23–35 CrossRef CAS.
- M. Kawasaki and S. Aoyama, Chem. Commun., 2004, 988–989, 10.1039/B400071D.
- Y.-S. Kim, K. Liang, K.-Y. Law and D. G. Whitten, J. Phys. Chem., 1994, 98, 984–988 CrossRef CAS.
- D. Liu, R. W. Fessenden, G. L. Hug and P. V. Kamat, J. Phys. Chem. B, 1997, 101, 2583–2590 CrossRef CAS.
- J. R. Mann, M. K. Gannon, T. C. Fitzgibbons, M. R. Detty and D. F. Watson, J. Phys. Chem. C, 2008, 112, 13057–13061 CAS.
- C. Nasr, D. Liu, S. Hotchandani and P. V. Kamat, J. Phys. Chem., 1996, 100, 11054–11061 CrossRef CAS.
- D. Liu and P. V. Kamat, J. Chem. Phys., 1996, 105, 965–970 CrossRef CAS.
- N. A. Treat, F. J. Knorr and J. L. McHale, J. Phys. Chem. C, 2016, 120, 9122–9131 CAS.
- F. Nüesch, J. E. Moser, V. Shklover and M. Grätzel, J. Am. Chem. Soc., 1996, 118, 5420–5431 CrossRef.
- S. Y. Bang, M. J. Ko, K. Kim, J. H. Kim, I. H. Jang and N. G. Park, Synth. Met., 2012, 162, 1503–1507 CrossRef CAS.
- D. Daphnomili, G. D. Sharma, S. Biswas, K. R. J. Thomas and A. G. Coutsolelos, J. Photochem. Photobiol., A, 2013, 253, 88–96 CrossRef CAS.
- T. Geiger, S. Kuster, J. H. Yum, S. J. Moon, M. K. Nazeeruddin, M. Gratzel and F. Nuesch, Adv. Funct. Mater., 2009, 19, 2720–2727 CrossRef CAS.
- L. Giribabu, V. K. Singh, C. V. Kumar, Y. Soujanya, P. Y. Reddy and M. L. Kantam, Sol. Energy, 2011, 85, 1204–1212 CrossRef CAS.
- J. J. He, G. Benko, F. Korodi, T. Polivka, R. Lomoth, B. Akermark, L. C. Sun, A. Hagfeldt and V. Sundstrom, J. Am. Chem. Soc., 2002, 124, 4922–4932 CrossRef CAS PubMed.
- Z. S. Huang, H. L. Feng, X. F. Zang, Z. Iqbal, H. P. Zeng, D. B. Kuang, L. Y. Wang, H. Meier and D. R. Cao, J. Mater. Chem. A, 2014, 2, 15365–15376 CAS.
- M. Ince, F. Cardinali, J. H. Yum, M. V. Martinez-Diaz, M. K. Nazeeruddin, M. Gratzel and T. Torres, Chem. – Eur. J., 2012, 18, 6343–6348 CrossRef CAS PubMed.
- M. Ishida, S. W. Park, D. Hwang, Y. B. Koo, J. L. Sessler, D. Y. Kim and D. Kim, J. Phys. Chem. C, 2011, 115, 19343–19354 CAS.
- T. Maeda, Y. Hamamura, K. Miyanaga, N. Shima, S. Yagi and H. Nakazumi, Org. Lett., 2011, 13, 5994–5997 CrossRef CAS PubMed.
- M. K. Nazeeruddin, R. Humphry-Baker, M. Gratzel and B. A. Murrer, Chem. Commun., 1998, 719–720, 10.1039/a708834e.
- A. Morandeira, I. Lopez-Duarte, B. O'Regan, M. V. Martinez-Diaz, A. Forneli, E. Palomares, T. Torres and J. R. Durrant, J. Mater. Chem., 2009, 19, 5016–5026 RSC.
- S. Feng, Q.-S. Li, P.-P. Sun, T. A. Niehaus and Z.-S. Li, ACS Appl. Mater. Interfaces, 2015, 7, 22504–22514 CAS.
- E. Palomares, M. V. Martinez-Diaz, S. A. Haque, T. Torres and J. R. Durrant, Chem. Commun., 2004, 2112–2113, 10.1039/B407860H.
- Y. Ooyama, A. Ishii, Y. Kagawa, I. Imae and Y. Harima, New J. Chem., 2007, 31, 2076–2082 RSC.
- J. H. Yum, P. Walter, S. Huber, D. Rentsch, T. Geiger, F. Nuesch, F. De Angelis, M. Gratzel and M. K. Nazeeruddin, J. Am. Chem. Soc., 2007, 129, 10320–10321 CrossRef CAS PubMed.
- J. Shi, J. Chen, Z. Chai, H. Wang, R. Tang, K. Fan, M. Wu, H. Han, J. Qin, T. Peng, Q. Li and Z. Li, J. Mater. Chem., 2012, 22, 18830–18838 RSC.
- H. Choi, C. Baik, S. O. Kang, J. Ko, M.-S. Kang, M. K. Nazeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2008, 47, 327–330 CrossRef CAS PubMed.
- L.-N. Yang, S.-C. Li, Z.-S. Li and Q.-S. Li, RSC Adv., 2015, 5, 25079–25088 RSC.
- K. Sayama, S. Tsukagoshi, K. Hara, Y. Ohga, A. Shinpou, Y. Abe, S. Suga and H. Arakawa, J. Phys. Chem. B, 2002, 106, 1363–1371 CrossRef CAS.
- N. Koumura, Z.-S. Wang, S. Mori, M. Miyashita, E. Suzuki and K. Hara, J. Am. Chem. Soc., 2006, 128, 14256–14257 CrossRef CAS PubMed.
- S. Qu, C. Qin, A. Islam, Y. Wu, W. Zhu, J. Hua, H. Tian and L. Han, Chem. Commun., 2012, 48, 6972–6974 RSC.
- M. Fang, H. Li, Q. Li and Z. Li, RSC Adv., 2016, 6, 40750–40759 RSC.
- Q. Li, J. Shi, H. Li, S. Li, C. Zhong, F. Guo, M. Peng, J. Hua, J. Qin and Z. Li, J. Mater. Chem., 2012, 22, 6689–6696 RSC.
- B. L. Watson, B. D. Sherman, A. L. Moore, T. A. Moore and D. Gust, Phys. Chem. Chem. Phys., 2015, 17, 15788–15796 RSC.
- Z. Ning, Q. Zhang, W. Wu, H. Pei, B. Liu and H. Tian, J. Org. Chem., 2008, 73, 3791–3797 CrossRef CAS PubMed.
- M. Pastore and F. De Angelis, ACS Nano, 2010, 4, 556–562 CrossRef CAS PubMed.
- S. Agrawal, M. Pastore, G. Marotta, M. A. Reddy, M. Chandrasekharam and F. De Angelis, J. Phys. Chem. C, 2013, 117, 9613–9622 CAS.
- T. Etienne, L. Chbibi, C. Michaux, E. A. Perpète, X. Assfeld and A. Monari, Dyes Pigm., 2014, 101, 203–211 CrossRef CAS.
- S. Feng, Q.-S. Li, L.-N. Yang, Z.-Z. Sun, T. A. Niehaus and Z.-S. Li, J. Power Sources, 2015, 273, 282–289 CrossRef CAS.
- L. Zhang and J. M. Cole, ACS Appl. Mater. Interfaces, 2014, 6, 15760–15766 CAS.
- H. Kusama and K. Sayama, J. Phys. Chem. C, 2012, 116, 23906–23914 CAS.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- T. N. Singh-Rachford and F. N. Castellano, Coord. Chem. Rev., 2010, 254, 2560–2573 CrossRef CAS.
- R. Katoh, A. Furube, T. Yoshihara, K. Hara, G. Fujihashi, S. Takano, S. Murata, H. Arakawa and M. Tachiya, J. Phys. Chem. B, 2004, 108, 4818–4822 CrossRef CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- M. B. Smith and J. Michl, Chem. Rev., 2010, 110, 6891–6936 CrossRef CAS PubMed.
- C. E. Swenberg and W. T. Stacy, Chem. Phys. Lett., 1968, 2, 327–328 CrossRef CAS.
- S. Singh, W. J. Jones, W. Siebrand, B. P. Stoicheff and W. G. Schneider, J. Chem. Phys., 1965, 42, 330–342 CrossRef CAS.
- I. Paci, J. C. Johnson, X. Chen, G. Rana, D. Popović, D. E. David, A. J. Nozik, M. A. Ratner and J. Michl, J. Am. Chem. Soc., 2006, 128, 16546–16553 CrossRef CAS PubMed.
- S. T. Roberts, R. E. McAnally, J. N. Mastron, D. H. Webber, M. T. Whited, R. L. Brutchey, M. E. Thompson and S. E. Bradforth, J. Am. Chem. Soc., 2012, 134, 6388–6400 CrossRef CAS PubMed.
- E. A. Margulies, C. E. Miller, Y. Wu, L. Ma, G. C. Schatz, R. M. Young and M. R. Wasielewski, Nat. Chem., 2016, 8, 1120–1125 CrossRef CAS PubMed.
- N. V. Korovina, S. Das, Z. Nett, X. Feng, J. Joy, R. Haiges, A. I. Krylov, S. E. Bradforth and M. E. Thompson, J. Am. Chem. Soc., 2016, 138, 617–627 CrossRef CAS PubMed.
- J. Zirzlmeier, D. Lehnherr, P. B. Coto, E. T. Chernick, R. Casillas, B. S. Basel, M. Thoss, R. R. Tykwinski and D. M. Guldi, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 5325–5330 CrossRef CAS PubMed.
- S. N. Sanders, E. Kumarasamy, A. B. Pun, M. T. Trinh, B. Choi, J. Xia, E. J. Taffet, J. Z. Low, J. R. Miller, X. Roy, X. Y. Zhu, M. L. Steigerwald, M. Y. Sfeir and L. M. Campos, J. Am. Chem. Soc., 2015, 137, 8965–8972 CrossRef CAS PubMed.
- J. C. Johnson, A. J. Nozik and J. Michl, J. Am. Chem. Soc., 2010, 132, 16302–16303 CrossRef CAS PubMed.
- J. N. Schrauben, Y. Zhao, C. Mercado, P. I. Dron, J. L. Ryerson, J. Michl, K. Zhu and J. C. Johnson, ACS Appl. Mater. Interfaces, 2015, 7, 2286–2293 CAS.
- N. J. Ekins-Daukes and T. W. Schmidt, Appl. Phys. Lett., 2008, 93, 063507 CrossRef.
- V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352 RSC.
- T. F. Schulze and T. W. Schmidt, Energy Environ. Sci., 2015, 8, 103–125 CAS.
- C. A. Parker, C. G. Hatchard and T. A. Joyce, Nature, 1965, 205, 1282–1284 CrossRef CAS.
- C. E. McCusker and F. N. Castellano, Inorg. Chem., 2015, 54, 6035–6042 CrossRef CAS PubMed.
- J. Zhao, W. Wu, J. Sun and S. Guo, Chem. Soc. Rev., 2013, 42, 5323–5351 RSC.
- J. S. Lissau, J. M. Gardner and A. Morandeira, J. Phys. Chem. C, 2011, 115, 23226–23232 CAS.
- J. S. Lissau, D. Nauroozi, M.-P. Santoni, S. Ott, J. M. Gardner and A. Morandeira, J. Phys. Chem. C, 2015, 119, 25792–25806 CAS.
- J. S. Lissau, D. Nauroozi, M.-P. Santoni, T. Edvinsson, S. Ott, J. M. Gardner and A. Morandeira, J. Phys. Chem. C, 2015, 119, 4550–4564 CAS.
- C. Simpson, T. M. Clarke, R. W. MacQueen, Y. Y. Cheng, A. J. Trevitt, A. J. Mozer, P. Wagner, T. W. Schmidt and A. Nattestad, Phys. Chem. Chem. Phys., 2015, 17, 24826–24830 RSC.
- K. Hanson, D. A. Torelli, A. K. Vannucci, M. K. Brennaman, H. Luo, L. Alibabaei, W. Song, D. L. Ashford, M. R. Norris, C. R. K. Glasson, J. J. Concepcion and T. J. Meyer, Angew. Chem., Int. Ed., 2012, 51, 12782–12785 CrossRef CAS PubMed.
- H. Lee, L. J. Kepley, H. G. Hong, S. Akhter and T. E. Mallouk, J. Phys. Chem., 1988, 92, 2597–2601 CrossRef CAS.
- K. Terada, K. Kobayashi, J. Hikita and M. Haga, Chem. Lett., 2009, 38, 416–417 CrossRef CAS.
- L. A. Vermeulen, J. L. Snover, L. S. Sapochak and M. E. Thompson, J. Am. Chem. Soc., 1993, 115, 11767–11774 CrossRef CAS.
- S. P. Hill, T. Banerjee, T. Dilbeck and K. Hanson, J. Phys. Chem. Lett., 2015, 6, 4510–4517 CrossRef CAS PubMed.
- S. P. Hill, T. Dilbeck, E. Baduell and K. Hanson, ACS Energy Lett., 2016, 1, 3–8 CrossRef CAS.
- T. Dilbeck, S. P. Hill and K. Hanson, J. Mater. Chem. A, 2017, 5, 11652–11660 CAS.
- S. P. Hill and K. Hanson, J. Am. Chem. Soc., 2017, 139, 10988–10991 CrossRef CAS PubMed.
- L. Frazer, J. K. Gallaher and T. W. Schmidt, ACS Energy Lett., 2017, 2, 1346–1354 CrossRef CAS.
- T. Dilbeck, J. C. Wang, Y. Zhou, A. Olsson, M. Sykora and K. Hanson, J. Phys. Chem. C, 2017, 121, 19690–19698 CAS.
- C. A. Kelly, F. Farzad, D. W. Thompson and G. J. Meyer, Langmuir, 1999, 15, 731–737 CrossRef CAS.
- F. Farzad, D. W. Thompson, C. A. Kelly and G. J. Meyer, J. Am. Chem. Soc., 1999, 121, 5577–5578 CrossRef CAS.
- C. Creutz, M. Chou, T. L. Netzel, M. Okumura and N. Sutin, J. Am. Chem. Soc., 1980, 102, 1309–1319 CrossRef CAS.
- V. Balzani, A. Juris, M. Venturi, S. Campagna and S. Serroni, Chem. Rev., 1996, 96, 759–834 CrossRef CAS PubMed.
- J. P. Sauvage, J. P. Collin, J. C. Chambron, S. Guillerez, C. Coudret, V. Balzani, F. Barigelletti, L. De Cola and L. Flamigni, Chem. Rev., 1994, 94, 993–1019 CrossRef CAS.
- L. M. Dupray, M. Devenney, D. R. Striplin and T. J. Meyer, J. Am. Chem. Soc., 1997, 119, 10243–10244 CrossRef CAS.
- W. E. Jones, S. M. Baxter, G. F. Strouse and T. J. Meyer, J. Am. Chem. Soc., 1993, 115, 7363–7373 CrossRef CAS.
- L. A. Worl, G. F. Strouse, J. N. Younathan, S. M. Baxter and T. J. Meyer, J. Am. Chem. Soc., 1990, 112, 7571–7578 CrossRef CAS.
- S. A. Trammell, J. Yang, M. Sykora, C. N. Fleming, F. Odobel and T. J. Meyer, J. Phys. Chem. B, 2001, 105, 8895–8904 CrossRef CAS.
- G. T. Higgins, B. V. Bergeron, G. M. Hasselmann, F. Farzad and G. J. Meyer, J. Phys. Chem. B, 2006, 110, 2598–2605 CrossRef CAS PubMed.
- S. Ardo and G. J. Meyer, J. Am. Chem. Soc., 2011, 133, 15384–15396 CrossRef CAS PubMed.
- W. Song, A. Ito, R. A. Binstead, K. Hanson, H. Luo, M. K. Brennaman, J. J. Concepcion and T. J. Meyer, J. Am. Chem. Soc., 2013, 135, 11587–11594 CrossRef CAS PubMed.
- S. E. Bettis, K. Hanson, L. Wang, M. K. Gish, J. J. Concepcion, Z. Fang, T. J. Meyer and J. M. Papanikolas, J. Phys. Chem. A, 2014, 118, 10301–10308 CrossRef CAS PubMed.
- J. R. Swierk, N. S. McCool, T. P. Saunders, G. D. Barber and T. E. Mallouk, J. Am. Chem. Soc., 2014, 136, 10974–10982 CrossRef CAS PubMed.
- D. Moia, U. B. Cappel, T. Leijtens, X. Li, A. M. Telford, H. J. Snaith, B. C. O’Regan, J. Nelson and P. R. F. Barnes, J. Phys. Chem. C, 2015, 119, 18975–18985 CAS.
- L. Yang, U. B. Cappel, E. L. Unger, M. Karlsson, K. M. Karlsson, E. Gabrielsson, L. Sun, G. Boschloo, A. Hagfeldt and E. M. J. Johansson, Phys. Chem. Chem. Phys., 2012, 14, 779–789 RSC.
- D. Moia, T. Leijtens, N. Noel, H. J. Snaith, J. Nelson and P. R. F. Barnes, Adv. Mater., 2015, 27, 5889–5894 CrossRef CAS PubMed.
- S. Ardo and G. J. Meyer, J. Am. Chem. Soc., 2010, 132, 9283–9285 CrossRef CAS PubMed.
- B. J. Brennan, A. C. Durrell, M. Koepf, R. H. Crabtree and G. W. Brudvig, Phys. Chem. Chem. Phys., 2015, 17, 12728–12734 RSC.
- B. J. Brennan, K. P. Regan, A. C. Durrell, C. A. Schmuttenmaer and G. W. Brudvig, ACS Energy Lett., 2017, 2, 168–173 CAS.
- D. Moia, V. Vaissier, I. Lopez-Duarte, T. Torres, M. K. Nazeeruddin, B. C. O'Regan, J. Nelson and P. R. F. Barnes, Chem. Sci., 2014, 5, 281–290 RSC.
- K. Hanson, M. K. Brennaman, A. Ito, H. Luo, W. Song, K. A. Parker, R. Ghosh, M. R. Norris, C. R. K. Glasson, J. J. Concepcion, R. Lopez and T. J. Meyer, J. Phys. Chem. C, 2012, 116, 14837–14847 CAS.
- P. Bonhôte, E. Gogniat, S. Tingry, C. Barbé, N. Vlachopoulos, F. Lenzmann, P. Comte and M. Grätzel, J. Phys. Chem. B, 1998, 102, 1498–1507 CrossRef PubMed.
- D. N. Blauch and J. M. Saveant, J. Am. Chem. Soc., 1992, 114, 3323–3332 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, M. K. Nazeeruddin, R. Humphry-Baker and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 4446–4452 CrossRef CAS PubMed.
- V. Vaissier, E. Mosconi, D. Moia, M. Pastore, J. M. Frost, F. De Angelis, P. R. F. Barnes and J. Nelson, Chem. Mater., 2014, 26, 4731–4740 CrossRef CAS.
- B. N. DiMarco, T. C. Motley, R. S. Balok, G. Li, M. A. Siegler, R. M. O’Donnell, K. Hu and G. J. Meyer, J. Phys. Chem. C, 2016, 120, 14226–14235 CAS.
- X. Wang, L. Guo, P. F. Xia, F. Zheng, M. S. Wong and Z. Zhu, J. Mater. Chem. A, 2013, 1, 13328–13336 CAS.
- N. Papageorgiou, M. Grätzel, O. Enger, D. Bonifazi and F. Diederich, J. Phys. Chem. B, 2002, 106, 3813–3822 CrossRef CAS.
- P. Qu and G. J. Meyer, Langmuir, 2001, 17, 6720–6728 CrossRef CAS.
- A. Fattori, L. M. Peter, H. Wang, H. Miura and F. Marken, J. Phys. Chem. C, 2010, 114, 11822–11828 CAS.
- X. Li, M. K. Nazeeruddin, M. Thelakkat, P. R. F. Barnes, R. Vilar and J. R. Durrant, Phys. Chem. Chem. Phys., 2011, 13, 1575–1584 RSC.
- E. Galoppini, W. Guo, W. Zhang, P. G. Hoertz, P. Qu and G. J. Meyer, J. Am. Chem. Soc., 2002, 124, 7801–7811 CrossRef CAS PubMed.
- S. A. Trammell and T. J. Meyer, J. Phys. Chem. B, 1999, 103, 104–107 CrossRef CAS.
- Q. Wang, S. M. Zakeeruddin, J. Cremer, P. Bäuerle, R. Humphry-Baker and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 5706–5713 CrossRef CAS PubMed.
- X. Li, M. K. Nazeeruddin, M. Thelakkat, P. R. F. Barnes, R. Vilar and J. R. Durrant, Phys. Chem. Chem. Phys., 2011, 13, 1575–1584 RSC.
- M. Pastore, T. Etienne and F. De Angelis, J. Mater. Chem. C, 2016, 4, 4346–4373 RSC.
- J. H. Delcamp, Y. R. Shi, J. H. Yum, T. Sajoto, E. Dell'Orto, S. Barlow, M. K. Nazeeruddin, S. R. Marder and M. Gratzel, Chem. – Eur. J., 2013, 19, 1819–1827 CrossRef CAS PubMed.
- D. B. Kuang, C. Klein, S. Ito, J. E. Moser, R. Humphry-Baker, S. M. Zakeeruddin and M. Gratzel, Adv. Funct. Mater., 2007, 17, 154–160 CrossRef CAS.
- J. Lim, Y. S. Kwon and T. Park, Chem. Commun., 2011, 47, 4147–4149 RSC.
- S. L. Lu, T. Wu, B. F. Ren and R. Geng, J. Mater. Sci.: Mater. Electron., 2013, 24, 2346–2350 CrossRef CAS.
- A. Reynal and E. Palomares, Energy Environ. Sci., 2009, 2, 1078–1081 CAS.
- H. P. Shen, H. Lin, Y. Z. Liu, X. Li, J. Zhang, N. Wang and J. B. Li, Electrochim. Acta, 2011, 56, 2092–2097 CrossRef CAS.
- Y. B. Shi, M. Liang, L. N. Wang, H. Y. Han, L. S. You, Z. Sun and S. Xue, ACS Appl. Mater. Interfaces, 2013, 5, 144–153 CAS.
- M. K. Wang, C. Gratzel, S. J. Moon, R. Humphry-Baker, N. Rossier-Iten, S. M. Zakeeruddin and M. Gratzel, Adv. Funct. Mater., 2009, 19, 2163–2172 CrossRef CAS.
- P. Wang, S. M. Zakeeruddin, P. Comte, R. Charvet, R. Humphry-Baker and M. Gratzel, J. Phys. Chem. B, 2003, 107, 14336–14341 CrossRef CAS.
- K. L. Wu, W. P. Ku, J. N. Clifford, E. Palomares, S. T. Ho, Y. Chi, S. H. Liu, P. T. Chou, M. K. Nazeeruddin and M. Gratzel, Energy Environ. Sci., 2013, 6, 859–870 CAS.
- T. Miyasaka, T. Watanabe, A. Fujishima and K. Honda, J. Am. Chem. Soc., 1978, 100, 6657–6665 CrossRef CAS.
- B. Oregan and M. Gratzel, Nature, 1991, 353, 737–740 CrossRef CAS.
- H. Y. Li, Y. Z. Yang, Y. Q. Hou, R. L. Tang, T. N. Duan, J. N. Chen, H. Wang, H. W. Han, T. Y. Peng, X. G. Chen, Q. Q. Li and Z. Li, ACS Sustainable Chem. Eng., 2014, 2, 1776–1784 CrossRef CAS.
- W. Q. Li, B. Liu, Y. Z. Wu, S. Q. Zhu, Q. Zhang and W. H. Zhu, Dyes Pigm., 2013, 99, 176–184 CrossRef CAS.
- Y. Ooyama, Y. Hagiwara, T. Mizumo, Y. Harima and J. Ohshita, New J. Chem., 2013, 37, 2479–2485 RSC.
- Z. S. Wang, Y. Cui, Y. Dan-oh, C. Kasada, A. Shinpo and K. Hara, J. Phys. Chem. C, 2007, 111, 7224–7230 CAS.
- Z. J. Ning, Y. Fu and H. Tian, Energy Environ. Sci., 2010, 3, 1170–1181 CAS.
- Y. R. Liu, J. R. Jennings, X. Z. Wang and Q. Wang, Phys. Chem. Chem. Phys., 2013, 15, 6170–6174 RSC.
- H. P. Shen, X. Li, J. B. Li, W. L. Wang and H. Lin, Electrochim. Acta, 2013, 97, 160–166 CrossRef CAS.
- M. K. Wang, X. Li, H. Lin, P. Pechy, S. M. Zakeeruddin and M. Gratzel, Dalton Trans., 2009, 10015–10020, 10.1039/b908673k.
- H. Lin, Y. Z. Liu, C. J. Liu, X. Li, H. P. Shen, J. Zhang, T. L. Ma and J. B. Li, J. Electroanal. Chem., 2011, 653, 81–85 CrossRef CAS.
- N. R. Neale, N. Kopidakis, J. van de Lagemaat, M. Gratzel and A. J. Frank, J. Phys. Chem. B, 2005, 109, 23183–23189 CrossRef CAS PubMed.
- X. M. Ren, Q. Y. Feng, G. Zhou, C. H. Huang and Z. S. Wang, J. Phys. Chem. C, 2010, 114, 7190–7195 CAS.
- T. Marinado, M. Hahlin, X. A. Jiang, M. Quintana, E. M. J. Johansson, E. Gabrielsson, S. Plogmaker, D. P. Hagberg, G. Boschloo, S. M. Zakeeruddin, M. Gratzel, H. Siegbahn, L. C. Sun, A. Hagfeldt and H. Rensmo, J. Phys. Chem. C, 2010, 114, 11903–11910 CAS.
- P. Lefebvre, B. Cariou, F. Lien, F. Kuipers and B. Staels, Physiol. Rev., 2009, 89, 147–191 CrossRef CAS PubMed.
- A. Kay and M. Gratzel, J. Phys. Chem., 1993, 97, 6272–6277 CrossRef CAS.
- Z. P. Zhang, S. M. Zakeeruddin, B. C. O'Regan, R. Humphry-Baker and M. Gratzel, J. Phys. Chem. B, 2005, 109, 21818–21824 CrossRef CAS PubMed.
- B. J. Song, H. M. Song, I. T. Choi, S. K. Kim, K. D. Seo, M. S. Kang, M. J. Lee, D. W. Cho, M. J. Ju and H. K. Kim, Chem. – Eur. J., 2011, 17, 11115–11121 CrossRef CAS PubMed.
- L. Y. Han, A. Islam, H. Chen, C. Malapaka, B. Chiranjeevi, S. F. Zhang, X. D. Yang and M. Yanagida, Energy Environ. Sci., 2012, 5, 6057–6060 CAS.
- S. Ruhle, M. Greenshtein, S. G. Chen, A. Merson, H. Pizem, C. S. Sukenik, D. Cahen and A. Zaban, J. Phys. Chem. B, 2005, 109, 18907–18913 CrossRef PubMed.
- T. Daeneke, T. H. Kwon, A. B. Holmes, N. W. Duffy, U. Bach and L. Spiccia, Nat. Chem., 2011, 3, 211–215 CrossRef CAS PubMed.
- I. R. Perera, A. Gupta, W. C. Xiang, T. Daeneke, U. Bach, R. A. Evans, C. A. Ohlin and L. Spiccia, Phys. Chem. Chem. Phys., 2014, 16, 12021–12028 RSC.
- P. Salvatori, G. Marotta, A. Cinti, C. Anselmi, E. Mosconi and F. De Angelis, J. Phys. Chem. C, 2013, 117, 3874–3887 CAS.
- P. Salvatori, G. Marotta, A. Cinti, E. Mosconi, M. Panigrahi, L. Giribabu, M. K. Nazeeruddin and F. De Angelis, Inorg. Chim. Acta, 2013, 406, 106–112 CrossRef CAS.
- S. Ito, H. Miura, S. Uchida, M. Takata, K. Sumioka, P. Liska, P. Comte, P. Pechy and M. Graetzel, Chem. Commun., 2008, 5194–5196, 10.1039/b809093a.
- M. Ikeda, N. Koide, L. Han, A. Sasahara and H. Onishi, Langmuir, 2008, 24, 8056–8060 CrossRef CAS PubMed.
- A. Dessi, G. B. Consiglio, M. Calamante, G. Reginato, A. Mordini, M. Peruzzini, M. Taddei, A. Sinicropi, M. L. Parisi, F. F. de Biani, R. Basosi, R. Mori, M. Spatola, M. Bruzzi and L. Zani, Eur. J. Org. Chem., 2013, 1916–1928, DOI:10.1002/ejoc.201201629.
- K. Hara, Y. Dan-Oh, C. Kasada, Y. Ohga, A. Shinpo, S. Suga, K. Sayama and H. Arakawa, Langmuir, 2004, 20, 4205–4210 CrossRef CAS PubMed.
- K. Hara, H. Sugihara, Y. Tachibana, A. Islam, M. Yanagida, K. Sayama, H. Arakawa, G. Fujihashi, T. Horiguchi and T. Kinoshita, Langmuir, 2001, 17, 5992–5999 CrossRef CAS.
- K. M. Lee, V. Suryanarayanan, K. C. Ho, K. R. J. Thomas and J. T. Lin, Sol. Energy Mater. Sol. Cells, 2007, 91, 1426–1431 CrossRef CAS.
- R. Y. Y. Lin, H. W. Lin, Y. S. Yen, C. H. Chang, H. H. Chou, P. W. Chen, C. Y. Hsu, Y. C. Chen, J. T. Lin and K. C. Ho, Energy Environ. Sci., 2013, 6, 2477–2486 Search PubMed.
- J. H. Yum, S. J. Moon, R. Humphry-Baker, P. Walter, T. Geiger, F. Nuesch, M. Graetzel and M. D. K. Nazeeruddin, Nanotechnology, 2008, 19 Search PubMed.
- Y. Numata, A. Islam, H. Chen and L. Y. Han, Energy Environ. Sci., 2012, 5, 8548–8552 CAS.
- V. S. Saji and M. Pyo, Curr. Appl. Phys., 2010, 10, S410–S413 CrossRef.
- B. Liu, Q. B. Liu, D. You, X. Y. Li, Y. Naruta and W. H. Zhu, J. Mater. Chem., 2012, 22, 13348–13356 RSC.
- H. P. Lu, C. L. Mai, C. Y. Tsia, S. J. Hsu, C. P. Hsieh, C. L. Chiu, C. Y. Yeh and E. W. Diau, Phys. Chem. Chem. Phys., 2009, 11, 10270–10274 RSC.
- M. K. Panda, G. D. Sharma, K. R. J. Thomas and A. G. Coutsolelos, J. Mater. Chem., 2012, 22, 8092–8102 RSC.
- S. Eu, T. Katoh, T. Umeyama, Y. Matano and H. Imahori, Dalton Trans., 2008, 5476–5483 RSC.
- S. Mori, M. Nagata, Y. Nakahata, K. Yasuta, R. Goto, M. Kimura and M. Taya, J. Am. Chem. Soc., 2010, 132, 4054–4055 CrossRef CAS PubMed.
- Y. Nagasawa and H. Miyasaka, Phys. Chem. Chem. Phys., 2014, 16, 13008–13026 RSC.
- B. S. Brunschwig and N. Sutin, Coord. Chem. Rev., 1999, 187, 233–254 CrossRef CAS.
- F. D. Lewis, T. Wu, Y. Zhang, R. L. Letsinger, S. R. Greenfield and M. R. Wasielewski, Science, 1997, 277, 673–676 CrossRef CAS PubMed.
- M. R. Wasielewski, Chem. Rev., 1992, 92, 435–461 CrossRef CAS.
- M. Gilbert and B. Albinsson, Chem. Soc. Rev., 2015, 44, 845–862 RSC.
- M. Natali, S. Campagna and F. Scandola, Chem. Soc. Rev., 2014, 43, 4005–4018 RSC.
- A. Arrigo, A. Santoro, M. T. Indelli, M. Natali, F. Scandola and S. Campagna, Phys. Chem. Chem. Phys., 2014, 16, 818–826 RSC.
- B. Albinsson and J. Mårtensson, J. Photochem. Photobiol., C, 2008, 9, 138–155 CrossRef CAS.
- M. Liang and J. Chen, Chem. Soc. Rev., 2013, 42, 3453–3488 RSC.
- A. Mahmood, Sol. Energy, 2016, 123, 127–144 CrossRef CAS.
- T. Ripolles-Sanchis, B.-C. Guo, H.-P. Wu, T.-Y. Pan, H.-W. Lee, S. R. Raga, F. Fabregat-Santiago, J. Bisquert, C.-Y. Yeh and E. W.-G. Diau, Chem. Commun., 2012, 48, 4368–4370 RSC.
- Y. Tang, Y. Wang, X. Li, H. Ågren, W.-H. Zhu and Y. Xie, ACS Appl. Mater. Interfaces, 2015, 7, 27976–27985 CAS.
- A. Yella, H.-W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W.-G. Diau, C.-Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- R. Argazzi, C. A. Bignozzi, T. A. Heimer, F. N. Castellano and G. J. Meyer, J. Am. Chem. Soc., 1995, 117, 11815–11816 CrossRef CAS.
- S. A. Haque, S. Handa, K. Peter, E. Palomares, M. Thelakkat and J. R. Durrant, Angew. Chem., Int. Ed. Engl., 2005, 44, 5740–5744 CrossRef CAS PubMed.
- J.-H. Yum, I. Jung, C. Baik, J. Ko, M. K. Nazeeruddin and M. Gratzel, Energy Environ. Sci., 2009, 2, 100–102 CAS.
- P. Bonhôte, J.-E. Moser, R. Humphry-Baker, N. Vlachopoulos, S. M. Zakeeruddin, L. Walder and M. Grätzel, J. Am. Chem. Soc., 1999, 121, 1324–1336 CrossRef.
- G. Li, K. Hu, C. Yi, K. L. Knappenberger, G. J. Meyer, S. I. Gorelsky and M. Shatruk, J. Phys. Chem. C, 2013, 117, 17399–17411 CAS.
- Y. Hao, E. Gabrielsson, P. W. Lohse, W. Yang, E. M. J. Johansson, A. Hagfeldt, L. Sun and G. Boschloo, Adv. Sci., 2015, 2, 1500174 CrossRef PubMed.
- A. Juris, V. Balzani, F. Barigelletti, S. Campagna, P. Belser and A. von Zelewsky, Coord. Chem. Rev., 1988, 84, 85–277 CrossRef CAS.
- K. Yuan Chiu, T. Xiang Su, J. Hong Li, T.-H. Lin, G.-S. Liou and S.-H. Cheng, J. Electroanal. Chem., 2005, 575, 95–101 CrossRef.
- J. Luo, M. Xu, R. Li, K.-W. Huang, C. Jiang, Q. Qi, W. Zeng, J. Zhang, C. Chi, P. Wang and J. Wu, J. Am. Chem. Soc., 2014, 136, 265–272 CrossRef CAS PubMed.
- L. N. Ashbrook and C. M. Elliott, J. Phys. Chem. C, 2013, 117, 3853–3864 CAS.
- Y. Hao, E. Gabrielsson, P. W. Lohse, W. X. Yang, E. M. J. Johansson, A. Hagfeldt, L. C. Sun and G. Boschloo, Adv. Sci., 2015, 2, 1500174 CrossRef PubMed.
- T. A. Shoker and T. H. Ghaddar, RSC Adv., 2014, 4, 18336–18340 RSC.
- R. Argazzi, C. A. Bignozzi, T. A. Heimer, F. N. Castellano and G. J. Meyer, J. Phys. Chem. B, 1997, 101, 2591–2597 CrossRef CAS.
- H. J. Snaith, C. S. Karthikeyan, A. Petrozza, J. Teuscher, J. E. Moser, M. K. Nazeeruddin, M. Thelakkat and M. Gratzel, J. Phys. Chem. C, 2008, 112, 7562–7566 CAS.
- M. Song, D. Kim, K. Ihn, S. Jo and D. Kim, Nanotechnology, 2004, 15, 1861–1865 CrossRef CAS.
- S. A. Haque, S. Handa, K. Peter, E. Palomares, M. Thelakkat and J. R. Durrant, Angew. Chem., Int. Ed., 2005, 44, 5740–5744 CrossRef CAS PubMed.
- R. Sivakumar, A. Manivel, M. Melendrez, J. Martinez-Oyanedel, M. Bunster, C. Vergara and P. Manidurai, Polyhedron, 2015, 87, 135–140 CrossRef CAS.
- S. Handa, H. Wietasch, M. Thelakkat, J. R. Durrant and S. A. Haque, Chem. Commun., 2007, 1725–1727 RSC.
- J. H. Yum, I. Jung, C. Baik, J. Ko, M. K. Nazeeruddin and M. Gratzel, Energy Environ. Sci., 2009, 2, 100–102 CAS.
- K. Willinger, K. Fischer, R. Kisselev and M. Thelakkat, J. Mater. Chem., 2009, 19, 5364–5376 RSC.
- A. El-Shafei, M. Hussain, A. Atiq, A. Islam and L. Han, J. Mater. Chem., 2012, 22, 24048–24056 RSC.
- L. Giribabu, T. Bessho, M. Srinivasu, C. Vijaykumar, Y. Soujanya, V. G. Reddy, P. Y. Reddy, J. H. Yum, M. Gratzel and M. K. Nazeeruddin, Dalton Trans., 2011, 40, 4497–4504 RSC.
- S. Lin-Qing, X. Pu. Hui, W. Xue-Song, H. Yuan-Jun, Z. Bao-Wen, C. Yi, L. Wei-Ying, Z. Jing-Bo, X. Xu-Rui and L. Yuan, Chin. J. Chem., 2003, 21, 644–649 CrossRef.
- L. Q. Song, H. Y. Ding, X. S. Wang, B. W. Zhang, Y. Cao, J. Feng, X. C. Ai and J. P. Zhang, J. Photochem. Photobiol., A, 2004, 165, 137–142 CrossRef CAS.
- G. Will, G. Boschloo, R. Hoyle, S. N. Rao and D. Fitzmaurice, J. Phys. Chem. B, 1998, 102, 10272–10278 CrossRef CAS.
- G. Will, G. Boschloo, S. N. Rao and D. Fitzmaurice, J. Phys. Chem. B, 1999, 103, 8067–8079 CrossRef CAS.
- M. Buchalska, J. Kuncewicz, E. Świętek, P. Łabuz, T. Baran, G. Stochel and W. Macyk, Coord. Chem. Rev., 2013, 257, 767–775 CrossRef CAS.
- F. Odobel, Y. Pellegrin, E. A. Gibson, A. Hagfeldt, A. L. Smeigh and L. Hammarstrom, Coord. Chem. Rev., 2012, 256, 2414–2423 CrossRef CAS.
- J. Warnan, J. Gardner, L. Le Pleux, J. Petersson, Y. Pellegrin, E. Blart, L. Hammarstrom and F. Odobel, J. Phys. Chem. C, 2014, 118, 103–113 CAS.
- Z. Ji and Y. Wu, J. Phys. Chem. C, 2013, 117, 18315–18324 CAS.
- Z. Ji, G. Natu and Y. Wu, ACS Appl. Mater. Interfaces, 2013, 5, 8641–8648 CAS.
- Z. Ji, G. Natu, Z. Huang, O. Kokhan, X. Zhang and Y. Wu, J. Phys. Chem. C, 2012, 116, 16854–16863 CAS.
- M. He, Z. Ji, Z. Huang and Y. Wu, J. Phys. Chem. C, 2014, 118, 16518–16525 CAS.
- L. Favereau, J. Warnan, Y. Pellegrin, E. Blart, M. Boujtita, D. Jacquemin and F. Odobel, Chem. Commun., 2013, 49, 8018–8020 RSC.
- Y. Farré, L. Zhang, Y. Pellegrin, A. Planchat, E. Blart, M. Boujtita, L. Hammarström, D. Jacquemin and F. Odobel, J. Phys. Chem. C, 2016, 120, 7923–7940 Search PubMed.
- T. T. T. Pham, S. K. Saha, D. Provost, Y. Farré, M. Raissi, Y. Pellegrin, E. Blart, S. Vedraine, B. Ratier, D. Aldakov, F. Odobel and J. Bouclé, J. Phys. Chem. C, 2017, 121, 129–139 CAS.
- A. Nattestad, Y. Y. Cheng, R. W. MacQueen, T. F. Schulze, F. W. Thompson, A. J. Mozer, B. Fückel, T. Khoury, M. J. Crossley, K. Lips, G. G. Wallace and T. W. Schmidt, J. Phys. Chem. Lett., 2013, 4, 2073–2078 CrossRef CAS PubMed.
- L. Le Pleux, A. L. Smeigh, E. Gibson, Y. Pellegrin, E. Blart, G. Boschloo, A. Hagfeldt, L. Hammarstrom and F. Odobel, Energy Environ. Sci., 2011, 4, 2075–2084 CAS.
- C. J. Wood, M. Cheng, C. A. Clark, R. Horvath, I. P. Clark, M. L. Hamilton, M. Towrie, M. W. George, L. Sun, X. Yang and E. A. Gibson, J. Phys. Chem. C, 2014, 118, 16536–16546 CAS.
- R. Hoyle, J. Sotomayor, G. Will and D. Fitzmaurice, J. Phys. Chem. B, 1997, 101, 10791–10800 CrossRef CAS.
- R. Hoyle, G. Will and D. Fitzmaurice, J. Mater. Chem., 1998, 8, 2033–2036 RSC.
- J. Sotomayor, G. Will and D. Fitzmaurice, J. Mater. Chem., 2000, 10, 685–692 RSC.
- H. M. Song, K. D. Seo, M. S. Kang, I. T. Choi, S. K. Kim, Y. K. Eom, J. H. Ryu, M. J. Ju and H. K. Kim, J. Mater. Chem., 2012, 22, 3786–3794 RSC.
- I. T. Choi, M. J. Ju, S. H. Kang, M. S. Kang, B. S. You, J. Y. Hong, Y. K. Eom, S. H. Song and H. K. Kim, J. Mater. Chem. A, 2013, 1, 9114–9121 CAS.
- I. T. Choi, M. J. Ju, S. H. Song, S. G. Kim, D. W. Cho, C. Im and H. K. Kim, Chem. – Eur. J., 2013, 19, 15545–15555 CrossRef CAS PubMed.
- Z. Jinlong, H. Bin, Z. Qin and H. Deyin, Dyes Pigm., 1998, 38, 41–47 CrossRef.
- M. Biancardo, R. Argazzi and C. A. Bignozzi, Inorg. Chem., 2005, 44, 9619–9621 CrossRef CAS PubMed.
- V. V. Matylitsky, L. Dworak and J. Wachtveitl, ChemPhysChem, 2010, 11, 2027–2035 CAS.
- K. Stranius, L. George, A. Efimov, T.-P. Ruoko, J. Pohjola and N. V. Tkachenko, Langmuir, 2015, 31, 944–952 CrossRef CAS PubMed.
- T. Hasobe, Phys. Chem. Chem. Phys., 2010, 12, 44–57 RSC.
- H. Imahori and T. Umeyama, J. Phys. Chem. C, 2009, 113, 9029–9039 CAS.
- H. Imahori, Angew. Chem., Int. Ed., 2002, 41, 2344–2347 CrossRef CAS PubMed.
- T. Hasobe, H. Imahori, S. Fukuzumi and P. V. Kamat, J. Phys. Chem. B, 2003, 107, 12105–12112 CrossRef CAS.
- H. Imahori, J. Mater. Chem., 2007, 17, 31–41 RSC.
- T. Hasobe, H. Murata, S. Fukuzumi and P. V. Kamat, Mol. Cryst. Liq. Cryst., 2007, 471, 39–51 CrossRef CAS.
- S. Fukuzumi and T. Kojima, J. Mater. Chem., 2008, 18, 1427–1439 RSC.
- T. Hasobe, H. Imahori, P. V. Kamat and S. Fukuzumi, J. Am. Chem. Soc., 2003, 125, 14962–14963 CrossRef CAS PubMed.
- T. Hasobe, Y. Kashiwagi, M. A. Absalom, J. Sly, K. Hosomizu, M. J. Crossley, H. Imahori, P. V. Kamat and S. Fukuzumi, Adv. Mater., 2004, 16, 975–979 CrossRef CAS.
- H. Imahori, A. Fujimoto, S. Kang, H. Hotta, K. Yoshida, T. Umeyama, Y. Matano and S. Isoda, Adv. Mater., 2005, 17, 1727–1730 CrossRef CAS.
- T. Hasobe, H. Imahori, P. V. Kamat, T. K. Ahn, S. K. Kim, D. Kim, A. Fujimoto, T. Hirakawa and S. Fukuzumi, J. Am. Chem. Soc., 2005, 127, 1216–1228 CrossRef CAS PubMed.
- T. Hasobe, P. V. Kamat, V. Troiani, N. Solladié, T. K. Ahn, S. K. Kim, D. Kim, A. Kongkanand, S. Kuwabata and S. Fukuzumi, J. Phys. Chem. B, 2005, 109, 19–23 CrossRef CAS PubMed.
- T. Hasobe, K. Saito, P. V. Kamat, V. Troiani, H. Qiu, N. Solladie, K. S. Kim, J. K. Park, D. Kim, F. D'Souza and S. Fukuzumi, J. Mater. Chem., 2007, 17, 4160–4170 RSC.
- H. Imahori, T. Hasobe, H. Yamada, P. V. Kamat, S. Barazzouk, M. Fujitsuka, O. Ito and S. Fukuzumi, Chem. Lett., 2001, 784–785 CrossRef CAS.
- H. Imahori and S. Fukuzumi, Adv. Funct. Mater., 2004, 14, 525–536 CrossRef CAS.
- A. Kira, T. Umeyama, Y. Matano, K. Yoshida, S. Isoda, J. K. Park, D. Kim and H. Imahori, J. Am. Chem. Soc., 2009, 131, 3198–3200 CrossRef CAS PubMed.
- H. Imahori, J.-C. Liu, H. Hotta, A. Kira, T. Umeyama, Y. Matano, G. Li, S. Ye, M. Isosomppi, N. V. Tkachenko and H. Lemmetyinen, J. Phys. Chem. B, 2005, 109, 18465–18474 CrossRef CAS PubMed.
- H. Hotta, S. Kang, T. Umeyama, Y. Matano, K. Yoshida, S. Isoda and H. Imahori, J. Phys. Chem. B, 2005, 109, 5700–5706 CrossRef CAS PubMed.
- H. Imahori, M. Ueda, S. Kang, H. Hayashi, S. Hayashi, H. Kaji, S. Seki, A. Saeki, S. Tagawa, T. Umeyama, Y. Matano, K. Yoshida, S. Isoda, M. Shiro, N. V. Tkachenko and H. Lemmetyinen, Chem. – Eur. J., 2007, 13, 10182–10193 CrossRef CAS PubMed.
- A. Kira, M. Tanaka, T. Umeyama, Y. Matano, N. Yoshimoto, Y. Zhang, S. Ye, H. Lehtivuori, N. V. Tkachenko, H. Lemmetyinen and H. Imahori, J. Phys. Chem. C, 2007, 111, 13618–13626 CAS.
- H. Hayashi, A. Kira, T. Umeyama, Y. Matano, P. Charoensirithavorn, T. Sagawa, S. Yoshikawa, N. V. Tkachenko, H. Lemmetyinen and H. Imahori, J. Phys. Chem. C, 2009, 113, 10819–10828 CAS.
- A. Varotto, L. Todaro, M. Vinodu, J. Koehne, G.-Y. Liu and C. M. Drain, Chem. Commun., 2008, 4921–4923 RSC.
- T. Hasobe, S. Hattori, H. Kotani, K. Ohkubo, K. Hosomizu, H. Imahori, P. V. Kamat and S. Fukuzumi, Org. Lett., 2004, 6, 3103–3106 CrossRef CAS PubMed.
- T. Hasobe, Y. Kashiwagi, M. A. Absalom, J. Sly, K. Hosomizu, M. J. Crossley, H. Imahori, P. V. Kamat and S. Fukuzumi, Adv. Mater., 2004, 16, 975–979 CrossRef CAS.
- T. Hasobe, H. Imahori, P. V. Kamat, T. K. Ahn, S. K. Kim, D. Kim, A. Fujimoto, T. Hirakawa and S. Fukuzumi, J. Am. Chem. Soc., 2005, 127, 1216–1228 CrossRef CAS PubMed.
- Y. Ooyama, K. Uenaka, T. Kamimura, S. Ozako, M. Kanda, T. Koide and F. Tani, RSC Adv., 2016, 6, 16150–16158 RSC.
- H. Imahori and T. Umeyama, J. Phys. Chem. C, 2009, 113, 9029–9039 CAS.
- H. Imahori and S. Fukuzumi, Adv. Funct. Mater., 2004, 14, 525–536 CrossRef CAS.
- B. H. Farnum, K.-R. Wee and T. J. Meyer, Nat. Chem., 2016, 8, 845–852 CrossRef CAS PubMed.
- B. Shan, B. H. Farnum, K.-R. Wee and T. J. Meyer, J. Phys. Chem. C, 2017, 121, 5882–5890 CAS.
- G. N. Lim, S. Hedström, K. A. Jung, P. A. D. Smith, V. S. Batista, F. D’Souza, A. van der Est and P. K. Poddutoori, J. Phys. Chem. C, 2017, 121, 14484–14497 CAS.
- W. Shockley and H. J. Queisser, J. Appl. Phys., 1961, 32, 510–519 CrossRef CAS.
- R. T. Ross and A. J. Nozik, J. Appl. Phys., 1982, 53, 3813–3818 CrossRef CAS.
- H. Gerischer and F. Willig, in Physical and Chemical Applications of Dyestuffs, ed. F. P. Schäfer, H. Gerischer, F. Willig, H. Meier, H. Jahnke, M. Schönborn and G. Zimmermann, Springer Berlin Heidelberg, Berlin, Heidelberg, 1976, pp. 31–84 DOI:10.1007/BFb0046057.
- A. Kirsh-de Mesmaeker, D. Maetens and R. Nasielski-Hinkens, J. Electroanal. Chem. Interfacial Electrochem., 1985, 182, 123–132 CrossRef.
- D. W. Thompson, C. A. Kelly, F. Farzad and G. J. Meyer, Langmuir, 1999, 15, 650–653 CrossRef CAS.
- C. A. Kelly, F. Farzad, D. W. Thompson, J. M. Stipkala and G. J. Meyer, Langmuir, 1999, 15, 7047–7054 CrossRef CAS.
- B. V. Bergeron, C. A. Kelly and G. J. Meyer, Langmuir, 2003, 19, 8389–8394 CrossRef CAS.
- B. V. Bergeron, A. Marton, G. Oskam and G. J. Meyer, J. Phys. Chem. B, 2005, 109, 937–943 CrossRef CAS PubMed.
- P. V. Kamat, S. Barazzouk, K. G. Thomas and S. Hotchandani, J. Phys. Chem. B, 2000, 104, 4014–4017 CrossRef CAS.
- C. C. Clark, A. Marton and G. J. Meyer, Inorg. Chem., 2005, 44, 3383–3385 CrossRef CAS PubMed.
- A. Marton, C. C. Clark, R. Srinivasan, R. E. Freundlich, A. A. Narducci Sarjeant and G. J. Meyer, Inorg. Chem., 2006, 45, 362–369 CrossRef CAS PubMed.
- P. Wang, B. Wenger, R. Humphry-Baker, J.-E. Moser, J. Teuscher, W. Kantlehner, J. Mezger, E. V. Stoyanov, S. M. Zakeeruddin and M. Grätzel, J. Am. Chem. Soc., 2005, 127, 6850–6856 CrossRef CAS PubMed.
- S. A. Berhe, H. B. Gobeze, S. D. Pokharel, E. Park and W. J. Youngblood, ACS Appl. Mater. Interfaces, 2014, 6, 10696–10705 CAS.
- B. Henderson and G. F. Imbusch, Optical spectroscopy of inorganic solids, Clarendon Press, Oxford University Press, Oxford, Oxfordshire, New York, 1989 Search PubMed.
- N. Sharifi, F. Tajabadi and N. Taghavinia, ChemPhysChem, 2014, 15, 3902–3927 CrossRef CAS PubMed.
- B. M. Klahr and T. W. Hamann, J. Phys. Chem. C, 2009, 113, 14040–14045 CAS.
- H. Deng, H. Mao, Z. Lu, J. Li and H. Xu, J. Photochem. Photobiol., A, 1997, 110, 47–52 CrossRef CAS.
- D. Huihua, Z. Hong, L. Bingjie and L. Zuhong, Jpn. J. Appl. Phys., 1998, 37, L132 Search PubMed.
- H. Deng, Y. Zhou, H. Mao and Z. Lu, Synth. Met., 1998, 92, 269–274 CrossRef CAS.
- T. Hasobe, H. Imahori, S. Fukuzumi and P. V. Kamat, J. Phys. Chem. B, 2003, 107, 12105–12112 CrossRef CAS.
- T. Horiuchi, H. Miura and S. Uchida, Chem. Commun., 2003, 3036–3037 RSC.
- H. Otaka, M. Kira, K. Yano, S. Ito, H. Mitekura, T. Kawata and F. Matsui, J. Photochem. Photobiol., A, 2004, 164, 67–73 CrossRef CAS.
- V. P. S. Perera, P. K. D. D. P. Pitigala, M. K. I. Senevirathne and K. Tennakone, Sol. Energy Mater. Sol. Cells, 2005, 85, 91–98 CAS.
- S. Kim, J. K. Lee, S. O. Kang, J. Ko, J. H. Yum, S. Fantacci, F. De Angelis, D. Di Censo, M. K. Nazeeruddin and M. Grätzel, J. Am. Chem. Soc., 2006, 128, 16701–16707 CrossRef CAS PubMed.
- J.-J. Cid, J.-H. Yum, S.-R. Jang, M. K. Nazeeruddin, E. Martínez-Ferrero, E. Palomares, J. Ko, M. Grätzel and T. Torres, Angew. Chem., Int. Ed., 2007, 46, 8358–8362 CrossRef CAS PubMed.
- K. Lee, S. W. Park, M. J. Ko, K. Kim and N.-G. Park, Nat. Mater., 2009, 8, 665–671 CrossRef CAS PubMed.
- T. Bessho, S. M. Zakeeruddin, C.-Y. Yeh, E. W.-G. Diau and M. Grätzel, Angew. Chem., Int. Ed., 2010, 49, 6646–6649 CrossRef CAS PubMed.
- P. J. Holliman, M. L. Davies, A. Connell, B. V. Velasco and T. M. Watson, Chem. Commun., 2010, 46, 7256–7258 RSC.
- X.-F. Wang, Y. Koyama, O. Kitao, Y. Wada, S.-I. Sasaki, H. Tamiaki and H. Zhou, Biosens. Bioelectron., 2010, 25, 1970–1976 CrossRef CAS PubMed.
- M. Planells, L. Pelleja, P. Ballester and E. Palomares, Energy Environ. Sci., 2011, 4, 528–534 CAS.
- K.-M. Lee, Y.-C. Hsu, M. Ikegami, T. Miyasaka, K. R. Justin Thomas, J. T. Lin and K.-C. Ho, J. Power Sources, 2011, 196, 2416–2421 CrossRef CAS.
- F. Huang, D. Chen, L. Cao, R. A. Caruso and Y.-B. Cheng, Energy Environ. Sci., 2011, 4, 2803–2806 CAS.
- M. J. Griffith, A. J. Mozer, G. Tsekouras, Y. Dong, P. Wagner, K. Wagner, G. G. Wallace, S. Mori and D. L. Officer, Appl. Phys. Lett., 2011, 98, 163502 CrossRef.
- P. J. Holliman, M. Mohsen, A. Connell, M. L. Davies, K. Al-Salihi, M. B. Pitak, G. J. Tizzard, S. J. Coles, R. W. Harrington, W. Clegg, C. Serpa, O. H. Fontes, C. Charbonneau and M. J. Carnie, J. Mater. Chem., 2012, 22, 13318–13327 RSC.
- M. Kimura, H. Nomoto, N. Masaki and S. Mori, Angew. Chem., Int. Ed., 2012, 51, 4371–4374 CrossRef CAS PubMed.
- V. Saxena, P. Veerender, A. K. Chauhan, P. Jha, D. K. Aswal and S. K. Gupta, Appl. Phys. Lett., 2012, 100, 133303 CrossRef.
- R. Yeh-Yung Lin, H.-W. Lin, Y.-S. Yen, C.-H. Chang, H.-H. Chou, P.-W. Chen, C.-Y. Hsu, Y.-C. Chen, J. T. Lin and K.-C. Ho, Energy Environ. Sci., 2013, 6, 2477–2486 CAS.
- L. Wei, Y. Yang, R. Fan, P. Wang, L. Li, J. Yu, B. Yang and W. Cao, RSC Adv., 2013, 3, 25908–25916 RSC.
- X. Lu, T. Lan, Z. Qin, Z.-S. Wang and G. Zhou, ACS Appl. Mater. Interfaces, 2014, 6, 19308–19317 CAS.
- L. Yang, W. W.-F. Leung and J. Wang, Nanoscale, 2013, 5, 7493–7498 RSC.
- A. Islam, M. Akhtaruzzaman, T. H. Chowdhury, C. Qin, L. Han, I. M. Bedja, R. Stalder, K. S. Schanze and J. R. Reynolds, ACS Appl. Mater. Interfaces, 2016, 8, 4616–4623 CAS.
- J.-H. Yum, S.-R. Jang, P. Walter, T. Geiger, F. Nuesch, S. Kim, J. Ko, M. Gratzel and M. K. Nazeeruddin, Chem. Commun., 2007, 4680–4682 RSC.
- K. Kakiage, Y. Aoyama, T. Yano, K. Oya, J.-i. Fujisawa and M. Hanaya, Chem. Commun., 2015, 51, 15894–15897 RSC.
- S. Chang, H. Wang, Y. Hua, Q. Li, X. Xiao, W.-K. Wong, W. Y. Wong, X. Zhu and T. Chen, J. Mater. Chem. A, 2013, 1, 11553–11558 CAS.
- C.-L. Wang, J.-Y. Hu, C.-H. Wu, H.-H. Kuo, Y.-C. Chang, Z.-J. Lan, H.-P. Wu, E. Wei-Guang Diau and C.-Y. Lin, Energy Environ. Sci., 2014, 7, 1392–1396 CAS.
- Y. Wang, B. Chen, W. Wu, X. Li, W. Zhu, H. Tian and Y. Xie, Angew. Chem., Int. Ed., 2014, 53, 10779–10783 CrossRef CAS PubMed.
- C.-M. Lan, H.-P. Wu, T.-Y. Pan, C.-W. Chang, W.-S. Chao, C.-T. Chen, C.-L. Wang, C.-Y. Lin and E. W.-G. Diau, Energy Environ. Sci., 2012, 5, 6460–6464 CAS.
- R. Y. Ogura, S. Nakane, M. Morooka, M. Orihashi, Y. Suzuki and K. Noda, Appl. Phys. Lett., 2009, 94, 073308 CrossRef.
- H. Ozawa, R. Shimizu and H. Arakawa, RSC Adv., 2012, 2, 3198–3200 RSC.
- D. D. Babu, D. Elsherbiny, H. Cheema, A. El-Shafei and A. V. Adhikari, Dyes Pigm., 2016, 132, 316–328 CrossRef CAS.
- S.-Q. Fan, C. Kim, B. Fang, K.-X. Liao, G.-J. Yang, C.-J. Li, J.-J. Kim and J. Ko, J. Phys. Chem. C, 2011, 115, 7747–7754 CAS.
- R. Y.-Y. Lin, Y.-S. Yen, Y.-T. Cheng, C.-P. Lee, Y.-C. Hsu, H.-H. Chou, C.-Y. Hsu, Y.-C. Chen, J. T. Lin, K.-C. Ho and C. Tsai, Org. Lett., 2012, 14, 3612–3615 CrossRef CAS PubMed.
- H.-P. Wu, Z.-W. Ou, T.-Y. Pan, C.-M. Lan, W.-K. Huang, H.-W. Lee, N. M. Reddy, C.-T. Chen, W.-S. Chao, C.-Y. Yeh and E. W.-G. Diau, Energy Environ. Sci., 2012, 5, 9843–9848 CAS.
- Y. Chen, Z. Zeng, C. Li, W. Wang, X. Wang and B. Zhang, New J. Chem., 2005, 29, 773–776 RSC.
- J. Chang, C.-P. Lee, D. Kumar, P.-W. Chen, L.-Y. Lin, K. R. J. Thomas and K.-C. Ho, J. Power Sources, 2013, 240, 779–785 CrossRef CAS.
- J. H. Delcamp, Y. Shi, J.-H. Yum, T. Sajoto, E. Dell'Orto, S. Barlow, M. K. Nazeeruddin, S. R. Marder and M. Grätzel, Chem. – Eur. J., 2013, 19, 1819–1827 CrossRef CAS PubMed.
- A. Connell, P. J. Holliman, M. L. Davies, C. D. Gwenin, S. Weiss, M. B. Pitak, P. N. Horton, S. J. Coles and G. Cooke, J. Mater. Chem. A, 2014, 2, 4055–4066 CAS.
- M. D. Brown, P. Parkinson, T. Torres, H. Miura, L. M. Herz and H. J. Snaith, J. Phys. Chem. C, 2011, 115, 23204–23208 CAS.
- C. Siegers, U. Würfel, M. Zistler, H. Gores, J. Hohl-Ebinger, A. Hinsch and R. Haag, ChemPhysChem, 2008, 9, 793–798 CrossRef CAS PubMed.
- M. Shrestha, L. Si, C.-W. Chang, H. He, A. Sykes, C.-Y. Lin and E. W.-G. Diau, J. Phys. Chem. C, 2012, 116, 10451–10460 CAS.
- J. N. Clifford, A. Forneli, H. Chen, T. Torres, S. Tan and E. Palomares, J. Mater. Chem., 2011, 21, 1693–1696 RSC.
- B. E. Hardin, A. Sellinger, T. Moehl, R. Humphry-Baker, J.-E. Moser, P. Wang, S. M. Zakeeruddin, M. Grätzel and M. D. McGehee, J. Am. Chem. Soc., 2011, 133, 10662–10667 CrossRef CAS PubMed.
- L. Martin-Gomis, F. Fernandez-Lazaro and A. Sastre-Santos, J. Mater. Chem. A, 2014, 2, 15672–15682 CAS.
- V. Balzani, L. Moggi and F. Scandola, in Supramolecular Photochemistry, ed. V. Balzani, Springer Netherlands, Dordrecht, 1987, pp. 1–28 DOI:10.1007/978-94-009-3979-0_1.
- D. Astruc, E. Boisselier and C. Ornelas, Chem. Rev., 2010, 110, 1857–1959 CrossRef CAS PubMed.
- T. Mirkovic, E. E. Ostroumov, J. M. Anna, R. van Grondelle, Govindjee and G. D. Scholes, Chem. Rev., 2017, 117, 249–293 CrossRef CAS PubMed.
- R. Amadelli, R. Argazzi, C. A. Bignozzi and F. Scandola, J. Am. Chem. Soc., 1990, 112, 7099–7103 CrossRef CAS.
- M. K. Nazeeruddin, P. Liska, J. Moser, N. Vlachopoulos and M. Grätzel, Helv. Chim. Acta, 1990, 73, 1788–1803 CrossRef CAS.
- C. A. Bignozzi, R. Argazzi, J. R. Schoonover, G. J. Meyer and F. Scandola, Sol. Energy Mater. Sol. Cells, 1995, 38, 187–198 CrossRef CAS.
- M. K. Nazeeruddin, R. Humphry-Baker, M. Gratzel, M. K. Nazeeruddin, R. Humphry-Baker, M. Gratzel and B. A. Murrer, Chem. Commun., 1998, 719–720 RSC.
- T. Rawling, C. Austin, F. Buchholz, S. B. Colbran and A. M. McDonagh, Inorg. Chem., 2009, 48, 3215–3227 CrossRef CAS PubMed.
- C. J. Kleverlaan, M. T. Indelli, C. A. Bignozzi, L. Pavanin, F. Scandola, G. M. Hasselman and G. J. Meyer, J. Am. Chem. Soc., 2000, 122, 2840–2849 CrossRef CAS.
- D. K. Panda, F. S. Goodson, S. Ray, R. Lowell and S. Saha, Chem. Commun., 2012, 48, 8775–8777 RSC.
- D. K. Panda, F. S. Goodson, S. Ray and S. Saha, Chem. Commun., 2014, 50, 5358–5360 RSC.
- H. Lee, L. J. Kepley, H. G. Hong and T. E. Mallouk, J. Am. Chem. Soc., 1988, 110, 618–620 CrossRef CAS.
- T. Ishida, K.-i. Terada, K. Hasegawa, H. Kuwahata, K. Kusama, R. Sato, M. Nakano, Y. Naitoh and M.-a. Haga, Appl. Surf. Sci., 2009, 255, 8824–8830 CrossRef CAS.
- O. O. Ogunsolu, I. A. Murphy, J. C. Wang, A. Das and K. Hanson, ACS Appl. Mater. Interfaces, 2016, 8, 28633–28640 CAS.
- D. Y. Lee, I. Lim, C. Y. Shin, S. A. Patil, W. Lee, N. K. Shrestha, J. K. Lee and S.-H. Han, J. Mater. Chem. A, 2015, 3, 22669–22676 CAS.
- W. A. Maza, A. J. Haring, S. R. Ahrenholtz, C. C. Epley, S. Y. Lin and A. J. Morris, Chem. Sci., 2016, 7, 719–727 RSC.
- D. Y. Lee, D. V. Shinde, S. J. Yoon, K. N. Cho, W. Lee, N. K. Shrestha and S.-H. Han, J. Phys. Chem. C, 2014, 118, 16328–16334 CAS.
- D. Y. Lee, E.-K. Kim, C. Y. Shin, D. V. Shinde, W. Lee, N. K. Shrestha, J. K. Lee and S.-H. Han, RSC Adv., 2014, 4, 12037–12042 RSC.
- H. C. Kolb, M. G. Finn and K. B. Sharpless, Angew. Chem., Int. Ed., 2001, 40, 2004–2021 CrossRef CAS PubMed.
- T. Duan, K. Fan, Y. Fu, C. Zhong, X. Chen, T. Peng and J. Qin, Dyes Pigm., 2012, 94, 28–33 CrossRef CAS.
- T. Duan, K. Fan, K. Li, W. Cao, C. Zhong, X. Chen, T. Peng and J. Qin, Dyes Pigm., 2015, 117, 108–115 CrossRef CAS.
- I. Stengel, N. Pootrakulchote, R. R. Dykeman, A. Mishra, S. M. Zakeeruddin, P. J. Dyson, M. Grätzel and P. Bäuerle, Adv. Energy Mater., 2012, 2, 1004–1012 CrossRef CAS.
- V. Nikolaou, P. A. Angaridis, G. Charalambidis, G. D. Sharma and A. G. Coutsolelos, Dalton Trans., 2015, 44, 1734–1747 RSC.
- E. E. Beauvilliers, M. R. Topka and P. H. Dinolfo, RSC Adv., 2014, 4, 32866–32875 RSC.
- P. K. B. Palomaki and P. H. Dinolfo, Langmuir, 2010, 26, 9677–9685 CrossRef CAS PubMed.
- P. K. B. Palomaki and P. H. Dinolfo, ACS Appl. Mater. Interfaces, 2011, 3, 4703–4713 CAS.
- P. K. B. Palomaki, M. R. Civic and P. H. Dinolfo, ACS Appl. Mater. Interfaces, 2013, 5, 7604–7612 CAS.
- E. L. Unger, S. J. Fretz, B. Lim, G. Y. Margulis, M. D. McGehee and T. D. P. Stack, Phys. Chem. Chem. Phys., 2015, 17, 6565–6571 RSC.
- P. K. D. D. P. Pitigala, M. K. I. Seneviratne, V. P. S. Perera and K. Tennakone, Langmuir, 2004, 20, 5100–5103 CrossRef CAS PubMed.
- J.-F. Gnichwitz, R. Marczak, F. Werner, N. Lang, N. Jux, D. M. Guldi, W. Peukert and A. Hirsch, J. Am. Chem. Soc., 2010, 132, 17910–17920 CrossRef CAS PubMed.
- N. K. Subbaiyan and F. D'Souza, Chem. Commun., 2012, 48, 3641–3643 RSC.
- Y. Kawashima, K. Ohkubo, V. M. Blas-Ferrando, H. Sakai, E. Font-Sanchis, J. Ortíz, F. Fernández-Lázaro, T. Hasobe, Á. Sastre-Santos and S. Fukuzumi, J. Phys. Chem. B, 2015, 119, 7690–7697 CrossRef CAS PubMed.
- G. Charalambidis, K. Karikis, E. Georgilis, B. L. M'Sabah, Y. Pellegrin, A. Planchat, B. Lucas, A. Mitraki, J. Boucle, F. Odobel and A. G. Coutsolelos, Sustainable Energy Fuels, 2017, 1, 387–395 CAS.
- S. K. Balasingam, M. Lee, M. G. Kang and Y. Jun, Chem. Commun., 2013, 49, 1471–1487 RSC.
- Y. Y. Cheng, A. Nattestad, T. F. Schulze, R. W. MacQueen, B. Fuckel, K. Lips, G. G. Wallace, T. Khoury, M. J. Crossley and T. W. Schmidt, Chem. Sci., 2016, 7, 559–568 RSC.
- T.-H. Wang, T.-W. Huang, Y.-C. Tsai, Y.-W. Chang and C.-S. Liao, Chem. Commun., 2015, 51, 7253–7256 RSC.
- G. Griffini, F. Bella, F. Nisic, C. Dragonetti, D. Roberto, M. Levi, R. Bongiovanni and S. Turri, Adv. Energy Mater., 2015, 5, 1401312 CrossRef.
- M. J. Y. Tayebjee, D. R. McCamey and T. W. Schmidt, J. Phys. Chem. Lett., 2015, 6, 2367–2378 CrossRef CAS PubMed.
- F. Inakazu, Y. Noma, Y. Ogomi and S. Hayase, Appl. Phys. Lett., 2008, 93, 093304 CrossRef.
- N. Yusuke, I. Keita, O. Yuhei, S. P. Shyam and H. Shuzi, Jpn. J. Appl. Phys., 2009, 48, 020213 CrossRef.
- P. Se Woong, L. Kyungtae, L. Doh-Kwon, K. Min Jae, P. Nam-Gyu and K. Kyungkon, Nanotechnology, 2011, 22, 045201 CrossRef PubMed.
- F. Lodermeyer, R. D. Costa, J. Malig, N. Jux and D. M. Guldi, Chem. – Eur. J., 2016, 22, 7851–7855 CrossRef CAS PubMed.
- Q. Miao, L. Wu, J. Cui, M. Huang and T. Ma, Adv. Mater., 2011, 23, 2764–2768 CrossRef CAS PubMed.
- E. Y. Kim, S. Yu, J. H. Moon, S. M. Yoo, C. Kim, H. K. Kim and W. I. Lee, Electrochim. Acta, 2013, 111, 261–267 CrossRef CAS.
- J. Lim, M. Lee, S. K. Balasingam, J. Kim, D. Kim and Y. Jun, RSC Adv., 2013, 3, 4801–4805 RSC.
- K. Cao, J. Lu, H. Li, Y. Shen and M. Wang, RSC Adv., 2015, 5, 62630–62637 RSC.
- G.-J. Yang, S.-Q. Fan, C.-J. Li and C.-X. Li, Nanosci. Nanotechnol. Lett., 2011, 3, 483–486 CrossRef CAS.
- J. Bandara, K. Willinger and M. Thelakkat, Phys. Chem. Chem. Phys., 2011, 13, 12906–12911 RSC.
- N. C. Jeong, H.-J. Son, C. Prasittichai, C. Y. Lee, R. A. Jensen, O. K. Farha and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 19820–19827 CrossRef CAS PubMed.
- Z. Xue, L. Wang and B. Liu, Nanoscale, 2013, 5, 2269–2273 RSC.
- J. N. Clifford, E. Palomares, M. K. Nazeeruddin, R. Thampi, M. Grätzel and J. R. Durrant, J. Am. Chem. Soc., 2004, 126, 5670–5671 CrossRef CAS PubMed.
- H. Choi, S. Kim, S. O. Kang, J. Ko, M. S. Kang, J. N. Clifford, A. Forneli, E. Palomares, M. K. Nazeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2008, 47, 8259–8263 CrossRef CAS PubMed.
- M. Dürr, A. Bamedi, A. Yasuda and G. Nelles, Appl. Phys. Lett., 2004, 84, 3397–3399 CrossRef.
- M. Yanagida, N. Onozawa-Komatsuzaki, M. Kurashige, K. Sayama and H. Sugihara, Sol. Energy Mater. Sol. Cells, 2010, 94, 297–302 CrossRef CAS.
- T. Yamaguchi, Y. Uchida, S. Agatsuma and H. Arakawa, Sol. Energy Mater. Sol. Cells, 2009, 93, 733–736 CrossRef CAS.
- W. S. Choi, I. T. Choi, B. S. You, J.-W. Yang, M. J. Ju and H. K. Kim, Isr. J. Chem., 2015, 55, 1002–1010 CrossRef CAS.
- B. Ajay Kumar, F. Naotaka, H. Azwar, O. Yuhei, S. P. Shyam, M. Tingli and H. Shuzi, Appl. Phys. Express, 2015, 8, 102301 CrossRef.
- W. Kubo, A. Sakamoto, T. Kitamura, Y. Wada and S. Yanagida, J. Photochem. Photobiol., A, 2004, 164, 33–39 CrossRef CAS.
- X. D. Zhang, W. M. Liao, W. Mu, D. J. Zheng, Y. S. Zhou, B. L. Xue, W. Liu, Z. Q. Lin and Y. L. Deng, J. Mater. Chem. A, 2014, 2, 11035–11039 CAS.
- K. Uzaki, S. S. Pandey and S. Hayase, J. Photochem. Photobiol., A, 2010, 216, 104–109 CrossRef CAS.
- U. Kenshiro, S. P. Shyam, O. Yuhei and H. Shuzi, Jpn. J. Appl. Phys., 2010, 49, 082301 CrossRef.
- J. He, H. Lindström, A. Hagfeldt and S.-E. Lindquist, Sol. Energy Mater. Sol. Cells, 2000, 62, 265–273 CrossRef CAS.
- F. Odobel, L. Le Pleux, Y. Pellegrin and E. Blart, Acc. Chem. Res., 2010, 43, 1063–1071 CrossRef CAS PubMed.
- A. Nakasa, H. Usami, S. Sumikura, S. Hasegawa, T. Koyama and E. Suzuki, Chem. Lett., 2005, 34, 500–501 CrossRef CAS.
- E. A. Gibson, A. L. Smeigh, L. Le Pleux, J. Fortage, G. Boschloo, E. Blart, Y. Pellegrin, F. Odobel, A. Hagfeldt and L. Hammarström, Angew. Chem., Int. Ed., 2009, 48, 4402–4405 CrossRef CAS PubMed.
- S. Powar, R. Bhargava, T. Daeneke, G. Götz, P. Bäuerle, T. Geiger, S. Kuster, F. A. Nüesch, L. Spiccia and U. Bach, Electrochim. Acta, 2015, 182, 458–463 CrossRef CAS.
- C. J. Wood, G. H. Summers and E. A. Gibson, Chem. Commun., 2015, 51, 3915–3918 RSC.
- H. Choi, T. Hwang, S. Lee, S. Nam, J. Kang, B. Lee and B. Park, J. Power Sources, 2015, 274, 937–942 CrossRef CAS.
- A. Nattestad, A. J. Mozer, M. K. R. Fischer, Y. B. Cheng, A. Mishra, P. Bauerle and U. Bach, Nat. Mater., 2010, 9, 31–35 CrossRef CAS PubMed.
- C. J. Cram and J. M. Cram, Science, 1974, 183, 803–809 Search PubMed.
- D. J. Cram, Angew. Chem., Int. Ed. Engl., 1988, 27, 1009–1020 CrossRef.
- G. Wenz, Clin. Drug Invest., 2000, 19, 21–25 CrossRef CAS.
- M. Freitag and E. Galoppini, Energy Environ. Sci., 2011, 4, 2482–2494 CAS.
- P. Piotrowiak, K. Deshayes, Z. S. Romanova, C. Pagba, S. Hore, G. Zordan, I. Place and A. Farrán, Pure Appl. Chem., 2003, 75, 1061–1068 CrossRef CAS.
- C. Pagba, G. Zordan, E. Galoppini, E. L. Piatnitski, S. Hore, K. Deshayes and P. Piotrowiak, J. Am. Chem. Soc., 2004, 126, 9888–9889 CrossRef CAS PubMed.
- S. A. Haque, J. S. Park, M. Srinivasarao and J. R. Durrant, Adv. Mater., 2004, 16, 1177–1181 CrossRef CAS.
- H. Choi, S. O. Kang, J. Ko, G. Gao, H. S. Kang, M.-S. Kang, M. K. Nazeeruddin and M. Grätzel, Angew. Chem., Int. Ed., 2009, 48, 5938–5941 CrossRef CAS PubMed.
- J. A. Bonacin, S. H. Toma, J. N. Freitas, A. F. Nogueira and H. E. Toma, Inorg. Chem. Commun., 2013, 36, 35–38 CrossRef CAS.
- S. H. Toma, J. A. Bonacin, K. Araki and H. E. Toma, Surf. Sci., 2006, 600, 4591–4597 CrossRef CAS.
- M. Porel, A. Klimczak, M. Freitag, E. Galoppini and V. Ramamurthy, Langmuir, 2012, 28, 3355–3359 CrossRef CAS PubMed.
- M. Freitag and E. Galoppini, Langmuir, 2010, 26, 8262–8269 CrossRef CAS PubMed.
- D. Cummins, G. Boschloo, M. Ryan, D. Corr, S. N. Rao and D. Fitzmaurice, J. Phys. Chem. B, 2000, 104, 11449–11459 CrossRef CAS.
- F. Campus, P. Bonhôte, M. Grätzel, S. Heinen and L. Walder, Sol. Energy Mater. Sol. Cells, 1999, 56, 281–297 CrossRef CAS.
- H.-J. Kim, W. S. Jeon, Y. H. Ko and K. Kim, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 5007–5011 CrossRef CAS PubMed.
- H. Li, F. Li, Y. Wang, L. Bai, F. Yu and L. Sun, ChemPlusChem, 2016, 81, 1056–1059 CrossRef CAS.
- W.-T. Deng, J.-C. Liu, J. Cao, D.-C. Hu, R.-Z. Li and N.-Z. Jin, Dalton Trans., 2014, 43, 626–631 RSC.
- J. Cao, D.-C. Hu, J.-C. Liu, R.-Z. Li and N.-Z. Jin, Org. Electron., 2014, 15, 509–516 CrossRef CAS.
- J. Cao, J.-C. Liu, W.-T. Deng, R.-Z. Li and N.-Z. Jin, Org. Electron., 2013, 14, 2713–2720 CrossRef CAS.
- J. Cao, D.-C. Hu, J.-C. Liu, R.-Z. Li and N.-Z. Jin, J. Coord. Chem., 2013, 66, 4211–4219 CrossRef CAS.
- M. T. Brumbach, A. K. Boal and D. R. Wheeler, Langmuir, 2009, 25, 10685–10690 CrossRef CAS PubMed.
- N. K. Subbaiyan, C. A. Wijesinghe and F. D'Souza, J. Am. Chem. Soc., 2009, 131, 14646–14647 CrossRef CAS PubMed.
- H. B. Gobeze, S. K. Das and F. D’Souza, J. Phys. Chem. C, 2014, 118, 16660–16671 CAS.
- N. K. Subbaiyan, J. P. Hill, K. Ariga, S. Fukuzumi and F. D'Souza, Chem. Commun., 2011, 47, 6003–6005 RSC.
- C. B. Kc, K. Stranius, P. D’Souza, N. K. Subbaiyan, H. Lemmetyinen, N. V. Tkachenko and F. D’Souza, J. Phys. Chem. C, 2013, 117, 763–773 Search PubMed.
- L. A. Martini, G. F. Moore, R. L. Milot, L. Z. Cai, S. W. Sheehan, C. A. Schmuttenmaer, G. W. Brudvig and R. H. Crabtree, J. Phys. Chem. C, 2013, 117, 14526–14533 CAS.
- C. F. A. Negre, R. L. Milot, L. A. Martini, W. Ding, R. H. Crabtree, C. A. Schmuttenmaer and V. S. Batista, J. Phys. Chem. C, 2013, 117, 24462–24470 CAS.
- O. O. Ogunsolu, J. C. Wang and K. Hanson, ACS Appl. Mater. Interfaces, 2015, 7, 27730–27734 CAS.
- J. C. Wang, I. A. Murphy and K. Hanson, J. Phys. Chem. C, 2015, 119, 3502–3508 CAS.
- J. C. Wang, K. Violette, O. O. Ogunsolu and K. Hanson, Phys. Chem. Chem. Phys., 2017, 19, 2679–2682 RSC.
- J. C. Wang, K. Violette, O. O. Ogunsolu, S. Cekli, E. Lambers, H. M. Fares and K. Hanson, Langmuir, 2017 DOI:10.1021/acs.langmuir.7b01964.
- O. O. Ogunsolu, J. C. Wang and K. Hanson, Inorg. Chem., 2017 DOI:10.1021/acs.inorgchem.7b01531.
| This journal is © The Royal Society of Chemistry 2018 |