Incremental NH stretching downshift through stepwise nitrogen complexation of pyrrole: a combined jet expansion and matrix isolation study

Abstract

Aggregates of pyrrole with nitrogen are studied by Fourier transform infrared spectroscopy in supersonic jet expansions as well as in neon, argon and nitrogen cryomatrices. The NH stretching vibration undergoes a significant downshift upon switching from isolated gas phase conditions to bulk nitrogen matrices, which can be reconstructed incrementally by stepwise cluster formation with an increasing number of nitrogen molecules both in supersonic expansions and neon or argon matrices. The modelling of the bulk matrix shift by finite cluster theory remains an interesting challenge. Self-aggregation of pyrrole also yields the first spectra of the homodimer and -trimer in a neon matrix, showing particularly small (up to 10 cm⁻¹) deviations from the isolated gas phase values.

---

1 Introduction

Isolation of transient species or weakly bound molecular aggregates in cryogenic matrices provides one of the most powerful and sensitive methods for subsequent spectroscopic studies of their structure and dynamics.¹ However, spectral shifts and splittings from unperturbed gas phase values due to the bulk environment are frequently observed even for light, soft and less perturbative matrix hosts such as parahydrogen² or neon.³ The significant electric quadrupole moment of molecular nitrogen⁴ results in a comparatively strong perturbation found in corresponding matrices.⁵ Partial positive charges at the centre and negative charges at the molecule ends⁶ lead to a more specific and directional guest–host interaction than for the similarly large argon host.⁷ Stepwise nanocoating of hydrogen-bonded organic compounds with matrix host molecules in supersonic expansions is a useful tool in understanding gas-to-matrix shifts^8–10 and may enable a more rigorous comparison of matrix isolation spectra to theoretical predictions.

In any molecular nitrogen solvation environment, the simple aromatic pyrrole (C₄H₄NH) ring offers the possibility of competition between more directional NH⋯N₂ hydrogen bonds and less directional aromatic π⋯N₂ interactions.¹¹ The NH stretching vibration provides a sensitive indicator for complex formation even with the weakly interacting nitrogen binding partner. Observable effects such as spectroscopic shifts and infrared intensity enhancements are much less pronounced in most other fundamental modes of the symmetric pyrrole molecule and therefore more difficult to judge experimentally. Observation of a possible infrared activation of the NN stretching vibration through complexation^12–14 is hindered by spectral overlap with the antisymmetric stretching vibration of atmospheric carbon dioxide.

Homoaggregates of pyrrole and their respective spectral fingerprints have been studied with a variety of different experimental techniques such as optothermal molecular beam,¹⁵ microwave,^16,17 cavity ring-down,¹⁸ infrared photodissociation¹⁹ and aromatically labelled UV/IR double resonance²⁰ spectroscopy as well as size selection by scattering.²¹ Broadband infrared spectroscopy in para-hydrogen,²² nitrogen^22,23 and argon matrices,⁷ solution^24,25 and supersonic expansions^26,27 as well as most other vibrational spectroscopy focus primarily on the NH stretching region. Corresponding infrared spectra in neon matrices provided in this work facilitate previously uncertain trimer band assignments in argon matrix.⁷

More importantly, NH stretching gas-to-matrix shifts are rationalised and incrementally reproduced by stepwise nitrogen complexation in neon and argon matrices as well as supersonic expansions. All spectra as well as harmonic density functional theory predictions show a weak, but distinct downshift of the NH stretching vibration upon hydrogen bond formation, clearly correcting a proposed unusual upshift based on anharmonic calculations and nitrogen matrix spectra²³ which has received considerable attention^22,28–30 despite being challenged by more reliable calculations.¹⁹

2 Experimental methods

For matrix isolation experiments,^31–34 pyrrole (Aldrich, >98%) was subjected to multiple freeze–pump–thaw cycles under primary vacuum to remove dissolved gases. Pyrrole was then mixed with matrix gases, neon (Air Liquide, N50 grade), argon and nitrogen (Air Liquide, N60 grade), in partial ratii Py/N₂/MG (Py, pyrrole, MG, matrix gas) ranging from 0.25/0/1000 to 0.28/55/1000. Mixtures were deposited onto a gold-plated copper cube cooled to 4.7 K in neon and 20 K in argon and nitrogen by a closed-cycle cryogenerator (Cryomech, PT-405). Cryostat and sample-carrier were protected from thermal background radiation by a chrome-plated brass shield kept at ≈32 K. Controlled heating (Lakeshore, Model 336) of the sample carrier was carried out with a 50 Ω resistor, while the background pressure in the vacuum chamber was kept at 10⁻⁷ mbar by a turbomolecular pump. Fourier transform IR (FTIR) spectra were all recorded at 4.7 K in the reflection mode using a Bruker IFS 66/S spectrometer (resolution: 0.12 cm⁻¹) equipped with a MCT detector.

For measurements in pulsed supersonic expansions,³⁵ helium (Linde, 99.996%) optionally mixed with nitrogen (Air Liquide, 99.996%) was guided through a thermostatted glass saturator containing liquid pyrrole (abcr, 99.8%), resulting in molar fractions of about 0.1% pyrrole in the gas mixture, depending on the vapour pressure controlled by the −20 °C saturator temperature. Hence, mixtures with partial ratii Py/N₂/He ranging from 1/25/1000 to 1/150/1000 were employed for the expansions. From a 67 L Teflon coated reservoir at a stagnation pressure of 0.75 bar the gas escaped through six solenoid valves into a preexpansion chamber connected with the vacuum chamber through a (600 × 0.2) mm² slit nozzle. A Bruker IFS 66v/S FTIR spectrometer equipped with a 150 W tungsten lamp, CaF₂ optics and a liquid nitrogen cooled 3 mm² InSb detector recorded synchronized broadband FTIR spectra of the resulting supersonic jet expansion at a resolution of 2 cm⁻¹ (as a compromise between spectral resolution power and signal-to-noise ratio) with the infrared beam crossing perpendicularly to the gas flow propagation direction. Maintenance of sufficiently low background pressures during 147 ms gas pulses was ensured by an attached 23 m³ buffer volume, continuously evacuated by a series of roots pumps at a speed of 2500 m³ h⁻¹ and a 25 s delay between subsequent pulses. A more detailed description of the setup (filet-jet) can be found in ref. 35.

3 Quantum chemical calculations and nomenclature

The studied molecules are abbreviated as P (pyrrole) and N (nitrogen). For the description of hydrogen bonded cluster compositions, these single letters are repeated in donor–acceptor sequence. The docking site of nitrogen at the pyrrole monomer is marked by a subscript to the N, discriminating between the NH proton (H), the aromatic π electron system (π) or the CH backbone (C). Structure optimisations and harmonic frequency calculations were performed at the B3LYP-D3(BJ)/aVTZ level of computation with the Gaussian09³⁶ (Rev. E01) program package. For selected clusters, these were complemented by additional anharmonic frequency calculations³⁷ (second order vibrational perturbation theory, VPT2) and CCSD(T)/aVTZ single point energies. A full list of all employed keywords can be found in Table S1 in the ESI.† No scaling of calculated harmonic wavenumbers is applied, because the focus is on very small shifts due to matrix interaction which are neither changed significantly by scaling factors nor expected to change much upon proper inclusion of anharmonicity (currently not possible for such weakly interacting, somewhat large molecular complexes).

Structures of P homoclusters (Fig. 1) were reoptimised from known literature models.²⁷ The PP dimer forms a NH⋯π hydrogen bond in a T-shape with the two molecule planes tilted from a perpendicular arrangement to about 55°,¹⁷ similar to pyrrole coordination of other aromatic acceptors.³⁸ The cyclic hydrogen bond topology in the PPP trimer allowing for substantial cooperativity which more than triples the dissociation energy has been experimentally demonstrated by complementary infrared and Raman NH stretching spectra.^18,27

Fig. 1 Stable structures of the pyrrole monomer (P), dimer (PP) and trimer (PPP) optimised at the B3LYP-D3(BJ)/aVTZ level. Harmonically zero-point corrected dissociation energies in kJ mol⁻¹ are provided in parentheses.

In comparison to P homoclusters, nitrogen solvation complexes are energetically substantially less favoured with predicted dissociation energies of about 6 kJ mol⁻¹ for the most stable heterodimers, reasonably close to the experimental value of (6.67 ± 0.08) kJ mol⁻¹ found for the mixed dimer of 1-naphthol and nitrogen.³⁹ For the first attached N₂ molecule with its quadrupole moment comprised of positive partial charge in the molecule centre and negative partial charge at its ends, P offers two almost equally attractive binding sites. The NH proton and the π-electron density above the aromatic ring plane (Fig. 2) compete for the solvent with the first motif winning for positively charged P¹⁹ and the latter being favoured in the most stable binary aggregate of neutral P and argon.⁴⁰ Only the hydrogen bonded N_H complex structure is predicted with a small NH stretching downshift in the double harmonic approximation (Table 1), while π binding is spectrally unimpressive. Both the π-system and the NH proton offer enough space for secondary N₂ attachment and those binding sites are subsequently filled upon increasing complexation. Interactions between attached N₂ molecules open up slightly different structural motifs in larger clusters, but the generally preferred binding sites at P remain the same. Up to the mixed tetramer with three N₂ molecules bound at P, increasing spectral NH stretching downshifts of N_H conformers are predicted harmonically as expected for cooperative solvation. However, for larger aggregates such as pentamers and hexamers the prediction for the most stable solvation complexes switches to small upshifts hinting at substantial difficulties of the employed theoretical method in accurately modelling N₂ embedding which will be demonstrated below. Additional conformers which are more than 1.0 kJ mol⁻¹ less stable than the respective minimum energy structures can be found in Fig. S1–S5 and the respective spectroscopic predictions are summarised in Table S2 in the ESI.† In the absence of detailed interconversion barrier analyses, it remains unclear which of the higher energy structures may contribute to the kinetically controlled jet experiments. For all cluster sizes, there are significantly (>5 cm⁻¹) downshifting structure representatives (typically involving N_H coordination), but they tend to move higher in relative energy with increasing coordination number. One evident trend in these computed data independent on complex binding energy is that directed NH⋯N₂ contacts often lead to downshifts of the NH stretching frequency, whereas structures with NH pointing between two N₂ units tend to show slight upshifts.

Fig. 2 Most stable structures found for heteroaggregates of the pyrrole monomer (P) with increasing N₂ coordination optimised at the B3LYP-D3(BJ)/aVTZ level. Relative energies in kJ mol⁻¹ calculated from CCSD(T)/aVTZ single-point calculations and harmonic zero-point vibrational energy from B3LYP-D3(BJ)/aVTZ are given in parentheses (bottom row exclusively B3LYP-D3(BJ)/aVTZ energies).

Table 1 Theoretically predicted properties of the most stable P and N₂ aggregates such as harmonic (ω_NH) and anharmonic ([small nu, Greek, tilde]_NH) NH stretching wavenumbers, lowest predicted harmonic (ω_L) and anharmonic ([small nu, Greek, tilde]_L) wavenumbers in cm⁻¹, harmonic (S_ω) and anharmonic (S_ν) infrared band strengths in km mol⁻¹, spectroscopic shifts (Δω_NH, Δ[small nu, Greek, tilde]_NH) relative to P in cm⁻¹ as well as relative electronic and harmonically zero-point corrected energies ΔE_e and ΔE₀ compared to the most stable cluster conformation in kJ mol⁻¹. All properties were calculated at the B3LYP-D3(BJ)/aVTZ level of approximation. Only the electronic energy was taken from CCSD(T)/aVTZ single-point calculations for all clusters except hexamers

Structure	ω NH	S ω	ΔωNH	ω L	[small nu, Greek, tilde] NH	S ν	Δ[small nu, Greek, tilde]NH	[small nu, Greek, tilde] L	ΔEe	ΔE0
P	3674	65	—	496	3508	51	—	492	—	—
PP	3669	72	−5	17	—	—	—	—	—	—
	3598	324	−76
PPP	3553	631	−121
	3553	631	−121	22	—	—	—	—	—	—
	3536	0	−138
PNπ	3674	65	0	21	3507	51	−1	(18 810)	0.0	0.0
PNH	3669	206	−5	11	3506	133	−2	(20)	0.8	0.7
PNπNπ	3673	65	−1	18	3517	52	9	(132)	0.0	0.0
PNπNH	3668	210	−6	10	3505	131	−3	(−22)	0.4	0.5
PNπNH	3675	94	1	8	3508	69	0	(23)	0.7	0.5
PNπNπNH	3667	214	−7	9	—	—	—	—	0.0	0.0
PNπNπNH	3674	98	0	12	—	—	—	—	0.5	0.1
PNπNHNH	3677	100	3	11	—	—	—	—	0.8	0.3
PNπNπNHNH	3676	122	2	10	—	—	—	—	0.0	0.0
PNπNπNHNH	3676	104	2	9	—	—	—	—	0.0	0.1
PNπNπNHNH	3678	168	4	4	—	—	—	—	0.1	0.3
PNπNπNHNHNH	3674	142	0	3	—	—	—	—	0.0	0.0
PNπNπNHNHNH	3674	174	0	8	—	—	—	—	0.1	0.1

---

Anharmonic predictions for low frequency large amplitude motions are unphysical in all tested cases except the rigid P monomer, indicating limitations of the VPT2 approach when treating soft, nonrigid molecular systems such as nitrogen aggregates.¹⁰ While localised high frequency modes such as NH stretching vibrations are typically less affected, errors are still introduced via coupling to the low frequency vibrations and could be of similar magnitude as the entire hydrogen bond induced shift.

4 Results and discussion

4.1 Neon, argon and nitrogen matrices

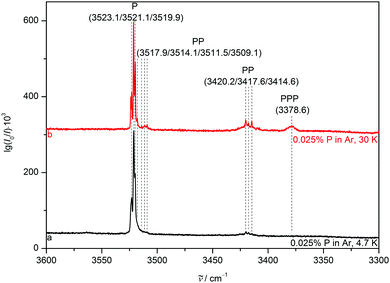
To reduce competition between the formation of energetically favoured P homoclusters and nitrogen complexation, P is highly diluted to concentrations as low as 0.025% for all matrices, minimising homoaggregation. NH stretching FTIR spectra of P in a neon (Fig. 3) matrix show a broad and structured monomer band, ranging from 3540 to 3525 cm⁻¹. This provides strong evidence for the sensitivity of the NH stretching mode to different lattice environments even for the partially quantum-delocalized and soft neon matrix and underscores the suitability of pyrrole for such a kind of study. After annealing to 9 K cluster formation is increased and the PP donor vibration at 3433.8 cm⁻¹ gains intensity as well as the PPP band at 3386.0 cm⁻¹. In the argon matrix⁷ (Fig. 4) site splitting between 3523.1, 3519.9 and the dominant site at 3521.1 cm⁻¹ is observed for P. After annealing to 30 K the PP donor vibrations at 3420.2, 3417.6 and 3414.6 cm⁻¹ gain intensity and various PP acceptor and PPP vibrations emerge at 3517.9, 3514.1, 3511.5, 3509.1 and 3378.6 cm⁻¹. The vibrational signal at 3378.6 cm⁻¹ was also observed in the previous work by Fausto and co-workers⁷ and very tentatively assigned to the tetramer. The gas phase shift trend²⁷ (Table 2) already makes an assignment to the trimer more likely, which is further corroborated by the new neon matrix value. It is not unexpected that the neon matrix shows the smallest deviations from the jet spectral positions.

Fig. 3 NH stretching FTIR spectra of 0.025% pyrrole in a neon matrix after deposition at 4.7 K (trace a) and after annealing to 9 K and recooling to 4.7 K (trace b). Wavenumbers and assignments are provided.

Fig. 4 NH stretching FTIR spectra of 0.025% pyrrole in an argon matrix after deposition at 20 K and subsequent cooling to 4.7 K (trace a) as well as after annealing to 30 K and recooling to 4.7 K (trace b). Wavenumbers and (tentative) assignments are provided.

Table 2 NH stretching band centre positions ([small nu, Greek, tilde]) in cm⁻¹ of the pyrrole monomer (P), dimer (PP) and trimer (PPP) measured in supersonic expansion and different cryomatrices as well as the gas-to-matrix wavenumber shift induced by matrix isolation (Δ[small nu, Greek, tilde]_mi) in cm⁻¹. Separate analysis for PP acceptor (upper row) and donor (lower row) vibrations is included

Structure	P		PP		PPP
	[small nu, Greek, tilde]	Δ[small nu, Greek, tilde]mi	[small nu, Greek, tilde]	Δ[small nu, Greek, tilde]mi	[small nu, Greek, tilde]	Δ[small nu, Greek, tilde]mi
Supersonic expansion^27	3531	—	3524	—	3393	—
			3444	—
Neon	3540, 3525	9, −6	3434	−10	3386	−7
para-Hydrogen^22	3520	−11	3515, 3512	−9, −12	3385	−8
			3424, 3417	−20, −27
Argon^7	3524, 3520	−7, −11	3418, 3409	−26, −35	3396^7	3
					[3378]^27	−15
Nitrogen^22,23	3520, 3509	−11, −22	3504, 3501	−20, −23	3385, 3380	−8, −13
			3424, 3415	−20, −29

---

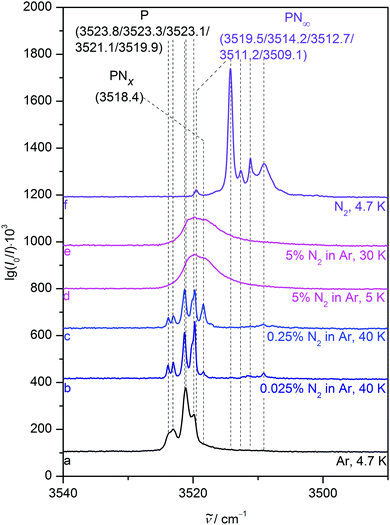
In a nitrogen matrix (Fig. 5), the monomer band also displays substantial site splitting with peaks at 3519.5, 3514.2, 3512.7, 3511.2 and 3509.1 cm⁻¹. After annealing to 30 K, unstable sites are depopulated in favour of mainly that at 3514.2 cm⁻¹. Only small fractions of the sites at 3509.1 and 3519.5 cm⁻¹ remain with the latter being falsely assumed as a sign of an upshifted NH stretching band position due to NH⋯N₂ hydrogen bonding in the binary aggregate of P and nitrogen in ref. 23. The PP donor and PPP vibrations also grow in at 3423.8, 3417.5, 3415.1, 3385.0 and 3379.6 cm⁻¹, alongside two acceptor vibrations at 3503.5 and 3501.1 cm⁻¹.

Fig. 5 NH stretching FTIR spectra of 0.025% pyrrole in a nitrogen matrix after deposition at 20 K and subsequent cooling to 4.7 K (trace a) as well as after annealing to 30 K and recooling to 4.7 K (trace b). Wavenumbers and (tentative) assignments are provided.

The gas-to-matrix shift of the monomer increases from the weakly interacting neon over para-hydrogen and the more polarisable argon to quadrupolar nitrogen (Table 2). Similar behaviour with larger shifts due to cooperative effects⁹ is found for the dimer, although para-hydrogen-, nitrogen- and argon-induced shifts are rather similar. The cyclic trimer does not offer the acceptor NH as an attractive interaction site for the matrix host molecules, therefore the gas-to-matrix shifts are smaller and more uniform across the different matrix hosts than the ones observed for the dimer, closely mirroring effects found for small aliphatic alcohols.⁹ The consistently smaller matrix shift for the trimer is further proof of its cyclic nature, also in a strongly perturbing matrix environment.

4.2 Nitrogen added to neon and argon matrices

A noticeable average NH stretching downshift of roughly 18 cm⁻¹ occurs for P when switching from neon to nitrogen hosts, most likely due to NH⋯N₂ interactions. Stepwise addition of small nitrogen fractions such as 0.025 and 0.5% to neon matrices (Fig. 6, traces b to e) incrementally reproduces this shift. The N₂ enriched neon matrices sustain annealing to 15 K for a few seconds and yield previously not observed downshifted bands at 3524.9, 3524.0, 3518.6, 3516.2 and 3514.7 cm⁻¹, which are attributed to complexes of P and N₂ in a neon environment, although assignment to certain calculated heteroaggregate structures (Fig. 2) is somewhat difficult in a bulk matrix. Annealing allows the different components to diffuse and create the molecular complexes, which most likely include a variety of NH and N_π aggregates as indicated by the broad range of observed downshifts. Addition of a larger nitrogen fraction of 5% (trace f) results in a broad NH stretching signal centred at 3520.2 cm⁻¹, which is further downshifted to a position at 3515.5 cm⁻¹ after annealing to 9 K (trace g), in close proximity to the dominant pure nitrogen matrix band position (trace h). We attribute the loss of structure upon increased N₂ admixture to an incomplete and amorphous N₂ embedding, i.e. interactions with N₂ enriched neon matrix grains. This incomplete N₂ embedding induces an inhomogeneous broadening due to a more dispersed distribution of nearly equivalent classes of oscillators.

Fig. 6 NH stretching FTIR spectra of 0.025% pyrrole in a neon matrix after deposition at 4.7 K (trace a). Spectra of neon matrices with increasing nitrogen addition (traces b to g) before and after annealing to the stated temperature and subsequent recooling to 4.7 K as well as a nitrogen matrix deposited at 20 K and subsequently cooled to 4.7 K (trace h) are also included. Wavenumbers and (tentative) assignments are provided.

Very similar behaviour is observed in argon matrices (Fig. 7), even though the band positions of P in pure argon are already closer to the N₂ matrix bands than corresponding neon transitions. Adding small amounts of 0.025 and 0.25% N₂ to the argon matrix and annealing to 40 K (traces b and c) results in new features at 3518.4 and 3509.1 cm⁻¹, most likely due to binary PN complexes. The larger 5% nitrogen fraction (traces d and e) again results in a broad band that is downshifted towards the pure N₂ matrix band position (trace f). Interestingly, this approach to pure N₂ is spectrally less complete for the argon host (3520 cm⁻¹) than for the neon host, in particular after annealing (3515 cm⁻¹). This probably reflects the softness of the neon matrix, which allows for a closer arrangement of the N₂ dopant around P, still sufficiently diluted by the matrix host to prevent sharp spectral features due to long range order. Indeed, neon is one of the softest matrices, exhibiting a crystal force constant⁴¹ of 3.6 compared to 5.4 and 8.2 mdyn Å⁻¹ in the case of nitrogen and argon matrices, respectively.

Fig. 7 NH stretching FTIR spectra of 0.025% pyrrole in an argon matrix after deposition at 20 K and subsequent cooling to 4.7 K (trace a). Spectra of argon matrices with increasing nitrogen addition (traces b to e) before and after annealing to the stated temperature and subsequent recooling to 4.7 K as well as a nitrogen matrix deposited at 20 K and cooled to 4.7 K (trace f) are also included. Wavenumbers and (tentative) assignments are provided.

4.3 Supersonic Expansions

Removing matrix-induced wavenumber shifts in a supersonic expansion (Fig. 8) yields the unperturbed P band position of 3531 cm⁻¹ and a hot band (P_hot) at 3507 cm⁻¹, in excellent agreement with previous studies.^18,26,27 The hot transition occurs due to insufficient vibrational cooling of the thermally excited out-of-plane bending mode ν₁₆ at 474.61 cm⁻¹ in the helium jet expansion.²⁷

Fig. 8 NH stretching FTIR jet spectra of about 0.1% pyrrole expanded in different mixtures of nitrogen and helium (traces a, c, e and g) as well as monomer-subtracting difference spectra (traces b, d and f). Trace h is taken from Fig. 5 (trace a) and divided by 2000. Wavenumbers and (tentative) assignments are provided.

Adding 2.5 and 5% N₂ to the gas mixture (traces c and e) results in a new feature at 3527 cm⁻¹, more clearly visible in the P-corrected difference spectra (traces b and d). Similar expansion conditions resulted in the formation of singly or doubly nitrogen coordinated clusters of alcohols^9,42 or carboxylic acids¹⁰ and the 5 cm⁻¹ downshift from the isolated monomer is in reasonable agreement with the nitrogen-induced shifts in neon and argon matrices as well as harmonic predictions for various small NH-coordinated PN clusters. If 15% nitrogen is added to the helium carrier gas (traces f and g), a band at 3518 cm⁻¹ emerges. The close proximity to the N₂ matrix band position suggests nitrogen nanocoating of P in the expansion, analogous to effects observed for alcohol dimers under similar expansion conditions.⁹ It would be desirable to quantify the spectral effects of stepwise N₂ coating of pyrrole using size-selective and/or high resolution ro–vibrational spectroscopy, but for the time being, the qualitative trends are unambiguous in terms of the direction of the wavenumber shift.

5 Conclusions

Stepwise nitrogen complexation of the pyrrole monomer in neon and argon matrices as well as supersonic expansions nicely bridges the gap between isolated gas phase and bulk nitrogen matrix environments (Fig. 9). The total gas-to-matrix downshift of the NH stretching vibration is incrementally reproduced, initially by coordination of a few nitrogen molecules at the NH proton. Density functional theory within the double harmonic approximation is able to describe this effect with reasonable accuracy. The final bulk matrix NH stretching band position is approached by embedding of pyrrole in larger amounts of nitrogen both in cryogenic matrices and the gas phase. Standard harmonic calculations for larger pyrrole nitrogen clusters clearly fail to accurately describe the bulk limit but it remains unclear whether this is due to their finite size and amorphous character or due to an electronic structure or anharmonicity deficiency. The −16.6 cm⁻¹ bulk N₂ wavenumber shift represents a challenging experimental benchmark which promises to provide deep insights into weak hydrogen bond and packing effects, if addressed properly by theory.⁴³ We anticipate that this may even be possible to a satisfactory degree in the harmonic oscillator approximation, if a possible ''forced contact'' nature of the NH⋯N₂ interaction in the bulk matrix is considered. For this, accurate pair potentials of dinitrogen⁴⁴ have to be combined with interaction potentials for pyrrole-N₂, perhaps in the form of neural networks.⁴⁵ This might confirm on a quantitative level what the present contribution shows qualitatively, based on multiple experimental evidence: significant upshifting of the NH stretching fundamental induced by N₂ is neither an issue in the matrix nor in the gas phase.

Fig. 9 NH stretching band positions of the pyrrole monomer in neon and argon cryomatrices as well as in supersonic helium expansions. Increasing nitrogen admixture causes progressive downshifts of the band position in all three environments, approaching the bulk N₂ matrix limit. High resolution gas phase²⁶ and nitrogen matrix spectra allow for an accurate determination of the total gas-to-matrix downshift to 16.6 cm⁻¹. The range of wavenumber shifts predicted for the most stable pyrrole-nitrogen complexes by harmonic B3LYP-D3(BJ)/aVTZ calculations nicely reproduces experimental findings with reasonable accuracy for the first three added nitrogen molecules, but the tested approach fails to describe continuous downshifts in more nitrogen-enriched environments and the bulk limit.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

S. Oswald thanks the FCI for a generous scholarship.

References

1. E. Whittle, D. A. Dows and G. C. Pimentel, J. Chem. Phys., 1954, 22, 1943–1944.
2. K. Yoshioka, P. L. Raston and D. T. Anderson, Int. Rev. Phys. Chem., 2006, 25, 469–496.
3. C. Pirim and L. Krim, Phys. Chem. Chem. Phys., 2011, 13, 19454–19459.
4. A. D. Buckingham, R. L. Disch and D. A. Dunmur, J. Am. Chem. Soc., 1968, 90, 3104–3107.
5. S. Coussan, Y. Bouteiller, J. P. Perchard and W. Q. Zheng, J. Phys. Chem. A, 1998, 102, 5789–5793.
6. G. L. D. Ritchie, J. N. Watson and R. I. Keir, Chem. Phys. Lett., 2003, 370, 376–380.
7. A. Gómez-Zavaglia and R. Fausto, J. Phys. Chem. A, 2004, 108, 6953–6967.
8. J. J. Lee, S. Höfener, W. Klopper, T. N. Wassermann and M. A. Suhm, J. Phys. Chem. C, 2009, 113, 10929–10938.
9. S. Oswald, M. Wallrabe and M. A. Suhm, J. Phys. Chem. A, 2017, 121, 3411–3422.
10. S. Oswald, E. Meyer and M. A. Suhm, J. Phys. Chem. A, 2018, 122, 2933–2946.
11. R. Kanakaraju and P. Kolandaivel, Int. J. Mol. Sci., 2002, 3, 777–789.
12. L. Fredin, B. Nelander and G. Ribbegård, J. Mol. Spectrosc., 1974, 53, 410–416.
13. L. Andrews and S. R. Davis, J. Chem. Phys., 1985, 83, 4983–4989.
14. J. Sadlej, B. Rowland, J. P. Devlin and V. Buch, J. Chem. Phys., 1995, 102, 4804–4818.
15. C. Douketis and J. P. Reilly, J. Chem. Phys., 1992, 96, 3431–3440.
16. U. Nygaard, J. Nielsen, J. Kirchheiner, G. Maltesen, J. Rastrup-Andersen and G. O. Sørensen, J. Mol. Struct., 1969, 3, 491–506.
17. G. Columberg and A. Bauder, J. Chem. Phys., 1997, 106, 504–510.
18. Y. Matsumoto and K. Honma, J. Chem. Phys., 2007, 127, 184310.
19. M. Schütz, Y. Matsumoto, A. Bouchet, M. Öztürk and O. Dopfer, Phys. Chem. Chem. Phys., 2017, 19, 3970–3986.
20. S. Kumar and A. Das, J. Chem. Phys., 2012, 136, 174302.
21. V. Profant, V. Poterya, M. Fárník, P. Slavícek and U. Buck, J. Phys. Chem. A, 2007, 111, 12477–12486.
22. S. Sarkar, N. Ramanathan, R. Gopi and K. Sundararajan, J. Mol. Struct., 2017, 1149, 387–403.
23. P. Pandey, RSC Adv., 2015, 5, 79661–79664.
24. M.-C. Bernard-Houplain and C. Sandorfy, Can. J. Chem., 1973, 51, 1075–1082.
25. V. Stefov, L. Pejov and B. Šoptrajanov, J. Mol. Struct., 2003, 649, 231–243.
26. A. Mellouki, R. Georges, M. Herman, D. L. Snavely and S. Leytner, Chem. Phys., 1997, 220, 311–322.
27. I. Dauster, C. A. Rice, P. Zielke and M. A. Suhm, Phys. Chem. Chem. Phys., 2008, 10, 2827–2835.
28. K. B. Moore, K. Sadeghian, C. D. Sherrill, C. Ochsenfeld and H. F. Schaefer, J. Chem. Theory Comput., 2017, 13, 5379–5395.
29. S. A. McDowell, Chem. Phys. Lett., 2017, 674, 146–150.
30. D. L. Jadhav, N. K. Karthick, P. P. Kannan, R. Shanmugam, A. Elangovan and G. Arivazhagan, J. Mol. Struct., 2017, 1130, 497–502.
31. A. Trivella, T. N. Wassermann, C. Manca Tanner, N. O. B. Lüttschwager and S. Coussan, J. Phys. Chem. A, 2018, 122, 2376–2393.
32. T. N. Wassermann, D. Luckhaus, S. Coussan and M. A. Suhm, Phys. Chem. Chem. Phys., 2006, 8, 2344–2348.
33. A. Trivella, T. N. Wassermann, J. M. Mestdagh, C. Manca Tanner, F. Marinelli, P. Roubin and S. Coussan, Phys. Chem. Chem. Phys., 2010, 12, 8300–8310.
34. T. N. Wassermann, M. A. Suhm, P. Roubin and S. Coussan, J. Mol. Struct., 2012, 1025, 20–32.
35. M. A. Suhm and F. Kollipost, Phys. Chem. Chem. Phys., 2013, 15, 10702–10721.
36. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, O. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian 09 Revision E.01, Gaussian Inc., Wallingford CT, 2009.
37. J. Bloino and V. Barone, J. Chem. Phys., 2012, 136, 124108.
38. C. Pfaffen, D. Infanger, P. Ottiger, H.-M. Frey and S. Leutwyler, Phys. Chem. Chem. Phys., 2011, 13, 14110–14118.
39. R. Knochenmuss, R. K. Sinha and S. Leutwyler, J. Chem. Phys., 2018, 148, 134302.
40. R. K. Bohn, K. W. Hillig and R. L. Kuczkowski, J. Phys. Chem., 1989, 93, 3456–3459.
41. L. Andrews and M. Moskovits, Chemistry and Physics of Matrix-Isolated Species, North-Holland, Amsterdam, 1989.
42. S. Oswald and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 12672–12676.
43. R. A. Mata and M. A. Suhm, Angew. Chem., Int. Ed., 2017, 56, 11011–11018.
44. A. van der Avoird, P. E. S. Wormer and A. P. J. Jansen, J. Chem. Phys., 1986, 84, 1629–1635.
45. J. Behler, Int. J. Quantum Chem., 2015, 115, 1032–1050.

---

Footnote

† Electronic supplementary information (ESI) available: Keywords for calculations, higher energy conformers, detailed theoretical predictions, coordinates of molecular structures. See DOI: 10.1039/c8cp07053a

---