Dimers of acetic acid in helium nanodroplets†
Abstract
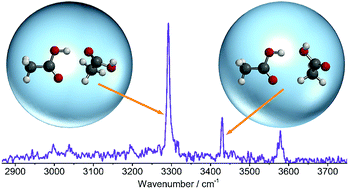
The structural arrangement of small carboxylic acid molecules in the liquid phase remains a controversial topic. Some studies indicate a dominance of the cyclic dimer that prevails in the gas phase, whilst other studies favor short fragments of the infinite catemer chains that are found in the crystalline phase. Furthermore, difficulties in preparing and probing size-selected catemer segments have resulted in a lack of benchmark data upon which theoretical models of the condensed phases can be built. To address these issues, we have combined infrared spectroscopy and quantum chemical calculations to explore regions of the intermolecular potential energy surface associated with the formation of metastable dimer isomers. The OH stretching region of the spectrum shows that aggregation of acetic acid molecules inside liquid helium nanodroplets yields two distinct metastable dimers, whilst negligible signal is observed from the cyclic dimer that typically overwhelms this spectral region. We deduce that the most abundant isomer in superfluid helium has one strong O–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C and one weak C–H⋯O
C and one weak C–H⋯O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C hydrogen bond. Since this bonding motif is common to the dimeric repeating unit of the catemer, it is of fundamental importance for understanding intermolecular interactions in the condensed phases of small carboxylic acids.
C hydrogen bond. Since this bonding motif is common to the dimeric repeating unit of the catemer, it is of fundamental importance for understanding intermolecular interactions in the condensed phases of small carboxylic acids.
- This article is part of the themed collections: Photodissociation and reaction dynamics and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...