Open Access Article
Open Access ArticleTuning phase transitions of aqueous protein solutions by multivalent cations†
Olga
Matsarskaia
 a,
Felix
Roosen-Runge
a,
Felix
Roosen-Runge
 *b,
Gudrun
Lotze
*b,
Gudrun
Lotze
 c,
Johannes
Möller
c,
Alessandro
Mariani
c,
Johannes
Möller
c,
Alessandro
Mariani
 c,
Fajun
Zhang
c,
Fajun
Zhang
 a and
Frank
Schreiber
a and
Frank
Schreiber
 *a
*a
aInstitut für Angewandte Physik, Universität Tübingen, Auf der Morgenstelle 10, 72076 Tübingen, Germany. E-mail: frank.schreiber@uni-tuebingen.de; Fax: +49 7071 295110; Tel: +49 7071 2978663
bDivision of Physical Chemistry, Lund University, Lund, Sweden. E-mail: felix.roosen-runge@fkem1.lu.se
cESRF, Grenoble, France
First published on 18th October 2018
Abstract
In the presence of trivalent cations, negatively charged globular proteins show a rich phase behaviour including reentrant condensation, crystallisation, clustering and lower critical solution temperature metastable liquid–liquid phase separation (LCST–LLPS). Here, we present a systematic study on how different multivalent cations can be employed to tune the interactions and the associated phase behaviour of proteins. We focus our investigations on the protein bovine serum albumin (BSA) in the presence of HoCl3, LaCl3 and YCl3. Using UV-Vis spectroscopy and small-angle X-ray scattering (SAXS), we find that the interprotein attraction induced by Ho3+ is very strong, while the one induced by La3+ is comparatively weak when comparing the data to BSA–Y3+ systems based on our previous work. Using zeta potential and isothermal titration calorimetry (ITC) measurements, we establish different binding affinities of cations to BSA with Ho3+ having the highest one. We propose that a combination of different cation features such as radius, polarisability and in particular hydration effects determine the protein–protein interaction induced by these cations. Our findings imply that subtle differences in cation properties can be a sensitive tool to fine-tune protein–protein interactions and phase behaviour in solution.
1 Introduction
A thorough understanding of phase transitions in protein solutions is of utmost importance for the design and stabilisation of protein-based therapeutics,1,2 disentangling cell-signalling processes,3 finding treatment options for protein condensation diseases4 as well as rationally manipulating pathways of protein crystallisation.5 The heterogeneous charge distribution and intricate interactions with their environment – the latter can additionally be influenced by various parameters including temperature, pH and pressure – make proteins highly complex molecules. In an attempt to better understand and investigate proteins and their interactions with their surroundings, it is thus helpful to make use of simplified physical models.In this context, the framework of colloid theory with corresponding model interaction potentials provides a successful approach. An important insight from colloid science describes the influence of the interaction range between particles on their phase behaviour. Specifically, interparticle attraction on a range smaller than the particle diameter is reflected in a metastable liquid–liquid coexistence region which shifts below the gas-crystal line.6–9 This liquid–liquid coexistence, also referred to as liquid–liquid phase separation (LLPS), can be considered analogous to the liquid–gas transition in the van der Waals gas.10 The experimental evidence for this phenomenon in colloidal systems, which also laid the foundation for its subsequent theoretical rationalisation by Gast et al.,11 was provided by Sperry and co-workers12 in a latex–polymer system with depletion attraction.
Importantly, such phenomena can also be observed in protein solutions. One of the earliest observations of LLPS in a protein system was documented by Tanaka et al. for an aqueous lysozyme–NaCl mixture.13 Since then, many more examples of LLPS in different protein solutions have been described. Examples include crystallins,14–17 different types of hemoglobin,18–20 lysozyme,8,21 polypeptides derived from elastin22 as well as cellular structures.23
Under physiological conditions, proteins and their interactions are influenced by cations such as Na+, K+, Ca2+, Mg2+ or Zn2+.24 Moreover, many proteins, notably serum albumins, can directly bind and transport cations.25 In addition to these physiologically occuring cation species, the interactions of proteins with less common cations such as lanthanides (Ln) are of fundamental interest in toxicology,26,27 the onset and development of neurodegenereative diseases,28,29 bacterial metabolism,30 tumour treatment31,32 as well as spectroscopic33 and diagnostic methods.34–36 Cation-specific effects are not limited to proteins, but similarly occur in soft matter systems. For example, a recent study by Yu et al.37 showed a strong decrease in polyelectrolyte brush lubricity upon the addition of multivalent cations such as Y3+.
Throughout the past years, our group has successfully established a rich phase behaviour induced in negatively charged globular proteins by trivalent salts such as YCl3. It has been found that Y3+ cations introduce a short-range attraction between the protein molecules by forming cation bridges between negatively charged residues of protein molecules,5 leading to a variety of phenomena including crystallisation,5,38,39 cluster formation,39 reentrant condensation,38,40,41 and metastable LLPS39 with a lower critical solution temperature (LCST–LLPS).42–44
A representative salt–protein concentration (cs–cp) phase diagram of a negatively charged globular protein in the presence of a trivalent salt describing our experimental systems is shown in Fig. 1. The dashed arrow in the right part shows the phase transitions at constant cp upon increasing cs. In regime I, at low cs, few cations bind to protein molecules. The overall protein surface charge is negative (left part of Fig. 1) and the net interactions are thus repulsive. An increasing cs leads to a weakened protein surface charge and a subsequent condensation of the protein solution. This area of the phase diagram is referred to as regime II and is separated from regime I by a critical salt concentration c*. Under appropriate conditions, a sample located in a certain region of the phase diagram (orange sphere on yellow ellipsoid) can undergo liquid–liquid phase separation into a protein-rich and a protein-poor phase (brown and yellow spheres on the high- and low-cp edges of the yellow ellipsoid, respectively), which is due to a short-range interprotein attraction induced by cation bridging.38 An even further increase of cs leads to a charge inversion of the protein surface due to an extensive binding of cations upon crossing a second critical salt concentration c**. These experimental findings can be rationalised from a theoretical point of view in the framework of an ion-activated patchy particle model45 which combines a hard-sphere repulsion of the proteins and a square-well attraction induced by cations binding to patches (negatively charged amino acid residues) on the protein surface. This mechanism features similarities to cation-mediated condensation of DNA.46,47 Interestingly, molecular dynamics and Monte Carlo studies by Pasquier et al.48 show an anomalous development of the protein–protein potential of mean force with increasing salt concentration in a system of human serum albumin (HSA) and YCl3. The results obtained by Pasquier et al.48 are in excellent agreement with the different regions of the experimental phase diagram shown in Fig. 1.
 | ||
| Fig. 1 Phase diagram showing regimes I, II and III, reentrant condensation and LLPS. See text for details. | ||
Previous studies showed that this phase behaviour also depends on the choice of the salt. We have found that trivalent salts other than YCl3 (such as FeCl3 and AlCl3) also induce reentrant condensation. However, we established that as opposed to YCl3, pH effects on the reentrant phase behaviour due to salt hydrolysis are significant in the case of FeCl3 and AlCl3.41 Furthermore, we found that for a protein solution with fixed YCl3 concentration, the addition of a monovalent salt could be used to shift the phase boundaries to higher critical concentrations, suggesting a subtle balance of charge repulsion and salt-induced attraction to be essential for the phase behaviour.49 The effect of different counterions of lanthanide cations on the phase behaviour of BSA is subject of a recent investigation.50
Given that details of the interaction potential have a strong influence on the phase behaviour of colloidal systems, we aim at investigating the influence of cations with different radii and chemical properties (Ho3+, La3+ and Y3+). Note that none of these cations cause strong pH effects by hydrolysis, and therefore the changes observed are due to different effective interactions due to subtle differences in the cation properties. Our main interest consists in fine-tuning and controlling the phase behaviour of protein solutions using different cations.
In the present work, we first describe macroscopic observations which evidence that different trivalent cations lead to remarkably strong differences in the phase behaviour of bovine serum albumin (BSA). Determining transition temperatures of different protein–cation mixtures by UV-Vis spectroscopy, we observe a strong interprotein attraction induced by Ho3+ in BSA solutions, whereas these attractions are weaker in the presence of La3+. Systems consisting of BSA and Y3+ are used as a reference. Reduced second virial coefficient values (B2/BHS2) obtained from small-angle X-ray scattering (SAXS) confirm this conclusion. In addition to cation-induced protein interactions, we study cation binding to BSA by zeta potential measurements and isothermal titration calorimetry (ITC) to obtain a comprehensive thermodynamic characterisation of cation–protein interactions.
2 Materials
Bovine serum albumin (BSA, product no. A7906), YCl3, HoCl3 and LaCl3 were purchased from Sigma Aldrich (Taufkirchen, Germany, now Merck, Darmstadt, Germany) and used without further purification. Protein and salt powders were dissolved in ultrapure degassed water (18.2 MΩ, Merck Millipore, Darmstadt, Germany). The exact protein concentration was determined using UV-Vis spectroscopy (Cary 50 UV-Vis spectrometer, Varian Inc., now Agilent Technologies, California, USA; absorbance at 280 nm). Samples were subsequently prepared by mixing appropriate volumes of aqueous protein and salt stock solutions.3 Experimental methods
3.1 Isothermal coexistence phase diagrams
c s–cp phase diagrams were determined at room temperature for 80 mg ml−1 (1.2 mM) BSA and increasing concentrations of HoCl3, LaCl3 and YCl3. The dilute phases were studied by visual inspection and light microscopy. Samples with dilute phases that were homogeneous under the microscope but appeared turbid upon visual inspection were classified as “turbid”. Where liquid–liquid phase separation was visible under the microscope, the samples were labelled as “LLPS”. In the absence of any inhomogeneity, samples were classified as “clear”.3.2 T-Dependent UV-Vis spectroscopy
All of the BSA–trivalent cation systems studied here show a LCST–LLPS-type behaviour. To elucidate the differences in protein–protein interactions induced by the different cations, cation mixtures were used. In order to determine the respective transition temperatures Ttrans from homogeneous to phase-separated states of the BSA–cation mixtures, temperature-dependent UV scans were performed using a Cary 50 UV-Vis spectrometer (Varian Inc., now Agilent Technologies, California, USA) connected to a water bath (Haake A 10B, Thermo Fisher Scientific, Schwerte, Germany). Samples were then subjected to temperature scans at a rate of 0.1 K min−1 while their absorbance was monitored over a wavelength range from 400 to 800 nm. The intensity values of the spectra obtained were summed and divided by the respective number of data points. Ttrans was determined from the maximum of the first derivatives with respect to temperature of the respective curves.3.3 Zeta potential measurements
Zeta potentials were measured by electrophoretic light scattering (ELS) using a Nano Zetasizer (Malvern Instruments, Malvern, United Kingdom). Samples containing 1 mg ml−1 (15 μM) BSA and increasing salt concentrations (0.1, 0.3, 0.5, 0.7 and 1 mM of HoCl3, YCl3 or LaCl3) were prepared shortly before the measurements. The low BSA concentration was chosen to avoid phase separation of the samples. Every sample was measured at 5 different temperatures, with 10 min of equilibration time before each measurement. The ζ potential values were subsequently converted into effective surface charge values Q in units of elementary charge e as explained in the ESI.†3.4 Isothermal titration calorimetry (ITC)
ITC measurements were performed using a MicroCal iTC200 (Malvern Instruments, formerly GE Healthcare). Salt solutions with concentrations of 800 μM or 3 mM were titrated into 1 mg ml−1 (15 μM) BSA solutions in 0.5 μl steps with a duration of 1 s each. A preliminary titration step of 0.2 μl with a duration of 0.5 s was used for equilibration. In the case of the titrations performed with 3 mM salt solution, the durations of these steps were 0.4 and 1 s, respectively. In order to correct for the heat of dilution of the salt, a background measurement was performed by titrating the 800 μM or 3 mM salt solutions into water. The background measurements were subtracted from the salt–protein measurements. For each measurement, 60 injections were performed in total. The time interval between each injection was 90 s with a filter period of 5 s. For titrations with 3 mM salt solutions, these time intervals were 180 and 2.5 s, respectively. The stirring speed of the syringe was 750 rpm and the reference power was set to 1.3 μcal s−1. All data sets were taken at 24 °C.3.5 Small-angle X-ray scattering (SAXS)
SAXS measurements were performed at beamline ID02 (ESRF, Grenoble, France) at a sample–detector distance of 2 m and an energy of 12.46 or 16 keV (λ = 0.8–0.9 Å). The scattered intensity was recorded using a Rayonix MX160 or a FReLoN Kodak CCD detector, covering a q range within 0.01 to 5 nm−1.Samples containing 80 or 85 mg ml−1 (=1.2 or 1.3 mM) BSA and increasing (0–50 mM) concentrations of HoCl3, LaCl3 or YCl3 were prepared at room temperature (ca. 21 °C) and centrifuged for 5 min at 9500 rcf to facilitate phase separation for those samples located in the LLPS region of their respective phase diagrams. Samples were loaded into a flow-through capillary and measured at a constant temperature of 20 °C controlled by a Peltier element connected to the flow cell. In the case of phase-separated samples, the dilute phases were measured. Per sample, 5–10 acquisitions were performed with an exposure time of 0.05–0.1 s. The data were calibrated to absolute intensity using water as a reference.51 Data were averaged and background-corrected using either water or pure salt solutions with appropriate concentrations.
In a SAXS experiment, the scattering intensity I(q) is measured as a function of momentum transfer  with a scattering angle 2θ.52 It can be expressed as
with a scattering angle 2θ.52 It can be expressed as
| I(q) = ΦVparticle(Δρ)2P(q)S(q) | (1) |
In systems with sufficiently high particle concentrations where intermolecular interactions cannot be neglected, the latter are accounted for by the structure factor
 | (2) |
Importantly, the structure factor at q → 0 is proportional to the osmotic compressibility (∂Π/∂c)−1 of the system in question54,55 which can be expanded into a series of virial coefficients An:54,56
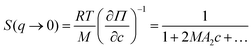 | (3) |
 | (4) |
For cs = 0–3 mM, the form factor was combined with a screened Coulomb (SC) structure factor.59,60 The screened Coulomb potential is expressed as
 | (5) |
For cs ≥ 4 mM, a sticky hard sphere structure (SHS) factor was used.61–63 The SHS potential is expressed as63
 | (6) |
| τ−1 = 4[exp(−ε/kBT) − 1][(a − σ)3 − 1] | (7) |
From τ, the reduced second virial coefficient is obtained via B2/BHS2= 1 − 1/(4τ).58 The fitting routine using the software Igor PRO64 employed here has been described in detail elsewhere (see ref. 38, 43 and 65).
4 Results
4.1 Macroscopic properties of phase-separated samples
Fig. 2 shows a series of samples consisting of aqueous solutions of 80 mg ml−1 (=1.2 mM) BSA and the same concentration (14 mM) of different trivalent salts prepared at 21 °C. In the sample containing YCl3, a moderate amount of a clear, yellowish, dense liquid phase is observed, consistent with earlier observations.5,40,42 The samples made with HoCl3 and GdCl3 form a substantial amount of dense phase; the dense phases are opaque, but still flow slowly. Using CeCl3 leads to a strong decrease of the amount of dense phase, which in this case is transparent. When LaCl3 is used, no dense phase is formed at 21 °C (see also ref. 43). The diffuse turbid region at the bottom of this sample and in the dilute phases of the samples prepared with YCl3 and CeCl3 is presumably due to cluster formation in regime II. This macroscopic observation thus indicates differences in protein–protein and protein–salt interactions induced by the different lanthanide salts used. Based on Fig. 2, the strongest protein–protein interactions are expected for HoCl3 and the weakest ones for LaCl3. We therefore focused our studies on HoCl3 and LaCl3, using YCl3 as a reference system based on extensive previous work.5,38–40,68 | ||
| Fig. 2 Comparison of dense phases of liquid–liquid phase separated samples containing 80 mg ml−1 BSA and different trivalent salts. The protein concentration (cp) is 80 mg ml−1, the salt concentration (cs) is 14 mM in every sample. All samples are located in the LLPS region of regime II of their respective cs–cp phase diagrams. Note that the dense phases obtained in the presence of Ho3+ and Gd3+ may correspond to an arrested state (see text for details). The cationic radii of the lanthanides are obtained from ref. 66 and that of Y3+ from ref. 67. The dashed vertical line between YCl3 and HoCl3 indicates that YCl3 is used as a reference system. | ||
4.2 Isothermal coexistence cs–cp phase diagram
As a first step towards a more quantitative description of the phase behaviours of our systems, phase diagrams were established for BSA in the presence of YCl3, LaCl3 and HoCl3. Homogeneous samples with salt concentrations below c* and beyond c** as well as liquid–liquid coexistence diagrams of phase-separated samples in regime II are shown in Fig. 3. | ||
| Fig. 3 Isothermal phase diagrams of BSA in the presence of LaCl3, HoCl3 and YCl3. Data in (a) are replotted based on ref. 43. In the presence of HoCl3, the dense phases formed feature network-like structures which may indicate aggregation. Nevertheless, these samples still show LCST behaviour and are therefore classified as showing both aggregation and LLPS. | ||
Fig. 3 illustrates the differences in the isothermal phase behaviour of BSA induced by the three different salts studied here. The most striking feature is the complete lack of LLPS at room temperature when LaCl3 is used.43 Using HoCl3, however, leads to a rather broad region of LLPS, larger still than the one induced by YCl3. The BSA–HoCl3 one shows more aggregation than the BSA–YCl3 one. A detailed characterisation of the properties of these dense phases is beyond the scope of the present publication. Nevertheless, the presence of aggregates suggests that the dense phases of the BSA–Ho3+ system may be in an arrested state caused by a stronger intermolecular attraction, as observed for other protein systems.21 This interpretation is further supported by the observation that dense BSA–Ho3+ (and BSA–Gd3+) phases appear turbid after preparation, but can mature into clear dense phases after several weeks.
4.3 Temperature-dependent UV spectroscopy
As an alternative route to investigate the effect of different cations on the macroscopic phase behaviour of our experimental systems, we systematically determined the cloud temperature Ttrans for BSA in the presence of cation mixtures. Fig. 4 shows a typical data set obtained for a constant BSA concentration of 80 mg ml−1 (1.2 mM). The total salt concentration was also kept constant at 10 mM while increasing the HoCl3 fraction and simultaneously decreasing that of LaCl3. Similar scans were also performed using different YCl3/LaCl3 and YCl3/HoCl3 ratio combinations. The transition temperature Ttrans of each system was determined as the maximum of the first derivatives with respect to temperature of the respective integrated absorbance curves. | ||
| Fig. 4 Typical series of T-dependent absorbance measurements (raw data) of samples containing a constant cp of 80 mg ml−1 (1.2 mM) BSA and a constant total ionic strength of 10 mM consisting of different salt ratios (here: HoCl3 & LaCl3). Similar series were also recorded for mixtures of HoCl3 & YCl3 as well as YCl3 and LaCl3. Ttrans values of all samples were compared to a sample with 10 mM pure YCl3 (Fig. 5). | ||
In order to quantify the influence of different cations on Ttrans of the different cation mixtures, the differences in Ttrans values (ΔTtrans) between different mixtures and samples containing 100% YCl3 (the Ttrans of which is 30.6 °C) were calculated (Fig. 5). As can be seen from the rightmost part (HoCl3/LaCl3 mixtures), the strongest ΔTtrans (−15 °C) is obtained in a mixture of 20% LaCl3 and 80% HoCl3. In other words, with higher fractions of HoCl3, the samples phase-separate already at lower T. This is also the lowest overall ΔTtrans observed amongst all mixtures investigated and supports the hypothesis that Ho3+ cations induce the strongest interprotein attraction of all cations studied here. This conclusion is also reflected in the fact that samples containing HoCl3 percentages higher than 80% already phase-separate at 12 °C, the initial equilibration temperature for the measurements presented here. Due to this behaviour, no measurements of BSA–HoCl3/LaCl3 samples containing more than 80% HoCl3 could be performed. When mixtures of YCl3 and HoCl3 (leftmost part of Fig. 5) are considered, any sample with a HoCl3/YCl3 ratio higher than 50/50 also phase-separates already at 12 °C. The higher the fraction of HoCl3, the higher the Ttrans difference to a sample containing only YCl3. Again, this indicates a strong interprotein attraction induced by Ho3+.
In the case of YCl3/LaCl3 mixtures (central part of Fig. 5), the highest ΔTtrans is obtained with the highest LaCl3 concentration. This implies that addition of LaCl3 shifts Ttrans towards higher values, confirming that Y3+ cations induce a stronger interprotein attraction than La3+ cations. Based on these measurements, the cations can be ranked according to the order of increasing cation-induced protein–protein interaction strengths as La3+ < Y3+ < Ho3+.
4.4 Effective interactions characterised by small-angle X-ray scattering
Small-angle X-ray scattering (SAXS) was performed in order to characterise the influence that the different cations investigated have on the protein–protein interactions of BSA. Background-corrected SAXS data obtained for BSA in the presence of an increasing HoCl3 concentration are shown in Fig. 6.Fig. 6 shows that the intensity at low q, I(0), increases and decreases in an alternating fashion. The intensity I(0) at low q was used to qualitatively estimate the strength of the interactions in the systems investigated (Fig. 7).
Fig. 7 shows three cs/cp regimes with consistent results: first, for cs/cp < 7, 1/I(0) behaves comparably for all cations, with a slightly lower 1/I(0) for Ho3+. For cs/cp in the range from 7 to 22, the different phase behaviours induced by Ho3+, Y3+ and La3+ are reflected in the strengths of the respective humps. While no hump is observed for La3+, the humps for Ho3+ and Y3+ are related to the reduced protein concentration in the dilute coexisting phases. As in Fig. 3, the LLPS appears more prominent for HoCl3 (i.e. the density difference between the corresponding dense and dilute phases is larger) than for YCl3, and is absent for LaCl3. Finally, at higher cs/cp (>22), 1/I(0) follows the order Ho3+ < Y3+ < La3+. Together with the trend towards lower Ttrans values for samples containing HoCl3 (Fig. 5), all these features indicate an interprotein attraction decreasing in the sequence HoCl3 > YCl3 > LaCl3, consistent with the above UV-Vis absorbance data in Section 4.3.
In order to further quantify the cation-induced protein–protein interactions, the SAXS curves were treated as follows: for salt concentrations cs < 6 mM, data were fitted using a screened Coulomb (SC) potential structure factor; at higher salt concentrations, a sticky hard sphere (SHS) potential structure factor was used (see model fit in Fig. 6). From the curves fitted with the SHS structure factor, stickiness parameters τ were extracted and used to calculate the reduced second virial coefficients (B2/BHS2 = 1 − 1/(4τ)58). Being related to the osmotic compressibility of the system investigated (see Methods section), these values can be used as a means to determine the overall strength of the interactions of the system in question. In particular, a positive B2/BHS2 indicates overall repulsion whereas negative values indicate net attraction. A value around −1.5 moreover indicates proximity to the critical point of LLPS in colloidal theory.69 The B2/BHS2 values obtained for BSA in the presence of HoCl3, LaCl3 and YCl3 are shown in Fig. 8 as functions of the cs/cp ratio.
 | ||
| Fig. 8 2nd virial coefficients determined from sticky hard sphere potential fits to background-corrected SAXS data. Dashed lines represent guides to the eye. cp is 80 mg ml−1 (1.2 mM) for the BSA–YCl3 and BSA–LaCl3 systems and 85 mg ml−1 (1.3 mM) for the BSA–HoCl3 system. The dark-red dotted line indicates the critical B2/BHS2 value below which phase separation is expected to occur.69 Where not visible, the error bars are smaller than the symbols. | ||
The B2/BHS2 values obtained for the BSA–LaCl3 system show that these samples nearly always show net attractive interactions, but, as confirmed by macroscopic experimental data, do not phase-separate under the given conditions. In the BSA–YCl3 and BSA–HoCl3 systems, however, the B2/BHS2 values indicate phase separation, as is confirmed from macroscopic observations. The systems containing YCl3 and HoCl3 therefore feature overall stronger attractive interactions.
The B2/BHS2 values of the BSA–HoCl3 system are overall more negative than those of YCl3 and differ in spite of the rather similar cationic radii of Y3+ and Ho3+. Note that the reason for the absence of humps as they are observed in the case of the 1/I(0) data in the B2/BHS2 values is the fact that the density difference between the two phases only manifests itself in the 1/I(0) values. The B2/BHS2 values, however, are equal in coexisting dense and dilute phases (see e.g.ref. 69), meaning that no density-dependent signature like the 1/I(0) hump is visible in the B2/BHS2 plot (Fig. 8).
The macroscopic phase behaviours observed here are linked to a combination of cation-induced interprotein interactions and cation–protein binding. To explore the cation binding behaviours to BSA and to explain potential differences between them, a comprehensive thermodynamic analysis using ζ potentials and isothermal titration calorimetry was performed. The results are summarised in the next section.
4.5 Thermodynamics of cation–protein binding: zeta potential and ITC measurements
In order to characterise the binding behaviour of cations to BSA, we measured BSA–salt sample series with increasing salt concentrations at different temperatures.In Fig. 9 an exemplary temperature-dependent raw zeta potential data set of BSA in the presence of HoCl3 system is shown. Corresponding data sets were also obtained for BSA in the presence of YCl3 and LaCl3. For further analysis, the data were fitted using the following equation (see ESI† for derivation):
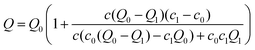 | (8) |
 | ||
| Fig. 9 Temperature-dependent ζ potential data of 1 mg ml−1 BSA with increasing HoCl3 concentrations. Each data point is an average of five measurements, error bars represent the standard deviation. The grey line indicates the point of zero charge (c0, Q = 0). The zeta potential values obtained were converted to elementary charge values using the calculations described in the ESI.† The dashed lines represent fits to the data (eqn (8)). | ||
A first quantitative parameter obtained from the fit is c0 as a function of temperature and type of salt. c0 can be regarded as a measure for the cation–protein affinity. As can be seen from Fig. 10, c0 decreases with temperature in every experimental system. This behaviour underlines the entropy-driven character of cation binding.42 Moreover, a strong difference between the BSA–HoCl3 system and the two other systems becomes obvious – overall, less Ho3+ cations are needed to neutralise the BSA charge, indicating a stronger binding affinity of Ho3+ to BSA.
 | ||
| Fig. 10 c 0 values for the BSA–YCl3, BSA–LaCl3 and BSA–HoCl3 systems (cp = 1 mg ml−1 = 15 μM). The c0 values were determined from fits (eqn (8)) to the raw ζ potential data as shown exemplarily in Fig. 9. Dashed lines are guides to the eye. | ||
The average number of cations binding to the protein surface, N, can be calculated via the relation N = (Q1 − Q0)/3 with Q0 = −9 exploiting the fact that every cation has a charge of +3. The respective values are shown in Fig. 11. As can be seen in Fig. 11, the average number again shows the sequence Ho3+ > Y3+ > La3+, with overall roughly 0.5–0.7 more cations bound for Ho3+ compared to La3+. We remark that the exact choice for Q0 is not essential for comparison between the cations, as the relative sequence in N is robust against variations of Q0.
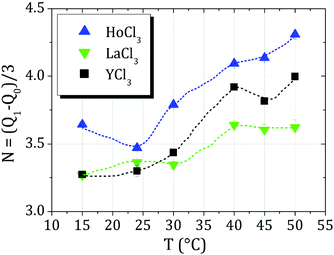 | ||
| Fig. 11 Average number of cations, N, binding to BSA as calculated from ζ potential data as (Q1 − Q0)/3, Q0 = −9. Dashes lines are guides to the eye. | ||
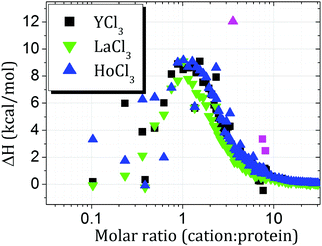
In order to thermodynamically quantify cation–protein binding, isothermal titration calorimetry (ITC) measurements were performed, as shown in Fig. 12. While the profiles for HoCl3 and YCl3 appear to be very similar, the systems with LaCl3 show a smaller enthalpic gain.
ΔHbind was calculated by determining the integral of the curve until the respective molar ratios of zero charge (=20.4 for HoCl3, 29.1 for LaCl3 and 30.9 for YCl3) and divided by Q0/−νs.42 The obtained values read 10.6 kcal mol−1 for HoCl3, 10.4 kcal mol−1 for YCl3 and 7.8 kcal mol−1 for LaCl3, reiterating the observation that LaCl3 shows a smaller value, while HoCl3 and YCl3 appear similar. We note that due to batch-to-batch variations of BSA,70 potentially due to different content of co-ions remaining after the purification process, the absolute values of ΔHbind should not be overinterpreted. Nevertheless, we argue that the values obtained here can be used for a semi-quantitative characterisation of our systems, in particular when comparing the cation–BSA binding for different cations within the same BSA batch.
5 Discussion
Based on the characterisation of cation–protein association and cation-induced protein interactions for different trivalent cations, we now discuss the implications for a general understanding which physicochemical parameters determine the interactions between proteins and multivalent cations.Cation radii are obvious parameters that can be seen as influencing the overall protein–ion interactions. In the present study, this is most clearly reflected in the B2/BHS2 values where stronger attractions go along with smaller cation radii. Similar findings were obtained by Schomäcker et al.71 in a study showing a clearly linear dependence of human serum albumin and human blood serum affinity to Ln cations on cation radius. A publication by Smolka et al.72 furthermore provides a detailed discussion of the role of the cation radius regarding the affinity of Ln cations to α-amylase, a system that is Ca2+-dependent under physiological conditions. According to the authors, the smallest cation is likely to experience the strongest attraction to the protein due to the fact that its charge is concentrated near its binding site on the protein. In the case of a strong cation binding site, this effect can compensate the high hydration free energy of the cation, which leads to an increased protein–cation affinity with decreasing cationic radius.72
While the relationship between cation radius and protein attraction strength appears straightforward in the case of the B2/BHS2 data, the c0 calculations and ITC measurements indicate that the situation is more complex. This suggests that cation–protein binding energies (measured by ITC and zeta potentials) and cation-induced protein–protein bridging energies (measured by Ttrans and B2/BHS2) are not directly coupled. In particular, c0, the salt concentration at the point of zero charge as a measure of cation–protein affinity, is rather similar for Y3+ and La3+, while the c0 values of Ho3+ differ strongly. In contrast, the B2/BHS2 values of Ho3+ and Y3+ resemble each other, whereas those of La3+ are clearly higher. In the case of ITC, the ΔHbind values are comparable for Y3+ and Ho3+ whereas they are lower for La3+, which indicates that no strong trends of cation–protein binding are seen in ITC. This may be caused by uncertainties of the experimental procedure and product purities. Since c0 and B2/BHS2 measure cation–protein binding and cation-mediated protein–protein bridging, respectively, these findings appear to indicate that binding and bridging strengths can be different for the same cation.
A probable explanation for this difference is the different surface geometry in the case of a cation being bound to one protein as opposed to when it is bridging two proteins. As the binding appears to be driven by entropy of hydration water,42 the dehydration due to the first bond to one protein molecule might be very different from that of the second bond to another protein. This explanation also emphasises that cation radii are not the only parameters that need to be taken into account in order to rationalise the influence of different cations on protein phase behaviour. This assumption is corroborated by a study conducted by Gomez et al.73 The authors investigated the abilities of lanthanide and Y3+ cations to restore the Ca2+-dependent biological activity of trypsinogen – another protein known to bind Ca2+ as well as lanthanide and Y3+ cations at aspartic acid residues – after depleting their trypsinogen system of Ca2+. At low lanthanide concentrations (around 10−4 M), the authors did not find a simple relationship between the cation radii and their efficiency in restoring the biological activity. Similarly, a non-monotonic relation between protein–lanthanide affinity and lanthanide radius has been found by Mulqueen et al.74
Gomez et al.73 attribute their findings to potentially incomplete dehydration of different cations upon trypsinogen binding and to different amounts of water molecules bound to the protein–lanthanide complex. This aspect is very important to consider since our experimental system is known to be driven and strongly influenced by hydration effects.42,43 Gomez et al.73 furthermore observe that Y3+ has a protein–cation affinity not fitting into the expected trend based on the cationic radii of the lanthanides. Along with findings indicating that the strengths of different Y3+–ligand complexes vary strongly depending on the ligand chosen and can thus interfere with a straightforward integration of yttrium into trends of the lanthanide series75,76 this provides further evidence that parameters other than radius can play a role in the interactions between proteins and multivalent cations. These can e.g. include electron configuration76,77 as well as cation polarisabilities and resulting dipoles.78
Previous work on the thermodynamic properties of lanthanides79 reports higher entropic contributions for the complexation of Ho3+ to ethylenediaminetetraacetic acid (EDTA). While a protein is certainly more complex than the rather simple EDTA molecule, coordination of lanthanide cations in the case of BSA nevertheless also proceeds via carboxylic groups, making EDTA–lanthanide complex formation a reasonable reference point. Our previous work42 was strongly supported by earlier results obtained for lanthanide and Y cations binding to amino acids in solution.80,81 Together with the zeta potential results which indicate a higher number of cations bound for Ho3+, this can help explain the stronger overall interprotein attraction induced by these cations.
The trypsinogen system investigated by Smolka et al.72 which we mentioned earlier is known to have two cation binding sites, whereas our system features several (around four) sites with varying local geometry. In addition to this, the cations used in the present work do not simply bind to BSA, but also bridge protein molecules and lead to an overall more complex phase behaviour of our system.42,45 The aspects mentioned by Gomez et al.,73 especially cation and complex hydration, might thus have even more intricate effects on our systems. We suggest that these two aspects can thereby help explain the differences in BSA phase behaviour induced by different cations and the difference between Y3+ and Ho3+ in spite of the closeness of their cationic radii. This finding is consistent with the lower Ttrans values in the presence of HoCl3 as well as the larger LLPS areas obtained for BSA with HoCl3.
From a broader perspective on biological matter, it is interesting to compare the protein system to the well-studied example of DNA: analogously to the observations in our protein–cation systems, cation-82 and polymer-83 induced attraction between DNA strands can similarly stabilise and shift the melting temperature of DNA to higher values. An additional factor influencing the melting transition of DNA is its degree of hydration,84 which provides another conceptual link between phase transitions of DNA and proteins. The crucial aspect of hydration in our protein–cation systems will be discussed in more detail in the following.
Computational results on lanthanide cations in the absence of proteins confirm the importance of hydration effects and differences in cation hydration along the lanthanide series. Duvail et al.85 performed an explicit polarisation molecular dynamics study on the exchange frequency (EF) of water molecules between the first hydration shell of lanthanide cations and bulk water. The EF shows a strongly non-monotonic behaviour along the lanthanide series with the maximum EF being observed for Tb3+, a lanthanide cation located close to Ho in the periodic system. Additionally, the authors provide evidence for a change in both hydration water structure and coordination number along the lanthanide series, a result corroborating earlier findings by Habenschuss and Spedding86–88 and studied in even more detail by Zhang et al.89 Persson et al.90 furthermore identified Ho3+ as the cation with the strongest change in hydration structure.
As a general caveat, it should be kept in mind that simulations and calculations for lanthanides and their properties encounter difficulties due to non-negligible relativistic effects89 caused by strong shielding of the nuclear charge,91 a generally large number of electrons and incomplete 4f electron orbital occupation.89 Nevertheless, the above examples show that a large number of such studies exhibits good reproducibility and consistency. We assume that these findings can potentially help explain non-monotonous effects that we observe in our experimental systems and that cannot be explained only by cation radii.
When discussing the effects the cations studied here have on protein phase behaviour, the classification of Y with respect to the lanthanide series is an important aspect to be mentioned. As apparent from the study by Gomez et al.,73 this is not always straightforward. On the one hand, the chemical properties of Y are sufficiently close to the lanthanide series for it to be treated like a lanthanide;92 on the other hand, extensive studies classifying lanthanide and Y complexes with various ligands show that depending on the ligand, Y can behave similarly either to the heavy or the light lanthanides.75,76 This is consistent with our own observations that points of zero charge or enthalpies of Y–BSA binding do not always follow a trend that could be expected based on cation radii or position in the periodic system. Our results confirm that while BSA phase behaviour induced by Y3+ cations is sufficiently similar to that induced by lanthanides, it cannot always be expected to follow similar trends.
6 Conclusions
The experiments presented here offer an insight into the differences in protein phase behaviours – in particular liquid–liquid phase separation (LLPS) – induced by the trivalent cations Y3+, Ho3+ and La3+. Whereas in the case of La3+ no phase separation is observed, Ho3+ leads to the formation of a dense phase which is potentially arrested. When Y3+ is used, the dense phase is more liquid-like. This difference in protein–protein attractions induced by the different cations is reflected in the increase and decrease of the transition temperature Ttrans upon LaCl3 and HoCl3 addition to the BSA samples, respectively. In addition, the stronger interprotein attraction manifests itself in lower reduced second virial coefficient B2/BHS2 values as determined from SAXS experiments. The different cations used in this work can therefore tune thermal sensitivity of the samples. We emphasise that cation radius may not be the only parameter that should be considered when quantifying both cation–protein binding as well as cation-induced protein–protein interactions, and that hydration effects can be particularly important.By carefully choosing multivalent cations, we are able to tune the phase transitions of aqueous BSA solutions. Our results thus provide a deeper understanding of thermodynamic fundamentals of colloidal and soft matter systems. Additionally, our findings are of relevance in the area of stimuli-responsive materials (e.g. for targeted drug delivery and release93 or water pollutant clearance94) where tuning the sensitivity to different environmental factors is of pivotal importance.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge financial support by the Deutsche Forschungsgemeinschaft (DFG) and thank the ESRF for beamtime on beamline ID02. O. M. acknowledges a PhD fellowship by the Studienstiftung des Deutschen Volkes (German Academic Scholarship Foundation) and thanks the PSCM (Grenoble), Thilo Stehle and Nina Jaspert (Tübingen) for sharing their laboratory resources as well as Pinelopi Christodoulou for help with the ITC measurements. F. R.-R. acknowledges funding from the Knut and Alice Wallenberg Foundation (project grant KAW 2014.0052). The authors are grateful to Theyencheri Narayanan (ESRF, Grenoble), Leonardo Chiappisi (ILL, Grenoble), Stefano Da Vela, Martin Oettel and Roland Roth (Tübingen) and Michael Dolg (Cologne) for valuable discussions.References
- Y. Wang, A. Lomakin, T. Hideshima, J. P. Laubach, O. Ogun, P. G. Richardson, N. C. Munshi, K. C. Anderson and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 13359–13361 CrossRef CAS PubMed.
- B. D. Mason, J. Z. van Enk, L. Zhang, R. L. Remmele, Jr. and J. Zhang, Biophys. J., 2010, 99, 3792–3800 CrossRef CAS PubMed.
- J. Berry, S. C. Weber, N. Vaidya, M. Haataja and C. P. Brangwynne, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, E5237–E5245 CrossRef CAS PubMed.
- G. B. Benedek, Invest. Ophthalmol. Visual Sci., 1997, 38, 1911–1921 CAS.
- F. Zhang, G. Zocher, A. Sauter, T. Stehle and F. Schreiber, J. Appl. Crystallogr., 2011, 44, 755–762 CrossRef CAS.
- E. Lomba and N. G. Almarza, J. Chem. Phys., 1994, 100, 8367–8372 CrossRef CAS.
- M. H. J. Hagen and D. Frenkel, J. Chem. Phys., 1994, 101, 4093–4097 CrossRef CAS.
- M. Muschol and F. Rosenberger, J. Chem. Phys., 1997, 107, 1953–1962 CrossRef CAS.
- V. J. Anderson and H. N. W. Lekkerkerker, Nature, 2002, 416, 811–815 CrossRef CAS PubMed.
- P. Papon, S. Schnur, J. Leblond and P. Meijer, The Physics of Phase Transitions: Concepts and Applications, Springer, Berlin Heidelberg, 2006 Search PubMed.
- A. P. Gast, C. K. Hall and W. B. Russel, Faraday Discuss. Chem. Soc., 1983, 76, 189–201 RSC.
- P. R. Sperry, H. B. Hopfenberg and N. L. Thomas, J. Colloid Interface Sci., 1981, 82, 62–76 CrossRef CAS.
- C. Ishimoto and T. Tanaka, Phys. Rev. Lett., 1977, 39, 474–477 CrossRef CAS.
- J. A. Thomson, P. Schurtenberger, G. M. Thurston and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7079–7083 CrossRef CAS.
- P. Schurtenberger, R. A. Chamberlin, G. M. Thurston, J. A. Thomson and G. B. Benedek, Phys. Rev. Lett., 1989, 63, 2064–2067 CrossRef CAS PubMed.
- M. L. Broide, C. R. Berland, J. Pande, O. O. Ogun and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1991, 88, 5660–5664 CrossRef CAS.
- C. R. Berland, G. M. Thurston, M. Kondo, M. L. Broide, J. Pande, O. Ogun and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1992, 89, 1214–1218 CrossRef CAS.
- P. L. San Biagio and M. U. Palma, Biophys. J., 1991, 60, 508–512 CrossRef CAS PubMed.
- O. Galkin, K. Chen, R. L. Nagel, R. E. Hirsch and P. G. Vekilov, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 8479–8483 CrossRef CAS PubMed.
- Q. Chen, P. G. Vekilov, R. L. Nagel and R. E. Hirsch, Biophys. J., 2004, 86, 1702–1712 CrossRef CAS PubMed.
- F. Cardinaux, T. Gibaud, A. Stradner and P. Schurtenberger, Phys. Rev. Lett., 2007, 99, 118301 CrossRef PubMed.
- D. W. Urry, C.-H. Luan, T. M. Parker, D. C. Gowda, K. U. Prasad, M. C. Reid and A. Safavy, J. Am. Chem. Soc., 1991, 113, 4346–4348 CrossRef CAS.
- C. F. Lee, C. P. Brangwynne, J. Gharakani, A. A. Hyman and F. Jülicher, Phys. Rev. Lett., 2013, 1962–1966 Search PubMed.
- A. L. Lehninger, D. L. Nelson and M. M. Cox, Lehninger Principles of Biochemistry, W. H. Freeman, New York, 2005 Search PubMed.
- K. A. Majorek, P. J. Porebski, A. Dayal, M. D. Zimmerman, K. Jablonska, A. J. Stewart, M. Chruszcz and W. Minor, Mol. Immunol., 2012, 52, 174–182 CrossRef CAS PubMed.
- L. M. Gaetke and C. K. Chow, Toxicology, 2003, 189, 147–163 CrossRef CAS PubMed.
- A. Pałasz and P. Czekaj, Acta Biochim. Pol., 2000, 47, 1107–1114 Search PubMed.
- D. R. C. McLachlan, C. Bergeron, J. Smith, D. Boomer and S. L. Rifat, Neurology, 1996, 46, 401–405 CrossRef CAS PubMed.
- V. Rondeau, D. Commenges, H. Jacqmin-Gadda and J.-F. Dartigues, Am. J. Epidemiol., 2000, 152, 59–66 CrossRef CAS PubMed.
- A. Pol, T. R. M. Barends, A. Dietl, A. F. Khadem, J. Eygensteyn, M. S. M. Jetten and H. J. M. Op den Camp, Environ. Microbiol., 2014, 16, 255–264 CrossRef CAS PubMed.
- R. Murthy, R. Nunez, J. Szklaruk, W. Erwin, D. C. Madoff, S. Gupta, K. Ahrar, M. J. Wallace, A. Cohen, D. M. Coldwell, A. S. Kennedy and M. E. Hicks, Oncol. Interv., 2005, 2, S41–S55 Search PubMed.
- R. S. Stubbs, R. J. Cannan and A. W. Mitchell, J. Gastrointest. Surg., 2001, 5, 294–302 CrossRef CAS PubMed.
- A. D. Sherry, E. R. Birnbaum and D. W. Darnall, J. Biol. Chem., 1972, 70, 3489–3494 Search PubMed.
- S. R. Vallabhajosula, J. F. Harwig, J. K. Siemsen and W. Wolf, J. Nucl. Med., 1980, 21, 650–656 CAS.
- P. Caravan, J. J. Ellison, T. J. McMurry and R. B. Lauffer, Chem. Rev., 1999, 99, 2293–2352 CrossRef CAS PubMed.
- E. Dadachova, S. Mirzaeh, S. V. Smith, F. F. Knapp Jr. and E. L. Hetherington, Appl. Radiat. Isot., 1997, 48, 477–481 CrossRef CAS PubMed.
- J. Yu, N. Jackson, X. Xu, Y. Morgenstern, Y. Kaufmann, M. Ruths, J. de Pablo and M. Tirrell, Science, 2018, 1438, 1434–1438 CrossRef PubMed.
- F. Zhang, R. Roth, M. Wolf, F. Roosen-Runge, M. W. A. Skoda, R. M. J. Jacobs, M. Sztucki and F. Schreiber, Soft Matter, 2012, 8, 1313–1316 RSC.
- F. Zhang, F. Roosen-Runge, A. Sauter, R. Roth, M. W. A. Skoda, R. Jacobs, M. Sztucki and F. Schreiber, Faraday Discuss., 2012, 159, 313–325 RSC.
- F. Zhang, M. W. A. Skoda, R. M. J. Jacobs, S. Zorn, R. A. Martin, C. M. Martin, G. F. Clark, S. Weggler, A. Hildebrandt, O. Kohlbacher and F. Schreiber, Phys. Rev. Lett., 2008, 101, 148101 CrossRef CAS PubMed.
- F. Roosen-Runge, B. S. Heck, F. Zhang, O. Kohlbacher and F. Schreiber, J. Phys. Chem. B, 2013, 117, 5777–5787 CrossRef CAS PubMed.
- O. Matsarskaia, M. K. Braun, F. Roosen-Runge, M. Wolf, F. Zhang, R. Roth and F. Schreiber, J. Phys. Chem. B, 2016, 120, 7731–7736 CrossRef CAS PubMed.
- M. K. Braun, M. Wolf, O. Matsarskaia, S. Da Vela, F. Roosen-Runge, M. Sztucki, R. Roth, F. Zhang and F. Schreiber, J. Phys. Chem. B, 2017, 121, 1731–1739 CrossRef CAS PubMed.
- S. Da Vela, M. K. Braun, A. Dörr, A. Greco, J. Möller, Z. Fu, F. Zhang and F. Schreiber, Soft Matter, 2016, 12, 9334–9341 RSC.
- F. Roosen-Runge, F. Zhang, F. Schreiber and R. Roth, Sci. Rep., 2014, 4, 7016 CrossRef CAS PubMed.
- I. Koltover, K. Wagner and C. R. Safinya, Proc. Natl. Acad. Sci. U. S. A., 2000, 97, 14046–14051 CrossRef CAS PubMed.
- A. G. Cherstvy, A. A. Kornyshev and S. Leikin, J. Phys. Chem. B, 2002, 106, 13362–13369 CrossRef CAS.
- C. Pasquier, M. Vazdar, J. Forsman, P. Jungwirth and M. Lund, J. Phys. Chem. B, 2017, 121, 3000–3006 CrossRef CAS PubMed.
- E. Jordan, F. Roosen-Runge, S. Leibfarth, F. Zhang, M. Sztucki, A. Hildebrandt, O. Kohlbacher and F. Schreiber, J. Phys. Chem. B, 2014, 118, 11365–11374 CrossRef CAS PubMed.
- M. K. Braun, A. Sauter, O. Matsarskaia, M. Wolf, F. Roosen-Runge, M. Sztucki, R. Roth, F. Zhang and F. Schreiber, in preparation.
- C. A. Dreiss, K. S. Jack and A. P. Parker, J. Appl. Crystallogr., 2006, 39, 32–38 CrossRef CAS.
- P. Lindner and T. Zemb, Neutrons, X-rays, and Light: Scattering Methods Applied to Soft Condensed Matter, Elsevier, North-Holland, 2002 Search PubMed.
- G. Nägele, The Physics of Colloidal Soft Matter, Institute of Fundamental Technological Research, Warsaw, Poland, 2004 Search PubMed.
- J. Gunton, A. Shiryayev and D. Pagan, Protein Condensation: Kinetic Pathways to Crystallization and Disease, Cambridge University Press, 2007 Search PubMed.
- A. Guinier and G. Fournet, Small-angle scattering of X-rays, Wiley, New York, 1955, vol. 14 Search PubMed.
- W. Schärtl, Light scattering from polymer solutions and nanoparticle dispersions, Springer, 2007 Search PubMed.
- F. Bonneté and D. Vivarès, Acta Crystallogr., Sect. D: Biol. Crystallogr., 2002, 58, 1571–1575 CrossRef.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS.
- J. B. Hayter and J. Penfold, Mol. Phys., 1981, 42, 109–118 CrossRef CAS.
- J.-P. Hansen and J. B. Hayter, Mol. Phys., 1982, 46, 651–656 CrossRef CAS.
- R. J. Baxter, J. Chem. Phys., 1968, 49, 2770–2774 CrossRef CAS.
- S. V. G. Menon, C. Manohar and K. S. Rao, J. Chem. Phys., 1991, 95, 9186–9190 CrossRef CAS.
- M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941–2944 CrossRef CAS.
- S. R. Kline, J. Appl. Crystallogr., 2006, 39, 895–900 CrossRef CAS.
- M. Wolf, F. Roosen-Runge, F. Zhang, R. Roth, M. W. Skoda, R. M. Jacobs, M. Sztucki and F. Schreiber, J. Mol. Liq., 2014, 200, 20–27 CrossRef CAS.
- P. D'Angelo, A. Zitolo, V. Migliorati, G. Chillemi, M. Duvail, P. Vitorge, S. Abadie and R. Spezia, Inorg. Chem., 2011, 50, 4572–4579 CrossRef PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767 CrossRef.
- F. Zhang, F. Roosen-Runge, A. Sauter, M. Wolf, R. M. J. Jacobs and F. Schreiber, Pure Appl. Chem., 2014, 86, 191–202 CAS.
- G. A. Vliegenthart and H. N. W. Lekkerkerker, J. Chem. Phys., 2000, 112, 5364–5369 CrossRef CAS.
- W. L. Hulse, J. Gray and R. T. Forbes, Int. J. Pharm., 2013, 453, 351–357 CrossRef CAS PubMed.
- K. Schomäcker, D. Mocker, R. Münze and G.-J. Beyer, Appl. Radiat. Isot., 1988, 39, 261–264 CrossRef.
- G. E. Smolka, E. R. Birnbaum and D. W. Darnall, Biochemistry, 1971, 10, 4556–4561 CrossRef CAS PubMed.
- J. E. Gomez, E. R. Birnbaum and D. W. Darnall, Biochemistry, 1974, 13, 3745–3750 CrossRef CAS PubMed.
- P. Mulqueen, J. M. Tingey and W. D. W. Horrocks, Biochemistry, 1985, 24, 6639–6645 CrossRef CAS PubMed.
- T. Moeller and R. Ferrús, J. Inorg. Nucl. Chem., 1961, 20, 261–273 CrossRef CAS.
- T. Moeller, D. F. Martin, L. C. Thompson, R. Ferrus, G. R. Feistel and W. J. Randall, Chem. Rev., 1965, 65, 1–50 CrossRef CAS.
- E. Y. Permyakov, Metalloproteomics, Wiley, Hoboken, New Jersey, 2009 Search PubMed.
- C. Clavaguéra and J. P. Dognon, Chem. Phys., 2005, 311, 169–176 CrossRef.
- G. R. Choppin, Pure Appl. Chem., 1971, 27, 23–41 CAS.
- R. S. Sandhu, Monatsh. Chem., 1977, 108, 51–55 CrossRef CAS.
- F. M. Elzawawy, Monatsh. Chem., 1991, 122, 921–925 CrossRef CAS.
- A. G. Cherstvy and A. A. Kornyshev, J. Phys. Chem. B, 2005, 109, 13024–13029 CrossRef CAS PubMed.
- A. González, A. Wildes, M. Marty-Roda, S. Cuesta-López, E. Mossou, A. Studer, B. Demé, G. Moiroux, J. L. Garden, N. Theodorakopoulos and M. Peyrard, J. Phys. Chem. B, 2018, 122, 2504–2515 CrossRef PubMed.
- F. Sebastiani, A. Pietrini, M. Longo, L. Comez, C. Petrillo, F. Sacchetti and A. Paciaroni, J. Phys. Chem. B, 2014, 118, 3785–3792 CrossRef CAS PubMed.
- M. Duvail, R. Spezia and P. Vitorge, Chem. Phys. Chem., 2008, 9, 693–696 CrossRef CAS PubMed.
- A. Habenschuss and F. H. Spedding, J. Chem. Phys., 1979, 70, 2797–2806 CrossRef CAS.
- A. Habenschuss and F. H. Spedding, J. Chem. Phys., 1979, 70, 3758–3763 CrossRef CAS.
- A. Habenschuss and F. H. Spedding, J. Chem. Phys., 1979, 73, 442–450 CrossRef.
- J. Zhang, N. Heinz and M. Dolg, Inorg. Chem., 2014, 53, 7700–7708 CrossRef CAS PubMed.
- I. Persson, P. D'Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Chem – Eur. J., 2008, 14, 3056–3066 CrossRef CAS PubMed.
- P. Pyykkö, Annu. Rev. Phys. Chem., 2012, 63, 45–64 CrossRef PubMed.
- F. G. N. Cloke, Chem. Soc. Rev., 1993, 22, 17–24 RSC.
- M. Constantin, eXPRESS Polym. Lett., 2011, 5, 839–848 CrossRef CAS.
- B. O. Okesola and D. K. Smith, Chem. Soc. Rev., 2016, 97, 219–243 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Calculation of effective protein surface charge from zeta potentials and derivation of zeta potential fitting equation. See DOI: 10.1039/c8cp05884a |
| This journal is © the Owner Societies 2018 |