Probing chirality recognition of protonated glutamic acid dimers by gas-phase vibrational spectroscopy and first-principles simulations†
Abstract
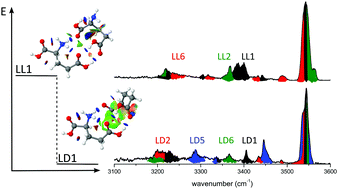
The homochirality of the amino acid metabolism still puzzles biochemists. Vibrational spectroscopy of mass-selected gas-phase amino acids and their clusters can precisely reveal their conformation and might ultimately help to decode the interactions responsible for chirality recognition. Infrared photodissociation (IRPD) and conformer-selective IR–IR hole burning spectra of protonated glutamic acid dimers (LL-/LD-Glu2H+) recorded in the fingerprint and XH stretch ranges (1100–1900 and 2600–3600 cm−1) provide direct insight into their stereospecific interactions. Glu2H+ dimers are generated by electrospray ionization and stored in a cryogenic quadrupole ion trap held at 10 K. The assignment of the IRPD spectra is supported by vibrational analysis using many-body dispersion-corrected hybrid density-functional theory. Sampling of the conformational space is accomplished by basin hopping and replica-exchange molecular dynamics simulations. The most stable LD-Glu2H+ dimer (LD1) is predicted to be more stable than the most stable LL-Glu2H+ dimer (LL1) by ΔE0 = 4.0 kJ mol−1, which relies on stronger secondary interactions in LD1 as demonstrated by the noncovalent interaction method. IR–IR hole burning spectroscopy reveals the coexistence of at least four LD-Glu2H+ and three LL-Glu2H+ conformers. Their IR-dip spectra are assigned to the most stable conformers at room and cryogenic temperature, revealing incomplete thermalization of the ions by kinetic trapping in the cold trap. We observe different population ratios of LL and LD conformers of Glu2H+, as revealed by specific νNH2 and νCO intensities (fingerprints of chirality recognition).
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...