Inelastic vibrational dynamics of CS in collision with H2 using a full-dimensional potential energy surface†
Abstract
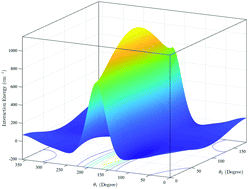
We report a six-dimensional (6D) potential energy surface (PES) for the CS–H2 system computed using high-level electronic structure theory and fitted using a hybrid invariant polynomial method. Full-dimensional quantum close-coupling scattering calculations have been carried out using this potential for rotational and, for the first time, vibrational quenching transitions of CS induced by H2. State-to-state cross sections and rate coefficients for rotational transitions in CS from rotational levels j1 = 0–5 in the ground vibrational state are compared with previous theoretical results obtained using a rigid-rotor approximation. For vibrational quenching, state-to-state and total cross sections and rate coefficients were calculated for the vibrational transitions in CS(v1 = 1,j1) + H2(v2 = 0,j2) → CS(v1′ = 0,j1′) + H2(v2′ = 0,j2′) collisions, for j1 = 0–5. Cross sections for collision energies in the range 1 to 3000 cm−1 and rate coefficients in the temperature range of 5 to 600 K are obtained for both para-H2 (j2 = 0) and ortho-H2 (j2 = 1) collision partners. Application of the computed results in astrophysics is also discussed.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...