Structural and electronic properties of a van der Waals heterostructure based on silicene and gallium selenide: effect of strain and electric field
Abstract
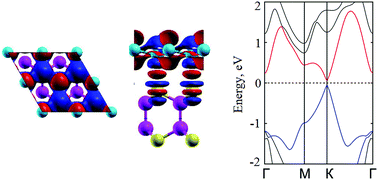
Combining van der Waals heterostructures by stacking different two-dimensional materials on top of each other layer-by-layer can enhance their desired properties and greatly extend the applications of the parent materials. In this work, by means of first principles calculations, we investigate systematically the structural and electronic properties of six different stacking configurations of a Si/GaSe heterostructure. The effect of biaxial strain and electric field on the electronic properties of the most energetically stable configuration of the Si/GaSe heterostructure has also been discussed. At the equilibrium state, the electronic properties of the Si/GaSe heterostructure in all its stacking configurations are well kept as compared with that of single layers owing to their weak van der Waals interactions. Interestingly, we find that a sizable band gap is opened at the Dirac K point of silicene in the Si/GaSe heterostructure, which could be further controlled by biaxial strain or electric field. These findings open up a possibility for designing silicene-based electronic devices, which exhibit a controllable band gap. Furthermore, the Si/GaSe heterostructure forms an n-type Schottky contact with a small Schottky barrier height of 0.23 eV. A transformation from the n-type Schottky contact to a p-type one, or from the Schottky contact to an ohmic contact may occur in the Si/GaSe heterostructure when strain or an electric field is applied.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...