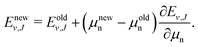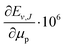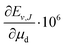Nonrelativistic energy levels of HD
Received
29th August 2018
, Accepted 8th October 2018
First published on 9th October 2018
Abstract
Nonadiabatic exponential functions are employed to solve the four-body Schrödinger equation. Nonrelativistic bound energy levels of the HD molecule are calculated to the relative accuracy of 10−12–10−13, which is the first step toward highly accurate prediction of dissociation and transition energies. Such energies, in connection with equally accurate experimental data, will enable refinement of the physical constant and aid the search for deviations caused by yet unknown interactions at the atomic scale.
1 Introduction
For the hydrogen molecule and its isotopic variants, contemporary spectroscopic measurements have reached the accuracy of 10−5–10−6 cm−1 for selected transition energies.1–7 However, different experiments do not always agree within the claimed accuracy. In particular, for the R(1) transition in the (2,0) overtone band in HD, Cozijn et al.5 have determined this transition energy to the accuracy of 7 × 10−7 cm−1 (20 kHz), whereas Tao et al.7 have reached the accuracy of 3 × 10−6 cm−1 (80 kHz) with results that differ among themselves by about 3 × 10−5 cm−1 (900 kHz). Theoretical calculations could resolve this discrepancy provided a sufficient accuracy (of ca. 10−5 cm−1) is achieved. This requires calculations of nonadiabatic corrections to the quantum electrodynamic contribution, which will be feasible in the near future.
The accuracy of theoretical predictions is ultimately limited by uncertainties in the nucleus–electron mass ratios. For example, the difference between the CODATA 2014 proton–electron mass ratio (μp = mp/me) and the value reported most recently8 leads to a difference of about 7 × 10−7 cm−1 (20 kHz) for the R(1) transition. This means that sufficiently accurate calculations of higher-order quantum electrodynamical effects may lead to the improved determination of the proton–electron mass ratio. Eventually, if one observes any discrepancies that can not be accommodated by physical constants, it will indicate the presence of yet unknown interaction that goes beyond the Standard model.
On the theoretical side, various relativistic and quantum electrodynamic corrections have recently been calculated to a high accuracy,9,10 but the principal problem up to now has been the insufficient accuracy of nonrelativistic energy levels. The purpose of this work is to present a method which enables the uncertainty originating from the nonrelativistic energy to be practically removed from the overall energy budget. This method aims at the precision level of 10−7 cm−1 for the dissociation energy of an arbitrary rovibrational energy level.
From a historical point of view, our work is related to the classic paper by Kołos and Wolniewicz.11 Although, our formalism differs significantly from the one used in their work, that article deserves a mention as the first attempt of a fully nonadiabatic description of the hydrogen molecule. Later on, the nonadiabatic corrections for rovibrational levels of HD were evaluated in the framework of the adiabatic approximation by Wolniewicz12 in 1995 and by us13 in 2010. Two lowest nonrotational levels were studied within a nonadiabatic formalism by Stanke et al.14 in 2009.
2 Theory
Our aim is to find highly accurate variational solutions to the stationary Schrödinger equation ĤΨ = EΨ for a heteronuclear diatomic molecule with the nuclei of charge ZA and ZB and finite masses MA and MB. The four-body Coulomb Hamiltonian for such a system, in atomic units and with a common notation, reads| | 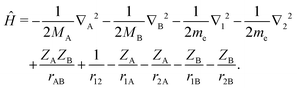 | (1) |
We search for both the eigenvalues E representing energy of bound rovibrational levels and the eigenfunctions Ψ which will be employed in future studies of relativistic and electrodynamic energy corrections.
A properly constructed trial wave function must reflect all symmetries and angular momenta present in the molecule. We assume that the rotational angular momentum of nuclei couples to the electronic angular momentum, ![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , to form the total angular momentum
, to form the total angular momentum ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) of the molecule. Therefore, for a given rotational level J the wave function ΨJ,M, which formally depends also on M—the projection of
of the molecule. Therefore, for a given rotational level J the wave function ΨJ,M, which formally depends also on M—the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) on the Z-axis in the laboratory frame, must involve ingredients describing the subsequent electronic states. The quantum number Λ—the eigenvalue of the
on the Z-axis in the laboratory frame, must involve ingredients describing the subsequent electronic states. The quantum number Λ—the eigenvalue of the ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ·
·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) operator and the inversion symmetry symbol g or u (for gerade or ungerade) are employed to distinguish between such states: Σg,u, Πg,u, Δg,u, Our Ansatz is a sum of components with growing Λ
operator and the inversion symmetry symbol g or u (for gerade or ungerade) are employed to distinguish between such states: Σg,u, Πg,u, Δg,u, Our Ansatz is a sum of components with growing Λ
| | 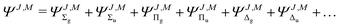 | (2) |
where
| | 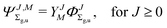 | (3) |
| | 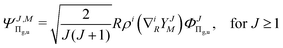 | (4) |
| | 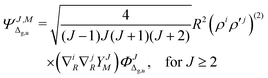 | (5) |
and so on for the higher electronic angular momenta. In the above equations we use the following notation
| | 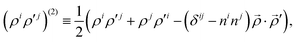 | (6) |
where
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif)
,
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif)
′ ≡
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 1
1 or
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 2
2,
ni ≡
Ri/
R and
ρia = (
δij −
ninj)
rjaB, with the Einstein summation convention assumed. The
YJM =
YJM(
![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif)
) denotes a spherical harmonic. The functions
ΦJΛ represent linear expansions
| | 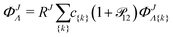 | (7) |
in the following nonadiabatic James-Coolidge (naJC) basis functions
| | 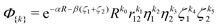 | (8) |
with
ζ1 =
r1A +
r1B,
η1 =
r1A −
r1B,
ζ2 =
r2A +
r2B,
η2 =
r2A −
r2B, and
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif)
=
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) AB
AB. The
α and
β denote nonlinear variational parameters and
ki are non-negative integers collectively denoted as {
k}. The basis functions with
k2 +
k3 even (odd) have the subscript g (u).
The trial four-particle wave function defined above depends explicitly on interparticle distances only, i.e. it is translationally invariant and our results do not depend on the choice of the origin in space.
Evaluation of the overlap and Hamiltonian matrix elements in the naJC basis Φ{k} was described in detail elsewere15 and will not be repeated here.
Due to the mutual orthogonality of the basis functions belonging to different electronic symmetries (〈ΦΛ|ΦΛ′〉 = δΛ′Λ), the overlap matrix ![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) has a block-diagonal structure whereas the Hamiltonian matrix
has a block-diagonal structure whereas the Hamiltonian matrix ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) is block-band diagonal because 〈ΦΛ|Ĥ|ΦΛ′〉 = 0 whenever |Λ − Λ′| > 1, see eqn (9) and (10).
is block-band diagonal because 〈ΦΛ|Ĥ|ΦΛ′〉 = 0 whenever |Λ − Λ′| > 1, see eqn (9) and (10).
| | 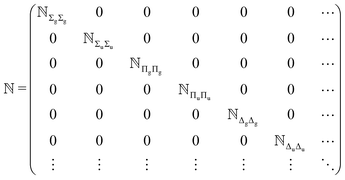 | (9) |
| |  | (10) |
3 Solving the matrix equation
The matrix Schrödinger equation (![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) − E
− E![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) )c = 0 can be solved directly, e.g. by the inverse iteration method, or perturbatively by utilizing the fact that all off-diagonal blocks are proportional to the inverse of nuclear mass, and thus are small. The latter approach is particularly advantageous for very large basis sets—the largest expansion employed in our calculations involved 445
)c = 0 can be solved directly, e.g. by the inverse iteration method, or perturbatively by utilizing the fact that all off-diagonal blocks are proportional to the inverse of nuclear mass, and thus are small. The latter approach is particularly advantageous for very large basis sets—the largest expansion employed in our calculations involved 445![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 basis functions. It is based on the Rayleigh–Schrödinger perturbation expansion of the total energy
498 basis functions. It is based on the Rayleigh–Schrödinger perturbation expansion of the total energy| | | E = E(0) + E(2) + E(3) + E(4)+ … | (11) |
with respect to off-diagonal blocks. The superscript n in E(n) corresponds to the power of the off-diagonal blocks appearing in subsequent energy corrections. The unperturbed energy E(0) = EΣg is obtained from the 0'th order equation| | 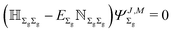 | (12) |
and is numerically several orders of magnitude larger than all the higher-order terms of the series.
The second-order term is expressed as the expectation value
| | 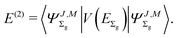 | (13) |
with the perturbation operator defined by
| | 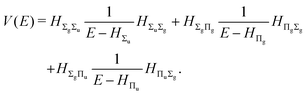 | (14) |
The third-order term reads
| | 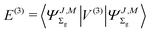 | (15) |
where
| | 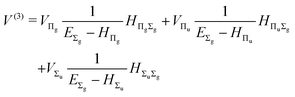 | (16) |
and involves a set of auxiliary operators appearing also in the expressions for
E(4) below
| | 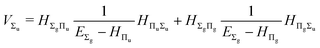 | (17) |
| | 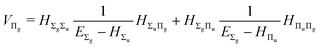 | (18) |
| | 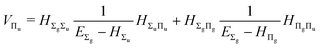 | (19) |
| | 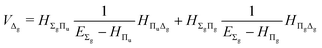 | (20) |
| | 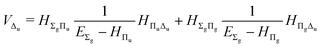 | (21) |
The fourth-order term involves the contributions from Δ states and can be evaluated from
| | 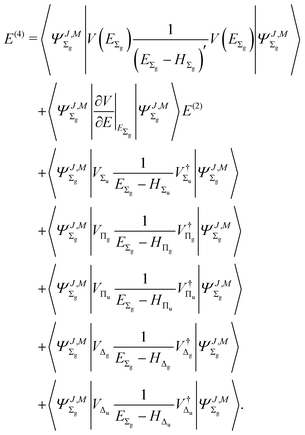 | (22) |
This perturbation expansion converges very rapidly, so including terms up to the fourth order appears to be sufficient to reach the desired accuracy.
4 Technical details and the convergence study
Calculations of the matrix elements as well as the linear algebra were performed in octuple-precision arithmetic.16 Apart from a trivial matrix elements parallelization, the linear algebra tasks were also efficiently parallelized for use on both distributed and shared memory systems. In the former case we applied the Elemental library17 in connection with MPI communication protocol, whereas in the latter—the PLASMA library18 with OpenMP interface. The multithreading has significantly lowered the time limitations of our calculations, additionally, the distributed memory program has lifted the memory barrier.
The nonlinear parameters α and β of the basis function Φ{k} (eqn (8)) were determined variationally. All the basis functions have a common α exponent but separate β exponents for different Λ states. In the first step, the number of basis functions kmaxi saturating the energy up to the 10−9 cm−1 threshold for given Λ were determined. Next, optimal α and βΣg were found. With these two exponents fixed, the βΣu, βΠg, and βΠu were optimized independently. The basis functions of Δ states appear in two variants necessary to make the wave function complete. One, for which (ρiρ′j)(2) of eqn (6) has ρ = ρ′, and the other with ρ ≠ ρ′. Both variants feature their own βΔg and βΔu exponents optimized in the presence of the other βs fixed.
As already mentioned, the E(0) contribution (see eqn (11)) is several orders of magnitude larger than the remaining ones. For this reason, we made a special effort to converge this energy component and we employed a double basis set for its description. Such a double basis set was composed of two sets of basis functions sharing the α exponent but having their own βΣg nonlinear parameters. The optimal parameters and the number of expansion terms were determined for both sets simultaneously.
An indispensable (and requiring serious additional effort) feature of the results of high-precision calculations is the estimated uncertainty assigned to a final result. For basis functions capable of forming a complete basis set, as it is in the present case, the uncertainty can be determined from a convergence pattern obtained by evaluation of the energy with a successively increasing expansion of the wave function. As a key parameter employed to control the energy convergence we have selected the 'shell' parameter Ω. This parameter limits the number of basis functions included in calculations to those fulfilling the inequality 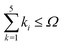 , while the maximum of k0 is fixed at the kmax0 value. The number of all basis functions K which meet this condition grows nonuniformly with Ω but ensures the saturation of the subsequent electronic 'shells'. The E(0) energy converges with growing K regularly according to the inverse power law which permits a firm extrapolation to the complete basis set and the estimation of the uncertainty. The convergence of the consecutive energy components E(2), E(3), and E(4) is less regular but also very rapid. As the final uncertainty changes very slowly between neighboring levels, the analysis of the convergence has been omitted for some of them. The features of the convergence are illustrated by the data collected in Table 1. The numerical convergence achieved for the individual E(n) terms is of the order of 10−13 a.u. and slowly grows with rotational or vibrational quantum number.
, while the maximum of k0 is fixed at the kmax0 value. The number of all basis functions K which meet this condition grows nonuniformly with Ω but ensures the saturation of the subsequent electronic 'shells'. The E(0) energy converges with growing K regularly according to the inverse power law which permits a firm extrapolation to the complete basis set and the estimation of the uncertainty. The convergence of the consecutive energy components E(2), E(3), and E(4) is less regular but also very rapid. As the final uncertainty changes very slowly between neighboring levels, the analysis of the convergence has been omitted for some of them. The features of the convergence are illustrated by the data collected in Table 1. The numerical convergence achieved for the individual E(n) terms is of the order of 10−13 a.u. and slowly grows with rotational or vibrational quantum number.
Table 1 Convergence of the E(0), E(2), E(3), and E(4) components (in a.u.) with the size of the basis set for the (0,0) and (0,16) levels. For the former level the E(3) vanishes
|
Ω
|
K
|
E
(0)
|
K
|
E
(2) × 107 |
E
(3) × 109 |
E
(4) × 1012 |
| (0,0) |
| 9 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415 415 |
−1.147171120265 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843 843 |
−2.12715216 |
|
−2.233 |
| 10 |
45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045 045 |
−1.16547171123917 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502 502 |
−2.12715184 |
|
−2.233 |
| 11 |
64![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680 680 |
−1.16547171124514 |
68![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712 712 |
−2.12715185 |
|
−2.233 |
| 12 |
90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860 860 |
−1.16547171124656 |
96![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992 992 |
−2.12715181 |
|
−2.233 |
| 13 |
124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740 740 |
−1.16547171124687 |
|
|
|
|
| 14 |
171![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360 360 |
−1.16547171124696 |
|
|
|
|
| ∞ |
∞ |
−1.16547171124699(3) |
∞ |
−2.1271518(1) |
|
−2.233 |
|
|
| (0,16) |
| 9 |
19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355 355 |
−1.117302461466 66 |
70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089 089 |
−45.529370 |
1.515796 |
−499.944 |
| 10 |
28![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665 665 |
−1.11730246150930 |
104![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647 647 |
−45.529401 |
1.515800 |
−499.969 |
| 11 |
41![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160 160 |
−1.11730246151685 |
151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524 524 |
−45.529403 |
1.515801 |
−499.991 |
| 12 |
57![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820 820 |
−1.11730246151855 |
213![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870 870 |
−45.529406 |
1.515802 |
−499.998 |
| 13 |
79![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380 380 |
−1.11730246151895 |
|
|
|
|
| 14 |
107![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100 100 |
−1.11730246151905 |
|
|
|
|
| ∞ |
∞ |
−1.11730246151909(3) |
∞ |
−45.529410(3) |
1.515802(1) |
−500.01(1) |
Another aspect of the convergence study is the saturation of these energy terms with respect to the presence of the basis functions with the growing quantum number Λ. For the nonrotational states only Σg,u functions are required. However, with increasing J, the contributions from the Πg and Πu functions become more and more significant so that already for J = 3 their sum supersedes that from the Σu functions. The contribution from Δg,u functions becomes larger than 10−7 cm−1 already for levels with J ≥ 4, but they appear only in the fourth and higher-order terms of expansion (11). Fig. 1 shows graphically how the contributions to dissociation energy from subsequent Λ states change with the growing J quantum number. The expected contribution from the Φg,u functions emerge only in terms E(6) and higher and may become noticeable only for the highest rotational excitations, which are not considered here. Therefore, we can safely claim that all the energy levels presented in this work are saturated with respect to the electronic angular momentum.
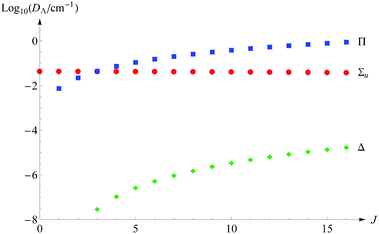 |
| | Fig. 1 The contributions from Σu, Π, and Δ states to the total nonrelativistic dissociation energy as a function of the rotational quantum number J (for v = 0). | |
The next question to be asked, is how large is the error in energy introduced by cutting off the series of eqn (11) after the fourth term. Table 2 presents the individual E(n) contributions for a few selected states. These contributions grow polynomially with increasing J. For the v = 0, J = 16 level the E(4) contribution is of the order of 10−4 cm−1, and it is justified to ask whether still higher-order terms are not necessary to guarantee the desired accuracy. We note that each Hamiltonian contains the 1/μn factor. Hence, we can expect that E(5)/E(4) ≈ 1/μn or even less, as observed in the case of the E(3)/E(2) relation, which is approximately −3 × 10−4. The above question can also be answered by a direct comparison of the energy obtained from the full matrix diagonalization with the energy evaluated using eqn (11). Results of such computations in comparison with the simple scaling of D(4) by the inverse of the nuclear reduced mass are shown in Fig. 2. As we can infer from this figure, the contribution from the omitted D(n), n ≥ 5 terms exceeds 10−8 cm−1 only for J ≥ 9 and remains smaller than 10−7 cm−1 for higher J. On the basis of the above arguments we conclude that even for the highest J considered here, the contributions from the neglected higher-order energy components are smaller than 10−7 cm−1.
Table 2 Convergence of the eigenvalue expansion E = E(0) + E(2) + E(3) + E(4) in terms of the corresponding dissociation energy components (in cm−1) for the selected levels of HD
| Term |
v = 0, J = 0 |
v = 0, J = 1 |
v = 0, J = 16 |
v = 2, J = 2 |
|
D
(0)
|
36406.46420530(1) |
36317.22941180(1) |
25834.53587789(1) |
29075.22038341(1) |
|
D
(2)
|
0.04668559 |
0.05472398 |
0.99925503(7) |
0.21758859(2) |
|
D
(3)
|
0.00000000 |
−0.00000290 |
−0.00033268 |
−0.00000977 |
|
D
(4)
|
0.00000049 |
0.00000053 |
0.00010974 |
0.00000298(1) |
|
D
|
36406.51089137(1) |
36317.28413342(1) |
25835.53490998(7) |
29075.43796520(3) |
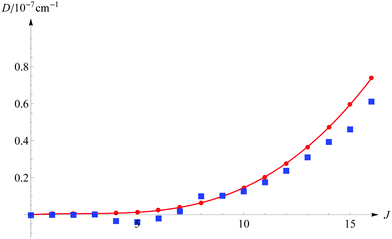 |
| | Fig. 2 The estimated contribution to the total nonrelativistic dissociation energy from the omitted D(n), n ≥ 5 terms as a function of the rotational quantum number J (for v = 0). The blue squares correspond to the computed contribution from the omitted higher order terms and the red line to the simple estimation D(5) ≈ D(4)/μn. | |
5 Numerical results
Table 3 contains the final nonrelativistic energies obtained for 41 rovibrational levels, which are located up to ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground level. The energy of remaining levels, obtained in frames of the nonadiabatic perturbation theory (NAPT) with the accuracy of ca. 0.0005 cm−1, is available in ref. 13. For each level, both the nonadiabatic eigenvalue Ev,J and the corresponding dissociation energy Dv,J are given in the table. The dissociation energy was obtained from
000 cm−1 above the ground level. The energy of remaining levels, obtained in frames of the nonadiabatic perturbation theory (NAPT) with the accuracy of ca. 0.0005 cm−1, is available in ref. 13. For each level, both the nonadiabatic eigenvalue Ev,J and the corresponding dissociation energy Dv,J are given in the table. The dissociation energy was obtained from| | Dv,j = 2![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) y(E(H) + E(D) − Ev,J), y(E(H) + E(D) − Ev,J), | (23) |
where the nonadiabatic atomic energies E(H) and E(D) are known from the exact solution of the Schrödinger equation. The Rydberg constant ![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) y = 109737.31568508(65)cm−1.19 All the eigenvalues listed in Table 3 have assigned an uncertainty estimated on the basis of the convergence analysis discussed above. These uncertainties are purely numerical and do not account for those due to physical constants. However, current uncertainties in the proton–electron (deuteron–electron) mass ratio and in the Rydberg constant are more significant than the numerical ones. For example, the CODATA 201419 proton–electron and deuteron–electron mass ratios have a relative standard uncertainty of 9.5 × 10−11 and 3.5 × 10−11, respectively. A change of this mass ratio by 1σ affects the eigenvalues of HD at the level of 10−12 a.u. and the corresponding dissociation energy at 10−7 cm−1. Hence, one cannot exclude the possibility of a refinement of these physical constants in future high-precision studies of HD. Similarly, the current uncertainty in the Rydberg constant affects the conversion of the dissociation energy value from a.u. to reciprocal centimeters at the level of 10−7 cm−1.
y = 109737.31568508(65)cm−1.19 All the eigenvalues listed in Table 3 have assigned an uncertainty estimated on the basis of the convergence analysis discussed above. These uncertainties are purely numerical and do not account for those due to physical constants. However, current uncertainties in the proton–electron (deuteron–electron) mass ratio and in the Rydberg constant are more significant than the numerical ones. For example, the CODATA 201419 proton–electron and deuteron–electron mass ratios have a relative standard uncertainty of 9.5 × 10−11 and 3.5 × 10−11, respectively. A change of this mass ratio by 1σ affects the eigenvalues of HD at the level of 10−12 a.u. and the corresponding dissociation energy at 10−7 cm−1. Hence, one cannot exclude the possibility of a refinement of these physical constants in future high-precision studies of HD. Similarly, the current uncertainty in the Rydberg constant affects the conversion of the dissociation energy value from a.u. to reciprocal centimeters at the level of 10−7 cm−1.
Table 3 Nonadiabatic eigenvalue (Ev,J) and dissociation energy (Dv,J) of the rovibrational energy levels of HD located up to ca. 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground level. The uncertainties assigned to Ev,J and Dv,J are due to the numerical convergence only and do not account for uncertainties transferred from the fundamental constants. The μn is the nucleus-to-electron mass ratio, with n = p, d
000 cm−1 above the ground level. The uncertainties assigned to Ev,J and Dv,J are due to the numerical convergence only and do not account for uncertainties transferred from the fundamental constants. The μn is the nucleus-to-electron mass ratio, with n = p, d
| (v,J) |
E
v,J/hartree |
D
v,J/cm−1 |
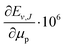
|
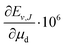
|
| (0,0) |
−1.16547192396439(3) |
36406.51089137(1) |
−1.69 |
−0.424 |
| (0,1) |
−1.16506537694165(3) |
36317.28413342(1) |
−1.84 |
−0.459 |
| (0,2) |
−1.16425508309094(3) |
36139.44518924(1) |
−2.13 |
−0.533 |
| (0,3) |
−1.16304657592944(3) |
35874.20852546(1) |
−2.55 |
−0.639 |
| (0,4) |
−1.16144799233927(6) |
35523.35998129(1) |
−3.12 |
−0.781 |
| (0,5) |
−1.15946988670851(8) |
35089.21597717(2) |
−3.81 |
−0.953 |
| (0,6) |
−1.15712499903903(9) |
34574.57262031(2) |
−4.61 |
−1.15 |
| (0,7) |
−1.1544279886395(1) |
33982.64725706(2) |
−5.53 |
−1.38 |
| (0,8) |
−1.1513951457706(1) |
33317.01518642(2) |
−6.54 |
−1.64 |
| (0,9) |
−1.1480440933964(1) |
32581.54420188(2) |
−7.64 |
−1.91 |
| (0,10) |
−1.1443934901810(1) |
31780.32940690(2) |
−8.82 |
−2.21 |
| (0,11) |
−1.1404627442859(1) |
30917.63040056(2) |
−10.1 |
−2.52 |
| (0,12) |
−1.1362717455822(2) |
29997.81250501(3) |
−11.3 |
−2.84 |
| (0,13) |
−1.1318406218566(3) |
29025.29325878(7) |
−12.7 |
−3.17 |
| (0,14) |
−1.1271895226147(3) |
28004.49496719(7) |
−14.0 |
−3.51 |
| (0,15) |
−1.1223384323217(3) |
26939.80371339(7) |
−15.4 |
−3.86 |
| (0,16) |
−1.1173070134442(3) |
25835.53490998(7) |
−16.8 |
−4.20 |
| (1,0) |
−1.14892259349461(3) |
32774.35268710(1) |
−4.54 |
−1.14 |
| (1,1) |
−1.14853361535671(3) |
32688.98185367(1) |
−4.68 |
−1.17 |
| (1,2) |
−1.14775837810983(3) |
32518.83694469(1) |
−4.95 |
−1.24 |
| (1,3) |
−1.14660225392289(4) |
32265.09701494(1) |
−5.35 |
−1.34 |
| (1,4) |
−1.14507314017112(4) |
31929.49533795(1) |
−5.88 |
−1.47 |
| (1,5) |
−1.1431812767341(1) |
31514.27930750(2) |
−6.52 |
−1.63 |
| (1,6) |
−1.1409390184852(1) |
31022.16050490(3) |
−7.27 |
−1.82 |
| (1,7) |
−1.1383605746595(2) |
30456.25749675(4) |
−8.13 |
−2.03 |
| (1,8) |
−1.1354617274586(1) |
29820.03407593(2) |
−9.07 |
−2.27 |
| (1,9) |
−1.1322595419602(3) |
29117.23559408(7) |
−10.1 |
−2.53 |
| (1,10) |
−1.1287720783053(3) |
28351.82579400(7) |
−11.2 |
−2.80 |
| (1,11) |
−1.1250181154717(4) |
27527.92618493(9) |
−12.3 |
−3.08 |
| (1,12) |
−1.1210168939675(2) |
26649.75957027(5) |
−13.5 |
−3.38 |
| (2,0) |
−1.13318174315629(4) |
29319.63536164(1) |
−7.11 |
−1.78 |
| (2,1) |
−1.13280998089048(6) |
29238.04297540(2) |
−7.23 |
−1.81 |
| (2,2) |
−1.13206909795027(6) |
29075.43796520(2) |
−7.49 |
−1.87 |
| (2,3) |
−1.13096431272305(8) |
28832.96563472(2) |
−7.86 |
−1.97 |
| (2,4) |
−1.12950329468599(8) |
28512.30923961(1) |
−8.35 |
−2.09 |
| (2,5) |
−1.1276959851255(2) |
28115.65064004(5) |
−8.95 |
−2.24 |
| (2,6) |
−1.1255543743172(2) |
27645.62139735(5) |
−9.65 |
−2.42 |
| (2,7) |
−1.1230922468621(2) |
27105.24688177(5) |
−10.4 |
−2.61 |
| (2,8) |
−1.1203249075122(2) |
26497.88609807(5) |
−11.3 |
−2.83 |
| (2,9) |
−1.1172688994405(2) |
25827.16985307(5) |
−12.3 |
−3.07 |
| (3,0) |
−1.11823351322064(5) |
26038.87810682(2) |
−9.39 |
−2.35 |
Over the decades the fundamental constants were determined with ever increasing accuracy. Not only their uncertainties change but also their estimated values tend to change slightly. This process seems to have accelerated in recent years. For this reason we decided to present the results of our calculations in a form which enables the small changes in the nucleus-to-electron mass ratio to be accounted for. Therefore, apart from the energy evaluated with the CODATA 2014 values of the ratios μp = mp/me and μd = md/me, we supply derivatives of the energy with respect to the change of these ratios δE/δμp and δE/δμd. In case a new recommendation of the proton or deuteron mass appears, the change in μp or μd can be immediately reflected in the energy of a level by using the derivatives given in Table 3 and the equation
| | 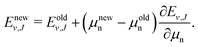 | (24) |
These derivatives enable also an assessment of the sensitivity of particular levels or pairs of levels to the nuclear mass variations and hence a selection of the best candidates for the future nuclear mass refinement.
The accuracy of the results presented in this work significantly exceeds the accuracy of previously known results. In particular, the best previous dissociation energy of the ground level was obtained from nonadiabatic, explicitly correlated Gaussian functions14,20 as well as in adiabatic calculations by solving the radial nonadiabatic Schrödinger equation.13 The comparison presented in Table 4 shows the progress in accuracy made by applying the naJC functions and enables assessment of the accuracy of the other results.
Table 4 Comparison of the best previous literature data with the dissociation energy obtained in this work for the ground level of HD
| Year, method, and reference |
D
0,0/cm−1 |
Difference |
| This work |
36406.51089137(1) |
|
| 2018, 2048-term naECG20 |
36406.510879 |
1.3 × 10−5 |
| 2010, NAPT13 |
36406.5108(10) |
1.1 × 10−4 |
| 2009, 10000-term ECG14 |
36406.51046 |
4.3 × 10−4 |
6 Conclusions
The method described in this work is an extension to the heteronuclear case of the approach presented previously for H2.15 As before, bound levels with an arbitrary rotational and vibrational quantum numbers can be accessed. Another extension of the previous approach, crucial from the practical point of view, is the parallelization of the diagonalization procedure. The accuracy achieved for the nonrelativistic energy levels using the nonadiabatic James-Coolidge functions surpasses that obtained with other methods by three or more orders of magnitude. From now the uncertainty of the nonrelativistic component of the total energy no longer limits the overall accuracy. Moreover, thanks to the recent progress in relativistic calculations for HD,20,21 the uncertainty of the relativistic correction has been significantly diminished (to 2 × 10−7 cm−1) and the current largest contribution to the error budget comes from the missing nonadiabatic quantum electrodynamic effects and amounts to less than 2 × 10−4 cm−1. It is our intention to employ the wave functions obtained within this project to accurately evaluate also the relativistic and QED corrections.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
The authors wish to acknowledge help from Michał Siłkowski with implementation of the PLASMA library and vectorisation of octuple-precision arithmetics, and from Piotr Kopta with implementation of the Elemental library. This research was supported by the National Science Center (Poland) Grant No. 2017/25/B/ST4/01024, as well as by a computing grant from the Poznan Supercomputing and Networking Center, and by the PRACE project.
References
- C.-F. Cheng, Y. R. Sun, H. Pan, J. Wang, A.-W. Liu, A. Campargue and S.-M. Hu, Phys. Rev. A: At., Mol., Opt. Phys., 2012, 85, 024501 CrossRef.
- D. Mondelain, S. Kassi, T. Sala, D. Romanini, D. Gatti and A. Campargue, J. Mol. Spectrosc., 2016, 326, 5–8 CrossRef CAS.
- R. K. Altmann, L. S. Dreissen, E. J. Salumbides, W. Ubachs and K. S. E. Eikema, Phys. Rev. Lett., 2018, 120, 043204 CrossRef CAS PubMed.
- P. Wcisło, F. Thibault, M. Zaborowski, S. Wójtewicz, A. Cygan, G. Kowzan, P. Masłowski, J. Komasa, M. Puchalski, K. Pachucki, R. Ciuryło and D. Lisak, J. Quant. Spectrosc. Radiat. Transfer, 2018, 213, 41–51 CrossRef.
- F. M. J. Cozijn, P. Dupré, E. J. Salumbides, K. S. E. Eikema and W. Ubachs, Phys. Rev. Lett., 2018, 120, 153002 CrossRef CAS PubMed.
- C. Cheng, J. Hussels, M. Niu, H. L. Bethlem, K. S. E. Eikema, E. J. Salumbides, W. Ubachs, M. Beyer, N. J. Hölsch, J. A. Agner, F. Merkt, L.-G. Tao, S.-M. Hu and C. Jungen, Phys. Rev. Lett., 2018, 121, 013001 CrossRef PubMed.
- L.-G. Tao, A.-W. Liu, K. Pachucki, J. Komasa, Y. R. Sun, J. Wang and S.-M. Hu, Phys. Rev. Lett., 2018, 120, 153001 CrossRef PubMed.
- F. Heiße, F. Köhler-Langes, S. Rau, J. Hou, S. Junck, A. Kracke, A. Mooser, W. Quint, S. Ulmer, G. Werth, K. Blaum and S. Sturm, Phys. Rev. Lett., 2017, 119, 033001 CrossRef PubMed.
- M. Puchalski, J. Komasa, P. Czachorowski and K. Pachucki, Phys. Rev. Lett., 2016, 117, 263002 CrossRef PubMed.
- M. Puchalski, J. Komasa and K. Pachucki, Phys. Rev. A: At., Mol., Opt. Phys., 2017, 95, 052506 CrossRef.
- W. Kołos and L. Wolniewicz, Rev. Mod. Phys., 1963, 35, 473 CrossRef.
- L. Wolniewicz, J. Chem. Phys., 1995, 103, 1792 CrossRef CAS.
- K. Pachucki and J. Komasa, Phys. Chem. Chem. Phys., 2010, 12, 9188 RSC.
- M. Stanke, S. Bubin, M. Molski and L. Adamowicz, Phys. Rev. A: At., Mol., Opt. Phys., 2009, 79, 032507 CrossRef.
- K. Pachucki and J. Komasa, Phys. Chem. Chem. Phys., 2018, 20, 247–255 RSC.
-
Y. Hida, X. S. Li and D. H. Bailey, Quad-Double Arithmetic: Algorithms, Implementation, and Application, Lbl-46996, Lawrence Berkeley National Laboratory Technical Report, 2000.
- J. Poulson, B. Marker, R. A. van de Geijn, J. R. Hammond and N. A. Romero, ACM Trans. Math. Softw., 2013, 39, 13:1–13:24 CrossRef.
- A. YarKhan, J. Kurzak, P. Luszczek and J. Dongarra, Int. J. Parallel Program, 2017, 45, 612–633 CrossRef.
- P. J. Mohr, D. B. Newell and B. N. Taylor, Rev. Mod. Phys., 2016, 88, 035009 CrossRef.
- M. Puchalski, A. Spyszkiewicz, J. Komasa and K. Pachucki, Phys. Rev. Lett., 2018, 121, 073001 CrossRef PubMed.
-
P. Czachorowski, M. Puchalski, J. Komasa and K. Pachucki, 2018, submitted.
|
| This journal is © the Owner Societies 2018 |
 b
b
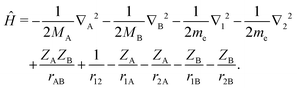
![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) , to form the total angular momentum
, to form the total angular momentum ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) of the molecule. Therefore, for a given rotational level J the wave function ΨJ,M, which formally depends also on M—the projection of
of the molecule. Therefore, for a given rotational level J the wave function ΨJ,M, which formally depends also on M—the projection of ![[J with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004a_20d1.gif) on the Z-axis in the laboratory frame, must involve ingredients describing the subsequent electronic states. The quantum number Λ—the eigenvalue of the
on the Z-axis in the laboratory frame, must involve ingredients describing the subsequent electronic states. The quantum number Λ—the eigenvalue of the ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ·
·![[L with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_004c_20d1.gif) operator and the inversion symmetry symbol g or u (for gerade or ungerade) are employed to distinguish between such states: Σg,u, Πg,u, Δg,u, Our Ansatz is a sum of components with growing Λ
operator and the inversion symmetry symbol g or u (for gerade or ungerade) are employed to distinguish between such states: Σg,u, Πg,u, Δg,u, Our Ansatz is a sum of components with growing Λ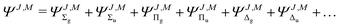
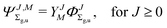
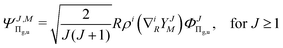
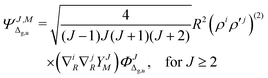
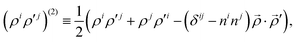
![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ,
, ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) ′ ≡
′ ≡ ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 1 or
1 or ![[small rho, Greek, vector]](https://www.rsc.org/images/entities/i_char_e137.gif) 2, ni ≡ Ri/R and ρia = (δij − ninj)rjaB, with the Einstein summation convention assumed. The YJM = YJM(
2, ni ≡ Ri/R and ρia = (δij − ninj)rjaB, with the Einstein summation convention assumed. The YJM = YJM(![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) ) denotes a spherical harmonic. The functions ΦJΛ represent linear expansions
) denotes a spherical harmonic. The functions ΦJΛ represent linear expansions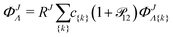
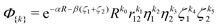
![[R with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0052_20d1.gif) =
= ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) AB. The α and β denote nonlinear variational parameters and ki are non-negative integers collectively denoted as {k}. The basis functions with k2 + k3 even (odd) have the subscript g (u).
AB. The α and β denote nonlinear variational parameters and ki are non-negative integers collectively denoted as {k}. The basis functions with k2 + k3 even (odd) have the subscript g (u).
![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) has a block-diagonal structure whereas the Hamiltonian matrix
has a block-diagonal structure whereas the Hamiltonian matrix ![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) is block-band diagonal because 〈ΦΛ|Ĥ|ΦΛ′〉 = 0 whenever |Λ − Λ′| > 1, see eqn (9) and (10).
is block-band diagonal because 〈ΦΛ|Ĥ|ΦΛ′〉 = 0 whenever |Λ − Λ′| > 1, see eqn (9) and (10).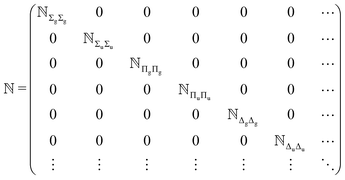

![[Doublestruck H]](https://www.rsc.org/images/entities/char_e16b.gif) − E
− E![[Doublestruck N]](https://www.rsc.org/images/entities/char_e171.gif) )c = 0 can be solved directly, e.g. by the inverse iteration method, or perturbatively by utilizing the fact that all off-diagonal blocks are proportional to the inverse of nuclear mass, and thus are small. The latter approach is particularly advantageous for very large basis sets—the largest expansion employed in our calculations involved 445
)c = 0 can be solved directly, e.g. by the inverse iteration method, or perturbatively by utilizing the fact that all off-diagonal blocks are proportional to the inverse of nuclear mass, and thus are small. The latter approach is particularly advantageous for very large basis sets—the largest expansion employed in our calculations involved 445![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 498 basis functions. It is based on the Rayleigh–Schrödinger perturbation expansion of the total energy
498 basis functions. It is based on the Rayleigh–Schrödinger perturbation expansion of the total energy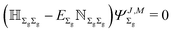
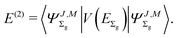
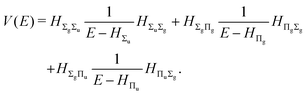
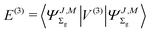
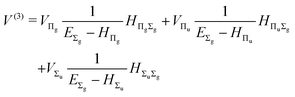
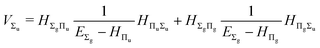
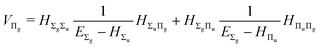
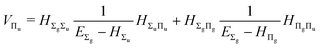
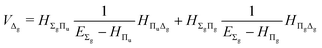
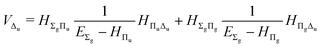

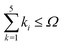 , while the maximum of k0 is fixed at the kmax0 value. The number of all basis functions K which meet this condition grows nonuniformly with Ω but ensures the saturation of the subsequent electronic 'shells'. The E(0) energy converges with growing K regularly according to the inverse power law which permits a firm extrapolation to the complete basis set and the estimation of the uncertainty. The convergence of the consecutive energy components E(2), E(3), and E(4) is less regular but also very rapid. As the final uncertainty changes very slowly between neighboring levels, the analysis of the convergence has been omitted for some of them. The features of the convergence are illustrated by the data collected in Table 1. The numerical convergence achieved for the individual E(n) terms is of the order of 10−13 a.u. and slowly grows with rotational or vibrational quantum number.
, while the maximum of k0 is fixed at the kmax0 value. The number of all basis functions K which meet this condition grows nonuniformly with Ω but ensures the saturation of the subsequent electronic 'shells'. The E(0) energy converges with growing K regularly according to the inverse power law which permits a firm extrapolation to the complete basis set and the estimation of the uncertainty. The convergence of the consecutive energy components E(2), E(3), and E(4) is less regular but also very rapid. As the final uncertainty changes very slowly between neighboring levels, the analysis of the convergence has been omitted for some of them. The features of the convergence are illustrated by the data collected in Table 1. The numerical convergence achieved for the individual E(n) terms is of the order of 10−13 a.u. and slowly grows with rotational or vibrational quantum number.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 415
415![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 843
843![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 045
045![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 502
502![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 680
680![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 712
712![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 860
860![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 992
992![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 740
740![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 360
360![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 355
355![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 089
089![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 665
665![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 647
647![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 160
160![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 524
524![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 820
820![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 870
870![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 380
380![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 100
100
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground level. The energy of remaining levels, obtained in frames of the nonadiabatic perturbation theory (NAPT) with the accuracy of ca. 0.0005 cm−1, is available in ref. 13. For each level, both the nonadiabatic eigenvalue Ev,J and the corresponding dissociation energy Dv,J are given in the table. The dissociation energy was obtained from
000 cm−1 above the ground level. The energy of remaining levels, obtained in frames of the nonadiabatic perturbation theory (NAPT) with the accuracy of ca. 0.0005 cm−1, is available in ref. 13. For each level, both the nonadiabatic eigenvalue Ev,J and the corresponding dissociation energy Dv,J are given in the table. The dissociation energy was obtained from![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) y(E(H) + E(D) − Ev,J),
y(E(H) + E(D) − Ev,J),![[scr R, script letter R]](https://www.rsc.org/images/entities/char_e531.gif) y = 109737.31568508(65)cm−1.19 All the eigenvalues listed in Table 3 have assigned an uncertainty estimated on the basis of the convergence analysis discussed above. These uncertainties are purely numerical and do not account for those due to physical constants. However, current uncertainties in the proton–electron (deuteron–electron) mass ratio and in the Rydberg constant are more significant than the numerical ones. For example, the CODATA 201419 proton–electron and deuteron–electron mass ratios have a relative standard uncertainty of 9.5 × 10−11 and 3.5 × 10−11, respectively. A change of this mass ratio by 1σ affects the eigenvalues of HD at the level of 10−12 a.u. and the corresponding dissociation energy at 10−7 cm−1. Hence, one cannot exclude the possibility of a refinement of these physical constants in future high-precision studies of HD. Similarly, the current uncertainty in the Rydberg constant affects the conversion of the dissociation energy value from a.u. to reciprocal centimeters at the level of 10−7 cm−1.
y = 109737.31568508(65)cm−1.19 All the eigenvalues listed in Table 3 have assigned an uncertainty estimated on the basis of the convergence analysis discussed above. These uncertainties are purely numerical and do not account for those due to physical constants. However, current uncertainties in the proton–electron (deuteron–electron) mass ratio and in the Rydberg constant are more significant than the numerical ones. For example, the CODATA 201419 proton–electron and deuteron–electron mass ratios have a relative standard uncertainty of 9.5 × 10−11 and 3.5 × 10−11, respectively. A change of this mass ratio by 1σ affects the eigenvalues of HD at the level of 10−12 a.u. and the corresponding dissociation energy at 10−7 cm−1. Hence, one cannot exclude the possibility of a refinement of these physical constants in future high-precision studies of HD. Similarly, the current uncertainty in the Rydberg constant affects the conversion of the dissociation energy value from a.u. to reciprocal centimeters at the level of 10−7 cm−1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 above the ground level. The uncertainties assigned to Ev,J and Dv,J are due to the numerical convergence only and do not account for uncertainties transferred from the fundamental constants. The μn is the nucleus-to-electron mass ratio, with n = p, d
000 cm−1 above the ground level. The uncertainties assigned to Ev,J and Dv,J are due to the numerical convergence only and do not account for uncertainties transferred from the fundamental constants. The μn is the nucleus-to-electron mass ratio, with n = p, d