Mapping the ultrafast vibrational dynamics of all-trans and 13-cis retinal isomerization in Anabaena Sensory Rhodopsin†
Abstract
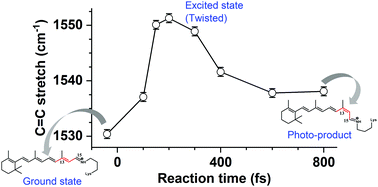
Discrepancies in the isomerization dynamics and quantum yields of the trans and cis retinal protonated Schiff base is a well-known issue in the context of retinal photochemistry. Anabaena Sensory Rhodopsin (ASR) is a microbial retinal protein that comprises a retinal chromophore in two ground state (GS) conformations: all-trans, 15-anti (AT) and 13-cis, 15-syn (13C). In this study, we applied impulsive vibrational spectroscopic techniques (DFWM, pump-DFWM and pump-IVS) to ASR to shed more light on how the structural changes take place in the excited state within the same protein environment. Our findings point to distinct features in the ground state structural conformations as well as to drastically different evolutions in the excited state manifold. The ground state vibrational spectra show stronger Raman activity of the C14–H out-of-plane wag (at about 805 cm−1) for the 13C isomer than that for the AT isomer, which hints at a pre-distortion of 13C in the ground state. Evolution of the Raman frequency after interaction with the actinic pulse shows a blue-shift for the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching and CH3 rocking mode for both isomers. For AT, however, the blue-shift is not instantaneous as observed for the 13C isomer, rather it takes more than 200 fs to reach the maximum frequency shift. This frequency blue-shift is rationalized by a decrease in the effective conjugation length during the isomerization reaction, which further confirms a slower formation of the twisted state for the AT isomer and corroborates the presence of a barrier in the excited state trajectory previously predicted by quantum chemical calculations.
C stretching and CH3 rocking mode for both isomers. For AT, however, the blue-shift is not instantaneous as observed for the 13C isomer, rather it takes more than 200 fs to reach the maximum frequency shift. This frequency blue-shift is rationalized by a decrease in the effective conjugation length during the isomerization reaction, which further confirms a slower formation of the twisted state for the AT isomer and corroborates the presence of a barrier in the excited state trajectory previously predicted by quantum chemical calculations.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...