Excited-state dynamics of a molecular dyad with two orthogonally-oriented fluorophores†
Abstract
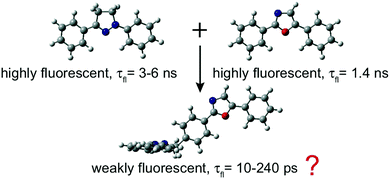
The excited-state dynamics of a T-shaped bichromophoric molecule, consisting of two strong fluorophores, diphenyloxazole and diphenylpyrazoline, directly linked in an orthogonal geometry, was investigated. Despite the weak coupling ensured by this geometry and confirmed by the electronic absorption spectra, this dyad exhibits only weak fluorescence in both apolar and polar solvents, with fluorescence lifetimes ranging from 200 ps in CHX to 10 ps in ACN. Ultrafast spectroscopic measurements reveal that the fluorescence quenching in polar solvents is due to the population of a charge-separated state. In non-polar solvents, this process is energetically not feasible, and a quenching due to an efficient intersystem crossing (ISC) to the triplet manifold is proposed, based on quantum-chemical calculations. This process occurs via the spin–orbit charge-transfer (SOCT) ISC mechanism, which is enabled by the charge-transfer character acquired by the S1 state of the dyad upon structural relaxation and by the orthogonal arrangement of the molecular orbitals involved in the transition. The same mechanism is proposed to explain why the recombination of the charge-separated state is faster in medium than in highly polar solvents, as well as to account for the fast decay of the lowest triplet state to the ground state.
- This article is part of the themed collection: 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...