How robust is the metallicity of two dimensional gallium?

Abstract

Atomically thin gallium layers have recently been experimentally produced via solid–melt exfoliation, and show promise as robustly metallic 2D materials for electronic applications. However, the extent to which the experimental technique can be extended to other metals relies on understanding how the 2D structures relate to the bulk form of gallium, which is itself unique as an elemental ‘molecular metal’. We relate the experimentally formed 2D materials to the theoretically predicted ‘bilayer gallium’ which has previously been shown to be stable in vacuum at the nanoscale, via density functional theory calculations. We also study the variation of electronic structure with lattice strain to confirm the extent to which the metallicity will be robust on a wide range of substrate materials.

---

1 Introduction

Very recently, the first experimental production of two-dimensional forms of gallium has been achieved, through exfoliation of atomically thin layers from the weakly bound solid–melt interface.¹ Unlike previously discovered 2D materials, which are more typically semiconducting,^2–7 2D gallium – so far nicknamed ‘gallenene’ – is a true metallic layer, in which the metallic character is robust with respect to the interaction with several different semiconducting substrates. This suggests that there are significant prospects for the use of 2D gallium in electronic devices.

However, the use of gallium raises questions about the generality of this approach for synthesising 2D metals, as the bulk metal is itself highly unique: long known to be the only elemental example of a ‘molecular metal’, it exhibits a rich phase diagram,⁸ with respect to size,^9–12 temperature¹³ and pressure dependence.^14,15 Under standard conditions, it adopts the α-phase,^16,17 an 8-atom unit cell in which the atoms are arranged in pairs, within a rhombohedral lattice. This is sometimes referred to as a dimeric structure^18–20 giving rise to the description of the metal as a molecular solid: this is a conceptually satisfying description, as it gives some explanation of the low melting temperature of the metal. Estimating the metallic contribution to the cohesive energy of the bulk crystal by subtracting the dimer bond energy from the total energy of the bulk gives an intermolecular energy that correlates with the low melting temperature; in contrast, the low melting temperatures of mercury and caesium correlate with their total cohesive energies. In summary, the relationship between the structure of gallium and its low melting temperature has been well established.

The electronic properties of the metal, however, are equally influenced by – if not responsible for – its unusual structure. Composed of covalently bonded-dimers, the metallic bonding is highly anisotropic, existing in the plane perpendicular to the average alignment of the dimers. In consequence, the conductivity of gallium metal has long been known to have a 2D character.^21,22

At the nanoscale, the relative stability of different polymorphs can change dramatically. In the case of gallium, this has been demonstrated both experimentally, and computationally, in studies of the finite temperature behaviour. The experimental observations of the higher-than-bulk melting temperatures of gallium clusters^23–26 contain numerous features in the observed specific heat signatures of solid–solid transitions. These have since been elucidated through extensive first-principles molecular dynamics simulations^27–31 which have also provided the first theoretical explanation of why the melting temperatures in these clusters are so high: relatively stable two-dimensional structures form in the liquid phase and lower its entropy, stabilising the nanoscale liquid relative to the solid and elevating the melting temperature compared to the bulk.³²

Following the discovery and extensive investigation of graphene^33–35 other atomically-thick two-dimensional materials have attracted much attention, due to their auspicious mechanical, thermal, optical, and electronic properties.^2–7 In this work, we look to place the experimental discovery of 2D gallium into the context of its previously known 2D character to answer the question: to what extent could other elemental metals be used to construct similar structures of reduced dimensionality?

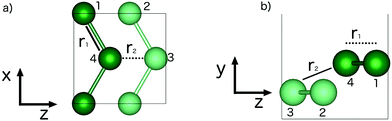
The two-dimensional structure first found in first principles molecular dynamics studies of clusters,³⁶ is a relaxed (010) bilayer surface of bulk α-gallium. The structure of bulk α-gallium is displayed in Fig. 1a with the covalent pairs of gallium atoms oriented vertically and the metallic conduction along horizontal planes.³⁷ It is along this conducting plane, and by slicing through the covalent pairs of atoms within bulk α-gallium, that the most stable surface structure of gallium is formed: the (010)-gallium surface where, despite the significance of the dimeric bonds for many of the properties of bulk gallium, these bonds are severed to allow significant relaxation, at the surface, resulting in a strengthening of the metallic character.

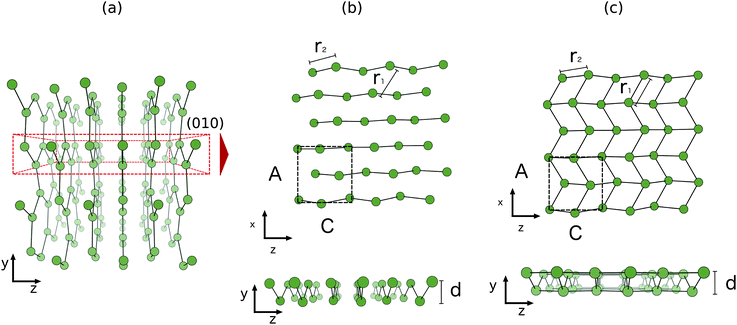Fig. 1 Structures of (a) bulk α-gallium, illustrating the (010) plane (b) bilayer gallium from bulk α-gallium and (c) optimized bilayer gallium.

Simply cutting through the bulk structure (see Fig. 1b) of α-gallium, as described above, leads to a two-layered surface that undergoes a strong relaxation (see Fig. 1c). The obtained structure is pseudo-hexagonal, whereby three of the six atoms that make up a hexagon are shifted vertically. This leads to a surface with an out-of-plane honeycomb structure parallel to the vacuum plane. Notably, and in contrast to the case of the relationship of graphene to graphite, this structure is formed by slicing through covalent bonds, rather than weak van der Waals bonds. This structure is the same as the most stable structure described by Kochat et al., as one of their two gallenene structures.¹

In the following, we examine the metallic character of this surface using Density Functional Theory (DFT) which we validate against state of the art hybrid calculations, to ensure that the metallic character is robust with respect to the inclusion of exact exchange, which has not been done in previous work. We also examine the electronic response to lattice deformation of a range of symmetries.

2 Methods

The gallium bilayer surface was simulated by employing a 4-atom unit cell with two periodic dimensions. This captures the periodicity of the larger unit cell version as employed in the prior molecular dynamics simulations.³⁶ We applied the projected augmented wave (PAW) method in combination with a plane-wave basis set as implemented in the VASP code.^38–43 We employed the DFT functional PW91,^44,45 as well as HSE06 computations for reference. The explicit valence states considered were the 4s,4p-states, based on previous testing that has shown the effect of the semi-core 3d-states to be negligible.²⁷ An energy cutoff of 175 eV ensured converged energies within the size of the SCF convergence criteria. The first-order smearing method of Methfessel–Paxton was employed.

Bilayer gallium was optimized with starting bond lengths of 2.69 Å between nearest Ga–Ga neighbours and an interplanar distance of 1.31 Å, taken from the bulk lattice. The cell volume was allowed to relax during optimization. A criterion of 10⁻⁴ eV was used for convergence within the electronic SC loop. An energy difference of 10⁻³ eV between steps was required for breaking of the ionic relaxation loop. After optimization, bond lengths between Ga–Ga nearest neighbours was 2.71 Å and the interplanar distance remained at 1.31 Å. As illustrated by Fig. 1, bilayer gallium is derived from the (010) surface of the bulk phase of α-gallium. The optimized structure has an interplanar distance, d = 1.31 Å. Along the y axis in bilayer gallium, there is 20.3 Å of vacuum space in order to prevent interaction between adjacent unit cells in the y axis within the periodic boundary conditions.

For optimizations and single point calculations, a 14 × 1 × 14 gamma-centered k-grid was employed. For band structure calculations, sampling was done within the cubic Brillouin zone.

3 Results and discussion

Fig. 2 illustrates the geometry of the bonds between the first and second coordination sphere in bilayer gallium, r₁ and r₂, respectively. The consequence of cutting through the covalent bonds of α-phase gallium to create the 2D sheet is that the two different types of bond, r₁ and r₂ are similar in bond length: 2.707 Å and 2.711 Å. The buckling of the 2D sheet is inherited from the buckling of the metallic planes in the original α-phase, but is reduced to 1.31 Å.

Fig. 2 Bilayer gallium structure, illustrating bonds from (a) bilayer from the y axis perspective (b) bilayer gallium from the x axis. Lines and dashed lines indicate bond is in or out of the perspective axis, respectively.

The effect of variation of the lattice parameters on the density of states (DOS) is studied to assess the response of the electronic structure, and metallicity, of 2D gallium to induced lattice strain. Changes in the bond lengths are investigated by varying the a, and c lattice parameters (in the x- and z-directions of the lattice), as a percentage of their equilibrium lengths, and the interplanar (buckling) distance, d (in the y-direction), of the bilayer gallium structure.

3.1 Projected band structure and density of states

The projected band structure and density of states (Fig. 3) illustrates that the main contribution to the bands around the Fermi level is from Ga p-orbitals. Below −2 eV, Ga s-orbitals dominate the contribution to the bands. The projected band structure illustrates disperse bands throughout the entire band structure (Fig. 3). The bands dominated by s-orbital contribution are more disperse, which is straightforwardly attributable to the fact that s-orbitals are more polarizable than p-orbitals.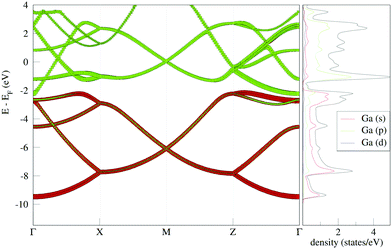

Fig. 3 Projected band structure and density of states for gallium bilayer with equilibrium interplanar distance.

The material is clearly metallic. In the region within 2 eV of the Fermi energy, the bands are almost linear between the Γ and X point, and this is also seen around the M point. At the point of crossing, these bands are offset from the Fermi energy by only 0.04 eV.

3.2 Variation of r₁via change of the lattice parameter a

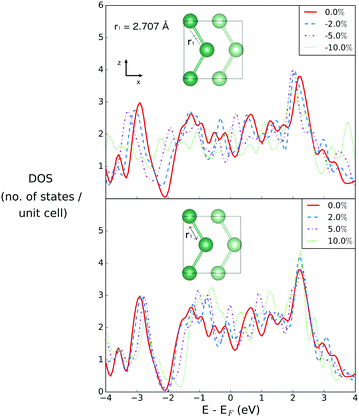
The density of states is first investigated as a function of compression and extension of the a lattice parameter in the x-direction. This changes only the first Ga–Ga bond length, r₁ (see Fig. 2). The r₁ bond is the bond that sits within the plane, and has no out of plane component.

The effect of changing r₁, the bond distance of gallium atoms within the plane, is shown in Fig. 4. This is changing the first coordination sphere for gallium in the optimized structure. The interplanar distance remains unchanged.

Fig. 4 Densities of states for bilayer gallium varying r₁. In order to vary r₁ by varying percentages, the lattice parameter a is compressed and extended along the x-axis. The equilibrium value of r₁ is given in the inset.

The DOS of the equilibrium structure itself is highly metallic, with few features of note other than a strong dip at 2 eV below the Fermi level, below which the states are primarily of s-character, and above which they are of p-character. Upon compression of r₁, the DOS changes only weakly at E_F, by values of −0.258, −0.0495 and 0.5145 for changes in bond length by −2%, −5% and −10%, respectively. The most significant change is a closing of the gap between s- and p-character states at 2 eV below the Fermi level, due to the compression.

On the other hand, when r₁ is extended, the gap between the s- and p-character states opens, resulting in a overall increase of the density of states between 1 eV above and below the Fermi level. This results in changes in the DOS value at E_F of 0.3485, 1.0285 and −0.007 for extension by 2%, 5% and 10%, respectively.

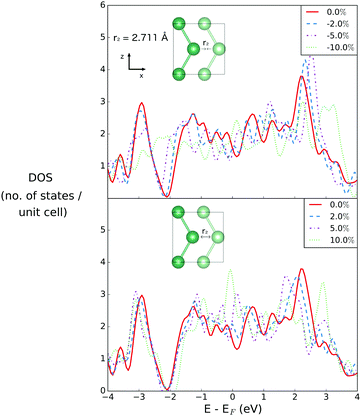
3.3 Variation of r₂via change of the interlayer distance d

The second nearest neighbour distance, r₂, is varied in the data shown in Fig. 5, by changing the interlayer distance d along the y-axis, which has no effect on r₁. The r₂ bond has an out of plane component, due to the buckling of the planes, but is effectively the same length as r₁ at equilibrium, at a length only 0.004 Å longer.

Fig. 5 Densities of states for bilayer gallium with compression and extension of r₂ length by various percentages, via changing the interplanar distance, d. The equilibrium value of r₂ is given in the inset.

As r₂ is compressed, the DOS at E_F changes by 0.308, −0.2145 and −0.0505 for changes in bond length by −2%, −5% and −10%, respectively. When r₂ is expanded, the DOS at E_F changes by 0.387, 0.758 and 1.675 for extension by 2%, 5% and 10%, respectively. As with compression and extension of r₁, the effect of compression and extension of r₂ results in most obvious changes at the pseudogap between the s- and p-character states, at 2 eV below the Fermi level. However in this case the changes are more significant, in particular seen for the extreme case of 10% compression, at which point this gap has been completely suppressed. As a consequence, we can conclude that the electronic structure of 2D gallium is more strongly dependent on this out-of-plane component than on the in-plane features of the structure, however, since this effect occurs only on a feature of the electronic structure well below the Fermi level it has relatively few implications for the metallicity of the material.

3.4 Variation of both r₁ and r₂via change of the z-direction lattice parameter

Both r₁ and r₂ may be simultaneously varied through variations of the lattice parameter in the z-direction (see Fig. 6).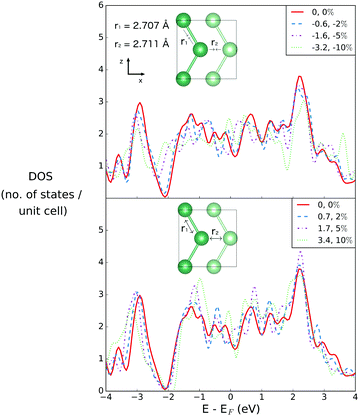

Fig. 6 Densities of states for bilayer gallium with compression and extension along the Z vector. The equilibrium values of r₁ and r₂ are given in the inset.

As r₁ and r₂ are simultaneously compressed or extended, the DOS at E_F shows the same small shifts previously described; in this sense, the directionality of the compression or extension matters less than the effect on the interatomic distances. As previously noted, it is the pseudogap region that occurs around 2 eV below the Fermi energy that is most sensitive, in particular to shortening of the interatomic distances. However these effects have no real implications for the metallicity of the structure, which remains robust.

3.5 The band structure

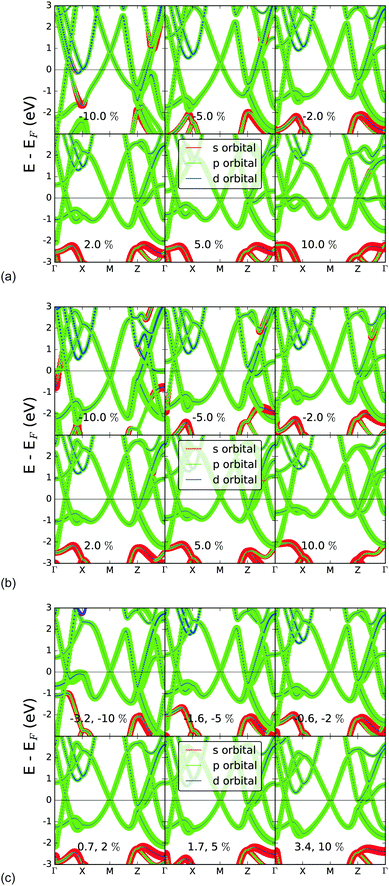
In Fig. 7, the changes induced in the band structure via bond strain induced in the x-, y-, and z-directions respectively are shown. In particular, the projection of orbital character onto the bands demonstrates the electronic nature of the previously described pseudogap in the density of states as being due to the change from bands of s-character to p-character, and the relative effect of strain on the band structure.

Fig. 7 Projected band structure for gallium bilayer with compression and extension of r₁ and r₂ by the percentage values shown, achieved via variation of the lattice parameters in the x-, y-, and z-directions respectively for the subplots (a), (b), and (c).

Straining the lattice in the x-direction results in clear changes of the band structure. At the M point, the two bands nearest to E_F in the equilibrium structure shift down with compression of r₁, and up with extension of r₁, thereby demonstrating the sensitivity of the electronic properties of bilayer gallium to bond strain. However, when the lattice strain is induced in the y-direction, the opposite trend is seen for r₂ than r₁; the two bands which nearly touch at the M point in the equilibrium structure are shifted upwards in the case of compression of r₂, and are shifted downwards in the case of extension of r₂. Lattice strain in the z-direction causes least shift of these bands, likely due to a cancelling effect of changing both r₁ and r₂. Compression of r₁ causes a downwards shift of the M-point band crossing, and compression of r₂ causes a shift upwards.

In summary, it is the variation of r₂ – the out of plane bond length – to which the band structure is most sensitive. This is also the dimension in which structural change is most directly induced by the interaction with a substrate. In particular, the pseudogap at ca. −2 eV is lost completely at 10% compression, while it is strongly opened at 10% extension in this direction. However the nature of the bands around the Fermi level is relatively unchanged.

3.6 The effect of exact exchange

In Fig. 8 the performance of hybrid functionals is tested for the band structure, based on the well-known underestimation of band gaps expected from standard GGA density functionals. The percentage of exact exchange derived from Hartree–Fock (HF) calculations is increased systematically to provide insight into the extent to which exchange might lead to the loss of metallic character due to the possible opening of a band gap.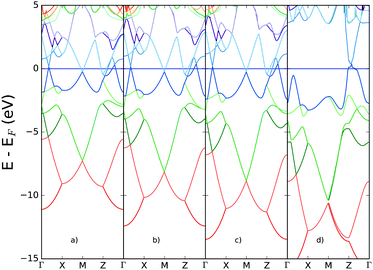

Fig. 8 Band structure for bilayer gallium derived from HSE06 functional with inclusion of exchange (a) default, 20% (b) 50% (c) 70% exchange and (d) HF calculation (100% exchange).

The band structure remains relatively unperturbed around the Fermi energy, for increasing percentages of exact exchange. However the Hartree–Fock calculation shows significant differences in the conduction bands: most notably, a gap opens at the M-point and between the Γ- and X-points. Even in this limiting case, however, the metallicity of two-dimensional gallium is retained, due to the bands crossing the Fermi energy at the Z-point.

The question remains, whether this robust metallicity could be expected to be found for other 2D metals in similar structures, in particular for those with similar electronic structure but much higher thermal stability, such as aluminium. The answer lies in the particular ability of gallium to combine covalent and metallic bonding – and the recognition that the extent of covalent bonding in the metallic lattice is itself anisotropic.

Analysis of changes in the Electron Localisation Function (ELF) (see ESI†) with the induced strain examined above provides the following picture. In the optimised bilayer structure, for an isosurface value of 0.6, the areas of localised electron density are connected along the x-direction, demonstrating that the covalent character is a contribution to the r₁ bonds, but not to the out of plane r₂ bonds, which remain more metallic in character. This is a direct inversion of the relative orientation of the covalent and metallic bonds in the α-gallium bulk structure, but results from reconstruction of the surface as it is obtained by cutting through the covalent bonds that exist in the bulk.

As r₁ is lengthened, the covalent nature of these bonds is weakened, as shown by the disconnection of the isosurface between individual atoms. However the sensitivity of the electronic structure to the out of plane distance, d, is explained by the induced overlap in localised electron density that occurs once the bilayer is compressed sufficiently in this direction, which may be interpreted as corresponding to the introduction of covalency into the r₂ bond. The recognition that the degree of covalent character in the interatomic bonds within the two-dimensional character varies with structural change leaves open the possibility that similar structures might be prepared from other elemental metals, given the right precursor structure.

4 Conclusions

The use of solid–melt exfoliation for the experimental realisation of a true two-dimensional metal opens new possibilities for the development of 2D materials and their device applications. While gallium has a low melting temperature which may limit device applications, the inherent metallicity of the 2D structure depends on the character of the electronic bands, which we have shown here to be robust with respect to significant lattice strain, and thus to the preparation of a wide range of interfaces.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We would like to thank Krista G. Steenbergen for helpful input. The authors wish to acknowledge the contribution of NeSI high-performance computing facilities to the results of this research. NZ's national facilities are provided by the NZ eScience Infrastructure and funded jointly by NeSI's collaborator institutions and through the Ministry of Business, Innovation & Employment's Research Infrastructure programme. URL https://www.nesi.org.nz. We would like to thank Lukas Eugen Marsoner Steinkasserer for computational advice and expertise.

References

1. V. Kochat, A. Samanta, Y. Zhang, S. Bhowmick, P. Manimunda, S. A. S. Asif, A. S. Stender, R. Vajtai, A. K. Singh and C. S. Tiwary, et al. , Sci. Adv., 2018, 4, e1701373.
2. M. Xu, T. Liang, M. Shi and H. Chen, Chem. Rev., 2013, 113, 3766–3798.
3. A. Manchon, H. C. Koo, J. Nitta, S. M. Frolov and R. A. Duine, Nat. Mater., 2015, 14, 871–882.
4. Z. Sun and H. Chang, ACS Nano, 2014, 8, 4133–4156.
5. J. Hong, C. Jin, J. Yuan and Z. Zhang, Adv. Mater., 2017, 29, 1606434.
6. J. S. Ponraj, Z.-Q. Xu, S. C. Dhanabalan, H. Mu, Y. Wang, J. Yuan, P. Li, S. Thakur, M. Ashrafi, K. Mccoubrey, Y. Zhang, S. Li, H. Zhang and Q. Bao, Nanotechnology, 2016, 27, 462001.
7. X. Peng, L. Peng, C. Wu and Y. Xie, Chem. Soc. Rev., 2014, 43, 3303–3323.
8. M. Bernasconi, G. L. Chiarotti and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 9988–9998.
9. H. He, G. Fei, P. Cui, K. Zheng, L. Liang, Y. Li and L. De Zhang, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 073310.
10. A. Petitmangin, C. Hébert, J. Perrière, B. Gallas, L. Binet, P. Barboux and P. Vermaut, J. Appl. Phys., 2011, 109, 013711.
11. B. F. Soares, K. F. MacDonald, V. A. Fedotov and N. I. Zheludev, Nano Lett., 2005, 5, 2104–2107.
12. B. Soares, F. Jonsson and N. Zheludev, Phys. Rev. Lett., 2007, 98, 153905.
13. S. Cajahuaringa, M. de Koning and A. Antonelli, J. Chem. Phys., 2012, 136, 064513.
14. K. Takemura, K. Kobayashi and M. Arai, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 58, 2482.
15. A. S. Mikhaylushkin, S. I. Simak, B. Johansson and U. Häussermann, J. Phys. Chem. Solids, 2006, 67, 2132–2135.
16. M. Olsen-Bar and R. W. Powell, Proc. R. Soc. London, Ser. A, 1951, 209, 542–550.
17. V. Heine, J. Phys.: Condens. Matter, 1968, 1, 222.
18. E. Voloshina, K. Rosciszewski and B. Paulus, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 045113.
19. X. G. Gong, G. L. Chiarotti, M. Parrinello and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 14277.
20. X. G. Gong, G. L. Chiarotti, M. Parrinello and E. Tosatti, EPL, 1993, 21, 469.
21. V. Heine, J. Phys. C: Solid State Phys., 1968, 222.
22. M. Yaqub and J. F. Cochran, Phys. Rev., 1965, 137, 1182.
23. G. A. Breaux, B. Cao and M. F. Jarrold, J. Phys. Chem. B, 2005, 109, 16575–16578.
24. S. Chacko, K. Joshi, D. Kanhere and S. Blundell, Phys. Rev. Lett., 2004, 92, 135506.
25. G. Breaux, R. Benirschke, T. Sugai, B. Kinnear and M. Jarrold, Phys. Rev. Lett., 2003, 91, 215508.
26. K. L. Pyfer, J. O. Kafader, A. Yalamanchali and M. F. Jarrold, J. Phys. Chem. A, 2014, 118, 4900–4906.
27. K. G. Steenbergen, D. Schebarchov and N. Gaston, J. Chem. Phys., 2012, 137, 144307.
28. K. G. Steenbergen and N. Gaston, Phys. Chem. Chem. Phys., 2013, 15, 15325.
29. K. G. Steenbergen and N. Gaston, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 161402.
30. K. G. Steenbergen and N. Gaston, Chem. – Eur. J., 2014, 21, 2862–2869.
31. K. G. Steenbergen and N. Gaston, J. Chem. Phys., 2014, 140, 064102.
32. K. G. Steenbergen and N. Gaston, Nano Lett., 2015, 16, 21–26.
33. A. K. Geim and K. S. Novoselov, Nat. Mater., 2007, 6, 183–191.
34. S. Das Sarma, S. Adam, E. H. Hwang and E. Rossi, Rev. Mod. Phys., 2011, 83, 407–470.
35. K. P. Loh, S. W. Tong and J. Wu, J. Am. Chem. Soc., 2016, 138, 1095–1102.
36. K. G. Steenbergen and N. Gaston, Nano Lett., 2016, 16, 21–26.
37. X. G. Gong, G. L. Chiarotti, M. Parrinello and E. Tosatti, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 43, 14277.
38. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
39. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
40. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
41. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
42. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
43. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
44. J. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
45. J. Perdew, J. Chevary, S. Vosko, K. Jackson, M. Pederson, D. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 4978.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05280h

---