4s to 5s and 4p photoexcitation dynamics of K atoms from the surface of helium nanodroplets: a theoretical study
Abstract
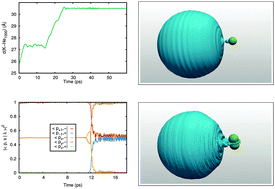
We study the photodissociation of the potassium atom from a superfluid helium nanodroplet upon 5s 2S or 4p 2P excitation using the time-dependent helium density functional method (He-TDDFT). The importance of quantum effects is assessed by comparing the absorption spectrum obtained for a classical or a quantum description of the K atom. In the case of the 5s 2S ← 4s 2S excitation the difference is rather large, and we use a quantum description for the ensuing direct dissociation dynamics. In the case of the 4p 2P ← 4s 2S absorption spectrum, the difference is much smaller, hence a classical description of K is used to describe 4p 2P excitation dynamics. Excitation to the 4p 2Σ1/2 state leads to the direct dissociation of the K atom, while the 4p 2Π3/2 state initially leads to the formation of an exciplex and the 4p 2Π1/2 state to a bouncing atom above the droplet surface. Remarkably, electronic relaxation can be observed for the latter two states, leading to spin–orbit relaxation and the binding of the initially departing one-atom excimer as a ring excimer for the 2P3/2 state and to the formation of a bound, ring excimer for the 2Π1/2 state.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...