Gravimetric tank method to evaluate material-enhanced hydrogen storage by physisorbing materials

Abstract

The most common methods to evaluate hydrogen sorption (volumetric and gravimetric) require significant experience and expensive equipment for providing reproducible results. Both methods allow one to measure excess uptake values which are used to calculate the total amount of hydrogen stored inside of a tank as required for applications. Here we propose an easy to use and inexpensive alternative approach which allows one to evaluate directly the weight of hydrogen inside a material-filled test tank. The weight of the same tank filled with compressed hydrogen in the absence of loaded material is used as a reference. We argue that the only parameter which is of importance for hydrogen storage applications is by how much the material improves the total weight of hydrogen inside of the given volume compared to compressed gas. This parameter which we propose to name Gain includes both volumetric and gravimetric characterization of the material; it can be determined directly without knowing the skeletal volume of the material or excess sorption. The feasibility of the Gravimetric Tank (GT) method was tested using several common carbon and Metal Organic Framework (MOF) materials. The best Gain value of ∼12% was found for the Cu-BTC MOF which means that the tank completely filled with this material stores a 12% higher amount of hydrogen compared to H₂ gas at the same P–T conditions. The advantages of the GT method are its inexpensive design, extremely simple procedures and direct results in terms of tank capacity as required for industrial applications. The GT method could be proposed as a standard check for verification of the high hydrogen storage capacity of new materials. The GT method is expected to provide even better accuracy for evaluation of a material's performance for storage of denser gases like e.g. CO₂ and CH₄.

---

1. Introduction

Hydrogen storage remains one of the main obstacles for broad implementation of hydrogen technology.^1,2 The low density of hydrogen gas at a standard commercial interval of pressures (<200 bar) and near ambient temperatures does not allow one to use simple compression to accommodate the required 4–5 kg of hydrogen inside of a tank reasonably sized for mobile applications. The only available industrial solution for hydrogen storage in fuel cell driven cars at the moment (e.g. as in the Toyota Mirai) is to use a very high pressure of 700 bar. Using materials which could reversibly adsorb hydrogen at near ambient temperatures is an attractive method to improve hydrogen storage.³ However, the progress in this field has been plagued by controversies in evaluation of hydrogen storage capacity, e.g. by carbon nanomaterials,^4–8 Metal Organic Frameworks (MOFs) and more recently graphene related materials.^9–21 Numerous reports of exceptionally high sorption of hydrogen have been reported over past years for graphene related materials either in the pristine state or after decoration with various nanoparticles.^13–16,22 Careful examination of hydrogen sorption by reduced graphene oxide (rGO), activated rGO and pillared graphene oxides performed in our group has not confirmed these claims.^17–20 Hydrogen sorption (excess wt%) has been found to correlate with Specific Surface Area (SSA) for all studied graphene materials following the trend standard for other nanostructured carbon materials.²¹ However, reports on extremely high hydrogen sorption by rGO and other graphene-related materials continue to appear. The reproducibility of hydrogen sorption measurements has become a major issue which hinders progress in materials based hydrogen storage.

Controversies have also continued over about 15 years for hydrogen storage by the “spillover” mechanism. Dissociation of molecular hydrogen on metal nanoparticles and migration of atomic hydrogen on the support material was reported typically as an explanation for nanoparticle-enhanced hydrogen storage by several materials. Some groups consistently reported the “spillover” effect for several materials^23–26 while other groups could not reproduce these results.^27–30 More recently multiple reports on nanoparticle induced enhancement of hydrogen storage were published for various graphene-related materials decorated with e.g. Pt, Pd, and TiO₂ providing an increase of hydrogen sorption by 10–500%.^9–12 For example, a number as high as 8.67 wt% already at 60 bar H₂ pressure was reported recently for Pd decorated rGO.³¹ Detailed discussion of the “spillover” effect and related controversies is outside of the scope of our paper and can be found elsewhere. Some artifacts in measurements of hydrogen sorption can easily be interpreted as “spillover.”¹⁸ However, these artifacts cannot explain all the observed variety of previous reports.

Overestimations in hydrogen storage for carbon materials at the end of the 1990s contributed to implementation of rather high target values set by the US DOE program (9 wt% by 2015). The targets were revised to lower values (4.5 wt% and 0.03 kg l⁻¹ by 2020) several years ago but even the lower values remain far away from the reliably verified levels of physisorption in high surface area materials.

The controversies mentioned above emphasize the need for a simple, reliable, inexpensive and undisputed method to evaluate hydrogen storage parameters of new materials.

It can be assumed that the reasons behind most of the controversies in hydrogen storage measurements originate from experimental errors of currently used gravimetric and volumetric methods. The gravimetric method uses accurate measurements of sample weight inside of a sealed cell filled with compressed hydrogen with main errors related to taking into account the buoyancy effect and evaluation of the sample skeletal volume.^32,33 The volumetric method is based on measurements of pressure drop over the adsorbing material and proved to be especially sensitive to the range of possible errors: e.g. leaks, poor temperature control, inaccurate calibration of dosing volume, cumulative errors associated with the gas dosing procedure etc. Since the main principle of the method is rather simple, very often some homemade systems are assembled for hydrogen sorption measurements without taking into account all important details and error sources. A detailed analysis behind the irreproducibility issues was presented recently by D. Broom and M. Hirscher.³⁴ A lot of work was recently done to analyze all sources of errors and to improve the reproducibility of hydrogen sorption measurements using gravimetric and especially volumetric methods.^34–38 However, these measurements will remain rather delicate, requiring a lot of experience.

It is important to emphasize that the quantities measured using both gravimetric and volumetric methods do not directly provide the value of the hydrogen storage capacity. The measured parameter in both cases is surface excess sorption which needs to be re-calculated into total sorption for practical applications. The calculation is also not that trivial as it requires exact knowledge of the sample skeletal density and the volume of free space not occupied by material. Additional characterization of the sample is required to quantify these parameters and additional errors are introduced once the excess sorption is recalculated into total sorption.

The problem of reproducibility in hydrogen storage measurements has been especially explicitly demonstrated by a blind test performed in 2009 in 14 different European laboratories. Hydrogen sorption isotherms measured from the same sample in different laboratories showed surprisingly strong differences, especially for high pressures (∼0.02 wt% to ∼0.6 wt% at ∼30 bar)³⁹ Note that much higher pressures above 100 bar are typically used for practical applications. The results of the blind test emphasize the strong need for development of a simple and reliable test method which could be used for evaluation of hydrogen storage at high pressures. It would be rather beneficial to develop some method capable of evaluating directly the amount of hydrogen stored inside of a tank with a known volume which is, in fact, the only parameter which is of interest for industrial applications.

One of the earlier attempts to measure the hydrogen amount stored inside of a material-filled tank was performed up to 200 bar using a tank connected to a flowmeter.⁴⁰ However, this method was demonstrated only for large tanks with several kilograms of material and has not received broad attention.

We argue here that the most direct method for evaluation of gas storage is based on a weight measurement of a whole test tank disconnected from the gas supply. Here we suggest to name it as the Gravimetric Tank (GT) method. To the best of our knowledge this method was proposed first by Zielinski et al. in 2007 but has not received broad attention.⁴¹ Very few attempts to use this method were presented over past years and only as a feasibility test for storage of methane using activated carbons.⁴² The paper by Zielinski et al.⁴¹ remains the only one where hydrogen storage evaluation was tested using weighing the whole test “capsule” with material and hydrogen inside. We believe that the reasons for the lack of attention to the GT method are the following:

– Previous publications⁴¹ mostly targeted evaluation of excess sorption isotherms. The excess uptakes are better evaluated by standard gravimetric and volumetric methods. The main advantage of the GT method is direct evaluation of total hydrogen storage for industry-related applications at high pressures (>100 bar).

– The standard balances available in 2007 did not provide the required accuracy for total weights of over 200–300 g. As a result, the design of light weight tanks for high pressures was one of the main problems. Recent technology advances provide a possibility to use a standard and relatively inexpensive desktop balance with 0.1 mg precision for total weights over 500 g. Therefore, the test tank can be assembled using a standard Swagelok valve and stainless steel connection parts.

– A relatively large amount of material was tested in the first report from 2007 (∼1.5–2 g). Smaller amounts of materials (∼100 mg) are often cited as a need for laboratory scale testing of hydrogen storage. However, many of the materials which were claimed to store 5–10 wt% of hydrogen at ambient temperature and pressures around 100 bar can be easily produced in gram amounts (e.g. decorated rGO, MOF-5 etc.)

One of the strongest motivations for the implementation of the GT method into standard hydrogen storage evaluation practice is recent advances in the automotive industry. The first mass produced hydrogen fuel cell car (Toyota Mirai) is supplied with tanks which store hydrogen at 700 bar pressure. The new definition of targets should be then to store the same amount of hydrogen as at 700 bar in the same volume but at lower pressures, ideally decreasing the pressure down to the standard ∼150–200 bar by using materials which physisorb or chemisorb hydrogen. We argue here that the best and most direct method to estimate the advantages of given material for hydrogen storage relative to compressed gas is to use the GT method. The final results obtained by the GT method do not require knowledge of the material skeletal density and do not include any errors connected to helium sorption. Note that helium sorption is not accounted for in standard volumetric and gravimetric methods while the errors associated with this problem are not negligible at high pressures.

As it is demonstrated in our study, the GT method provides reasonable precision and accuracy by using a standard commercially available balance at pressures above 100 bar and gram amounts of material. Feasibility tests were performed for the GT method using several common high surface area materials with known physisorption of hydrogen: carbon nanotubes (CNTs), activated carbon (AC), reduced graphene oxide (rGO), and KOH activated rGO (a-rGO) and several kinds of MOFs. The GT method provided satisfactory reproducibility for all studied materials. The method is simple, relatively inexpensive and free from obvious overestimation issues assuming that several possible sources of errors are taken into account. Therefore, we believe that the GT method can efficiently end twenty years of controversies in hydrogen storage measurements.

2. Experimental

2.1 Gravimetric tank method

The prototype of the hydrogen tank was prepared using a stainless steel container and standard Swagelok valve (Fig. 1). The GT method provides a simple and direct estimation of the hydrogen amount inside of the small test tank. The stainless steel hydrogen tank can be closed using the valve under vacuum conditions or after filling with gas (Fig. 1). The closed tank can be disconnected from the dosing system and weighted. The amount of stored hydrogen can be then evaluated by comparing the weight of the tank loaded with hydrogen and the weight of the tank closed with vacuum inside (m_total), see Fig. 1a and b.

Fig. 1 (a) Scheme of the gravimetric tank method. The test tank can be filled with H₂ gas at certain P–T conditions, closed and disconnected from the system. The whole tank is then weighted using a standard balance. (b) Test tank closed with vacuum inside and weighted; (c) the same tank closed at ambient temperature with 120 bar of hydrogen inside. The hydrogen storage capacity of the tank (m_total) is evaluated by taking the weight difference between (b and c) values (95 mg).

The sample cell provided as a standard part of the Hiden Isochema IMI system (immersion reactor) was connected to a Swagelok stainless steel integral bonnet needle valve and a Swagelok VCR face seal fitting was used as a connection between the valve and the reactor. The inner volume of this assembly measured by pycnometry was 10.31 ml with a useful volume (excluding the volume of the connection parts) of ∼7.2 ml. Note that the volume of the container can be determined also without pycnometry by filling the tank with helium (which is a heavier gas compared to hydrogen) and weighing it (see the ESI† file). The volume of our test tank is sufficient for experiments with gram amounts of common materials. Any gas dosing system which provides a precise pressure of hydrogen can be used to fill the test tank.

Weight measurements were performed using a Radwag AS 510.3Y balance with a maximum load of 510 g and readability of 0.1 mg. All weight measurements were repeated 9–10 times and averaged to improve repeatability (see ESI† for examples). The reactor was typically weighed first in empty state, then weighed filled with material (∼0.5–2.0 g). The reactor with the sample inside was then connected to turbopump providing 10⁻⁵ bar pressure and degassed using external heater at 150 °C under dynamic vacuum for 10–20 hours, cooled down to ambient temperature, disconnected and weighted again with vacuum inside. Gas dosing was performed using a Hiden Isochema IMI volumetric system with a typical pressure of 120 bar and temperature of 23 °C. The sample was covered by a layer of silica wool in order to prevent outflow of material in the process of gas compression and release. A circulation liquid thermostat was used to maintain a stable temperature at the conditions of gas loading. The pressure and temperature inside of the reactor were stabilized for about 10–15 minutes, and the tank was then closed, disconnected and weighted with hydrogen inside. The weight of hydrogen stored in the tank (m_total) was calculated as a difference between the weight of the material filled tank under vacuum and with hydrogen inside (Fig. 1b). The weight of the test tank was also verified after hydrogen release to ensure the absence of material loss.

The following materials were tested for hydrogen storage performance in this study:

– graphite powder, flake (−325 mesh) purchased from Alfa Aesar;

– commercial reduced graphene oxide (rGO) provided by Graphenea;

– highly purified carboxylic single-walled carbon nanotubes (CNT) by ACS Materials (USA);

– iron(III) carboxylate (MIL-100), see details in the ESI† file;

– 1,4-Benzodicarboxylate (MOF-5), see details in the ESI† file;

– copper benzene-1,3,5-tricarboxylate Basolite® C 300 (Cu-BTC MOF) purchased from Sigma-Aldrich;

– porous carbon (AC) provided by ACS Materials;

– high surface area “graphene scaffolds” prepared using KOH activation of thermally exfoliated rGO (a-rGO). Details of the synthesis are provided in the ESI† file.

The Specific Surface Area (SSA) of these materials was verified using analysis of nitrogen sorption isotherms recorded (Quantachrome Nova 1200e surface area analyzer) before and after hydrogen storage tests to detect a possible effect of pore structure collapse related to degassing procedures or pressure driven effects. The SSA remained unchanged or slightly decreased (<5% change) after H₂ testing for all studied materials.

The excess hydrogen sorption of studied materials was verified using standard gravimetric and volumetric methods routinely used in our laboratory over the past decade.^20,43,44 Rubotherm GmbH gravimetric sorption analyzer and Hiden Isochema IMI volumetric systems were used; details of measurement procedures were reported elsewhere.^20,43,44 FLUIDCAL software was used for calculation of the fluid density of hydrogen and helium. The skeletal density of materials was in both methods determined using helium dosing and not corrected to the sorption of helium.

2.2 Definitions of parameters used to characterize hydrogen storage in the gravimetric tank method

Below we introduce some parameters for characterization of the hydrogen storage properties of materials in the GT method.

The Total Storage Density (TSD) specific for the test tank is defined as the amount of stored hydrogen divided by the total volume of the tank:

TSD_tank = m_total/V_tank (1)

where m_total is the total mass of stored hydrogen and V_tank is the total inner volume of the test tank. Note that this definition is general and can be in principle used not only for physisorbing but also for chemisorbing materials.

The material related Tank Storage Density (TSD_mat) is defined as a density of H₂ gas within the volume occupied by the sample (useful volume V_useful, see Fig. 1). The total weight of hydrogen in the material filled volume (TSD_mat) can be calculated by subtracting the amount of hydrogen stored as gas in the dead volume V_dead from the total storage m_total.

TSD_mat = (m_total − V_dead × ρ_H2(P,T))/V_useful (2)

ρ_H2(P,T) – density of hydrogen at given P–T conditions.

The dead volume (V_dead) is the part of the tank which is not filled with material due to e.g. sample size limitations (incompletely filled volume) and includes also the volume of connection pipes and the inside of the valve. See the ESI† file for details of calculation of V_useful and V_dead.

TSD_mat can be higher or lower compared to the density of compressed hydrogen at the same P–T conditions. Therefore, the hydrogen storage (or storage of any gas) performance of the given material in a tank can be then estimated using a simple parameter which we name as hydrogen (or any other gas) storage Gain (or simply Gain in the following discussions).

Gain(P,T) = 100% × (TSD × ρ_H2(P,T))/ρ_H2(P,T) (3)

By definition, the Gain value shows the change in the density of hydrogen inside of the test tank due to addition of material relative to the density of hydrogen gas and is expressed in percent. A positive value of Gain will be found for materials which store hydrogen better compared to compressed gas and negative for materials which store hydrogen less well. For example, the material with a Gain value of 10% added into the tank will provide a 10% increase in the weight of hydrogen compared to material-free tank filled with hydrogen gas the same P–T conditions.

The Gain (G_tank) calculated using the total volume of the tank (TSD_tank), eqn (3), is specific only for a certain construction of the test tank and dead volume. The material-related Gain (G_mat) can be calculated by eqn (3) using TSD_mat, the known bulk density of the material and the mass of material (see ESI† for details).

The G_mat parameter includes both volumetric and gravimetric characterization of the material's hydrogen storage properties as it depends on the bulk density of the material. In principle, TSD_mat and Gain are the only important parameters which are of interest for hydrogen storage applications.

Note that evaluation of the G_mat value using the GT method does not require evaluation of the skeletal volume of the material and includes only the bulk density of the material which is easy to find.

Once again, evaluation of excess sorption is NOT the target of the GT method but it can be calculated in order to compare results with the data obtained by standard gravimetric and volumetric methods. The material's wt% of hydrogen storage can be calculated using the GT method by subtracting the weight of hydrogen stored as a gas in pores and free volume from m_total. The exact skeletal volume of the material can be found e.g. using pycnometry or the known real density of the material or using the GT method with helium dosing (see details and example in ESI†). The latter method suggests dosing the material-filled test tank with helium, measuring the weight of helium and comparing with the weight of helium in the material-free tank. The volume not occupied by material multiplied by the density of hydrogen gas will provide the part of hydrogen storage not included in the excess sorption.

Note that GT method provides the experimental total storage of hydrogen which is then used for calculation of wt%. This procedure is opposite to the standard volumetric and gravimetric methods which provide excess wt% and the total storage is then calculated using the known skeletal volume of the material.

Since most of the literature data provide only excess wt% storage we also derived an equation which allows us to calculate Gain (G_mat) starting from the data obtained by standard methods (see details of the derivation in ESI†):

Gain = V_skeletal/V_tank (wt% × ρ_sample − 100ρ_H2(P,T))/ρ_H2(P,T) (4)

Eqn (4) allows us to estimate the value of wt% excess sorption required to exceed the hydrogen storage of the compressed gas. See also earlier reports for calculation of excess isotherms into absolute uptake for methane sorption in ref. 45. For example, if we take a material with a real density of 2.23 g cm⁻³ (typical for graphitic carbon materials) and hydrogen density at 120 bar and 23 °C (0.009157 g cm⁻³) a positive sign of the Gain will be found if the excess sorption is higher than 0.41 wt%.

The GT method proposed here is simple and inexpensive, but not error free. We learned about several types of errors affecting the measurements, most importantly contamination of the tank surface (e.g. moisture condensation), mechanical damage in the process of connecting/disconnecting (rubber protected tools must be used to prevent scratching), poor thermal stabilization etc. These errors need to be taken into account and minimized; see more details in the ESI† file. Our experience shows that the errors associated with using GT methods are relatively easy to take into account if some simple routines are followed. Moreover, eventual errors are easy to detect. For example, leaks are directly detected during repeated weighing of the tank, and mechanical wear of connection parts can be easily detected by taking a reference weight measurement of the empty tank after the end of the experiment with the material.

The main limitation of the GT method is given by the balance precision (±0.2 mg in our tests) relative to the total amount of hydrogen inside of the tank at given P–T conditions (see Fig. 2). The GT method with our specific tank design provides a reliable estimation of hydrogen storage at high pressures (∼100 bar), but not for low pressures of a few bars due to higher errors. Note that the repeatability of weight measurements is the most important parameter in our method, not the accuracy for the measurements of the total weight of the test tank (∼330 g). The weight difference between the hydrogen free and hydrogen filled tank could be reproducibly measured with error ±0.2 mg.

Fig. 2 (a) Amount of hydrogen per unit of useful tank volume (TSD_mat) experimentally evaluated using the GT method for several common physisorbing materials at 120 bar and 23 °C. Blue arrows show the difference compared to the density of hydrogen. (b) Material specific gain G_mat for the same materials.

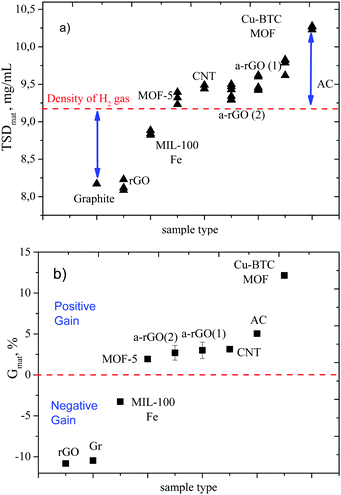
3. Results and discussion

The GT method was tested in this study using several materials with a broad variation of Specific Surface Area (SSA) (up to ∼2800 m² g⁻¹): CNTs, graphene-related materials and several MOFs. The results are summarized in Fig. 2 and Table 1. Fig. 2a shows TSD values calculated using the procedure described above. Once again, TSD is simply the weight of hydrogen divided by the total volume of the tank (TSD_tank) or normalized to the useful volume of the tank (volume filled by material) thus providing material specific TSD_mat.

Table 1 Characterization of sorption properties for several common physisorption materials at 120 bar and 23 °C. From left to right: G_mat – material related Gain; G_tank – Gain specific for the whole tank (includes the volume not occupied by material); TSD_mat – material specific tank storage density, TSD_tank – tank storage density, BET SSA determined using analysis of nitrogen sorption isotherms, excess wt% of hydrogen sorption and bulk density of the material. The hydrogen storage data are averaged over 3–6 tests for each material, see expanded table with all data in ESI

Name (mass of sample, g)	G mat (Gtank), %	TSDmat (TSDtank), mg cm^−3	BET SSA, m^2 g^−1	wt%	p bulkmat, g cm^−3
Graphite	−10.47 ± 0.05	8.17	0	0.00 ± 0.02	0.36
(m = 0.9812)	(−2.818 ± 0.008)	(8.87)
rGO	−10.82 ± 0.07	8.14	445	0.14 ± 0.01	0.33
(m = 1.9654)	(−6.24 ± 0.02)	(8.56)
MIL-100	−3.27 ± 0.02	8.85	1467	0.35 ± 0.02	0.19
(m = 0.9043)	(−1.500 ± 0.004)	(9.01)
MOF-5	1.94 ± 0.01	9.32	2604	0.53 ± 0.02	0.37
(m = 1.2095)	(0.620 ± 0.002)	(9.20)
a-rGO (2)	2.7 ± 0.9	9.39	2263	0.9 ± 0.1	0.10
(m = 0.5800)	(1.6 ± 0.5)	(9.29)
a-rGO (1)	3 ± 1	9.5	2750	0.8 ± 0.1	0.10
(m = 0.5952)	(2.3 ± 0.7)	(9.38)
CNT	3.14 ± 0.02	9.45	1093	0.47 ± 0.02	0.04
(m = 0.9088)	(1.940 ± 0.005)	(9.34)
ACT=const	5.04 ± 0.04	9.62	2007	0.67 ± 0.02	0.17
(m = 1.0958)	(3.14 ± 0.01)	(9.44)
AC	7.35 ± 0.05	9.81	2007	0.68 ± 0.02	0.17
(m = 1.4230)	(4.16 ± 0.01)	(9.51)
Cu-BTC-MOF	12.15 ± 0.07	10.26	1593	0.64 ± 0.02	0.44
(m = 1.0706)	(2.91 ± 0.01)	(9.41)

---

The dashed line in Fig. 2a represents the density of hydrogen gas at a given temperature and pressure. Materials which fall below this line do not provide an advantage compared to compressed gas. Materials which help to improve hydrogen storage exhibit TSD values above the density of hydrogen gas.

The position of points on the graph depends on the bulk density of the material. For poorly sorbing materials most of the hydrogen is stored as compressed H₂ gas in the voids between powder grains. Therefore, the more material we add to the tank, the smaller will be the total amount of hydrogen which we can store in the tank. The trend is opposite for materials with a positive sign of the Gain: the higher the bulk density of the material, the higher the amount of material we can insert into the tank and the better will be the hydrogen storage. The Gain values experimentally obtained at 120 bar and 23 °C are summarized in Table 1.

G _mat provides direct information about the advantage or disadvantage of the material compared to storage of hydrogen as compressed gas at given P–T conditions and includes both volumetric and gravimetric characterization. For example the value G_mat = 7.3% means that the mass of hydrogen stored in the tank filled with AC material is 7.3% higher compared to the mass of hydrogen in the same tank filled with compressed gas at the same P–T conditions.

Note that the material with higher surface area and better excess sorption of hydrogen (a-rGO) shows almost exactly twice smaller G_mat compared to AC due to twice smaller bulk density of material. It is clear that the same material can possibly be compacted better (e.g. using compression and binders) providing higher bulk density and improving the Gain. However, the change in the bulk density of material will never change the sign of the Gain. It is obvious also that the Gain is a function of temperature and pressure. Both hydrogen gas density and sorption of hydrogen improve upon cooling and at higher pressure but not at the same rate.

The data presented in Fig. 2 and Table 1 provide full characterization of materials for hydrogen storage applications. Once again, the value of the Gain is found directly without the need to evaluate excess wt%. Note that a similar idea to use compressed hydrogen as a reference was earlier proposed in ref. 46 but the “net adsorption” parameter introduced in this study is less trivial for understanding and refers to some kind of “adsorption” rather than to the total hydrogen amount stored within a given volume. The main purpose of the GT method is not to evaluate the sorption of gas by a material, but to find the true gas storage capacity of a material-filled tank. Therefore, we believe that the “Gain” introduced in this study is a more straightforward parameter.

Evaluation of excess wt% is not the primary target of the GT method, but it can be used with satisfactory accuracy for the high pressure part of isotherms, see Fig. 3. The isotherm recorded for the AC sample (60–140 bar) using the GT method shows slightly higher uptakes but in general it is in good agreement with the data obtained using standard volumetric and gravimetric methods. Note that the errors of the wt% measurement increase at higher pressures for volumetric and standard gravimetric methods but decrease for the GT method. The absolute value of error in weight measurements provided by the precision of the balance (±0.2 mg) remains unchanged at any pressure, but the smaller amount of hydrogen loaded at lower pressures results in higher error.

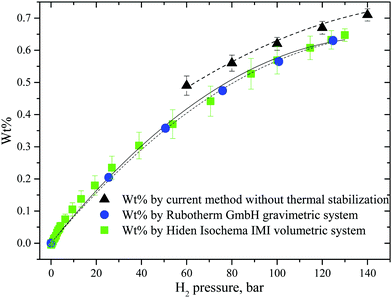Fig. 3 Hydrogen sorption isotherms obtained for AC using GT, and standard gravimetric and volumetric methods.

Fig. 4 shows a summary for wt% data obtained using the GT method for several test materials with a broad range of SSA and hydrogen sorption capacity (see also Table 1). It shows also the trend reported in our earlier studies for SSA vs. wt% at 120 bar H₂ pressure.^17,19,21 This trend is in agreement with the so called “Chahine rule”.^48,49 The trends estimated using standard gravimetric and volumetric methods for carbon materials (AC, rGO and a-rGO) are in rather good agreement with data points collected using the GT method.

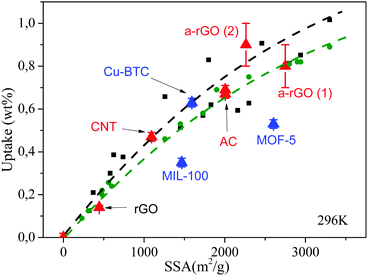Fig. 4 Hydrogen uptake wt% vs. SSA measured by the GT method at 120 bar and 296 K for several common carbon materials and MOFs , compared to our earlier measurements^17,47 performed for rGO and a-rGO materials using standard gravimetric () and volumetric (■) methods.

Samples of MIL-100 and MOF-5 showed somewhat smaller wt% uptakes compared to the “standard“ trend. Therefore, we re-measured the sorption for these specific samples. Standard gravimetric measurement of the MOF-5 excess uptake provided a 0.57 wt% value compared to 0.53 wt% found by the GT method; for MIL-100 identical values of 0.35 wt% were recorded by both methods. Sorption properties of Cu-BTC materials were also verified providing good agreement between excess uptakes measured using GT (0.57 wt%) and volumetric (0.59 wt%) methods. Detailed understanding of the reasons for somewhat lower sorption by these two MOF materials is out of the scope of this study.

It is interesting to estimate approximately the maximal possible Gain value for carbon materials using a simple calculation. The real density of graphite is about 2.3 g cm⁻³ and the distance between graphene layers is about 3.3 Å. To make the space between graphene layers accessible to hydrogen we need to expand the lattice approximately by two times which will result in a twice lower real density of about 1 g cm⁻³. That is roughly 6 times higher than the bulk density of AC in Table 1. Assuming a maximal theoretical SSA of graphene 2650 m² g⁻¹ and using well established sorption vs. excess wt% trends^17,21 the maximal value of Gain can be estimated as ∼35%. Moreover, theoretical studies predict at least a 30% increase of hydrogen sorption in sub-nanometer size graphene pores.⁵⁰ Including this enhancement factor, the maximal Gain value for physisorbing carbon materials can be estimated as ∼45% at 120 bar and ambient temperatures. Considering that the bulk density of realistic materials will be always smaller than their real density, the maximal Gain value which could possibly be achieved for applications is about 30%. Once again, it means that full loading of the tank with material will improve the hydrogen storage capacity by 30% compared to the material free tank with compressed hydrogen at 120 bar and 23 °C as in our experiments. At the same time the tank will become heavier due to the addition of material.

Summarizing our experience, the advantages of the GT method are the following:

– Direct estimation of the hydrogen storage amount using an industry-related tank of a given volume.

– The new parameter introduced for evaluation of a material's performance in gas storage (Gain) provides a very simple and intuitively clear characteristic of the material related to real and bulk densities. For example, we demonstrate that hydrogen storage improvement due to physisorption by ideal carbon materials is limited by G_mat ∼ 30% which mean that at most a 30% higher amount of hydrogen can be stored in the material filled tank compared to a tank filled with compressed hydrogen at the same P–T conditions.

– Reasonable accuracy of the GT method is demonstrated for gram amounts of materials using a standard commercial balance. It is obvious that the GT method can be used also for larger industrial tanks capable of storing kg amounts of gases.

– The method is technically very simple, inexpensive and easy to learn. The test system can easily be assembled using common parts and does not require long experience to take into account typical errors. Note that further improvements are certainly possible. Using e.g. lighter tanks with larger volume and smaller dead volume will improve the accuracy of the method.

– The GT method is especially reliable for evaluation of hydrogen storage at high pressures (>60 bar): the amount of storage gas increases at higher pressures while errors become smaller. With proper tank design the whole pressure range up to commercially used 700 bar (as in the Toyota Mirai) can be studied. That is in contrast with standard gravimetric and volumetric methods. The volumetric method is especially vulnerable for large magnitudes of errors at pressures above 100 bar.

– The GT method was tested here for the gas with smallest density (H₂). It will be even easier to use for estimation of the tank storage capacity of other denser gases (e.g. CH₄ or CO₂).

4. Conclusions

In summary, the hydrogen storage properties of several materials were evaluated relative to the storage capacity of compressed hydrogen gas using the gravimetric tank method. The best Gain value of ∼12% was found for the Cu-BTC MOF which means that the tank completely filled with this material stores a 12% higher amount of hydrogen compared to H₂ gas at the same P–T conditions. The method is based on a weight measurement of a gas filled test tank containing a gram amount of material using a standard commercial balance. The GT method will not replace accurate measurements of hydrogen sorption isotherms using e.g. standard gravimetric and volumetric methods due to insufficient accuracy at low pressures of a few bars. However, the method presents clear advantages for industry-related measurements of the gas storage capacity of a tank at high pressures (tens and hundreds of bars). Our experiments demonstrate that currently available physisorbing materials provide a maximal Gain (increase of hydrogen storage capacity relative to compressed gas) of about 12% and unlikely to exceed ∼30%. We propose to use the GT method as a simple and reliable test to verify reports of exceptionally high hydrogen storage for various novel materials. The GT method can also be used for routine evaluation of a material's performance in storage of any gases like methane or carbon dioxide.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

A. T. and A. I acknowledge funding from the European Union Horizon 2020 research and innovation program under grant agreements No. 696656 and N785219, and support from Kempestiftelserna and Swedish Research Council (N 2017-04173). We thank FNRS for a FRIA fellowship for T. S. We thank also Graphenea for providing a sample of rGO.

Notes and references

1. L. Schlapbach and A. Zuttel, Nature, 2001, 414, 353–358.
2. Q. W. Lai, M. Paskevicius, D. A. Sheppard, C. E. Buckley, A. W. Thornton, M. R. Hill, Q. F. Gu, J. F. Mao, Z. G. Huang, H. K. Liu, Z. P. Guo, A. Banerjee, S. Chakraborty, R. Ahuja and K. F. Aguey-Zinsou, ChemSusChem, 2015, 8, 2789–2825.
3. V. Tozzini and V. Pellegrini, Phys. Chem. Chem. Phys., 2013, 15, 80–89.
4. C. Liu, Y. Y. Fan, M. Liu, H. T. Cong, H. M. Cheng and M. S. Dresselhaus, Science, 1999, 286, 1127–1129.
5. A. C. Dillon, K. M. Jones, T. A. Bekkedahl, C. H. Kiang, D. S. Bethune and M. J. Heben, Nature, 1997, 386, 377–379.
6. M. Becher, M. Haluska, M. Hirscher, A. Quintel, V. Skakalova, U. Dettlaff-Weglikovska, X. Chen, M. Hulman, Y. Choi, S. Roth, V. Meregalli, M. Parrinello, R. Strobel, L. Jorissen, M. M. Kappes, J. Fink, A. Zuttel, I. Stepanek and P. Bernierg, Crop Physiol., 2003, 4, 1055–1062.
7. B. Panella, M. Hirscher and S. Roth, Carbon, 2005, 43, 2209–2214.
8. E. Poirier, R. Chahine, P. Benard, D. Cossement, L. Lafi, E. Melancon, T. K. Bose and S. Desilets, Appl. Phys. A: Mater. Sci. Process., 2004, 78, 961–967.
9. V. B. Parambhath, R. Nagar, K. Sethupathi and S. Ramaprabhu, J. Phys. Chem. C, 2011, 115, 15679–15685.
10. V. B. Parambhath, R. Nagar and S. Ramaprabhu, Langmuir, 2012, 28, 7826–7833.
11. H. Jung, K. T. Park, M. N. Gueye, S. H. So and C. R. Park, Int. J. Hydrogen Energy, 2016, 41, 5019–5027.
12. R. Kumar, J. H. Oh, H. J. Kim, J. H. Jung, C. H. Jung, W. G. Hong, H. J. Kim, J. Y. Park and I. K. Oh, ACS Nano, 2015, 9, 7343–7351.
13. L. F. Wang, N. R. Stuckert and R. T. Yang, AIChE J., 2011, 57, 2902–2908.
14. A. Ghosh, K. S. Subrahmanyam, K. S. Krishna, S. Datta, A. Govindaraj, S. K. Pati and C. N. R. Rao, J. Phys. Chem. C, 2008, 112, 15704–15707.
15. Z. Jin, W. Lu, K. J. O’Neill, P. A. Parilla, L. J. Simpson, C. Kittrell and J. M. Tour, Chem. Mater., 2011, 23, 923–925.
16. K. Spyrou, D. Gournis and P. Rudolf, ECS J. Solid State Sci. Technol., 2013, 2, M3160–M3169.
17. A. Klechikov, G. Mercier, T. Sharifi, I. A. Baburin, G. Seifert and A. V. Talyzin, Chem. Commun., 2015, 51, 15280–15283.
18. A. Klechikov, J. H. Sun, G. Z. Hu, M. B. Zheng, T. Wagberg and A. V. Talyzin, Microporous Mesoporous Mater., 2017, 250, 27–34.
19. J. H. Sun, F. Morales-Lara, A. Klechikov, A. V. Talyzin, I. A. Baburin, G. Seifert, F. Cardano, M. Baldrighi, M. Frasconi and S. Giordani, Carbon, 2017, 120, 145–156.
20. G. Mercier, A. Klechikov, M. Hedenstrom, D. Johnels, I. A. Baburin, G. Seifert, R. Mysyk and A. V. Talyzin, J. Phys. Chem. C, 2015, 119, 27179–27191.
21. A. G. Klechikov, G. Mercier, P. Merino, S. Blanco, C. Merino and A. V. Talyzin, Microporous Mesoporous Mater., 2015, 210, 46–51.
22. T. H. Kim, J. Bae, T. H. Lee, J. Hwang, J. H. Jung, D. K. Kim, J. S. Lee, D. O. Kim, Y. H. Lee and J. Ihm, Nano Energy, 2016, 27, 402–411.
23. A. Lueking and R. T. Yang, J. Catal., 2002, 211, 565.
24. Y. W. Li and R. T. Yang, J. Am. Chem. Soc., 2006, 128, 726–727.
25. A. Lueking and R. T. Yang, J. Catal., 2002, 206, 165–168.
26. N. R. Stuckert, L. F. Wang and R. T. Yang, Langmuir, 2010, 26, 11963–11971.
27. R. Campesi, F. Cuevas, M. Latroche and M. Hirscher, Phys. Chem. Chem. Phys., 2010, 12, 10457–10459.
28. S. M. Luzan and A. V. Talyzin, Microporous Mesoporous Mater., 2010, 135, 201–205.
29. N. P. Stadie, J. J. Purewal, C. C. Ahn and B. Fultz, Langmuir, 2010, 26, 15481–15485.
30. R. Prins, Chem. Rev., 2012, 112, 2714–2738.
31. C. Y. Zhou and J. A. Szpunar, ACS Appl. Mater. Interfaces, 2016, 8, 25933–25940.
32. G. De Weireld, M. Frere and R. Jadot, Meas. Sci. Technol., 1999, 10, 117–126.
33. A. Herbst, R. Staudt and P. Harting, J. Therm. Anal. Calorim., 2003, 71, 125–135.
34. D. P. Broom and M. Hirscher, Energy Environ. Sci., 2016, 9, 3368–3380.
35. D. P. Broom and P. Moretto, J. Alloys Compd., 2007, 446, 687–691.
36. D. P. Broom and C. J. Webb, Int. J. Hydrogen Energy, 2017, 42, 29320–29343.
37. D. P. Broom, C. J. Webb, K. E. Hurst, P. A. Parilla, T. Gennett, C. M. Brown, R. Zacharia, E. Tylianakis, E. Klontzas, G. E. Froudakis, T. A. Steriotis, P. N. Trikalitis, D. L. Anton, B. Hardy, D. Tamburello, C. Corgnale, B. A. van Hassel, D. Cossement, R. Chahine and M. Hirscher, Appl. Phys. A: Mater. Sci. Process., 2016, 122.
38. K. E. Hurst, P. A. Parilla, K. J. O'Neill and T. Gennett, Appl. Phys. A: Mater. Sci. Process., 2016, 122, 42.
39. C. Zlotea, P. Moretto and T. Steriotis, Int. J. Hydrogen Energy, 2009, 34, 3044–3057.
40. S. J. Hynek and W. D. Fuller, Hydrogen Energy Prog. XI, Proc. World Hydrogen Energy Conf., 11th, 1996, 1–3, 1197–1202.
41. J. M. Zielinski, P. McKeon and M. F. Kimak, Ind. Eng. Chem. Res., 2007, 46, 329–335.
42. J. Burress, D. Bethea and B. Troub, Rev. Sci. Instrum., 2017, 88, 053902.
43. S. M. Luzan, H. Jung, H. Chun and A. V. Talyzin, Int. J. Hydrogen Energy, 2009, 34, 9754–9759.
44. A. V. Talyzin and A. Jacob, J. Alloys Compd., 2005, 395, 154–158.
45. M. E. Casco, M. Martinez-Escandell, E. Gadea-Ramos, K. Kaneko, J. Silvestre-Albero and F. Rodriguez-Reinoso, Chem. Mater., 2015, 27, 959–964.
46. S. Gumma and O. Talu, Langmuir, 2010, 26, 17013–17023.
47. A. Klechikov and A. V. Talyzin, ACS Nano, 2016, 10, 9055–9056.
48. E. Poirier, R. Chahine and T. K. Bose, Int. J. Hydrogen Energy, 2001, 26, 831–835.
49. N. P. Stadie, J. J. Vajo, R. W. Cumberland, A. A. Wilson, C. C. Ahn and B. Fultz, Langmuir, 2012, 28, 10057–10063.
50. M. Rzepka, P. Lamp and M. A. de la Casa-Lillo, J. Phys. Chem. B, 1998, 102, 10894–10898.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05241g

---