Comparing the molecular and global rheology of a fluid under high pressures

Abstract

The viscosity of liquids is a strong function of pressure. While viscosity is relatively easy to measure at low pressure, high-pressure rheology presents significant experimental challenges. As a result, rheological models are often used to extrapolate viscosity from low pressure measurements to higher pressures. Techniques to obtain data over a wide range of pressures and shear rates, as well as understanding the validity and limitations of methods to fill the gaps in the available data, are therefore of crucial practical and theoretical importance. This work examines the viscosity of polyalphaolefin (PAO) by combining average global area averaged measurements at high pressure and local molecular viscosity measurements at moderate pressures. Viscosities spanning five orders of magnitude are examined at pressures up to 720 MPa. High pressure results were obtained with friction measurements where the fluid is sheared between two surfaces in a loaded point contact. The local molecular microviscosity at medium and low pressures was measured by applying a technique based on fluorescence anisotropy, which probes the rotational motion of dye molecules in a nanoscale film under shear. Both sets of measurements are taken in the same configuration, an elastohydrodynamic (EHD) contact. This is the first set of quantitative local viscosity measurements that have been verified against both friction and high pressure rheometry measurements. Commonly used rheological models were compared to experimental results. Our work shows that fluorescence anisotropy and friction measurements can be used to determine the viscosity of liquids over a wide range of conditions from a single experimental setup. The results obtained match results from low- and high-pressure rheometry for PAO. The importance of correcting friction data for pressure non-uniformity, temperature and shear thinning is also highlighted.

---

Introduction

The availability of accurate viscosity data over a wide range of pressures and shear rates plays a critical role in our understanding of natural phenomena and our ability to design and operate machinery in an efficient and reliable way. As a result, viscometers and rheometers of various geometries are standard equipment in many laboratories. Most of these devices, however, are not suitable for high-pressure, high-shear rheology because of the cost and complexity of high-pressure instruments. Yet high-pressure rheology is relevant to conditions commonly experienced by crucial engineering components, such as bearings, fuel injectors and gears. To make matters worse, the behaviour of fluids at high-pressure can deviate substantially from observations at low to moderate pressures. Hence, extrapolation of high-pressure behaviour from low-pressure data may be inaccurate, if not altogether misleading. There is, therefore, a clear need for methods to measure viscosities over a broad range of pressures and shear rates. At the same time, it is crucial to understand how rheological models can best help bridge the gap between the available data and the application needs.

High-pressure rheological data are normally obtained experimentally or by using rheological models. The former approach demands the use of high-pressure rheometers.^1,2 Even high-pressure rheometers may not reach pressures and shear rates of engineering interest. Furthermore, some factors of practical importance, such as the degree of confinement and the thermal conductivity of the environment, may not be easily accounted for.³ Because of the complexity of the equipment involved, in situ measurements are not always possible. Molecular dynamics simulations have also been used to study the high-pressure rheology of model lubricants.^3–5 However, due to computational limitations, such studies are currently limited to relatively small molecules with short relaxation times.⁶

As an alternative, hydrodynamic friction⁷ can be used to infer the viscosity of liquids from relatively straightforward force measurements. Friction measurements involve shearing the test fluid between two surfaces in a loaded contact (an elastohydrodynamic or EHD contact). This approach may provide information that is more relevant to engineering applications. However, flow conditions across an EHD contact are not uniform and the quantity obtained is an average viscosity. The onset of shear thinning and temperature changes due to frictional heating further complicate the use of friction data as a source of rheological information. When the measured friction is very low, as observed in low-pressure conditions, the experimental errors can be substantial.

Novel in situ methods have recently been developed to provide local viscosity measurements of a sheared fluid under high-pressure conditions. These methods make use of EHD contacts and involve the addition of sensing probes, such as fluorescent molecules or particles, to the fluid of interest. The fluorescence characteristics of the probes are affected by the viscosity of the surrounding fluid, thereby allowing local information about its rheology to be gathered. Particle tracking has also been conducted by Strubel et al.⁸ to collect information about the lubricant flow field in an EHD contact. Since the particles rarely enter the contact, only information on the peripheral areas of the contact is obtained.

Dench et al. have measured the viscosity heterogeneity of liquids in EHD contacts based on fluorescence lifetime measurements with molecular rotors.^9,10 Otsu and Imado¹¹ used pyrene excimer fluorescence intensity and showed similar observations. Fluorescence-based methods, however, may have a limited operational viscosity range. In addition, in order for a fluorescence probe to be used to measure viscosity, the effects of temperature and pressure on its fluorescence properties must be ascertained and duly taken into consideration.

The experimental challenges described show the importance of devising methods to measure the viscosity of liquids over a broad range of operating conditions, with equipment of manageable complexity.

The difficulty of obtaining data at high-pressure, high-shear conditions also makes the use of rheological models attractive to obtain estimates where no experiments are available. Commonly used rheological models include Barus,¹² Roelands,¹³ and the Hybrid model¹⁴ (details in section ‘Common rheological models’), although their applicability and limitations require verification.

The goal of this work is to demonstrate the use of an EHD contact as a rheometer with a wide range of operating conditions, and to assess the appropriateness of rheological models in describing the high-pressure viscosity of a fluid. To achieve our goal, the viscosity of a model fluid, polyalphaolefin (PAO), was measured up to a pressure of 720 MPa. The measurements span five orders of magnitude of viscosity.

A newly developed, fluorescence anisotropy-based method (see section ‘Fluorescence anisotropy measurements’), which monitors the rotational diffusion of molecular probes in a fluid, was used for the first time to obtain spatial information of the local viscosity of a PAO in an EHD contact at low and medium pressures. Fluorescence anisotropy has previously been used to measure the viscosity of fluids under high pressure in bulk,^15,16 but not in a lubricated contact. Friction measurements were performed to examine area-averaged viscosity of the PAO above 300 MPa. Fluorescence anisotropy-based measurements and conventional friction measurements examine properties of fluids at very different length scales, i.e. nm and 100's μm respectively. These measurements were combined and then compared to high-pressure rheology data to examine the validity of the combined approach. The limitations and applicability of commonly used rheological models to our results is then investigated.

Definitions of pressure viscosity coefficients

Pressure-viscosity coefficients are frequently used to describe the sensitivity of the viscosity, η, to pressure, p. Pressure-viscosity coefficients are not constants, but rather functions of pressure.¹⁷ Their variability reflects compressibility of the fluid due to (1) a reduction in free volume – dominant at low pressures,¹⁸ and (2) the compression of the molecules themselves.¹⁹ A pressure viscosity coefficient α_p can be assigned over a defined pressure range by fitting viscosity data up to a pressure p. α₀ is the initial pressure-viscosity coefficient defined by the logarithmic derivative of viscosity with respect to pressure at zero pressure under ambient conditions,¹ as shown in eqn (1).Liquids are generally more compressible at low pressures. Hence α₀ is significantly higher than α_p>0 while α is relatively constant at moderate pressure.

Common rheological models

Barus equation and single exponential fit

As a first approximation, a single exponential relationship, e.g.

η = be^α_p (2)

may be used to describe the pressure-viscosity relationship of a fluid. b and α are fitting parameters. The Barus equation (eqn (3)) is a single exponential model fitted through the zero pressure viscosity η₀.

The Barus equation

η = η₀e^α_p (3)

is obtained at low pressure and is popular due to easy access of experimental data. It should however only be used to describe fluids at low pressures.^20,21 Extrapolating the Barus equation to higher pressures can lead to over-prediction of the high-pressure viscosity. Note engineering fluids commonly show a relatively constant α in the moderate pressure range.^17,22

Some fluids show a faster than exponential dependence of viscosity at very high pressure.²³ This phenomenon may be caused by the vitrification of the fluid at very high pressure. Faster-than-exponential behaviour gives rise to an inflection point in the pressure-viscosity relationship, which cannot be represented by a single exponential fit. For PAOs, Nakamura et al. showed that no inflection occurred up to 1 GPa and the initial reduction in free volume is mostly over by 200 MPa so that α is relatively constant.²⁴

Roelands equation

Roelands equation empirically fits the viscosity variation with pressure of mineral oils and hydrocarbon-based fluids. The equation accounts for the variation of α with pressure through the Roelands parameter Z. Z can be expressed as²³where the values η_r = 6.3 × 10⁻⁵ Pa s and p_r = 0.196 GPa are commonly adopted. For an isothermal case, the viscosity at a given pressure can be expressed by²³Variations accounting for temperature^20,25 also exist. Sargent²¹ found Roelands equation to be accurate up to 500 MPa for common lubricants. Like a single exponential fit, Roelands equation is incapable of showing an inflection point in the relationship.

Hybrid model

The Paluch equation²⁶ when combined with the McEwen equation²⁷ forms the Hybrid equation (eqn (6)).¹⁴ The Paluch equation is used to model faster than exponential response and the McEwen term the slower than exponential response. C_f is the Fragility parameter, q is the McEwen exponent and p_∞ is the pressure where the viscosity tends towards infinity. Due to the conditions tested, only the McEwen equation term (eqn (7)) is required in this work.

An EHD contact as a rheometer

A circular point EHD contact, shown in Fig. 1(b) and (c), is formed when a rotating ball is pressed against a spinning disc, with a thin fluid film being sheared, separating the two surfaces. The fluid surrounding the contact (the out-of-contact region) experiences ambient pressure and is relatively thick compared to the fluid in the EHD contact, which is submicron in thickness. The film thickness h is controlled by the entrainment speed U_e

U_e = (U_disc + U_ball)/2 (8)

The speeds of both the ball and the disc, U_ball and U_disc, are controlled separately to set the slide roll ratio SRRAs U_e increases, the volume of lubricant drawn into the contact, and hence h increases. When the film is thick enough, the two surfaces are separated and the fluid film fully supports the load. This lubrication regime is known as full fluid film lubrication. At sufficiently high loads, elastic deformation of the surfaces occurs. The high contact pressure changes the viscosity of the entrained lubricant. This contact geometry (Fig. 1(b) and (c)) is chosen because it easily provides a large range of pressure, over 1 GPa, without requiring hydrostatic systems. The size of the contact and the pressure exerted in the fluid are governed by Hertzian contact mechanics. The contact radius a (eqn (10)) is set by the load N, the effective radius (which is the radius of the rotating ball in this study) R′ and the combined elastic modulus E*. The local contact pressure p(x) varies with radial position normalised by the contact radius a and can be approximated by a Hertzian pressure distribution (eqn (11)). The maximum contact pressure p_max, shown in eqn (12), is at the centre of the contact. The average pressure p_a is defined by eqn (13).

p(x) = p_max(1 − x²)^1/2 (11)

In this study, two types of friction measurements were performed in an EHD point contact. Firstly, the frictional force experienced by the contact can be measured with a force transducer. This force measurement can be turned into a stress value if the contact area is known:μ being a friction coefficient, N the applied load and a the contact radius. The stress value in turn yields an area average viscosity value η^Fwhere

[small gamma, Greek, dot above] = U_s/h_c (16)

where U_s = U_ball− U_disc, and the central fluid film thickness in the EHD contact, h_c. η^F is normally related to the average contact pressure p_a (see Table 1 for the definition of all viscosities used in this paper).

Fig. 1 (a) Schematic of the setup. Beam expander (BE), polarising beam splitter (PBS), polariser (P), dichroic (D), long pass filter (LP), mirror (M), tube lens (TL), lens (L), 1/2 waveplate (λ/2), objective (O); (b) schematic of a point contact under elastohydrodynamic (EHD) conditions from the side. (c) Schematic of a point contact under EHD conditions from below showing the imaged (point by point) area. The imaged area in this figure is obtained with white light interferometry for a typical EHD contact. The arrow shows the flow direction of the fluid.

Table 1 Definitions of viscosities used in this work

Parameter	Definition
η 0	Viscosity at zero pressure
η r	Reference viscosity value used in the Roeland equation (eqn (4) and (5))
η	True viscosity of the fluids. This is taken as the value obtained from the high pressure rheometry and can be modelled by the Barus equation with the exponent represented as a polynomial.
η ^M	Area averaged viscosity taken from friction measurement with an EHD point contact
η ^F	Theoretical area averaged viscosity based on an EHD point contact (see eqn (21))
η ^A	Local viscosity in an EHD point contact obtained with fluorescence anisotropy measurements
η ^R	Theoretical area averaged viscosity obtained using an EHD point contact if the true viscosity of the fluid is modelled by the Barus equation with the exponent represented as a polynomial (see eqn (23) and (24)). This is calculated from the value obtained from the high pressure rheometry η. The derivation is in eqn (25).
η ^E	True viscosity of a fluid considering the effect of shear thinning (see eqn (26)).
η ^G	Theoretical area averaged viscosity obtained using an EHD point contact if the true viscosity of the fluid is modelled by the Barus equation with the exponent represented as a polynomial and the effect of shear-thinning is incorporated. This is calculated from the value obtained from the high pressure rheometry, i.e. η (see eqn (27)).
η ^T	Theoretical area averaged viscosity obtained using an EHD point contact if the true viscosity of the fluid is modelled by the Barus equation with the exponent represented as a polynomial and the effects of shear-thinning and shear heating are incorporated. This is calculated from the value obtained from the high pressure rheometry, i.e. η (see eqn (27), where η0 is the value of viscosity at zero pressure and at the contact flash temperature based on the test condition)
η*	Estimated true viscosity of the fluid based on area-average viscosity from friction measurements, η^M, taken into account of effects of shear thinning and shear heating and the effect of applied pressure distribution has been removed.

---

In this study, a molecular probe is added to a fluid. The viscosity of the fluid results in friction that affects the translational and rotational motion of the probe. This friction is a nanoscale phenomenon and can be determined through optical techniques (see details in methodology). The pressure heterogeneity (see eqn (11)) in an EHD contact provides a unique opportunity to obtain local viscosity maps across a large range of pressure with a simple contact geometry.

Two remarks should be made about the use of an EHD contact as a rheometer. Firstly rheological data represents the viscosity of fluids at the low shear rate limit. At finite shear rates, the linearity of the relation between shear strain and shear stress breaks down and, for some fluids, shear thinning takes place. The stress at which shear thinning starts is the Eyring stress. Friction measurements are by nature finite shear rate measurements. In order to minimise the occurrence of shear thinning, measurements are taken at the lowest possible shear rate to obtain an adequate friction force signal. As the maximum shear stress at the centre of the contact can still be high, shear thinning cannot be ruled out from the present experiments. Secondly the applied pressure in a point contact is spatially heterogeneous. This has important consequence to the validity of using friction measurement for viscosity measurements. A method will be shown in the section ‘Processing friction data to obtain viscosity from spatially heterogeneous contacts’ on how friction data can be processed for rheological purposes.

Fluorescence anisotropy – molecular friction

With fluorophores added to the model fluid as molecular probes, a technique called fluorescence anisotropy was used to obtain information on the local viscosity of the fluid. The technique is commonly used in the life sciences²⁸ and polymer physics²⁹ research, for measurements in cells,^30,31 protein dynamics,²⁸ structural changes and interactions among molecules.^32,33 The principle on how fluorescence anisotropy can be used to measure viscosity with a non-segmental fluorophore will be described briefly in this section. Details can be found in Lakowicz.³⁴

Fluorescence anisotropy involves exciting fluorophores in a fluid with plane polarised light. Fluorophores with their absorption transition moments aligned with the polarised light are more likely to be excited. The initial emission light thus has a certain polarisation state. Fluorescence anisotropy, r, relates the emission intensity that is plane polarised, I_‖, and horizontally polarised, I_⊥, to the total emission intensity, I_T (see eqn (17) and (18)). I_‖ and I_⊥ are detected using separate sensors. G is a constant that accounts for differences in the sensitivity of the two detectors and the polarisation optics, see Fig. 1.

The theoretical maximum fluorescence anisotropy r₀ at time t = 0 after excitation is 0.4 and occurs when the absorption and emission dipoles of fluorophores are parallel. As fluorophores rotate with time due to Brownian motion, their emission transition moments rotate and their emission becomes depolarised and r drops. The characteristic time of depolarisation is therefore governed by the friction the fluorophore experiences, i.e. the viscosity of the lubricant surrounding the probe, which hinders the rotation of the fluorophores. The more viscous the fluid, the longer the fluorescence anisotropy remains at its initial value. If a continuous wave laser is used for excitation, as in this study, then fluorophores are continuously being excited, hence a steady state fluorescence anisotropy value is obtained. The average fluorescence anisotropy of a fluorophore in a fluid is related to the viscosity of the fluids, described by eqn (19). Note A and B are fitting coefficients that are specific to the interaction between the fluid and the probe. It is assumed that their interaction is not affected by temperature and applied pressure.

I_T = I_‖ + 2GI_⊥ (17)

r = A ln(η) + B (19)

Using local molecular friction to represent fluid rheology has been achieved in the authors previous works^9,10 by measuring the fluorescence lifetime of molecular rotors in model fluids. Since molecular rotors are mostly used in biological samples, few are applicable to high viscosity conditions and are soluble in non-polar fluids. Fluorescence anisotropy measurements of fluid viscosity can utilise any soluble fluorophore that is sensitive in the viscosity range of interest. Hence a switch from fluorescence lifetime to fluorescence anisotropy measurements increases the number of available fluorophores. The reasoning behind the choice of steady state over time resolved fluorescence anisotropy measurements was to make the technique more accessible.

Experimental

Materials

Spectrasyn 8 (PAO 8), a chemical grade polyalphaolefin (PAO) from Exxon Mobil, was the main working fluid in this work. The polydispersity is not known. Based on the calibration results shown in Fig. 4, the polydispersity of PAO has no effect on our results.

Test fluids, listed in Table 2, were used for viscosity-fluorescence anisotropy calibration (see section ‘Viscosity-fluorescence anisotropy calibration’). Durasyn is PAO manufactured by Ineos. GTL 8 is a branched alkane based commercial base oil manufactured by Shell Global Solutions Ltd. They were used as received. Viscosities of test solutions were measured with a viscometer (Stabinger SVM3000) at 22 °C and are listed in Table 2. Their viscosities span 0.0004–3.451 Pa s. n-Heptane and toluene, both spectroscopic grades, were from Sigma Aldrich. Their viscosities were provided by the supplier. Structures of these chemicals are shown in Fig. 2.

Table 2 Viscosity of the fluids tested at 22 °C

Fluid	Viscosity (Pa s)
n-Heptane	0.0004
Toluene	0.0010
Spectrasyn 8	0.088
Spectrasyn 40	0.951
Spectrasyn 100	3.451
Durasyn 174	0.874
Durasyn 145	0.041
Durasyn 164	0.029
GTL8	0.139
GTL8 & Durasyn 174 blend	0.159
Spectrasyn 40 & Durasyn 164 blend	0.136

---

Fig. 2 Chemical structures of fluids used.

Nile red (see Fig. 2) was used as the fluorophore. It was dissolved into test fluids with magnetic stirring at 100 °C for 1 h. Mixtures were then filtered with 1 μm filters (514-4027 Syringe Filters, Acrodisc®, glass fibre VWR), and the final fluorophore concentration in the test solutions was 0.1–0.4 mM.

Fluorescence anisotropy measurements

The test rig consisted of a circular EHD contact created by pressing a steel ball against a glass disc. Test conditions, shown in Table 3, with SRR = 0, are chosen to give good quality data while minimising shear heating. The test rig was mounted on an automatic translation stage, which was placed over an inverted microscope as described previously by the authors.^9,10 This provided optical access to the contact area. Material properties of the rubbing surfaces are provided in Table 4. A 488 nm continuous-wave laser (Spectra Physics) was used as the excitation light source. The laser beam was expanded and collimated using a telescope. It then passed through a λ/2 waveplate and a polariser. The light reached the back of the microscope and was directed to the objective with a dichroic mirror. A 20× Zeiss Neofluor objective (NA = 0.4) was used to focus the laser (Gaussian spot size of collected confocal emission ≈2 μm FWHM) into the fluid in the contact. The resulting fluorescence emission was collected through the same objective. The fluorescence passed through the dichroic mirror, an emission filter and the tube lens. It then passed through a pin hole and was collimated. After that, it passed through a polarising beam splitter to separate the horizontal and plane polarised emission before being focused onto two detectors (em-ccd cameras, Raptor Falcon). The setup is shown in detail in Fig. 1. Since the local pressure in the EHD contact varies according to eqn (11), the local viscosity in the contact is not uniform. To explore this viscosity heterogeneity, the contact was moved so that 400 locations distributed on a regular 20 × 20 lattice were probed in each image. The total imaged area (see Fig. 1(c)) was 325 × 325 μm which covered the contact and its surrounding area. Each fluorescence anisotropy map was generated from 21 images averaged at each point, with the first and last 2 images discarded (25 images taken) to ensure the contact was in-position and was as stable as possible during the measurement. A viscosity map was obtained by applying a relationship between viscosity and fluorescence anisotropy based on the calibration detailed in section ‘Viscosity-fluorescence anisotropy calibration’.

Table 3 Conditions of contact for fluorescence anisotropy measurements

Load, N, (N)	3
Average pressure, pa (MPa)	182
Peak pressure, pmax (MPa)	273
Entrainment speed, Ue (mm s^−1)	145
Film thickness, h (nm)	≈115

---

Table 4 Material properties of the ball and the disc. Youngs modulus E and the Poissons ratio ν

E (GPa) and ν of AISI52100 steel	220 and 0.3
E (GPa) and ν of glass	70 and 0.2

---

The detection system needs to be calibrated before use. Firstly, the polarising beam splitter leakage was determined. Then the sensitivity of the two detectors to emission of different polarisations were assessed (see section, ‘Fluorescence anisotropy – molecular friction’). Finally, to ensure the detectors were on their respective focal planes, their positions were checked using an aqueous solution of glycogen. Initially 0.1 mM solution was used. It was then diluted until the measured fluorescence anisotropy with the emission (long pass) filters removed reached its peak value. At the correct concentration, glycogen scatters light almost completely which results in a fluorescence anisotropy close to 1. The position of each detector was then optimised until the fluorescence anisotropy reached its maximum value.

For static, bulk measurements, which were required for the calibration of the response of the fluorophore, the EHD contact was replaced with a cuvette on a slide holder.

The temperature of the fluorescence experiments was managed by the temperature control of the room and was set to 22 ± 1 °C.

Data collection and analysis of fluorescence measurements in nanoscale films with microscale vertical displacement

In this setup, the focal plane is fixed once the position of the objective is fixed. The depth of field of a typical 20× microscope objective is around 6 μm while the typical thickness of a fluid film in our test is less than 1 μm. This means that if the thin film in which fluorescence measurements are to be taken is displaced vertically (i.e. in z-direction, see Fig. 1) more than the depth of field, then a significant amount of fluorescence signal is lost. Such displacement is possible in our EHD contact due to rotation of the disc or the ball, rendering the fluid film to become out of focus periodically (precession). This results in intensity fluctuations which are not related to properties of the fluid film. This problem is amplified when more than one detector is used. If the positions of the detectors deviate from their respective focal planes by a different amount, the fluorescence anisotropy changes in a way unrelated to the properties of the fluid film. To account for this problem, two constants, D₁ and D₂ are introduced into eqn (18) to make eqn (20).Eqn (20) shows that when the thin film moves out of focus, there is a linear shift in the fluorescence anisotropy. This shift is governed by the relative distance between the two detectors from their respective focal planes and the average run out (vertical displacement as a function of radial position of the disc) of the fluid film verses the exposure time of the detector. To take this linear shift in fluorescence anisotropy into consideration, a systematic offset is required. Two offset values are needed. It is vital that they are meaningful and based on measured values. The reference value for the offset is the value of the fluorescence anisotropy in bulk solutions taken in static condition in a cuvette. Then an out-of-contact average fluorescence anisotropy (all area outside of the red circle in Fig. 3) as well as an in-contact average around the edge of the contact (area between the red and green circles in Fig. 3) are taken. The latter has a local pressure close to zero and corresponds to the region that lies 1 pixel (≈17 μm) away from the contact. This is where the film thickness is of a similar order of magnitude to that of the fluid film in the contact. These values are compared with the static bulk fluorescence anisotropy, giving the two necessary offsets. The exact offset values vary among fluorescence anisotropy maps. The offsets are then applied to all the values taken from their corresponding regions. This offset procedure gives consistent results.

Fig. 3 Contour plot of viscosity vs. position for PAO 8 in an EHD point contact under pure rolling condition. Peak pressure = 273 MPa, entrainment speed = 145 mm s⁻¹, h ≈ 115 nm measured using optical interferometry. Cross sections of the figure in both the flow (black dash line) and orthogonal to the flow (red dash line) directions are shown in Fig. 6. The white arrow indicates the direction of fluid flow.

Since the film thickness in the out of contact region is much thicker than that in the EHD contact, the intensity obtained from the former is much stronger than that from the latter at a fixed exposure time. Thus, fluorescence anisotropy maps were taken at different exposure times to resolve different parts of map. An exposure time of 30 ms allows fluorescence anisotropy outside the contact to be resolved. Exposure times of 70 and 100 ms increase the signal-to-noise ratio of data from the in-contact region. An exposure time of 50 ms is also used. These four fluorescence anisotropy maps taken at different exposure times are averaged on a point by point basis to produce the final averaged map. To do so, the contact and its centre in each map are found by smoothing the map with an averaging spatial filter and then fitting the cross sections of the map with a polynomial, locating the position of the peak fluorescence anisotropy.⁹ Recall the fluorescence anisotropy map consists of 20 × 20 grid points. Once the location of the peak fluorescence anisotropy of the smoothed contact is found, the positions of the grid points are shifted so that the peak fluorescence anisotropy of each image lies at the position (0,0). It was found that this shift never exceeds one grid point in each direction and the difference in spatial position from map to map was cancelled out in the averaging process. The pressure was calculated from the Hertzian relationship (eqn (11)) after the centre was found from the averaged map.

Friction measurement

Friction and film thickness measurements were performed with a circular EHD contact. To obtain the film thickness required to calculate the viscosity (see eqn (14)–(16)), an EHD 2 (PCS instruments) was used. This instrument measures film thickness using optical interferometry.^35,36 In this case, an EHD contact was created with a steel ball against a glass disc and the test conditions were matched to those applied in friction measurements.

Friction measurements were taken using a mini traction machine (PCS Instruments). Traction curves (coefficient of friction against shear rate) were obtained at temperatures between 20 and 50 °C in 5 °C increments, and loads between 15 and 45 N in 5 N increments. To achieve a wide pressure range, EHD contacts were created with steel ball against steel disc, steel ball against glass disc, and glass ball against glass disc. Friction data were then used to calculate the area-averaged viscosity η^F at each average pressure p_a and temperature (see eqn (14)–(16)). Then for each average pressure, η^F at each temperature was fitted using an exponential fit and the viscosity at 22 °C was estimated. Details on η^F estimation with friction measurement can be found in the authors previous work.⁹ Procedures to take into account effects of shear thinning and shear heating on η^F are described in the section ‘Processing friction data to obtain viscosity from spatially heterogeneous contacts’.

Results and discussion

Viscosity-fluorescence anisotropy calibration

Solutions listed in Table 2 were used to calibrate the response of Nile red in fluids of various viscosities. The fluorescence anisotropy of Nile red in each solution was measured at least 3 times and averaged. As suggested by eqn (19), the measured fluorescence anisotropy values all lay on a straight line when plotted against the logarithm of viscosity (see Fig. 4). Data from blends made of a mixture of high and low molecular weight PAO, and PAO and GTL (left-facing, and right-facing triangles, Fig. 4) obey the same relationship, confirming that the polydispersity of the solutions do not affect our results. The results also show that the setup was well aligned for fluorescence anisotropy measurements.

Fig. 4 Calibration of Nile red fluorescence anisotropy with viscosity in bulk solution under static conditions. Insert shows the calibration on linear–linear axis. Error bars are one standard deviation. Solvents here are heptane and toluene.

Fluorescence anisotropy of Nile red in n-heptane and toluene are negative (diamonds, Fig. 4). This is due to difficulties in calibrating the system with very low r where I_‖ ≈ GI_⊥. So, any small fluctuation or offset affects the fluorescence anisotropy value substantially. Note if a single calibration relationship is used and it is linear as in Fig. 4, a small offset is not of any concern.

Mapping viscosity with fluorescence anisotropy

Fluorescence anisotropy maps of EHD contacts were used to generate viscosity maps (Fig. 3) based on the fluorescence anisotropy-viscosity calibration (Fig. 4). As expected, the local fluorescence anisotropy (Fig. 5(a)), and hence local fluid viscosity η^A (Fig. 5(b)), increases from the edge of the contact and reaches a maximum near the centre of the contact where pressure is the highest. The cross-sections of the viscosity map shown in Fig. 3 (also in Fig. 5(b)) through the centre of the contact parallel (black line) and orthogonal (red line) to the flow direction are presented in Fig. 6. Note the inlet, where the fluid is entrained into the contact, has a viscosity around 0.25 Pa s (see insert in Fig. 6), which suggests a pressure rise at the inlet of around 70 MPa. Pressure build-up at the inlet is part of the fluid film generation process to keep the two rubbing surfaces separated. The result is consistent with the authors’ previous findings (50–100 MPa)⁹ using a different fluid, and the findings of Glovena and Spikes³⁷ and Otsu and Imado.¹¹ This pressure rise can extend up to half the contact width behind the contact.³⁸

Fig. 5 (a) Fluorescence anisotropy vs. position for PAO 8 in an EHD point contact under pure rolling conditions. (b) Viscosity map from (a) using the calibration in Fig. 4. Arrows indicate flow direction. Peak pressure = 273 MPa, entrainment speed = 145 mm s⁻¹, h ≈ 115 nm measured using optical interferometry.

Fig. 6 Cross-sections showing local viscosity in both parallel (black) and orthogonal (red) to the fluid flow directions as shown in Fig. 3. Blue line corresponds to the prediction based on Hertzian contact pressure and Barus equation fit to high pressure viscometry data up to 280 MPa. Arrow indicates the flow direction. Insert highlights the increase in viscosity at the inlet of the contact. Hertzian contact radius 72.5 μm.

The predicted in-contact viscosity distribution based on Hertzian contact pressure distribution and results from high pressure viscometry at 22 °C³⁹ (black square with solid line, Fig. 7, see also Table S2, ESI†) is shown as the blue line in Fig. 6. While the results obtained from the orthogonal direction (red line, Fig. 6) match well with the prediction (blue line), results from the flow direction (black line) show broadening. This is not always the case.⁹ In this case, the contact has shifted slightly in the flow direction due to the imaging stage returning more accurately to the centre, between maps, in the orthogonal-to-flow direction. This is likely due to the forces exerted in the flow direction to drive the ball, working against the imaging stage. Hence more accurate pressure-viscosity distribution is obtained in the measurements orthogonal to the flow direction.

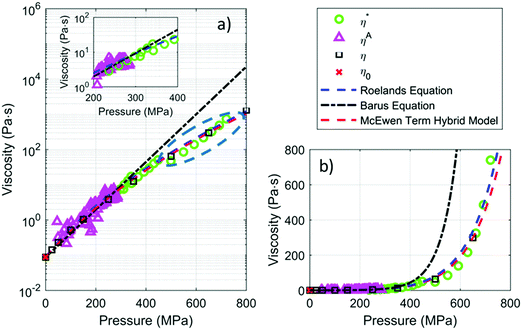Fig. 7 (a) Viscosity of PAO 8 from friction measurements with all necessary adjustments (see text for details), η*; from in situ local fluorescence anisotropy measurement η^A; and from high pressure viscometry, η,³⁹ log-linear axis. η₀ is viscosity of PAO at ambient pressure and was obtained with Stabinger viscometer. Fits from commonly used rheological models are included (lines). Viscosity results from friction measurements using a steel–steel EHD point contact lie in the blue dashed ellipse. Insert shows the region where η* and η^A overlap. (b) Figure (a) shown on a linear–linear axis. Note Roeland equation (blue dash line) and the McEwen term (red dash line) almost overlap.

Comparison of local viscosity data from fluorescence anisotropy measurements with high pressure viscometry data

Direct quantification of viscosity in an EHD contact with local in situ fluorescence anisotropy measurements is limited to the moderate pressure range due to the sensitivity of the chosen probe. In the viscosity range studied, results from in situ fluorescence anisotropy measurements (η^A triangles, Fig. 7) matches well with the low shear viscosity of PAO 8 at ambient pressure obtained using a Stabinger viscometer (red square) and also data from high pressure low shear rheometry at 22 °C³⁹ (η, black square with solid line). This supports that local viscosity measurements in an EHD contact are conducted in close to isothermal conditions.

Processing friction data to obtain viscosity from spatially heterogeneous contacts

Viscosities for PAO 8 at mean contact pressures between 240 and 720 MPa obtained from friction data are shown in Fig. 8 (η^M, red crosses, see Table 1 for definitions of η^M and η^F).

Fig. 8 Breakdown of how friction is corrected to obtain true viscosity of PAO 8. Insert for clarity in the region of interest. See Table 1 for definitions of symbols.

Due to the non-uniform pressure experienced by the fluid in an EHD point contact and the non-linear relationship between pressure and viscosity,¹⁴ the area-averaged viscosity does not correspond to the “true” viscosity η at the same p_a. To illustrate the potential issues, we examine a fluid with true viscosity obeying Barus law (eqn (3)). Assuming that the pressure distribution in the contact is Hertzian (eqn (11)), the area average viscosity from a point contact η^F can be calculated by applying eqn (11) and (14) with τ = [small gamma, Greek, dot above]η(p(x))

Let ν be the ratio between η and η^F. Then ν can be determined in closed form:where β = αp_max. ν is always less than 1 (solid black line, Fig. 9), i.e. η^F overestimates η and is a good approximation of η only if β is small. If 30% deviation is acceptable, then the limiting β is 4. For PAO assuming α = 15.6 GPa⁻¹, this translates to p_max and p_a of 260 and 170 MPa respectively.

Fig. 9 Effect of β on the ratio ν, when the rheology is modelled by the Barus equation (black solid line) and when α_p is replaced by a 3rd order polynomial.

High pressure rheometry data (black square with solid line, Fig. 8) show that if it is modelled with the Barus equation, the pressure-viscosity coefficient must be modelled as a polynomial

Q(p) = a + bp + cp² + dp³ (23)

The true viscosity of the fluid is now represented by eqn (24)

η = η₀e^Q(p(x)) (24)

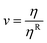The area average viscosity obtained in an EHD point contact is then given by the following equation:A new value of for PAO is calculated numerically (red dashed line, Fig. 9). It shows that η^R should be a good approximation for η up to approximately p_a = 210 MPa. η^R (blue dashed line, Fig. 8) actually exceeds η by a considerable margin beyond p_a = 210 MPa.

The area average η^M measured from friction, however, is very close to η up to p_a = 350 MPa. One possible reason is shear thinning may happen locally in the high-pressure regions of the contact. The effect of shear thinning on viscosity can be accounted for by the Eyring model.³⁸ The resulting viscosity η^E is related to the Eyring stress τ_e, the shear stress at the onset of shear thinning. Combining with eqn (23) and (24), the viscosity under shear thinning conditions η^E is

The corresponding area-averaged viscosity η^G is then given by:where τ_e = 2.5 MPa was obtained by friction tests at several shear rates, and is assumed constant. This value is within the range for common engineering fluids.^40,41 The maximum average shear stress in the friction tests is 7–10 MPa, although most measurements are taken at significantly lower stress levels. η^G (blue triangles, Fig. 8) fits η^M (red crosses, Fig. 8) obtained from friction tests relatively well, supporting that shear thinning effect pushes η^M closer to true η at high pressure (open squares with solid line, Fig. 8) when in fact PAO is experiencing different amount of shear in each of these cases.

Shear heating also affects friction results. The flash temperature in the contact, temperature rise caused by the friction between the two rubbing surfaces, is estimated using Blok, Jaeger and Archard theory as outline by Stachowiak and Batchelor⁴² for each contact case. It is less than 15 °C in the worst case and usually less than 2 °C. To estimate the contribution of shear heating to the discrepancy between η^G (blue triangles) and η^M (red crosses), we assume eqn (23) is unaffected by temperature. The area-averaged viscosity in an EHD point contact taken into considerations of both shear thinning and shear heating, η^T, can be obtained with eqn (27) by having η₀ as the low shear ambient-pressure viscosity at the flash temperature of the contact. The larger difference in η^T (blue squares, Fig. 8) and η^G (blue triangles, Fig. 8) shows that the effect of shear heating is more obvious for lower pressure glass–glass contacts where the temperature rise is high due to the lower thermal conductivity of glass.

The ratio , with η₀ as the low shear ambient-pressure viscosity at the flash temperature of the contact, is computed. Multiplying η^M measured from friction tests by ν′ gives η*, where the effects of pressure heterogeneities, shear thinning and shear heating in an EHD point contact are removed. η* (green circles, Fig. 8) can be used to estimate the true viscosity of a fluid and it matches η from the high-pressure rheology (open squares with solid line, Fig. 8) well.

It should be noted that even though in this work the coefficients in Q(p) are inferred from the high-pressure rheology data, they can also be obtained in principle from the combined friction/fluorescence anisotropy data. The analysis shown models the true rheology of the fluid as a single exponential with the pressure-viscosity coefficient models as a third-order polynomial. The use of different rheological models do not affect the universality of the analysis.

Exploration of common rheological models: combining fluorescence anisotropy and friction measurements

Based on the discussion in previous sections, a combined fluorescence anisotropy and friction approach for examining fluid viscosity is possible and works best when applied in low and moderate pressure range, provided the effects of shear thinning and shear heating are considered. For the following analysis, the viscosity of PAO 8 is obtained by the combined approach for p_a < 480 MPa. At the same applied pressure (around 300 MPa), η* from friction measurements (circles, Fig. 7) and η^A from fluorescence anisotropy measurements (triangles, Fig. 7) overlap.

While data from friction measurements for p_a > 480 MPa are available, the potential of more substantial shear thinning at these pressures may render these data less reliable. Hence at p_a > 480 MPa, only viscosity³⁹ from high pressure rheometry at 22 °C is used. Viscosity³⁹ from high pressure rheometry for p_a < 480 MPa matches results from the combined approach (see Fig. 8) and is included in this analysis.

The Roelands equation (blue dash lines, Fig. 7 and 10) and the Hybrid model (red dash lines, Fig. 7) fit data for the whole range of pressure applied well.

Fig. 10 Fitting rheological data using Roeland's equation, Barus equation and a free single exponential fit.

The Barus relationship (eqn (3)), with η₀ = 0.088 Pa s, were obtained based on η^A up to 280 MPa, giving

η = η₀e^{15.6×10−9p} (28)

with α = 15.6 GPa⁻¹ (R² = 0.80). Calculating α*, which is the average α up to the pressure at which η → ∞, using the method of Gold et al.⁴³ yields an α* of 14 GPa⁻¹. The application of the McEwen term of the hybrid model to the data estimates α₀ to be 17.7 GPa⁻¹. Our estimated α lies between α_o and α*. Therefore, the estimation for α seems reasonable. Note eqn (28) (black dot-dash lines, Fig. 7) fails to describe the viscosity of PAO 8 at high pressure.

A single exponential fit with no predetermined constant (red solid line, Fig. 10) was used to fit the pressure-viscosity relationship of PAO 8. The equation of best fit

η = 0.46e^{9.95×10−9p} (29)

describes the results well except in the low-pressure range, where it overestimates the viscosity of the fluid. It exceeds the ambient low shear viscosity of PAO 8 by an order of magnitude (0.46 vs. 0.088 Pa s).

Since the pressure-viscosity coefficient changes with pressure, its values will depend on the pressure range viscosity data is available for fitting. How the available of viscosity data affects the goodness of fit, and its implications on the use of film thickness and friction measurements for the determination of the pressure-viscosity coefficient is discussed in ESI,† Section S1.

Since single exponential models failed to describe data obtained in the full pressure range tested, Roelands model was used. The Roelands parameter Z is estimated to be 0.42 (see eqn (4)) with η₀ = 0.088 Pa s and α₀ = 15.6 GPa⁻¹ taken from eqn (28). While there is issue concerning the procedure for estimating Z,²³ this is nevertheless commonly done and is used here. The resulting equation fits our experimental data obtained up to 700 MPa (see blue dash line, Fig. 7 and 10), with a goodness of fit R² = 0.991. Hence in this case the Roelands equation, determined with low-pressure viscosity data, can predict the viscosity of PAO 8 at high pressure, at least up to 720 MPa. Note Roelands equation is known to have limitations at describing viscosity at higher pressure when the faster than exponential effect comes into place.⁴⁴ This is not seen within the range of pressures tested.

For completeness, the McEwen term of the hybrid model that describes our results is obtained by fitting eqn (7) to viscosity data up to 480 MPa (see red dash line, Fig. 7). This gives α₀ = 18.7 GPa⁻¹ and q = 10.76 and fits the data well with a R² = 0.997. To assess the predictive power of the hybrid model in this work, fitting parameters of eqn (7) are obtained from low-pressure viscosity data, by limiting the maximum pressure to be considered for fitting purpose. The resulting equation is then used to predict high-pressure viscosity. Predicted and experimental results are compared. Varying the range of pressure for fitting the hybrid model affects both the value of α₀ and the goodness of fit R², as shown in Fig. 11. A stable α₀ and high R² are only achieved when viscosity data from up to p = 660 MPa is used to fit the Hybrid mode, although α₀ starts to stabilise from p = 500 MPa. Hence for PAO 8 and in the range of pressure investigated, the Hybrid model is more suitable for interpolation, rather than extrapolation purpose. When all the data is used for fitting the Hybrid model, it describes the experimental data well (see Fig. 7). Table 5 shows a summary of fitting parameters.

Fig. 11 Effect of maximum fitting pressure on α₀ within the McEwen term of the Hybrid model.

Table 5 Summary on fitting parameters, see conditions of fitting in the text

Model/equation number	Parameter	Value
Barus equation (up to 280 MPa)/eqn (3)	η 0	0.088 Pa s
	α	15.6 GPa^−1
Single exponential fit with no predetermined constant/eqn (2)	b	0.460 Pa s
	α	9.95 GPa^−1
Roelands equation/eqn (5)	η 0	0.088 Pa s
	α	15.6 GPa^−1
	Z	0.42
McEwen term of the hybrid model/eqn (7)	α 0	18.7 GPa^−1
	q	10.76
Eyring stress	τ e	2.5 MPa
Polynomial fit for the exponent in the Barus equation/eqn (24) (pressure in MPa and viscosity in Pa s)	a	0.0593
	b	0.0179
	c	−1.3414 × 10^−5
	d	7.4605 × 10^−9

---

Potential applications of fluorescence anisotropy viscosity measurements in non-Newtonian conditions

Local fluorescence anisotropy measurements allow the local viscosity of a fluid to be obtained. With minimal/no averaging (just across the spot size), the true rheology of the fluids at its local conditions can be determined. Any heterogeneity of viscosity can be detected. When applied to a point EHD contact, it provides fluid viscosity at medium pressure range. The applicable pressure range is limited by the viscosity the fluorophore is sensitive to and may be extended by using smaller fluorophores.

Shear thinning is governed by the local structure of the fluid. Fluorescence anisotropy spectroscopy can be used to detect molecular changes in the fluid that may cause shear thinning, due to for example, a change in degree of entanglement, a change in domain size or permeant shear thinning⁴⁵ caused by chain scission of the molecule. The authors have detected shear thinning in a polar fluid previously using molecular rotors.¹⁰ This was however not quantitative. The response of the fluorophore may not match macroscale measurements, and this would shed light on relationships between nanoscale and microscale rheological phenomena.

Structural changes in a fluid due to shear can lead to changes in, apart from its viscosity, also its flow profile. While these changes are related, no clear relationship has been established. Velocity profile measurements in EHD contacts^46,47 have been obtained previously and it has been shown that the fluid velocity profile is pressure dependent in some cases. Similar profiles have also been obtained through non-equilibrium molecular dynamics simulations.⁴⁸ The methodology developed in this work thus allows the relationship between local flow and local viscosity of a fluid to be investigated systematically.

Conclusions

In this work, the viscosity of a model fluid (PAO 8) is examined across 5 orders of magnitude range at pressure up to 720 MPa using a point EHD contact.

A fluorescence anisotropy-based technique has been developed, which together with proper calibration and data analysis methods, allows the examination of the local viscosity of a fluid in a point EHD contact. While the pressure in an EHD contact is spatially heterogeneous, its pressure distribution is known. Hence, a viscosity map which correlates local viscosity with local pressure can be generated. This is the first time direct quantitative viscosity measurements have been made in a rubbing contact in situ without a correction for environmental conditions. High-pressure viscosity is accessed by friction measurements with an EHD point contact. The procedures on how meaningful viscosity data can be obtained from friction measurements is described in detail. This is crucial for our understanding of rheology of lubricants at high pressure and high shear conditions.

Results from fluorescence anisotropy and friction measurements were combined. They match well results from high pressure low shear rheometry.³⁹ This shows that local viscosity measured in molecular scale for a homogenous fluid in an EHD contact at the pressure range studied is the same viscosity obtained on the macroscale. It also shows that results from fluorescence anisotropy (viscosity range 0.0004–7.6 Pa s) and friction measurements (viscosity range 3.4–710 Pa s) can be combined and this approach is a viable alternative to examining high pressure rheology of fluids at viscosities up to 710 Pa s and pressures of 720 MPa.

Various rheological models have been used to describe our viscosity results. Both the hybrid model¹⁴ and the Roelands equation¹³ fit the experimentally obtained pressure-viscosity relationship well. Roelands model obtained based on low-pressure (up to 280 MPa) viscosity predicts high-pressure viscosity successfully within our tests pressure range. No single exponential model can describe viscosity of PAO 8 in the whole pressure range tested. This is due to changing compressibility of the fluids with pressure. At low pressures, the fluid is more compressible (hence α is larger) and the rate of change of α with pressure decreases rapidly with pressure. As a result, single exponential model that tries to fit data from wide pressure range tends to overestimate the fluid's low-pressure viscosity while the commonly used Barus equation overestimates high-pressure viscosity substantially.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

JD is funded by the Shell University Technology Centre for Fuels and Lubricants at Imperial College London. This work is also supported by EPSRC research grant numbers EP/L023202/1 and Taiho Kogyo Tribology Research Foundation. The authors would like to acknowledge Prof. H. Spikes, Dr A. Ponjavic, Dr J. Ewen and Mr S. Jeffreys for the supportive discussions they provided throughout this work. The authors would like to thank Dr N. Marx for the design of the ultra-low run-out ball on flat rheometer, without which this work would not be possible. The authors would also like to thank Dr J. Zhang for his advice on friction measurements and Dr S. Bair for his help characterising the PAO using high-pressure viscometry and fitting of the Hybrid model. The authors thank Exxon Mobil for providing Spectrasyn and Dr A. Kadric and Dr N. De Laurentis for providing Durasyn.

References

1. S. Bair, Proc. Inst. Mech. Eng., Part J, 2002, 216, 139–149.
2. S. Bair, in Tribology Series, Vol 30, Lubricants and Lubrication—Proceedings of the 21th leeds-Lyon Symposium on Tribology, ed. G. Dowson, D. Taylor, C. Childs and T. Dalmaz, Elsevier, 1995, pp. 169–187.
3. C. McCabe, S. Cui, P. T. Cummings, P. A. Gordon and R. B. Saeger, J. Chem. Phys., 2001, 114, 1887–1891.
4. P. Liu, H. Yu, N. Ren, F. E. Lockwood and Q. J. Wang, Tribol. Lett., 2015, 60, 1–9.
5. V. Jadhao and M. O. Robbins, Proc. Natl. Acad. Sci. U. S. A., 2017, 201705978.
6. J. P. Ewen, D. M. Heyes and D. Dini, Friction, 2018, 6, 349–386.
7. C. R. Evans and K. L. Johnson, Proc. Inst. Mech. Eng., Part C, 1986, 200, 303–312.
8. V. Strubel, S. Simoens, P. Vergne, N. Fillot, F. Ville, M. El Hajem, N. Devaux, A. Mondelin and Y. Maheo, Tribol. Lett., 2017, 65, 75.
9. J. Dench, N. Morgan and J. S. S. Wong, Tribol. Lett., 2017, 65, 25.
10. A. Ponjavic, J. Dench, N. Morgan and J. S. S. Wong, RSC Adv., 2015, 5, 99585–99593.
11. T. Otsu and K. Imado, Tribol. Lett., 2018, 66, 40.
12. C. Barus, Am. J. Sci., 1893, s3–45, 87–96.
13. C. Roelands, PhD thesis, TU Delft, 1966.
14. S. S. Bair, O. Andersson, F. S. Qureshi and M. M. Schirru, Tribol. Trans., 2018, 61, 247–255.
15. N. Ito, O. Kajimoto and K. Hara, J. Phys. Chem. A, 2002, 106, 6024–6029.
16. N. Kometani and A. Tai, J. Solution Chem., 2014, 43, 1529–1538.
17. P. Vergne and S. Bair, Tribol. Lett., 2014, 54, 1–12.
18. S. Bair, C. Mary, N. Bouscharain and P. Vergne, Proc. Inst. Mech. Eng., Part J, 2013, 227, 1056–1060.
19. B. Schuler, A. Soranno, H. Hofmann and D. Nettels, Annu. Rev. Biophys., 2016, 45, 207–231.
20. G. W. Stachowiak and A. W. Batchelor, Engineering Tribology, Elsevier, 2006, pp. 11–50.
21. L. B. Sargent, ASLE Trans., 1983, 26, 1–10.
22. H. van Leeuwen, Proc. Inst. Mech. Eng., Part J, 2011, 225(6), 449–464.
23. S. Bair, J. Tribol., 1993, 115, 333.
24. Y. Nakamura, S. Hiraiwa, F. Suzuki and M. Matsui, Tribol. Online, 2016, 11, 444–449.
25. J. Seabra, A. Sottomayor and A. Campos, Tribology Series, Elsevier, 1993, pp. 215–225.
26. M. Paluch, Z. Dendzik and S. J. Rzoska, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 2979–2982.
27. E. McEwen, J. Inst. Pet., 1952, 38, 646–672.
28. D. M. Jameson and J. A. Ross, Chem. Rev., 2010, 110, 2685–2708.
29. S. Jeon, S. C. Bae and S. Granick, Macromolecules, 2001, 34, 8401–8404.
30. J. A. Levitt, P.-H. Chung, M. K. Kuimova, G. Yahioglu, Y. Wang, J. Qu and K. Suhling, ChemPhysChem, 2011, 12, 662–672.
31. K. Suhling, J. Siegel, P. M. P. Lanigan, S. Lévêque-Fort, S. E. D. Webb, D. Phillips, D. M. Davis and P. M. W. French, Opt. Lett., 2004, 29, 584.
32. D. R. Matthews, L. M. Carlin, E. Ofo, P. R. Barber, B. Vojnovic, M. Irving, T. Ng and S. M. Ameer-Beg, J. Microsc., 2010, 237, 51–62.
33. A. N. Bader, E. G. Hofman, J. Voortman, P. M. P. Van Bergen En Henegouwen and H. C. Gerritsen, Biophys. J., 2009, 97, 2613–2622.
34. J. R. Lakowicz, Principles of fluorescence spectroscopy, Springer, 3rd edn, 2006.
35. A. Cameron and R. Gohar, Proc. R. Soc. A, 1966, 291, 520–536.
36. R. P. Glovnea, A. K. Forrest, A. V. Olver and H. A. Spikes, Tribol. Lett., 2003, 15, 217–230.
37. R. P. Glovnea and H. A. Spikes, Tribol. Trans., 1995, 38, 932–940.
38. H. Spikes and Z. Jie, Tribol. Lett., 2014, 56, 1–25.
39. S. S. Bair, private communication, 2018.
40. K. L. Johnson and J. L. Tevaarwerk, Proc. R. Soc. A, 1977, 356, 215–236.
41. C. R. Gentle and A. Cameron, ASLE Trans., 1975, 18, 222–228.
42. G. W. Stachowiak and A. W. Batchelor, Engineering Tribology, Elsevier, 2006, pp. 287–362.
43. P. W. Gold, A. Schmidt, H. Dicke, J. Loos and C. Assmann, J. Synth. Lubr., 2001, 18, 51–79.
44. S. Bair, L. Martinie and P. Vergne, Tribol. Lett., 2016, 63, 1–10.
45. N. Marx, A. Ponjavic, R. I. Taylor and H. A. Spikes, Tribol. Lett., 2017, 65, 1–15.
46. A. Ponjavic, M. Chennaoui and J. S. S. Wong, Tribol. Lett., 2013, 50, 261–277.
47. B. Galmiche, A. Ponjavic and J. S. S. Wong, J. Phys.: Condens. Matter, 2016, 28, 134005.
48. J. P. Ewen, C. Gattinoni, J. Zhang, D. M. Heyes, H. A. Spikes and D. Dini, Phys. Chem. Chem. Phys., 2017, 19, 17883–17894.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05155k

---