Effect of the degree of inversion on optical properties of spinel ZnFe₂O₄

Abstract

Spinel ferrites (^T[M_1−xFe_x]^O[M_xFe_2−x]O₄ with 0 ≤ x ≤ 1, where M is a bivalent metal ion and the superscripts denote tetrahedral and octahedral sites) are materials commonly used in electronics due to their outstanding magnetic properties. Thus, the effect of the degree of inversion, x, on these properties is well known. However, its effect on other properties of these materials has rarely been investigated in detail. Since ferrites gained much attention during the last decade as visible light active photocatalysts and photoelectrocatalysts, understanding the effect of the degree of inversion on the optical properties became necessary. Among photocatalytically and photoelectrocatalytically active spinel ferrites, zinc ferrite (ZnFe₂O₄, ZFO) is one of the most widely studied materials. In this work, five ZFO samples with degrees of inversion varying from 0.07 to 0.20 were prepared by a solid-state reaction employing different annealing temperatures and subsequent quenching. Raman and UV-Vis-NIR spectra were measured and analyzed together with theoretical results obtained from ab initio calculations. Changes in the UV-Vis-NIR spectra associated with electronic transitions of tetrahedrally and octahedrally coordinated Fe³⁺ ions are distinguished. However, the optical band gap of the material remains unchanged as the degree of inversion varies. Based on the experimental and theoretical results, a new assignment for the Raman active internal modes and the electronic transitions of ZFO is proposed.

---

1. Introduction

Spinel ferrites are versatile materials with several applications in the fields of information storage,¹ magnetic fluids,² microwave devices,³ and catalysis.⁴ Undoubtedly, their outstanding magnetic properties make spinel ferrites such interesting materials for these purposes.⁵ However, other properties, such as semiconductivity, are nowadays scientifically explored. Recently, semiconducting spinel ferrites (MFe₂O₄, M = metal ion) have attracted attention in the fields of photocatalysis and photoelectrocatalysis.^6,7 Applications of spinel ferrites in these research areas include artificial photosynthesis,⁷ carbon dioxide conversion,⁸ hydrogen and oxygen generation via water splitting,^9–11 and water treatment.¹² Properties such as narrow band gaps (≈2 eV), high chemical stability, abundance, and low cost make spinel ferrites promising materials for the applications mentioned above.^6,7

MFe₂O₄ crystallizes in a face-centered cubic structure like the mineral spinel (MgAl₂O₄), after which this class of materials is named. In the so-called normal structure, M²⁺ and Fe³⁺ ions occupy 1/8 of the tetrahedral sites and 1/2 of the octahedral sites available in the O²⁻ lattice, respectively. However, when all the M²⁺ ions at the tetrahedral sites are exchanged by Fe³⁺ ions from the octahedral sites, the material adopts a so-called inverse structure. The parameter commonly employed to characterize the cation disorder is the degree of inversion, x, defined as the fraction of M²⁺ ions occupying octahedral sites, according to ^T[M_1−xFe_x]^O[M_xFe_2−x]O₄.

Among photocatalytically and photoelectrocatalytically active spinel ferrites, zinc ferrite (ZnFe₂O₄, ZFO) is one of the most widely studied materials.^13,14 At standard conditions (273.15 K and 100 kPa), the normal structure is the thermodynamically most stable configuration for bulk ZFO.¹⁵ Nevertheless, it is known that ZFO does not usually exhibit a normal structure and the degree of inversion closely depends on the synthetic conditions.^15–20 This effect is especially pronounced when nanoparticulate ZFO samples are synthesized. Akhtar et al.¹⁸ reported the sol–gel synthesis of ZFO nanoparticles having degrees of inversion of 0.5 or 0.25 when urea or citric acid, respectively, are used as precursors. Kamiyama et al.¹⁹ reported the co-precipitation synthesis of ZFO nanoparticles with a degree of inversion of 0.142 and Nakashima et al.²⁰ prepared nanoparticulate ZFO with a degree of inversion of 0.6 by radio-frequency sputtering. ZFO nanoparticles having a high degree of inversion have been prepared by Kurian and Mathew²¹ using a solvothermal technique. They reported a degree of inversion of 0.54.²¹ Šepelák et al.²² investigated the effect of high-energy ball-milling in the cation distribution of nanoscaled ZFO. The authors showed an increase in the degree of inversion from 0 to 0.94, i.e., from normal spinel to almost completely inversed spinel by increasing the milling time.

Mozaffari et al.²³ and Yuan et al.²⁴ reported that the magnetization of ZFO increases as the degree of inversion becomes larger. Harris et al.²⁵ reviewed the effect of the degree of inversion of mechanochemically processed ZFO nanoparticles not only on the magnetization but also on the Néel temperature and the nuclear magnetic properties, including hyperfine field distributions, isomer shifts, and quadrupole interactions. ZFO samples prepared by mechanochemical methods show degrees of inversion close to 2/3.²⁵ As a consequence, a ferrimagnetic behavior is observed at room temperature for the highly disordered ZFO samples. Conversely, an antiferromagnetic behavior with a Néel temperature of 10.5 K is observed for normal ZFO.²⁵

Although the effect of the degree of inversion on the magnetic properties is well known, some other physicochemical properties have not been until now investigated in detail. Among these, the optical properties are of utmost importance for the characterization of a material with applications in optoelectronics, photocatalysis, and photoelectrocatalysis. On the one hand, the UV and visible light absorptivity of a material is directly related with the maximum photonic efficiency that can be expected under defined experimental conditions. On the other hand, Raman spectroscopy is a commonly employed technique for the characterization of ZFO. Wang et al.²⁶ reported a first order Raman spectrum of a ZFO sample having a degree of inversion of 0.10. The authors correlated the observed signals with the five Raman active internal modes predicted by the factor group analysis.²⁶ The experimental data presented in the current study demonstrate that some of the signals detected by Wang et al. are originated due to a symmetry perturbation because of the cation disordering and, thus, are not active internal modes. Regarding the absorptivity of ZFO, Pailhé et al.²⁷ reported a diffuse reflectance Vis-NIR spectrum of a sample with a degree of inversion of 0.140. For the interpretation of some of the electronic transitions, the authors considered the splitting of the Fe(3d) orbitals on the basis of the Russell–Saunders coupling.²⁷ However, they also assigned some transitions on the basis of a simple splitting of the Fe(3d) orbitals (into t_2g and e_g orbitals), thus presenting ambiguous results.

To the best of our knowledge, the effect of the degree of inversion on the Raman scattering and UV-Vis-NIR absorptivity of ZFO has not been studied in detail before. For the first time, Raman spectra of normal and inverted ZFO were calculated, obtaining an excellent agreement with the experimental results. The combination of ab initio calculations and experimental data allowed to describe how the optical properties of ZFO evolve as the degree of inversion increases from x ≈ 0.07 to x ≈ 0.20. Furthermore, fundamental properties such as the assignment of the Raman active internal modes and the electronic transitions were analyzed. The experimental and theoretical evidence presented in this work supports a new interpretation for both, the Raman active internal modes and the electronic transitions of spinel ZFO.

2. Materials and methods

Polycrystalline ZFO samples were synthesized by means of a solid-state reaction. Stoichiometric amounts of ZnO (Sigma Aldrich, ≥99.0%) and Fe₂O₃ (Sigma Aldrich, ≥99.0%) powders were mixed together using an agate mortar. The mixture was calcined in air at 1073 K with a heating rate of 350 K h⁻¹. After 12 hours, the sample was cooled to room temperature and grinded again in an agate mortar. Aliquots of 0.500 g were pressed into 13 mm diameter pellets applying a pressure of 55 MPa. The pellets were calcined at 1273 K with a heating rate of 150 K h⁻¹. After 2 hours at this temperature, the samples were cooled to 1073 K with a cooling rate of 100 K h⁻¹, then kept at 1073 K for 12 hours, cooled to 773 K at a rate of 100 K h⁻¹, kept at 773 K for 50 hours, and finally quenched in cold water. Some of the pellets (referred from now as ZFO_773) were retained for further characterization. The rest were divided into four sets of samples. The samples were heated up with a rate of 300 K h⁻¹ and calcined at 873, 973, 1073, and 1173 K for 25, 20, 12, and 10 hours, respectively. After this period of time, the calcined pellets were immediately quenched in cold water. These samples will be referred as ZFO_873, ZFO_973, ZFO_1073, and ZFO_1173.

Powder X-ray diffraction data were collected with an StadiMP diffractometer (Stoe & Cie., Darmstadt, Germany) using monochromatized MoKα₁ radiation (λ = 70.9300 pm) and a Mythen2 1K detector (Dectris, Baden-Daettwil, Switzerland). Flat samples for transmission measurements were prepared by placing the sample between two thin mylar foils and fixing these with a metal ring providing a 3 mm hole. The diffraction pattern were recorded in transmission geometry in the 2θ range from 2° to 92°, collecting 5977 data points with a step width of 0.015° 2θ and 270 s measurement time per step. Rietveld refinements were carried out using the Bruker DIFFRAC^plus TOPAS V4.2 software (Bruker AXS Inc., Madison, Wisconsin, USA). The space group Fd3̄m, with the zinc and iron ions placed in tetrahedral and octahedral sites, respectively, was assumed as starting point for the refinement. The scale factors, lattice parameters, oxygen positional parameters, inversion parameters, the three isotropic displacement parameters, and the zero point were optimized during the refinements. The standard instrumental parameters were determined with a LaB₆ standard (SRM 660c, NIST).

Mössbauer measurements were performed in transmission mode using a Miniaturized Mössbauer Spectrometer MIMOS II with the sample perpendicular to the ⁵⁷Co/Rh source. The samples were placed into a spherical sample holder and the cap was subsequently rotated to align the crystals in the xy-plane. All isomer shifts are given relative to α-Fe at room temperature. The data were fitted by least-squares method using Lorentzian line shapes with the Recoil 1.05 Mössbauer Analysis software.²⁸

Raman measurements were made employing a confocal Bruker Senterra micro-Raman spectrometer. Depolarized spectra were collected at ambient conditions in backscattering geometry using an Olympus BX 51 microscope that allows the incident 785 nm, 633 nm, or 532 nm laser beam to be focused on the sample as a spot of about 2 μm in diameter. An integration time of 5 s, 20 co-additions, and a power of 50 mW, 2 mW, and 2 mW for the 785 nm, 633 nm, and 532 nm lasers, respectively, were used. The instrumental precision was within ±3 cm⁻¹.

Raman spectra were calculated using the CRYSTAL14 program package,²⁹ employing triple-ζ basis sets. The frequencies were calculated using the range separated functional HSE06,³⁰ while the intensities were calculated with B3LYP.³¹ A well-converged Monkhorst–Pack grid of 8 × 8 × 8 was sufficient. The atomic positions of normal and inverse ZFO were optimized using an experimental lattice parameter of a = 844.32 pm.³²

UV-Vis-NIR spectroscopy was carried out with an Agilent Carry 5000 device equipped with an external DRA-2500 Diffuse Reflectance Accessory. The spectra were collected in the range of 200 nm to 2000 nm with a data acquisition interval of 1 nm, an averaging time of 0.1 s, a scan rate of 600 nm min⁻¹, and a spectral bandwidth of 2 nm. The instrumental precision was within ±0.5 nm. The optical band gaps were determined by the derivation of absorption spectrum fitting method (DASF).³³

Optical spectra of normal and inverse ZFO were calculated using the Vienna ab initio Simulation Package (VASP)³⁴ version 5.4.4. A carefully converged quasi-particle GW0³⁵ algorithm was employed and to gain insight about the optical properties, the Bethe–Salpeter-Equations (BSE)³⁶ were solved afterwards. For normal ZFO, an experimental structure³² was used, while for inverse ZFO, an optimization of atomic positions was performed.

The composition of the samples was determined analytically by means of inductively coupled plasma optical emission spectrometry (ICP-OES) using a Spectroflame and Spectro Arcos from Spectro Analytical Instruments. Fe and Zn were quantified by measuring the optical emission at 259.941 nm and 213.856 nm, respectively, and comparing with the calibration curve prepared using the respective ICP standards (Carl Roth). Prior to the analysis, the samples were dissolved in freshly distilled 16% HCl (Carl Roth) at 473 K using an ultraWAVE microwave digestion system from MLS GmbH.

The structural and morphological properties of the samples were analyzed using a JEOL JSM-6700F scanning electron microscope provided with a lower secondary electron image detector. An acceleration voltage of 2.0 kV and a 25 000 times magnification were employed.

3. Results and discussions

ZFO samples with degree of inversion of approximately 0.07, 0.10, 0.13, 0.16, and 0.20 were synthesized by means of a solid-state reaction. An initial calcination at 1273 K was carried out for all the samples in order to ensure the homogeneity of the crystallinity and the crystallite size between them. The degree of inversion was modified by further calcination steps at temperatures ranging from 773 K to 1173 K and subsequent quenching of the samples in cold water. The samples were characterized employing XRD and Rietveld refinement (Fig. S1, ESI†), Mössbauer spectroscopy (Table S1 and Fig. S2, ESI†), Raman spectroscopy (Fig. 2 and Fig. S5, ESI†), and elemental analysis. The elemental analysis revealed a Fe to Zn ratio close, within the experimental error, to 2 : 1 as expected for ZFO. This ratio will also hold in the case that a mixture of equal amounts of Fe₂O₃ and ZnO is present. However, XDR (Fig. S1, ESI†) and Raman (Fig. 2) data give no indication of the presence of ZnO or hematite (α-Fe₂O₃). Maghemite (γ-Fe₂O₃), having a spinel structure, might not be distinguished from ZFO in an XRD diffractogram. However, the presence of γ-Fe₂O₃ is excluded based on the Raman (Fig. S6, ESI†) and Mössbauer data (Fig. S3, ESI†). The strongest Raman scattering signal of γ-Fe₂O₃, located at 670 cm⁻¹, might not be differentiated from the broad ZFO band at ca. 647 cm⁻¹.³⁷ However, the next strongest and characteristic band of γ-Fe₂O₃, located at 718 cm⁻¹,³⁷ is not observed in the Raman spectra of ZFO (Fig. S6, ESI†). A more conclusive evidence of the absence of γ-Fe₂O₃ comes from the Mössbauer data. A sextet is observed in the Mössbauer spectrum of γ-Fe₂O₃ (Fig. S3, ESI†) due to its room temperature ferrimagnetism.³⁷ However, only two duplets (due to the Fe³⁺ cations present in tetrahedral and octahedral sites) are observed in the Mössbauer spectra of the ZFO samples (Fig. S2, ESI†). This is because of the room temperature paramagnetism of the ZFO samples. Therefore, the presence of γ-Fe₂O₃ as secondary phase in the ZFO samples is excluded.

The values deduced from Rietveld refinement and Mössbauer spectroscopy together with the structural parameters and the iron to zinc molar ratios obtained from the elemental analysis of the different quenched ZFO samples are given in Table 1. Neither secondary phases nor impurities could be detected from the XRD patterns. Furthermore, none of the samples showed Mössbauer signals attributable to Fe²⁺. Hence, the absence of Fe²⁺ and, therefore, of oxygen vacancies has been confirmed by Mössbauer spectroscopy.

Table 1 Refined structural parameters, degree of inversion deduced from Mössbauer spectroscopy, and Fe to Zn molar ratios of the different temperature annealed ZFO samples. n_Fe/n_Zn is the Fe to Zn molar ratio, x is the degree of inversion, a is the lattice parameter, x(O) is the oxygen positional parameter on 32e: x,x,x in Fd3̄m, L_Vol(IB) is the average crystallite size, and B_Zn, B_Fe, and B_o are the isotropic displacement parameters concerning the Zn²⁺, Fe³⁺, and O²⁻ ions, respectively

Calcination temperature/K	n Fe/nZn	Degree of inversion x			a/pm	x(O)	L Vol(IB)/nm	B Zn/Å^2	B Fe/Å^2	B o/Å^2
		Rietveld refinement (RR)	Mössbauer spectroscopy (MS)
773	1.98 ± 0.04	0.073(7)	0.074 ± 0.015	0.074 ± 0.011	844.285(5)	0.26025(13)	306(6)	0.38(1)	0.37(1)	0.39(3)
873	1.98 ± 0.05	0.106(6)	0.102 ± 0.020	0.104 ± 0.013	844.433(5)	0.26001(11)	293(5)	0.48(1)	0.37(1)	0.50(2)
973	1.97 ± 0.04	0.131(6)	0.136 ± 0.010	0.134 ± 0.008	844.374(5)	0.26001(11)	302(5)	0.53(1)	0.52(1)	0.56(2)
1073	1.98 ± 0.03	0.161(7)	0.156 ± 0.012	0.159 ± 0.010	844.432(5)	0.25996(12)	327(6)	0.50(1)	0.53(1)	0.53(2)
1173	1.98 ± 0.07	0.196(7)	0.210 ± 0.028	0.203 ± 0.017	844.427(5)	0.25954(13)	283(6)	0.34(1)	0.36(1)	0.41(3)

---

As becomes obvious from Fig. 1A, the degree of inversion increases linearly with the calcination temperature from 0.074 ± 0.011 at 773 K to 0.203 ± 0.017 at 1173 K. A similar behavior was reported by O’Neill¹⁵ using powder XRD structure refinements, and by Pavese et al.¹⁶ from in situ high-temperature neutron powder diffraction data evaluation (Fig. 1B). The results from O’Neill show a monotonic increase in the degree of inversion from 0.019 at 773 K to 0.149 at 1073 K, and then a plateau. The author suggested that this plateau results from the re-ordering kinetics at temperatures higher than 1173 K being too fast to allow a quenching of the sample.¹⁶ This effect was not observed by Pavese et al. because their measurements were done in situ.¹⁶

Fig. 1 (A) Degree of inversion, x, versus the annealing temperature. (B) Comparison of the present result with values obtained by O’Neill¹⁵ and Pavese et al.¹⁶

A comprehensible work regarding the thermodynamics of the cation disorder and the dependence of the degree of inversion with the temperature have been done by Callen et al.,³⁸ Navrotsky and Kleppa,³⁹ O’Neill and Navrotsky,^40,41 and O’Neill.¹⁵ The cation distribution in ZFO can be treated as a dynamic equilibrium according to the following interchange reaction between ions being present in tetrahedral (subscript “T”) and octahedral sites (subscript “O”):

^TZn + ^OFe ⇄ ^OZn + ^TFe

A summary reviewing the thermodynamic analysis of the temperature effect on the degree of inversion is presented in the ESI† (Fig. S4).

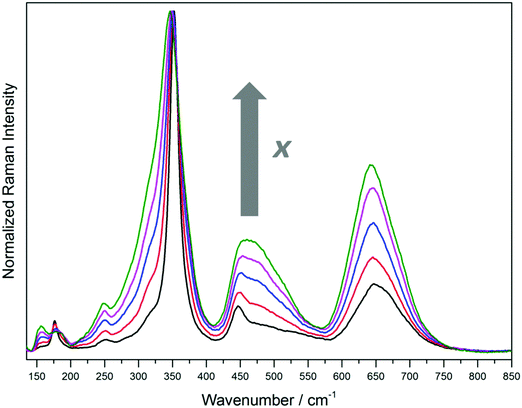
The Raman spectra of the different ZFO samples are shown in Fig. 2. In agreement with the XRD data, no signals attributed to impurities or secondary phases are identified. The ZFO sample with the lowest degree of inversion (ZFO_773, x = 0.074 ± 0.011) shows five bands at 176.5 ± 3 cm⁻¹, 251 ± 3 cm⁻¹ (weak), 352 ± 3 cm⁻¹, 447 ± 3 cm⁻¹, and 647 ± 3 cm⁻¹ and one minor signal at 155 ± 3 cm⁻¹. The sharp signal at 352 ± 3 cm⁻¹ exhibits a broad shoulder at smaller wavenumbers while the band at 447 ± 3 cm⁻¹ presents a broad shoulder at higher wavenumbers. The broad signal at 647 ± 3 cm⁻¹ can be deconvoluted into two Gaussian-shape signals at ca. 644 cm⁻¹ and 675 cm⁻¹ (Fig. S7, ESI†). Comparing with the Raman spectra measured with 532 nm and 633 nm laser excitations (Fig. S5, ESI†), the relative intensities of the bands change markedly. Interestingly, a signal not present in the spectra obtained with 785 nm laser excitation is observed at 573.5 ± 3 cm⁻¹ for the samples having a low degree of inversion. This signal decreases rapidly as the degree of inversion of the samples increases. A group-theoretical analysis of the vibrational spectrum for the spinel structure made by White and DeAngelis⁴² predicted five Raman active internal modes: A_1g, E_g, and three T_2g.⁴² Because normal and inverse spinel crystallize in the same space group, no change is expected in the number of active internal Raman modes. Nevertheless, when the degree of inversion is neither 0 nor 1 (0 < x < 1), the symmetry is perturbed and the number of normal modes increases.⁴³ The five predicted Raman active internal modes for the normal structure can be attributed to the signals at 176.5 ± 3 cm⁻¹, 352 ± 3 cm⁻¹, 447 ± 3 cm⁻¹, 573.5 ± 3 cm⁻¹, and 647 ± 3 cm⁻¹. The weak band at 251 ± 3 cm⁻¹, and the shoulders and broadening observed for most of the signals are direct consequences of the non-zero degree of inversion, as will be discussed below. Even the sample with a degree of inversion close to 0 (ZFO_773, x = 0.074 ± 0.011) shows all the mentioned deviations.

Fig. 2 Normalized Raman spectra of the ZFO samples with increasing degree of inversion (— ZFO_773, x = 0.074 ± 0.011; ZFO_873, x = 0.104 ± 0.013; ZFO_973, x = 0.134 ± 0.008; ZFO_1073, x = 0.159 ± 0.010; ZFO_1173, x = 0.203 ± 0.017) obtained using a 785 nm laser as the excitation source.

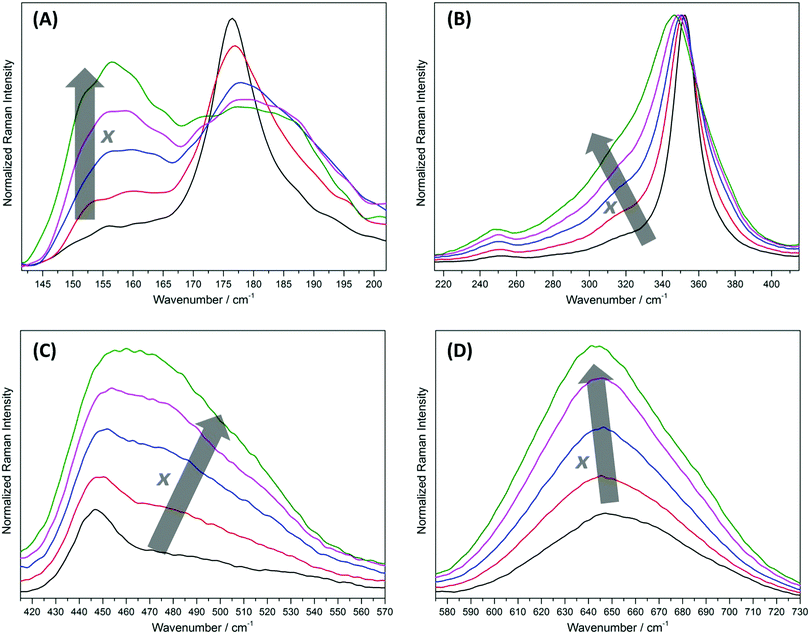
Distinctive changes can be observed in the Raman scattering as the degree of inversion of the ZFO samples increases. Fig. 3 shows the magnification of four different regions of the Raman spectra presented above. The first interval, from 141.5 cm⁻¹ to 202 cm⁻¹ (Fig. 3A), exhibits pronounced changes. As the degree of inversion increases, a band almost imperceptible for x = 0.074 ± 0.011 becomes higher in intensity at 156 ± 3 cm⁻¹ and the sharp signal observed at 176.5 ± 3 cm⁻¹ decreases in intensity. Interestingly, this decrease is accompanied by a growth of a shoulder at higher wavenumbers, resulting in a broad band from 168 cm⁻¹ to 198 cm⁻¹. Supposing that the Raman mode at 176.5 ± 3 cm⁻¹ is due to vibrations of the AO₄ tetrahedral groups, the broadening of this band can be explained by the exchange of Zn atoms by lighter Fe atoms, resulting in a shift in the vibration frequency to higher wavenumbers.

Fig. 3 Raman spectra (785 nm excitation source) from (A) 141.5 cm⁻¹ to 202 cm⁻¹, (B) 215 cm⁻¹ to 415 cm⁻¹, (C) 415 cm⁻¹ to 570 cm⁻¹, and (D) 575 cm⁻¹ to 730 cm⁻¹ of the ZFO samples with increasing degree of inversion (— ZFO_773, x = 0.074 ± 0.011; ZFO_873, x = 0.104 ± 0.013; ZFO_973, x = 0.134 ± 0.008; ZFO_1073, x = 0.159 ± 0.010; ZFO_1173, x = 0.203 ± 0.017).

In the region from 215 cm⁻¹ to 415 cm⁻¹ (Fig. 3B), an increase in the intensity of the weak signal at 251 ± 3 cm⁻¹ and a broadening of the main band at 352 ± 3 cm⁻¹ with a small shift of the maximum to smaller wavenumbers are observed as the degree of inversion of the samples increases. The broadening is due to the growth of the shoulder situated at 315 ± 3 cm⁻¹. This shoulder exhibits a weak intensity for the sample with x = 0.074 ± 0.011. Supposing that the signals in this spectral region are predominantly ruled by the vibration of the AO₆ octahedral groups, the growth of this shoulder at lower wavenumbers is in concordance with the exchange of Fe atoms by heavier Zn atoms. Regarding the behavior of the weak signal at 251 ± 3 cm⁻¹, it can be assumed that it arises due to the perturbation in the symmetry produced by the cation disordering. Hence, this signal is not one of the five predicted Raman active internal modes for the normal structure.

Prominent changes in the Raman spectra are noticed in the interval from 415 cm⁻¹ to 570 cm⁻¹ (Fig. 3C). As the degree of inversion increases, the shoulder of the band observed at 447 ± 3 cm⁻¹ for the sample with x = 0.074 ± 0.011 grows markedly. This finally results in a broad band from 415 cm⁻¹ to 560 cm⁻¹ with a maximum at 460 ± 3 cm⁻¹ for the sample with x = 0.203 ± 0.017. Supposing that the signal at 447 ± 3 cm⁻¹ arises from the vibrations of the AO₄ tetrahedral groups, the increase in the intensity of the shoulder at higher wavenumbers is again a direct consequence of the exchange of Zn atoms by lighter Fe atoms. As was mentioned above, the Raman active internal mode at 573.5 ± 3 cm⁻¹ is not intense enough to be detected using a 785 nm excitation source. Despite this signal is observed in the spectra obtained using 532 nm and 633 nm laser excitations, the intensity decreases rapidly as the degree of inversion increases (Fig. S5, ESI†). This suggests that the vibration of Zn atoms in the tetrahedral sites is also related to this Raman band. Because the signal decreases in intensity with the increasing degree of inversion, the weak band becomes rapidly imperceptible.

A particular change is observed in the region between 575 cm⁻¹ and 730 cm⁻¹ (Fig. 3D). As the degree of inversion increases from 0.074 ± 0.011 to 0.203 ± 0.017, the intensity of the broad band at 647 ± 3 cm⁻¹ grows markedly. The increase in the relative intensity of this band in comparison to the main signal at 352 ± 3 cm⁻¹ can clearly be seen in Fig. 2. In the Raman spectra measured with 532 nm and 633 nm laser excitations, the band at 647 ± 3 cm⁻¹ becomes the main signal for the samples having higher degrees of inversion (Fig. S5, ESI†). This increase in intensity is accompanied by a shift of the position of the maximum from 647 ± 3 cm⁻¹ to 642 ± 3 cm⁻¹.

It should be noticed that the ratio between two Raman scattering signals seems to depend on the degree of inversion. The intensity ratio between the Raman shifts at 352 and 647 cm⁻¹vs. the degree of inversion was fitted with an exponential decay function. The obtained results are shown in the supporting information (Fig. S8, ESI†).

Fig. 4A shows the calculated Raman spectra of normal and inverse ZFO. The position and relative intensity of the calculated frequencies for a degree of inversion of x = 0 show a reasonably good agreement with the experimental result obtained for x ≈ 0.073. It is worth mentioning that the FWHM of the Raman signals cannot be calculated (therefore, an arbitrary value of 8 cm⁻¹ was used to plot the results) and that vibrational wavenumbers from DFT calculations are typically larger than the observed experimentally.⁴⁴ This is not only due to the harmonic approximation but also to the finite basis sets.⁴⁴ Furthermore, the computation of vibrational wavenumbers was shown to be dependent on the method.^44,45 Howard et al. considered vibrational wavenumbers within 20 cm⁻¹ of the reference values as accurate. Thus, the calculated spectrum for x = 0, with deviations of 15.5 to 48 cm⁻¹ (5.7 to 8.8%, respectively) from the experimental data obtained for a ZFO sample with x ≈ 0.073, is reasonably good. Scaling factors are often applied to improve the agreement between the calculated and experimental results.⁴⁴ Using scaling factors would also align the calculated spectrum presented in Fig. 4B with the experimental spectrum obtained for ZFO with x ≈ 0.073. However, this is not scientifically reasonable since the degree of inversion of the calculated ZFO (x = 0) and the synthesized ZFO (x ≈ 0.073) are not equal. Since the maximal inversion achieved experimentally is x = 0.203 ± 0.017, the calculated spectrum with an inversion of x = 1 cannot be compared directly. Nevertheless, the trends observed experimentally upon increasing disorder may be related to the theoretical spectra.

Fig. 4 (A) Calculated Raman spectra of ZFO with x = 0 and x = 1. (B) Comparison between the calculated Raman spectrum of ZFO with x = 0 and the experimental Raman spectrum of ZFO with x = 0.074 ± 0.011.

In the region from 150 cm⁻¹ to 250 cm⁻¹ it can be seen a prominent signal shift to higher wavenumbers with increasing intensity as the inversion increases. In agreement with the experimental result, the Raman signal observed in this region for x = 0 is shifted to higher wavenumbers in the calculated spectrum for x = 1. Vibrational analysis confirms the assumption that this signal arises from wagging of the tetrahedral ion, explaining the shift to higher wavenumbers when Zn atoms are replaced by the lighter Fe atoms.

The Raman signal located at 375 cm⁻¹ for the normal ZFO shifts to 325 cm⁻¹ and exhibits a shoulder at 310 cm⁻¹. This trend is once more in very good agreement with the experimental results. Vibrations of both, the octahedrally and tetrahedrally coordinated ions contribute to this signal.

The double peak obtained at 464 cm⁻¹ and 472 cm⁻¹ for x = 0 shifts to slightly smaller wavenumbers (459 cm⁻¹ and 462 cm⁻¹) under inversion and increases in intensity, being the most pronounced signal for x = 1. Although the vibrational analysis mainly ascribes these signals to the wagging of the tetrahedrally coordinated ions, as was supposed above, this behavior is not completely in line with the experimental results shown in Fig. 3C.

The calculated spectrum for x = 0 shows a small signal at 600 cm⁻¹, which splits into three signals at 541 cm⁻¹, 563 cm⁻¹, and 586 cm⁻¹ for x = 1. This effect cannot be observed in the experimental spectrum obtained with 785 nm laser excitation since those signals vanish between the rather broad bands located at higher and lower wavenumbers. Nevertheless, the spectra measured with 532 nm and 633 nm laser excitations (Fig. S5, ESI†) show a weak signal at 573 ± 3 cm⁻¹, comparable with the calculated signal at 600 cm⁻¹, for the sample with x = 0.074 ± 0.011. The intensity of this signal decreases as the degree of inversion increases. This decrease might be attributed to the split of this signal into three bands at lower wavenumbers, which contribute to the broadness of the band observed between 415 cm⁻¹ and 560 cm⁻¹.

The calculated signal at 695 cm⁻¹ undergoes a slight shift to 699 cm⁻¹ upon inversion, accompanied by a decreased intensity, which is contradictory to the experimental results (see Fig. 3D). This signal can mainly be ascribed to a symmetrical stretching of the ZnO₄-tetrahedra in the normal ZFO, and FeO₄-tetrahedra in the inverse ZFO.

As becomes clear from the above discussion, the degree of inversion has a great effect on the Raman scattering properties of ZFO. It is not surprising to find spectra in the literature showing different signal positions as well as diverse assignments.^26,46 Furthermore, most authors presume a normal structure for the ZFO samples, thus not determining the degree of inversion. This assumption is not necessarily correct as the ordering of the sample can be easily modified by the temperature of preparation. Moreover, there are reports showing low-temperature synthesized ZFO nanoparticles with high degrees of inversion.^18–20 Wang et al.²⁶ presented a Raman spectrum of ZFO with x = 0.10 together with an assignment of the bands. The signals at 221 cm⁻¹, 246 cm⁻¹, 355 cm⁻¹, 451 cm⁻¹, and 647 cm⁻¹ were identified as the five Raman active internal modes predicted by the group-theoretical analysis, having F_2g, E_g, F_2g, F_2g, and A_1g symmetry, respectively. The authors attributed the signals above 600 cm⁻¹ to the motion of oxygen in the tetrahedral AO₄ groups. The low-frequency modes were attributed to vibrations in the octahedral BO₆ sites. The distinctive signals at 355 cm⁻¹, 451 cm⁻¹, and 647 cm⁻¹ agree with the results presented in this work but a discrepancy is found with the vibrations at 221 cm⁻¹ and 246 cm⁻¹. As was mentioned above, the weak band at 251 ± 3 cm⁻¹ arises from the disorder of the sample and is not one of the Raman active internal modes for the normal structure predicted by the group-theoretical analysis. The signal at 221 cm⁻¹ was not observed in the present work neither for the 785 nm nor for the 532 nm and 633 nm laser excitations (Fig. S5, ESI†). A signal at 176.5 cm⁻¹ appears in the result presented by Wang et al. but the resolution in this region, close to the acquisition limit of the spectrum, is poor. Finally, the internal mode reported in the present work at 573.5 ± 3 cm⁻¹ is not observed by Wang et al. because this signal becomes very weak while using a 785 nm laser excitation. The assignment of the Raman active internal modes proposed in this work and the assignment made by Wang et al. are presented in Table 2.

Table 2 Assignment of the Raman active internal modes for normal ZFO proposed in the present work together with the assignment made by Wang et al.²⁶

Raman active internal mode	Frequency/cm^−1
	This work		Wang et al.
	Theoretical	Experimental
F2g	191	176.5 ± 3	221
Eg	375	352 ± 3	246
F2g	464/472	447 ± 3	355
F2g	600	573 ± 3	451
A1g	695	647 ± 3	647

---

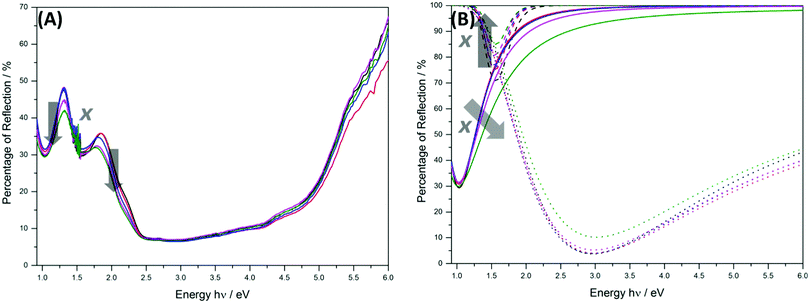
The UV-Vis-NIR diffuse reflectance spectra of the different ZFO samples are shown in Fig. 5. Three predominant absorption bands are observed in the regions from 220 nm to 670 nm, 670 nm to 950 nm, and 950 nm to 1600 nm. The bands around 795 nm (ca. 1.56 eV) and 1200 nm (ca. 1.03 eV) present typical Gaussian shapes, whereas the band with a maximum around 425 nm saturates the detector and then decreases in intensity from ca. 400 nm. The former band exhibits masked signals around 451 nm, 532 nm, and 614 nm. The determination and origin of these signals will be discussed below. Less reflectivity, namely more absorption, in the region between 500 nm and 700 nm is observed as the degree of inversion of the sample increases. This explains the darkening of the samples as x changes from 0.074 ± 0.011 to 0.203 ± 0.017 (Fig. S9, ESI†). The reflectivity of NIR radiation between 1400 nm and 2000 nm also decreases as the degree of inversion increases.

Fig. 5 UV-Vis-NIR diffuse reflectance spectra of the ZFO samples with increasing degree of inversion (— ZFO_773, x = 0.074 ± 0.011; ZFO_873, x = 0.104 ± 0.013; ZFO_973, x = 0.134 ± 0.008; ZFO_1073, x = 0.159 ± 0.010; ZFO_1173, x = 0.203 ± 0.017).

Three types of electronic transitions are found in Fe³⁺ rich oxides: ligand field transitions, transitions due to ligand-to-metal charge-transfer, and transitions resulting from simultaneous excitation of magnetically-coupled Fe³⁺ neighboring cations.⁴⁷ The latter transitions are expected to be negligible for ZFO since there are no face-sharing FeO₆ structures. The ligand field transitions for a Fe³⁺ ion occupying an octahedral site are due to the excitation of electrons from t_2g into e_g orbitals. These orbitals are formed by the splitting of the 3d orbitals due to the electrical field of the surrounding O²⁻ anions. Furthermore, both the t_2g and e_g orbitals are also split because of the exchange energy (Russell–Saunders coupling) and the resulting energetic states can be found in the respective Tanabe–Sugano diagram (Fig. S10, ESI†). According to this diagram, a high spin Fe³⁺ ion exhibits a ⁶A_1g ground state and the first three possible electronic transition are: ⁶A_1g(G) → ⁴T_1g(G) [(t^α_2g)³(e^α_g)² → (t^α_2g)³(e^α_g)¹(t^β_2g)¹], ⁶A_1g(G) → ⁴T_2g(G) [(t^α_2g)³(e^α_g)² → (t^α_2g)³(e^α_g)¹(t^β_2g)¹], and ⁶A_1g(G) → ⁴A_1g(G) [(t^α_2g)³(e^α_g)² → (t^α_2g)²(t^β_2g)¹(e^α_g)²]. Although all the transitions from the ground ⁶A_1g state are spin and parity-forbidden, they become allowed due to the magnetic coupling of electronic spins of neighboring Fe³⁺ cations.^48–50

On the basis of the Tanabe–Sugano diagram, an assignment of the experimentally observed UV-Vis-NIR bands was done (Table 3). The signals at 1200 nm and 795 nm can be assigned to the ⁶A_1g → ⁴T_1g(G) and ⁶A_1g → ⁴T_2g(G) transitions, respectively. This corresponds with a value of ca. 14 164 cm⁻¹ (1.76 eV) for the energy of the octahedral crystal field, and ca. 624 cm⁻¹ for the Racah parameter (Fig. S10, ESI†). Additionally, the energy for the ⁶A_1g → ⁴A_1g(G) and ⁶A_1g → ⁴T_2g(D) transitions is estimated to be ca. 20 248 cm⁻¹ (494 nm, 2.51 eV) and 22 300 cm⁻¹ (448 nm, 2.76 eV), respectively. The latter value is in good agreement with the signal at 451 nm masked within the broad band from 220 to 670 nm. Transitions from non-bonding molecular orbitals localized on the oxygen atoms to the antibonding t_2g Fe(3d) orbitals are reported in the literature for a vast variety of iron-based oxides.^47,51 Because this electronic excitation is responsible for the optical band gap of the semiconducting ZFO, the derivation absorption spectrum fitting method (DASF)³³ was applied to get more insight into the energy and the nature of the transition. Because the measured diffuse reflectance spectra do not correlate directly to the absorption spectra, the Kubelka–Munk radiative transfer model⁴⁵ was first applied to determine the absorption coefficient. Rietveld refinement (Table 1) and SEM pictures (Fig. S11, ESI†) reveal that the particles have similar size and shape. Thus, it was assumed that the different ZFO samples have the same scattering properties. The full mathematical deduction of the DASF model for diffuse reflectance data is presented in the supporting information. As can be seen from Fig. 6, three clear bands are observed at 2.02 eV (614 nm), 2.33 eV (532 nm), and 2.75 eV (451 nm), and a weak signal is observed at 2.58 eV (481 nm). The bands at 2.58 eV and 2.75 eV can be assigned to the ⁶A_1g → ⁴A_1g(G) and ⁶A_1g → ⁴T_2g(D) transitions, respectively (Fig. S10, ESI†). Consequently, the signal observed at 2.02 eV can be attributed to the O²⁻ + Fe³⁺ → O⁻ + Fe²⁺ transition. Moreover, the DASF analysis shows that this is an allowed and indirect transition (Fig. S12, ESI†). Finally, the band at 2.33 eV can be attributed to a direct O²⁻ + Fe³⁺ → O⁻ + Fe²⁺ transition. Table 3 lists the proposed assignment for the experimentally observed electronic transitions of ZFO.

Table 3 Assignment of the experimentally observed electronic transitions of ZFO according to the ligand field theory considering Russell–Saunders coupling

Wavelength/nm	Transition
1200	^6A1g → ^4T1g(G)
795	^6A1g → ^4T2g(G)
614	O^2− + Fe^3+ → O^− + Fe^2+ (indirect)
532	O^2− + Fe^3+ → O^− + Fe^2+ (direct)
481	^6A1g → ^4A1g(G)
451	^6A1g → ^4T2g(D)

---

Fig. 6 Derivation of absorption spectrum fitting (DASF) method calculated from 670 nm to 400 nm for the ZFO samples with increasing degree of inversion (— ZFO_773, x = 0.074 ± 0.011; ZFO_873, x = 0.104 ± 0.013; ZFO_973, x = 0.134 ± 0.008; ZFO_1073, x = 0.159 ± 0.010; ZFO_1173, x = 0.203 ± 0.017).

Surprisingly, all the bands can be assigned considering only electronic transitions in the octahedrally coordinated Fe³⁺ ions. Similar results are known for other iron-based oxides having Fe³⁺ in both tetrahedral and octahedral positions.⁴⁷ Pailhé et al.²⁷ also assigned the UV-Vis-NIR absorption bands of a ZFO sample with x = 0.140 to transitions involving Fe³⁺ in octahedral sites. Nevertheless, despite the authors deduced some of the transitions considering the orbital splitting due to the Russell–Saunders coupling, they mixed two different models by assigning transitions on the basis of a simple splitting of the Fe(3d) orbitals (into t_2g and e_g orbitals) as well.

By comparing the spectra for the ZFO samples with different degrees of inversion, the presence of transitions involving tetrahedrally coordinated Fe³⁺ ions can be analyzed. The UV-Vis-NIR spectra from 0.90 to 6.0 eV and the deconvolution of the three distinctive reflection bands employing Gaussian shaped curves are shown in Fig. 7. As the degree of inversion of the samples increases, the percentage of reflection at ca. 1.5 eV becomes higher (absorption decreases), and a broadening is observed for the band at ca. 1.0 eV (absorption increases). The amount of Fe³⁺ ions in octahedrally coordinated sites has a considerable effect on the signal around 1.5 eV. As this value decreases, the absorption in this region becomes smaller. This effect is consistent with the assignment of this band to a transition involving Fe³⁺ ions in octahedral sites. On the other hand, an increasing amount of Fe³⁺ ions in tetrahedrally coordinated sites generates a higher absorption in the region around 1.0 eV. This signal cannot be attributed solely to transitions involving Fe³⁺ ions in tetrahedral sites because the intensity is already very high for the sample containing only 3.8% (x = 0.074 ± 0.011) of tetrahedrally coordinated Fe³⁺ ions and does not grow proportionally as the degree of inversion increases. Nevertheless, considering that the transitions originating from tetrahedrally coordinated Fe³⁺ ions might not be significantly different in energy than those arising from the octahedrally coordinated,⁵¹ an overlapping of both types of transitions can be expected at around 1.0 eV. Therefore, the broadening of the band in the NIR region close to 1.0 eV can be explained by the contribution of the ligand field transitions due to Fe³⁺ ions occupying tetrahedral sites.

Fig. 7 (A) UV-VIS-NIR diffuse reflectance spectra from 0.9 to 6.0 eV of the ZFO samples with increasing degree of inversion. (B) Deconvolution of the UV-VIS-NIR diffuse reflectance spectra employing Gaussian-shaped curves. The full line, dash line, and pointed line corresponds to the reflection bands at 1.03 eV, 1.56 eV, and 3.00 eV, respectively. — ZFO_773, x = 0.074 ± 0.011; ZFO_873, x = 0.104 ± 0.013; ZFO_973, x = 0.134 ± 0.008; ZFO_1073, x = 0.159 ± 0.010; ZFO_1173, x = 0.203 ± 0.017.

The imaginary part of the dielectric function, ε₂, which is directly related to the probability of photon absorption,⁵² was calculated in dependency on the excitation energy for ZFO with a degree of inversion of x = 0 and x = 1. The resulting spectra are given in Fig. 8.

Fig. 8 Calculated imaginary part of the dielectric function ε₂ for optical spectrum of ZFO for ZFO with x = 0 and x = 1.

Since the used theoretical approach is no multideterminantal ansatz, intra-atomic transitions cannot be described. The onset of the spectrum for the normal and the inverse ZFO is located at 2.3 and 2.1 eV, respectively. The position of the O²⁻ + Fe³⁺ → O⁻ + Fe²⁺ transition is in excellent agreement with the experimental result. Furthermore, both experiment and theory state that there is no difference in the band gap energy for different degrees of inversion. The theoretical spectrum in Fig. 8 shows that, upon inversion, the intensity of the band gap excitation decreases dramatically. A similar effect can be seen in Fig. 6 for the signal attributed to the direct band gap transition. As the degree of inversion increases, the area of the signal, and thus the absorption coefficient, decreases.

4. Conclusions

The effect of the degree of inversion on the Raman scattering and the UV-VIS-NIR reflectivity of spinel ZFO is elucidated. Based on the strong evidence collected, a new assignment for both, the Raman active internal modes and the electronic transitions is proposed for normal ZFO. As the degree of inversion increases, a larger contribution from the ligand field transitions of the tetrahedrally coordinated Fe³⁺ ions into the visible light absorptivity of the material is observed, producing a characteristic darkening of the sample. Conversely, no effect is observed on the energies of the transitions due to ligand-to-metal charge-transfer between O²⁻ and Fe³⁺ ions. Thereby, the band gap energy, with values of 2.02 eV and 2.33 eV for the indirect and direct transition, respectively, is found to be independent of the degree of inversion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank the Laboratory of Nano- and Quantum-Engineering (LNQE) and Dr Dirk Dorfs and MSc Rasmus Himstedt for their support concerning the UV-Vis-NIR diffuse reflectance measurements. Financial support from the Deutsche Forschungsgemeinschaft in the large facility support INST144/435-1FUGG @ University of Bremen and under the program SPP 1613 (BA 1137/22-1) and the Niedersächsisches Ministerium für Wissenschaft und Kultur (NTH-research group “ElektroBak”), is gratefully acknowledged.

References

1. R. Sharma, P. Thakur, P. Sharma and V. Sharma, Ferrimagnetic Ni²⁺ doped Mg–Zn spinel ferrite nanoparticles for high density information storage, J. Alloys Compd., 2017, 704, 7–17.
2. M. P. Pileni, Magnetic fluids: Fabrication, magnetic properties, and organization of nanocrystals, Adv. Funct. Mater., 2001, 11, 323–336.
3. M. Pardavi-Horvath, Microwave applications of soft ferrites, J. Magn. Magn. Mater., 2000, 215, 171–183.
4. K. Yan, X. Wu, X. An and X. Xie, Facile synthesis and catalytic property of spinel ferrites by a template method, J. Alloys Compd., 2013, 552, 405–408.
5. A. B. Van Groenou, P. F. Bongers and A. L. Stuyts, Magnetism, microstructure and crystal chemistry of spinel ferrites, Mater. Sci. Eng., 1968, 3, 317–392.
6. D. H. Taffa, R. Dillert, A. C. Ulpe, K. C. L. Bauerfeind, T. Bredow, D. W. Bahnemann and M. Wark, Photoelectrochemical and theoretical investigations of spinel type ferrites (M_xFe_3−xO₄) for water splitting: a mini-review, J. Photonics Energy, 2016, 7, 012009.
7. R. Dillert, D. H. Taffa, M. Wark, T. Bredow and D. W. Bahnemann, Research Update: Photoelectrochemical water splitting and photocatalytic hydrogen production using ferrites (MFe₂O₄) under visible light irradiation, APL Mater., 2015, 3, 104001.
8. G. Song, F. Xin and X. Yin, Photocatalytic reduction of carbon dioxide over ZnFe₂O₄/TiO₂ nanobelts heterostructure in cyclohexanol, J. Colloid Interface Sci., 2015, 442, 60–66.
9. S. Boumaza, A. Boudjemaa, A. Bouguelia, R. Bouarab and M. Trari, Visible light induced hydrogen evolution on new hetero-system ZnFe₂O₄/SrTiO₃, Appl. Energy, 2010, 87, 2230–2236.
10. A. A. Tahir and K. G. U. Wijayantha, Photoelectrochemical water splitting at nanostructured ZnFe₂O₄ electrodes, J. Photochem. Photobiol., A, 2010, 216, 119–125.
11. J. H. Kim, J. H. Kim, J. W. Jang, J. Y. Kim, S. H. Choi, G. Magesh, J. Lee and J. S. Lee, Awakening solar water-splitting activity of ZnFe₂O₄ nanorods by hybrid microwave annealing, Adv. Energy Mater., 2015, 5, 1401933.
12. M. A. Valenzuela, P. Bosch, J. Jiménez-Becerrill, O. Quiroz and A. I. Páez, Preparation, characterization and photocatalytic activity of ZnO, Fe₂O₃ and ZnFe₂O₄, J. Photochem. Photobiol., A, 2002, 148, 177–182.
13. E. Casbeer, V. K. Sharma and X. Z. Li, Synthesis and photocatalytic activity of ferrites under visible light: A review, Sep. Purif. Technol., 2012, 87, 1–14.
14. A. Arimi, L. Megatif, L. I. Granone, R. Dillert and D. W. Bahnemann, Visible-light photocatalytic activity of zinc ferrites, J. Photochem. Photobiol., A, 2018 DOI:10.1016/j.jphotochem.2018.03.014.
15. H. S. C. O’Neill, Temperature dependence of the cation distribution in zinc ferrite (ZnFe₂O₄) from powder XRD structural refinements, Eur. J. Mineral., 1992, 4, 571–580.
16. A. Pavese, D. Levy and A. H. Hoser, Cation distribution in synthetic zinc ferrite (Zn_0.97Fe_2.02O₄) from in situ high-temperature neutron powder diffraction, Am. Mineral., 2000, 85, 1497–1502.
17. F. Bræstrup, B. C. Hauback and K. K. Hansen, Temperature dependence of the cation distribution in ZnFe₂O₄ measured with high temperature neutron diffraction, J. Solid State Chem., 2008, 181, 2364–2369.
18. M. J. Akhtar, M. Nadeem, S. Javaid and M. Atif, Cation distribution in nanocrystalline ZnFe₂O₄ investigated using x-ray absorption fine structure spectroscopy, J. Phys.: Condens. Matter, 2009, 21, 1–9.
19. T. Kamiyama, K. Haneda, T. Sato, S. Ikeda and H. Asano, Cation distribution in ZnFe₂O₄ fine particles studied by neutron powder diffraction, Solid State Commun., 1992, 81, 563–566.
20. S. Nakashima, K. Fujita, K. Tanaka, K. Hirao, T. Yamamoto and I. Tanaka, First-principles XANES simulations of spinel zinc ferrite with a disordered cation distribution, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 2–9.
21. J. Kurian and M. J. Mathew, Structural, optical and magnetic studies of CuFe₂O₄, MgFe₂O₄ and ZnFe₂O₄ nanoparticles prepared by hydrothermal/solvothermal method, J. Magn. Magn. Mater., 2018, 451, 121–130.
22. V. Šepelák, K. Tkáčová, V. V. Boldyrev, S. Wigmann and K. D. Becker, Mechanically induced cation redistribution in ZnFe₂O₄ and its thermal stability, Phys. B, 1997, 234–236, 617–619.
23. M. Mozaffari, M. Eghbali Arani and J. Amighian, The effect of cation distribution on magnetization of ZnFe₂O₄ nanoparticles, J. Magn. Magn. Mater., 2010, 322, 3240–3244.
24. Q. Yuan, L. Pan, R. Liu, J. Wang, Z. Liao, L. Qin, J. Bi, D. Gao and J. Wu, Cation distribution and magnetism in quenched ZnFe₂O₄, J. Electron. Mater., 2018, 47, 3608–3614.
25. V. G. Harris and V. Šepelák, Mechanochemically processed zinc ferrite nanoparticles: Evolution of structure and impact of induced cation inversion, J. Magn. Magn. Mater., 2018, 465, 603–610.
26. Z. Wang, D. Schiferl, Y. Zhao and H. S. C. O’Neill, High pressure Raman spectroscopy of spinel-type ferrite ZnFe₂O₄, J. Phys. Chem. Solids, 2003, 64, 2517–2523.
27. N. Pailhé, A. Wattiaux, M. Gaudon and A. Demourgues, Correlation between structural features and vis-NIR spectra of α-Fe₂O₃ hematite and AFe₂O₄ spinel oxides (A = Mg, Zn), J. Solid State Chem., 2008, 181, 1040–1047.
28. K. Lagarec and D. G. Rancourt, Recoil 1.05 Mössbauer Analysis software, Dep. Physics, Univ. Ottawa, Ottawa, ON, Canada, 2002.
29. R. Dovesi, R. Orlando, B. Civalleri, R. Roetti, V. R. Saunders and C. M. Zicovich-Wilson, CRYSTAL: a computational tool for the ab initio study of the electronic properties of crystals, Z. Kristallogr. – Cryst. Mater., 2005, 220, 571–573.
30. A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, Influence of the exchange screening parameter on the performance of screened hybrid functionals, J. Chem. Phys., 2006, 125, 224106.
31. P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields, J. Phys. Chem., 1994, 98, 11623–11627.
32. R. J. Hill, J. R. Craig and G. V. Gibbs, Systematics of the spinel structure type, Phys. Chem. Miner., 1979, 4, 317–339.
33. D. Souri and Z. E. Tahan, A new method for the determination of optical band gap and the nature of optical transitions in semiconductors, Appl. Phys. B: Lasers Opt., 2015, 119, 273–279.
34. G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. L. Hedin, New method for calculating the one-particleGreen's function with application to the electron-gas-problem, Phys. Rev., 1965, 139, A796–A823.
36. M. Rohlfing and S. G. Louie, Electron-hole excitations and optical spectra from first principles, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944.
37. R. M. Cornell and U. Schwertmann, in The Iron Oxides: Structure, Properties, Reactions, Occurences and Uses, WILEY-VCH, Darmstadt, 2nd edn, 2004, pp. 139–183.
38. H. B. Callen, S. E. Harrison and C. J. Kriessman, Cation distributions in ferrospinels. Theoretical, Phys. Rev., 1956, 103, 851–856.
39. A. Navrotsky and O. J. Kleppa, The thermodynamics of cation distributions in simple spinels, J. Inorg. Nucl. Chem., 1967, 29, 2701–2714.
40. H. S. C. O’Neill and A. Navrotsky, Simple spinels: crystallographic parameters, cation radii, lattice energies, and cation distribution, Am. Mineral., 1983, 68, 181–194.
41. H. S. C. O’Neill and A. Navrotsky, Cation distributions and thermodynamic properties of binary spinel solid solutions, Am. Mineral., 1984, 69, 733–753.
42. W. B. White and B. A. DeAngelis, Interpretation of the vibrational spectra of spinels, Spectrochim. Acta, Part A, 1967, 23A, 985–995.
43. P. R. Graves, C. Johnston and J. J. Campaniello, Raman scattering in spinel structure ferrites, Mater. Res. Bull., 1988, 23, 1651–1660.
44. A. P. Scott and L. Radom, Harmonic vibrational frequencies: An evaluation of Hartree-Fock, Møller-Plesset, quadratic configuration interaction, density functional theory, and semiempirical scale factors, J. Phys. Chem., 1996, 100, 16502–16513.
45. J. C. Howard, J. D. Enyard and G. S. Tschumper, Assessing the accuracy of some popular DFT methods for computing harmonic vibrational frequencies of water clusters, J. Chem. Phys., 2015, 143, 214103.
46. Z. Ž. Lazarević, D. L. Sekulić, V. N. Ivanovski and N. Ž. Romčević, A structural and magnetic investigation of the inversion degree in spinel NiFe₂O₄, ZnFe₂O₄ and Ni_0.5Zn_0.5Fe₂O₄ ferrites prepared by soft mechanochemical synthesis, Int. J. Chem. Mol. Nucl. Mater. Metall. Eng., 2015, 9, 1066–1070.
47. D. M. Sherman and T. D. Waite, Electronic spectra of Fe³⁺ oxides and oxide hydroxides in the near IR to near UV, Am. Mineral., 1985, 70, 1262–1269.
48. J. Ferguson, H. J. Guggenheim and Y. Tanabe, The effects of exchange interactions in the spectra of octahedral manganese. II. Compounds, J. Phys. Soc. Jpn., 1966, 21, 692–704.
49. J. J. Krebs and W. G. Maisch, Exchange effects in the optical-absorption spectrum of Fe³⁺ in Al₂O₃, Phys. Rev. B: Condens. Matter Mater. Phys., 1971, 4, 757–769.
50. L. L. Lohr, Spin-forbidden electronic excitations in transition metal complexes, Coord. Chem. Rev., 1972, 8, 241–259.
51. D. M. Sherman, The electronic structures of Fe³⁺ coordination sites in iron oxides: Applications to spectra, bonding, and magnetism, Phys. Chem. Miner., 1985, 12, 161–175.
52. P. Yu and M. Cardona, Fundamentals of Semiconductors, Springer, 4th edn, 2010.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp05061a

---