Quantum approaches to vibrational dynamics and spectroscopy: is ease of interpretation sacrificed as rigor increases?
Abstract
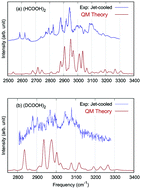
The subject of this Perspective is quantum approaches, beyond the harmonic approximation, to vibrational dynamics and IR spectroscopy. We begin with a pedagogical, unifying review of the most widely used quantum approaches. Some of the key details that lead to steep computational scaling of these approaches are reviewed, as well as some effective strategies to overcome or at least mitigate them. Considering in particular the application to IR spectroscopy, we stress the strength and weakness of each approach for spectral features that evolve from “simple” to “complex”. We use the 10-atom formic acid dimer as an ideal example of this evolution. The IR spectrum of this dimer and two isotopologs has been obtained computationally using our software, MULTIMODE, and approaches to obtain accurate, ab initio, full-dimensional potential energy and dipole moment surfaces, also developed by our group. The IR spectra obtained with the widely used “ab initio molecular dynamics” approach are also presented and assessed. The extension of quantum approaches to molecular clusters and even condensed phase applications, where molecular dynamics approaches are typically used, is discussed mainly in the context of the local monomer model. This approach is illustrated for a methane clathrate hydrate, where vibrational energies of the symmetric and asymmetric stretches of methane are given for a number of water cages and compared to experiment. The question about interpretation is also addressed throughout the Perspective.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases, PCCP Perspectives and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...