Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Trimeric coiled coils expand the range of strength, toughness and dynamics of coiled coil motifs under shear†
Ana E.
Bergues-Pupo
 a,
Kerstin G.
Blank
a,
Kerstin G.
Blank
 b,
Reinhard
Lipowsky
b,
Reinhard
Lipowsky
 a and
Ana
Vila Verde
a and
Ana
Vila Verde
 *a
*a
aMax Planck Institute of Colloids and Interfaces, Department of Theory & Bio-Systems, 14424 Potsdam, Germany. E-mail: Ana.Vilaverde@mpikg.mpg.de; Fax: +49 331 567 9602; Tel: +49 331 567 9608
bMax Planck Institute of Colloids and Interfaces, Mechano(bio)chemistry, 14424 Potsdam, Germany
First published on 6th November 2018
Abstract
Coiled coils are widespread protein motifs in nature, and promising building blocks for bio-inspired nanomaterials and nanoscale force sensors. Detailed structural insight into their mechanical response is required to understand their role in tissues and to design building blocks for applications. We use all-atom molecular dynamics simulations to elucidate the mechanical response of two types of coiled coils under shear: dimers and trimers. The amino acid sequences of both systems are similar, thus enabling universal (vs. system-specific) features to be identified. The trimer is mechanically more stable – it is both stronger and tougher – than the dimer, withstanding higher forces (127 pN vs. 49 pN at v = 10−3 nm ns−1) and dissipating up to five times more energy before rupture. The deformation mechanism of the trimer at all pull speeds is dominated by progressive helix unfolding. In contrast, at the lowest pull speeds, dimers deform by unfolding/refolding-assisted sliding. The additional helix in the trimer thus both determines the stability of the structure and affects the deformation mechanism, preventing helix sliding. The mechanical response of the coiled coils is not only sensitive to the oligomerization state but also to helix stability: preventing helix unfolding doubles the mechanical strength of the trimer, but decreases its toughness to half. Our results show that coiled coil trimers expand the range of coiled coil responses to an applied shear force. Altering the stability of individual helices against deformation emerges as one possible route towards fine-tuning this response, enabling the use of these motifs as nanomechanical building blocks.
1 Introduction
Coiled coils (CCs) are bundles of two or more alpha helices, present in the structure of around 10% of natural proteins.1,2 They appear in intracellular architectures, such as molecular motors and cytoskeleton fibers, as well as extracellular structures, such as the cartilage, blood clots and the basal lamina. They are also part of transmembrane proteins involved in membrane fusion.3–5 Natural CCs thus play an important role in a variety of mechano-biological processes, like cellular transport, force sensing, gene expression and cell signaling.1 The amino acid sequence motifs associated with CC formation are well understood, enabling the de novo design of such motifs.6 Making use of their controlled self-assembling properties, they are increasingly used as nanoscale building blocks in bio-engineered materials, e.g. as physical cross-links in hydrogels7–9 and for functionalizing nanoparticles.10In all these scenarios, CCs bear mechanical load and are either capable of maintaining their mechanical integrity or of undergoing structural transitions to transmit or dissipate force. Unraveling the sequence–structure–function relationships of CCs is therefore essential for understanding their many mechanical roles and for designing CC-based nano-materials with targeted mechanical properties. Intuitively, one expects that the mechanical response of CCs depends on the specific amino acid sequence, while simultaneously displaying universal features correlating with the CC length, degree of oligomerization, and pulling geometry, (i.e. tensile vs. shear vs. unzip).
CCs have been well-studied in the tensile12–16 and unzip17,18 geometries using single molecule force spectroscopy (SMFS) together with molecular dynamics simulations; however, much less so in the shear geometry.11,19 Most studies have focused on short dimeric CCs or on natural proteins containing CC domains, often differing in the number and relative orientation of the helices, as well as in the amino acid sequences. A straightforward distinction between universal and motif-specific features is thus difficult; however, a few universal features have emerged:11–16,19
(i) Shear and tensile loading of topologically different CC motifs exhibits an almost universal response: the force first increases linearly with extension and, upon reaching a threshold extension, a force plateau develops. Atomistic simulations have revealed that the force plateau originates from the unfolding of the individual helices in the CC bundle.11,13,14 In the tensile geometry, the plateau force appears to increase with an increasing number of helices in the CC.14,16 This response is expected in the tensile geometry because CC deformation involves the simultaneous stretching of all the helices. It remains an open question, however, if this is also the case in the shear geometry.
(ii) When pulled in the shear geometry, short dimeric CCs show a complex structural response characterized by a hierarchy of timescales.11 At very fast pulling velocities, progressive helix unfolding propagates from the points of force application. When decreasing the pulling velocities below 10−2 nm ns−1, helix refolding becomes possible, which facilitates a net displacement between the helices without permanent deformation, a mechanism termed unfolding/refolding-assisted helix sliding. At even lower pulling velocities, usually realized in SMFS experiments, helix sliding competes with thermally assisted inter-chain dissociation of the helices perpendicular to the force axis. This especially applies to short CCs (3–4 heptads) where the force required for dissociation is below or similar to the plateau force (in the range of 20–50 pN).
It remains unclear how the oligomerization state affects the nanomechanical response in the shear pulling geometry (Fig. 1): do trimeric CCs possess a higher plateau force than dimeric CCs also in this case? What are the molecular mechanisms governing trimer deformation, and do they follow the same hierarchy of timescales found in the dimeric CCs? Answers to these questions are essential for extending the force range of CCs for applications. The shear geometry is particularly useful for applications that benefit from inter-chain dissociation, such as hydrogels that include CCs as dynamic physical cross-links7–9 and molecular force sensors.20,21 A wider use of CCs in these applications is currently restricted as dimeric CCs exhibit a force plateau of maximally 50 pN (ref. 11). In this context, higher order oligomers represent a promising, but to be tested strategy, to reach this important goal.
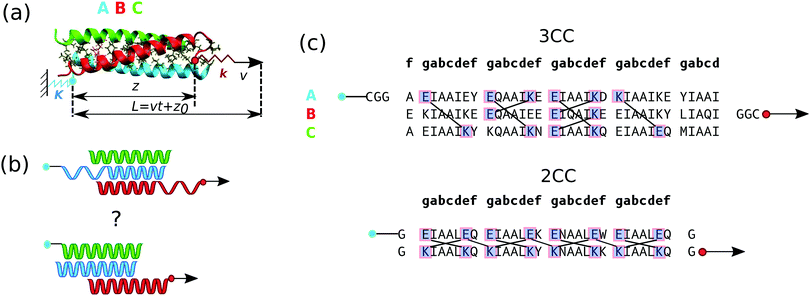 | ||
| Fig. 1 Simulation setup. (a) Shear pulling geometry applied to the trimeric CC. The component of the force acting on the pulled spring (red) along the z direction is calculated as F = k(L − z). Each of the three helices A, B and C is represented in a different color to indicate its distinct amino acid composition. Helix A (blue) is attached to the wall on the left and helix B (red) is pulled via the spring on the right. (b) Possible deformation mechanisms in the shear geometry (top: helix unfolding; and bottom: helix sliding). (c) Amino acid sequences of the trimeric coiled coil (3CC) used in this study and of the dimeric coiled coil (2CC) previously investigated by us.11 The amino acids are grouped by heptads and those forming inter-helical salt bridges in the crystal structure (3CC) or in the equilibrium simulation without force (2CC) are marked with blue squares and linked by solid lines. | ||
In this work, we answer these questions by using molecular dynamics simulations with all-atom resolution in implicit solvent. We compare a synthetic heterotrimeric CC (3CC) with a heterodimeric CC (2CC) of similar sequence composition and length (Fig. 1c) that we have studied previously.11
Despite a large number of similarities between the two CC motifs, we find that the trimeric 3CC is mechanically more stable – it is both tougher and stronger – than the dimeric 2CC. The presence of an additional helix not only increases the plateau force, it also affects the deformation mechanism at low pulling velocities: 3CC always responds with progressive helix unfolding and does not show any evidence of helix sliding, which is observed for 2CC at comparable pulling velocities. We further demonstrate that trimers can withstand forces higher than 200 pN if the stability of the individual helices in the bundle is increased so that unfolding is prevented. The stabilization of individual helices increases the mechanical strength of the 3CC while decreasing its toughness, suggesting that this parameter is also used by nature to tune CC properties. Our findings evidence the potential of short trimeric CCs to be used for extending the force range of nanomechanical building blocks that find application in nanostructured materials, molecular force sensors and others.
2 Materials and methods
Synthetic trimeric coiled coil system
We use the heterotrimeric CC (3CC) introduced by Nautiyal et al.22,23 (see Fig. 1c). Each alpha helix in the CC is 34 amino acids long and is characterized by a periodic repetition of 7 amino acids, conventionally denoted as gabcdef, called heptad. Amino acids at positions a and d are hydrophobic and pack towards the center of the bundle. Isoleucine residues are found at all a and d positions, except at the a positions of the second heptad where the polar amino acid glutamine is found. Charged amino acids are found at positions e and g and determine heterotrimer specificity, introducing salt bridges between the helices. For this 3CC, 7 inter-helical salt bridges are visible in the crystal structure. We added two glycines and a cysteine to the termini of helices A and B where the pulling force is applied (CGG) to stay closer to typical experimental stretching setups. This sequence is slightly different when compared to 2CC we previously studied, where a single glycine was added at both ends of both helices.11 The negative chloride ion which, in the crystal structure, is coordinated to the polar glutamine residues (Q) at positions a in the second heptad of the trimer was removed. In this way, we avoid possible artifacts originating from the ion force field interaction parameters. Equilibrium simulations show that the CC is stable under these conditions (Fig. 2).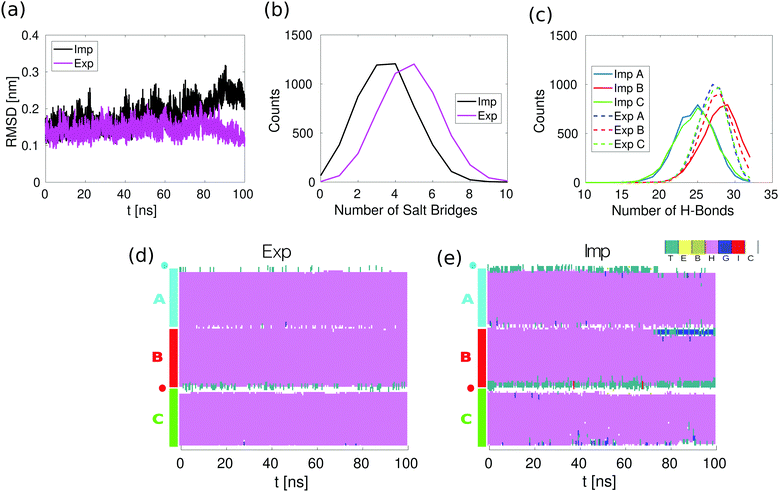 | ||
| Fig. 2 Equilibrium simulations in implicit and explicit solvent. (a) Root Mean Square Deviation (RMSD) of the backbone atoms as determined from the explicit (Exp) and implicit (Imp) solvent simulations. (b) Distribution of the number of salt bridges in the last 50 ns of the equilibrium simulations. A salt bridge is considered to be formed if any of the oxygen atoms of acidic side chains are within 0.32 nm of any of the nitrogen atoms of basic side chains. (c) Distribution of the number of the intra-helical hydrogen bonds in the last 50 ns of the equilibrium simulation. A hydrogen bond is considered to be formed if the two following geometric criteria hold: the distance between the donor and acceptor atoms is equal to or smaller than 0.35 nm and the angle between the hydrogen, the donor and the acceptor atoms is equal to or smaller than 30 degrees. (d) Secondary structure in the explicit solvent simulations. (e) Secondary structure in the implicit solvent simulations. Secondary structure is assigned with the stride algorithm25 as implemented in VMD.26 The color/letter code specifies the type of secondary structure for each amino acid: turn (T); extended configuration (E); isolated bridge (B); α helix (H); 3–10 helix (G); π helix (I) and random coil (C). | ||
This trimeric sequence is chosen because of its high similarity with the dimer we have investigated previously.11 Both sequences (see Fig. 1c) are highly repetitive, have similar length and are characterized by a parallel orientation of the helices. They contain buried polar amino acids in one of the hydrophobic positions and have a high thermal stability, with melting temperatures of approximately 80 °C.22,24 Despite this high degree of similarity, these two CCs also exhibit crucial differences that are intrinsically associated with their oligomerization state: the packing of the hydrophobic residues at both hydrophobic positions a and d follows an acute geometry for the trimer, whereas parallel and perpendicular packing are found at positions a and d for the dimer, respectively. Also, the distribution of salt bridges in the dimer is highly regular, because heterodimer specificity can easily be achieved with two oppositely charged helices. Heterospecificity is more difficult to obtain in trimers and the pattern of charged amino acids was carefully optimized to disfavor helix assemblies other than the desired ABC structure (Fig. 1c).
Molecular dynamics simulations
All simulations were conducted in GROMACS 5.1.1, using the Amber99SB-ILDN force field.27 To explore a wide range of pulling velocities, constant velocity simulations were performed in implicit solvent, using the Generalized Born (GB) and surface area algorithms. The Still approximation was used for calculating the GB part. The initial structure of 3CC was taken from the Protein Data Bank, ID code 1bb1. The positions of missing atoms in the original crystal structure were generated with the analysis Amber tool pdb4amber. The structure was minimized using 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with the steepest descent algorithm, followed by another 50
000 steps with the steepest descent algorithm, followed by another 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps with the conjugate gradient algorithm. The equilibration was conducted in three steps of 200 ps each and the system was heated from 10 K (step 1), to 150 K (step 2) and finally to 300 K (step 3). All the subsequent simulations were conducted at T = 300 K. Constraints on all covalent bonds were applied with the LINCS algorithm, which allows using an integration time step of 2 fs. The cutoff distances for the Coulomb and the van der Waals interactions are 5 and 1 nm, respectively.
000 steps with the conjugate gradient algorithm. The equilibration was conducted in three steps of 200 ps each and the system was heated from 10 K (step 1), to 150 K (step 2) and finally to 300 K (step 3). All the subsequent simulations were conducted at T = 300 K. Constraints on all covalent bonds were applied with the LINCS algorithm, which allows using an integration time step of 2 fs. The cutoff distances for the Coulomb and the van der Waals interactions are 5 and 1 nm, respectively.
In the pulling simulations, the external force was applied to the Cα atoms of the terminal cysteines (see Fig. 1). We added a restraint harmonic potential with spring constant K to the position of the cysteine in helix A to prevent the displacement of the whole system during the pulling simulations. The elastic constant, k, in the spring acting on helix B, where the force is measured, is lower than the one of the spring used to prevent the displacement of helix A, namely K = 10k = 1000 kJ (mol nm2)−1. Pulling of the spring acting on helix B is done along the z-direction. The force reported throughout this work is calculated as F = k(L − z) (see Fig. 1a).
A comparison between explicit and implicit solvent was initially performed for equilibrium simulations without pulling force to establish the validity of the implicit solvent simulations. The explicit solvent simulations were conducted with the TIP3P water model,28 the chloride ion of Smith and Dang29 and the sodium ion of Åqvist30 modified for Amber31 (σNa,Na = 3.32840 Å, εNa,Na = 0.0115897 kJ mol−1). These ion parameters are included with the Amber99SB-ILDN force field. A total of 13886 water molecules, 44 Na+ and 37 Cl− ions (37 Na+ and 37 Cl− corresponding to a salt concentration of 0.15 mol L−1 and 7 Na+ to have an electrically neutral system) were used in the simulations. After energy minimization (same steps as for the implicit solvent simulations), equilibration was performed by carrying out 100 ps simulation in the NVT ensemble (T = 300 K), followed by 1 ns in the NPT ensemble (T = 300 K, P = 1 bar). The cutoff distance for the Coulomb and the van der Waals interactions is 1 nm.
3 Results
Conformational stability in implicit and explicit solvent
To compare the conformational stability of the 3CC in both implicit and explicit solvent, we analyzed 100 ns simulations without force. The Root Mean Square Deviation (RMSD) of the positions of the backbone atoms as a function of time shows that the conformation of 3CC is more stable when simulated with explicit solvent (Fig. 2a). This behavior is reflected in the higher number of salt bridges and hydrogen bonds in the explicit solvent simulations, as can be seen from the distributions of salt bridges and hydrogen bonds in Fig. 2b and c. It is likely that the 3CC structure is over-stabilized in the explicit solvent simulations, because salt bridges are known to be over-stabilized in the Amber99SB-ILDN force field with TIP3P water.32 The difference in the average number of intrahelical hydrogen bonds between implicit and explicit solvent should not significantly impact the CC energy (Fig. S1, ESI†). Despite the lower conformational stability of 3CC in implicit solvent, spontaneous opening of complete helical turns, of more than three or more consecutive amino acids, does not occur as can be seen from the secondary structure as a function of time during the equilibrium simulation (Fig. 2e), in agreement with the explicit solvent simulations (Fig. 2d).The effects of the explicit/implicit solvents on the outcome of the pulling simulations were previously investigated in the dimeric 2CC system.11 The shape of the force–distance curves at various retract speeds did not differ between solvent models, with the value of the plateau force differing by less than 20%. Given the similarity between the 2CC and 3CC systems, we would expect the effect of the solvent model to be comparable for 3CC. We therefore use implicit solvent in the present study to be able to perform multiple simulations at different retract speeds.
The mechanical response of trimeric coiled coils under shear pull is velocity-dependent
Using the shear pulling geometry depicted in Fig. 1a, only the helices A and B are directly loaded. We measured both the force F at the rightmost spring and the position L of this spring when displaced at constant velocity v. The leftmost spring is very stiff, so we calculate the extension as ΔL ≈ v·t where t is the simulation time. The force–distance curves, shown in Fig. 3a, were obtained at four different pulling velocities, ranging from 1 to 10−3 nm ns−1, thus covering the same interval as for the dimer we have studied previously.11Fig. 3a shows that the mechanical response is velocity-dependent as expected for a thermally activated non-equilibrium process: larger pulling velocities result in larger forces.33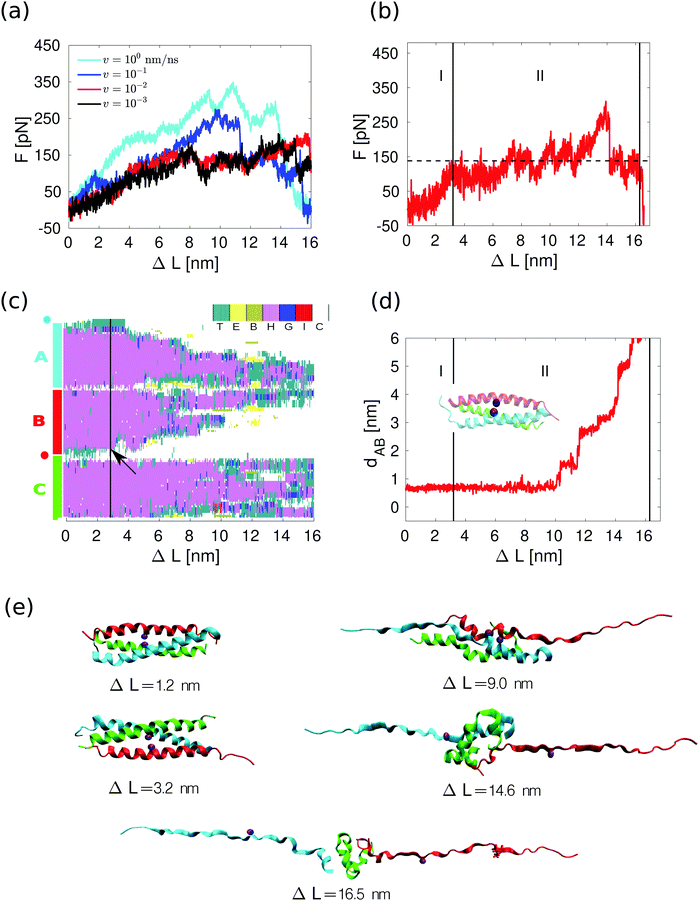 | ||
| Fig. 3 Response of 3CC to the applied shear force. (a) Average force as a function of extension at different pulling velocities. The average is calculated over 4 different force traces at each velocity except for v = 10−3 nm ns−1, where 3 traces were used. (b) Individual force trace at v = 10−3 nm ns−1. The average value of the force within the force plateau in region II corresponds to the horizontal dashed line. (c) Changes in the secondary structure of the three helices A, B and C for the force trace shown in panel b. The positions of the amino acids where the external force is applied are represented by the blue and red circles. The color/letter code specifies the type of secondary structure for each amino acid: turn (T); extended configuration (E); isolated bridge (B); α helix (H); 3–10 helix (G); π helix (I) and random coil (C). The unfolding event used to define the beginning of region II is marked with an arrow. (d) Relative displacement between helices A and B for the force trace shown in panel b. The distance dAB is measured between the Cβ atoms (inset, purple spheres) at position a in the third heptad of helices in A and B, see Fig. 1c. (e) Several snapshots of the force trace shown in panel b. | ||
To characterize the mechanical response of the trimeric coiled coil in detail, we consider only v = 10−3 nm ns−1, the lowest velocity we can access. This value is 2 orders of magnitude lower than for a previous simulation study of a trimeric CC of similar length,34 and was also used for the 2CC sequence we studied earlier. Simulations at v = 10−3 nm ns−1 have a run time of 12 months and are thus at the limit of what is computationally accessible.
The trimeric coiled coil is mechanically more stable than the dimer
A force–distance curve at v = 10−3 nm ns−1 is shown in Fig. 3b, and snapshots taken at different extensions during the simulation are shown in Fig. 3e. Similar results (Fig. S3a, ESI†) were obtained for other force traces at the same velocity. The shape of the curve is similar to what has been observed for 2CC in the shear geometry11 (Fig. S2a, ESI†) as well as for other CCs pulled in a tensile geometry.12–16 The force–distance curve consists of two main regions: an elastic region (I) and a region where the force fluctuates around an almost constant value (II). Due to the thermal noise, it is difficult to define the exact boundary between I and II. We define the beginning of region II as the extension where four consecutive amino acids unfold at one of the points of force application. This criterion was selected because four amino acids define approximately a helical turn, and helical turns never opened during the equilibrium simulation in the absence of force (Fig. 2e). The force in region II in this force trace has an average value of approximately 140 pN. The average value in region II over three different simulations at v = 10−3 nm ns−1 is 127 ± 17 pN. In contrast, for the 2CC at the same velocity the average force plateau is 49 ± 8 pN (see ref. 11 and Fig. S2a, ESI†). In region II, 3CC can be extended by approximately 12 nm – almost twice its equilibrium length – before helix B separates from the others. In the case of 2CC, the extension in region II is only ≈4 nm at v = 10−3 nm ns−1, corresponding to one time its equilibrium length. These features of the force–extension curves reveal different mechanical properties of 2CC and 3CC, to which we refer when comparing their mechanical stability: the mechanical strength, namely the average force in the region II of the force–extension curve, and the toughness, namely the energy needed to reach the displacement ΔLs at which the helices separate. The toughness is calculated as the work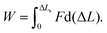 | (1) |
Because both the plateau force and the total extension are larger for 3CC than for 2CC, the trimeric coiled coil is both mechanically stronger and tougher than the dimer, with the trimer dissipating up to five times more energy than the dimer before rupture. Table 1 summarizes the mechanical properties of 2CC and 3CC at the two slowest velocities used in the simulations. Estimates for the highest velocities are not provided because the large fluctuations in the force values prevent the estimate of the mechanical strength.
| v (nm ns−1) | 2CC11 | 3CC |
|---|---|---|
| Mechanical strength (pN) | ||
| 10−2 | 64 | 142 |
| 10−3 | 49 | 127 |
| Toughness (kcal mol−1) | ||
| 10−2 | 44 | 271 |
| 10−3 | 31 | 191 |
The trimeric coiled coil deforms predominantly by progressive helix unfolding
For 2CC, the force plateau observed in the simulations originated from two different processes:11 progressive helix unfolding starting from the pulled ends of the CC at high velocities, and helix sliding assisted by transient unfolding (termed unfolding/refolding-assisted helix sliding) at the slowest velocities (Fig. S2, ESI†). In contrast, for 3CC the main process is helix unfolding starting from the pulled ends of helices A and B, even at low velocities (Fig. 3e, ESI†). Helix C remains folded during large parts of the simulation and is bound to helix A in most simulations (Fig. 3c and Movie M1, ESI†). The stronger interaction of helix C with helix A originates from four inter-helical salt bridges formed between these helices; in contrast, helices B and C share only one salt bridge. Helix C deforms, e.g., by changing its secondary structure (Fig. 3c) or by bending (snapshots of Fig. 3e), when helices A and B are mostly unfolded. These deformations show that the loss of native contacts affects the stability of the individual helix. The deformed helix C may, however, establish energetically favorable, non-native contacts with the other helices, which transiently stabilize the deformed CC. This stabilizing effect explains the force peaks visible in some of the single-run force–extension curves (Fig. 3b and Fig. S3a, ESI†).The process of unfolding is visualized in more detail in Fig. 3c, which shows a progressive transition from helix (pink color) to random coil (white) as a function of the spring position. Some unfolding/refolding events are observed in the central part of the helices, but they only involve a single amino acid. Unfolding of a full helical turn in a CC necessarily involves two types of events: amino acids must undergo a transition from alpha-helical to extended structure configurations, and hydrophobic CC contacts must break. To clarify the order in which these events occur, we compare the secondary structure of the amino acids closest to the pulled ends of 3CC with the average distance between the amino acids forming a hydrophobic contact in the same section of the coiled coil. An increase in this distance signals the disappearance of a hydrophobic contact. Our results (Fig. S4, ESI†) demonstrate that, on average, hydrophobic contacts break at the same time as the amino acids preceding them lose their alpha-helical configuration. In contrast, metadynamics and restrained simulations by Hamed et al. in the unzipping geometry suggested that the loss of helical structure precedes the separation of the hydrophobic residues.34
Visual inspection of the simulated CC configurations suggests that sliding also occurs in 3CC, but only once the CC is substantially deformed via progressive unfolding. To identify the onset of sliding, we calculate the relative displacement between helices A and B. Specifically, we calculate the distance between the atoms of the isoleucines at the a position of the third heptads of helices A and B as in Fig. 3d. If this distance remains constant, there is no relative displacement between the helices. Fig. 3d shows that both helices remain pinned until the middle of region II, supporting the qualitative description of progressive helix unfolding as the main process responsible for the force plateau. Additional simulations at the same velocity and with different seeds in the integration of the Langevin equations of motion show the same trends (see Fig. S3, ESI†), with the onset of the force plateau correlating with the onset of progressive unfolding, and inter-helix displacement occurring only after significant unfolding has taken place. In contrast, for 2CC the relative displacement between helices A and B starts approximately at the beginning of the force plateau for 2CC (Fig. S2a and b, ESI†).
Preventing helix unfolding increases the strength but decreases the toughness of the trimeric coiled coil
In the previous section, we showed that the force plateau of 3CC is associated with progressive helix unfolding. To demonstrate that the measured forces indeed originate from helix unfolding, we ask how the mechanical response of 3CC is affected if helix unfolding is suppressed. This effect can be achieved by increasing the helical strength of individual helices in the CC bundle. This strategy has already been used experimentally for increasing the thermodynamic stability of short helix-forming peptides, by including metal-coordinating amino acids at adjacent positions along one face of the helix35i.e., separated by 4 amino acids in the linear sequence or, alternatively, covalent staples in the same positions.36–38 To implement a similar strategy in our simulations, we chose to introduce harmonic restraint potentials in all dihedral angles of the peptide backbone, except for the CGG overhangs and the last isoleucine residues in the C-terminus of the three helices because they exhibit large fluctuations in the equilibrium simulation. The equilibrium values for the restraint potentials were obtained at the end of the equilibrium simulation without force, where most of the dihedral angles correspond to an alpha-helical structure. The restraints were strong enough to prevent the dihedrals from deviating more than 6 degrees from their initial values during the simulation.Fig. 4a shows the average force–distance relationships as obtained by averaging over three individual force traces with (black) and without (red) restraint potentials, for pulling velocity v = 10−2 nm ns−1. The response of 3CC is similar for v = 10−2 nm ns−1 and for 10−3 nm ns−1 (Fig. 3a). Thus, working with v = 10−2 nm ns−1 enables faster runtimes while giving similar insight into the response of the system. The force–distance curves show clear differences: in the restrained system, the force increases continuously with extension and does not reach a plateau before rupture. Moreover, the maximum force at rupture is substantially higher than the plateau force observed in the simulations without restraint potentials. Because unfolding of helical turns is suppressed, all hydrophobic contacts break simultaneously instead of progressively (Fig. 4c and d). As a direct result of this altered deformation process, the restrained CC ruptures at about half the extension ΔL of the unrestrained one. Suppressing helix unfolding thus limits the amount of energy that the CC can dissipate before rupture, as shown in Fig. 4b. Here, the toughness W is calculated using eqn (1) and plotted as a function of the extension ΔL together with the toughness values (indicated by arrows) at the moment of helix separation. Increasing helix stability by suppressing helix unfolding thus increases the mechanical strength but reduces the toughness of 3CC.
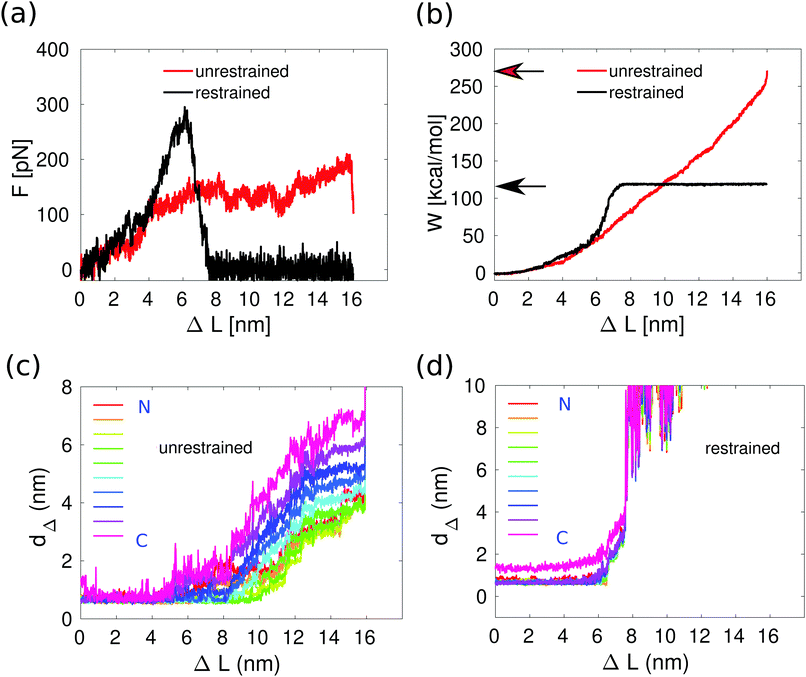 | ||
| Fig. 4 Effect of helix stability on the deformation and rupture of the trimeric coiled coil at v = 10−2 nm ns−1. (a) Force–distance relationships with and without restraint potentials. The curves are obtained by averaging over four individual force traces for the unrestrained case (red) and over three such traces for the restrained case (black). (b) Toughness W as a function of extension ΔL, calculated viaeqn (1) from the forces in panel a. The arrows point to the toughness obtained when helix B separates from helices A and C. (c) Hydrophobic contacts as function of the extension: without restraint potentials. (d) Hydrophobic contacts as function of the extension: with restraint potentials. The hydrophobic contacts are quantified by the distances dΔ at each hydrophobic position a and d. dΔ is the average of distance of the sides of the triangle formed by the Cβ atoms of the hydrophobic residues of each of the helices at the same position a or d. The colors indicate the position of these triangles along the CC bundle (up-to-down corresponds to the N-to-C terminus direction). | ||
Different time scales for the mechanical relaxation of 2CC and 3CC
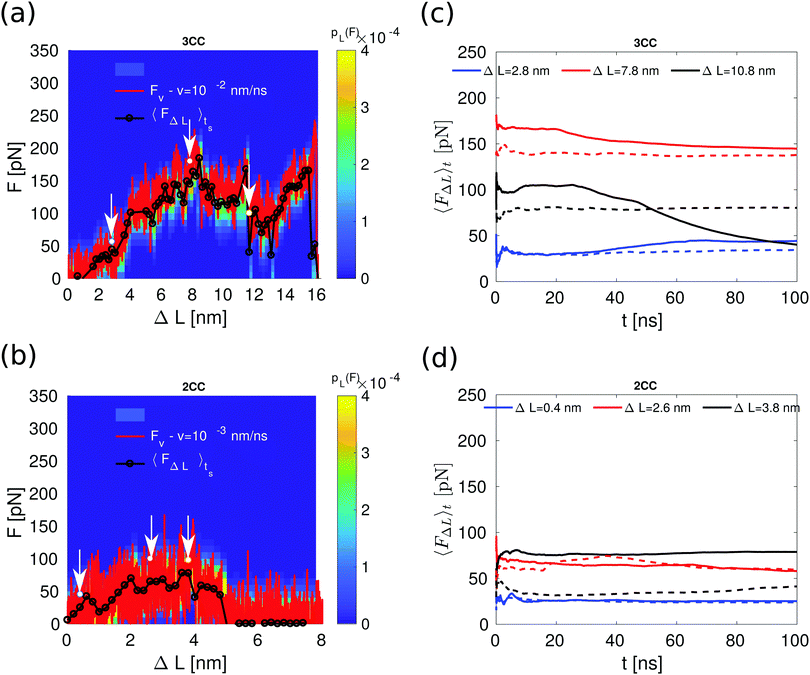
The constant velocity simulations show that 3CCs are mechanically more stable than the previously studied 2CCs. At the lowest pulling velocities, the corresponding force plateaus originate from different processes: progressive helix unfolding for 3CCs vs. unfolding/refolding-assisted sliding for 2CCs. Because the lowest pulling velocity explored in the simulations is still higher than the pulling velocities that can be investigated experimentally, the question arises whether the same differences in the mechanical stability will apply for the pulling velocities accessible with, e.g., the atomic force microscope or generated by cells probing the mechanical properties of their environment.To answer this question, we performed additional simulations, which we term constant length simulations. Different intermediate conformations were taken from the constant velocity simulations at v = 10−2 nm ns−1 for the 3CCs and at v = 10−3 nm ns−1 for the 2CCs, and used as starting points for a new round of simulations. Each of these conformations has a different value of ΔL, enforced by fixing the position of the rightmost spring during the entire simulation time (ts = 100 ns). For each of these constant length simulations, we measured the average force, 〈FΔL〉ts, at the spring during the time interval between 0 and ts. We compare 〈FΔL〉ts at each ΔL with the force Fv at t = 0, which corresponds to the measured force in the constant velocity simulation at the corresponding position of the spring. Differences between these two force values indicate that the selected conformation requires additional time to equilibrate.
When performing the constant length simulations, marked differences are observed between 〈FΔL〉ts and Fv only for the 3CCs at spring positions with ΔL > 10 nm (Fig. 5a), i.e., after the relative displacement between the helices has started. At these extensions, the force 〈FΔL〉ts is sometimes smaller than Fv. In contrast, for the 2CCs, the average force 〈FΔL〉ts and Fv overlap at all the spring positions (Fig. 5b).
We look in more detail into the force behavior at the spring positions marked with arrows in Fig. 5a and b. Specifically, the average force 〈FΔL〉t at each of these positions was calculated as a function of the time t, within the interval 0 < t < ts. If 〈FΔL〉t does not saturate, equilibrium is not reached during the time scale of the simulations. To check the influence of different initial conditions on the force saturation, we use two different initial conformations (see Fig. S5, ESI†) with the same ΔL taken from different individual force traces at the same velocity for each of the three spring positions and each of the CC systems. The results (Fig. 5c and d) again indicate that increasing the simulation time scale has a stronger effect on the 3CCs after the onset of relative helix displacement (ΔL = 10.8 nm). At this extension, the average force for one of the force traces decreases continuously with time because the helices A and B dissociate after t = 73 ns. This simple test shows that even though the dimer starts unfolding at a lower force than the trimer, the dimer's intermediate conformations after helix displacement resist shear force for longer periods of time than trimers. Thus, longer time scales in the trimer simulation may decrease the length of the force plateau, as helix dissociation is likely to occur. In contrast, the longer time scales we accessed with our simulations do not change the mechanical response of the dimer, suggesting that the unfolding/refolding-assisted sliding mechanism will still hold at velocities lower than those used in the simulations. We do not propose, however, that these differences will also determine helix dissociation/separation in the experiment.
4 Discussion
Using molecular dynamics simulations, we have examined the response of a short, synthetic trimeric CC to mechanical shear strain. Comparing the force–extension behavior of 3CCs and 2CCs, we observe that the number of helices influences several properties of the mechanical response to the applied force.Under the same loading conditions and for similar helix length, 3CCs withstand considerably higher forces than 2CCs, with a plateau force of 127 ± 17 pN compared to 49 ± 8 pN. The substantial difference in the plateau forces between 3CCs and 2CCs suggests that the third helix has a stabilizing effect which is more than additive; if the effect was additive, the ratio between the plateau force and the number of helices should be approximately the same for both CCs. A qualitatively similar increase in the mechanical strength with degree of oligomerization is also seen for coiled coils strained in the tensile geometry, but we emphasize that the mechanisms underlying this similarity are different. In the tensile geometry the force is shared homogeneously between the helices, whereas this is not the case in the shear geometry. The deformation processes are also different between 2CCs and 3CCs in the range of pulling velocities tested. At the highest velocities, both CCs show progressive helix unfolding, initiated at the points of force application. Whereas this is also the process observed for 3CCs at the slowest velocities v = 10−2 nm ns−1 and v = 10−3 nm ns−1 (see Movie M1, ESI†), for 2CCs at these velocities the helices are able to slide against each other via an unfolding/refolding mechanism.11
The larger plateau force and the altered deformation mechanism observed for 3CCs suggest that the additional helix affects the mechanical response of coiled coils in several ways. In comparison to 2CCs, 3CCs have an extended hydrophobic core, characterized by a larger number of hydrophobic contacts. Consequently, more contacts have to be broken simultaneously to complete the unfolding of each turn of the pulled helices. This leads to a larger plateau force. At the same time, the neighboring helices stabilize each individual helix against unfolding, thus preventing sliding of the helical segments further away from the force application point via the unfolding/refolding mechanism, seen in 2CCs.
Would unfolding/refolding-assisted sliding be observed for trimeric coiled coils if the pulling velocity was below v = 10−3 nm ns−1? Our results from the constant L simulations suggest that sliding would not occur for the trimer even at slower velocities. Instead, dissociation of helix B from helices A and C may occur in the plateau region after unfolding.
Two structural differences between 2CCs and 3CCs could in principle prevent the occurrence of sliding in 3CC even at experimentally accessible pulling velocities. 2CCs possess a highly periodic charge distribution, whereas the charge distribution is irregular for 3CCs. This irregularity ensures the highest possible thermodynamic stability of the heterotrimer relative to other possible assembly states.22 As charge interactions contribute much less to the overall stability of CCs than hydrophobic interactions,39 however, we conclude that charge repulsion in off-registry conformations is not sufficient to prevent unfolding/refolding-assisted sliding.
It appears more likely that the packing of the hydrophobic residues determines the deformation mechanism. The hydrophobic amino acids of 3CCs are packed in an acute knobs-into-holes geometry at both a and d positions. In contrast, 2CCs show parallel knobs-into-holes packing in the a position and perpendicular packing in the d position.24 To facilitate sliding, the helices in the central part of the coiled coil need to unfold locally, and the hydrophobic amino acids need to be flexible enough to break and reform new contacts; these two rare events need to occur on a similar timescale. We propose that the more densely packed hydrophobic core of 3CCs and the different packing geometry reduce the hydrophobic core flexibility so that the individual amino acids do not possess the necessary conformational space required for unfolding/refolding-assisted sliding. This leaves progressive unfolding as the major response to the applied shear force.
When increasing the stability of individual helices, their unfolding is suppressed and helix separation takes place without unfolding. Thus, tuning helix stability provides a strategy for controlling the mechanical properties of the CC. In the limit in which all helical turns are prevented from unfolding, the mechanical strength of 3CCs increases up to 200 pN (Fig. 4a). Under these conditions, all hydrophobic contacts have to be broken simultaneously to facilitate CC rupture (Fig. 4d). This larger strength comes at the expense of a decrease in toughness because CC rupture occurs at much smaller extensions. The correlation between the mechanical response of CCs and the intrinsic stability of the individual helices should not be limited to trimeric coiled coils. This issue requires further investigation, both using experiments and simulations.
5 Concluding remarks
We show that trimeric coiled coils under shear loads withstand larger forces compared to dimeric coiled coils, with a plateau force of 127 ± 17 pN compared to 49 ± 8 pN. In addition, trimers dissipate up to five times more energy before rupture than dimers of comparable length and sequence. Helix stability is a key parameter to tune the mechanical response of coiled coils: in the limit in which helix unfolding is prevented, the rupture force of the trimer increases up to 200 pN but the dissipated energy or toughness, see eqn (1), decreases to half. These features of the mechanical response of CC trimers and dimers under shear are directly relevant for understanding the function of CCs in biological systems and for using CCs as nanomechanical building blocks in applications. In mammalian tissues, the majority of intracellular CC-containing proteins consist of dimeric CCs, while CCs in the extracellular matrix are frequently trimers.4 The distinct mechanical responses of trimers and dimers as observed in our simulations should be functionally relevant, implying that the oligomerization state of CC structures has been evolutionary optimized.From an application point of view, trimeric CCs increase the force range of CC motifs over 100 pN, expanding the possible use of CCs as versatile motifs for creating nanostructured materials40 and as nanoscale force sensors.20,21 Considering that the force plateau of CC dimers reaches only 25–50 pN (in phase II11,12) and only about 65 pN for DNA (in the so called overstretching transition),41–43 CC trimers may emerge as the first synthetic building block with tunable mechanics in the force range between 100 and 200 pN. This force range is highly interesting for a number of applications, in particular for the further development of molecular force sensors for measuring cellular traction forces, which have been shown to exceed the force range of currently used force sensor building blocks.21 Importantly, the increase of the mechanical strength by increasing the oligomerization state is advantageous compared to the potential increase with the CC length,11 because some studies indicate that the rupture force for the shear geometry gets almost constant after a critical length.44
Our results demonstrate that the combination of oligomerization state and helix stability are key design parameters for tuning the strength and toughness of CCs. The chosen 3CC is experimentally accessible, enabling further characterization of this motif, e.g., comparing its mechanical response with natural trimeric CCs of similar length and different sequence composition.45 The acute knobs-into-holes packing of trimeric CCs has been shown to tolerate different combinations of hydrophobic amino acids at the a and d positions46 so that a systematic investigation of these differences is not only expected to shed further light on the proposed mechanism, but may also emerge as an additional design parameter for tuning the mechanical response of trimeric CCs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Dr Chuanfu Luo for providing two of the simulations of the 2CC at the slowest velocity that allowed a more clear comparison with the 3CC. We gratefully acknowledge Marco Ehlert and René Genz from the IT team of Max Planck Institute of Colloids and Interfaces (MPIKG) for their help with computational facilities. Open Access funding provided by the Max Planck Society.Notes and references
- L. Truebestein and T. A. Leonard, BioEssays, 2016, 38, 903–916 CrossRef CAS PubMed.
- E. Wolf, P. S. Kim and B. Berger, Protein Sci., 1997, 6, 1179–1189 CrossRef CAS PubMed.
- P. Burkhard, J. Stetefeld and S. V. Strelkov, Trends Cell Biol., 2001, 11, 82–88 CrossRef CAS PubMed.
- A. N. Lupas and M. Gruber, Fibrous Proteins: Coiled-Coils, Collagen and Elastomers, Academic Press, 2005, vol. 70, pp. 37–38 Search PubMed.
- D. A. Parry, R. B. Fraser and J. M. Squire, J. Struct. Biol., 2008, 163, 258–269 CrossRef CAS PubMed.
- D. N. Woolfson, G. J. Bartlett, A. J. Burton, J. W. Heal, A. Niitsu, A. R. Thomson and C. W. Wood, Curr. Opin. Struct. Biol., 2015, 33, 16–26 CrossRef CAS PubMed.
- C. Wang, R. J. Stewart and J. Kopeček, Nature, 1999, 397, 417 CrossRef CAS PubMed.
- P. Jing, J. S. Rudra, A. B. Herr and J. H. Collier, Biomacromolecules, 2008, 9, 2438–2446 CrossRef CAS PubMed.
- S. Dånmark, C. Aronsson and D. Aili, Biomacromolecules, 2016, 17, 2260–2267 CrossRef PubMed.
- M. M. Stevens, N. T. Flynn, C. Wang, D. A. Tirrell and R. Langer, Adv. Mater., 2004, 16, 915–918 CrossRef CAS.
- M. Goktas, C. Luo, R. M. A. Sullan, A. E. Bergues-Pupo, R. Lipowsky, A. V. Verde and K. Blank, Chem. Sci., 2018, 9, 4610–4621 RSC.
- I. Schwaiger, C. Sattler, D. R. Hostetter and M. Rief, Nat. Mater., 2002, 1, 232 CrossRef CAS PubMed.
- D. D. Root, V. K. Yadavalli, J. G. Forbes and K. Wang, Biophys. J., 2006, 90, 2852–2866 CrossRef CAS PubMed.
- B. B. Lim, E. H. Lee, M. Sotomayor and K. Schulten, Structure, 2008, 16, 449–459 CrossRef CAS PubMed.
- J. Block, H. Witt, A. Candelli, E. J. Peterman, G. J. Wuite, A. Janshoff and S. Köster, Phys. Rev. Lett., 2017, 118, 048101 CrossRef PubMed.
- K. A. Minin, A. Zhmurov, K. A. Marx, P. K. Purohit and V. Barsegov, J. Am. Chem. Soc., 2017, 139, 16168–16177 CrossRef CAS PubMed.
- T. Bornschlögl and M. Rief, Phys. Rev. Lett., 2006, 96, 118102 CrossRef PubMed.
- Y. Gao, G. Sirinakis and Y. Zhang, J. Am. Chem. Soc., 2011, 133, 12749–12757 CrossRef CAS PubMed.
- Z. Qin and M. J. Buehler, Phys. Rev. Lett., 2010, 104, 198304 CrossRef PubMed.
- C. Albrecht, K. Blank, M. Lalic-Mülthaler, S. Hirler, T. Mai, I. Gilbert, S. Schiffmann, T. Bayer, H. Clausen-Schaumann and H. E. Gaub, Science, 2003, 301, 367–370 CrossRef CAS PubMed.
- M. Goktas and K. G. Blank, Adv. Mater. Interfaces, 2017, 4, 1600441 CrossRef.
- S. Nautiyal, D. N. Woolfson, D. S. King and T. Alber, Biochemistry, 1995, 34, 11645–11651 CrossRef CAS PubMed.
- S. Nautiyal and T. Alber, Protein Sci., 1999, 8, 84–90 CrossRef CAS PubMed.
- F. Thomas, A. L. Boyle, A. J. Burton and D. N. Woolfson, J. Am. Chem. Soc., 2013, 135, 5161–5166 CrossRef CAS PubMed.
- D. Frishman and P. Argos, Proteins: Struct., Funct., Bioinf., 1995, 23, 566–579 CrossRef CAS PubMed.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef CAS PubMed.
- K. Lindorff-Larsen, S. Piana, K. Palmo, P. Maragakis, J. L. Klepeis, R. O. Dror and D. E. Shaw, Proteins, 2010, 78, 1950–1958 CAS.
- W. L. Jorgensen, J. Chandrasekhar, J. D. Madura, R. W. Impey and M. L. Klein, J. Chem. Phys., 1983, 79, 926–935 CrossRef CAS.
- D. E. Smith and L. X. Dang, J. Chem. Phys., 1994, 100, 3757–3766 CrossRef CAS.
- J. Åqvist, J. Phys. Chem., 1990, 94, 8021–8024 CrossRef.
- A. A. Chen and R. V. Pappu, J. Phys. Chem. B, 2007, 111, 11884–11887 CrossRef CAS PubMed.
- K. T. Debiec, A. M. Gronenborn and L. T. Chong, J. Phys. Chem. B, 2014, 118, 6561–6569 CrossRef CAS PubMed.
- E. Evans, Annu. Rev. Biophys. Biomol. Struct., 2001, 30, 105–128 CrossRef CAS PubMed.
- E. Hamed and S. Keten, Biophys. J., 2014, 107, 477–484 CrossRef CAS PubMed.
- F. H. Arnold and J.-H. Zhang, Trends Biotechnol., 1994, 12, 189–192 CrossRef CAS PubMed.
- C. E. Schafmeister, J. Po and G. L. Verdine, J. Am. Chem. Soc., 2000, 122, 5891–5892 CrossRef CAS.
- Y.-W. Kim and G. L. Verdine, Bioorg. Med. Chem. Lett., 2009, 19, 2533–2536 CrossRef CAS PubMed.
- L. D. Walensky and G. H. Bird, J. Med. Chem., 2014, 57, 6275–6288 CrossRef CAS PubMed.
- A. N. Lupas and J. Bassler, Trends Biochem. Sci., 2017, 42, 130–140 CrossRef CAS PubMed.
- D. N. Woolfson, Pept. Sci., 2010, 94, 118–127 CrossRef CAS PubMed.
- S. B. Smith, Y. Cui and C. Bustamante, Science, 1996, 271, 795–799 CrossRef CAS PubMed.
- P. Cluzel, A. Lebrun, C. Heller, R. Lavery, J.-L. Viovy, D. Chatenay and F. Caron, Science, 1996, 271, 792–794 CrossRef CAS PubMed.
- P. Gross, N. Laurens, L. B. Oddershede, U. Bockelmann, E. J. Peterman and G. J. Wuite, Nat. Phys., 2011, 7, 731 Search PubMed.
- M. Mosayebi, A. A. Louis, J. P. Doye and T. E. Ouldridge, ACS Nano, 2015, 9, 11993–12003 CrossRef CAS PubMed.
- R. A. Kammerer, D. Kostrewa, P. Progias, S. Honnappa, D. Avila, A. Lustig, F. K. Winkler, J. Pieters and M. O. Steinmetz, Proc. Natl. Acad. Sci. U. S. A., 2005, 102, 13891–13896 CrossRef CAS PubMed.
- P. B. Harbury, P. S. Kim and T. Alber, Nature, 1994, 371, 80 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Potential energy of 3CC and its correlation with the number of intrahelical hydrogen bonds; summary of the mechanical response of 2CC to shear pull; for 3CC: sequence of events associated with helix unfolding, additional force traces, hydrophobic contacts as a function of extension with and without dihedral constraints, initial conformations for the simulations at constant Li; movie M1. See DOI: 10.1039/c8cp04896g |
| This journal is © the Owner Societies 2018 |