Theoretical insight into joint photodynamic action of a gold(i) complex and a BODIPY chromophore for singlet oxygen generation†
Abstract
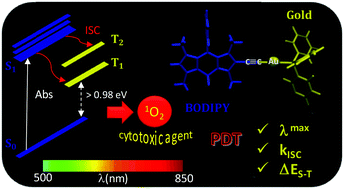
Density functional theory is herein employed to provide theoretical insight into the mechanism involved in 1O2 photosensitization by a gold–BODIPY combined complex proposed as a promising photodynamic therapy agent. The protocol is thus used to compute the non-radiative rate constants for the S1 → Tj intersystem crossing transitions. Calculations show that while the incorporation of an iodine atom into the core skeleton of BODIPY enhances the singlet–triplet intersystem crossing (ISC) efficiency due to the occurrence of the singlet–triplet transition between states with different orbital characters (ππ* → πn*), the presence of a gold atom, even if not directly anchored to the chromophore core but through a triplet bond, equally entails an increase of the spin–orbit coupling constant due to the heavy atom effect. In this way, the system is able to generate singlet molecular oxygen, the key cytotoxic agent in PDT. Our results fit well with the experimental singlet oxygen quantum yield and cytotoxicity determination.
- This article is part of the themed collections: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases and 2018 PCCP HOT Articles


 Please wait while we load your content...
Please wait while we load your content...