Unveiling anharmonic coupling by means of excited state ab initio dynamics: application to diarylethene photoreactivity†
Abstract
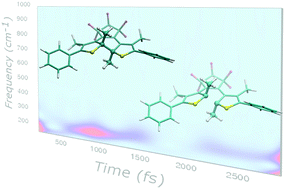
In this work, excited state ab initio molecular dynamics together with a time resolved vibrational analysis is employed to shed light on the vibrational photoinduced dynamics of a well-known diarylethene molecule experiencing a ring opening reaction upon electronic excitation. The photoreactivity of diarylethenes is recognized to be controlled by a non-adiabatic intersection point between the ground and the first excited state surfaces. The computation of an energy scan, along a suitable reaction coordinate, allows us to identify the region of potential energy surfaces in which the ground (S0) and the first excited (S1) state are well separated. The adiabatic sampling of that region in S1 shows that in the first 3 picoseconds, the central CC bond, which is subject to break, oscillates in an antiphase with respect to the energy gap ΔE(S1 − S0). A multiresolution analysis based on the wavelet transform was then applied to the structural parameters extracted from the excited state dynamics. The wavelet maps show characteristic oscillations of the frequencies, mainly CC stretching and CCC bending localized on the central 4-ring moiety. Moreover, we have identified the main frequency (methyl wagging motion) involved in the modulation of these oscillations. The anharmonic coupling within a group of vibrational modes was therefore highlighted, in good agreement with experimental evidence. For the first time, a quantitative analysis of time resolved signals from a wavelet transform/ab initio molecular dynamics approach was performed.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...