The first stages of oxide growth at the low index Al surfaces (100), (110), (111): clusters and stripes vs. homogeneous growth

Abstract

We performed a density functional theory (DFT) investigation of the mechanisms of oxide growth at Al(100), Al(110) and Al(111) up to 1 monolayer (ML) coverage of O-atoms with 0.125 ML increments. We found that the surface binding site preferences of O-atoms are largely affected by the presence of neighboring O-atoms. Based on this we constructed two oxide growth models: the formation of clusters that evolve to stripes with increasing coverage and the formation of a more homogeneous distribution of O-atoms. While the former model is characterized by a lower symmetry of distribution of O-atoms at the surfaces, the latter corresponds to higher symmetries. We found that the prevalence of each oxide growth mode depends on the coverage of O-atoms and that this dependency is different for each surface. For Al(100) and Al(110), up to coverages of 1 ML the oxide grows preferably via the formation of clusters that evolve to stripes with increasing coverage, while for Al(111) the stripes and clusters are the preferred growth mode for coverages up to 0.375 ML, beyond which the homogeneous growth mode is energetically favored. The calculated Al–O pair distribution functions show that the formation of clusters and stripes leads to shorter Al–O bond lengths when compared to the homogeneous growth. The oxides formed at Al(100) and Al(110) have Al–O bond lengths and geometries typical of the shorter bonds of α-alumina while at Al(111) the bond lengths are typical of γ-alumina and β-alumina. These results suggest that for low coverages, the oxides formed at Al(100) and Al(110) are resemblant of defective α-alumina while the oxide formed at Al(111) is similar to less disordered γ-alumina and β-alumina. For Al(111), the small energy difference between the growth of clusters and stripes and homogeneous growth does not exclude the coexistence of both growth modes; this could lead to the formation of a defective or amorphous oxide.

---

1. Introduction

The first stages of the growth of oxides at metal surfaces are often envisioned to follow mechanisms that involve the binding of O-atoms with the surfaces in ways that lead to the higher symmetries possible of disposition of O in the plane of the surface. This largely empirical picture is based on the fact that adsorbate distributions with higher symmetries minimize local stresses induced by the adsorption process and result in smaller local surface dipole moments than distributions with lower symmetries.^1–4 Such views have emerged to a large extent from the centenary Langmuir adsorption model.⁵ However, there are other factors that affect the disposition of adsorbates at surfaces such as the interactions between adsorbates and the fine energetic balance that exists between forming surface–adsorbate bonds and displacing the surface atoms from their equilibrium positions via surface reconstruction and relaxation.^1–4 All these parameters affect the geometries of disposition of adsorbates at surfaces, including the growth of oxide layers.

Aluminum reacts readily with oxygen and there are plenty of experimental^6–13 and computational^14–21 data available on these reactions especially at low Miller index surfaces such as the (111) and (100). However, the mechanisms of the initial stages of oxide growth remain fairly obscure and mechanistic data is scarce. These two surfaces have been the main focus due to their lower surface energies when compared to the Al(110).^22,23 But for practical applications Al(110) can also be of relevance because it appears in facets at surfaces of polycrystals.²⁴ Additionally, the Al(110) has a lower workfunction than the above mentioned two surfaces,^25–28 and can form strong bonds with O-atoms for low coverages, before a large number of surface bound O-atoms starts to have a large impact on the workfunction.^29,30

The experimental studies on the first-stages of oxide growth at Al surfaces have been focused almost solely on Al(111). The current knowledge is that right after dissociation of O₂, the O-atoms are “hot” and highly mobile, so that they can travel distances of around 80 Å on the surface.^31,32 Simultaneously there are studies that report high energy barriers of around 0.8 eV for diffusion of O-atoms on the surface.³³ These observations might sound incompatible but the phenomenon has been attributed to the highly dynamical natures of both the oxidation process and of the Al surfaces.^34,35 The “hot” O-atoms carry considerable amounts of kinetic energy right after the O₂ molecule dissociates, but latter they “cool down” and adsorb to become less mobile.³⁶ At this stage they can become nucleation sites and promote the oxide growth as clusters.^13,32,36,37 Diffusion of Al-atoms has also been proposed as being involved in the mechanism of growth of such structures.³⁸ In previous computational studies, it has been shown that for Al(111), increasing the coverage of oxygen implies large relaxations of the first layer of Al atoms and even at coverages lower than one monolayer (ML) it is favorable for O to bind to the second surface layer which results in the formation of clusters of O-atoms.^29,39,40 The authors found further that there is a cooperative effect between the O-atoms that facilitates the oxidation. This mechanism of has been recently confirmed in an experimental investigation.¹³ In a previous computational study we reported the occurrence of a similar phenomenon for Al(110).³⁰ In that work we compared two different modes for the initial growth of oxide, as clusters and a homogeneous mode. We found that for coverages of 1.5 ML and below the preferred mode of growth is as clusters (or islands), but as the coverage increases above that value the homogeneous mode becomes more favorable. The phenomena responsible for this are related with increased resistance to surface reconstruction and changes in the workfunction. For Al(100) indirect measurements have suggested that upon reaction with O₂(g), after a certain coverage has been reached, O-atoms penetrate the surface lifting the outmost Al-atoms,⁴¹ and a computational study using the embedded cluster method suggests that single O-atoms prefer to bind at four-fold hollow sites.⁴² A recent experimental investigation has shown that for Al(100) the oxide grows as islands that with increasing coverage of O-atoms expand laterally to form stripes.¹³

Growth of oxides implies continuous changes in the structural symmetry of the interface between the metal substrate and the oxide layer as the oxide increases in thickness.^28,43–45 Therefore the computational modelling of such phenomena is limited by the constraints imposed by the symmetrically constructed supercell to model the growth of oxide. Because of this, computational modelling is limited to either initial stages—where the structure of the growing oxide is constrained by the symmetry of the substrate metal—or to latter stages where the oxide has become thick to such an extent that its structure is similar to its bulk structure. Because of the highly dynamical nature of the growth of oxide on Al, which poses difficulties for experimental studies,^38,46,47 and being aware of the intrinsic limitations of the computational models, the computational investigation of the initial stages of oxide growth can give valuable information for understanding the further growth of layers of oxide at Al surfaces.^43,48,49

Besides our cited work³⁰ where we studied the increase in coverage of O-atoms at Al(110) from 0 to 2 ML with DFT and ab initio molecular dynamics, there are no first-principles mechanistic studies that focus on the increase in coverage of O-atoms at low Miller index Al surfaces. Most of the computational studies have focused on single or pairs of O-atoms at the surfaces. In this work we extend further the systematic study to include all the low index surfaces of Al. We found that the coordination modes of O-atoms and the dependency of these coordination modes with increasing coverage of O-atoms differs significantly for the three surfaces. Up to 1 ML, for Al(100) and Al(110) forming clusters and stripes is more favorable than forming a homogeneous coverage of O-atoms while for Al(111) after 0.25 ML of O-atoms it is more favorable to form homogeneous distributions of O-atoms. These findings together with the observed tendency to form different oxide structures already at these coverages, indicate that these surfaces can form oxide films with different amounts of defects and roughness, parameters that ultimately will affect the quality of the oxide films.

2. Computational details

The density functional theory (DFT) calculations were performed with the Vienna ab initio simulation package⁵⁰ (VASP 5.4.1) with the exchange–correlation functional by Perdew–Burke–Ernzerhof, PBE (ref. 51 and 52) with ultrasoft pseudopotentials of the projector augmented wave^53,54 (PAW) type. The supercells with periodic boundary conditions were composed of Al slabs with thicknesses of five layers along the direction perpendicular to the surface for Al(100) and Al(110), and seven layers for Al(111). Vacuum layers of 24 Å were used for all cases making supercells with 80 atoms for Al(100), 80 atoms for Al(110) and 112 atoms for Al(111). The reactions with oxygen were investigated at one of the surfaces of the slabs with a periodicity of p(4 × 4). During geometry optimization the three top layers of Al atoms as well as all adsorbates were allowed to relax while the two bottom layers of Al atoms were kept fixed. For the geometry optimization, a plane wave cutoff energy of 500 eV and a k-point mesh of (4 × 4 × 1) in the Monkhorst–Pack sampling scheme⁵⁵ were used together with Gaussian smearing with a width of 0.2 eV. The cutoff energy was increased to 900 eV for the computation of the single point energies after geometry optimization.

The adsorption energies reported herein are defined as follows

ΔE_ads = E_{adsorbate/slab} − (E_adsorbate + E_slab) (1)

where E_{adsorbate/slab}, E_adsorbate and E_slab, represent the electronic energies in gas phase for the adsorbate bound to the Al slab, free adsorbate and bare Al slab respectively. A more negative value for the electronic adsorption energy implies stronger adsorption. All values for adsorption of O-atoms are normalized per adsorbing O₂ molecule, that is, per two surface bound O-atoms.

The convergence criterion used for the self-consistent field (SCF) electronic energy was 1 × 10⁻⁴ eV. For the computation of the dissociative adsorption of O₂ that leads to the adsorption of 2 O-atoms, the supercells used with symmetry p(4 × 4) produce values for ΔE_ads per O-atom that differ at most 0.200 eV when compared to results obtained with p(8 × 8) supercells. Similarly, the k-point mesh used produces values that differ at most 0.021 eV from a k-point mesh of (12 × 12 × 1). In what concerns the thicknesses of the slabs employed, the same ΔE_ads per O-atom differs at most by 0.050 eV when compared to values obtained with slabs with thicknesses of seven layers for Al(100) and Al(110), and nine layers for Al(111). Tests of the van der Waals corrections using the empirical dispersion correction scheme (D3) as implemented in VASP were done.⁵⁶ The geometries optimized with PBE-D3 are extremely close to those obtained with PBE. Similarly to what we found in a previous work for adsorption of O-atoms at the surface of Cu,⁵⁷ the dispersion component of the adsorption energy of O-atoms is very small—in the range of 0.05 to 0.15 eV—in comparison with the magnitude of the adsorption energies of the O-atoms—in the range of 5.5 to 9.5 eV. Because D3 is an empirical parameter that depends on the geometries employed in the parameterization set, and because we do not have experimental data to benchmark our results, we do not include the PBE-D3 results in the discussion because there are no guarantees that it performs better than PBE for the systems under study in this work.

3. Results and discussion

3.1. The oxide growth models

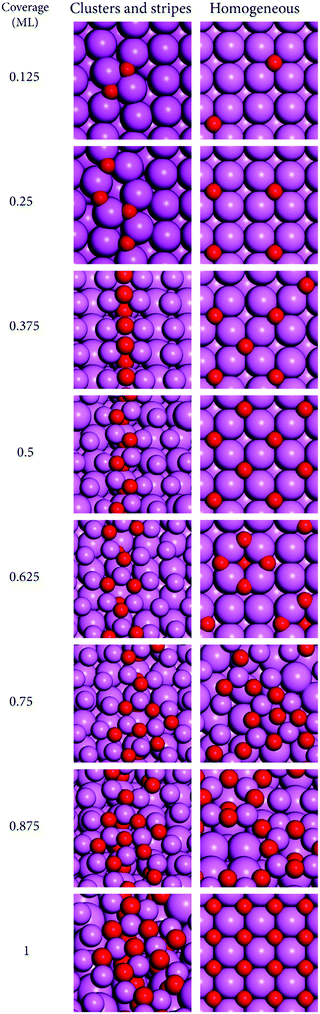
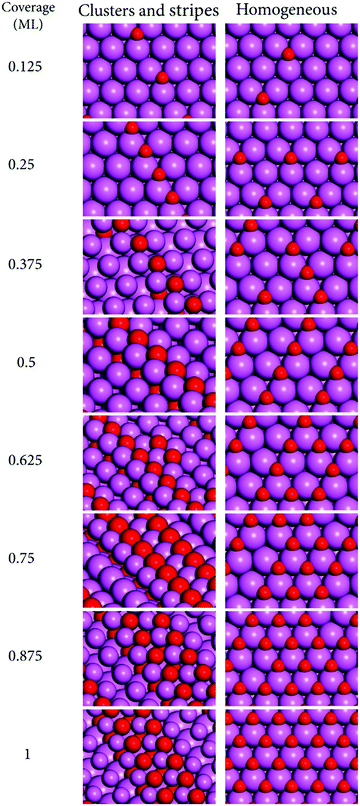
The increase in coverage of O-atoms was studied starting from the bare surfaces up to 1 ML with increments of 0.125 ML. The surface disposition of O-atoms followed two distinct models based on our previous study of the oxide growth at Al(110),³⁰ and on experimental observations for Al(111).³² These are the cluster-stripe model—where the O-atoms are placed at neighboring sites forming clusters that evolve to stripes with increasing coverage; and the homogeneous model—where the O-atoms are placed as further away as possible from each other obeying the constraints of being placed at the preferred adsorption sites. The former model leads to a lower symmetry of disposition of surface products while the latter leads to a higher symmetry. The supercells showing the bare surfaces employed in this investigation are shown in Fig. 1.

Fig. 1 The three Al surfaces employed in this study. The white boxes represent the supercells with p(4 × 4) periodicity used.

For the homogeneous model, the reactions with oxygen were investigated by placing the O-atoms at their preferred binding sites following the existing knowledge on the binding sites for single O-atoms at these surfaces, based on our and other groups’ previous studies.^20,21,30 This approach is valid to a large extent because for non-neighboring sites, even though the adsorbate–adsorbate interactions can change the reaction energies considerably and be long ranged, reaching several Å distance, the long range adsorbate–adsorbate interactions seldom change the preferences for binding sites.^58,59 These effects have been studied in our previous works and will not be discussed here with further detail. The preferred binding sites for single O-atoms are: Al(110), [short-bridge, sb]; Al(111), [fcc threefold hollow, 3fh], and Al(100), [fourfold hollow, 4fh]. For the cluster models where the O-atoms are placed at neighboring sites, however, we observed that for many of the cases the initial guesses based on the preferred binding sites for single O-atoms led to other geometries after optimization. It became clear that the co-adsorption of O-atoms affects their preferences for the surface binding sites. Given this, we performed a systematic search for the preferred binding sites for clusters of O-atoms at the low coverages of 0.125 and 0.25 ML. Those site preferences were used further in the construction of the cluster models for higher coverages. A similar phenomenon previously observed in our work for Al(110) was tackled with this approach and we were capable of obtaining structures close to “real-global minima”.³⁰ The validity of the approach was verified in that work with ab initio molecular dynamic calculations at finite temperatures, and the results obtained here agree with the modelling approach that was carefully benchmarked in that work. Following this, the results here discussed are based on the lower energy structures obtained for the two growth models constructed as detailed above.

3.2. The growth of oxides at Al(100), Al(110) and Al(111)

It can be seen that for all cases shown in Fig. 2–4 the formation of clusters that become stripes with increasing coverages leads to larger reconstructions of the surfaces than a more homogeneous disposition of O-atoms. The formation of O-atom clusters has been reported previously for Al(100) and Al(111) in experimental and computational investigations.^{13,30,32,36,37} It can be seen (Fig. 2–4) that in the cluster growth modes there is a tendency for the O-atoms to have a disposition that resembles stripes after a certain coverage has been reached. The result that the cluster growth leads to the formation of stripes had been previously obtained in our calculations for Al(110) and the finite temperature stability of this oxide growth model was there confirmed with ab initio molecular dynamics.³⁰ These structures involve the formation of Al–O bonds between the second layer of Al-atoms and O-atoms that are buried under the first layer of Al-atoms. In turn the first layer Al-atoms are bound to additional O-atoms that terminate the surface. This is visible in the stripes that form already at the low coverage of 0.375 ML for Al(100) and Al(111), and at the slightly higher coverage of 0.625 ML for Al(110). This growth mode has been observed in a recent experimental investigation for Al(111) at low coverages of O-atoms.¹³ There the authors observed that the oxide grows into the aluminum lattice beneath the islands, that exfoliate with a 10° angle relative to the bulk, forming structures similar to those shown in Fig. 4. In this mechanism the first-layer Al-atoms that are part of the stripes have increased coordination number with O when compared to the first layer Al-atoms involved in bonding with O in the homogeneous models. For low coverages, the growth of oxide via the formation of clusters or islands that grow laterally forming stripes has also been observed for Al(100) in a recent experimental investigation.¹³ In that work, the growth modes are similar to those here obtained and shown in Fig. 2. In the cluster-stripe models the coordination number of those Al-atoms becomes closer to the coordination number of Al in aluminum oxides than in the homogeneous models as it will be discussed below. This suggests that the driving force for the formation of the clusters and stripes is that these lead to coordination numbers and geometries that are closer to those of aluminum oxides. Because the vacancy formation energies at Al surfaces are lower than those at transition metal surfaces,⁶⁰ the formation of stripes of oxide that imply breaking bonds between the first and second layers of Al-atoms is more favorable for this metal than for the other metals. As such this oxide growth mechanism should be more favorable for metals with low surface vacancy formation energies. This is because of the lower energetic cost of breaking Al–Al bonds at Al surfaces than the correspondent bonds at the surface of metals with higher vacancy formation energies.

Fig. 2 Increasing coverage of O-atoms at the Al(100) surface according to two different models: formation of clusters that evolve to stripes with increasing coverage (left-hand panels); a more homogeneous distribution of O-atoms at the surface (right-hand panels). Al (), O (). The radius of some of the atoms has been reduced to ease the visualization of their environment.

Fig. 3 Increasing coverage of O-atoms at the Al(110) surface according to two different models: formation of clusters that evolve to stripes with increasing coverage (left-hand panels); a more homogeneous distribution of O-atoms at the surface (right-hand panels). Al (), O (). The radius of some of the atoms has been reduced to ease the visualization of their environment.

Fig. 4 Increasing coverage of O-atoms at the Al(111) surface according to two different models: formation of clusters that evolve to stripes with increasing coverage (left-hand panels); a more homogeneous distribution of O-atoms at the surface (right-hand panels). Al (), O (). The radius of some of the atoms has been reduced to ease the visualization of their environment.

From an energetic perspective, the formation of clusters and stripes increases the coordination number of Al-atoms to O-atoms, which leads to a considerable stabilization of the structures for the majority of the cases here studied because the bonds between Al and O are very exoergic. For Al(100) and Al(110) the energetic cost of breaking Al1–Al2 bonds (between the surface (Al1) and subsurface (Al2) layer of Al) is compensated by the formation of O–Al bonds in the clusters and stripes, making such surface structures more favorable than the homogeneous disposition of O-atoms for every coverage here studied as it can be seen in the data shown in Fig. 5. Al(111) has a turnover point already at 0.375 where the homogeneous growth becomes more stable than the formation of stripes. This is in agreement with experimental observations on the turnover point of about 0.2 ML where the formation of a homogeneous oxide becomes more favorable than the formation of clusters.³² From the three surfaces here studied, Al(111) is the surface with the highest first-layer vacancy formation energy.²³ In a previous study we have shown that for Al(110) the turnover point where the homogeneous growth becomes more favorable than the stripes occurs at 1.5 ML.³⁰

Fig. 5 Adsorption energies per dissociating O₂ molecule (ΔE_ads (eV)) that gives rise to the corresponding coverage of O-atoms at the surfaces (ML) for the two oxide growth modes here studied: clusters and stripes (), homogeneous ().

In Fig. 6 are shown the Al–O pair distribution functions (PDF) for all the geometries studied here, with a cutoff of 2.3 Å in order to include only the nearest neighbors. It can be seen that the cluster growth models tend to produce shorter Al–O bond distances than the homogeneous models. It can also be seen that the surface reconstruction driven by the growth of oxide as clusters and stripes makes the Al–O bond lengths lay closer to the range of the shorter bond lengths typical of α-alumina, 1.85 Å,⁶¹ while the homogeneous growth tends to produce Al–O bond lengths more similar to the longer bonds of α-alumina, 1.97 Å, and to the average bond lengths in γ-alumina, 1.97 Å.⁶² For the lower coverages, the formation of clusters allows the Al–O bond lengths to lay in the range of bond lengths typically found in Al₂O₃ polymorphs, while in the homogeneous models these bond lengths are larger and even outside of the range of the bond lengths found in Al₂O₃. It can be seen, by comparison of the PDF of Fig. 6 with the corresponding energy data for each structure shown in Fig. 5, that the energetically stable structures are those that have a higher frequency of occurrence of shorter Al–O bonds, in the range from 1.72 to 1.9 Å.

Fig. 6 Pair distribution functions g(r) for the nearest neighbor Al–O bonds as a function of the Al–O bond distance (r (Å)). Clusters and stripes growth models (); homogeneous growth models ().

The PDF (Fig. 6) and the energy (Fig. 5) data show that the most stable oxides at Al(110) and Al(100) surfaces are those that tend to have the shortest Al–O bonds, with distances in the range of those in bulk α-alumina, while the most stable oxides formed at Al(111) have bond lengths more resembling of those in bulk γ-alumina and other polymorphs of alumina such as β-alumina and magnetoplumbite where Al–O bond lengths are slightly lower than and greater than 2 Å.⁶³ In these two Al₂O₃ polymorphs the tetrahedral Al-atoms are undercoordinated and this agrees well with the fact that, in the homogeneous model which is the most stable growth model at Al(111) for 0.375 ML and above, the Al-atoms coordinate with O to form disordered tetrahedral structures. These Al-atoms are also undercoordinated when compared to the corresponding cluster-stripe growth models.

The fact that the formation of clusters and stripes is favored for Al(100) and Al(110) and the formation of a homogeneous layer is favored for Al(111), together with the knowledge of the vacancy formation energies and the data here obtained for the PDF, indicates that the bonds with O at Al(111) cause smaller stresses at this surface than for the two other surfaces. For low coverages this leads to the growth of a more homogeneous and less defective oxide than for the other two surfaces.

4. Conclusions

The systematic investigation of the co-adsorption of O-atoms at Al(100), Al(110) and Al(111) showed that the presence of neighboring O-atoms affects their surface binding site preferences. In this way modelling oxide growth with basis on single O-atom data should be avoided because it can lead to erroneous geometries.

Based on the results of our systematic search for preferred binding modes of O-atoms we constructed two models for the growth of oxide at these surfaces: the formation of clusters that evolve to stripes with increasing coverage and the formation of a more homogeneous distribution of O-atoms. The prevalence of each oxide growth mode is dependent on the coverage and on the surface. For Al(100) and Al(110), up to coverages of 1 ML the preferred oxide growth mode is via the formation of clusters—or islands—that evolve to stripes with increasing coverage, while for Al(111) the stripes-clusters are the preferred growth mode for coverages lower than 0.375 ML. Here there is a turnover point after which the homogeneous growth mode is preferred.

Overall the formation of clusters and stripes leads to shorter Al–O bond lengths when compared to the homogeneous growth of oxides. The Al–O pair distribution function shows that the most favorable oxide growth modes for Al(100) and Al(110) are those that lead to shorter Al–O bonds, of 1.72 to 1.9 Å, while for Al(111) the most favorable growth mode leads to larger Al–O bonds close to or larger than 2 Å. The oxides grown at Al(100) and Al(110) have Al–O bonds lengths typical of the shorter bond lengths of α-alumina while in the oxide grown at Al(111) the bonds lengths are typical of γ and β-alumina. The mechanisms here analyzed suggest that for low coverages, the oxides formed at Al(100) and Al(110) are disordered α-alumina while the oxide formed at Al(111) is less disordered γ or β alumina. However, the small energy difference between clusters and stripes and homogeneous growth for Al(111) does not exclude the coexistence of both modes, which in this case could lead to the formation of a defective or amorphous oxide.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

Financial support from the Swedish Foundation for Strategic Research (SSF, project ALUX, RMA11-0090) and from the Russian Science Foundation (grant 18-12-00366) is gratefully acknowledged. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at the PDC Center for High Performance Computing at the KTH – Royal Institute of Technology, Stockholm.

References

1. R. Westerström, C. J. Weststrate, A. Resta, A. Mikkelsen, J. Schnadt, J. N. Andersen, E. Lundgren, M. Schmid, N. Seriani, J. Harl, F. Mittendorfer and G. Kresse, Surf. Sci., 2008, 602, 2440–2447.
2. B. Jeon, S. K. R. S. Sankaranarayanan, A. C. T. van Duin and S. Ramanathan, Philos. Mag., 2011, 91, 4073–4088.
3. Y. Yang, J. Zhou, M. Nakayama, L. Nie, P. Liu and M. G. White, J. Phys. Chem. C, 2014, 118, 13697–13706.
4. R. Stumpf and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 4958–4973.
5. I. Langmuir, J. Am. Chem. Soc., 1918, 40, 1361–1403.
6. M. Schmid, G. Leonardelli, R. Tscheließnig, A. Biedermann and P. Varga, Surf. Sci., 2001, 478, L355–L362.
7. M. Kurahashi and Y. Yamauchi, Phys. Rev. Lett., 2013, 110, 246102.
8. L. Österlund, I. Zoric-acute and B. Kasemo, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 15452–15455.
9. H. Brune, J. Wintterlin, R. J. Behm and G. Ertl, Phys. Rev. Lett., 1992, 68, 624–626.
10. I. P. Batra and L. Kleinman, J. Electron Spectrosc. Relat. Phenom., 1984, 33, 175–241.
11. J. Trost, H. Brune, J. Wintterlin, R. J. Behm and G. Ertl, J. Chem. Phys., 1998, 108, 1740–1747.
12. J. Jacobsen, B. Hammer, K. W. Jacobsen and J. K. Norskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14954–14962.
13. L. Nguyen, T. Hashimoto, D. N. Zakharov, E. A. Stach, A. P. Rooney, B. Berkels, G. E. Thompson, S. J. Haigh and T. L. Burnett, ACS Appl. Mater. Interfaces, 2018, 10, 2230–2235.
14. Y. Yourdshahyan, B. Razaznejad and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 075416.
15. Y. F. Zhukovskii, P. W. M. Jacobs and M. Causá, J. Phys. Chem. Solids, 2003, 64, 1317–1331.
16. A. Kiejna and B. I. Lundqvist, Surf. Sci., 2002, 504, 1–10.
17. J. Behler, K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 115421.
18. J. Behler, B. Delley, S. Lorenz, K. Reuter and M. Scheffler, Phys. Rev. Lett., 2005, 94, 036104.
19. H.-R. Liu, H. Xiang and X. G. Gong, J. Chem. Phys., 2011, 135, 214702.
20. C. M. Lousada and P. A. Korzhavyi, Phys. Chem. Chem. Phys., 2015, 17, 1667–1679.
21. C. M. Lousada and P. A. Korzhavyi, J. Comput. Chem., 2016, 37, 787–794.
22. C. Fiolhais, L. M. Almeida and C. Henriques, Prog. Surf. Sci., 2003, 74, 209–217.
23. S. S. Gupta, M. A. van Huis, M. Dijkstra and M. H. F. Sluiter, Phys. Rev. B, 2016, 93, 085432.
24. A. Leybovich and T. Kuniya, J. Vac. Sci. Technol., A, 1993, 11, 1553–1557.
25. M. T. Greiner, L. Chai, M. G. Helander, W.-M. Tang and Z.-H. Lu, Adv. Funct. Mater., 2012, 22, 4557–4568.
26. S. V. Faleev, O. N. Mryasov and T. R. Mattsson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 205436.
27. J. K. Grepstad, P. O. Gartland and B. J. Slagsvold, Surf. Sci., 1976, 57, 348–362.
28. R. M. Eastment and C. H. B. Mee, J. Phys. F: Met. Phys., 1973, 3, 1738.
29. A. Kiejna and B. I. Lundqvist, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 085405.
30. C. M. Lousada and P. A. Korzhavyi, Appl. Surf. Sci., 2018, 441, 174–186.
31. H. Brune, J. Wintterlin, R. J. Behm and G. Ertl, Phys. Rev. Lett., 1992, 68, 624–626.
32. H. Brune, J. Wintterlin, J. Trost, G. Ertl, J. Wiechers and R. J. Behm, J. Chem. Phys., 1993, 99, 2128–2148.
33. J. Jacobsen, B. Hammer, K. W. Jacobsen and J. K. Nørskov, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 14954–14962.
34. C. Carbogno, A. Groß, J. Meyer and K. Reuter, in Dynamics of Gas-Surface Interactions: Atomic-level Understanding of Scattering Processes at Surfaces, ed. R. Díez Muiño and F. H. Busnengo, Springer Berlin Heidelberg, Berlin, Heidelberg, 2013, pp. 389–419.
35. E. V. Chulkov and I. Y. Sklyadneva, Surf. Sci., 1995, 331–333(part B), 1414–1421.
36. L. C. Ciacchi and M. C. Payne, Phys. Rev. Lett., 2004, 92, 176104.
37. D. E. Oner, H. Ternow, R. Chakarova, B. Kasemo and I. Zorić, Surf. Sci., 2002, 512, L325–L330.
38. N. Cai, G. Zhou, K. Müller and D. E. Starr, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 125445.
39. C. Lanthony, J. M. Ducéré, M. D. Rouhani, A. Hemeryck, A. Estève and C. Rossi, J. Chem. Phys., 2012, 137, 094707.
40. A. Kiejna and B. I. Lundqvist, Surf. Sci., 2002, 504, 1–10.
41. U. Memmert and P. R. Norton, Surf. Sci., 1988, 203, L689–L694.
42. H. A. Duarte and D. R. Salahub, J. Chem. Phys., 1998, 108, 743–756.
43. K. Aleksander, J. Phys.: Condens. Matter, 2014, 26, 053001.
44. H. Mei, Q. Liu, L. Liu, X. Lai, W. She and P. Zhai, Appl. Surf. Sci., 2015, 324, 538–546.
45. G. Pilania, B. J. Thijsse, R. G. Hoagland, I. Lazić, S. M. Valone and X.-Y. Liu, Sci. Rep., 2014, 4, 4485.
46. J. D. Osorio, J. Giraldo, J. C. Hernández, A. Toro and J. P. Hernández-Ortiz, Heat Mass Transfer, 2014, 50, 483–492.
47. T.-S. Shih and Z.-B. Liu, Mater. Trans., 2006, 47, 1347–1353.
48. J. D. Baran, H. Grönbeck and A. Hellman, Phys. Rev. Lett., 2014, 112, 146103.
49. E.-G. Kim and J.-L. Brédas, Org. Electron., 2013, 14, 569–574.
50. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
51. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
52. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1997, 78, 1396.
53. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
54. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
55. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
56. S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465.
57. C. M. Lousada, A. J. Johansson and P. A. Korzhavyi, J. Phys. Chem. C, 2015, 119, 14102–14113.
58. Y. Tiwary and K. A. Fichthorn, Surf. Sci., 2011, 605, 1391–1396.
59. C. M. Lousada, A. J. Johansson and P. A. Korzhavyi, ChemPhysChem, 2018, 19, 2159–2168.
60. H. M. Polatoglou, M. Methfessel and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 1877–1883.
61. N. Ishizawa, T. Miyata, I. Minato, F. Marumo and S. Iwai, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 228–230.
62. L. Smrcok, V. Langer and J. Krestan, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2006, 62, i83–i84.
63. T. R. Wagner and M. O'Keeffe, J. Solid State Chem., 1988, 73, 211–216.

---