Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Manipulating molecular order in nematic liquid crystal capillary bridges via surfactant adsorption: guiding principles from dissipative particle dynamics simulations†
Zeynep
Sumer
 and
Alberto
Striolo
and
Alberto
Striolo
 *
*
Department of Chemical Engineering, University College London, London WC1E 7JE, UK. E-mail: a.striolo@ucl.ac.uk
First published on 20th November 2018
Abstract
The ability of liquid crystals (LCs) to change orientational order is used in applications, ranging from sensors to displays. The aim of this work is to computationally investigate how surfactant adsorption on cylindrical LC bridges can be used to control such orientational order. Building from classical fundamental lessons, understanding the ordering of mesogens along a preferred axis with the help of molecular modelling contributes to investigations of systems that could be a platform for LC-based sensing applications. The coarse-grained dissipative particle dynamics (DPD) simulation method is implemented here, because it allows us to quantify the effect of molecular features on the properties of meso-scopic systems containing LC bridges, an aqueous solvent, and surfactants at various concentrations. Three surfactant types are modelled with short, medium, and long tail lengths, respectively. All surfactants adsorb at the LC–water interface. It is found that the length of the surfactant hydrophobic tail determines the effectiveness by which the LC order is affected. Short tails are not as effective as long ones. Surfactants with long tails affect the LC order, but, in agreement with experiments, predominantly only within a short distance from the LC–water interface. For these surfactants, the surface density at the LC–water interface is an important knob that can be used to control the order of the LCs. As the effective LC–surfactant interactions change, so does the distribution of the surfactants at the interface. Consistent with theoretical expectations, the results presented here elucidate the effect of molecular features on the anchoring mechanism between surfactants and mesogens within cylindrical bridges dispersed in aqueous systems and could be helpful for designing novel surface-active compounds in the development of advanced sensing devices based on LCs.
1. Introduction
Liquid crystals (LCs) continue to receive significant attention due to their tunable orientation. LCs can be used in various applications such as optoelectronics devices and biosensors. LCs are mesophases, between crystalline solids and isotropic liquids.1 In general terms, LCs are classified in two categories: lyotropic and thermotropic. At high temperatures, thermotropic LCs exhibit isotropic liquid phases, with no positional or orientational order. As the temperature decreases, the phase changes from isotropic to nematic. The nematic phase is the most common phase of LCs, in which LCs exhibit an orientational order. As the temperature is lowered further, LCs yield smectic phases with both orientational and positional ordering; the solid crystalline phase is obtained at very low temperatures.1,2Applications in which LCs are utilized build on the ability of controlling the orientation of mesogens with respect to a direction vector. Controlled alignment enables the potential applications of LCs in optical devices.3 To advance applications such as sensing and displays, it is required to detect and control, respectively, changes in LCs’ order due to external stimuli. To control LCs’ order, it is possible to use light,4–6 temperature,7 or adding amphiphiles to systems in which LC–solvent interfaces are present.3,8 One example of the latter approach is provided by the interface between thermotropic LCs and immiscible aqueous phases.9 For such systems, one fundamental question of wide interest concerns how mesogens anchor at the LC–water interface, in the presence or absence of surfactants. Recently, De Pablo and co-workers illustrated that the transport of water through a LC assembly can also affect anchoring.10 We are here interested in the effect of surfactants. Because surfactants adsorb at interfaces, they could affect the LCs’ anchoring. Anchoring between LCs and other molecules in an aqueous media can be used to manipulate the direction profile of LCs. Both experimental and computational studies investigated how the transition from a planar to homeotropic orientation takes place by adding surfactants. Haseloh et al. conducted dispersion polymerization experiments and found that surface anchoring is strongly dependent on the type of the mesogens and stabilizers.11 Amundson and Srinivasarao reported that the appropriate choice of polymer side groups in polymer-dispersed liquid crystal (PDLC) films enables to control anchoring without using additives.12 Their results also show that the anchoring transition temperature decreases as the chain length decreases.
LCs’ aggregates such as spherical droplets,13–20 flat surfaces9,12,21–25 or cylindrical formations (capillaries and bridges)26–30 have been investigated. Kim et al. quantified the optical, structural and topological features of tetrapodes assembled in flat layers, round capillaries and spherical droplets; the results for round capillaries revealed different textures depending on the inner diameter and system temperature.28 In the experimental observations, two tubes having 50 μm and 150 μm inner diameters were used; it was reported that LCs within narrow capillary tubes exhibit defects below a transition temperature, whereas LCs within the wider capillary tubes preserve smooth texture. Williams et al., investigated capillary tubes filled with nematic LCs to study topological singularities, and reported that orientation of LC molecules is sensitive to surface conditions.31 The same group also demonstrated how to tune nematic director fields using surface-alignment agents in cylindrical capillary tubes.32 It was found that the minimum energy corresponds to a nematic phase with perpendicular anchoring, with the LCs at the core of the cylindrical structure showing orientation parallel to the cylinder axis.33 Using experiments34 and theoretical calculations,35 Meyer showed that external stimuli can affect the topological singularity. It should be noted that theoretical calculations such as those reported by Meyer are based on continuum mechanics, and are effective in identifying the macroscopic properties of matter; on the other hand, molecular simulations can provide complimentary information, as they allow investigators to probe how the structure and dynamics of individual molecules depend on their interactions with the surroundings.
In a recent study, Busch et al. concluded that a thermal-history independent phase behaviour of ferroelectric LC 2MBOCBC can be achieved by using polymer coated walls in cylindrical nanopores.36 The pioneering studies concerning nematic LC alignment in cylindrical structures focused on homeotropic anchoring, and defined the escaped radial structure (ER).37 ER is the shift of direction vector from parallel to perpendicular with respect to the cylindrical axis due to the presence of external structures, such as a cylindrical confining wall or surface agents.32 Later, Ondris-Crawford et al. showed that the strength of interactions, i.e., surface coupling, between the cavity wall and the LC molecules increases with the length of LC molecules.37 Recently, Ellis et al. investigated topological defects on waist-like and barrel-like bridges with respect to their aspect ratios.27 They concluded that the aspect ratio determines ring and point defects. Their observations elucidated the role of shape and elasticity in dictating the LC structure in confined homeotropic nematic phases.
This brief overview demonstrates the importance of understanding LCs’ anchoring. In short, molecules at the LC/water interface contribute to orient the mesogens, starting from the interface, but also within inner regions, and eventually across the whole LC structure system.25 Simulations, in which the effective attraction between surfactant tails and LCs was increased systematically,24,25 have been conducted to better understand this observation.
Our understanding of LC structures builds from continuum theoretical calculations,35,38 which can identify driving forces and general guiding principles. Complementarily to such analysis, computational modelling and simulations, at the molecular scale, offer the opportunity of revealing how the details of the molecular compounds in LC-containing systems could affect macroscopic observables. Coarse-grained simulation methods have attracted interest in the investigation of LC anchoring due to relatively large time and length scales that they can probe. Zhang and co-workers39 developed different coarse-grained models representing 5CB molecules. Using these models, Zhang and co-workers were able to obtain isotropic–nematic transitions as well as diffusion coefficients. One of their models successfully reproduced experimental results for the nematic phase of 5CB at 300 K and 1 atm. The simulated density was 1.003 g cm−3, orientational order was calculated as 0.48, and the nematic-to-isotropic transition temperature was obtained at 305–310 K. The corresponding experimental data are 1.02 g cm−3, 0.54, and 306.7–308 K, respectively. Although the simulated diffusion coefficients were larger than experimental values, they provided a better match than atomistic simulations. In another coarse-grained study, the structural properties of self-assembled surfactant aggregates were investigated at the LC/water interface. Depending on the LC–surfactant tail affinity, it was possible to detect ‘condensed amphiphile monolayers’, and, above a critical surfactant coverage, LCs’ homeotropic anchoring was induced, in agreement with experiments.24
One coarse-grained simulation method that is attracting vast interest in materials modelling and simulation is dissipative particle dynamics (DPD).40,41 DPD is a coarse-grained simulation technique that allows researchers to achieve longer time and larger length scales, in some cases approaching experimentally-relevant conditions.42,43 DPD has been extensively used for studying soft materials, such as copolymers,43–45 nanoparticles,46–48 surfactants,49–53 and liquid crystals.25,54,55 The results of these simulations are in general consistent with experiments, and sometimes explain phenomena that are hard to observe with experimental techniques alone. Al Sunaidi et al.54 used DPD to study the phase transitions encountered by rod-like molecules, and described the conditions at which isotropic, nematic, smectic A and crystalline phases are stable. Zhang and Guo25 studied the interactions between LCs and amphiphilic rod–coil polymers in an aqueous environment. Their parametric study showed the effect of soft potential coefficients to the anchoring of LCs. Inokuchi and Arai55 studied LCs, water, and surfactants confined in a spherical geometry. They studied the self-assembly with respect to temperature and surfactant concentration. In all the DPD studies just summarized, the parameters that were systematically changed were either temperature or soft repulsion coefficients, and the target of the investigations was the anchoring between LCs and amphiphilic polymers.
The present study implements DPD to study cylindrical LCs formations dispersed in water, in the presence of surfactants. Because of computational limitations, the cylindrical structures considered are effectively infinitely long (see Section 2). As a consequence, the resulting probe regions are away from the basal terminations of the LC cylinders. In most cylindrical formations studied, LCs are injected to capillary tubes with the addition of amphiphiles such as lecithin26,28 and N,N-dimethyl-N-octadecyl-3-aminopropyl-trimethoxysilyl chloride (DMOAP)29 to induce homeotropic anchoring of LC molecules with tube walls. The system modelled here allows us to systematically investigate the effect of surfactant morphology on LC anchoring on a curved interface, without the presence of a tube.
Three different rod–coil amphiphiles are modelled. These amphiphiles have the same length, but they have different hydrophobic tail lengths: short, moderate, and long, respectively. The results show that varying the number of hydrophilic coils and hydrophobic rods in our simple surfactant model can largely affect LCs’ anchoring. When the surfactant density at the interface is high enough, phase segregation of surfactants at the interface causes the mesogens to shift from planar to homeotropic anchoring. Such transition is short-ranged in most of the systems considered here. However, our parametric analysis showed that a small decrease in the repulsion parameter that describes surfactant tail–LC interactions is sufficient to cause changes in mesogen orientation throughout the tube, which is in general agreement with literature results obtained at flat LC–solvent interfaces.
The remainder of this manuscript is organized as follows: in Section 2 we describe the models and algorithms implemented in the study. In Section 3 we discuss representative results. In Section 4 we summarize our main observations, and we comment on their possible relevance for practical applications and future research.
2. Computational details
2.1 Molecular models
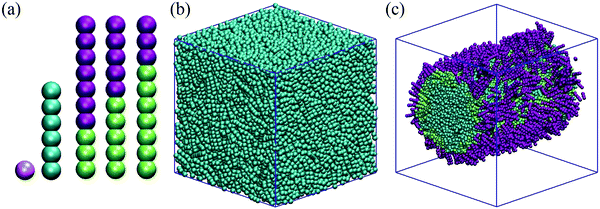
We implement here a model inspired by the work of Zhang and Guo.25 These authors prepared a coarse-grained model composed of mesogens, rod–coil amphiphiles and water molecules, which is suitable for DPD simulations. The coarse-grained models are schematically shown in Fig. 1(a). All simulations in this work are conducted in water, unless otherwise stated. Building on our prior simulations for surfactant systems,53,56,57 one water bead (W) represents five water molecules. It should be noted that in the coarse-grained model implemented here, electrostatic effects and hydrogen bonds are not considered. Some of the experimental properties of bulk liquid water were considered in the original derivation of the DPD parameters.58We consider three amphiphiles (surfactants). Each surfactant molecule (S) is composed of 10 beads, connected to form a chain; the head-group represents the coil block and the tail-group represents the rod block of each surfactant. Hydrophilic surfactant heads are indicated as Shead, whereas hydrophobic surfactant tails are identified as Stail. While all surfactants considered are composed of 10 beads, the number of beads assigned to head- and tail-groups distinguishes the various surfactants. The three surfactants are characterized by: Shead/Stail = 7/3, 5/5 and 3/7 as can be seen in Fig. 1(a).
It has been reported previously that the length of the surfactant head-group does not measurably affect the overall orientation of LCs.8 Our simulations show that the overall length of the surfactants affects the time required for achieving lateral phase separation among the surfactants adsorbed at the LC–water interface, but that the head-group length does not significantly affect LCs’ orientation. To test whether this was the case even in our system, we simulated three systems with 1000 surfactant molecules, in which the surfactant Shead/Stail beads are 3/5, 7/5 and 5/7, respectively. It was found that the surfactant models with the same tail length gave similar results, despite of differences in the head-group length, as shown in the ESI.† Therefore, throughout this paper we focus on changes in anchoring with respect to tail-length by keeping the overall surfactant length at 10 beads.
The liquid crystal molecules (LCs) considered here are composed of 6 beads connected in a rod-like arrangement. A harmonic spring is defined for surfactant beads and LC beads. Bond potential Ebond = kbond × (r − r0)2 and bond bending potential Eangle = kangle × (θ − θ0)2 are used, where r0 is 0.6 and θ0 is 180°. The kbond and kangle parameters are defined in two different ways: to preserve the rigidity of rod-like LCs and surfactant tails, both kbond and kangle are defined as 100kBT/rc2 for every consecutive bead. For the surfactant head, different kbond and kangle are set: 50kBT/rc2 and 30kBT/rc2, respectively. The stiffness was considered lower for the surfactant head beads to allow them with some flexibility.
2.2 Simulation details
The simulations were conducted using the dissipative particle dynamics (DPD) algorithm.58 The LAMMPS software package was utilized.59 All simulations are performed in the NVT ensemble. All simulations are run for 3 × 106 steps, with integration time Δt defined as 0.01τ. The DPD time scale was calculated by using simulated water self-diffusion coefficient Dsim = 0.0123Rc2/τ, as explained elsewhere.60 Each system was simulated for 0.447 μs, with the last 0.149 μs used for data analysis. To ensure reproducibility, each system was simulated twice, with different initial configurations. Test simulations were conducted in the NPT ensemble. For these simulations, the system with lower pressure (95% of that observed in the system containing only water, 23.0kBT/rc3, at the same temperature and density, 3 beads/rc3) obtained at the end of NVT simulations was chosen. NPT simulations were conducted for 0.149 μs, during which time the simulation box size changed from 30 × 30 × 30rc3 to 29.78 × 29.78 × 29.78rc3 (the correspondent density increased from 3 to 3.07 beads/rc3). This change in box size was considered negligible, and all subsequent simulations were conducted in the NVT ensemble. Additional details regarding the various simulated systems are reported in the ESI.†Full details of the DPD simulation methodology can be found elsewhere.42,50,58 In DPD, the positions and momenta of the beads present within a simulation box are updated along a series of discrete time steps. One important feature of DPD is that the bead–bead interaction potentials are ‘soft’, which allows researchers to probe length and time scales that are approaching experimental ones.42 The outcome of DPD simulations depend strongly on the parameterization, and in particular on self-repulsion parameters (αii) and inter-species repulsion coefficients. To determine such parameters, we followed the protocol proposed by Groot and Warren.58 They concluded that αii = 75kBT/ρ is representative of soft interactions in an aqueous environment. Because the density chosen here is 3, αii is defined to be 25 among same beads. Other repulsion coefficients are set as follows: αLC–Stail = αW–Shead = 25 and αLC–W = αLC–Shead = αW–Stail = αShead–Stail = 50.
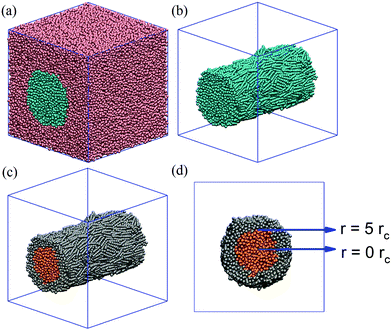
Initial configurations of simulation boxes are prepared by simulating the system at reduced temperature 1.0kBT and with repulsion coefficient set to 25.0 between LC and surfactant tail, as schematically shown in Fig. 1(c). The friction coefficient and the random force which are related by the equation σ2 = 2γkBT, were taken as γ = 4.5 and σ = 3, respectively.58 Pure LC simulations are run in a 20 × 20 × 20rc3 simulation box, whereas simulations for LC–surfactant interaction are run in a 30 × 30 × 30rc3 simulation box. Periodic boundary conditions are applied in all directions. In each simulation, 3000 LC molecules are used. Within the systems and conditions investigated in this work, 3000 mesogens were sufficient to yield a cylindrical structure that spans the length of the simulation box. In our initial configurations, the LC molecules are arranged in a cylindrical bridge that spans the entire length of the simulation box along the x-axis. Because the periodic boundary conditions are applied in 3 dimensions, the LC cylinder is effectively infinitely long. This allowed us to investigate the effect of surfactants on LC anchoring within a curved interface, while allowing for relatively easy analysis of results such as density profiles and also removing steric constraints on both mesogens and surfactant aggregates. The basal terminations of the LC cylinders are not included in this study.
It is envisioned that surfactants could be used to stabilize aqueous dispersions of LCs. Different amounts of surfactant molecules are used to investigate the effect of surface coverage. We started with 1000 surfactant molecules (55% coverage) and then increased to 1500 (80% coverage). Surface coverage is calculated by estimating the amount of beads required to cover the surface of a cylinder with radius 10rc and length 30rc, based on similar studies in the literature.24,25 Mahajan and co-workers noted that LC bridges in a nematic phase act as an ordinary Newtonian liquid bridge, which might collapse above a certain length-to-diameter ratio.61 In our simulations this collapse is prevented by using a very low ratio of length-to-diameter, by the fact that gravity is not considered, and by the fact that periodic boundary conditions effectively stabilise the bridges.
Note that in our simulations all surfactants are adsorbed at the LC–water interface. The remaining parts of the simulation box are filled with water beads.
2.3 Algorithms
The orientational order parameter (S) is a quantitative alignment tensor that characterizes the distribution of the LC molecules of a certain volume.62 This orientational order parameter can be obtained by taking the ensemble average of the traceless second-rank tensor, Q:63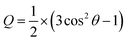 | (1) |
3. Results and discussion
3.1 Bulk liquid crystals
The purpose of this work is to investigate the dependency of LC anchoring to the length of hydrophobic rods in model surfactants. The first required step is to determine the simulation temperature at which bulk LCs undergo the isotropic-to-nematic phase transition. We conducted bulk simulations at different temperatures in the 0.1–1.0kBT range. At each temperature, we computed the order parameter (S). The results are shown in Fig. 2. The results clearly show that in the 0.8–1.0kBT temperature range, the LCs are in an isotropic phase, as expected because of the high temperature. Under these conditions the S parameter varies within the 0.00–0.02 range.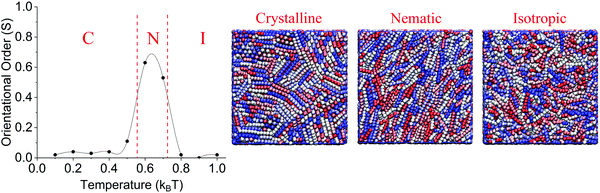 | ||
| Fig. 2 Orientational order parameter (S) of bulk LC vs. scaled temperature and snapshots of LCs in crystalline (C), nematic (N) and isotropic (I) phases. Line between data points is guide to eye. | ||
As the simulated temperature is decreased, the results show an increase in the order parameter S in the 0.6–0.7kBT temperature range, where S becomes 0.63 and 0.53, respectively. These results indicate that the LCs are in the nematic phase under these conditions.
When the temperature is reduced further, below 0.6kBT, a solid phase is observed. The results in Fig. 2 show low values for the order parameter S (between 0.02–0.11). However, analysis of simulation snapshots indicate that the LC molecules in the bulk yield small grains that are locally aligned, but dis-aligned with respect to each other. The relative disorder between different grains yields the overall low S.
The results from the bulk simulations show that in the 0.6–0.7kBT temperature range, the LCs are in the nematic phase. We select the highest of these temperatures for our subsequent simulations, so that the LCs can show orientation order, yet the individual molecules have significant thermal energy to allow the system to escape from metastable states.
3.2 Liquid crystal bridges in water
We prepare our model for a cylindrical LC bridge immersed in water, and we conduct simulations at 0.7kBT. The goal of these simulations is to ensure that the model is suitable to replicate the experimental expectations, as well as to prepare the reference system for assessing quantitatively the effect of surfactant adsorption on LC order. One representative simulation snapshot for the LC/water system (no surfactant present) is shown in Fig. 3(a). The simulation results show that the mesogens are aligned parallel to the cylindrical axis, exhibiting an order parameter S equal to 0.70. The LC cylinder is shown in Fig. 3(b). In summary, our control simulations at 0.7kBT showed that (i) LC molecules exhibit nematic alignment within the mesogen cylindrical formation dispersed in water (no other chemical is present), (ii) planar anchoring is observed at the interface between the LCs and water. All subsequent simulations are conducted at 0.7kBT.To quantify changes in the LC order within the cylinder, we arbitrarily divided the cylindrical LCs into two regions, shown with different colours in Fig. 3(c) and (d): the ‘core’ region is composed of mesogens within a radius of 5rc from the centre of the cylinder; the ‘shell’ region comprises those mesogens found within a radius from 5 up to 12rc from the centre. Note that the outer radius changes for the various simulations because as different surfactants are introduced, the shell region can expand slightly up to 12rc.
3.3 Effect of surfactant adsorption on LC orientational order
Starting from the base case discussed in Fig. 3, we systematically investigate the effect of surfactant adsorption on LC anchoring. A representative simulation snapshot is shown in Fig. 1(c). Unless otherwise noted, the interaction between LC and surfactant molecules is described by αLC–Stail = 25, and the repulsion parameter is chosen identical to the self-repulsion parameter, αself = 25. The surfactants considered have different tail lengths, as shown in Fig. 1(a). The number of Stail beads is increased from 3, 5 and 7, respectively. Note that the total number of beads per surfactant molecule is always 10, thus the number of beads in the head-groups reduces from 7, to 5, to 3, respectively, for the three surfactants simulated. The results obtained when the three surfactants are adsorbed at the LC–water interface are shown in Fig. 4. In these simulations, the number of surfactant molecules are 1000, which yields an overall surface coverage of ∼55%. The surface coverage is estimated following the procedure discussed in Section 2.2.The results shown for the surfactants with 3 beads in the tail-groups are shown in Fig. 4(a). Visual inspection of multiple simulation snapshots (∼100 per simulation run, separated from each other by 104 time steps) reveals that the surfactants are aligned homeotropically (perpendicularly to the interface). The surfactant tail lengths are too short to penetrate into the LCs. The overall order parameter of LCs is calculated as 0.63 ± 0.02, which is slightly lower than S found in the control simulation of Fig. 3(a) (0.70). In the core of the LC cylinder, orange in Fig. 4(d), LCs exhibit S ∼ 0.64 ± 0.03, whereas in the shell region S ∼ 0.63 ± 0.02. These results show that the addition of the surfactants with 3 beads in their tail-groups do not affect the orientation of the LCs. In addition, LC molecules are found to preserve planar anchoring.
As the number of beads in the tail-groups of the surfactants is increased from 3 to 5, the orientation of the mesogens at the shell region starts to shift from planar to homeotropic, as can be seen in Fig. 4(b and e). Although the surfactant tails are shorter than the LC molecules, they interpenetrate the LCs and affect their orientation. Within the bridge, the overall S decreased to 0.49 ± 0.03. Analysis of the order within the cylindrical bridge, Fig. 4(e), shows that, at the core, S equals ∼0.57 ± 0.05, suggesting that the LCs within a radius rc of 5 are not affected by the surfactant molecules. At the shell region, S decreases to 0.43 ± 0.03.
Similar results are observed in Fig. 4(c and f) when the surfactants have 7-bead-long tails, in which case the overall order parameter decreases to 0.38 ± 0.04. Although in this case the surfactant tail-groups are longer than the LCs, the mesogens at the core are not affected by surfactant adsorption at the surface. The results show that while at the core S remains 0.53 ± 0.05, in the shell it sharply decreases to 0.27 ± 0.04 (see Fig. 4(f)). These data suggest that, compared to the results obtained for shorter LCs, either more LCs shift from planar to homeotropic, or the same number of LCs shift orientation, but orient in a perfectly perpendicular direction with respect to the cylindrical axis.
Analysis of the simulation snapshots reveals a perhaps unexpected observation: the surfactants adsorbed at the LC–water interface are not homogeneously distributed on the surface. Instead, they segregate. As a consequence, the LCs near the surfactants are perpendicular at the interface, while the LCs near the water beads remain parallel to the interface. Such distribution of the surfactants is attributed to the lateral phase separation of the amphiphiles at the LC–water interface. When LCs are in a nematic phase, they present elastic properties that have been shown to be able to affect the properties of interfaces, in some cases leading to new phases and phase separations.22,64 Our results suggest that perhaps the elastic energy stored in the LCs causes the surfactants to undergo a lateral phase separation. In addition, Moreno-Razo et al.17 showed that packing of LC molecules at the interface is affected by nearby surface accumulation of other agents. Changes in the surfactant density at the interface are also expected to yield changes in energetically favourable sites, and as a result it is possible that LCs are packed differently due to the local surfactant concentration. Our results, combined with those in the literature, suggest that cooperative phenomena take place at the LC–water interface in the presence of surfactants: nematic LC phases trigger the lateral phase separation of amphiphiles, while amphiphiles, at a large enough local concentration, trigger the homeotropic alignment of LC molecules near the interface.
3.4 Effect of surfactant surface density
To quantify the effect of surfactant surface density on LCs’ anchoring, we conducted simulations similar to those described in Section 3.3, but we increased the number of the surfactant molecules to 1500. This yields a surface coverage of ∼80%. The results are summarized in Fig. 5. As the surfactant concentration is increased compared to the simulations discussed in Section 3.3, lateral phase separation is also observed. As a result, the morphology of the cylindrical LCs appears to be slightly deformed, simply as a consequence of the uneven surfactant distribution.One similarity with the systems described above is that LC molecules located at the core are not affected by the interactions with surfactant molecules. Therefore, we concluded that, within our model, the surfactant effect on mesogen order is short-ranged, mostly driven by steric interactions.
In Fig. 5(a and d), the results are shown for surfactants with short tail-groups (3 beads). Overall, S is found to be ∼0.59 ± 0.03, and it appears to be similar in the core and shell regions (0.62 ± 0.03 and 0.58 ± 0.03, respectively). These results show that the surfactants with short tails considered here do not affect the order of the mesogens even though their concentration is rather high. This observation changes when the surfactants with longer tail-groups are considered. Simulation snapshots for the LCs at contact with surfactants with tail-groups of 5 beads are shown in Fig. 5(b and e). Visual inspection reveals that that LC orientation is affected by the surfactant. The over-all order parameter S decreases to 0.43 ± 0.04. As seen in Fig. 5(e), while LCs at the core preserve high order with S = 0.60 ± 0.04 and LCs at the shell region show S = 0.32 ± 0.06. The effect is more pronounced when the surfactants with tail-groups of 7 beads are considered. The results are visualized in Fig. 5(c and f). At this 80% surfactant coverage, the overall order parameter S decreases to ∼0.25 ± 0.03. We note that S in the shell region becomes 0.05 ± 0.03, while the order in the core region is preserved (S ∼ 0.57 ± 0.04). The results for the order parameter, corroborated by visual inspection, show that at this surface coverage, the surfactants with tail-groups of 7 beads cause almost all LC molecules in the shell region to assume homeotropic alignment.
3.5 Effect of LC–surfactant interactions
As discussed above, the simulation results obtained here, as well as the results in the literature, suggest that there is a cooperative effect between surfactants and LC molecules, which determines both the distribution of the surfactants on the LC bridge and the anchoring of the mesogens. Because it is possible that the lateral phase separation between surfactant aggregates affect LC anchoring, we conducted a parametric study in which we reduce the repulsion between mesogens and surfactant tails. The correspondent repulsion parameter is decreased to αLC–Stail = 20. This decrease in repulsion, to a value lower than the self-repulsion parameter, 25, could be representative of coarse-grained models used to describe the self-assembly of ionic LCs and their interactions with ionic surfactants.65,66 Although coulombic interactions are not taken into consideration explicitly in our simulations, the effective attraction between surfactant tails and LCs is meant to reproduce, qualitatively, the combined effect of multiple interactions. Once αLC–Stail = 20, it is expected that the surface segregation evident from the snapshots shown in Fig. 4 and 5 is weakened. For this study we only consider systems with 1000 surfactants. The results are summarized in Fig. 6. For all surfactants considered, the results show a homogeneous distribution on the LCs. The simulation snapshots also reveal that once the repulsion between LCs and surfactant tail-groups has been reduced, the change in the mesogen order becomes longer ranged. In fact, the LCs at the core shift their orientation, which becomes isotropic. We now discuss the results for each of the three architectures considered for the surfactants.In Fig. 6(a and d), the results are shown for the surfactants with tail-groups of 3 beads. The overall order parameter S is found to be ∼−0.03 ± 0.03. This negative second order tensor (Q) indicates that the mesogen molecules are oriented almost perpendicularly with respect to cylindrical axis, as explained in eqn (1). The mesogens within the core yield S ∼ −0.06 ± 0.04, while those in the shell S ∼ 0.00 ± 0.03.
We observed a similar trend for the surfactants with 5 beads in their tail-groups (Fig. 6(b and e)): overall S is −0.14 ± 0.02. Orientational order in Fig. 6(b) has a slightly lower value than in Fig. 6(a), due to relatively longer surfactant tail-groups. For this surfactant, the results show that the order for the mesogens in the core (S ∼ −0.12 ± 0.04) is similar to that for the mesogens in the shell (S ∼ −0.16 ± 0.01), which suggests that the range of interaction between the surfactants adsorbed on the LC bridge and the mesogens is large enough to affect equally all mesogens within the cylinder.
The results obtained for the surfactants with 7 beads in their tail-groups are shown in Fig. 6(c and f). The results show that, in addition to affecting the order of the mesogens, the surfactants also affect the shape of the cylindrical droplet. The overall, core and shell order parameters are ∼−0.18 ± 0.03, 0.04 ± 0.05, and −0.31 ± 0.02, respectively. Due to the length and rigidity of surfactant tail-groups, and because the surfactants cause homeotropic order for the LCs, the original cylinder is deformed into a triangular prism by the adsorption of the surfactants. Presumably, the deformation prevented us from observing long-range interactions between surfactants and LCs at the inner region of the cylinder.
Parametric studies such as those discussed in Fig. 6 could be extended to consider various surfactant–LC interactions, and also the effect of branching in the surfactant molecule. While this is beyond the scope of the present manuscript, we point out that previous studies show that branching affects the orientation of LC molecules.8,9
3.6 Orientation of LCs with respect to surfactant density and radius
To further quantify the mesogens order as a function of surfactant architecture and density, we analysed the second-rank tensor of each mesogen within the LC bridge. The results are shown in Fig. 7, where we distinguish LCs based on their orientations: mesogens with an order parameter S in the range of −0.5 to 0.0 are defined ‘homeotropically aligned’; 0.5–1.0 as ‘in planar alignment’; 0.0–0.5 as ‘tilted’. When there is no surfactant in the system, the S distribution is shown as black bars. In this system, 5% of the mesogens are homeotropically aligned; 17% are tilted; the vast majority, 78%, are ‘in planar alignment’.When 1000 surfactants are present, the results (Fig. 7(a)) are shown in red, blue, and green bars for surfactants with 3, 5, and 7 beads in their tail-groups, respectively. As the tail length increases, the amount of mesogens in planar alignment decreases (69%, 58% and 49%, respectively), that of homeotropically aligned LCs increases (10%, 21% and 29%), and that of ‘tilted’ LCs remains approximately constant ∼20–22%. These results show that as the surfactant tail length increases, anchoring becomes more and more homeotropic. Two reasons explain why many LCs preserve their planar orientation: (a) the LCs in the core region are not affected by surfactants, as explained above; (b) only 55% of the surface is covered by surfactants, with the LCs in the remaining surface maintaining planar anchoring.
When 1500 surfactants are present (Fig. 7(b)), the results are similar. As the tail length increases, the amount of mesogens in planar alignment decreases (65%, 54% and 42%, respectively), that of mesogens homeotropically aligned increases (12%, 25% and 40%, respectively), and that of tilted LCs decreases (23%, 21% and 18%, respectively). Our results are qualitatively consistent with the experimental results, which show that when surfactants with short alkyl chain lengths are introduced, LC molecules remain anchored parallel to the interface until the surfactant concentration is so large that the mesogens are dispersed by the surfactants.8 In addition, our simulation results suggest that when the surfactants have a sufficiently long tail-group, they can promote homeotropic anchoring of the mesogens, and that the effect increases with the surfactant density at the LC–water interface.
The results obtained when the LC–tail repulsion is decreased (αLC–Stail = 20) and 1000 surfactants are on the surface, are shown in Fig. 7(c). As the tail length increases the amount of mesogens in planar alignment decreases (16%, 12% and 12%, respectively), that of mesogens homeotropically aligned increases (65%, 75% and 77%, respectively), and that of tilted LCs decreases (19%, 13% and 11%). These results show that when the repulsion between LCs and surfactant tails is decreased below the self-repulsion parameter, LCs align with the surfactant molecules, which strongly increases the amount of mesogens with homeotropic anchoring.
Lastly, we provide structural information regarding the LC bridges. We display the order parameter S as a function of the distance from the cylindrical diameter centre, coupled with the radial density profiles obtained for the surfactant tail-groups in Fig. 8. To calculate the density of the tail-groups we consider each bead in the surfactant tail-group. In Fig. 8(a), we display the result relative to those discussed in Fig. 4. The results show that LCs possess planar orientation at r ≤ 5rc. At larger distances, surfactants interact with LC molecules, and S decreases. In general, the results in Fig. 8(a) corroborate two findings: (i) short tails do not affect the LC orientation at any part of the cylinder; and (ii) as surfactant tail length increases, LCs at the outer surface align homeotropically. The latter observation is due to the physical interaction between surfactant tail-groups and LCs molecules, as suggested by the density profiles of the surfactant tail-groups.
Results relative to those discussed in Fig. 5 are shown in Fig. 8(b). The results corroborate our previous comments, according to which increasing the density of the surfactants is effective in changing LCs’ anchoring only for those surfactants with long tails. It should be pointed out that the results shown in Fig. 8(a) and (b) are consistent with the experimental observations reported by Williams et al., who found that for LCs confined in a cylindrical geometry it is possible that the minimum energy configuration corresponds to homeotropic anchoring coupled with LCs oriented parallel to the cylinder axis near the centre of the cylinder.32
Results relative to those discussed in Fig. 6 are shown in Fig. 8(c). The results clearly show the penetration of the change into mesogen orientation due to the surfactants from the interface towards their centre. The results show that the LC order in the core region is isotropic for all surfactants considered, highlighting the importance of LC–surfactant tail interactions in controlling the behaviour of the mesogens.
4. Conclusions
Control of mesogen orientation is fundamental for further developing optical devices and sensors, among other applications that involve liquid crystals (LCs). LC anchoring could be affected by surfactant adsorption. We investigated anchoring between LC molecules within a cylindrical bridge. In our computational model, the LC bridge is effectively infinitely long, and our study focused on the lateral surface, not on the bases of the cylinder. In particular, the effect of surfactant adsorption on LCs’ anchoring was quantified, simulating surfactants of three different morphologies. Three rod–coil diblock amphiphiles were modelled, which have short, moderate, and long surfactant tails, respectively. We investigated systems in which 55% of the surface is covered by surfactants. It was found that short surfactant tails do not significantly affect the anchoring of LC molecules. On the other hand, surfactants with long tails affect LCs’ orientation, but only at a short range, in agreement with experiments. When the surface coverage was increased from 55% to ∼80%, surfactants with long tail-groups had a more pronounced effect on the number of LC molecules that changed their anchoring from planar to homeotropic. If the surfactant tail length is short, increasing surfactant density at the LC–water interface did not affect LCs’ anchoring. For all surfactants at moderate surface density, a lateral phase separation was observed for the surfactants at the LC–water interface, which causes effects on LCs’ anchoring to be non-uniform across the interface.Parametric investigations such as those considered here can be conducted to quantify the effect of many parameters that could affect LCs’ anchoring, including surfactant tail-group branching, ionic strength, etc. For example, it was discussed here how decreasing the soft repulsion between surfactant tail-groups and LCs prevented lateral phase separation from occurring and strongly affected LCs’ anchoring. It is seen that, within the conditions considered here, regardless of the interaction parameters chosen to describe surfactant tail–LC interactions, surfactants with longer tails were the most effective in promoting homeotropic anchoring at the LC–water interface.
Consistent with both expectations from continuum theories and experimental observations, the simulation results presented here quantify the effect of changes in surfactant morphology on the orientation of LC molecules. The results could guide the selection of promising surfactants for future studies on controlling homeotropic LC anchoring within a capillary bridge.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported, in part, by the Engineering and Physical Sciences Research Council (EPSRC), via grant number EP/N007123/1. Generous allocations of computing time were provided by the National Energy Resources Supercomputer Center (NERSC) and the Research Computing Platforms Support (LEGION) – University College London. The Authors acknowledge useful discussions with Dr Stefan Guldin and his group at University College London.References
- D.-K. Yang, Fundamentals of Liquid Crystal Devices, John Wiley & Sons, 2014 Search PubMed.
- S. F. Sun, Physical Chemistry of Macromolecules: Basic Principles and Issues, John Wiley & Sons, 2004 Search PubMed.
- J. Patel and H. Yokoyama, Nature, 1993, 362, 525 CrossRef CAS.
- M. Feller, W. Chen and Y. Shen, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 6778 CrossRef CAS.
- W. M. Gibbons, P. J. Shannon, S.-T. Sun and B. J. Swetlin, Nature, 1991, 351, 49 CrossRef CAS.
- N. A. Vaz, G. W. Smith and G. P. Montgomery Jr, Mol. Cryst. Liq. Cryst., 1987, 146, 1–15 CrossRef CAS.
- L. A. Serrano, M. J. Fornerod, Y. Yang, S. Gaisford, F. Stellacci and S. Guldin, Soft Matter, 2018, 14, 4615–4620 RSC.
- J. M. Brake, A. D. Mezera and N. L. Abbott, Langmuir, 2003, 19, 6436–6442 CrossRef CAS.
- N. A. Lockwood, J. J. de Pablo and N. L. Abbott, Langmuir, 2005, 21, 6805–6814 CrossRef CAS PubMed.
- H. Ramezani-Dakhel, M. Sadati, R. Zhang, M. Rahimi, K. Kurtenbach, B. Roux and J. J. de Pablo, ACS Cent. Sci., 2017, 3, 1345–1349 CrossRef CAS PubMed.
- S. Haseloh, P. van der Schoot and R. Zentel, Soft Matter, 2010, 6, 4112–4119 RSC.
- K. R. Amundson and M. Srinivasarao, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, R1211 CrossRef CAS.
- V. J. Alino, J. Pang and K.-L. Yang, Langmuir, 2011, 27, 11784–11789 CrossRef CAS.
- J. H. Erdmann, S. Žumer and J. W. Doane, Phys. Rev. Lett., 1990, 64, 1907 CrossRef CAS PubMed.
- I.-H. Lin, D. S. Miller, P. J. Bertics, C. J. Murphy, J. J. De Pablo and N. L. Abbott, Science, 2011, 332, 1297–1300 CrossRef CAS PubMed.
- U. Manna, Y. M. Zayas-Gonzalez, R. J. Carlton, F. Caruso, N. L. Abbott and D. M. Lynn, Angew. Chem., Int. Ed., 2013, 52, 14011–14015 CrossRef CAS PubMed.
- J. Moreno-Razo, E. Sambriski, N. Abbott, J. Hernandez-Ortiz and J. De Pablo, Nature, 2012, 485, 86 CrossRef CAS PubMed.
- K. Peddireddy, P. Kumar, S. Thutupalli, S. Herminghaus and C. Bahr, Langmuir, 2012, 28, 12426–12431 CrossRef CAS PubMed.
- S. Sivakumar, K. L. Wark, J. K. Gupta, N. L. Abbott and F. Caruso, Adv. Funct. Mater., 2009, 19, 2260–2265 CrossRef CAS.
- X. Wang, Y. Zhou, Y.-K. Kim, D. S. Miller, R. Zhang, J. A. Martinez-Gonzalez, E. Bukusoglu, B. Zhang, T. M. Brown and J. J. de Pablo, Soft Matter, 2017, 13, 5714–5723 RSC.
- X. Feng, A. Mourran, M. Möller and C. Bahr, Soft Matter, 2012, 8, 9661–9668 RSC.
- J. K. Gupta, M.-V. Meli, S. Teren and N. L. Abbott, Phys. Rev. Lett., 2008, 100, 048301 CrossRef PubMed.
- D. Hartono, C. Y. Xue, K. L. Yang and L. Y. L. Yung, Adv. Funct. Mater., 2009, 19, 3574–3579 CrossRef CAS.
- Y.-t. Ouyang and H.-x. Guo, Chin. J. Polym. Sci., 2014, 32, 1298–1310 CrossRef CAS.
- Z. Zhang and H. Guo, Soft Matter, 2012, 8, 5168–5174 RSC.
- G. P. Crawford, W. Doane and S. Zumer, Liq. Cryst. Today, 1995, 5, 8–11 Search PubMed.
- P. W. Ellis, S. Huang, S. Klaneček, J. Vallamkondu, E. Dannemiller, M. Vernon, Y.-W. Chang, P. M. Goldbart and A. Fernandez-Nieves, Phys. Rev. E, 2018, 97, 040701 CrossRef PubMed.
- Y.-K. Kim, B. Senyuk, S.-T. Shin, A. Kohlmeier, G. H. Mehl and O. D. Lavrentovich, Soft Matter, 2014, 10, 500–509 RSC.
- X. Wang, Y.-K. Kim, E. Bukusoglu, B. Zhang, D. S. Miller and N. L. Abbott, Phys. Rev. Lett., 2016, 116, 147801 CrossRef PubMed.
- X. Wang, D. S. Miller, E. Bukusoglu, J. J. De Pablo and N. L. Abbott, Nat. Mater., 2016, 15, 106 CrossRef CAS PubMed.
- C. Williams, P. Cladis and M. Kleman, Mol. Cryst. Liq. Cryst., 1973, 21, 355–373 CrossRef CAS.
- C. Williams, P. Pierański and P. Cladis, Phys. Rev. Lett., 1972, 29, 90 CrossRef CAS.
- G. P. Crawford and S. Zumer, Liquid Crystals in Complex Geometries Formed by Polymer and Porous Networks, Taylor and Francis, New York, 1996 Search PubMed.
- R. B. Meyer, Mol. Cryst. Liq. Cryst., 1972, 16, 355–369 CrossRef CAS.
- R. B. Meyer, Philos. Mag., 1973, 27, 405–424 CrossRef CAS.
- M. Busch, A. V. Kityk, W. Piecek, T. Hofmann, D. Wallacher, S. Całus, P. Kula, M. Steinhart, M. Eich and P. Huber, Nanoscale, 2017, 9, 19086–19099 RSC.
- R. Ondris-Crawford, G. Crawford, J. Doane, S. Žumer, M. Vilfan and I. Vilfan, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1993, 48, 1998 CrossRef CAS.
- P. Cladis and M. Kleman, J. Phys., 1972, 33, 591–598 CrossRef CAS.
- J. Zhang, J. Su, Y. Ma and H. Guo, J. Phys. Chem. B, 2012, 116, 2075–2089 CrossRef CAS PubMed.
- P. Hoogerbrugge and J. Koelman, EPL, 1992, 19, 155 CrossRef.
- J. Koelman and P. Hoogerbrugge, EPL, 1993, 21, 363 CrossRef CAS.
- P. Español and P. B. Warren, J. Chem. Phys., 2017, 146, 150901 CrossRef PubMed.
- Y.-L. Lin, H.-Y. Chang, Y.-J. Sheng and H.-K. Tsao, Macromolecules, 2012, 45, 7143–7156 CrossRef CAS.
- Z. Wang, H. Wang, M. Cheng, C. Li, R. Faller, S. Sun and S. Hu, ACS Nano, 2018, 12, 1413–1419 CrossRef CAS PubMed.
- S. Yamamoto, Y. Maruyama and S.-A. Hyodo, J. Chem. Phys., 2002, 116, 5842–5849 CrossRef CAS.
- H. Fan and A. Striolo, Soft Matter, 2012, 8, 9533–9538 RSC.
- F. Sicard and A. Striolo, Nanoscale, 2017, 9, 8567–8572 RSC.
- Z. Yang, L. Xin-Ping and Z. Qing-Xuan, Polymer, 2011, 52, 6110–6116 CrossRef CAS.
- F.-L. Dong, Y. Li and P. Zhang, Chem. Phys. Lett., 2004, 399, 215–219 CrossRef CAS.
- R. D. Groot and K. Rabone, Biophys. J., 2001, 81, 725–736 CrossRef CAS PubMed.
- P. Prinsen, P. Warren and M. Michels, Phys. Rev. Lett., 2002, 89, 148302 CrossRef CAS PubMed.
- Y. Shi-Ling, C. Zheng-Ting and X. Gui-Ying, Chin. J. Chem., 2003, 21, 112–116 CrossRef.
- M. Suttipong, B. P. Grady and A. Striolo, Soft Matter, 2017, 13, 862–874 RSC.
- A. AlSunaidi, W. K. den Otter and J. Clarke, Philos. Trans. R. Soc., A, 2004, 362, 1773–1782 CrossRef CAS.
- T. Inokuchi and N. Arai, Mol. Simul., 2017, 43, 1218–1226 CrossRef CAS.
- M. Suttipong, B. P. Grady and A. Striolo, Phys. Chem. Chem. Phys., 2014, 16, 16388–16398 RSC.
- M. Suttipong, B. P. Grady and A. Striolo, J. Phys. Chem. B, 2015, 119, 5467–5474 CrossRef CAS.
- R. D. Groot and P. B. Warren, J. Chem. Phys., 1997, 107, 4423–4435 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- H. Fan and A. Striolo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 051610 CrossRef.
- M. P. Mahajan, Liq. Cryst., 1999, 26, 443–448 CrossRef CAS.
- B. Jerome, Rep. Prog. Phys., 1991, 54, 391 CrossRef CAS.
- M. Greschek, M. Melle and M. Schoen, Soft Matter, 2010, 6, 1898–1909 RSC.
- J. K. Gupta and N. L. Abbott, Langmuir, 2009, 25, 2026–2033 CrossRef CAS PubMed.
- K. Binnemans, Chem. Rev., 2005, 105, 4148–4204 CrossRef CAS PubMed.
- C. F. Faul and M. Antonietti, Adv. Mater., 2003, 15, 673–683 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Molecular composition for all systems simulated in this work. Pressure of selected simulated systems as a function of simulation time. The volume of the box for the system simulated within the NPT ensemble. Orientational order parameters (S) of LC molecules when different surfactants are adsorbed on the surface with Shead/Stail = (a) 3/5, (b) 7/5, and (c) 5/7 at 0.7kBT. Configurations of LC and 1000 surfactant molecules with Shead/Stail = (a) 3/5, (b) 7/5, and (c) 5/7 at 0.7kBT. Orientational order as a function of position within the LC cylinder covered by 1000 surfactant molecules. See DOI: 10.1039/c8cp04492a |
| This journal is © the Owner Societies 2018 |