Bridging solution properties to gas hydrate nucleation through guest dynamics

Abstract

By investigating the aqueous solution properties of several hydrate guests with molecular simulations, we find that with increasing guest concentration, the guest's hydration shell becomes more ordered and the system entropy decreases. A common critical value of the self-diffusion coefficient of different guest molecules is identified, below which hydrates will nucleate very readily.

---

Nucleation and growth of multicomponent crystals are of great importance to material science.^1,2 It is known that small changes in the conditions may have a significant impact on the nucleation process.³ Thus, a firm understanding of the role of each component in a nucleation process is required. Compared to the difficulty of achieving ice nucleation through unbiased molecular dynamics (MD) simulations,⁴ gas hydrates, ice-like clathrate compounds,⁵ can be nucleated very readily at smaller relative undercooling by the addition of small guest molecules, such as methane, CO₂, and propane, to the water.⁶ Clearly, these guests play a vital role in the gas hydrate nucleation process.

The mechanism of gas hydrate nucleation has received considerable attention in recent times.^7–15 The first gas hydrate nucleation hypothesis, known as the labile cluster hypothesis (LCH), was proposed by Sloan and coworkers.⁷ This hypothesis imagined that water cages formed around the guest molecules in solution and then tended to combine to form the crystal. Radhakrishnan and Trout⁸ proposed the local structuring hypothesis (LSH) which suggested that guest molecules arrange in a configuration similar to that of the crystal due to concentration fluctuations, and then the water molecules rearrange around the guest molecules to form a hydrate structure. Though these hypotheses capture important aspects of the hydrate nucleation mechanism, it missed the point that hydrate nucleation is a cooperative process, where hydrate cages can be stabilized by the guest molecules both inside the cage and surrounding it.⁹ At the same time, the association of guest molecules with cages can help to form a region of high-concentration in solution. Guo et al.¹⁰ proposed the cage adsorption hypothesis (CAH) to describe this behavior, and according to the location of the adsorption barrier in the potential of mean force (PMF) between the water cage and guest, the CAH predicts a critical concentration of ∼0.04 mol fraction for methane aqueous solution,¹⁶ above which methane hydrate begins to nucleate.^17–19 However, it cannot explain the observed critical concentration for CO₂ hydrate nucleation, as large as ∼0.09 mol fraction,²⁰ because the location of the adsorption barrier for CO₂ is almost the same as that for methane.²¹ We suspect that this is due to the different dynamical features of guest molecules in aqueous solution, which have not been considered in the CAH.

In this study, aqueous solution properties of various guest species (CH₄, CO₂, Ar, Kr, Xe, Rn, and C₃H₈) are investigated through molecular dynamics simulations at 250 K and 273.15 K, and 50 MPa, where the relationship between the solution structure, dynamical properties, and gas hydrate nucleation will be elucidated. The simulation details can be found in the ESI.†

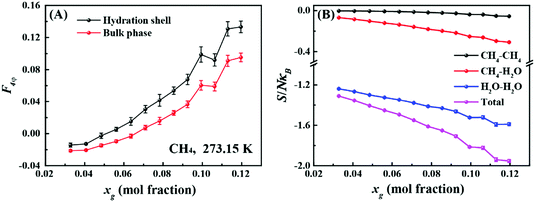
First, we investigated the differences in the structure of the hydration shells of the guest molecules. Fig. 1A compares average values of the F_4φ order parameter²² for water molecules in the first hydration shell and in the bulk phase. The F_4φ order parameter is based on the torsion angle between two hydrogen-bonded water molecules, and can be used to identify ice, liquid water, and hydrates according to their characteristic values of −0.4, −0.04, and 0.7, respectively.²²Fig. 1A shows that the hydrogen-bond network in the hydration shell is more hydrate-like than in the bulk phase and this difference increases with increasing guest molecule concentration, x_g. It is known that the hydration shell of a small hydrophobic molecule has an enhanced water structure and stronger hydrogen bonds relative to those in the bulk water.^23–25 Consequently, with increasing x_g, the hydrogen-bond topology appears to become more hydrate-like as shown in Fig. 1A (additional examples are shown in Fig. S2 and S3, ESI†).

Fig. 1 (A) The change in the average F_4φ for water molecules within 0.54 nm of methane molecules (hydration shell) and others (bulk phase) with increasing methane concentration at 273.15 K. (B) The change in the pair correlation entropy and methane–methane, methane–water, and water–water contributions with increasing methane concentrations at 273.15 K. Details of how the pair correlation entropy was determined can be found in the ESI.†

Fig. 1B shows the dependence of the pair correlation entropy on the guest molecule concentration for a methane–water system. It should be noted that the pair correlation entropy is a major component of hydration entropy, which has been previously used to calculate the entropy of hydrophobic hydration.^26–29 Clearly, the ordering in solution results in a decrease of system entropy, where the contributions from methane–methane, methane–water, and water–water correlations all decrease with increasing guest concentration (further examples are given in Fig. S2 and S3, ESI†). To further understand this phenomenon, we tracked the radial distribution functions (RDFs) for the guest species in solution with increasing x_g. Fig. 2 shows the RDFs for methane at 273.15 K (other examples are shown in Fig. S4 and S5, ESI†). We can see that the probability of the contact pairs (the first peak in Fig. 2) decreases with increasing x_g, while the probability of solvent-separated pairs (the second peaks in Fig. 2) increases, in agreement with previous studies.^22,30,31 With increasing x_g, we also see that the location of the solvent-separated peak in Fig. 2 shifts (see the arrow) to slightly smaller separations more consistent with values for a gas hydrate (i.e., 0.62 nm). Evidently, the ordering of the hydration shell acts to suppress the formation of contact pairs in solution. This interplay can impact gas hydrate nucleation because the increased order within the hydration shell can help compensate for the entropy penalty associated with the formation of the gas hydrate. That is to say, with increasing x_g, the system entropy decreases, and the structure in the system becomes more like that of the solid phase.

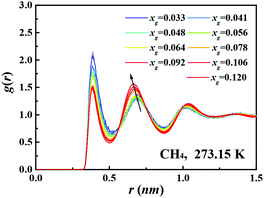Fig. 2 Methane–methane radial distribution functions for solutions with different methane concentrations at 273.15 K. The black arrow is to aid the eyes.

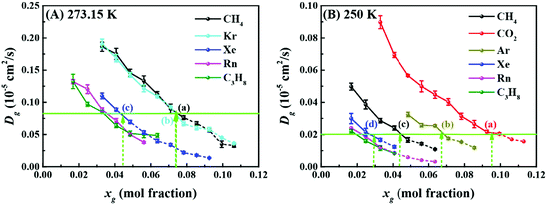
We now shift our attention to the mobility of guest molecules in solution. Fig. 3 shows the dependence of the self-diffusion coefficients of the guest molecules in solution upon increasing x_g at 273.15 K and 250 K. We can see that the self-diffusion coefficient decreases with increasing x_g, which was previously found for xenon solution.³¹ This is reasonable given the increasing order in the hydration shell (as noted above). In Fig. 3, we have also identified two series of points (i.e., a, b, and c in (A), and a, b, c, and d in (B)) corresponding to a critical concentration of each guest except for radon and propane, above which hydrate nucleation occurs readily. The details of the method to identify the guests’ critical concentration for hydrate nucleation can be found in the ESI.† Surprisingly, these points have an almost identical value of the self-diffusion coefficient for each temperature (see Fig. 3 and Table S6, ESI†). This suggests that a common critical self-diffusion coefficient of guest molecules must be reached in order to trigger rapid hydrate nucleation where this value is temperature dependent. Since CO₂ diffuses faster than methane at the same x_g at 250 K and 50 MPa (seeing Fig. 3B), this helps to account for why the critical concentration of CO₂ (∼0.09)²⁰ is nearly double that of methane (∼0.04),^16,19 although the locations of the adsorption barrier of methane and CO₂ to water cages are identical.²¹ To the best of our knowledge, this is the first report connecting guest dynamics with hydrate nucleation. This provides an easily determined proxy, i.e. the self-diffusion coefficient of the guest, for predicting the critical concentration for nucleation of hydrates. Note that the value of the self-diffusion coefficient of water is apparently not appropriate as an indicator for hydrate nucleation, which is clearly indicated in the ESI.†

Fig. 3 The dependence of the self-diffusion coefficients of guest molecules on increasing concentrations at 273.15 K (A) and 250 K (B). The green arrows indicate values of the critical concentration for each guest, labeled as (a), (b), (c), and (d), at which gas hydrates nucleate quickly and that also correspond to two common critical values of D_g. Hydrate nucleation was not observed for Ar and CO₂ at 273.15 K with the concentrations considered in this work. Results for krypton are not shown in (B) because of their similarity to those for methane. The dashed part of the lines implies that data may be affected due to hydrate nucleation.

It should be noted that all the guests having a common critical self-diffusion coefficient (Fig. 3) are sI hydrate formers.⁵ For propane and radon, which are sII hydrate formers, it is apparent that they need much smaller self-diffusion coefficients than the sI hydrate formers to readily nucleate hydrates (see Fig. 3 and Table S6, ESI†). We note that for pure propane or radon hydrates, the 5¹²6⁴ cages will be occupied but not the 5¹² cages. This implies that more 5¹²6⁴ cages are needed to promote the formation of a critical cluster of cages than is required for sI hydrates where both cage types will be occupied. Consequently, suppressed values of the self-diffusion coefficient for propane and radon in solution are expected at the critical concentration.

To help elucidate the underlying origins of the critical self-diffusion coefficient, we show several trajectories of methane molecules at different x_g as shown in Fig. 4. Clearly, the guest molecules are more diffusive at a lower concentration (Fig. 4A). Since the guest hydration shell becomes more ordered and the system entropy reduces with increasing x_g, guest mobility decreases and molecules are often localized within their hydration shells (see Fig. 4D, the displacement of 0.45 nm being smaller than the diameter of a 5¹² cage, 0.79 nm³³), and as a result, hydrate cages are more likely to form. A typical hydration shell from Fig. 4D is shown in Fig. 5. Correspondingly, the diffusion mechanism of guest molecules changes from more Brownian-like motion in the liquid phase to hopping-like behavior more consistent with a solid phase.^34,35 Using the funnel-shaped potential energy landscape for gas hydrate nucleation,³⁶ a system with high x_g can be seen to approach the narrow neck region of its funnel-shaped energy landscape so that water cages can readily form and trigger hydrate nucleation. Addressing the question of ice nucleation is apparently more difficult than for gas hydrates at comparable undercooling,³⁶ the present results confirm that the presence of guest molecules in water does decrease the system entropy, and accordingly, the configurational space of the system (on its funnel-shaped energy landscape) is narrowed, so the system can more readily find a pathway to the solid phase.

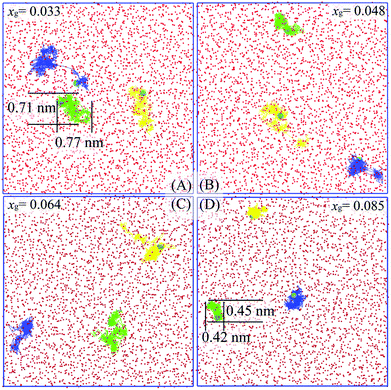Fig. 4 Trajectory traces of three randomly selected methane molecules during the 1 ns-length time window in systems with different methane concentrations at 273.15 K. Methane molecules and oxygen atoms of water molecules from the initial configuration are represented as cyan spheres and red spheres, respectively. Molecular trajectories are shown as yellow, green, and blue lines. Images were generated using VMD.³²

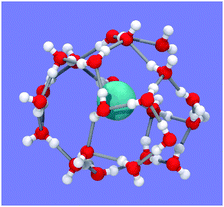Fig. 5 Snapshot of one typical hydration shell from Fig. 4D. The shell is identifiable as a 4¹5⁴6¹7³8¹ water cage. Methane is in cyan. Oxygen and hydrogen atoms are in red and white, respectively.

In conclusion, with increasing guest concentration, the hydration shell of guest molecules is observed to become more ordered, resulting in a drop of the system entropy. The guest mobility also decreases correspondingly. A common critical self-diffusion coefficient value for different guest molecules is identified, below which hydrates will nucleate readily, at least for sI hydrates. These observations can be used to explain the difference in nucleation behaviors of CO₂ and methane hydrate. Because CO₂ has a larger mobility at the same concentration, CO₂ requires a larger concentration compared to methane to achieve the nucleation. From a practical viewpoint, since the self-diffusion coefficient is relatively easy to measure and is sensitive to entropy changes, it can be used as an easily determined proxy for predicting hydrate nucleation. One can then employ this measure when considering the possible influence of various factors on hydrate nucleation e.g. addition of other species that might promote or inhibit gas hydrate formation. Moreover, our results may have implications on the nucleation of other multicomponent systems, and the dynamical properties for such systems deserve more attention.

This work was supported by the National Natural Science Foundation of China (Grant No. 41602038 and 41372059), the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDB10020301) and the China Scholarship Council (CSC). PK is grateful for the financial support from the Natural Sciences and Engineering Research Council of Canada (RGPIN-2016-03845) and acknowledges a Wenner-Gren Foundation Fellowship.

Conflicts of interest

There are no conflicts to declare.

Notes and references

1. Nucleation Theory and Applications, ed. J. W. P. Schmelzer, Wiley-VCH, 2005.
2. Y. Min, J. Kwak, A. Soon and U. Jeong, Acc. Chem. Res., 2014, 47, 2887–2893.
3. D. Wang and Y. Li, Adv. Mater., 2011, 23, 1044–1060.
4. J. R. Espinosa, C. Navarro, E. Sanz, C. Valeriani and C. Vega, J. Chem. Phys., 2016, 145, 211922.
5. E. D. Sloan and C. A. Koh, Clathrate Hydrates of Natural Gasses, CRC Press, Boca Raton, FL, 3rd edn, 2008.
6. G. C. Sosso, J. Chen, S. J. Cox, M. Fitzner, P. Pedevilla, A. Zen and A. Michaelides, Chem. Rev., 2016, 116, 7078–7116.
7. E. D. Sloan and F. A. Fleyfel, AIChE J., 1991, 37, 1281–1292.
8. R. Radhakrishnan and B. L. Trout, J. Chem. Phys., 2002, 117, 1786–1796.
9. G.-J. Guo, Y.-G. Zhang and H. Liu, J. Phys. Chem. C, 2007, 111, 2595–2606.
10. G.-J. Guo, M. Li, Y.-G. Zhang and C.-H. Wu, Phys. Chem. Chem. Phys., 2009, 11, 10427–10437.
11. M. R. Walsh, C. A. Koh, E. D. Sloan, A. K. Sum and D. T. Wu, Science, 2009, 326, 1095–1098.
12. L. C. Jacobson, W. Hujo and V. Molinero, J. Am. Chem. Soc., 2010, 132, 11806–11811.
13. J. Vatamanu and P. G. Kusalik, Phys. Chem. Chem. Phys., 2010, 12, 15065–15072.
14. G.-J. Guo, Y.-G. Zhang, C.-J. Liu and K.-H. Li, Phys. Chem. Chem. Phys., 2011, 13, 12048–12057.
15. Y. Bi, A. Porras and T. Li, J. Chem. Phys., 2016, 145, 211909.
16. G.-J. Guo and P. M. Rodger, J. Phys. Chem. B, 2013, 117, 6498–6504.
17. S. Sarupria and P. G. Debenedetti, J. Phys. Chem. Lett., 2012, 3, 2942–2947.
18. F. Jiménez-Ángeles and A. Firoozabadi, J. Phys. Chem. C, 2014, 118, 11310–11318.
19. Z. Zhang, C.-J. Liu, M. R. Walsh and G.-J. Guo, Phys. Chem. Chem. Phys., 2016, 18, 15602–15608.
20. Z. He, P. Linga and J. Jiang, Phys. Chem. Chem. Phys., 2017, 19, 15657–15661.
21. C. Liu, Z. Zhang and G.-J. Guo, RSC Adv., 2016, 6, 106443–106452.
22. P. M. Rodger, T. R. Forester and W. Smith, Fluid Phase Equilib., 1996, 116, 326–332.
23. D. Chandler, Nature, 2005, 437, 640–647.
24. J. G. Davis, K. P. Gierszal, P. Wang and D. Ben-Amotz, Nature, 2012, 491, 582–585.
25. J. Grdadolnik, F. Merzel and F. Avbelj, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 322–327.
26. M. Kinoshita, N. Matubayasi, Y. Harano and M. Nakahara, J. Chem. Phys., 2006, 124, 024512.
27. M. E. Paulaitis, H. S. Ashbaugh and S. Garde, Biophys. Chem., 1994, 51, 349–357.
28. H. S. Ashbaugh and M. E. Paulaitis, J. Phys. Chem., 1996, 100, 1900–1913.
29. M. Y. Liu, Q. A. Besford, T. Mulvaney and A. Gray-Weale, J. Chem. Phys., 2015, 142, 114117.
30. C. Moon, P. C. Taylor and P. M. Rodger, J. Am. Chem. Soc., 2003, 125, 4706–4707.
31. V. I. Artyukhov, A. Y. Pulver, A. Peregudov and I. Artyuhov, J. Chem. Phys., 2014, 141, 034503.
32. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
33. E. D. Sloan, Nature, 2003, 426, 353–359.
34. S. Liang, D. Liang, N. Wu, L. Yi and G. Hu, J. Phys. Chem. C, 2016, 120, 16298–16304.
35. H. Lo, M.-T. Lee and S.-T. Lin, J. Phys. Chem. C, 2017, 121, 8280–8289.
36. K. W. Hall, S. Carpendale and P. G. Kusalik, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 12041–12046.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp04466j

---