Computing vibration–rotation-tunnelling levels of HOD dimer
Abstract
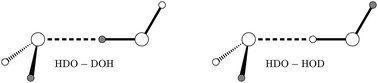
Using an accurate 6D water dimer potential energy surface, we compute vibration–rotation-tunnelling levels of HOD dimer, by assuming that the two monomers are rigid. HOD dimer has two isomers, a D-bonded isomer and an H-bonded isomer, and the wavefunctions of both isomers have amplitude in four wells. HOD dimer is important because, unlike the case of H2O dimer or D2O dimer, it is possible to measure the largest tunnelling splitting. Results for HOD dimer, therefore facilitate the testing of H2O dimer potentials. In J. Chem. Phys., 1995, 102, 1114, experimental results were interpreted in terms of 1D models. Experimental splittings of both isomers, obtained by fitting an energy level equation to spectra, are in good agreement with those we compute.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...