Open Access Article
Open Access ArticlePotential models for the simulation of methane adsorption on graphene: development and CCSD(T) benchmarks†
J.
Vekeman
 ab,
I.
G. Cuesta
*ac,
N.
Faginas-Lago
ab,
I.
G. Cuesta
*ac,
N.
Faginas-Lago
 *b,
J.
Wilson
a,
J.
Sánchez-Marín
a and
A.
Sánchez de Merás
*b,
J.
Wilson
a,
J.
Sánchez-Marín
a and
A.
Sánchez de Merás
 *ac
*ac
aInstituto de Ciencia Molecular, Parc cientifico de la Universidad de Valencia, C/Catedrático José Beltrán 2, E-46980 Paterna, Spain. E-mail: sanchez@uv.es; garciain@uv.es
bDipartimento di Chimica, Biologia e Biotecnologie, Università di Perugia, Via Elce di Sotto 8, 06123 Perugia, Italy. E-mail: noelia.faginaslago@unipg.it
cDepartamento de Química Física, Universidad de Valencia, Avda Dr. Moliner 50, 46100 Burjassot, Spain
First published on 2nd October 2018
Abstract
Different force fields for the graphene–CH4 system are proposed including pseudo-atom and full atomistic models. Furthermore, different charge schemes are tested to evaluate the electrostatic interaction for the CH4 dimer. The interaction parameters are optimized by fitting to interaction energies at the DFT level, which were themselves benchmarked against CCSD(T) calculations. The potentials obtained with both the pseudo-atom and full atomistic approaches describe accurately enough the average interaction in the methane dimer as well as in the graphene–methane system. Moreover, the atom–atom potentials also correctly provide the energies associated with different orientations of the molecules. In the atomistic models, charge schemes including small charges allow for the adequate representation of the stability sequence of significant conformations of the methane dimer. Additionally, an intermediate charge of −0.63e on the carbon atom in methane leads to bond energies with errors of ca. 0.07 kcal mol−1 with respect to the CCSD(T) values for the methane dimer. For the graphene–methane interaction, the atom–atom potential model predicts an average interaction energy of 2.89 kcal mol−1, comparable to the experimental interaction energy of 3.00 kcal mol−1. Finally, the presented force fields were used to obtain self-diffusion coefficients that were checked against the experimental value found in the literature. The no-charge and Hirshfeld charge atom–atom models perform extremely well in this respect, while the cheapest potential considered, a pseudo-atom model without charges, still performs reasonably well.
1 Introduction
Methane capture has gained a lot of interest because of two main reasons. First of all there is an increasing urgency to reduce greenhouse gas emissions, as was highlighted by the recently signed Paris agreement.1 While less methane is emitted than carbon dioxide, its higher energy-uptake makes it a big contributor to the greenhouse effect,2 and thus materials capable of filtering methane from exhaust gas mixtures are highly welcomed. On the other hand, methane is often suggested as a transition fuel until alternative energy sources become feasible for large-scale use. It is fairly easily acquired from natural gas and current technologies only need minimal changes to incorporate it and, most importantly in this context, it is less harmful for the environment than use of crude oil or coal.3 Furthermore, earth's natural resources of natural gas are larger than for more traditional fossil fuels.3 However, the use of any gas as energy resource poses problems of safe storage and transportation in useful amounts and thus materials are needed that can safely trap the gas in high concentrations and release it in a controlled fashion when necessary.4For these reasons, a wide range of materials have been investigated for adsorption of methane. Amongst them, water chlatrates used to solidify methane have been proposed,5 as well as adsorption onto metal–organic frameworks,6,7 zeolites,8,9 activated carbon10 and graphite.11,12 Furthermore, due to their unique properties, ordered nanocarbon materials like graphene and carbon nanotubes have been shown to possess adsorptive qualities for gases like methane.13,14 Previous studies have shown promising first results for the adsorption of gases like H2,15,16 H2O,17 NO18 and CO219 on graphene. These results motivate the development of graphene–CH4 interaction potentials that are capable of describing the processes present in the adsorption of the gas, especially for a large number of molecules as this is crucial for practical applications.
The interaction between graphene and CH4 is mainly of dispersive character and, consequently, associated to the instantaneous fluctuations of the electron density and resulting multipoles. Similar to other van der Waals contributions, although always attractive, dispersive interactions are not isotropic, making the relative orientation of the molecules an important factor to be considered. Being extremely weak, these interactions are the most difficult to be successfully computed, making their correct description an important challenge for any theoretical investigation.
In order to well represent the adsorption of a gas on graphene, accurate potentials are needed for the interactions between the adsorbates as well as between the adsorbent and the adsorbate. Although high-level potentials for these small systems are quite easily produced for the simplest gases, an equilibrium between accuracy and simplicity should be maintained to be feasible for molecular dynamics.
For this purpose, often the Lennard-Jones (LJ) potential is used.20,21 However, the deficiencies of the LJ scheme at both the short and long ranges are well known.22–24 Beyond this model, Pirani et al. proposed an Improved Lennard-Jones (ILJ) potential,22,23 simple and accurate, which offers greater flexibility by adding an extra parameter in such a way that it eliminates most of the shortcomings of the LJ model. This potential has been shown to have a good performance for dispersion interactions in noble gas systems and in conditions of high angular resolution and energy, adequately reproducing vibrational springs.23,24 By means of a careful selection of the appropriate parameters, it seems to be particularly useful for molecular dynamics simulations of, especially, non-covalent interactions.
Another factor to take into account is the interaction model. Often, when studying these interactions, molecules are represented as point masses, especially if they are highly symmetric like methane.11,25 This way, the orientation-dependence of the interaction energy is completely lost in the model. To avoid this, it has been proposed to consider bond–bond interactions by placing an interaction centre on the midbond-point of the carbon–hydrogen bonds22 of methane. Or, more commonly, the molecule can be described by directly taking into account the interactions of all involved atoms in atom–atom potentials.14,26
Electrostatic contributions to the interaction are often included through a Coulombic expression by assigning partial charges to the system,25,26 but this is commonly done without much consideration of the actual added accuracy of this term. The partial charges that are being assigned have no true physical value—since they are not quantum observables—and often there is no real indication that their inclusion is actually important for the results. Indeed, there is often no agreement on the charge model and the actual values to be used for a given molecule, and this is especially so for the symmetrical structure of methane.27
In this work we adopt the ILJ functional to develop a set of force fields capable of evaluating van der Waals interactions like those present in the graphene–CH4 system. We propose two different types of force fields: one representing each methane molecule only by its centre of mass, while in the other an atomistic model of five sites is used. We also consider the influence of the electrostatic part on the parameters using different charge schemes whose viability will be evaluated.
The ILJ interaction potentials were derived from first principles calculations at the level of dispersion-corrected density functional theory. In particular, the B97D functional was used, which includes an empirical dispersion term. From a practical point of view, it seems to be a very robust functional and, among semi-empirical GGA functionals, it is suggested as an efficient and precise method for the study of large systems interacting through dispersion forces.28 Although the B97D functional has proven its value for non-covalent interactions,28–31 this does not guarantee accurate results in a systematic manner for all systems. To overcome this issue, we benchmarked important geometries against CCSD(T) calculations that provide the most trustable physical description of non-covalent interactions in computational chemistry and can therefore be used as reference calculations. Similar approaches have been applied using the LJ potential for the interaction with metal–organic frameworks by Rana et al.,26 while Stassen27 compared several schemes for the methane dimer.
Summarizing, this work aims to present a number of systematic potentials describing the methane dimer and graphene–CH4 interactions based on the ILJ potential. The potentials introduced are accurate, but simple enough for use in molecular dynamics. The models we present will be tested and compared by calculating self-diffusion coefficients via molecular dynamics simulations. Comparison of these with the experimental value from the literature gives us the possibility to assess the performance of the different force fields proposed. Furthermore, highly accurate and reliable predictions of the preferred interaction sites of gas molecules on graphene—as well as the most favorable orientation of CH4—are provided by means of CCSD(T) and DFT studies in which graphene is modeled by coronene (C24H12) and circumcoronene (C54H18) respectively.
In Section 2, the computational details will be outlined. Section 3 will discuss the interaction energies obtained at the DFT and CCSD(T) level. The obtained force fields will be discussed in Section 4, while the diffusion coefficients will be presented in Section 5. Finally Section 6 will present concluding remarks.
2 Computational details
Since graphene is in principle an infinite molecule, we used two truncated systems for the single point energy calculations. These models are large enough as to represent the interactions, but at the same time sufficiently small to allow for high-level CCSD(T) calculations. Previous research has shown that coronene and circumcoronene are suitable models to represent graphene at CCSD(T) and B97D levels of theory, respectively.31–34 Circumcoronene can be seen as a benzene ring with two concentric rings of benzenes whereby the outermost ring is terminated by dangling hydrogen atoms to avoid wrong electronic structures.All monomers were optimized at the B3LYP/6-31G**35,36 level. The C–H distance in CH4 was 1.09 Å, and the average C–C and C–H distances were 1.42 Å and 1.09 Å respectively for coronene and circumcoronene. After this optimization, the structures were considered rigid in all further interaction energy calculations.
The single point DFT energy calculations of the CH4 dimer, the circumcoronene–CH4 system and the coronene–CH4 system were computed at the B97D/TZV2P28,37 level using Gaussian 0938 and the EMSL Basis Set Exchange.39,40 This combination of the B97D functional and the split-valence triple-zeta basis set supplemented with two polarizations (TZV2P) has previously been found to be sufficient to represent the polarization effects in similar systems.32,33
To benchmark the interaction energies obtained at the DFT level, we have calculated the corresponding interaction energies at the CCSD(T) level, using coronene as a model for graphene as stated above. The CCSD(T) interaction energies were calculated using the Dalton program41,42 and the Cholesky decomposition of orbital denominators up to six vectors,43 as it was checked that including more vectors was of little importance for the system of interest. The aug-cc-pVDZ basis set44 was used supplemented with a unique set of functions (3s3p2d1f1g)45 placed midway between the interacting systems. This procedure substantially improves the description of the interaction at a reasonable cost.46 As it can be seen in Table 1, where the CBS values are given in parentheses, the obtained interaction energy values are very close to the corresponding CBS-extrapolated ones with differences not larger than 0.01 kcal mol−1, with the only exception of the F conformation of the methane dimer. All calculations were counterpoise corrected in order to minimize the basis set superposition error.47
| Coronene–CH4 | D e (kcal mol−1) | R e (Å) | ||
|---|---|---|---|---|
| Site | Orientation | DFT | CCSD(T) | DFT |
| a MP2/(T,Q) + ΔCCSD(T)/local-DZ, site T H-up. b DFT/CC (PBE/aQZ), site T H-up. c BLYP-D3/aTZ, site C H-up. d Circumcoronene–CH4, B3LYP-D3/aDZ, site T H-up. e Graphene–CH4, MP2/aTZ, site T H-up and site C H-up, respectively. f Graphene–CH4, vdW-DF(refPBE)/aTZ, site T H-up and site C H-up, respectively. g C72H24, M06-2X/6-31G*:AM1, site B H-up. h C126H36, M06-2X/6-31G*:AM1, site B H-up. i Recommended experimental value of the zero-coverage adsorption well depth of methane on the (0001) surface of graphite and the distance between the methane carbon and the surface. j The CBS limit is given in parentheses. | ||||
| C | H-up | 2.928 | 2.584 | 3.4 |
| 2H-up | 2.810 | 2.312 | 3.4 | |
| 3H-up | 2.539 | 2.018 | 3.6 | |
| T | H-up | 2.908 | 2.571 | 3.3 |
| 2H-up | 2.605 | 2.177 | 3.5 | |
| 3H-up | 2.228 | 1.652 | 3.7 | |
| B | H-up | 2.887 | 2.446 | 3.3 |
| 2H-up | 2.683 | 1.905 | 3.3 | |
| 3H-up | 2.293 | 1.713 | 3.7 | |
| Other work | 2.85,a49 2.80,b50 3.32,c51 3.36,d49 3.00,e13 3.92,e13 3.69,f13 3.23,f13 3.47,g52 3.48h52 | 3.32,a49 3.31,b50 3.37,c51 3.32,d49 3.29,e13 3.28,e13 3.64,f13 3.60,f13 2.79,g52 2.81h52 | ||
| Experimenti53 | 3.00 ± 0.23 | 3.45 | ||
| CH4–CH4 | D e (kcal mol−1) | R e (Å) | |||
|---|---|---|---|---|---|
| Site | Orientation | DFT | CCSD(T)j | DFT | CCSD(T) |
| A | 3H–3H | 0.558 | 0.548 (0.538) | 3.8 | 3.7 |
| B | 3H–2H | 0.515 | 0.464 (0.455) | 3.9 | 3.8 |
| C | 2H–2H | 0.474 | 0.424 (0.423) | 4.0 | 4.0 |
| D | 3H–1H | 0.523 | 0.434 (0.436) | 4.0 | 4.1 |
| E | 2H–1H | 0.499 | 0.357 (0.349) | 4.3 | 4.3 |
| F | 1H–1H | 0.220 | 0.145 (0.190) | 4.7 | 4.8 |
For the methane dimer, 99 random orientations were generated and a scan over the intermolecular distance between 3.2 Å and 20 Å (with much more sampling around the equilibrium distance) was carried out for each conformation of the dimer. This led to a total of 39 distances that were considered for all of the 99 relative orientations. For all of the 3861 conformations thus obtained, the interaction energy was calculated at the B97D/TZV2P level.
Interaction energies were then calculated for the circumcoronene–CH4 system at the same level of theory as for the methane dimer. Ten different CH4 orientations were generated with respect to the circumcoronene molecule at random positions above the circumcoronene plane. The CH4 position was restricted as to exclude the outer benzene rings in order to minimize interactions with dangling hydrogens and other edge effects. Interaction energies at distances between 2.8 Å and 20 Å were calculated, again sampling more closely to the equilibrium distance, giving a total of 32 intermolecular distances for each of the ten orientations considered.
The force fields were created by fitting suitable potentials directly to the energies obtained from DFT. Following the results of ref. 33 we have not averaged the energies over the orientations before fitting, but instead included all the energies in the fitting.
Molecular dynamics calculations were done using DL_POLY v2.2.48 Periodic boundary conditions were used in the x, y and z-direction under standard conditions (273 K and 1 atm) in the microcanonical (NVE) ensemble. A timestep of 1 fs was used for a run time of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps including an equilibration of 3
000 steps including an equilibration of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps, leading to a total run time of 5 ns, while monitoring of temperature and energy showed convergence. van der Waals and Coulombic cutoffs were set to 18 Å, while 100 CH4 molecules were randomly distributed in a cubic cell with sides of 160 Å to ensure the density of methane under standard conditions.
000 steps, leading to a total run time of 5 ns, while monitoring of temperature and energy showed convergence. van der Waals and Coulombic cutoffs were set to 18 Å, while 100 CH4 molecules were randomly distributed in a cubic cell with sides of 160 Å to ensure the density of methane under standard conditions.
We have calculated the diffusion coefficient using the following Einstein equation:
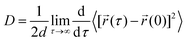 | (1) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) is the position of the particle of interest at time τ. The term 〈[
(τ) is the position of the particle of interest at time τ. The term 〈[![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (τ) −
(τ) − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) (0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time.
(0)]2〉 is called the mean squared displacement (MSD) and varies linearly over time.
To ensure good statistics, we have calculated the diffusion coefficient from 5 different starting configurations and for each starting configuration we have sampled 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 MSD values versus time. We evaluated the diffusion coefficient over 1
000 MSD values versus time. We evaluated the diffusion coefficient over 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 different time origins by taking timestep 1 to 1
000 different time origins by taking timestep 1 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 as a first time interval, then timestep 2 to 1
000 as a first time interval, then timestep 2 to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000
000![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 001 and so on.
001 and so on.
3 CCSD(T) and DFT interaction energies
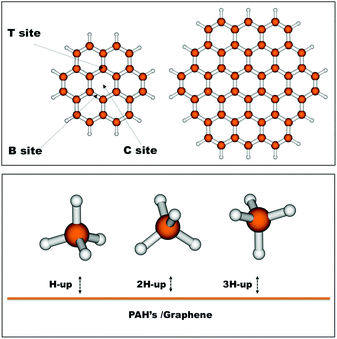
In order to benchmark our DFT interaction energies, we have selected relevant geometries of the methane molecule over coronene. More specifically, we have selected three different interaction sites, namely the centre of the coronene molecule (C site), a position above a carbon atom of the inner benzene ring (T site) and lastly above the midbond-point of a bond of this inner benzene (B site). Furthermore we have selected three relevant ‘attacking’ geometries of methane, one with a hydrogen pointing up (H-up), one with two hydrogens pointing up (2H-up) and a last one with three hydrogens pointing up (3H-up). The selected geometries can be seen in Fig. 1. The intermolecular distance for the nine different geometries was optimized at the DFT level after which CCSD(T) calculations were performed.Table 1 gives a comparison between the interaction energies at different levels of theory for several conformations of the methane dimer and of the coronene–methane cluster. It can be seen that the interaction energies calculated with the B97D functional are in general in good agreement with the CCSD(T) results for the considered coronene–CH4 interaction. In fact, the DFT method correctly reproduces the stability sequence obtained at the CCSD(T) level for both the three different interaction sites over coronene on the one hand and for the different methane orientations on the other hand. However, in all studied cases B97D slightly overestimates the interaction energies at the CCSD(T) level by about 0.5 kcal mol−1. The overestimation decreases as the number of H(CH4)-ring interactions increases which benefits our study since the latter are the most numerous as they are more favorable energetically. Moreover, the interaction of methane with benzene and naphthalene is similar to that with coronene, as shown in the ESI.†
It is seen that the position of the methane molecule over coronene is not too important as was found in a previous work for the CO molecule.32 The T and B sites are actually very similar in energy, while the C site is more stable by about 0.2 kcal mol−1. More important is the orientation of the methane molecule, with the lowest energy structure being the orientation H-up, with the three hydrogens pointing downwards equidistant from the surface. This preference of orientation is encountered for the three positions (C, T and B) of the methane molecule, all providing very similar bonding energies.
Similar results are found in the literature at both MP2/(T,Q) + ΔCCSD(T) and DFT/CC, while slightly higher values are determined using BLYP-D3 in the upper range of the experimental values. In larger graphene–methane clusters the energy increases, being above, in some cases, the experimental upper limit. Some methods, like MP2 and B2LYP-D3, are especially sensitive to this. Conversely, the M06-2X energy seems to be stabilized at 3.5 kcal mol−1. The most stable geometry obtained by Thierfelder et al. (MP2/aTZ) matches our results, even though they report a significantly higher interaction energy.13 It is known, however, that MP2 overestimates the dispersion energy. Thierfelder et al. have not considered the B position and their second lowest energy structure coincides with ours if the B position is left out. It should be noted that in some cases different minimum structures were found in previous studies. Specifically, Umadevi and Sastri found, through a geometry optimization at the M06-2X/6-31G*:AM1 level, the minimum energy structure to be site B H-up.52 Smith and Patkowski on the other hand found site T H-up to have the lowest energy at the MP2/aDZ level.49 This is due to the fact that the three positions for adsorption (C, B and T) have very similar energy (Table 1) with differences inferior to the precision of the method. The molecular distances from the surface obtained from the computational studies included in Table 1 give mostly adsorption distances within the wide experimental range, with only M06-2X falling below.
Compared to the experimental bond energy, our results are quite close. Our lowest DFT energy values are within the experimental uncertainty interval whereby it is noteworthy that these most stable configurations contribute the strongest to the experimental value. The agreement of the equilibrium distances for the discussed geometries is also very good.
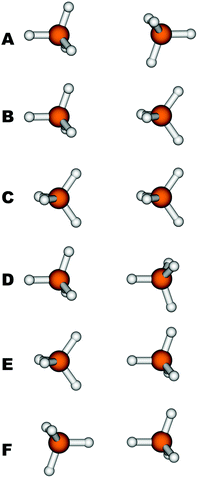
The quality of the B97D method has also been tested for the CH4–CH4 interaction by means of CCSD(T) calculations; more specifically six orientations (labelled from A to F in Fig. 2) of the CH4 dimer have been evaluated. They cover different situations, from the most stable configuration (A) with the face of the first CH4 tetrahedron facing the face of the second, to the least stable (F), with the vertices of the tetrahedra facing each other. The intermolecular distances for the six orientations of methane molecules were optimized with both B97D and CCSD(T). The interaction energy, De, and the bond distance, Re, defined as the distance between the carbon atoms, are shown in Table 1. It can be seen that the interaction energy for the methane dimer is primarily of the dispersive type and depends on the orientation as well. The sequence of energies found at the CCSD(T) level decreases in the order A > B > D ≈ C > E > F. However, only the extremes, A and F, show a clear difference in energy, of the order of 0.4 kcal mol−1. The remaining intermediate orientations, B–E, are very close in energy to each other, so that in some cases they are too close for the B97D functional to be able to reproduce the correct order. The stability sequence with B97D is A > B ≈ D > E > C > F, with extremes coinciding with those from CCSD(T). In general, they are in good agreement with the reference results, since they correctly reproduce three differentiated, maximum, minimum and intermediate interaction ranges. In the intermediate range, the correct order is not retained because the B97D functional does not reproduce precisely enough the orientations where the interaction occurs through a vertex of the tetrahedron, which leads to an overestimation of the energies of conformers D and E larger than the energy differences. Despite this, we can point out that the average interaction energy for the calculated CH4–CH4 interaction at the B97D level (0.46 kcal mol−1) is in excellent agreement with the CCSD(T) value, which is only 0.06 kcal mol−1 below. The results obtained for the bond distances are even better, both for the considered orientations, with errors smaller than 0.1 Å, and for the average distance, whose deviation with respect to CCSD(T) is only of the order of 0.01 Å.
In brief, the comparison of B97D and CCSD(T) results for the studied systems shows that B97D is able to give a satisfactory picture of non-local dispersive effects and, consequently, makes feasible the numerous first principles calculations needed to build force fields capable of describing the processes associated with the adsorption of methane on graphene through dispersion contributions.
4 Force fields
In this work it is assumed that the total interaction energy can be split into two independent parts, the nonelectrostatic part (Vnelec) and the electrostatic part (Velec). The first will be represented by the semiempirical ILJ potential developed by Pirani et al.,23 while the latter will be represented as a Coulombic sum| Vtot(R) = Vnelec(R) + Velec(R) = VILJ(R) + VCoul(R). | (2) |
The ILJ potential assumes pairwise additivity of the nonelectrostatic energy part and was introduced as an improvement over the well-known LJ potential, especially at both short and long ranges where LJ is known to have shortcomings. The function was proven to give a reliable physical representation of non-bonded systems, while remaining simple and using only a small amount of parameters that are physically relevant.54,55 The potential describes the distance dependence of the interaction energy as follows:
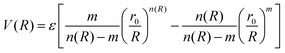 | (3) |
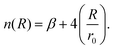 | (4) |
This function is determined by three parameters, ε, r0 and β, which will be specific to different interactions. ε is the well depth of the Morse curve depicted by the ILJ potential, while r0 is its location. β on the other hand is a dimensionless parameter that adds extra flexibility. Its value is loosely related to the hardness of the interaction partners and is usually limited within a range depending on the type of interaction. For pure dispersion interactions, as in this work, β is assumed to lie between 7 and 9. This is evident by noting that the ILJ potential will reduce to the LJ potential when β = 8 and R is close to the equilibrium distance. For interactions between neutral systems, as all the molecules in this work are, m is taken to be 6 as suggested in the original papers.
We have represented the methane molecule by two different models. In the first, an interaction centre was placed at the centre of mass, coinciding with the carbon atom, treating the methane molecule as a sphere effectively reduced to a point mass. Note that all the information on relative orientation of the monomers will therefore be lost. This approach is justified by the 3D structure, which is almost spherical, and has proven its worth before.25 A potential of this form describing the methane dimer will simply equal eqn (3) and will be denoted as the CM–CM model from now on.
A next step in complexity in the framework of pair potentials is to use a multicentre (multi-site) model to represent each methane molecule. Placing an interaction site at each atom, we need 25 ILJ potentials to describe the methane dimer. Three independent sets of ILJ parameters are then required, namely C–C, C–H and H–H parameters.
When representing interactions for the circumcoronene molecule, the methane molecule will mainly interact with the carbon atoms on circumcoronene that are close by. If only a single interaction centre is taken into account, only interaction with the inner benzene ring would be effectively considered. When methane is located more on the side of the circumcoronene, the interaction will be stronger with benzene rings that are closer by than the central one; hence we will always treat circumcoronene with interaction centres on all carbon atoms. Dangling hydrogen atoms are not considered. The ignored interactions will be very small, since we have ensured that methane was positioned far away from the edges as mentioned before.
In the literature, electrostatic interactions are often included in molecular dynamics even for neutral molecules without dipole or quadrupole. Usually this is done via the Coulombic sum
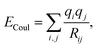 | (5) |
As we aim to look at the influence of different charge schemes on the parameters, besides the one representing the octupole, we will also use the charges calculated by population analysis methods such as Mulliken, APT,56 NBO57 and Hirshfeld.58
4.1 Methane dimer
Table 2 gives the three parameters—the well depth, ε, the equilibrium distance, r0, and the additional, β—defining the ILJ potential for the methane dimer using the CM–CM model and the atom–atom representations and both with and without explicit inclusion of a Coulombic electrostatic term through different charge schemes, charges are indicated in the table.| ILJ parameters | No charges | APT (0.026) | Hirshfeld (−0.148) | Mulliken (−0.471) | Albertí (−0.626) | NBO (−0.823) | |
|---|---|---|---|---|---|---|---|
| CM–CM | |||||||
| ε (kcal mol−1) | 0.421 | 0.421 | 0.421 | 0.424 | 0.427 | 0.431 | |
| r 0 (Å) | 4.169 | 4.169 | 4.168 | 4.165 | 4.163 | 4.159 | |
| β | 8.216 | 8.216 | 8.215 | 8.208 | 8.202 | 8.192 | |
| Atom–atom free | |||||||
| C–C | ε (kcal mol−1) | 0.109 | 0.109 | 0.108 | 0.070 | 0.125 | 0.140 |
| r 0 (Å) | 3.800 | 3.800 | 3.800 | 3.829 | 3.815 | 3.797 | |
| β | 8.027 | 8.027 | 8.024 | 8.149 | 7.464 | 7.421 | |
| C–H | ε (kcal mol−1) | 0.075 | 0.075 | 0.075 | 0.088 | 0.067 | 0.068 |
| r 0 (Å) | 3.628 | 3.628 | 3.628 | 3.604 | 3.639 | 3.632 | |
| β | 4.932 | 4.933 | 4.941 | 4.798 | 5.414 | 5.490 | |
| H–H | ε (kcal mol−1) | 0.005 | 0.005 | 0.005 | 0.004 | 0.003 | 0.003 |
| r 0 (Å) | 3.419 | 3.419 | 3.411 | 3.401 | 3.373 | 3.365 | |
| β | 4.363 | 4.363 | 4.364 | 4.437 | 4.938 | 4.989 | |
| Atom–atom restricted | |||||||
| C–C | ε (kcal mol−1) | 0.198 | 0.198 | 0.198 | 0.196 | 0.195 | 0.194 |
| r 0 (Å) | 4.141 | 4.141 | 4.139 | 4.122 | 4.106 | 4.077 | |
| β | 7.645 | 7.645 | 7.645 | 7.642 | 7.643 | 7.647 | |
| C–H | ε (kcal mol−1) | 0.047 | 0.047 | 0.047 | 0.047 | 0.048 | 0.048 |
| r 0 (Å) | 3.368 | 3.368 | 3.370 | 3.389 | 3.404 | 3.426 | |
| β | 7.279 | 7.279 | 7.278 | 7.268 | 7.260 | 7.249 | |
| H–H | ε (kcal mol−1) | 0.013 | 0.013 | 0.013 | 0.013 | 0.013 | 0.013 |
| r 0 (Å) | 2.610 | 2.610 | 2.610 | 2.608 | 2.607 | 2.606 | |
| β | 7.038 | 7.038 | 7.037 | 7.034 | 7.032 | 7.028 | |
The CM–CM potential is the simplest representation of the CH4–CH4 interaction presented here as it only considers a single interaction site for every methane molecule at their centres of mass. By explicitly including the electrostatic part in this model, we introduce, to some extent, the orientation of the molecules in the potential. It is clear that with increasing electrostatic interaction—larger absolute partial charges—the parameters of the ILJ potential change systematically; more precisely, ε increases, while r0 and β decrease with increasing electrostatic interaction. However, one can also note that the parameters only change significantly when the partial charges become high and even then the changes are limited. We thus conclude that for the CM–CM model an electrostatic part is not explicitly needed for the methane dimer as is widely accepted in the literature.
For a CM–CM model without charges, Albertí et al. have reported an ε of 0.345 kcal mol−1, r0 of 4.04 Å while they fixed the β to 8.5 Note, however, two important differences. Firstly, we have allowed β to change as a fitting parameter. Secondly, they determined the parameters via correlation formulae deduced from experiment, while we have done a pure mathematical fit to DFT interaction energies.
The atom–atom model takes into account the interaction of all the atoms present in the system, using a specific potential for each of the possible pairs, with the aim of including the dependence of the interaction energy on the orientation. Consequently, for the methane dimer, three sets of atom–atom potential parameters (C–C, C–H and H–H) were optimized using the same charge schemes mentioned before. In Table 2, the interaction parameters are given under the section “atom–atom free”. The introduction of the electrostatic part changes the parameters to a greater extent than in the CM–CM model. It is, however, noticeable that the parameters hardly change for the three schemes with the lowest charges; apparently a certain threshold is needed for the electrostatic part to become influential. The electrostatic contribution affects fundamentally the C–C interaction and the β parameter which in turn affects mainly the description at medium distances. Contrarily, r0 does not vary substantially in any of the three interactions. The model using Mulliken charges behaves especially unexpected since it gives a stronger ε for the C–H interaction than for the C–C interaction, contradicting chemical intuition which would assume larger interaction energies between centres with a larger polarizability.
As mentioned before, originally the ILJ potential assumes that the different parameters can be derived from (atomic) static polarizabilities and dispersion coefficients from a semi-empirical expression relying itself on the same static polarizabilities.59 In particular, the β parameter should vary between 7 and 9, while those we have determined from DFT calculations can be as small as 4.5. This significant diminution can be explained by two reasons. Firstly, since Pascal's rule of polarizability is only approximate, the definition of atomic polarazibilities introduces a degree of arbitrariness that makes the conversion of global molecular properties into atomic contributions not necessarily unique and, therefore, there is no reason to expect that a purely statistical fitting is going to reproduce such atomic distributions. Secondly, as usual in MD simulations, the electrostatic contribution of the interactions has been represented by a simple Coulombic term with—again more or less arbitrary—atomic charges. However, the first non-zero term of the multipole expansion of the electrostatic interaction in the methane dimer corresponds to octupoles and such interaction decreases faster with distance (as R−7) than the used Coulomb formula (R−1). Consequently, the non-electrostatic part of our potential must somehow compensate this issue through a variation of its defining parameters.
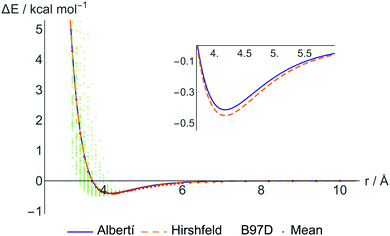
Still, in order not to completely lose the simple physical interpretation of the ILJ potential, we have refitted the DFT data restricting the β parameters to within the recommended interval (7–9) and giving to each DFT point a weight inversely related to its distance from the CM–CM predicted value. These are the parameters shown in the third section of Table 2, denoted “atom–atom restricted”. Further restrictions to keep also the standard physical meaning of ε's and r0's lead to parameters that slightly worsen the equivalence between fit-predicted and DFT-calculated interactions, especially at short distances, and these parameters are thus not included in the results. In Fig. 3 some selected fitted potentials are represented.
The same atom–atom model was used by Vela et al.14 and Stassen et al.27 although they used the standard LJ model. Although the potentials are not the same, we would like to point out that the ILJ potential mimics the LJ potential in the equilibrium region meaning that the position and the value of the well-depth should be directly comparable. Vela et al. have reported values of ε = 0.056 kcal mol−1 and r0 = 3.82 Å for the C–C interaction, ε = 0.061 kcal mol−1 and r0 = 3.57 Å for the C–H interaction and ε = 0.066 kcal mol−1 and r0 = 3.33 Å for the H–H interaction. Although the values of r0 are in close agreement with ours, those of ε are not. It is especially surprising that they propose rising interactions in the series C–C, C–H, H–H since dispersion energies are determined by the size of the polarizability of the involved systems and these contradict their rising series. It should finally be noted that they did not discriminate the carbon atoms in methane from the ones in the carbon nanotubes they investigated, something which may have influenced the choice of parameters. Moreover, as mentioned before, the intrinsic arbitrariness of expressing global molecular properties in terms of atomic contributions should also be taken into account. Stassen et al. used ε = 0.102 kcal mol−1 and r0 = 3.76 Å for the C–C interaction, ε = 0.047 kcal mol−1 and r0 = 3.36 Å for the C–H interaction and ε = 0.017 kcal mol−1 and r0 = 3.16 Å for the H–H interaction. Since no charges are included in this model, it is comparable with our no-charge model, with which it compares well. Furthermore, they report an atom–atom model including a partial charge on the carbon atom of −0.240e. This is a situation somewhere in between our Hirshfeld and Mulliken models. They report the following parameter values: ε = 0.066 kcal mol−1, r0 = 3.929 Å, ε = 0.044 kcal mol−1, r0 = 3.367 Å, ε = 0.030 kcal mol−1, r0 = 2.806 Å for the C–C, C–H and H–H interactions, respectively.
The quality of the proposed force fields and the different charge schemes has been evaluated by determining the capacity of the adjusted potentials to reproduce the energies and interaction distances of the six, previously mentioned, highly symmetric configurations of the CH4 dimer. In this way, the ability of each of them to describe not only average situations, but also specific orientations is analyzed. The results are compared with CCSD(T) values since those are the most accurate. Table 3 shows the values obtained.
| A | B | C | D | E | F | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D e | R e | D e | R e | D e | R e | D e | R e | D e | R e | D e | R e | |
| CCSD(T) | ||||||||||||
| 0.548 | 3.660 | 0.464 | 3.849 | 0.424 | 3.992 | 0.434 | 4.106 | 0.357 | 4.341 | 0.145 | 4.811 | |
| CM–CM model | ||||||||||||
| No charges | 0.417 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 |
| APT | 0.417 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 | 0.418 | 4.197 | 0.417 | 4.197 | 0.417 | 4.197 |
| Hirshfeld | 0.416 | 4.197 | 0.417 | 4.196 | 0.419 | 4.194 | 0.421 | 4.192 | 0.419 | 4.194 | 0.412 | 4.202 |
| Mulliken | 0.404 | 4.207 | 0.413 | 4.200 | 0.435 | 4.179 | 0.455 | 4.159 | 0.434 | 4.176 | 0.366 | 4.259 |
| Albertí | 0.394 | 4.217 | 0.411 | 4.204 | 0.472 | 4.144 | 0.515 | 4.088 | 0.453 | 4.163 | 0.326 | 4.309 |
| NBO | 0.377 | 4.232 | 0.405 | 4.210 | 0.473 | 4.145 | 0.539 | 4.085 | 0.470 | 4.137 | 0.278 | 4.387 |
| Atom–atom free model | ||||||||||||
| No charges | 0.650 | 3.817 | 0.576 | 3.944 | 0.531 | 4.037 | 0.391 | 4.315 | 0.384 | 4.353 | 0.297 | 4.654 |
| APT | 0.650 | 3.817 | 0.576 | 3.944 | 0.531 | 4.037 | 0.391 | 4.315 | 0.384 | 4.353 | 0.297 | 4.654 |
| Hirshfeld | 0.646 | 3.818 | 0.574 | 3.944 | 0.533 | 4.035 | 0.393 | 4.312 | 0.384 | 4.352 | 0.294 | 4.656 |
| Mulliken | 0.656 | 3.816 | 0.595 | 3.937 | 0.579 | 4.011 | 0.439 | 4.279 | 0.417 | 4.332 | 0.296 | 4.657 |
| Albertí | 0.543 | 3.864 | 0.509 | 3.968 | 0.524 | 4.014 | 0.407 | 4.272 | 0.376 | 4.322 | 0.237 | 4.684 |
| NBO | 0.527 | 3.878 | 0.513 | 3.970 | 0.568 | 3.986 | 0.459 | 4.227 | 0.402 | 4.299 | 0.214 | 4.721 |
| Atom–atom restricted model | ||||||||||||
| No charges | 0.458 | 3.935 | 0.457 | 3.968 | 0.466 | 3.988 | 0.382 | 4.169 | 0.417 | 4.155 | 0.345 | 4.434 |
| APT | 0.458 | 3.935 | 0.457 | 3.968 | 0.466 | 3.988 | 0.382 | 4.169 | 0.417 | 4.155 | 0.345 | 4.434 |
| Hirshfeld | 0.456 | 3.935 | 0.456 | 3.968 | 0.469 | 3.986 | 0.385 | 4.166 | 0.418 | 4.154 | 0.341 | 4.437 |
| Mulliken | 0.442 | 3.937 | 0.453 | 3.966 | 0.492 | 3.966 | 0.416 | 4.138 | 0.429 | 4.146 | 0.306 | 4.466 |
| Albertí | 0.430 | 3.939 | 0.450 | 3.965 | 0.512 | 3.949 | 0.443 | 4.115 | 0.439 | 4.140 | 0.277 | 4.491 |
| NBO | 0.409 | 3.942 | 0.445 | 3.962 | 0.548 | 3.921 | 0.491 | 4.078 | 0.455 | 4.130 | 0.231 | 4.537 |
| Other potentials | ||||||||||||
| TraPPE | 0.292 | 4.248 | 0.292 | 4.248 | 0.292 | 4.248 | 0.292 | 4.248 | 0.292 | 4.248 | 0.292 | 4.248 |
| Stassen-A | 0.296 | 4.251 | 0.296 | 4.251 | 0.296 | 4.251 | 0.296 | 4.251 | 0.296 | 4.251 | 0.296 | 4.251 |
| Vela | 1.118 | 3.843 | 0.971 | 4.052 | 0.892 | 4.119 | 0.664 | 4.476 | 0.498 | 4.700 | 0.303 | 5.200 |
| Stassen-B | 0.543 | 3.670 | 0.475 | 3.871 | 0.470 | 3.933 | 0.320 | 4.297 | 0.267 | 4.500 | 0.157 | 5.000 |
| Stassen-C | 0.506 | 3.625 | 0.472 | 3.771 | 0.491 | 3.835 | 0.336 | 4.181 | 0.317 | 4.200 | 0.194 | 4.700 |
| Amber | 0.422 | 3.729 | 0.420 | 3.848 | 0.499 | 3.858 | 0.367 | 4.183 | 0.268 | 4.158 | 0.136 | 4.900 |
It can be observed that the CM–CM model is not capable of reproducing, neither in direction nor in magnitude, the energy differences associated with the different orientations of methane, even when introducing large charges such as Albertí's or NBO. However, the average of all of them has an acceptable low error. The latter is not the case for the distances which are generally overestimated.
The atom–atom model, on the other hand, is capable of reproducing the sequence of stability of the different orientations, with practically all the considered charge schemes. Using the potentials obtained with small charges such as APT, Hirshfeld or Mulliken, the energies are generally overestimated by about 0.1 kcal mol−1. The NBO charges give a good description of most of the conformations with some difference in the order of the intermediate orientations, as was already observed in the comparison of the DFT and CCSD(T) energies for the six dimer conformations (see Section 3). Finally, in the case of the potential using Albertí's charges, which are intermediate in the range of charges used, a rather accurate reproduction of the bond energies of all conformers is observed, thus providing the appropriate energy ordering of all different relative orientations. A reduction of the error in the intermolecular distances is also observed compared to the CM–CM model, although they are still overestimated.
When the restriction over the β parameters is applied, even though the average error is essentially maintained due to arithmetic cancellations, it is observed that the conformations with the highest interaction energies get destabilized, while those with the lowest interaction energies are stabilized. Subsequently, there is a significant reduction of the energy interval and the correct ordering of the different conformations is completely lost. Paradoxically, such order is recovered by introducing new restrictions, but these have been discarded because of the large errors that they produce in the diffusion coefficients discussed below.
Finally, to compare the performance of our parameters in reproducing the CCSD(T) interaction energies to existing force fields, we have selected a number of relevant sets of parameters to calculate the interaction energies of the six methane dimers shown in Fig. 2. More specifically, we have selected three force fields from the work of Stassen27 that are of comparable types as ours, and the same nomenclature is used as in the original paper, leading to the discussion of Stassen-A, Stassen-B and Stassen-C. The force field presented by Vela et al.14 was included as well as popularly used force fields such as TraPPE60 and Amber.61 All these potentials are based on the standard LJ potential and this comparison can thus be seen as a validation of the ILJ potential over the LJ potential. The obtained values of dissociation energies and equilibrium distances for the different conformations are shown in the last rows of Table 3 and dissociation curves comparing B97-D, CCSD(T) Stassen-B and ILJ are presented in the ESI.†
As expected, and similar as for our parameters, the CM–CM models are not able to grab the orientations of the dimer; however, the average interaction is predicted to be about 0.1 kcal mol−1 lower than predicted by our parameters. The average CCSD(T) value of the dimers considered is 0.395 kcal mol−1 and is thus better reproduced by our CM–CM model without charges or with small charges.
Looking at atom–atom LJ potentials, we see that Vela et al. severely overestimate the interaction energies, by about a factor of two to be more specific. The other three force fields perform from reasonably well in the Amber case to very well in the Stassen case. Especially Stassen-B performs exceptionally well. Actually, our force fields perform slightly worse in some cases than Stassen-B at the equilibrium region, although it does better in other conformations. Moreover, it is worth noting that the improvement of the ILJ potential is not in the prediction of the equilibrium region, but in the prediction of the behaviour at long and short ranges; we are thus confident that although, our force fields perform slightly worse than Stassen-B at the equilibrium region, they outperform it at regions outside the equilibrium range.
4.2 Circumcoronene–methane
In Table 4, two sets of potentials for the graphene–methane interaction (graphene modeled by circumcoronene) are shown. In the first, methane is represented by the CM-model, while in the second, it is represented by the atomistic model. No electrostatic interactions are included since they are negligible in the virtually infinite graphene sheet. Tsuzuki et al. have reported weak electrostatic interactions to play an important role in the interaction of CH4 with benzene. However, passing to bigger molecules like naphthalene and pyrene, the relative importance of such contributions to the interaction energy is comparatively much smaller, justifying our assumption that electrostatic energies are of minor importance in polycyclic aromatic hydrocarbons (PAHs).62 This was further confirmed by the energy decomposition and the CCSD(T) interaction energies presented in the same article for the naphthalene–methane and pyrene–methane systems.| ε (kcal mol−1) | r 0 (Å) | β | |
|---|---|---|---|
| C–CM(CH4) | 0.210 | 3.938 | 8.185 |
| C–C(CH4) | 0.195 | 3.671 | 7.745 |
| C–H(CH4) | 0.099 | 3.727 | 5.476 |
A study by Albertí et al.25 gives parameters for interactions between the carbon atoms of benzene and the centres of mass of methane. It should be noted however that they included explicitly the interactions with the hydrogen atoms on benzene via a second set of parameters. In our case, because of the larger size of circumcoronene and the restriction of the location of methane above the plane, we have not included these interactions explicitly. Nevertheless we can make a crude comparison between the values. Values of 0.155 kcal mol−1 and 4.093 Å are reported for ε and r0 respectively. These are in the same range as our values of 0.210 kcal mol−1 and 3.938 Å, especially considering that they have fixed the β value to 9.4, while we allowed it to relax to a value of 8.185.
Finally we present in this section, parameters for the circumcoronene–CH4 interaction whereby an atomistic model is used for methane. To the best of our knowledge, this has not been presented before. We report values of 0.195 kcal mol−1, 3.671 Å and 7.745 for ε, r0 and β respectively for the C–C interaction and, in the same order, 0.099 kcal mol−1, 3.727 Å and 5.476 for the C–H interaction.
As there are no experimental data nor high-level theoretical results that we are aware of, the reliability of the adjusted potentials is then analyzed indirectly by a procedure analogous to that used for the methane dimer. However, the computational cost of obtaining benchmark energies and distances for graphene or circumcoronene makes us resort to smaller polycyclic hydrocarbons. The equilibrium distances and the binding energies were determined by the ILJ potentials fitted to B97D/TZV2P calculations for the three representative orientations of methane, shown in Fig. 1, above the centres of mass of coronene, naphthalene and benzene and compared to either accurate CCSD(T) estimates or experimental values, and the results are shown in Table 5.
| C24H12–CH4 | C10H8–CH4 | C6H6–CH4 | ||||
|---|---|---|---|---|---|---|
| D e | R e | D e | R e | D e | R e | |
| a Graphite–CH4, best estimate. b Mass analyzed threshold ionization (MATI) technique on the benzene–methane cluster. Values corrected with zero-point energies (ZPE = 0.291 kcal mol−1). | ||||||
| C–CM(CH4) | 2.930 | 3.502 | — | — | 1.293 | 3.673 |
| C-Atom(CH4)/H-up | 3.295 | 3.404 | 2.109 | 3.501 | 1.497 | 3.562 |
| C-Atom(CH4)/2H-up | 2.977 | 3.499 | 1.875 | 3.598 | 1.314 | 3.667 |
| C-Atom(CH4)/3H-up | 2.384 | 3.675 | 1.388 | 3.787 | 0.970 | 3.912 |
| CCSD(T)/H-up | 2.584 | 3.4 | 2.12649 | — | 1.2363 | 3.663 |
| CCSD(T)/2H-up | 2.312 | 3.4 | 1.86,62 2.08849 | 3.662 | 1.3263 | 3.663 |
| CCSD(T)/3H-up | 2.018 | 3.6 | — | — | 1.4563 | 3.863 |
| Exp. | 3.00 ± 0.23a53 | 3.45a53 | — | — | 1.321–1.421b64 | — |
The analysis of the results reveals that the CM potential function overestimates the average CCSD(T) coronene–methane interaction by 0.6 kcal mol−1 as could be expected for the B97D functional. However, it reproduces excellently the experimental value of the interaction energy for graphite–CH4.53 This is also the case for the average bond distance obtained from the fitting which matches the CCSD(T) result and the experimental value closely. Even though the average values are acceptable, this model is by construction not able to reproduce the effect of the orientation of methane relative to the aromatic surface.
The atom–atom model, on the contrary, is able to include the orientation effect and to correctly reproduce the sequence of stability found in the CCSD(T) calculations. The H-up complex is the most stable, while the 3H-up is the least stable. The interaction energies of the conformers, which are overestimated by values between 0.4 kcal mol−1 and 0.7 kcal mol−1 relative to the CCSD(T) value, on average reproduce excellently the experimental value found for the graphite–CH4 interaction and the distances in the conformers are also well reproduced, especially taking into account that the lowest energy conformers (H-up and 2H-up) contribute most to the experimental value.53
The atom–atom potential was tried with smaller aromatic systems like naphthalene and benzene in order to test its limits. We must point out that our parametrization of the ILJ potential is specifically designed for large PAHs since the contribution of the dangling hydrogens of the model is not explicitly included in the potential function. Nevertheless, the results obtained are reasonably satisfactory. For the naphthalene–CH4 system there is a good agreement with the CCSD(T) values both in the interaction energy and in the bond distance for all conformations.62,63 Not surprisingly, for the benzene–CH4 cluster, the stability sequence found from the determined semi-empirical potential is not correct. Actually, the preferred structure as predicted by the fitted potential is H-up (tridentate) in which three C–H bonds of methane point towards benzene, similar to the minimum energy structure in the coronene–CH4 complex as well as in other clusters with PAHs.62 However, in reality, benzene shows a different behavior, preferring a 3H-up (monodentate) structure. Tsuzuki et al. have justified such behaviour in terms of the dissimilar nature of the interaction of methane with benzene compared to other PAHs.62 Even though bonding is due in all cases to dispersion contributions, in the former the weak electrostatic interaction stabilizes the 3H-up structure, while in naphthalene such electrostatic contribution is not enough to stabilize the 3H-up structure and the dispersion-favoured structure H-up orientation of methane results to be the most stable.62,63 Since our potential is derived from DFT data of the interaction of methane with circumcoronene, where the dispersion forces are strongly dominant, it is by construction not capable of accurately evaluating the comparatively strong electrostatic component of the interaction with benzene. Even so, the average values agree well with the calculated CCSD(T) and the experimental energies.
5 Diffusion coefficients
As a way of comparing the different force fields we created, we have calculated for all of them the self-diffusion coefficient of methane under standard conditions (273 K and 1 atm) and the corresponding gas density, since this property is well-documented from experiment. Table 6 gives the resulting diffusion coefficients together with the experimental reference value.| Model | No charges | APT | Hirshfeld | Mulliken | Albertí | NBO | Exp. |
|---|---|---|---|---|---|---|---|
| CM–CM | |||||||
| 105 × D (m2 s−1) | 1.699 | 1.683 | 1.831 | 1.643 | 1.552 | 1.157 | 1.880 |
| Atom–atom free | |||||||
| 105 × D (m2 s−1) | 1.876 | 2.041 | 1.937 | 1.571 | 1.541 | 1.232 | |
| Atom–atom restricted | |||||||
| 105 × D (m2 s−1) | — | 1.963 | 1.999 | 1.785 | 1.619 | 1.280 | |
Firstly, it can be seen that there is no systematic better behaviour of either the CM–CM model or the atom–atom model over the different charge schemes. Also, the other way around, no charge scheme performs consistently better for both the CM–CM and atom–atom model.
The model that performs best of all is the atom–atom no-charge model, which shows an absolute error (Ea) of only −0.004 m2 s−1 compared to the experimental value. In general, when atom–atom models are considered, the schemes providing small charges seem to be those of choice; using Hirshfeld charges in the free atom–atom model an Ea of −0.06 m2 s−1 is obtained. Also, the restricted atom–atom model describes reasonably well the diffusion coefficients, with Eas around 0.1 m2 s−1. In particular, errors of 0.095 m2 s−1, 0.08 m2 s−1 and 0.1 m2 s−1 are got for Mulliken, APT and Hirshfeld charges respectively. It is worthwhile to stress that, despite the fact that the Hirshfeld charges provide the best estimation only for the CM–CM model, in general this scheme delivers a good description for the three potential functions. On the contrary, the charges proposed by Albertí, which gave an excellent description of the methane–methane interaction, now only give a qualitative description with an Ea of the order of 0.3 m2 s−1. Notably, although widely used in static energy calculations, NBO charges perform quite badly in our molecular dynamics simulations with an Ea of 0.65 m2 s−1.
Looking at the CM–CM models, the best performing one is the Hirshfeld scheme with an Ea of −0.05 m2 s−1. Notable here is that the no-charge CM–CM model, which is the cheapest among the considered models, still performs acceptably well with an Ea of −0.18 m2 s−1. For large systems, it may be worthwhile to use this model saving considerable computing time.
6 Conclusions
We have proposed a set of force fields for the graphene–CH4 system by fitting different potentials to interaction energies at the DFT level. The potentials include CM–CM and atom–atom potential models as well as different charge schemes to describe the electrostatic interaction within the CH4 dimer. Graphene was represented with an atomistic potential.The B97D interaction energies obtained were benchmarked against CCSD(T) calculations and were in good agreement with the latter. The comparison clearly shows that the B97D functional is able to give a good description of the correlation contributions producing the dispersive effects in these systems and is, consequently, adequate for the construction of force fields capable of describing the adsorption of methane on graphene.
For the graphene–methane and methane–methane systems, the proposed potentials were proven to reproduce well the interaction energies and equilibrium distances experimentally determined or theoretically computed by means of the CCSD(T) method. Accordingly, together with the use of charge schemes containing relatively small atomic charges (such as APT, Hirshfeld or Mulliken), the atom–atom potentials adequately describe the stability sequence of significant conformations of the methane dimer. The description is improved with the slightly larger Albertí charges, so that binding energies are predicted very well. Likewise, the atom–atom potential for graphene–methane is able to accurately reproduce the interaction with PAHs such as naphthalene or coronene as compared to the CCSD(T) and experimental reference values. Accordingly, a very good agreement should be expected for the interaction with other extended carbon systems such as, for instance, nanotubes. In particular, an average interaction energy for the coronene–methane complex of approximately 2.89 kcal mol−1 has been determined, very close to the experimental value of 3.00 kcal mol−1 for the graphene–methane system.
Both CM–CM and atom–atom models were tested via calculation of the diffusion coefficient, and neither showed a consistently better performance over the other. We found however that the atom–atom no-charge model performed the best, with a very accurate prediction of the diffusion coefficient compared to the experimental value. Introduction of small charges, like Hirshfeld's, also gives good results, while larger atomic charges like Albertí's can provide only a qualitative picture. The cheapest of the considered models, the CM–CM no-charge model, performs acceptably well.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The project leading to this publication has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement no. 642294. N. F.-L. acknowledges financial support from the “Fondazione Cassa di Risparmio di Perugia” (Project code: P2014/2015, ACT 2014/6167). N. F.-L. further thanks MIUR and the University of Perugia for the financial support of the AMIS project through the “Dipartimenti di Eccellenza” program. J. W. acknowledges the University of Valencia for a “VLC Campus de Excelencia Internacional” grant in the “2012-0147-Euromaster on Theoretical Chemistry and Computational Modelling” programme.References
- UNFCCC, Conference of the Parties (COP), Adoption of the Paris Agreement, Proposal by the President, 2015.
- D. T. Shindell, G. Faluvegi, D. M. Koch, G. A. Schmidt, N. Unger and S. E. Bauer, Science, 2009, 326, 716–718 CrossRef CAS PubMed.
- N. H. Afgan, P. A. Pilavachi and M. G. Carvalho, Energy Policy, 2007, 35, 704–713 CrossRef.
- P.-s. Choi, J.-m. Jeong, Y.-k. Choi, M.-s. Kim, G.-j. Shin and S.-j. Park, Carbon Lett., 2016, 17, 18–28 CrossRef.
- M. Albertí, A. Costantini, A. Laganá and F. Pirani, J. Phys. Chem. B, 2012, 116, 4220–4227 CrossRef PubMed.
- Y. Peng, V. Krungleviciute, I. Eryazici, J. T. Hupp, O. K. Farha and T. Yildirim, J. Am. Chem. Soc., 2013, 135, 11887–11894 CrossRef CAS PubMed.
- E. Bichoutskaia, M. Suyetin, M. Bound, Y. Yan and M. Schröder, J. Phys. Chem. C, 2014, 118, 15573–15580 CrossRef CAS.
- S. Cavenati, C. A. Grande and A. E. Rodrigues, J. Chem. Eng. Data, 2004, 49, 1095–1101 CrossRef CAS.
- J. Kim, A. Maiti, L.-C. Lin, J. K. Stolaroff, B. Smit and R. D. Aines, Nat. Commun., 2013, 4, 1694–1697 CrossRef PubMed.
- E. Salehi, V. Taghikhani, C. Ghotbi, E. Nemati Lay and A. Shojaei, J. Nat. Gas Chem., 2007, 16, 415–422 CrossRef CAS.
- A. G. Albesa, J. L. Llanos and J. L. Vicente, Langmuir, 2008, 24, 3836–3840 CrossRef CAS PubMed.
- M. A. Razak, D. D. Do and G. R. Birkett, Adsorption, 2011, 17, 385–394 CrossRef.
- C. Thierfelder, M. Witte, S. Blankenburg, E. Rauls and W. G. Schmidt, Surf. Sci., 2011, 605, 746–749 CrossRef CAS.
- S. Vela and F. Huarte-Larrañaga, Carbon, 2011, 49, 4544–4553 CrossRef CAS.
- D. Henwood and J. D. Carey, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 245413 CrossRef.
- J. Petucci, C. Leblond, M. Karimi and G. Vidali, J. Chem. Phys., 2013, 139, 44706–44712 CrossRef PubMed.
- J. Kysilka, M. Rubeš, L. Grajciar, P. Nachtigall and O. Bludský, J. Phys. Chem. A, 2011, 115, 11387–11393 CrossRef CAS PubMed.
- O. Leenaerts, B. Partoens and F. M. Peeters, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125416 CrossRef.
- H. J. Yoon, D. H. Jun, J. H. Yang, Z. Zhou, S. S. Yang and M. M. C. Cheng, Sens. Actuators, B, 2011, 157, 310–313 CrossRef CAS.
- C.-D. Wu, T.-H. Fang, J.-Y. Lo and Y.-L. Feng, J. Mol. Model., 2013, 19, 3813–3819 CrossRef CAS PubMed.
- E. Dundar, P. Boulet, C. Wexler, L. Firlej, P. Llewellyn and B. Kuchta, J. Chem. Phys., 2016, 145, 144704 CrossRef CAS PubMed.
- F. Pirani, M. Albertí, A. Castro, M. Moix Teixidor and D. Cappelletti, Chem. Phys. Lett., 2004, 394, 37–44 CrossRef CAS.
- F. Pirani, S. Brizi, L. F. Roncaratti, P. Casavecchia, D. Cappelletti and F. Vecchiocattivi, Phys. Chem. Chem. Phys., 2008, 10, 5489–5503 RSC.
- A. Lombardi and F. Palazzetti, J. Mol. Struct. THEOCHEM, 2008, 852, 22–29 CrossRef CAS.
- M. Albertí, A. Aguilar, J. M. Lucas and F. Pirani, J. Phys. Chem. A, 2012, 116, 5480–5490 CrossRef PubMed.
- M. K. Rana, H. S. Koh, H. Zuberi and D. J. Siegel, J. Phys. Chem. C, 2014, 118, 2929–2942 CrossRef CAS.
- H. Stassen, J. Mol. Struct., 1999, 464, 107–119 CrossRef CAS.
- S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473 CrossRef CAS PubMed.
- R. Peverati and K. K. Baldridge, J. Chem. Theory Comput., 2008, 4, 2030–2048 CrossRef CAS PubMed.
- J. Vekeman, N. Faginas-Lago, I. G. Cuesta, J. Sánchez-Marín and A. Sánchez de Merás, in LNCS. ICCSA 2018, ed. O. Gervasi, B. Murgante, S. Misra, E. Stankova, C. Torre, A. Rocha, D. Taniar, B. Apduhan, E. Tarantino and Y. Riu, Springer International Publishing, Cham, 2018, pp. 563–578 Search PubMed.
- J. Wilson, N. Faginas-Lago, J. Vekeman, I. G. Cuesta, J. Sánchez-Marín and A. Sánchez de Merás, ChemPhysChem, 2018, 19, 774–783 CrossRef CAS PubMed.
- M. Bin Yeamin, N. Faginas-Lago, M. Albertí, I. G. Cuesta, J. Sanchez-Marin and A. M. J. Sanchez de Meras, RSC Adv., 2014, 4, 54447–54453 RSC.
- P. Lazar, F. Karlický, P. Jurecka, M. Kocman, E. Otyepková, K. Safárová and M. Otyepka, J. Am. Chem. Soc., 2013, 135, 6372–6377 CrossRef CAS PubMed.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- W. J. Hehre, R. Ditchfield and J. A. Pople, J. Chem. Phys., 1972, 56, 2257–2261 CrossRef CAS.
- A. Schäfer, C. Huber and R. Ahlrichs, J. Chem. Phys., 1994, 100, 5829–5835 CrossRef.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, V. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, J. J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski and D. J. Fox, Gaussian-09 Revision D.01, 2009 Search PubMed.
- D. Feller, J. Comput. Chem., 1996, 17, 1571–1586 CrossRef CAS.
- K. L. Schuchardt, B. T. Didier, T. Elsethagen, L. Sun, V. Gurumoorthi, J. Chase, J. Li and T. L. Windus, J. Chem. Inf. Model., 2007, 47, 1045–1052 CrossRef CAS PubMed.
- Dalton, a molecular electronic structure program, Release Dalton2016.1, 2016.
- K. Aidas, C. Angeli, K. L. Bak, V. Bakken, R. Bast, L. Boman, O. Christiansen, R. Cimiraglia, S. Coriani, P. Dahle, E. K. Dalskov, U. Ekström, T. Enevoldsen, J. J. Eriksen, P. Ettenhuber, B. Fernández, L. Ferrighi, H. Fliegl, L. Frediani, K. Hald, A. Halkier, C. Hättig, H. Heiberg, T. Helgaker, A. C. Hennum, H. Hettema, E. Hjertenæs, S. Høst, I. M. Høyvik, M. F. Iozzi, B. Jansík, H. J. A. Jensen, D. Jonsson, P. Jørgensen, J. Kauczor, S. Kirpekar, T. Kjærgaard, W. Klopper, S. Knecht, R. Kobayashi, H. Koch, J. Kongsted, A. Krapp, K. Kristensen, A. Ligabue, O. B. Lutnæs, J. I. Melo, K. V. Mikkelsen, R. H. Myhre, C. Neiss, C. B. Nielsen, P. Norman, J. Olsen, J. M. H. Olsen, A. Osted, M. J. Packer, F. Pawlowski, T. B. Pedersen, P. F. Provasi, S. Reine, Z. Rinkevicius, T. A. Ruden, K. Ruud, V. V. Rybkin, P. Sałek, C. C. M. Samson, A. S. de Merás, T. Saue, S. P. A. Sauer, B. Schimmelpfennig, K. Sneskov, A. H. Steindal, K. O. Sylvester-Hvid, P. R. Taylor, A. M. Teale, E. I. Tellgren, D. P. Tew, A. J. Thorvaldsen, L. Thøgersen, O. Vahtras, M. A. Watson, D. J. D. Wilson, M. Ziolkowski and H. Ågren, WIREs Comput. Mol. Sci., 2014, 4, 269–284 CrossRef CAS PubMed.
- J. L. Cacheiro, T. B. Pedersen, B. Fernández, A. S. De Merás and H. Koch, Int. J. Quantum Chem., 2011, 111, 349–355 CrossRef CAS.
- T. H. Dunning, J. Chem. Phys., 1989, 90, 1007–1023 CrossRef CAS.
- F.-M. Tao and Y.-K. Pan, Mol. Phys., 1994, 81, 507–518 CrossRef CAS.
- H. Koch, B. Fernández and J. Makarewicz, J. Chem. Phys., 1999, 111, 198–204 CrossRef CAS.
- S. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- W. Smith and T. R. Forester, J. Mol. Graphics, 1996, 14, 136–141 CrossRef CAS PubMed.
- D. G. Smith and K. Patkowski, J. Chem. Theory Comput., 2013, 9, 370–389 CrossRef CAS PubMed.
- M. Rubeš, J. Kysilka, P. Nachtigall and O. Bludský, Phys. Chem. Chem. Phys., 2010, 12, 6438–6444 RSC.
- N. X. Qiu, Y. Xue, Y. Guo, W. J. Sun and W. Chu, Comput. Theor. Chem., 2012, 992, 37–47 CrossRef CAS.
- D. Umadevi and G. N. Sastry, Curr. Sci., 2014, 106, 1224–1234 CAS.
- G. Vidali, G. Ihm, H. Y. Kim and M. W. Cole, Surf. Sci. Rep., 1991, 12, 135–181 CrossRef.
- M. I. Hernández, M. Bartolomei and J. Campos-Martínez, J. Phys. Chem. A, 2015, 119, 10743–10749 CrossRef PubMed.
- N. Faginas Lago, F. Huarte Larranaga and M. Albertí, Eur. Phys. J. D, 2009, 55, 75–85 CrossRef.
- J. Cioslowski, J. Am. Chem. Soc., 1989, 111, 8333–8336 CrossRef CAS.
- J. P. Foster and F. Weinhold, J. Am. Chem. Soc., 1980, 102, 7211–7218 CrossRef CAS.
- F. L. Hirshfeld, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- F. Pirani, D. Cappelletti and G. Liuti, Chem. Phys. Lett., 2001, 350, 286–296 CrossRef CAS.
- J. M. L. Martin, Computational Thermochem. Predict. Estim. Mol. Thermodyn., ACS Symp. Ser., 1998, vol. 677, pp. 212–236.
- Z. Hu, L. Zhang and J. Jiang, J. Chem. Phys., 2012, 136, 244703 CrossRef PubMed.
- S. Tsuzuki, K. Honda, A. Fujii, T. Uchimarua and M. Mikami, Phys. Chem. Chem. Phys., 2008, 10, 2860–2865 RSC.
- S. Tsuzuki, K. Honda, T. Uchimaru, M. Mikami and K. Tanabe, J. Am. Chem. Soc., 2000, 122, 3746–3753 CrossRef CAS.
- K. Shibasaki, A. Fujii, N. Mikami and S. Tsuzuki, J. Phys. Chem. A, 2006, 110, 4397–4404 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp03652g |
| This journal is © the Owner Societies 2018 |