Systematic analysis of electron energy-loss near-edge structures in Li-ion battery materials

Abstract

Electrical conductivity, state of charge and chemical stability of Li-ion battery materials all depend on the electronic states of their component atoms, and tools for measuring these reliably are needed for advanced materials analysis and design. Here we report a systematic investigation of electron energy-loss near-edge structures (ELNES) of Li-K and O-K edges for ten representative Li-ion battery electrodes and solid-state electrolytes obtained by performing transmission electron microscopy with a Wien-filter monochromator-equipped microscope. While the peaks of Li-K edges are positioned at about 62 eV for most of the materials examined, the peak positions of O-K edges vary within a range of about 530 to 540 eV, and the peaks can be categorised into three groups based on their characteristic edge shapes: (i) double peaks, (ii) single sharp peaks, and (iii) single broad peaks. The double peaks of group (i) are attributable to the d⁰ electronic configuration of their transition metal ions bonded to O atoms. The origin of the different peak shapes of groups (ii) and (iii) is more subtle but insights are gained using density functional theory methods to simulate O-K ELNES edges of group (ii) material LiCoO₂ and group (iii) material LiFePO₄. Comparison of their densities of states reveals that in LiCoO₂ the Co–O hybrid orbitals are separated from Li–O hybrid orbitals, resulting in a sharp peak in the O-K edge, while Fe–O, Li–O and P–O hybrid orbitals in LiFePO₄ partially overlap each other and produce a broad peak.

---

1 Introduction

Li-ion batteries (LIBs) are widely used in a myriad of applications such as portable devices, electric vehicles and renewable energy storage systems. In an effort to develop superior LIBs, many candidate electrode materials have been investigated in terms of energy density, output voltage, charge–discharge rates and cycle lifetimes.^1–3 At the same time, efforts to improve battery safety, compactness and stability have led to the development of solid electrolytes that exhibit good Li-ion conductivities and structural integrity after many charge–discharge cycles when used in all-solid-state LIBs.⁴

At the microscopic level, charging and discharging of LIBs involves diffusion of Li atoms, conduction of electrons and changes in valence states of the transition-metal (TM) atoms. Characterisation of the structural and chemical changes that take place during battery operation is thus of fundamental importance in the development of improved LIB materials.

Electrodes and electrolytes in LIBs typically contain TM and Li cations bonded to anions such as O, S and sometimes F. Energy-loss near-edge structure (ELNES) spectra of these elements, obtained by performing electron energy-loss spectroscopy (EELS) within a transmission electron microscope (TEM), can provide useful data about their energetics and coordination environments with a spatial resolution of a few nanometres.^5–12 In this work we focus on a number of actively investigated oxide LIB materials, some of whose EELS spectra have not yet been reported.

TM-L_2,3 ELNES spectra, ranging over energies between 450 and 900 eV depending on the element in question and its coordination environment,¹³ are widely used to characterise TM valence states because TM-L spectra change markedly when the valence state changes.^14–16 Similarly, the shapes of O-K ELNES at around 530 eV and Li-K ELNES at around 60 eV depend strongly on the local crystal environments of these atoms and the nature of the interatomic bonding.^11,17,18 In these cases, ELNES simulations using density functional theory (DFT) are indispensable for identifying the electronic transitions producing the fine structures observed experimentally.^7,11,19,20

In the low-energy region (less than 100 eV) in which Li-K edges appear, high energy resolution is necessary to obtain peak shapes accurately. While measurements with resolutions up to 0.3 eV (as determined by the full width half maximum (FWHM) of the zero-loss peak) can be obtained using cold-FE guns,²¹ to obtain resolutions better than 0.1 eV requires use of monochromators.^22–24 The latter allows Li-K edge spectra to be used to measure Li concentrations and distributions quantitatively with nanoscale resolution, as reported for materials LiCoO₂,^25,26 LiFePO₄^27,28 and Li₂MnO₃.²⁹ One drawback of this method, however, is that TM-M_2,3 (or TM-N_2,3) edges lie near to Li-K edges, making their peaks difficult to deconvolute.

Although measurements of Li-K and O-K edges of many LIB materials have been reported,^{14,15,30–36} to the best of our knowledge, the dependence of the ELNES spectra on the type of TM, the crystal structure, and the bonding environment has not been studied systematically. This lack of systematic comparison has sometimes led to conflicting results in the literature, and hampers deeper understanding of the relationship between electronic structure, chemical environment and electrochemical properties of these materials.

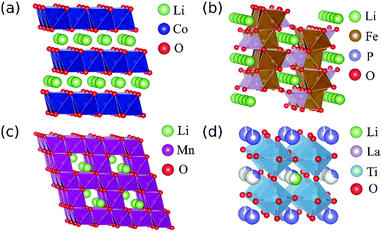
In this study, using a monochromator-equipped TEM, we carried out a systematic comparison of the effect of different TM elements and crystal environments on Li-K and O-K ELNES spectra for ten typical LIB-related materials. The structure types of each material and the coordination numbers (CN), valence states and d-electron configurations of their component TM elements are listed in Table 1, with representative crystal structures depicted in Fig. 1. The materials examined include six cathode materials, two solid electrolyte materials, one anode material, and one non-conductive material (as reference). The cathode materials include two layer-type materials, LiCoO₂ and Li₂MnO₃; two olivine-type materials, LiFePO₄ and LiCoPO₄; and two spinel-type materials, LiMn₂O₄ and LiNi_0.5Mn_1.5O₄. LiCoO₂,^37,38 LiMn₂O₄^39,40 and LiFePO₄^41,42 have been widely investigated and are used commercially. Li₂MnO₃ is a lithium-excess material with superior capacity to LiCoO₂; LiCoPO₄ exhibits higher output voltage than LiFePO₄,^43,44 and LiNi_0.5Mn_1.5O₄ also exhibits higher output voltage than LiMn₂O₄.^45,46 The latter three are being actively researched as next-generation cathode materials. The two solid-state electrolytes examined were perovskite-related materials Li_0.33La_0.56TiO₃ and Li_0.14La_0.29NbO₃. Li site occupancy factors in these materials are low compared to the others, so LiNbO₃ was also characterised as a reference material because it shares their perovskite-like structure but with fully occupied crystallographic Li sites. The anode material was spinel-type Li₄Ti₅O₁₂.

Table 1 Li-ion battery materials examined in this study, their composition, structure type, and atomic coordination numbers (CNs), together with charge states and d-electron configurations of their transition metal (TM) ions

Composition	Structure type	CN			TM
		O	Li	TM	ion	d config.
LiFePO4	Olivine	4	6	6	Fe^2+	d^6 (HS)
LiCoPO4	Olivine	4	6	6	Co^2+	d^7 (HS)
LiCoO2	Layered rocksalt	6	6	6	Co^3+	d^6 (LS)
Li2MnO3	Layered rocksalt	6	6	6	Mn^4+	d^3
LiMn2O4	Spinel	4	4	6	Mn^3+	d^4
					Mn^4+	d^3
LiNi0.5Mn1.5O4	Spinel	4	4	6	Ni^2+	d^8
					Mn^4+	d^3
Li4Ti5O12	Spinel	4	4,6	6	Ti^4+	d^0
LiNbO3	Trigonal perovskite	4	∼12	6	Nb^5+	d^0
Li0.33La0.56TiO3	Layered perovskite	6	∼12	6	Ti^4+	d^0
Li0.14La0.29NbO3	Layered perovskite	6	∼12	6	Nb^5+	d^0

---

Fig. 1 Representative structures of Li-ion battery materials examined in this study: (a) LiCoO₂ with layered rocksalt structure, (b) LiFePO₄ with olivine structure, (c) LiMn₂O₄ with spinel structure and (d) Li_xLa_(2−x)/3TiO₃ with layered perovskite structure. Multicoloured spheres in (d) represent partially occupied sites.

These materials all exhibit differently shaped EELS spectra, especially in the case of O-K ELNES. To understand the origins of these differences, we carried out DFT-based calculations of LiCoO₂ and LiFePO₄, which exhibit representative spectrum shapes. Although several theoretical investigations have been reported for both compounds,^20,47–49 the reported results are not sufficiently detailed to provide explanations for the differences in ELNES peak positions and shapes. In particular, electronic structures of excited states have not yet been reported, so in this study we performed ELNES simulations of LiCoO₂ and LiFePO₄ taking into account the electronic structures of the excited state, and compared the results with experimental spectra.

2 Methods

2.1 Specimen preparation

Samples of the ten compounds were prepared by different methods, as described below:

(1) LiFePO₄. Powder was prepared by solid-state reaction between stoichiometric amounts of Li₂CoO₃, FeC₂O₄·2H₂O and (NH₄)₂HPO₄ at 600 °C for 6 h, followed by annealing at 800 °C for 24 h under pure Ar gas flow.⁵⁰

(2) LiCoPO₄. A thin film of LiCoPO₄ was prepared via an aqueous sol–gel route using citric acid as the chelating agent.⁵¹ Stoichiometric amounts of CH₃COOLi, Co(NO₃)₂·6H₂O and NH₄H₂PO₄ were dissolved in distilled water and citric acid was added to the solution. The precursor solution was spread on an Au-coated Al₂O₃ substrate by spin-coating and annealed first at 350 °C for 1 h and then at 700 °C for 1 h.

(3) LiCoO₂. LiCoO₂ single crystals were prepared via a flux method using LiCoO₂, Li₂O and LiCl. The mixture was heated at 900 °C for 10 h, cooled to 700 °C at a rate of 2 °C h⁻¹ and then allowed to cool naturally down to room temperature. Platelet-like LiCoO₂ single crystals were separated by rinsing the frozen flux in hot water.

(4) Li₂MnO₃. Li₂MnO₃ nanocrystals were fabricated by a hydrothermal method. LiOH·H₂O was dissolved in distilled water and γ-MnO₂ powder was added to the solution. The mixture was heated at 180 °C for 24 h in an autoclave, centrifuged, washed with water and ethanol, and dried at 120 °C.

(5) LiMn₂O₄. LiMn₂O₄ thin film was fabricated by chemical solution deposition of chemically modified LiOC₂H₄OC₂H₅ and Mn(OC₂H₄OC₂H₅)₄ solutions by refluxing in C₂H₅OC₂H₄OH.⁵² The precursor solution was spin-coated onto an Au-coated Al₂O₃ substrate to form a thin film after heat treatment at 750 °C for 1 h.

(6) LiNi_0.5Mn_1.5O₄. LiNi_0.5Mn_1.5O₄ polycrystalline powder was prepared by a sol–gel method. LiCH₃COO·2H₂O, Mn(CH₃COO)₂·4H₂O, Ni(CH₃COO)₂·4H₂O and glycolic acid were dissolved in distilled water and gelated. After calcining the precursor gel at 250 °C for 1 h, the powder was sintered at 800 °C for 20 h.

(7) Li₄Ti₅O₁₂. Li₄Ti₅O₁₂ thin film was fabricated by a sputtering method using a pristine Li₄Ti₅O₁₂ target.⁵³ The deposited film was annealed at 900 °C.

(8) LiNbO₃. LiNbO₃ powder was prepared by a conventional solid-state reaction method from Li₂CO₃ and Nb₂O₅ by sintering at 1000 °C for 5 h.⁵⁴

(9) Li_0.33La_0.56TiO₃. Li_0.33La_0.56TiO₃ powder was prepared by a solid-state reaction method by sintering mixtures of Li₂CO₃, TiO₂ and La₂O₃.⁵⁵

(10) Li_0.14La_0.29NbO₃. A single crystal of Li_0.14La_0.29NbO₃ was fabricated by a conventional unidirectional solidification method.⁵⁴ LiNbO₃ and LaNb₃O₉ precursor powders were mixed, compacted into a cylindrical shape and sintered at 1200 °C for 20 h. The sintered polycrystalline Li_0.14La_0.29NbO₃ rod that resulted was melted in a Pt crucible at 1380 °C and then gradually passed downward through a unidirectional solidification furnace.

X-ray diffraction measurements were used to confirm that materials (1) to (10) were each prepared successfully as a single phase with the appropriate crystal structure under ambient conditions (see Fig. S1 in ESI†).

2.2 EELS measurements

TEM specimens of thin films of LiCoPO₄, LiMn₂O₄ and Li₄Ti₅O₁₂ were prepared using low-temperature (liquid N₂-cooled to below −100 °C) and low-voltage (3.0 kV to 0.2 kV) ion-milling (PIPS, Gatan Inc.). Special care was taken to minimise damage to the samples, and surfaces were cleaned using a plasma cleaner (Solarus, Gatan Inc.) to remove residual amorphous phases. TEM specimens of the other bulk samples were prepared by careful crushing, and the resulting powders dispersed and deposited onto lacey carbon films (above copper substrates).

EELS measurements were carried out using a JEM-2400FCS atomic resolution microscope (JEOL Ltd.) equipped with a spherical-aberration corrector (CEOS GmbH), an EELS spectrometer (GIF Tridiem ERS, Gatan Inc.) and a Wien-filter type monochromator. The microscope was installed in a room designed and constructed to minimise AC magnetic fields, floor vibrations, air-flow volume, temperature fluctuations and acoustic vibrations. In this stable environment, a high energy resolution below 30 meV was achieved.²⁴

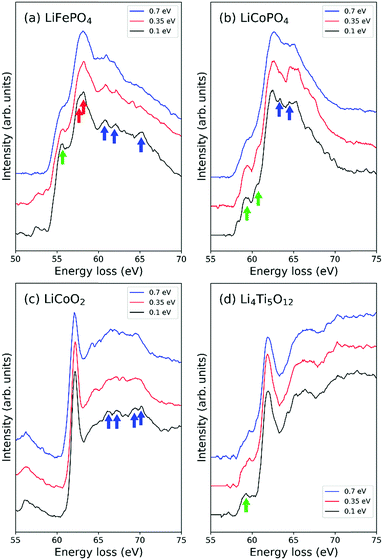
EELS spectra were recorded with an accelerating voltage of 60 kV to reduce irradiation damage and a convergence/collection semi-angle of 30/35 mrad. The energy resolution, ΔE, specified in terms of the FWHM of the zero-loss peak, was controlled by changing the width of an energy selection slit in the monochromator. To examine the effect of energy resolution on ELNES spectra, we measured Li-K edges of LiFePO₄, LiCoPO₄, LiCoO₂ and Li₄Ti₅O₁₂ under various slit conditions, viz., no slit, slit of width 4 μm, and slit of width 1 μm, keeping the dispersion value constant at 0.05 eV per pixel. The resulting ΔE were 0.7 eV, 0.35 eV and 0.1 eV, respectively.

Measurements to compare Li-K edges of all materials were performed using a dispersion value, slit width, and measurement exposure time of 0.05 eV per pixel, 1 μm and 0.2 s, respectively. Similarly, for O-K edges, values of 0.1 eV per pixel, 4 μm and 1 s, respectively, were used. The dispersion value of 0.1 eV per pixel used for O-K edge measurements was larger than that for Li-K edges, but is comparable to the natural line width of the O-K edge, 0.12 eV.⁵⁶ These conditions provided resolutions of ΔE = 0.1 and 0.3 eV for Li-K and O-K edges, respectively. Integration times per measurement for both edges were 10–20 s. Energy alignment was carried out by measuring the zero-loss peak just before and after recording edge spectra. The standard deviation of the zero-loss peak position was 0.03 eV over a time span of 10 minutes (see Fig. S2 in ESI†).

2.3 ELNES simulations

Theoretical O-K ELNES spectra of LiCoO₂ and LiFePO₄ were generated from first-principles calculations using the DFT+U method including spin polarisation.⁵⁷ In all calculations, the GGA-PBE functional was used for the exchange-correlation term.⁵⁸ Values of U of 4.91 eV and 3.71 eV, respectively, were applied to d electrons in Co³⁺ in LiCoO₂ and Fe²⁺ in LiFePO₄.⁵⁹ In LiFePO₄, although the most stable spin configuration is anti-ferromagnetic, the temperature of the anti-ferromagnetic-to-ferromagnetic transition is below room temperature,⁴⁹ so we assumed LiFePO₄ to be in the ferromagnetic state for the calculations.

Before generating ELNES spectra, lattice parameters of LiCoO₂ and LiFePO₄ were determined by performing structural optimisation using the VASP code⁶⁰ with a planewave cut-off energy of 500 eV. The hexagonal R3̄m unit cell (12 atoms) of LiCoO₂ was optimised using a 15 × 15 × 3 Brillouin zone k-point mesh, and the orthorhombic Pnma unit cell (28 atoms) of LiFePO₄ using a 6 × 9 × 15 k-point mesh.

O-K ELNES spectra were generated using the core-hole method implemented in the WIEN2k code with an all-electron basis set (APW + lo method).⁶¹ In this method, the transition probabilities were calculated using a supercell with an electron removed from the 1s orbital of an O atom (core hole) and placed in the conduction band.⁶² According to the spin selection rule, we need to consider the probability of each spin state of the excited electron. In the case of an up-spin excited electron, only up-spin orbitals are relevant to the transition calculation, and vice versa for down-spin excited electrons. Because LiCoO₂ in its ground state is non-magnetic, the probabilities of up-spin excitation and down-spin excitation are identical, so we only performed calculations for an up-spin excitation. In the case of LiFePO₄, although up- and down-spin excitations are not equivalent, our test calculations revealed that the differences between the two excited states are small. The theoretical ELNES spectra of LiFePO₄ reported here were generated by averaging contributions of up- and down-spin orbitals from calculation of a down-spin excitation.

Muffin tin radii (R_MT) for Li, O, P, Co and Fe were 1.70, 1.60 (LiCoO₂)/1.45 (LiFePO₄), 1.45, 2.00 and 2.10 bohr, respectively. The cutoff parameter that determines the maximum wave number of plane waves, R_kmax, was set at 7.0, and O-1s states were treated as core levels for both LiCoO₂ and LiFePO₄. A 4 × 4 × 1 (192 atom) supercell was constructed from the LiCoO₂ unit cell and a 1 × 2 × 2 (112 atom) supercell from the LiFePO₄ unit cell, with 3 × 3 × 2 and 4 × 3 × 3 k-point meshes, respectively, for integrating over the Brillouin zone. In LiFePO₄, as there are three non-equivalent O sites, we calculated the contribution of each type of O separately and took the weighted average when calculating the projected density of states (PDOS) of O-p orbitals and ELNES spectra. The core level of the most distant O atom from the excited O atom in each supercell was used as reference to adjust the PDOS position. The transition energy obtained from the difference in total energies between ground and excited states was used to adjust ELNES edge positions.

3 Results and discussion

3.1 Effect of energy resolution on Li-K ELNES

The effect of different energy resolutions, i.e., ΔE = 0.7, 0.35 and 0.1 eV, on EELS spectra in the low-loss region around Li-K edges was examined for LiFePO₄, LiCoPO₄, LiCoO₂ and Li₄Ti₅O₁₂ (Fig. 2). As can be seen in Fig. 2(c) and (d), the positions and shapes of the strongest peaks change little with ΔE in the cases of Li₄Ti₅O₁₂ and LiCoO₂. In the case of LiCoPO₄, when ΔE = 0.35 eV, a small trough appears at higher energy than the largest peak, around 64 eV, and when ΔE = 0.1 eV, small peaks appear on both sides of this trough as indicated by the blue arrow in Fig. 2(b). The splitting of the peak on the left side of the trough from the largest peak is accompanied by a shift of the largest peak to slightly lower energy, allowing the edge position to be determined with higher accuracy. In the case of LiFePO₄, the single peak at 58.2 eV apparent when ΔE = 0.7 eV changes into a main peak and shoulder peak at 57.6 and 58.3 eV, respectively, when ΔE = 0.1 eV, as indicated by the red arrows in Fig. 2(a).

Fig. 2 Li-K edges of EELS spectra using energy resolutions, ΔE, of 0.7, 0.35 and 0.1 eV for (a) LiFePO₄, (b) LiCoPO₄, (c) LiCoO₂ and (d) Li₄Ti₅O₁₂. Fine structures emerging when an energy resolution of 0.1 eV is used are indicated by arrows. Green arrows indicate pre-edge peaks, blue arrows indicate post-edge peaks and red arrows indicate splitting of main edges.

In the cases of LiFePO₄, LiCoPO₄ and Li₄Ti₅O₁₂, pre-edge peaks become more distinct with decreasing ΔE as indicated by green arrows in Fig. 2(a), (b) and (d). In LiCoO₂ and LiFePO₄ small bumps appear in the tails of the largest peaks at higher energies when ΔE ≤ 0.35 eV, as indicated by blue arrows in Fig. 2(a) and (c). Although such peaks are small, they are useful for checking the accuracy of calculated spectra. For example, the spectral shape including tail peaks of LiCoO₂ has been verified by DFT calculations using the Z + 1 method by Kikkawa et al.³⁰ In the case of LiFePO₄, while the largest peak in Fig. 2(a) at around 58 eV corresponds to the Fe-M_2,3 edge, the peaks above 60 eV indicated by the blue arrows are thought to be components of the Li-K edge because it has been reported that the intensities of these peaks decrease with decreasing Li content.³² In this case, performing EELS measurements with high resolution becomes critically important as such features may otherwise be missed.

3.2 Comparison of Li-K ELNES

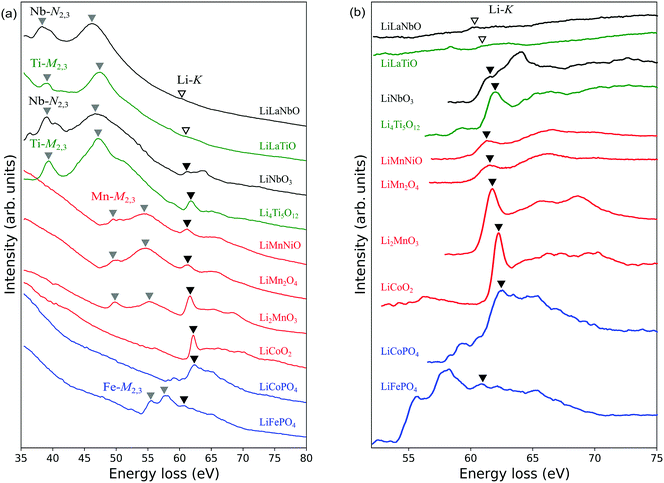
Fig. 3(a) shows experimentally obtained ELNES spectra for all materials measured with a resolution of ΔE = 0.1 eV. The main peak positions of TM-M_2,3 (or N_2,3 for Nb) edges and Li-K edges are indicated by grey and black inverted triangles, respectively. The weak peaks assumed to be Li-K edges in the spectra of Li_0.14La_0.29NbO₃ and Li_0.33La_0.56TiO₃ are indicated by open inverted triangles. Fig. 3(b) shows a magnified view of the energy region around the Li-K edges after background subtraction. TM-M_2,3 (or N_2,3 for Nb) edges have also been subtracted, except for the Fe-M_2,3 edge for LiFePO₄. Table 2 compares these peak positions with data available in the literature.^{13,14,30,32–34,36} Agreement to within 1 eV was obtained in all cases.

Fig. 3 EELS spectra of Li-ion battery materials: (a) comparison of total spectra from 10 materials; (b) magnified view of Li-K edges in the energy range 52 to 75 eV after background subtraction. LiLaNbO, LiLaTiO and LiMnNiO stand for Li_0.14La_0.29NbO₃, Li_0.33La_0.56TiO₃ and LiMn_1.5Ni_0.5O₄, respectively. Peaks of the TM edges (M_2,3 for Mn, Fe, Co, Ni and Ti; N_2,3 for Nb) and the main peaks of Li-K edges are indicated by grey and black inverted triangles, respectively. Open inverted triangles in the case of LLNO and LLTO indicate weak peaks assumed to be Li-K edges. The tails of Mn/Fe-M_2,3 edges overlap Li-K edges, and Co/Ni-M_2,3 edges merge completely with Li-K edges.

Table 2 Peak positions of TM-M,N and Li-K edges compared with data in the literature. Values obtained by background subtraction are given in parentheses

Composition	TM-M,N edges (eV)		Li-K edge (eV)
	This work	Previous work	This work	Previous work
a Ref. 20. b Ref. 36. c Ref. 14. d Ref. 33. e Ref. 51. f Ref. 30. g Ref. 34.
LiFePO4	55.9, 58.3	55.5, 57.4^a	60.9	60.3^a
LiCoPO4	—		62.4	63.0^e
LiCoO2	—		62.2	62.0^f
Li2MnO3	50.0, 55.5	50.4, 55.4^b	61.7	62.6^b
LiMn2O4	50.2, 54.9	49.5, 54.5^c	61.4	60.6^c
LiNi0.5Mn1.5O4	49.7, 54.6		61.2
Li4Ti5O12	39.3, 47.3	39.5, 47.3^d	61.8	61.6^d
LiNbO3	39.0, 46.6		61.3
Li0.33La0.56TiO3	39.2, 47.4		(58.8)	59.1^g
Li0.14La0.29NbO3	38.4, 46.4		(60.4)

---

TM-M_2,3 (Nb-N_2,3) edges are known to correspond to transitions from 3p_3/2,1/2 (or 4p_3/2,1/2) core states to the unoccupied conduction bands. A systematic comparison of the spectra reveals peak positions shift to higher energies as the atomic number increases. This trend reflects the shift to lower core energy levels with increasing atomic number.

In LiNi_0.5Mn_1.5O₄, LiFePO₄, LiCoPO₄ and LiCoO₂, the M_2,3 edges of Ni, Fe and Co are close to and partially overlap the Li-K edges, complicating detection of the latter. As mentioned in the previous section, in the case of LiFePO₄, we cannot assign the weak protrusion at around 62 eV to the Li-K edge without comparison with measurements from delithiated samples. Similarly, the Li-K edge in LiCoO₂ has been identified by comparison with spectra from delithiated samples.³⁰ In the case of LiCoPO₄, no such data are available, so we here assume the peak at around 62 eV to be the Li-K edge, similar to the case for LiCoO₂. The Ni-M_2,3 edge of LiNi_0.5Mn_1.5O₄ is assumed to occur at energies higher than the Li-K edge by several electron-volts because in Ni metal it appears at 68 eV.¹³ Based on this, the small protrusion at 61.9 eV to the right of the Mn-M_2,3 edges was assigned to the Li-K edge.

In the magnified spectra of Li_0.14La_0.29NbO₃ and Li_0.33La_0.56TiO₃, very slight peaks are visible at around 60 eV. However, it is difficult to distinguish these Li-K edges from Nb-N₁ and Ti-M₁ edges which also exist at around 60 eV,³⁴ so it is difficult to identify the Li-K edges with certainty. The chief reason for this is the lower Li concentrations in these solid electrolytes compared to the other materials; the volume densities of Li atoms in these two materials are approximately 2.3 and 5.7 atoms per nm³, respectively, while those of the other materials are between 13 and 40 atoms per nm³.

Previous studies of other Li-containing materials by ELNES or XANES showed that the positions of Li-K edges can vary by more than 5 eV depending on the particular chemical environment of the Li atoms, as reflected in the Mulliken electronegativities or oxidation numbers of neighbouring atoms.^18,63 In our work, the main Li-K peaks were observed to lie at around 61–62 eV for all materials except Li_0.33La_0.56TiO₃ and Li_0.14La_0.29NbO₃. This suggests that, although there are differences between the compounds, such as the CN of Li, Li–O bond lengths, and the types of second nearest neighbour cations, the positions of the main peaks are only slightly affected by the local environments around Li.

For some materials, the fine structures of Li-K edges contain small pre-edge peaks and/or sub-peaks above the main peak. These structures are expected to contain valuable information about the chemical bonding states in these compounds. It remains difficult, however, to extract these details because of the overlap with TM-M_2,3 edges mentioned above. Furthermore, although DFT calculations can help explicate these fine structures, simulation of a Li-K edge requires a calculation scheme that includes electron-hole coupling effects, e.g., the Bethe-Salpeter equation (BSE) method,⁶⁴ which is beyond the scope of the present work.

3.3 O-K ELNES

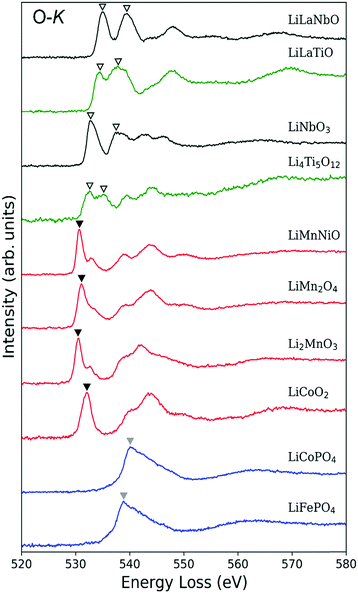
Fig. 4 shows O-K ELNES spectra of the LIB materials examined in this study obtained with ΔE = 0.3 eV. The peak positions occur at energies between 530 eV and 550 eV. Based on the peak shapes, the materials can be categorised into the following three groups: (i) Li_0.14La_0.29NbO₃, Li_0.33La_0.56TiO₃, LiNbO₃ and Li₄Ti₅O₁₂, with double peaks split by a few electron-volts (indicated by inverted open triangles); (ii) LiCoO₂, Li₂MnO₃, LiMn₂O₄ and LiNi_0.5Mn_1.5O₄, with a single sharp, strong peak at the edge position (indicated by black inverted triangles); and (iii) LiCoPO₄ and LiFePO₄, with a single broad peak (indicated by grey inverted triangles). In Table 3, the peak positions are listed for all ten materials and compared with available reported values. In all cases, differences in energy are less than 2 eV.

Fig. 4 EELS spectra around O-K edges of the Li-ion battery materials. LiLaNbO, LiLaTiO and LiMnNiO stand for Li_0.14La_0.29NbO₃, Li_0.33La_0.56TiO₃ and LiMn_1.5Ni_0.5O₄, respectively. Spectra can be classified into three groups according to edge shape: (i) double peaks of similar intensity (open inverted triangles); (ii) single sharp peak (black inverted triangles) with relatively weak sub-peak; and (iii) a single broad peak (grey inverted triangles).

Table 3 Peak positions and shapes of O-K edges compared with data in the literature

Composition	O-K edge (eV)		Shape
	This work	Previous work
a Ref. 35. b Ref. 51. c Ref. 30. d Ref. 36. e Ref. 14. f Ref. 33. g Ref. 34.
LiFePO4	538.7	537.0^a	Broad single
LiCoPO4	540.1	540.4^b	Broad single
LiCoO2	532.0	530.5^c	Sharp single
Li2MnO3	530.5	530.9^d	Sharp single
LiMn2O4	531.1	529.5^e	Sharp single
LiNi0.5Mn1.5O4	530.7		Sharp single
Li4Ti5O12	532.6, 535.2	532.7, 535.4^f	Double
LiNbO3	532.7, 537.8		Double
Li0.33La0.56TiO3	534.5, 537.7	532.9, 536.1^g	Double
Li0.14La0.29NbO3	535.1, 539.6		Double

---

The observed trends can be partly interpreted in terms of the effect of TM-d orbitals overlapping with neighbouring O-2p orbitals. As reported in Table 1, TM atoms in group (i) materials have a d⁰ configuration, while TM atoms in the other two groups have partially occupied d orbitals. Since all TM atoms of the materials examined here are in octahedral coordination environments, their d orbitals are split into t_2g and e_g bands.

In group (i) materials, the t_2g and e_g bands hybridise with unoccupied O-2p orbitals to form part of the conduction band. Such hybridisation results in splitting of the O-2p states into which an O-1s electron is excited, resulting in the double peak in the O-K ELNES spectra.

In the case of group (ii) materials, the origin of the single sharp peak and small sub-peaks can also be explained in terms of the TM-d orbitals, with d orbitals in the conduction band splitting by different amounts as a result of their partial occupation (for details see Section S3 in ESI†).

O-K ELNES spectra of group (iii) materials contain only one broad peak, and are distinctly different to those of group (ii) materials despite also containing partially occupied TM-d orbitals. In addition, the peak positions of group (iii) materials are energetically higher than those of the other groups. These differences cannot be explained satisfactorily using a simple model of the electronic structure, so we simulated the ELNES of a group (ii) material, LiCoO₂, and a group (iii) material, LiFePO₄, using the core-hole method within the framework of DFT, analysing and comparing their electronic structures in detail.

3.4 O-K ELNES simulations of LiCoO₂ and LiFePO₄

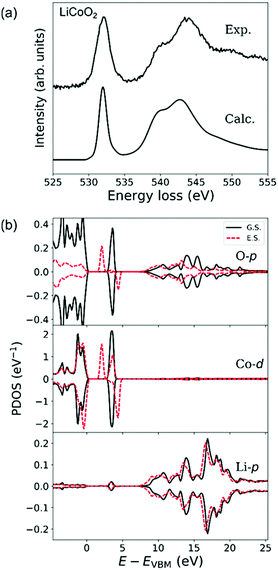
Fig. 5(a) shows experimental and simulated O-K ELNES spectra of LiCoO₂ when ΔE = 0.3 eV. The simulated spectrum matches the shape of the experimental spectrum well, as well as the calculated O-K X-ray absorption near edge structure.^47,48Fig. 5(b) shows PDOSs of O-p, Co-d and Li-p orbitals, with ground-state and excited-state PDOSs plotted as solid and dashed lines, respectively. The excited-state PDOSs are from the O atom containing the core hole in the case of the O-p orbital, and from Co and Li atoms neighbouring the excited O atom in the case of Co-d and Li-p orbitals, respectively.

Fig. 5 (a) Experimental and calculated ELNES spectra of the O-K edge of LiCoO₂ and (b) projected densities of states (PDOSs) of O-p, Co-d and Li-p orbitals in LiCoO₂. Solid lines are PDOSs for the ground state (G.S.) and dashed lines are for the excited state (E.S.). PDOSs of Co and Li in the excited state were extracted from atoms neighbouring the excited O atom.

In ground-state LiCoO₂, the valence band consists of Co-3d (t_2g) and O-2p orbitals and the conduction band of Co-3d (e_g), O-2p and Li-2p orbitals.^30,47 The octahedral environment of the Co atom causes Co-d orbitals to split into fully occupied t_2g states and unoccupied e_g states. The calculated band gap of 2.5 eV is consistent with previous DFT calculations.⁴⁸

Formation of an O-1s hole reduces the symmetry reduction of CoO₆ octahedra resulting in splitting of Co-d (e_g) orbitals hybridised with 2p orbitals of the excited O atom. This splitting lowers the conduction band minimum by about 1.5 eV, resulting in a lowering of the energy of the O-K edge, and produces the very small shoulder-like sub-peak in the tail of the main peak in the ELNES. Other changes in the shape of the broad hybridisation band between O-2p and Li-2p orbitals at energies higher than 7 eV in the excited state are also noticeable in the PDOS plots in Fig. 5(b). Since the O-K ELNES spectrum is produced by the transition of an O-1s electron to unoccupied O-p states, Fig. 5(b) shows that the single sharp ELNES peak at around 532 eV and the broad peak at energies higher than 536 eV originate from hybridisation of O-p orbitals with Co-d and Li-p orbitals, respectively.

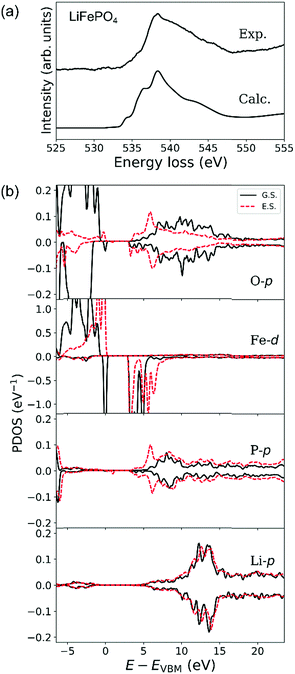
Experimental and calculated O-K ELNES spectra of LiFePO₄ using ΔE = 0.3 eV are compared in Fig. 6(a). Fig. 6(b) shows PDOSs of O-p, Fe-d, P-p and Li-p orbitals in ground and excited states in the same manner as for LiCoO₂ in Fig. 5(b) where PDOSs of the excited O atom and Fe, P and Li atoms neighbouring it have been averaged over contributions from crystallographically independent sites.

Fig. 6 (a) Experimental and calculated ELNES spectra of the O-K edge of LiFePO₄ and (b) projected densities of states (PDOSs) of O-p, Fe-d, P-p and Li-p orbitals in LiFePO₄. Solid lines are PDOSs for the ground state (G.S.) and dashed lines are for the excited state (E.S.). PDOSs of Fe, P and Li in the excited state were extracted from atoms neighbouring the excited O atom. Calculated O-p PDOSs and ELNES spectra are averages of data from O atoms on the three non-equivalent crystallographic sites in the olivine-type structure.

The calculated O-K ELNES spectrum in Fig. 6(a) has a single broad peak and appears more similar to the experimental spectrum compared to those previously calculated using the Z + 1 method¹⁹ or from dielectric function calculations.²⁰ This result demonstrates the efficacy of using the core–hole method to simulate the ELNES spectra with reasonable accuracy.⁶²

In the ground state, while the top of the valence band of LiFePO₄ consists of O-2p and Fe-3d orbitals, in the energy range from 3 to 5 eV above the valence band maximum (VBM), the conduction band mainly consists of O-2p and Fe-3d orbitals and the region with energies higher than 5 eV consists of O-p, P-p and Li-p orbitals (Fig. 6(b)). The relatively large differences between up- and down-spin contributions in PDOSs of Fe-d and O-p orbitals reflect the high-spin states of Fe²⁺ ions with a d⁶ electronic configuration, i.e., (t_2g)⁴(e_g)². The observed broad distribution of the O-p PDOS in the conduction band is a result of hybridisation between O-p orbitals and neighbouring Fe, P and Li orbitals. This overlapping of several orbitals in the conduction band is characteristic of LiFePO₄, in contrast to the clear separation between hybrid O–Co and Li–O orbitals in the conduction band of LiCoO₂.

When an electron is elevated from an O-1s shell in LiFePO₄, the PDOSs of O-p, Fe-d and P-p orbitals at the bottom of the conduction band (around 3 to 7 eV above the VBM) change dramatically, while their PDOSs at higher energies undergo relatively little change. Introduction of the core hole shifts the bottom of the conduction band, which in the ground state consists mainly of Fe-d electrons between 3 and 5 eV above the VBM, higher by about 1.5 eV. The PDOS of P-p orbitals between 5 and 7 eV above the Fermi level also increases dramatically, a consequence of the strong covalent bonding between P and O atoms. The band gap, however, remains essentially unchanged because Fe-d orbitals at the top of the valence band in the ground state are elevated to the bottom of the conduction band in the excited state. These changes enhance the energetic overlap between the Fe–O, Li–O and P–O hybrid orbitals, resulting in the characteristic broad peak in the O-K ELNES of LiFePO₄, in contrast to that of LiCoO₂. The broad single peaks observed for group (iii) materials (LiFePO₄ and LiCoPO₄) can thus be attributed to the presence of tetrahedral PO₄ units in addition to the TM–O polyhedra. Group (ii) materials, which lack PO₄ tetrahedral units, exhibit single, sharp O-K edges regardless of the overall crystal structure, e.g., layered-rocksalt in the case of LiCoO₂ or spinel in the case of LiMn₂O₄.

Although the band gaps of LiCoO₂ and LiFePO₄ are almost the same, the peak positions of O-K edges in LiCoO₂ and LiFePO₄ differ by about 6.7 eV. Our ELNES simulations also demonstrated a similar trend, with a calculated difference in peak positions of 4.9 eV. Analysis of the electronic structures showed that this difference arises from the difference in changes in the conduction bands in the excited state. As mentioned above, the peak in the O-K edge of LiCoO₂ corresponds to the conduction band minimum composed of hybrid O–Co orbitals, and decreases by about 1.5 eV upon introduction of a core hole. In the case of LiFePO₄, the conduction band minimum is not decreased when a core hole is introduced, and neither are there isolated hybrid O–TM orbitals. This difference provides one explanation for why the main peak of the O-K edge in LiFePO₄ appears at higher energy than in LiCoO₂.

4 Conclusions

Li-K and O-K ELNES spectra of ten different representative LIB materials were systematically investigated by EELS using an aberration-corrected TEM equipped with a monochromator. Measurements with a high energy resolution of ΔE = 0.1 eV revealed fine structures in Li-K ELNES spectra that can otherwise remain hidden. The peak positions of Li-K edges were found to be about 62 eV for most of the LIB materials because of the similar coordination environments of their Li ions. In contrast, the peak positions of O-K edges varied over a range of about 10 eV.

The shapes of O-K edges could be divided into three groups. Group (i) materials contained octahedrally coordinated TM ions with empty d orbitals, and these materials produced ELNES with double peaks at the O-K edges because of splitting of TM-d orbitals into t_2g and e_g levels. Group (ii) and (iii) materials both contained TM ions with partially filled d orbitals, but the shapes of their O-K edges were found to be distinctly different, the former with a single sharp peak and the latter with a single broad peak.

ELNES simulations based on DFT revealed that the single sharp peak in the O-K edge of group (ii) material LiCoO₂ results from hybridisation of O-p and Co-d e_g orbitals with energies close to the conduction band minimum. In contrast, the broad peak of the O-K edge of group (iii) material LiFePO₄ results from hybridisation between O-p orbitals with P-p, Fe-d and Li-p orbitals in the conduction band at similar energy levels.

Our systematic analysis of EELS spectra demonstrates how a combination of high-resolution ELNES measurements and simulations based on DFT calculations provides useful insights into the electronic structures and coordination environments of atoms in LIB materials.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was partially supported by the Research & Development Initiative for Scientific Innovation of New Generation Batteries 2 (RISING 2) project from the New Energy and Industrial Technology Development Organization (NEDO), Japan. The authors thank Toyota Motor Corporation for providing some of the samples.

References

1. J. M. Tarascon and M. Armand, Nature, 2001, 414, 359–367.
2. M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301.
3. J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603.
4. C. Sun, J. Liu, Y. Gong, D. P. Wilkinson and J. Zhang, Nano Energy, 2017, 33, 363–386.
5. P. E. Batson, Ultramicroscopy, 1992, 47, 133–144.
6. K. Suenaga, Science, 2000, 290, 2280–2282.
7. S. Muto and K. Tatsumi, Microscopy, 2016, 1–11.
8. K. J. Carroll, D. Qian, C. Fell, S. Calvin, G. M. Veith, M. Chi, L. Baggetto and Y. S. Meng, Phys. Chem. Chem. Phys., 2013, 15, 11128–11138.
9. R. Senga and K. Suenaga, Nat. Commun., 2015, 6, 7943.
10. W. Zhou, M. P. Oxley, A. R. Lupini, O. L. Krivanek, S. J. Pennycook and J.-C. Idrobo, Microsc. Microanal., 2012, 18, 1342–1354.
11. T. Mizoguchi, T. Sasaki, S. Tanaka, K. Matsunaga, T. Yamamoto, M. Kohyama and Y. Ikuhara, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 74, 1–10.
12. R. Huang, Y. H. Ikuhara, T. Mizoguchi, S. D. Findlay, A. Kuwabara, C. A. J. Fisher, H. Moriwake, H. Oki, T. Hirayama and Y. Ikuhara, Angew. Chem., Int. Ed., 2011, 50, 3053–3057.
13. R. F. Egerton, Electron Energy-Loss Spectroscopy in the Electron Microscope, Springer, US, Boston, MA, 3rd edn, 2011.
14. X. Gao, Y. H. Ikuhara, C. A. J. Fisher, H. Moriwake, A. Kuwabara, H. Oki, K. Kohama, R. Yoshida, R. Huang and Y. Ikuhara, Adv. Mater. Interfaces, 2014, 1, 1400143.
15. R. Huang, T. Hitosugi, C. A. J. Fisher, Y. H. Ikuhara, H. Moriwake, H. Oki and Y. Ikuhara, Mater. Chem. Phys., 2012, 133, 1101–1107.
16. L. Laffont, C. Delacourt, P. Gibot, M. Y. Wu, P. Kooyman, C. Masquelier and J. M. Tarascon, Chem. Mater., 2006, 18, 5520–5529.
17. T. Mizoguchi, J. P. Buban, K. Matsunaga, T. Yamamoto and Y. Ikuhara, Ultramicroscopy, 2006, 106, 92–104.
18. F. Wang, J. Graetz, M. S. Moreno, C. Ma, L. Wu, V. Volkov and Y. Zhu, ACS Nano, 2011, 5, 1190–1197.
19. S. C. Nagpure, S. S. S. Babu, B. Bhushan, A. Kumar, R. Mishra, W. Windl, L. Kovarik and M. Mills, Acta Mater., 2011, 59, 6917–6926.
20. M. K. Kinyanjui, P. Axmann, M. Wohlfahrt-Mehrens, P. Moreau, F. Boucher and U. Kaiser, J. Phys.: Condens. Matter, 2010, 22, 275501.
21. K. Kimoto and Y. Matsui, J. Microsc., 2002, 208, 224–228.
22. P. C. Tiemeijer, Inst. Phys. Conf. Ser., 1999, 161, 191.
23. M. Mukai, J. S. Kim, K. Omoto, H. Sawada, A. Kimura, A. Ikeda, J. Zhou, T. Kaneyama, N. P. Young, J. H. Warner, P. D. Nellist and A. I. Kirkland, Ultramicroscopy, 2014, 140, 37–43.
24. M. Mukai, E. Okunishi, M. Ashino, K. Omoto, T. Fukuda, A. Ikeda, K. Somehara, T. Kaneyama, T. Saitoh, T. Hirayama and Y. Ikuhara, Microscopy, 2015, 64, 151–158.
25. Z. Wang, D. Santhanagopalan, W. Zhang, F. Wang, H. L. Xin, K. He, J. Li, N. Dudney and Y. S. Meng, Nano Lett., 2016, 16, 3760–3767.
26. N. Taguchi, H. Sakaebe, K. Tatsumi and T. Akita, e-J. Surf. Sci. Nanotechnol., 2015, 13, 284–288.
27. X. Mu, A. Kobler, D. Wang, V. S. K. K. Chakravadhanula, S. Schlabach, D. V. Szabó, P. Norby and C. Kübel, Ultramicroscopy, 2016, 170, 10–18.
28. S. Kobayashi, C. A. J. Fisher, T. Kato, Y. Ukyo, T. Hirayama and Y. Ikuhara, Nano Lett., 2016, 16, 5409–5414.
29. P. Yan, L. Xiao, J. Zheng, Y. Zhou, Y. He, X. Zu, S. X. Mao, J. Xiao, F. Gao, J.-G. Zhang and C.-M. Wang, Chem. Mater., 2015, 27, 975–982.
30. J. Kikkawa, S. Terada, A. Gunji, M. Haruta, T. Nagai, K. Kurashima and K. Kimoto, Appl. Phys. Lett., 2014, 104, 114105.
31. J. Graetz, A. Hightower, C. C. Ahn, R. Yazami, P. Rez and B. Fultz, J. Phys. Chem. B, 2002, 106, 1286–1289.
32. P. Moreau and F. Boucher, Micron, 2012, 43, 16–21.
33. M. Kitta, T. Akita, S. Tanaka and M. Kohyama, J. Power Sources, 2013, 237, 26–32.
34. C. Ma, K. Chen, C. Liang, C.-W. Nan, R. Ishikawa, K. More and M. Chi, Energy Environ. Sci., 2014, 7, 1638.
35. Y. Honda, S. Muto, K. Tatsumi, H. Kondo, K. Horibuchi, T. Kobayashi and T. Sasaki, J. Power Sources, 2015, 291, 85–94.
36. J. Kikkawa, T. Akita, E. Hosono, H. Zhou and M. Kohyama, J. Phys. Chem. C, 2010, 114, 18358–18365.
37. K. Mizushima, P. Jones, P. Wiseman and J. Goodenough, Solid State Ionics, 1981, 3–4, 171–174.
38. A. K. Padhi, K. S. S. Nanjundaswamy and J. B. Goodenough, J. Electrochem. Soc., 1997, 144, 1188–1194.
39. M. M. Thackeray, W. I. F. David, P. G. Bruce and J. B. Goodenough, Mater. Res. Bull., 1983, 18, 461–472.
40. G. G. Amatucci, N. Pereira, T. Zheng and J.-M. Tarascon, J. Electrochem. Soc., 2001, 148, A171.
41. A. Yamada, S. C. Chung and K. Hinokuma, J. Electrochem. Soc., 2001, 148, A224.
42. L.-X. Yuan, Z.-H. Wang, W.-X. Zhang, X.-L. Hu, J.-T. Chen, Y.-H. Huang and J. B. Goodenough, Energy Environ. Sci., 2011, 4, 269–284.
43. J. M. Lloris, C. Pérez Vicente and J. L. Tirado, Electrochem. Solid-State Lett., 2002, 5, A234.
44. F. Zhou, M. Cococcioni, K. Kang and G. Ceder, Electrochem. Commun., 2004, 6, 1144–1148.
45. Q. Zhong, A. Bonakdarpour, M. Zhang, Y. Gao, J. R. Dahn, A. Bonakclarpour, M. Zhang, Y. Gao and J. R. Dahn, J. Electrochem. Soc., 1997, 144, 205.
46. K. Zhang, X. Han, Z. Hu, X. Zhang, Z. Tao and J. Chen, Chem. Soc. Rev., 2015, 44, 699–728.
47. M. T. Czyzyk, R. Potze and G. A. Sawatzky, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 3729–3735.
48. A. Juhin, F. de Groot, G. Vankó, M. Calandra and C. Brouder, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 1–12.
49. G. Rousse, J. Rodriguez-Carvajal, S. Patoux and C. Masquelier, Chem. Mater., 2003, 15, 4082–4090.
50. A. Nakamura, S. Furutsuki, S. Nishimura, T. Tohei, Y. Sato, N. Shibata, A. Yamada and Y. Ikuhara, Chem. Mater., 2014, 26, 6178–6184.
51. Y. H. Ikuhara, X. Gao, C. A. J. Fisher, A. Kuwabara, H. Moriwake, K. Kohama, H. Iba and Y. Ikuhara, J. Mater. Chem. A, 2017, 5, 9329–9338.
52. Y. H. Ikuhara, X. Gao, R. Huang, C. A. J. Fisher, A. Kuwabara, H. Moriwake and K. Kohama, J. Phys. Chem. C, 2014, 118, 19540–19547.
53. A. Kumatani, S. Shiraki, Y. Takagi, T. Suzuki, T. Ohsawa, X. Gao, Y. Ikuhara and T. Hitosugi, Jpn. J. Appl. Phys., 2014, 53, 058001.
54. Y. Fujiwara, K. Hoshikawa and K. Kohama, J. Cryst. Growth, 2016, 433, 48–53.
55. X. Gao, C. A. J. Fisher, T. Kimura, Y. H. Ikuhara, H. Moriwake, A. Kuwabara, H. Oki, T. Tojigamori, R. Huang and Y. Ikuhara, Chem. Mater., 2013, 25, 1607–1614.
56. M. O. Krause, J. Phys. Chem. Ref. Data, 1979, 8, 307–327.
57. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
58. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
59. F. Zhou, M. Cococcioni, C. A. Marianetti, D. Morgan and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 235121.
60. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
61. G. K. H. H. Madsen, P. Blaha, K. Schwarz, E. Sjöstedt and L. Nordström, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 64, 195134.
62. T. Mizoguchi, W. Olovsson, H. Ikeno and I. Tanaka, Micron, 2010, 41, 695–709.
63. J. Tsuji, H. Nakamatsu, T. Mukoyama, K. Kojima, S. Ikeda and K. Taniguchi, X-Ray Spectrom., 2002, 31, 319–326.
64. W. Olovsson, I. Tanaka, T. Mizoguchi, P. Puschnig and C. Ambrosch-Draxl, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 041102.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp03390k

‡ Authors contributed equally.

---