Interband transitions in closed-shell vacancy containing graphene quantum dots complexed with heavy metals

Abstract

High-performance optical detection of toxic heavy metals by using graphene quantum dots (GQDs) requires a strong interaction between the metals and GQDs, which can be reached through a functionalization/immobilization procedure or doping effect. However, commonly used surface activation approaches induce toxicity into the analysis system and, therefore, are ineligible from the environmental point of view. Here, we show that artificial creation of vacancy-type defects in GQDs can be a helpful means of intentional control of the active sites available for reaction with cadmium (Cd), mercury (Hg) and lead (Pb). Using restricted density functional theory (DFT) and time-dependent DFT (TD-DFT) methods, we predict the effect of vacancy complexes not previously studied to describe the binding ability of GQDs towards metal adsorbates. We also show that the interband absorption in closed-shell GQDs complexed with Cd, Hg and Pb is strongly dependent on the vacancy type and can be efficiently tuned to attain the desired coloration of the analysis system. The results suggest that the vacancy defects play an important role in governing the hybridization between locally-excited (LE) and charge-transfer (CT) states of the GQDs. Based on the molecular orbital analysis and in-depth knowledge of excited states, the mechanisms underlying the interband absorption are discussed.

---

1. Introduction

Toxic heavy metals (HMs) as a factor of environmental pollution are still one of the main problems of the present day.^1,2 Their high toxicity at relatively low concentrations³ and their exceptionally large bioaccumulation ability⁴ have a harmful effect not only on individual living creatures,^5,6 but also on the planetary ecosystem.^7,8 In response to this global challenge, the World Health Organization (WHO) has implemented environmental regulations to protect humankind from the most dangerous heavy metal pollutants.⁹ In accordance with the WHO requirements, first of all, it is necessary to control the content of the three most toxic heavy metals, namely cadmium (Cd),¹⁰ mercury (Hg),¹¹ and lead (Pb),¹² in food, soil, drinking water, outdoor and indoor air, and biological fluids. At present, the permissible levels of these hazardous elements in each of the categories have been determined.^10–12 To meet the WHO guidelines for minimal acceptable heavy metal concentrations in water, air and food, it is vitally important to realize fast methods for real-time detection of HMs and their removal/filtration.

During the last decades, extensive research efforts have mostly been focused on development/improvement of effective “bulky” detection methods (chromatography, mass spectrometry, etc.),^13–15 design of sensitive materials and devices (electrodes, hybrid structures, field emission transistors, and Schottky diodes),^16–25 and fabrication of potent adsorbents (filters, and membranes).^26–35 Considering the drawbacks of the traditional “bulky” time-consuming techniques, numerous research groups, nowadays, investigate graphene-family materials (graphene quantum dots, reduced graphene oxide, epitaxial graphene, etc.) as possible candidates for conceptualization of both sensors and adsorbents.^36–41

Being a two-dimensional (2D) monoatomic sheet of sp²-conjugated carbon atoms,⁴² graphene possesses unprecedentedly high sensitivity towards detection of individual atoms and molecules adsorbed onto its planar surface.⁴³ The basic physics underlying such detection is related to the possibility of local modulation of the charge-transfer reactions. It is reasonable to assume that providing as high a rate as possible of the electron-transfer reaction between graphene and adsorbates is an imperative requirement to consider graphene as an appropriate sensitive and adsorbing material. In other words, the most important parameters of a sensing device and an adsorbent (namely, the response time and the adsorption capacity) strongly depend on the interaction strength between graphene and the adsorbates we are interested in. The optimization of these parameters requires a deep understanding of the interaction mechanism. With respect to heavy metals, there are two fundamental processes governing this mechanism: (i) chemisorption of the HM divalent ions and (ii) physisorption of the HM neutral atoms. An ideal defect-free basal plane of graphene offers several high-symmetry adsorption sites (so-called bridge, hollow and on-top sites) for reaction with HMs. While the divalent Cd, Hg and Pb ions are found to be strongly bonded preferentially to these sites (providing large charge transfer conditions), the elemental HMs are differently physisorbed and bonded to graphene through weak dispersion (van der Waals) forces.⁴⁴ Furthermore, in the case of charged ions and neutral atoms of HMs immersed in liquids the interaction strength is very sensitive to the solvent effect and is significantly weakened due to the so-called solvent-involved cation–π interaction.⁴⁵ A major disadvantage of the basal plane of graphene towards HM adsorption is the poor sensitivity in those cases when the interaction mechanism is driven predominantly by the physisorption of neutral metal adatoms. For example, the most frequently used electrochemical techniques for HM detection (anodic stripping voltammetry, cyclic voltammetry and chronoamperometry) imply that the output signal of the graphene working electrode is related to HM-involved spontaneous redox reactions.⁴⁶ As the result of such reactions, the subsequent signal is proportional to the number of metal adatoms physisorped onto the graphene surface. Additionally, optical detection methods, namely UV-vis absorption spectroscopy and colorimetric detection, are also inappropriate approaches for recognition of elemental heavy metals because of insufficient quenching of the optical signal and negligible color changes, which remain invisible to the unaided eye.⁴⁶ Therefore, the effective adsorption of HMs requires that the graphene-family materials are appreciably functionalized/modified to provide the necessary reactive surface area.

Various materials were suggested for the activation of graphene surfaces to improve the sensitivity towards Cd, Hg and Pb.^47–57 Among them, special emphasis has been given to hybrid composites based on graphene-family nanomaterials^47–52 and surface-functionalized graphene with chemical moieties and immobilized recognition elements.^53–57 Unfortunately, in most cases the entire preparation procedure of the working electrode, sensitive solution electrolyte and active recognition element in sensing devices is still very complicated as it involves surface functionalization and multistage chemical reactions. Furthermore, as has been demonstrated for other carbon materials, especially for multi-wall carbon nanotubes, the surface functionalization with carbonyl, carboxyl, and hydroxyl groups can increase their toxicity.⁵⁸ In the light of global trends towards development of “green” fabrication technologies for new less harmful materials and chemicals,⁵⁹ utilizing highly-toxic functionalized graphene-based materials for detection and removal of heavy metals becomes less safe and less desirable. There is, therefore, a strong demand for development of an easy-to-use versatile platform (including only the key benefits of graphene) that allows both high-performance detection and effective removal of heavy metals. In this regard, introducing defects (mono-vacancies and vacancy complexes) into graphene-family materials can be an effective tool to enhance the adsorption ability of heavy metals, thereby avoiding surface functionalization/immobilization steps. Recently, it has been demonstrated that the defect-engineering approach in the case of graphene can promote the increase of the binding energy of alkaline-earth metals and hydrogen,⁶⁰ gas molecules and water,^61,62 Li,⁶³ Pt,⁶⁴ Cd,⁶⁵ Co⁶⁶ and 3d transition metals (from Sc to Zn).⁶⁷ Nevertheless, there is still a limited amount of data in the literature on the role of vacancy-related defects in the complexation between elemental toxic heavy metals and graphene-like structures.

In this article, we report a first-principles study of vacancy-assisted interactions between elemental heavy metals (Cd, Hg and Pb) and graphene quantum dots. Since the formation of vacancy-type defects may be accompanied by the appearance of unpaired electrons, we realize that heavy metal adsorption may occur on GQDs in the singlet and triplet states, i.e. on closed-shell and opened-shell structures. Nevertheless, the main aim of this work is to understand how the metal adsorbates will affect structural, electronic and optical properties of closed-shell GQDs having vacancy complexes. In this case, the increase in the local density of states at dangling bonds is expected to be responsible for the tuning of reactivity of GQDs, while the effect of the unpaired electrons (in the triplet state) on the binding ability is not considered here. Special focus will be given to understanding of the interband transitions that drive the optical response of GQDs after HM exposure and to the influence of the vacancy type on the excited states of the interacting constituents. We anticipate that this understanding will importantly advance the research on GQD-based sensing devices. The choice of GQDs as a representative of the graphene-family materials is justified by the fact that GQD-related systems are multifunctional platforms, which can be used for production of micron-sized solid sheets (a promising working electrode material for electrochemical detection of heavy metals),⁶⁸ catalysts accelerating the reaction with HMs,⁶⁹ modified working electrodes,^70,71 aqueous solution electrolytes for optical and colorimetric detection of heavy metals^72–82 and adsorbent agents for removal of heavy metals.^83–85

2. Theoretical approach

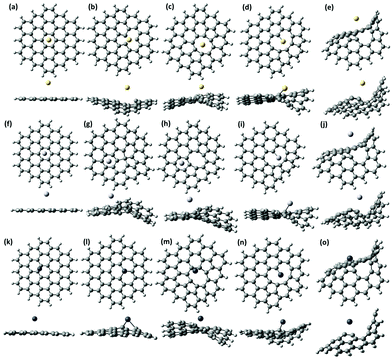
All quantum chemical calculations were carried out with the Gaussian 09 Rev. D.01 program package, using the default convergence criteria.⁸⁶ The zigzag-edged C₅₄H₁₈ (circumcoronene) polycyclic aromatic hydrocarbon (PAH) comprising 19 hexagonal benzene-like rings was chosen as a model structure of GQDs. This type of GQDs can absorb light very efficiently in the visible part of the spectrum and, therefore, can be used for colorimetric detection of heavy metals.⁴⁵ The creation of a monovacancy and complex vacancies can be simply modelled by removing one carbon atom and the nearest neighbour 2, 3, and 4 carbon atoms from the GQDs. Thus, five sets of geometrical configurations of GQDs were considered – the pristine defect-free GQDs and others with monovacancy, divacancy, trivacancy and tetravacancy defects in closed-shell singlet states (Fig. 1). All structures were terminated with the same number of hydrogen atoms. The equilibrium HM adsorption configurations were found by relaxing the HM@GQD (HM = Cd, Hg and Pb) complexes under gas-phase conditions using the PBE1PBE-D3 level of restricted DFT (which includes the empirical dispersion correction)⁸⁷ with a 6-311G(d,p) basis set for carbon and hydrogen atoms as well as a basis set developed by the Stuttgart–Dresden–Bonn group (SDD) for the heavy metal atoms.⁸⁸ Starting coordinates before geometry optimization were the same for all three metals in GQD@HMs complexes. In other words, we placed the HMs directly on the vacancy-type site of GQDs and then the structures were allowed to fully relax. Therefore, it is reasonable to assume that unique binding patterns for the GQDs and HM atoms only originate from the unique metal properties and the specific interaction between defects and metals. It should be mentioned that the PBE1PBE-D3 method takes explicitly London dispersion forces (or van der Waals forces) into account by using an additional term (which is proportional to R⁻⁶) and, therefore, this approach is suitable to describe the weak physisorption of elemental HMs onto the sp² plane. Since the main aim of the current work is to investigate the possible ways of enhancement of the interaction strength in the “HM@GQD” complex via artificial creation of vacancy defects (playing a role of reactive sites), a special focus is placed on the achievement of full control of the binding energy and charge transfer from adsorbates to GQDs. The binding energy of the heavy metal species to the defect-free and vacancy-containing GQDs was calculated by using the following equation:

E_b = −[E_GQD+HM − (E_GQD + E_HM)] (1)

where E_GQD+HM is the total energy of the GQD after complexation with the HM, E_GQD is the total energy of the isolated individual GQD, and E_HM is the total energy of an individual HM.

Fig. 1 Optimized structures of the pristine defect-free GQD (a) and GQDs with a carbon monovacancy (b), a divacancy (c), a trivacancy (d) and a tetravacancy (e).

The binding energies have been corrected for the basis set superposition error (BSSE) by means of the counterpoise method.⁸⁹ The charge transfer is calculated using Mulliken population analysis (MPA).⁹⁰ It should be mentioned that MPA is sensitive to the basis set and can, therefore, cause overestimation of the charge transfer magnitude in the interacting complexes, especially in those cases when diffuse and polarization functions are added to basis sets.⁹¹ These disadvantages mainly originate from the fact that MPA deals with nonorthogonal basis sets. On the other hand, Natural Population Analysis (NPA) can help to overcome this bottleneck, since this model implies the use of orthonormal natural atomic functions.^92,93 In contrast to MPA and NPA, the Hirshfeld model⁹⁴ can provide a clear partitioning of the electron density between all atoms belonging to the interacting complex and is regarded as a less basis-set dependent approach to predict atomic charges. To investigate the applicability of the MPA model for calculation of partial atomic charges on elemental heavy metals placed on GQDs, we compare the Mulliken population analysis to the Hirshfeld analysis, popular natural population analysis, and available reference data.

In the next step, in order to obtain the absorption spectra, density transition matrices and oscillator strengths for the most probable excited states, time-dependent density functional theory (TD-DFT) calculations were carried out on the full set of the GQD structures before and after complexation with elemental heavy metals using the same level of DFT theory (PBE1PBE-D3/6-311G(d,p)/SDD). The first 12 excited states were investigated and analyzed. In most cases any changes in the ultraviolet-visible (UV-vis) absorption spectra of GQDs after complexation with heavy metals can lead to changes in coloration of the interacting complexes. To estimate the possible colour changes perceived by the naked eye, we performed ab initio colorimetric calculations under daylight conditions based on the absorption spectra and colour-matching functions. The theoretical approach for simulation of the perceived colour can be found elsewhere.⁹⁵ It is obvious that understanding the fundamental physics underlying the colour changes of GQDs after interaction with Cd, Hg and Pb is an important step towards designing a printed and easy-to-use sensing platform for the real-time detection of elemental heavy metals.

3. Results and discussion

3.1 Equilibrium structures, reactivity and binding energies

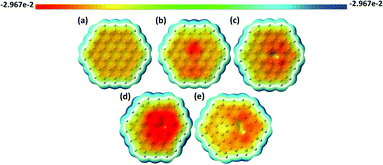
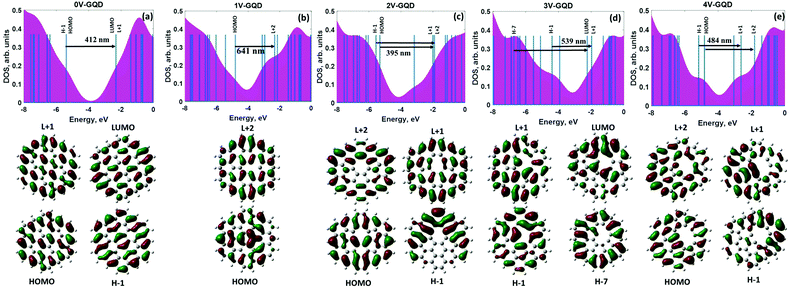
The mean size of vacancy-type defects should unambiguously define the local adsorption of heavy metals at the atomic scale.⁹⁶ In this regard, one of the most important parameters which allows us to estimate the role of the vacancies in affecting the interaction energy between elemental heavy metals and graphene quantum dots is the ability of the vacancy defects to trap electric charges. It is reasonable to assume that the changes in the spatial distribution of the wave-function near the carbon vacancies imply an enhancement of the electron density between the closest to the vacancy carbon species. This can be interpreted as the formation of shorter C–C bonds within inner carbon rings and even five-membered pentagonal carbon rings (Fig. 1). The first type of vacancy defect considered in our calculations is the monovacancy (Fig. 1b). In this configuration, after a vacancy is created, three sp² chemical bonds are broken and the atoms surrounding the vacancy site displace from their initial lattice positions. Consequently, the electrons that participate in broken bonds tend to localize around the single vacancy. Due to this reason localized vacancy energy levels can appear among the allowed molecular orbitals in GQDs. The second defect structure (the so-called 5–8–5 divacancy defect) is related to the removal of two carbon atoms, and, consequently, to the formation of an octagon at the vacancy site with two carbon pentagons (Fig. 1c). It is interesting to note that Liu et al.,⁹⁷ in a recent study, demonstrated that the most stable electronic state of the even-numbered vacancy-type graphene nanofragments (with the 5–8–5 divacancy defect) is a closed shell singlet state without unpaired electrons, while the presence of unpaired electrons was observed for the less stable structure with the 555777 divacancy in the triplet state. In contrast to this, Yumura et al.⁹⁶ showed that the triplet state of C₉₆H₂₆ with vacancy defects is more stable than singlet states and, thus, the available unpaired electrons improve the reactivity of the graphene structure towards platinum clusters. Although the single vacancy and double vacancy geometries are expected to be the most stable in graphene quantum dots, the formation of high-order vacancy-complexes, namely trivacancy⁹⁸ and tetravacancy⁹⁹ is also possible (Fig. 1d and e). A complete description of the binding ability of the GQDs containing vacancy complexes towards heavy metals requires accurate knowledge not only of the vacancy-induced redistribution of the carrier wave-function in GQDs, but also the DOS of a certain structure. For instance, the energetic positions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) levels with respect to the metal work function can affect the direction of the charge transfer between the metal adsorbate and the GQDs.¹⁰⁰ Before discussing the DOS for each structure presented in Fig. 1, the molecular electrostatic potential (MEP) will be examined to analyse the reactivity of the defective GQDs towards charge-controlled interaction with metals adsorbates. It should be mentioned that the deep analysis of the MEP surface enables determination of the most reactive sites across the sp²-plane of the GQDs, namely electron-sufficient and/or electron-deficient sites.¹⁰¹ As demonstrated in Fig. 2a, the basal plane of defect-free graphene does not provide efficient reactive sites for the chemical adsorption of elemental heavy metals. Indeed, according to electrochemical investigations of graphene,¹⁰² the basal plane of graphene is inactive. It is demonstrated by the homogenous distribution of the electrostatic potential (Fig. 2a). On the other hand, graphene is highly electrochemically active at the edge plane and near defect sites.¹⁰³

Fig. 2 Molecular electrostatic potential (MEP) surfaces for the pristine defect-free GQD (a) and GQDs with a carbon monovacancy (b), a divacancy (c), a trivacancy (d) and a tetravacancy (e). MEP surfaces were computed at the PBE1PBE-D3/6-311g(d,p) level of theory at an iso-value electron density of 0.004 atomic units. The values of the MEPs (in atomic units) are depicted by the colour bar at the top. The blue colour corresponds to excess positive charge, while the red colour represents the negatively charged regions.

In the case of defective GQDs, the MEP exhibits some local inhomogeneities near the vacancy defects (Fig. 2b–e). We note that we found a significant difference between the structures with odd and even numbers of missing carbon atoms. The spatial regions within monovacancy and trivacancy defects become more negatively charged than those within divacancy and tetravacancy defects. From the point of view of the GQD reactivity, the presence of negatively charged regions means that the vacancy defects with odd numbers of removed carbon atoms have a preferential ability to attract electrons belonging to elemental heavy metals compared to the structures with even numbers of missing carbon atoms (divacancy and tetravacancy). In other words, negatively charged carbon atoms around the monovacancy and trivacancy would allow enhancement of the interaction strength between graphene quantum dots and neutral metal adsorbates. A similar trend was observed for vacancy-containing graphene nanofragments interacting with Pt.⁹⁶ To support the aforementioned findings and to elucidate the nature of the enhanced chemical reactivity we further consider the effect of vacancy defects on the HOMO–LUMO energy gap (the difference between the energies of the lowest unoccupied molecular orbital and the highest occupied molecular orbital) of the GQDs. Table 1 summarizes the calculated dipole moment, HOMO (LUMO) energy position and HOMO–LUMO energy gap for each considered structure. We found that the main parameters of the molecular systems that we used to mimic GQDs are strongly correlated with the chemical reactivity. The calculated energy gap of the defect-free GQDs is approximately 3.07 eV, suggesting a pronounced semiconductor behavior of the GQDs. While the energy gap is found to decrease, when a vacancy defect is added. It is generally accepted that the HOMO–LUMO energy gap is related to the chemical hardness of the molecular system. In this regard, the systems with larger HOMO–LUMO gaps are more stable than those with small energy gaps. This is due to the fact that the narrow-band-gap materials have a reduced resistance to polarization of the electron cloud after interaction with external adsorbates. We also noticed that the energy gap of ONVTGQDs decreases much more compared with the even-numbered-vacancy-type GQDs (ENVTGQDs). One can assume that the presence of negatively charged regions in the defective GQDs plays an important role in providing high chemical reactivity. Naturally, the vacancy-induced HOMO–LUMO gap shrinking is explained by lowering of the LUMO level and upward movement of the HOMO level. Since the LUMO energy is the lowest energy orbital that can accept electrons, one can expect that its lowering will promote the charge transfer from the metallic adsorbate to the GQDs. Bearing this in mind, from Table 1 it is clearly seen that the GQDs with monovacancy and trivacancy defects are highly desired materials for strong chemisorption of neutral metal adatoms. The high magnitudes of the induced dipole moment for these systems would also translate into their enhanced ability to interact chemically with adsorbates. Finally, we revealed that the vacancy defects in GQDs play a role of perturbations that break the degeneracy of the electronic states near the HOMO and LUMO levels, thereby causing a lowering of the energy of unoccupied states and raising that of the occupied states.

Table 1 Calculated parameters of graphene quantum dots depending on the type of vacancy defect

Number of removed C atoms	Parameters
	Total energy, Hartree	HOMO, Hartree	LUMO, Hartree	HOMO–LUMO gap, eV	Dipole moment, Debye
0	−2067.03705028	−0.19785	−0.08501	3.0705	0
1	−2028.62547931	−0.17689	−0.11438	1.7010	1.3708
2	−1990.66580078	−0.19537	−0.11649	2.1464	0.8057
3	−1952.37281095	−0.15990	−0.14392	0.4348	1.0449
4	−1914.15744370	−0.17709	−0.11217	1.7666	0.2856

---

To find the equilibrium structures and the position of the adsorbed heavy metals we carried out geometry optimization using relaxed structures of the vacancy-containing GQDs presented in Fig. 1. By positioning heavy metal adatoms (Cd, Hg and Pb) above the centre of the vacancy defect, we investigated the favourable binding sites and binding energies. As can be seen from Fig. 3a, f and k, the physisorption of Cd, Hg and Pb on defect-free graphene quantum dots, which is predominantly regulated by van der Waals interactions, suggests no significant structural changes and therefore the GQDs complexed with HMs retain their planar structure. Expectedly, among the three heavy metals, our calculations yielded the lowest total energy for Cd and Hg atoms located at the hollow site (the center of the hexagonal ring), and 3.41 Å and 3.29 Å above the surface, respectively. While the Pb adatom tends to occupy the bridge site (above the centre of the C–C bond) at the equilibrium height 2.81 Å. It is interesting to note that the heavy metal adsorption onto defective GQDs induces a strong buckling into the system, propagating away from the adsorption site (Fig. 3). Such structural modifications accompany strong chemical bonding. We found that Pb adatoms located above the vacancy defects as if they saturate the vacancy-induced dangling bonds form shorter bonds with the closest carbon atoms belonging to GQDs than other metals. Even though all heavy metals for each considered configuration behave as electron donors (Table 2), the electron transfer occurring from Pb to GQDs is always significantly enhanced. The difference in the charge transfer between GQDs and Cd⁰, Hg⁰ and Pb⁰ adatoms can be understood in terms of the ionization energy of the metal.¹⁰⁴ The ionization potential of Pb⁰ is approximately equal to 7.41 eV,¹⁰⁵ whereas Cd and Hg have larger ionization energies of 8.99 eV and 10.43 eV,¹⁰⁵ respectively. Thus, Pb⁰ transfers electrons much more easily to the GQDs than Cd⁰ and Hg⁰ adatoms. This clearly explains why the Pb adatom behaves differently compared to the other atoms, which form weaker chemical bonds with the carbon atoms. As was predicted by the MEP mapping analysis, the charge transfer between GQDs with trivacancy defects and heavy metals reaches the highest value in comparison to the other interacting systems. We note that the aforementioned discussion is mainly related to explanation of the difference in partial atomic charges on heavy metals calculated by Mulliken population analysis. Nevertheless, as was mentioned before the results of MPA analysis are still questionable and the accuracy of this method needs to be addressed. In principle, the accuracy of population analysis is typically estimated by comparing it to data from experimental measurements.¹⁰⁶ To quantify the match between predicted and real data the experimental dipole moments of the molecules of interest can be used.¹⁰⁷ Nevertheless, due to the lack of high accuracy experimental benchmark data, it is a challenge to validate the existing charge analysis models. In our case, the results of supercell calculations using periodic boundary conditions to describe the charge transfer between graphene and elemental heavy metals can be, to some extent, regarded as reference data. According to the results of the Bader charge analysis of the 4  ×  4 graphene supercell interacting with heavy metals,⁴⁴ the atomic charges on Cd, Hg and Pb were estimated to be approximately +0.02, +0.05 and +0.27, respectively. It means that they behave as typical electron-donating adsorbates, providing effective charge transfer from the metal to the graphene. The tendency of charge transfer is consistent with that of ionization potential of the considered metals, implying that Pb can transfer electrons more easily to the graphene than other metals. Table S1 and Fig. S1 (ESI†) describe the calculated atomic charges on elemental heavy metals bound to the vacancy-free and vacancy-containing GQDs, in which the charge transfer directions predicted by Mulliken population analysis for all three metals on vacancy-free GQDs are similar to reference data. The results of Hirshfeld analysis and NPA are quite surprising because they contradict in some way reference data (with some exceptions). The Hirshfeld charge is found to be in good agreement with the Bader charge only for cadmium, while the NPA model well describes only the lead case. In other cases, these two models predicted the negative charges on heavy metals and, consequently, electron-accepting behaviour. Despite the numerical instability (dependence on the basis set) of the Mulliken population analysis, this model of partial atomic charge gives a reasonable picture of charge transfer processes between elemental heavy metals and GQDs and can be effectively used to understand the overall trend of the binding ability of GQDs to HMs.

Fig. 3 Optimized structures of pristine and defective GQDs (with monovacancies, divacancies, trivacancies and tetravacancies, respectively) after complexation with elemental heavy metals (top view and side view): Cd (a–e), Hg (f–j) and Pb (k–o). The number of the carbon vacancies in GQDs increases from the left to the right of the image.

Table 2 Calculated parameters of GQDs interacting with elemental heavy metals as a function on the number of removed C atoms

Number of removed C atoms	Parameters
	Total energy, Hartree			HOMO–LUMO gap, eV			Binding energy, eV			Charge on the HM atom
	HM@GQD
	Cd	Hg	Pb	Cd	Hg	Pb	Cd	Hg	Pb	Cd	Hg	Pb
0	−2234.782565	−2220.557882	−2070.413613	3.072	3.072	0.964	0.288	0.308	0.505	0.050	0.069	0.205
1	−2196.412087	−2182.216648	−2032.171152	1.992	2.738	1.739	1.406	2.222	5.107	0.067	0.085	0.364
2	−2158.421403	−2144.195379	−1994.141086	2.048	2.211	2.595	0.563	0.546	3.192	0.122	0.072	0.765
3	−2120.197808	−2105.937907	−1955.974080	1.466	1.219	2.372	2.451	1.513	6.620	0.902	0.576	0.772
4	−2082.026331	−2067.800643	−1917.744325	1.866	1.863	1.569	3.645	3.638	6.228	0.098	0.062	0.571

---

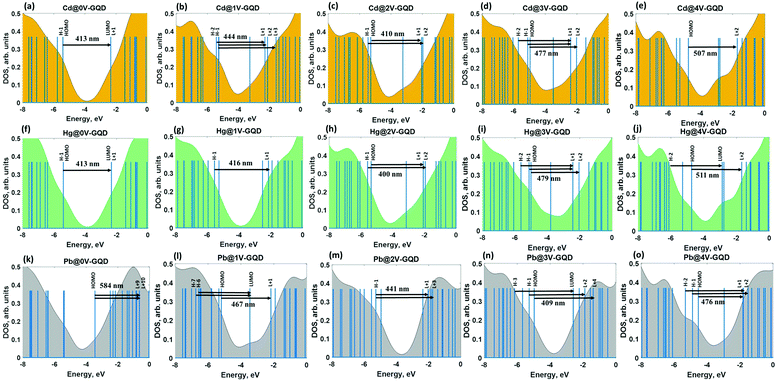
Having determined the relaxed structures, we next estimate the binding energy. All calculated parameters are summarized in Table 2. It is obvious that the artificial creation of vacancies in GQDs causes a significant increase of the binding energy of elemental heavy metals, allowing switching from a weakly physiosorbed state to a strongly chemisorbed state. These changes in the nature of the interaction between metal adsorbates and GQDs can be interpreted in terms of redistribution of the components contributing to the total binding energy. Considering the case of adsorption on defect-free GQDs, it is reasonable to assume that the interaction between Cd and Hg and GQDs occurs predominantly through dispersion forces, while the binding of Pb includes both the charge transfer and van der Waals interactions. On the other hand, the chemisorption of metals on defective GQDs involves also electrostatic interactions. Due to this reason, the binding energies are almost an order of magnitude higher compared to those describing the metal adsorption on the basal plane of defect-free GQDs. A significant point to note, however, is that the charge transfer contribution to the binding energy is more pronounced for Pb than Cd and Hg. Except for Cd and Hg adsorbed on GQDs with trivacancy defects, the binding in all remaining structures involves strong electrostatic interactions. It is not too surprising since Pb, by virtue of its low ionization potential, is able to easily donate electrons to GQDs, independently of the type of vacancy defects. Moving from the adsorbate-free defective GQDs (Table 1) to such with adsorbed HMs (Table 2) we notice that similarly to the previous case the increase of the removed number of carbon atoms causes significant HOMO–LUMO gap shrinking after Cd (Hg) adsorption. While HOMO–LUMO gap widening takes place for defective GQDs complexed with Pb adatoms. This is mainly due to the appearance of the hybridization states in vacancy-mediated interacting systems (this will be discussed below).

3.2 Interbrand absorption

Bearing in mind the knowledge about the adsorption ability of defective GQDs to heavy metals, we are aiming to understand the fundamental correlation between the binding energies of HMs and the optical properties of vacancy-containing GQDs. Such a holistic understanding will promote the correct interpretation of the experimental absorption spectra, thereby facilitating design of high-performance sensing devices. At the first step of our analysis we resolve the absorption spectra into partial contributions corresponding to the most probable excited interband transitions between occupied and unoccupied energy levels. Then we focus on the orbital composition analysis, which provides information about the nature of the molecular levels involved in these transitions.

3.2.1 Excited states in defective GQDs. The resulting spectra of the adsorbate-free defective GQDs are shown in Fig. 4a, while corresponding peak assignments can be seen in Tables S2–S6 (ESI†).

Fig. 4 Changes of the UV-vis absorption spectra with the introduction of the vacancy defects in GQDs before (a) and after complexation with Cd (b), Hg (c) and Pb (d). (e) Colour changes of the defect-free and defective GQDs after interaction with elemental heavy metals. 0 V, 1 V, 2 V, 3 V and 4 V designate monovacancy, divacancy, trivacancy and tetravacancy defects in GQD structures, respectively. (f) Histogram showing the oscillator strength ratios (f₀/f) of the GQDs in the absence and presence of elemental metal adatoms, where f₀ and f correspond to oscillator strengths of the most probable optical excited transitions in the pristine defect-free GQDs and defective GQDs after binding with Cd, Hg and Pb, respectively.

From this figure we conclude that the intensity of the absorption peak drastically decreases with increasing the vacancy defect size and the absorption band line-width tends to become broader. This effect can be attributed to the reduction of the oscillator strength caused by the defect-induced symmetry breaking. In addition, we notice the difference between absorption spectra of structures with odd and even numbers of missing carbon atoms. Particularly, ONVTGQDs exhibit a shift of the absorption peak towards the long-wavelength side and larger quenching of the absorption intensity, as is seen in Fig. 4a and 5(a–e). It is noteworthy that the red-shift of the absorption spectra in the visible range leads to changes in perceived coloration of the GQDs from a mustard green colour (defect-free GQDs) to dark blue (GQDs with monovacancies and trivacancies, respectively) and even black (GQDs with tetravacancies). While the system with the divacancy demonstrates no coloration changes compared to defect-free GQDs. The corresponding simulated colours are displayed in Fig. 4g. To understand the origin of the absorption peaks we performed DOS calculations for all considered structures. Since the HOMO−1 and HOMO as well as the LUMO+1 and LUMO are degenerate π and π* orbitals in defect-free GQDs (Fig. 5a), the absorption peak at 412 nm originates from the degenerate multi-level electronic transitions from the ground state to the S3 and S4 singlet excited states. Molecular orbitals which are involved in these transitions are shown in the bottom panel of Fig. 5a. Wave-functions of the aforementioned molecular orbitals are highly delocalized over the GQDs. Contrary to the doubly degenerate LUMO and HOMO in defect-free GQDs, the lowest orbitals in vacancy-containing GQDs split into nondegenerate orbitals (see Fig. 5b–e). Such a splitting is responsible for the change in the nature of the electronic excitations: from the doubly degenerate excited state in defect-free GQDs to a set of excited states in defective GQDs. The detailed description of the electronic transitions which involve the corresponding excited states is provided in ESI.†

Fig. 5 Density of states (DOS) of GQDs with different vacancy defects (shaded area): (a) no defects, (b) monovacancies, (c) divacancies, (d) trivacancies and (e) tetravacancies. The number of the removed carbon atoms from the GQD increases from the left to the right of the image. Blue vertical lines denote the molecular orbitals. The excited transitions between available occupied and unoccupied electronic levels are shown by horizontal black arrowed lines. The bottom panel exhibits the spatial distribution of wave-functions corresponding to the occupied and unoccupied orbitals which are involved in electronic transitions in GQDs. The red and green colours indicate positive and negative phases in the wave function, respectively. The orbitals are drawn at an isosurface value of 0.02.

To shed more light on the nature of the interband absorption in GQDs we computed the transition density matrix¹⁰⁸ for the lowest excited states in each GQD (Fig. 6a–e). It should be mentioned that in most cases the excited state can have two components: a locally-excited (LE) state and a charge-transfer (CT) state.¹⁰⁹ Detailed analysis of the matrix elements allows us two distinguish between them. Indeed, the diagonal terms of the transition density matrix correspond to the charge variation of the corresponding atoms and, consequently, represent the LE character of the excited state, while the off-diagonal terms are related to the CT component exhibiting electron–hole coherence between the corresponding atoms.¹¹⁰ The 2D-grid map for the defect-free GQDs (Fig. 6a) indicates the LE character dominates in the S4 state. Additional evidence for the correct determination of the type of electron excitation can be found through comparing the charge-transfer length (Δr), the electron–hole wave-function overlap integral (S) and the distance between centroids of holes and electrons (D) for the corresponding excited state.¹¹¹ All these parameters are listed in Dataset 1 (ESI†). Δr and D of the S4 state are negligibly small, as shown in Dataset 1, while this state is characterized by a large overlap integral. It means that the electrons and holes are localized without obvious charge transfer. This is because the graphene quantum dot is a highly delocalized system and thus a strong coherence between sp²-bonded carbon atoms is observed. It is interesting to note that the S0 → S4 transition preferentially involves “edge” carbon atoms labeled 25–54, while central carbon atoms (labeled 1–24) belonging to inner hexagonal rings are less involved in excited transitions. In the case of ONVTGQDs (Fig. 6b and d), the contribution of the CT component to the lowest excited states, namely S5 and S11 (for monovacancy and trivacancy), becomes larger compared to that of the defect-free GQDs and the bright regions within the corresponding maps are distributed more homogeneously over the GQD plane. In line with this, S5 and S11 states have larger charge-transfer lengths (0.71 Å and 1.16 Å, respectively), and smaller overlap integrals. Therefore, one can classify these states as LE–CT hybridized states. When two carbon atoms are removed from a GQD, the brightest zones are concentrated across the diagonal of the color-filled map (Fig. 6c), indicating the partial LE character of the S10 state. This implies preferential participation of the edge carbon atoms labeled 41–52 and inner carbon atoms labeled 16–21 (which surround the divacancy complex) in optical transitions. We also noticed that due to the large charge-transfer length (1.935 Å) the S5 excited state in GQDs with tetravacancies (Fig. 6e) can be explained as originating from the formation of a hybridized state with increased contribution from the CT component.

Fig. 6 Two-dimensional colour-filled representation of the TDM for the most probable S4 ← S0, S5 ← S0, S10 ← S0, S11 ← S0, and S5 ← S0 excited states in GQDs without interaction with elemental heavy metals: (a) no defects, (b) monovacancies, (c) divacancies, (d) trivacancies and (e) tetravacancies. A colour scale bar is shown on the right of each contour plot. A brighter colour indicates a higher probability of finding the generated electron–hole pair.

3.2.2 Excited states in defective GQDs interacting with elemental HMs. In comparison to the adsorbate-free defective GQDs, the charge transfer from metal adsorbates to GQDs leads to changes in the DOS spectra of GQDs and, consequently, to a redistribution of the molecular levels involved in the excited states. It clearly manifests itself in many ways, from coloration changes (Fig. 4e) to signal quenching (Fig. 4g). Furthermore, we revealed a direct correlation between the perceived colour and binding energy. Weakly interacting systems (Cd or Hg adatoms with defect-free and divacancy-containing GQDs) do not change their coloration compared to the corresponding adsorbate-free GQDs. Contrary to this, the complexes with high interaction energy exhibit large difference in the perceived colour. Converting our theoretical data into colorimetric parameters, we also noticed that the ONVTGQDs are more desirable systems for colorimetric sensing of Cd and Hg. Since Pb interacts with defect-free and vacancy-containing GQDs in a much stronger manner than Cd and Hg, we observed completely different pictures of the interband absorption with large contributions from hybridized and localized energy levels to excited states. This is consistent with the coloration of GQDs complexed with Pb. Fig. 4g shows that monitoring of the interband absorption in defective GQDs is a sensitive method for metal identification, since f₀/f increases after interaction with metals in a unique manner depending on the type of the vacancy defect. In this case, the oscillator strength ratio can be related to the quenching efficiency. From a practical point of view, this means that sensor arrays consisting of GQDs with different types and densities of vacancy defects can enable discriminative multi-metal analysis. To move toward a more detailed description of the excited transitions in ONVTGQDs and ENVTGQDs after adsorption of elemental heavy metals, in the following we consider the features of the interband absorption for each of the considered metal adsorbates. The main trends we noticed are that the charge-transfer length (Δr) for the most probable excited states increased significantly with increasing the size of vacancy-type defects in GQDs interacting with Cd and Hg (see Dataset 1, ESI†), while Δr was found to decrease for excited states in defective GQDs after lead adsorption. This implies the fundamental role of carbon vacancies in the redistribution of the charge density during the interband transition in strongly interacting complexes. Therefore, it is important to gain deep insights into the nature of the excited states depending on the type of vacancy and kind of heavy metal.

3.2.3 Excited states in defective GQDs interacting with elemental Cd. As can be seen from Fig. 4b, Fig. 7(a–e) and Table 2, the interband absorption in GQDs complexed with neutral Cd adatoms depends on the binding energy. The increase in the number of removed carbon atoms causes a stronger interaction between Cd and GQDs and significant HOMO–LUMO gap shrinking, followed by the red-shift of the absorption peak, except in the case of GQDs with divacancies (where a slight blue-shift is observed). It is interesting to note that the adsorbate-free GQDs with monovacancies and trivacancies yielded a larger redshift of the broad excitation band than similar GQDs with adsorbed Cd (Fig. 7). This is mainly due to the vacancy-assisted strengthening of the interaction between Cd and GQDs. For the defect-free GQDs complexed with Cd through weak van der Waals interactions (Fig. 7a), the absorption spectrum is dominated by an intense peak at 413 nm with an oscillator strength of 0.9509. Like the pristine GQDs, two degenerate excited states contribute to this absorption band (S5 ← S0 and S6 ← S0). The corresponding electronic transitions which are involved in these excited states are listed in Table S7 (ESI†). Wave functions for the molecular orbitals are highly delocalized over the defect-free GQDs (Fig. 8a). Fig. 9a indicates that the electron–hole coherence for the S5 state (dominated by π–π* transitions) is quite strong within the inner carbon atoms labelled 1–6. The electrons and holes are all localized in the bottom left corner of the map, and therefore the S5 state can be classified as a LE state. The absorption spectra of the GQDs with monovacancies and divacancies after interaction with elemental Cd originate from the S11 excited states observed at 444 nm and 410 nm (Tables S7 and S8, ESI†), respectively. The 444 nm-peak is associated with a combination of electronic transitions: H−6 → LUMO (15%), H−2 → L+1 (25%), H−1 → L+2 (29%), and H−1 → L+3 (26%). We noticed the hybrid nature of the H−2 level, with partial contribution of Cd, as low as 9% (Fig. 8b), while the strongly hybridized HOMO level is not involved in these transitions. According to the TDM map for the S11 excited state (Fig. 9b), the electrons still strongly cohere with holes within inner carbon atoms labelled 1–6, but the contribution of the intermolecular charge transfer component to the excited state increases. The nature of the S11 state in GQDs with divacancies can be interpreted as a combination of the following electronic transitions: H−5 → LUMO (10%), H−1 → L+2 (50%), and HOMO → L+1 (24%), while the second less intense feature at 426 nm (the S10 state) can be assigned to H−7 → LUMO (23%), H−1 → L+1 (47%) and HOMO → L+2 (23%) transitions (Table S9, ESI†). The orbital composition analysis provides evidence that the hybridized H−1 (Fig. 8c) and LUMO molecular orbitals are involved in these transitions. The contribution of Cd to these levels is found to be 41% and 5%, respectively. Since the Cd-related occupied H−1 molecular level plays an important role in the S11 excited state, the transition density matrix should reflect this role. Indeed, as can be seen from Fig. 9c intermolecular charge transfer dominates over the LE component. It is obvious that electron–hole coherence occurs at both the right and top edges of the map. In other words, S11 is an intermolecular electric charge transfer state, in which electrons and holes cohere between cadmium and outer carbon atoms belonging to GQDs. Analysis of the absorption spectrum of the GQDs with divacancy defects indicates that the S11 excited state has a larger electronic transition probability compared to other excited states (Fig. 7d and Table S10, ESI†). The most notable result of the complexation of trivacancy-containing GQDs with elemental Cd is the appearance of the hybridized CT–LE state (Fig. 9d). Since the hybridized LUMO level participates in electronic transitions, we observe that electrons and holes cohere between cadmium and edge carbon atoms. In addition, the bright regions in the left bottom corner of the map suggest both electrons and holes are localized on the inner carbon atoms. The interband absorption in GQDs with tetravacancies (Fig. 7e and Table S11, ESI†) is characterized by the appearance of two dominating features at 507 nm (with an oscillator strength of 0.1892) and 632 nm (0.1097). The band at 507 nm is assigned to the HOMO → L+2 transition, while the most likely transitions contributing to the 632 nm absorption are H−2 → LUMO (23%), and H−1 → L+1 (61%). The full assignments of the corresponding transitions are summarized for each transition in Table S11 (ESI†). The orbital compositional analysis suggests that among all aforementioned molecular orbitals only H−2 is highly hybridized (Cd contribution, 74%), whereas the wave-functions of the remaining molecular orbitals are delocalized over the defective GQDs. Since the Cd-related orbitals are not involved in the S7 excited state (Fig. 8e), both electrons and holes are localized on the inner carbon atoms, thereby indicating the dominating role of the LE state.

Fig. 7 Calculated DOS (shaded area) of the GQDs (without and with vacancy defects) interacting with elemental heavy metals: (a–e) Cd, (f–j) Hg and Pb (k–o). Blue vertical lines denote the molecular orbitals. The excited transitions between available occupied and unoccupied electronic levels are shown by horizontal black arrowed lines.

Fig. 8 Images demonstrating the spatial distribution of wave-functions corresponding to occupied and unoccupied orbitals which are involved in electronic transitions in defect-free and defective GQDs after interaction with elemental heavy metals: (a–e) Cd, (f–j) Hg and Pb (k–o) Pb. The number of the carbon vacancies in GQDs increases from the left to the right of the image. The red and green colours indicate positive and negative phases in the wave function, respectively. The orbitals are drawn at an isosurface value of 0.02.

Fig. 9 Contour plots of transition density matrices of defect-free and defective GQDs after interaction with elemental heavy metals: (a–e) Cd, (f–j) Hg and Pb (k–o). The number of the carbon vacancies in GQDs increases from the left to the right of the image. A colour scale bar is shown on the right of each colour-filled map. A brighter colour indicates a higher probability of finding the generated electron–hole pair.

3.2.4 Excited states in defective GQDs interacting with elemental Hg. Fig. 7(f–j) illustrates the transitions from the occupied electronic states to the empty levels, which contribute to the intensive peak in the absorption curves demonstrated in Fig. 4c. Based on the analysis of the existing transitions in defect-free GQDs interacting with Hg (Fig. 7f), one can observe that the dominant contribution to the S4 excited state at 413 nm arises from the combination of the electronic transitions: H−1 → LUMO (25%), H−1 → L+1 (22%), HOMO → LUMO (22%), and HOMO → L+1 (25%). The wave-functions for all these molecular orbitals are delocalized over the GQD (Fig. 8f). Like the adsorbate-free GQD case, the 2D-grid map for defect-free GQDs interacting with Hg (Fig. 9f) indicates the LE character dominates in the S4 state. Nevertheless, electron–hole coherence occurs mainly within the inner carbon atoms in the central part of the GQDs. Three intense features can be distinguished in the absorption spectrum of the monovacancy-containing GQDs complexed with Hg (Table S12, ESI†). The dominant feature at 416 nm (with an oscillator strength of 0.360) can be ascribed to H−1 → L+1 electronic transitions. According to the orbital compositional analysis, neither H−1 nor L+1 have contributions from Hg (Fig. 8g). Only GQD-related levels are involved in these transitions. Since Hg-related orbitals do not participate in the electronic transitions, the LE character is prevailing in the S8 state (Fig. 9g). In the case of the divacancy the absorption peak is blue-shifted by 16 nm (Fig. 7h), and the nature of the electronic transitions becomes more complicated (Table S14, ESI†). This is due to the fact that the hybrid H−6 (GQD: 89%, Hg: 11%) orbital starts to participate in the excited transitions. The most intense peak at 400 nm is due to the combination of two close transitions, such as H−1 → L+2 (54%), and HOMO → L+1 (14%). These frontier molecular orbitals are completely delocalized over the GQD (Fig. 8h). The mercury adatom does not participate in the optical excitation S11 ← S0 (Fig. 9h). In this case, the nature of excited transitions can be understood in terms of a strongly hybridized CT–LE state. On one hand, we observe a large electron transfer (off-diagonal coherence) from the edge carbon atoms to the inner carbon atoms and vice versa. On the other hand, one can see the bright regions in the bottom left corner of the map and the top right corner of the map (diagonal coherence), indicating partial LE character of the S11 excited state. A further increase in the number of the removed carbon atoms (from 2 to 3) causes localization of the HOMO and the LUMO level mainly on the Hg adsorbate (Fig. 8i), followed by a significant drop in the absorption intensity and a red-shift of the absorption band from 400 to 479 nm (Fig. 7i). The adsorption spectrum of tri-vacancy containing GQDs is dominated by the single excited state S12 with an oscillator strength of 0.2915. The nature of this state can be attributed to the following transitions: H−2 → L+1 (23%), H−1 → L+1 (14%), and HOMO → L+2 (38%). Because of the appearance of the hybridized HOMO (the Hg contribution is about 86%) level, we revealed off-diagonal coherences between Hg and edge carbon atoms, which implies that the CT character dominates in the S12 state. Being complexed with Hg tetravacancy-containing GQDs demonstrates an observable decrease in the oscillator strength of the major transitions. We can ascribe this decrease to the non-symmetric nature of the GQD, which manifest itself in large splitting of the lowest occupied and highest unoccupied levels belonging to the GQD into a set of well-distinguished energy levels (Fig. 7j). As an important consequence, the transitions from H−2 to the LUMO (23%) and from the HOMO to L+2 (45%) become allowed and generate the most intense absorption feature at 511 nm (with an oscillator strength of 0.1219). The second peak with an oscillator strength of 0.1168 appears at 617 nm and involves the transitions from H−1 to L+1 (83%) and from the HOMO to L+2 (11%). Among these molecular levels only H−2 has a small contribution from the Hg adsorbate (less than 19%). Analysis of the TDM map indicates that the S5 excited state is dominating the matrix elements (the bottom left corner of the map), implying a dominant contribution of the LE component (Fig. 9j).

3.2.5 Excited states in defective GQDs interacting with elemental Pb. Moving our attention to the absorption spectra of GQDs complexed with Pb, in the following we gain insights into the origin of the electronic transitions in the presence of vacancy defects. The corresponding absorption spectra are illustrated in Fig. 4c, while peak assignments are presented in Tables S16–S20 (ESI†). In the absorption spectrum of defect-free GQDs interacting with Pb three weak bands at 539, 584 and 672 nm can be observed (Table S17, ESI†). The most intense peak at 584 nm can be identified as an overlapped multi-level transition, including contributions from HOMO → L+7 (14%), HOMO → L+9 (16%) and HOMO → L+10 (59%). In this case, hybrid HOMO and L+10 levels are involved in the S10 excited state (Fig. 8k). As can be seen for the TDM map, the nature of the S10 excited state can be interpreted as a hybridized state with large contribution from the CT component. As can be seen from the Dataset (ESI†) this state is characterized by the large value of Δr (2.13 Å) and small value of the overlap integral (0.29). The dualistic nature of this state is related to the fact that the electrons and holes are localized on the inner carbon atoms labelled 1–21 (see the bright region in the bottom left corner of the map) and the electron–hole coherence is strong because of the electron transfer between Pb and GQDs (see the bright regions across the right edge and top edge of the map). Like in the vacancy-mediated interband absorption in GQDs interacting with Cd and Hg, the vacancies also play an important role in the redistribution of the excited states in GQDs after complexation with Pb. We explain these phenomena by vacancy-induced strengthening of the charge transfer and electrostatic interaction between Pb and GQDs. A clear blue-shift of the most prominent absorption peaks can be seen in Fig. 7(k–o). Passing from the pristine GQDs to monovacancy-containing GQDs, we noticed that the absorption spectrum is mainly dominated by a peak at 467 nm with an oscillator strength of 0.1896. A detailed analysis of the calculated results indicates that three transitions contribute to the S10 excited state, including H−7 → LUMO (26%), H−6 → LUMO (26%) and HOMO → L+1 (27%). These transitions contribute almost equally to the absorption peak. The contribution of Pb to the LUMO, H−6, and H−7 is found to be negligibly small (Table S18, ESI†). Fig. 8l illustrates the contributing orbitals which are involved in the corresponding transitions. In this case, we noticed the presence of the CT–LE state with increased contribution from the LE state (Fig. 9l). This is also evidenced by a simultaneous increase in the overlap integral and a decrease in the charge-transfer length (see Dataset 1, ESI†). Further increase of the number of removed carbon atoms from 1 to 2 and 3 leads to a subsequent shift of the absorption peak of Pb²⁺@GQD towards the short-wavelength side and an enhancement of the absorption intensity, as seen in Fig. 4c. Considering the absorption spectrum of GQDs with divacancies one can see that two bands, at 421 and 441 nm, can be distinguished. The dominating peak at 441 nm is related to the following transitions: H−1 → L+1 (60%) and H−1 → L+3 (15%). The matrix elements associated with the S8 state (Fig. 9m) are rather homogeneously distributed across the map, suggesting a large degree of hybridization between CT and LE modes. The absorption spectrum of the trivacancy-containing GQDs complexed with Pb mainly originates from two excited states – S6 at 482 nm and S11 at 409 nm. The S6 state is dominated by two transitions, from the HOMO to L+2 (61%) and from the HOMO to L+3 (15%). The Pb is contributing to both L+2 (10%) and L+3 (32%). The last feature at 409 nm is dominated by three transitions from the GQD-related occupied levels to unoccupied levels: H−3 → LUMO (14%), H−1 → L+2 (36%) and HOMO → L+4 (20%). For L+4, the contribution of Pb is approximately 30%. The transition density matrix describing the S11 state shows strong mixing between LE and CT states (Fig. 9n) implying a high degree of hybridization. It is evidenced by the simultaneous presence of electron–hole coherence in both diagonal and off-diagonal directions (bright regions in the bottom corner of the map as well as off-diagonal matrix elements corresponding to the charge transfer between inner and outer carbon atoms). Finally, due to significant structural modifications, which appear in tetravacancy-containing GQDs after adsorption of elemental Pb adatoms, the interband absorption is characterized by small oscillator strengths for the main transitions (see Table S21, ESI†). The major feature at 476 nm corresponding to the S10 excited state (see Fig. 7o) is related to a mixture of three transitions: H−2 → L+1 (11%), H−1 → L+2 (61%) and HOMO → L+1 (17%). The wave-functions for all these orbitals are shared between the Pb adsorbate and the defective GQD (Fig. 8o). The matrix elements related to the S10 state are distributed in both the diagonal and off-diagonal directions (Fig. 9o), indicating the hybridized nature of this state. The brightest region is located in the bottom left corner of the map, representing the dominating role of LE character, which includes inner carbon atoms labelled 1–15.

4. Conclusions

We have employed DFT and time dependent (TD) DFT methods to theoretically investigate the structure, electronic and optical properties of vacancy-containing closed-shell GQDs (monovacancy, divacancy, trivacancy and tetravacancy) complexed with elemental heavy metals (Hg, Cd and Pb). We have provided evidence that the vacancy engineering can promote a strong interaction between graphene quantum dots and metal adsorbates, which allows for better optical detection of Cd, Hg and Pb. We found that the monovacancy and trivacancy defects are very active for the reaction with HMs compared to the defect-free and even-numbered vacancy type GQDs, which originates from the presence of negatively charged regions facilitating the charge transfer between metal adsorbates and GQDs. Since the interaction mechanism between Pb and GQDs is mainly governed by charge transfer, the adsorbed Pb atoms tend to bind more strongly near vacancy defects compared to Cd and Hg. An important finding is that the vacancy-assisted interaction with HMs causes atomic-scale buckling of the initially flat sp² plane of GQDs, which becomes larger with an increase in the size of the vacancy defect. Therefore, a trade-off between the stability of GQDs and their reactivity must be reached to provide effective local modulation of the density of active surface sites. We revealed the fundamental correlation between the coloration of the GQDs and interaction strength of the HM@GQD complexes implying that the color changes can be distinguished only for strongly interacting systems. Furthermore, we find that there are two different mechanisms of interband absorption in GQDs interacting with HMs depending on the presence of the vacancy defects: the locally-excited character dominates the lowest excited singlet transitions in the defect-free GQDs complexed with Cd and Hg, while the hybrid coupled states with charge-transfer and locally excited components are more favorable for vacancy-containing GQDs after adsorption of Cd and Hg. Through the analysis of the excited states in GQDs interacting with Pb, we found strong charge-transfer channels between defect-free GQDs and Pb as well as a decrease of the charge-transfer length in the presence of vacancies. The transformation of the excited state character from the pure locally-excited (LE) state and/or pure CT state to the hybridized state is found to be accompanied by redistribution of the molecular energy orbitals which are involved in the allowed electronic transitions as well as participation of the HM-related orbitals affecting the electron–hole coherence under excitation conditions. Our work provides deep insights into the nature of the mechanisms underlying the vacancy-mediated interaction between graphene quantum dots and elemental heavy metals. The output from this advanced understanding will promote the fabrication of colorimetric sensor arrays based on vacancy-containing GQDs.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to thank financial support via VR grant 621-2014-5805 and SSF (SSF GMT14-0077, SSF RMA15-0024). Dr I. Shtepliuk acknowledges the support from Wallenberg foundation and Ångpanneföreningens Forskningsstiftelse (Grant 16-541). All calculations were performed using the supercomputer resources of the Swedish National Infrastructure for Computing (SNIC), National Supercomputing Center (NSC).

Notes and references

1. https://www.eea.europa.eu/data-and-maps/indicators/eea32-heavy-metal-hm-emissions-1 .
2. S. A. Mansour, in Heavy Metal Contamination as a Global Problem and the Need for Prevention/Reduction Measurements, in Practical Food Safety: Contemporary Issues and Future Directions, ed. R. Bhat and V. M. Gómez-López, John Wiley & Sons, Ltd, Chichester, UK, 2014.
3. P. B. Tchounwou, C. G. Yedjou, A. K. Patlolla and D. J. Sutton, Heavy Metals Toxicity and the Environment, EXS, 2012, 101, 133–164.
4. A. Khan, S. Khan, M. Amjad Khan, Z. Qamar and M. Waqa, The uptake and bioaccumulation of heavy metals by food plants, their effects on plants nutrients, and associated health risk: a review, Environ. Sci. Pollut. Res., 2015, 22, 13772.
5. M. Jaishankar, T. Tseten, N. Anbalagan, B. B. Mathew and K. N. Beeregowda, Toxicity, mechanism and health effects of some heavy metals, Interdiscip. Toxicol., 2014, 7(2), 60–72.
6. R. Singh, N. Gautam, A. Mishra and R. Gupta, Heavy metals and living systems: An overview, Indian J. Pharmacol., 2011, 43(3), 246–253.
7. J. Puhe and B. Ulrich, Global Climate Change and Human Impacts on Forest Ecosystems: Postglacial Development, Present Situation and Future Trends in Central Europe, Springer, Heidelberg, Germany, 2001.
8. E. Rosenberg, in Heavy Metals in Water: Presence, Removal and Safety, ed. S. K. Sharma, Royal Society of Chemistry, Cambridge, 2015.
9. http://www.who.int/ipcs/assessment/public_health/chemicals_phc/en/ .
10. http://www.who.int/ipcs/assessment/public_health/cadmium/en/ .
11. http://www.who.int/ipcs/assessment/public_health/mercury/en/ .
12. http://www.who.int/ipcs/assessment/public_health/lead/en/ .
13. H. M. Hussein, Analysis of trace heavy metals and volatile chemical compounds of Lepidium sativum using atomic absorption spectroscopy, gas chromatography-mass spectrometric and fourier-transform infrared spectroscopy, Res. J. Pharm., Biol. Chem. Sci., 2016, 7(4), 2529–2555.
14. S. L. Stegall, K. M. Ashraf, J. R. Moye, D. A. Higgins and M. M. Collinson, Separation of transition and heavy metals using stationary phase gradients and thin layer chromatography, J. Chromatogr. A, 2016, 1446, 141–148.
15. L. J. Paliwal, S. M. Waiyari and L. Deshmukh, Rapid separation of some toxic heavy metal ions by thin layer chromatography, Rasayan J. Chem., 2011, 4(3), 630–635.
16. Y. Lu, X. Liang, C. Niyungeko, J. Zhou, J. Xu and G. Tian, A review of the identification and detection of heavy metal ions in the environment by voltammetry, Talanta, 2018, 178, 324–338.
17. G. Zhao, H. Wang and G. Liu, Recent advances in chemically modified electrodes, microfabricated devices and injection systems for the electrochemical detection of heavy metals: A review, Int. J. Electrochem. Sci., 2017, 12(9), 8622–8641.
18. B. Bansod, T. Kumar, R. Thakur, S. Rana and I. Singh, A review on various electrochemical techniques for heavy metal ions detection with different sensing platforms, Biosens. Bioelectron., 2017, 94, 443–455.
19. R. Mahmoudi, M. Kazeminia, A. Kaboudari, S. F. R. Pir-Mahalleh and B. Pakbin, A review of the importance, detection and controlling of heavy metal in milk and dairy products, Malays. J. Sci., 2017, 36(1), 1–16.
20. M. R. Saidur, A. R. A. Aziz and W. J. Basirun, Recent advances in DNA-based electrochemical biosensors for heavy metal ion detection: A review, Biosens. Bioelectron., 2017, 90, 125–139.
21. S. Zhan, Y. Wu, L. Wang, X. Zhan and P. Zhou, A mini-review on functional nucleic acids-based heavy metal ion detection, Biosens. Bioelectron., 2016, 86, 353–368.
22. M. B. Gumpu, S. Sethuraman, U. M. Krishnan and J. B. B. Rayappan, A review on detection of heavy metal ions in water – An electrochemical approach, Sens. Actuators, B, 2015, 213, 515–533.
23. B. Lv, Q. Jiang and C. Zhu, A review of heavy metals immunoassay detection, Adv. J. Food Sci. Technol., 2015, 8(8), 559–565.
24. M. Li, H. Gou, I. Al-Ogaidi and N. Wu, Nanostructured sensors for detection of heavy metals: A review, ACS Sustainable Chem. Eng., 2013, 1(7), 713–723.
25. I. Shtepliuk, J. Eriksson, V. Khranovskyy, T. Iakimov, A. L. Spetz and R. Yakimova, Monolayer graphene/SiC Schottky barrier diodes with improved barrier height uniformity as a sensing platform for the detection of heavy metals, Beilstein J. Nanotechnol., 2016, 7, 1800–1814.
26. R. Bisht, M. Agarwal and K. Singh, Heavy metal removal from wastewater using various adsorbents: A review, J. Water Reuse Desalin., 2017, 7(4), 387–419.
27. Z. Al-Qodah and M. Al-Shannag, Heavy metal ions removal from wastewater using electrocoagulation processes: A comprehensive review, Sep. Sci. Technol., 2017, 52(17), 2649–2676.
28. C. F. Carolin, P. S. Kumar, A. Saravanan, G. J. Joshiba and M. Naushad, Efficient techniques for the removal of toxic heavy metals from aquatic environment: A review, J. Environ. Chem. Eng., 2017, 5(3), 2782–2799.
29. A. Habineza, J. Zhai, T. Ntakirutimana, F. P. Qiu, X. Li and Q. Wang, Heavy metal removal from wastewaters by agricultural waste low-cost adsorbents: Hindrances of adsorption technology to the large scale industrial application – a review, Desalin. Water Treat., 2017, 78, 192–214.
30. V. N. Thekkudan, V. K. Vaidyanathan, S. K. Ponnusamy, C. Charles, S. Sundar, D. Vishnu, S. Anbalagan, V. K. Vaithyanathan and S. Subramanian, Review on nanoadsorbents: A solution for heavy metal removal from wastewater, IET Nanobiotechnol., 2017, 11(3), 213–224.
31. V. K. Gupta, O. Moradi, I. Tyagi, S. Agarwal, H. Sadegh, R. Shahryari-Ghoshekandi, A. S. H. Makhlouf, M. Goodarzi and A. Garshasbi, Study on the removal of heavy metal ions from industry waste by carbon nanotubes: Effect of the surface modification: A review, Crit. Rev. Environ. Sci. Technol., 2016, 46(2), 93–118.
32. E. Bazrafshan, L. Mohammadi, A. Ansari-Moghaddam and A. H. Mahvi, Heavy metals removal from aqueous environments by electrocoagulation process – A systematic review, J. Environ. Health Sci. Eng., 2015, 13(1), 74.
33. A. P. Lim and A. Z. Aris, A review on economically adsorbents on heavy metals removal in water and wastewater, Rev. Environ. Sci. Bio/Technol., 2014, 13(2), 163–181.
34. A. K. Dwivedi and D. P. S. Rajput, A review on adsorptive removal of heavy metal (Cu, Cd) from aqueous solution using low cost adsorbent, Ecol., Environ. Conserv., 2014, 20(1), 175–180.
35. F. Fu and Q. Wang, Removal of heavy metal ions from wastewaters: A review, J. Environ. Manage., 2011, 92(3), 407–418.
36. J. Xu, Z. Cao, Y. Zhang, Z. Yuan, Z. Lou, X. Xu and X. Wang, A review of functionalized carbon nanotubes and graphene for heavy metal adsorption from water: Preparation, application, and mechanism, Chemosphere, 2018, 195, 351–364.
37. A. I. A. Sherlala, A. A. A. Raman, M. M. Bello and A. Asghar, A review of the applications of organo-functionalized magnetic graphene oxide nanocomposites for heavy metal adsorption, Chemosphere, 2018, 193, 1004–1017.
38. W. Peng, H. Li, Y. Liu and S. Song, A review on heavy metal ions adsorption from water by graphene oxide and its composites, J. Mol. Liq., 2017, 230, 496–504.
39. Z.-Y. Yang, N.-N. Dai, R.-T. Lu, Z.-H. Huang and F.-Y. Kang, A review of graphene composite-based sensors for detection of heavy metals, Xinxing Tan Cailiao, 2015, 30(6), 511–518.
40. J. Chang, G. Zhou, E. R. Christensen, R. Heideman and J. Chen, Graphene-based sensors for detection of heavy metals in water: A review Chemosensors and Chemoreception, Anal. Bioanal. Chem., 2014, 406(16), 3957–3975.
41. L. Xu and J. Wang, The application of graphene-based materials for the removal of heavy metals and radionuclides from water and wastewater, Crit. Rev. Environ. Sci. Technol., 2017, 47(12), 1042–1105.
42. K. S. Novoselov, D. Jiang, F. Schedin, T. J. Booth, V. V. Khotkevich, S. V. Morozov and A. K. Geim, Two-dimensional atomic crystals, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(30), 10451–10453.
43. F. Schedin, A. K. Geim, S. V. Morozov, E. W. Hill, P. Blake, M. I. Katsnelson and K. S. Novoselov, Detection of individual gas molecules adsorbed on graphene, Nat. Mater., 2007, 6(9), 652–655.
44. I. Shtepliuk, N. M. Caffrey, T. Iakimov, V. Khranovskyy, I. A. Abrikosov and R. Yakimova, On the interaction of toxic Heavy Metals (Cd, Hg, Pb) with graphene quantum dots and infinite grapheme, Sci. Rep., 2017, 7(1), 3934.
45. I. Shtepliuk, V. Khranovskyy and R. Yakimova, Insights into the origin of the excited transitions in graphene quantum dots interacting with heavy metals in different media, Phys. Chem. Chem. Phys., 2017, 19(45), 30445–30463.
46. J. Baron-Jaimez, M. R. Joya and J. Barba-Ortega, Anodic stripping voltammetry – ASV for determination of heavy metals, J. Phys.: Conf. Ser., 2013, 466, 012023.
47. S. Lee, J. Oh, D. Kim and Y. Piao, A sensitive electrochemical sensor using an iron oxide/graphene composite for the simultaneous detection of heavy metal ions, Talanta, 2016, 160, 528–536.
48. M. Cao, H. Zhang, C. Zhang and Z. Sheng, Graphene-containing composite materials for heavy metal ions adsorption, Gongneng Cailiao, 2016, 47(8), 08001–08007.
49. S. Lee, S.-K. Park, E. Choi and Y. Piao, Voltammetric determination of trace heavy metals using an electrochemically deposited graphene/bismuth nanocomposite film-modified glassy carbon electrode, J. Electroanal. Chem., 2016, 766, 120–127.
50. S. Lee, S. Bong, J. Ha, M. Kwak, S.-K. Park and Y. Piao, Electrochemical deposition of bismuth on activated graphene-nafion composite for anodic stripping voltammetric determination of trace heavy metals, Sens. Actuators, B, 2015, 215, 62–69.
51. X. Li, H. Zhou, W. Wu, S. Wei, Y. Xu and Y. Kuang, Studies of heavy metal ion adsorption on Chitosan/Sulfydryl-functionalized graphene oxide composites, J. Colloid Interface Sci., 2015, 448, 389–397.
52. Y. Zhang, C. Zhong, Q. Zhang, B. Chen, M. He and B. Hu, Graphene oxide-TiO₂ composite as a novel adsorbent for the preconcentration of heavy metals and rare earth elements in environmental samples followed by on-line inductively coupled plasma optical emission spectrometry detection, RSC Adv., 2015, 5(8), 5996–6005.
53. Z. Dong, F. Zhang, D. Wang, X. Liu and J. Jin, Polydopamine-mediated surface-functionalization of graphene oxide for heavy metal ions removal, J. Solid State Chem., 2015, 224, 88–93.
54. Z. Dong, D. Wang, X. Liu, X. Pei, L. Chen and J. Jin, Bio-inspired surface-functionalization of graphene oxide for the adsorption of organic dyes and heavy metal ions with a superhigh capacity, J. Mater. Chem. A, 2014, 2(14), 5034–5040.
55. M. Karimi, F. Aboufazeli, H. R. L. Z. Zhad, O. Sadeghi and E. Najafi, Cadmium Ions Determination in Sea Food Samples Using Dipyridyl-Functionalized Graphene Nano-sheet, Food Anal. Methods, 2014, 7(3), 669–675.
56. S. Muralikrishna, K. Sureshkumar, T. S. Varley, D. H. Nagaraju and T. Ramakrishnappa, In situ reduction and functionalization of graphene oxide with l-cysteine for simultaneous electrochemical determination of cadmium(II), lead(II), copper(II), and mercury(II) ions, Anal. Methods, 2014, 6(21), 8698–8705.
57. C. Göde, M. L. Yola, A. Yılmaz, N. Atar and S. Wang, A novel electrochemical sensor based on calixarene functionalized reduced graphene oxide: Application to simultaneous determination of Fe(III), Cd(II) and Pb(II) ions, J. Colloid Interface Sci., 2017, 508, 525–531.
58. A. Magrez, S. Kasas, V. Salicio, N. Pasquier, J. Won Seo, M. Celio, S. Catsicas, B. Schwaller and L. Forró, Cellular Toxicity of Carbon-Based Nanomaterials, Nano Lett., 2006, 6(6), 1121–1125.
59. S. E. Crawford, T. Hartung, H. Hollert, B. Mathes, B. van Ravenzwaay, T. Steger-Hartmann, C. Studer and H. F. Krug, Green Toxicology: a strategy for sustainable chemical and material development, Environ. Sci. Eur., 2017, 29(1), 16.
60. G. Kim, S.-H. Jhi, S. Lim and N. Park, Effect of vacancy defects in graphene on metal anchoring and hydrogen adsorption, Appl. Phys. Lett., 2009, 94, 173102.
61. B. Sanyal, O. Eriksson, U. Jansson and H. Grennberg, Molecular adsorption in graphene with divacancy defects, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79, 113409.
62. Y. You, J. Deng, X. Tan, N. Gorjizadeh, M. Yoshimura, S. C. Smith, V. Sahajwalla and R. K. Joshi, On the mechanism of gas adsorption for pristine, defective and functionalized graphene, Phys. Chem. Chem. Phys., 2017, 19, 6051–6056.
63. H. Yildirim, A. Kinaci, Z.-J. Zhao, M. K. Y. Chan and J. P. Greeley, First-Principles Analysis of Defect-Mediated Li Adsorption on Graphene, ACS Appl. Mater. Interfaces, 2014, 6(23), 21141–21150.
64. I. Fampiou and A. Ramasubramaniam, Binding of Pt Nanoclusters to Point Defects in Graphene: Adsorption, Morphology, and Electronic Structure, J. Phys. Chem. C, 2012, 116(11), 6543–6555.
65. J. Liao, L. Yanga, C. Z. Wangd and S. Lin, Tuning Cd adsorption behaviours on graphene by introducing defects: a first-principles study, Mater. Technol., 2017, 32(14), 840–844.
66. A. Johll Harman Low Raelynn, Density Functional Theory Study of Metal Adatoms at or Near a Stone-wales Defect in Graphene, Procedia Eng., 2014, 93, 2–7.
67. K. Li, Y. Li, H. Tang, M. Jiao, Y. Wang and Z. Wu, A density functional theory study on 3d metal/graphene for the removal of CO from H₂ feed gas in hydrogen fuel cells, RSC Adv., 2015, 5, 16394.
68. G. Bharathi, D. Nataraj, S. Premkumar, M. Sowmiya, K. Senthilkumar, T. Daniel Thangadurai, O. Yu Khyzhun, M. Gupta, D. Phase, N. Patra, S. Nath Jha and D. Bhattacharyya, Graphene Quantum Dot Solid Sheets: Strong blue-light-emitting & photocurrent-producing band-gap opened nanostructures, Sci. Rep., 2017, 7, 10850.
69. L. Zhang, D. Peng, R.-P. Liang and J.-D. Qiu, Nitrogen-Doped Graphene Quantum Dots as a New Catalyst Accelerating the Coordination Reaction between Cadmium(II) and 5,10,15,20-Tetrakis(1-methyl-4-pyridinio) porphyrin for Cadmium(II) Sensing, Anal. Chem., 2015, 87, 10894–10901.
70. S. L. Ting, S. J. Ee, A. Ananthanarayanan, K. C. Leong and P. Chen, Graphene quantum dots functionalized gold nanoparticles for sensitive electrochemical detection of heavy metal ions, Electrochim. Acta, 2015, 172, 7–11.
71. C. Zhou, W. Jiang and B. K. Via, Facile synthesis of soluble graphene quantum dots and its improved property in detecting heavy metal ions, Colloids Surf., B, 2014, 118, 72–76.
72. S. Bian, C. Shen, H. Hua, L. Zhou, H. Zhu, F. Xi, J. Liu and X. Dong, One-pot synthesis of sulfur-doped graphene quantum dots as a novel fluorescent probe for highly selective and sensitive detection of lead(II), RSC Adv., 2016, 6(74), 69977–69983.
73. Z. S. Qian, X. Y. Shan, L. J. Chai, J. R. Chen and H. Feng, A fluorescent nanosensor based on graphene quantum dots-aptamer probe and graphene oxide platform for detection of lead(II) ion, Biosens. Bioelectron., 2015, 68, 225–231.
74. Y.-X. Qi, M. Zhang, Q.-Q. Fu, R. Liu and G.-Y. Shi, Highly sensitive and selective fluorescent detection of cerebral lead(II) based on graphene quantum dot conjugates, Chem. Commun., 2013, 49(90), 10599–10601.
75. M. H. Amini, F. Faridbod, M. R. Ganjali and P. Norouzi, Functionalized graphene quantum dots as a fluorescent “off–on” nanosensor for detection of mercury and ethyl xanthate, Res. Chem. Intermed., 2017, 43(12), 7457–7470.
76. N. T. N. Anh, A. D. Chowdhury and R.-A. Doong, Highly sensitive and selective detection of mercury ions using N, S-codoped graphene quantum dots and its paper strip based sensing application in wastewater, Sens. Actuators, B, 2017, 252, 1169–1178.
77. Z. Yan, X. Qu, Q. Niu, C. Tian, C. Fan and B. Ye, A green synthesis of highly fluorescent nitrogen-doped graphene quantum dots for the highly sensitive and selective detection of mercury (II) ions and biothiols, Anal. Methods, 2016, 8(7), 1565–1571.
78. B. Shi, L. Zhang, C. Lan, J. Zhao, Y. Su and S. Zhao, One-pot green synthesis of oxygen-rich nitrogen-doped graphene quantum dots and their potential application in pH-sensitive photoluminescence and detection of mercury(II) ions, Talanta, 2015, 142, 131–139.
79. M. Hua, C. Wang, J. Qian, K. Wang, Z. Yang, Q. Liu, H. Mao and K. Wang, Preparation of graphene quantum dots based core-satellite hybrid spheres and their use as the ratiometric fluorescence probe for visual determination of mercury(II) ions, Anal. Chim. Acta, 2015, 888, 173–181.
80. T. V. Tam, S. H. Hong and W. M. Choi, Facile synthesis of cysteine-functionalized graphene quantum dots for a fluorescence probe for mercury ions, RSC Adv., 2015, 5(118), 97598–97603.
81. B. Wang, S. Zhuo, L. Chen and Y. Zhang, Fluorescent graphene quantum dot nanoprobes for the sensitive and selective detection of mercury ions, Spectrochim. Acta, Part A, 2014, 131, 384–387.
82. Z. Li, Y. Wang, Y. Ni and S. Kokot, A rapid and label-free dual detection of Hg (II) and cysteine with the use of fluorescence switching of graphene quantum dots, Sens. Actuators, B, 2015, 207(A), 490–497.
83. M. Lü, J. Li and X. Yang, et al., Applications of graphene-based materials in environmental protection and detection, Chin. Sci. Bull., 2013, 58, 2698.
84. J. Xu, X. Jie, F. Xie, H. Yang, W. Wei and Z. Xia, Flavonoid moiety-incorporated carbon dots for ultrasensitive and highly selective fluorescence detection and removal of Pb²⁺, Nano Res., 2018, 11(7), 3648–3657.
85. H. Xu, L. Xie and M. Hakkarainen, Coffee-Ground-Derived Quantum Dots for Aqueous Processable Nanoporous Graphene Membranes, ACS Sustainable Chem. Eng., 2017, 5(6), 5360–5367.
86. M. J. Frisch, G. W. Trucks, H. B. Schlegel and G. E. Scuseria, et al., Gaussian 09, Revision D.01, Gaussian Inc., Wallingford CT, 2009.
87. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
88. J. M. L. Martin and A. Sundermann, J. Chem. Phys., 2001, 114, 3408–3420.
89. S. F. Boys and F. Bernardi, Mol. Phys., 1970, 19, 553.
90. R. S. Mulliken, J. Chem. Phys., 1955, 23, 1833–1840.
91. J. D. Thompson, J. D. Xidos, T. M. Sonbuchner, C. J. Cramer and D. G. Truhlar, More reliable partial atomic charges when using diffuse basis sets, PhysChemComm, 2002, 5, 117–134.
92. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926.
93. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746.
94. F. L. Hirshfeld, Bonded-atom fragments for describing molecular charge densities, Theor. Chim. Acta, 1977, 44, 129–138.
95. O. BarisMalcıoglu, A. Calzolari, R. Gebauer, D. Varsano and S. Baroni, Dielectric and Thermal Effects on the Optical Properties of Natural Dyes: A Case Study on Solvated Cyanin, J. Am. Chem. Soc., 2011, 133, 15425–15433.
96. T. Yumura, T. Awano, H. Kobayashi and T. Yamabe, Platinum Clusters on Vacancy-Type Defects of Nanometer-Sized Graphene Patches, Molecules, 2012, 17, 7941–7960.
97. L. Liu and S. Chen, Geometries and Electronic States of Divacancy Defect in Finite-Size Hexagonal Graphene Flakes, J. Chem., 2017, 8491264.
98. A. W. Robertson, G.-D. Lee, K. He, E. Yoon, A. I. Kirkland and J. H. Warner, The role of the bridging atom in stabilizing odd numbered graphene vacancies, Nano Lett., 2014, 14(7), 3972–3980.
99. A. W. Robertson, G.-D. Lee, K. He, E. Yoon, A. I. Kirkland and J. H. Warner, Stability and Dynamics of the Tetravacancy in Graphene, Nano Lett., 2014, 14(3), 1634–1642.
100. R. Otero, A. L. Vázquez de Parga and J. M. Gallego, Electronic, structural and chemical effects of charge-transfer at organic/inorganic interfaces, Surf. Sci. Rep., 2017, 72, 105–145.
101. D. Cortés Arriagada, Global and local reactivity indexes applied to understand the chemistry of graphene oxide and doped graphene, J. Mol. Model., 2013, 19, 919–930.
102. A. Ambrosi, C. K. Chua, A. Bonanni and M. Pumera, Electrochemistry of graphene and related materials, Chem. Rev., 2014, 114(14), 7150–7188.
103. I. Shtepliuk, M. Vagin, I. G. Ivanov, T. Iakimov, G. Reza Yazdia and R. Yakimova, Lead (Pb) interfacing with epitaxial graphene, Phys. Chem. Chem. Phys., 2018, 20, 17105–17116.
104. M. Legesse, F. El Mellouhi, E. T. Bentria, M. E. Madjet, T. S. Fisher, S. Kais and F. H. Alharbi, Reduced work function of graphene by metal adatoms, Appl. Surf. Sci., 2017, 394, 98–107.
105. W. C. Martin, A. Musgrove and S. Kotochigova, Ground Levels and Ionization Energies for Neutral Atoms, National Institute of Standards and Technology, Gaithersburg, MD, 2002, http://physics.nist.gov/IonEnergy.
106. H. Lu, D. Dai, P. Yanga and L. Li, Atomic orbitals in molecules: general electronegativity and improvement of Mulliken population analysis, Phys. Chem. Chem. Phys., 2006, 8, 340–346.
107. R. D. Nelson, D. R. Lide and A. A. Maryott, Selected Values of Electric Dipole Moments for Molecules in the Gas Phase, National Bureau of Standards, Washington DC, 1967.
108. S. Tretiak and S. Mukamel, ensity Matrix Analysis and Simulation of Electronic Excitations in Conjugated and Aggregated Molecules, Chem. Rev., 2002, 102, 3171–3212.
109. Z. R. Grabowski, K. Rotkiewicz and W. Rettig, Chem. Rev., 2003, 103, 3899.
110. S. Tretiak, V. Chernyak and S. Mukamel, Collective electronic oscillators for nonlinear optical response of conjugated molecules, Chem. Phys. Lett., 1996, 259, 55.
111. B. Moore, H. Sun, N. Govind, K. Kowalski and J. Autschbach, Charge-Transfer Versus Charge-Transfer-Like Excitations Revisited, J. Chem. Theory Comput., 2015, 11, 3305–3320.

---

Footnote

† Electronic supplementary information (ESI) available: Full assignments of the excited transitions in GQDs complexed with HMs. See DOI: 10.1039/c8cp03306d

---