Molecular dynamics simulations of ammonium/phosphonium-based protic ionic liquids: influence of alkyl to aryl group

Abstract

The variation of the center atom in the cation from an N to a P-atom leads to improved physiochemical properties of protic ionic liquids (PILs) which are suitable for electrolyte applications. We present an atomistic simulations study to compare the effect of an alkyl or aryl group on trioctylammonium triflate ([HN(Oct)₃][TFO]) and triphenylammonium triflate ([HN(Ph)₃][TFO]) with their phosphonium analogues. We have computed the binding energy from quantum chemical calculations and physical properties such as the viscosity and the electrical conductivity of PILs from molecular dynamics simulations. The influence of the aromatic character in PILs is found to be significant to the physical properties. Gas phase quantum chemical calculations on clusters of ion pairs have revealed the presence of C–H/π interactions in aromatic PILs along with hydrogen bonding. The variation in strength of the ion-pair affinities is examined using electric-current correlation and velocity autocorrelation functions. The qualitative differences observed are due to the aromatic rings and change in the central atom of the quaternary cation from an N to a P-atom, substantiated quantitatively by diffusion coefficients and electrical conductivities. The relatively weaker ion-pair interactions and low binding energy (−73.34 kcal mol⁻¹) lead to the highest electrical conductivity in [HP(Ph)₃][TFO].

---

1 Introduction

Electrochemical properties at wide temperature ranges popularized ionic liquids (ILs) as successful electrolytes in batteries, dye-sensitized solar cells, capacitors and fuel cells.^1–16 In the past few decades, tremendous effort has been put towards the investigation of the compatibility of ILs with different electrochemical devices in anhydrous or aqueous phases.^4,9,17 Parallel to the experimental findings, substantial support through a molecular-level understanding has been provided over the years^18,19 to explore ionic mobility, vibrational signatures of various interactions^20–22 and ion hopping.^23,24 Recently, the existence of one or more than one solid–solid phase transition in ionic liquid plastic crystals has drawn attention due to the specific contribution of various solid phases to the electrolytic properties.^24–31

Protic ionic liquids (PILs) were favoured for their potential use in portable and long life cycle energy devices over acid electrolytes mainly due to a high energy density, a large electro-chemical window and a wide range of thermal stabilities. In the search for proton conducting ILs, the applicability of ammonium-based PILs has been well examined in the past decade. Rana et al.³² synthesized tri-butylphosphonium cation-based ammonium analogue PILs and demonstrated their facile ionic conductivity compared to ammonium-based PILs. The use of phosphonium-based ILs as an electrolyte is interesting due to their competent/improved physical and electrochemical properties with the ammonium-based PILs.^32,33 Luo et al.³⁴ explored a comparative study of tri-octylphosphonium triflate and tri-phenylphosphonium triflate with ammonium analogues. The authors found a higher cation conductivity in phosphonium salts compared to their ammonium analogues which was attributed to weaker hydrogen bonding in phosphonium cation-based ILs. Apart from these protic ILs, the effect of the variation of the center atom species of the cation from an N to a P atom on the physicochemical properties of aprotic quaternary cation-based ILs also revealed similar results. For example, tri-n-ethylpentylphosphonium bis-trifluoromethanesulfonyl amide ([TEPP][TFSA]) showed a lower viscosity and higher self-diffusion coefficient compared to its ammonium analogues (i.e. tri-n-ethylpentylammonium bis-trifluoromethanesulfonyl amide ([TEPA][TFSA])).³⁵ Recently, Salem et al.³⁶ evaluated tri-methylpropylphosphonium bis-fluorosulfonyl imide ([P1113][FSI]), tri-methyl-iso-butylphosphonium bis-fluorosulfonyl imide ([P111i4][FSI]) and tri-methyl-iso-butylphosphonium bis-trifluoromethylsulfonyl imide ([P111i4][TFSI]) as electrolytes along with Li salt and showed improved battery performance in the presence of a phosphonium-based IL.

Previously, molecular dynamics (MD) simulations have been applied to explore the microstructural interactions in phosphonium-based aprotic ILs such as tetrabutylphosphonium amino acids,³⁷ [PC₆C₆C₆C₁₄][Tf₂N] IL,³⁸ alkoxyphosphonium IL with [Tf₂N] anion,³⁹ and tetradecyltrihexylphosphonium ([P14,6,6,6]⁺) based ILs with various anions.⁴⁰ In the present study, we have performed classical MD simulations on alkyl/aryl ammonium triflate protic ILs and their respective phosphonium analogues. We have chosen tri-octylammonium triflate ([HN(Oct)₃][TFO]), tri-phenylammonium triflate ([HN(Ph)₃][TFO]), tri-octylphosphonium triflate ([HP(Oct)₃][TFO]) and tri-phenylphosphonium triflate ([HP(Ph)₃][TFO]) PILs (see Fig. 1). The computational details of the gas phase calculations and MD simulations are provided in the next section.

Fig. 1 The chemical structures of tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs.

2 Computational details

A. Gas phase

The initial structures of the ion pairs of these PILs were constructed using GaussView⁴¹ software. We have carried out geometry optimizations on five different initial configurations (for the monomer, dimer, trimer, and tetramer respectively) which were chosen randomly from the MD simulations' trajectories. For e.g., five different initial configurations of the [HN(Ph)₃][TFO] dimer are shown in Fig. S1 of the ESI.† The geometry optimized structures correspond to the minimum energy among the five different configurations analysed.

(i) Calculations using atom-centered basis sets. For the geometry optimization of an isolated ion pair (monomer) in the gas phase, a M06/aug-cc-pVDZ level of theory was implemented using the Gaussian09 code.⁴² Vibrational frequencies were calculated at the same level of theory and the absence of any imaginary frequency confirmed that the ion pairs were in their true minimum energy configuration.

(ii) Calculations using plane-wave basis sets. DFT calculations for clusters of two (dimer), three (trimer) and four ion pairs (tetramer) for all of these PILs were carried out using CP2K software.⁴³ The effect of the core electrons and nuclei on the valence electrons were considered by using Geodecker–Teter–Hutter (GTH) pseudopotentials.⁴⁴ Triple-ζ double-polarized basis sets with an energy cutoff of 280 Ry were employed to treat the valence electrons. A Perdew, Burke, and Ernzerhof (PBE) exchange–correlation functional was employed.⁴⁵ The van der Waals interactions were incorporated through Grimme's DFT-D3 scheme.⁴⁶ A cluster of these PILs was quenched in an isolated condition with convergence criteria of 10⁻⁵ and 10⁻⁷ for nuclear coordinates and gradient of wave functions, respectively. The minimized structures were used for further analysis.

B. Liquid phase

Classical molecular dynamics simulations were performed on the liquid phases of these PILs using the LAMMPS package.⁴⁷ We used 256 ion-pairs for each system and the simulations were carried out at 393 K, 417 K, 441 K and 465 K. All bonded interaction parameters were taken from the OPLS-AA force field.⁴⁸ Non-bonded potential parameters for these salts were taken from the work of different groups. In our previous study, for alkylammonium-based PILs we used the van der Waals parameters of Chang et al.⁴⁹ which showed reliable agreement with experiment in predicting various physical properties. Thus, for [HN(Oct)₃][TFO] and [HP(Oct)₃][TFO] similar parameters were used to model non-bonded interactions, except for the phosphorus in [HP(Oct)₃][TFO], for which Lennard-Jones parameters were taken from the work of Wang et al.⁵⁰ For the other two triphenyl-based PILs, [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO], OPLS-AA Lennard-Jones parameters were used. In order to include the effect of electronic polarization, which plays a crucial role in determining the structure and dynamics of ILs,^51–53 the atomic site charges for these PILs were calculated using the DDEC/c3 program.^54,55 For this purpose, an isolated ion pair of these salts was optimized within the DFT framework using the CP2K package.⁴³ The minimized coordinates were used to generate the valence electron density and were saved in a cube file. This density information was used as an input to the DDEC/c3 code to obtain atomic charges. Other details of the calculations are the same as those described in the DFT calculations for clusters. The atomic site charges obtained for these salts are tabulated in Tables S1–S3 of the ESI.† The remaining non-bonded and bonded force field parameters are provided in Tables S4 and S5 of the ESI.† The total ion charges were in a range between ±0.70 to ±0.78e which can be understood as an effect of the electronic polarization and charge transfer present in these systems.

Energy minimization was performed on the initial configuration created using Packmol.⁵⁶ A distance cutoff of 12 Å was employed to calculate the pairwise interactions in real space. Long-range interactions were computed through a particle–particle particle mesh (PPPM) solver with a precision of 10⁻⁵. All of the C–H covalent bonds were constrained using the SHAKE algorithm as implemented in LAMMPS.⁴⁷ The velocity Verlet algorithm was used to integrate the equations of motion with a timestep of 1 fs. The Nosé–Hoover thermostat and barostat^57,58 were employed to control the temperature and pressure of the system. All the systems were equilibrated in an NPT ensemble for 15 ns. The computed densities from the NPT simulations are given in Table 1. A trajectory of 48 ns was generated for each system in the NVT ensemble to calculate several equilibrium properties. The systems were visualized in VMD.⁵⁹

Table 1 The density (in g cc⁻¹) calculated from MD simulations of tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs

PIL	393 K	417 K	441 K	465 K
[HN(Oct)3][TFO]	0.877	0.861	0.846	0.830
[HP(Oct)3][TFO]	0.884	0.868	0.852	0.836
[HN(Ph)3][TFO]	1.201	1.180	1.159	1.138
[HP(Ph)3][TFO]	1.190	1.168	1.146	1.123

---

3 Results and discussion

3.1 Binding energy and structure

The binding energy (BE) is estimated as follows

BE = E_IL − (E_Cation + E_Anion) (1)

where E_IL, E_Cation, and E_Anion represent the energy of an isolated ion-pair, cation and anion, respectively. The binding energies are corrected for the basis set superposition error (BSSE). The computed binding energies at a M06/aug-cc-pVDZ level of theory are [HP(Ph)₃][TFO]: −73.34, [HP(Oct)₃][TFO]: −76.81, [HN(Oct)₃][TFO]: −83.36 and [HN(Ph)₃][TFO]: −85.65 kcal mol⁻¹, respectively. The strength of the cation–anion binding interaction increases in the following order: [HP(Ph)₃][TFO] < [HP(Oct)₃][TFO] < [HN(Oct)₃][TFO] < [HN(Ph)₃][TFO]. Thus, the binding strength in the aryl group substituted quaternary phosphonium-based cation is lowest among all the cations with a [TFO] anion. In order to investigate the impact of the aryl group of neighboring cations on ion-pairs, dimer, trimer and tetramer structures of [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO] are optimized using the CP2K⁴³ program. The optimized structures show hydrogen-bonding interactions between acidic hydrogen (N–H or P–H) and the oxygen atom of the [TFO] anion. For clarity, the optimized structures are shown in Fig. 2 for dimer and trimer only. The N–H⋯O hydrogen-bonding distance is found to be comparatively shorter (1.4 Å) than that of P–H⋯O (∼1.6–1.8 Å). Interestingly, depending on the variation in structural orientation of the phenyl ring in aryl PILs, the geometry parameters of hydrogen bonds (bond length and angle) vary with the growth of the cluster from dimer to tetramer. The electronegativity difference for N–H compared to P–H is quite significant and the environmental effects along with the electron withdrawing nature of the phenyl group could only perturb the N–H⋯O hydrogen-bonding distance from 1.4 Å to 1.5 Å. In the case of P–H⋯O, a significant effect of perturbations due to the phenyl rings is observed in the hydrogen-bonding distance (∼1.5–1.8 Å) from monomer to tetramer. Apart from the hydrogen bonding interaction, weak intermolecular C–H/π (with phenyl ring) interactions are also observed in the case of the dimer, trimer and tetramer of [HN(Ph)₃][TFO]. Similarly, these C–H/π (with phenyl ring) interactions are seen in phosphonium analogues. The hydrogen-bonding distances and respective hydrogen-bonding angle observed in optimized structures are shown in Table S6 (ESI†) for [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO], respectively. Thus, the notable difference for aryl substituted cations of ammonium and their phosphonium analogues is the relative strength and distance of the hydrogen-bonds. The longer P–H⋯O distance compared to the N–H⋯O hydrogen bond leads to a significant deviation in their binding strength.

Fig. 2 The distances depicted for N–H⋯O or P–H⋯O hydrogen-bonding interactions and C–H/π interactions with respect to the center of mass of the phenyl ring obtained from quantum chemical calculation for (a) dimer & (b) trimer of [HN(Ph)₃][TFO], and (c) dimer & (d) trimer of [HP(Ph)₃][TFO] PILs, respectively [color scheme for (i) cation: N – blue (CPK), H_N/P – cyan (CPK), P – ochre (CPK), C_Phynylring – gray (Paperchain), ring H-white (CPK) and (ii) anion C – gray, F – green, S – yellow, O – red (CPK)].

These hydrogen bonding interactions are further characterized using the radial distribution functions (RDFs) obtained from MD simulations of 256 ion-pairs of ILs. RDFs between the acidic hydrogen atom attached to the cationic N-atom or P-atom with anionic oxygen atoms are shown in Fig. 3. The peak profile for [HN(Oct)₃][TFO] around 2 Å is similar to that of [N222][TFO] obtained in our recent work.⁶⁰ The peak position for [HP(Oct)₃][TFO] shows a slight shift towards a longer distance around 2.2 Å. In the case of aromatic PILs, RDF peaks occur at relatively shorter distances at around 1.45 Å for [HN(Ph)₃][TFO] and 1.75 Å for [HP(Ph)₃][TFO], respectively. It is due to the influence of charge transmission from the N/P to the electron withdrawing phenyl ring compared to positive electrostatic induction by the octyl chain. These results clearly support a previous finding by Fumino et al.²⁰ where an enhancement in the electron releasing nature of the ammonium cation of protic molten salts/PILs leads to weaker hydrogen bonds. A similar trend in aryl to alkyl substitution in these PILs is seen on N–H stretching frequencies from the experimental findings of Luo et al.³⁴ due to a weakening of the hydrogen bond. Moreover, these RDF peak profiles are in excellent agreement with hydrogen-bond distances obtained from quantum chemical calculations. The high peak intensity at a relatively lower distance of N–H⋯O interaction in [HN(Ph)₃][TFO] among all PILs leads to a strong ion-pair binding affinity. Similar observations are seen in the center of mass RDFs calculated for cation–cation and cation–anion interactions (Fig. S2 of ESI†).

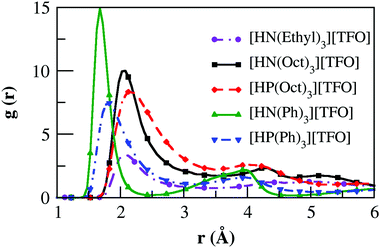Fig. 3 Radial distribution functions between the acidic hydrogen (N/P–H) and the anionic oxygen atom in the PILs [the RDF data for [HN(Ethyl)₃][TFO] (i.e. [N222][TFO]) is shown for comparison from our previous work⁶⁰ with copyright (2015) permission of Royal Society of Chemistry].

In order to examine the distribution of anions around the cation, the spatial density distribution maps of anions (S-atom and O-atoms) around the center of mass of the cation were calculated from MD simulations at 393 K. Fig. 4 shows the spatial density maps where the anion distribution over the acidic hydrogen is more dense for aliphatic ILs compared to aromatic PILs. Moreover, the presence of bulky octyl chains leads to a more condensed anion distribution above or below the acidic hydrogen (N–H or P–H bond vector). A random orientation of the aromatic rings is seen for the cation in [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO] instead of a planar orientation (similar to Fig. 2 from quantum chemical calculations). For [HN(Ph)₃][TFO] it results in a circular distribution of anions in a narrow region which seem to be influenced by shorter and stronger hydrogen bonding interactions. The density of anion distribution around the acidic hydrogen in [HP(Ph)₃][TFO] is comparatively lower than [HN(Ph)₃][TFO]. It might be a result of a longer hydrogen bonding distance in [HP(Ph)₃][TFO] compared to [HN(Ph)₃][TFO]. The interactions of anions with the ring hydrogen atoms of the cation are insignificant. The influence of the above ion-pair interactions and binding energy on physico-chemical properties is illustrated in the next section by calculating the shear viscosity and dynamics of PILs.

Fig. 4 Spatial density maps of anions (S-atom and O-atoms) around the center of mass of the cation calculated from MD simulation at 393 K for tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs at an iso-surface value of 0.004745 ų [color scheme for (i) cation: N – blue (CPK), P – ochre (CPK), H_N/P – cyan (CPK), C_Alkyl – violet (Polyhedra), alkyl H-white (CPK), phenyl ring – paper chain and (ii) anion iso-surface: S – yellow-green, O – orange-red].

3.2 Shear viscosity

The shear viscosity of these systems is computed using the equilibrium Green–Kubo relation,⁶¹where V is the system volume, and P̃ is the symmetric, traceless part of the pressure tensor. Pressure tensors were stored at each step for a 4 ns duration and twelve such independent trajectories were generated. The block average of these trajectories was used to compute the shear viscosity from the time integral of the stress autocorrelation function (eqn (2)). The viscosity (in mPa s) calculated from the MD simulations of tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs is shown in Table 2. At 393 K, the viscosity computed from the MD simulations increases in the following order: [HP(Ph)₃][TFO] < [HP(Oct)₃][TFO] < [HN(Oct)₃][TFO] < [HN(Ph)₃][TFO]. The increasing order of viscosity complies with the increasing order of the binding strength or binding energy. As the binding strength of the ion-pair is lowest in [HP(Ph)₃][TFO] it leads to the lowest viscosity among all the PILs. The existence of a strong ion-pair affinity along with N–H⋯O hydrogen-bonding in [HN(Ph)₃][TFO] result in the highest viscosity among the studied PILs. A similar observation is seen at higher temperatures.

Table 2 The shear viscosity (in mPa s) calculated from MD simulations of PILs

PIL	393 K	417 K	441 K	465 K
[HN(Oct)3][TFO]	37.5	27.6	12.3	9.9
[HP(Oct)3][TFO]	33.1	25.2	8.8	6.6
[HN(Ph)3][TFO]	45.0	36.7	16.8	9.1
[HP(Ph)3][TFO]	14.8	9.3	4.8	3.6

---

3.3 Mobility or dynamics of PILs

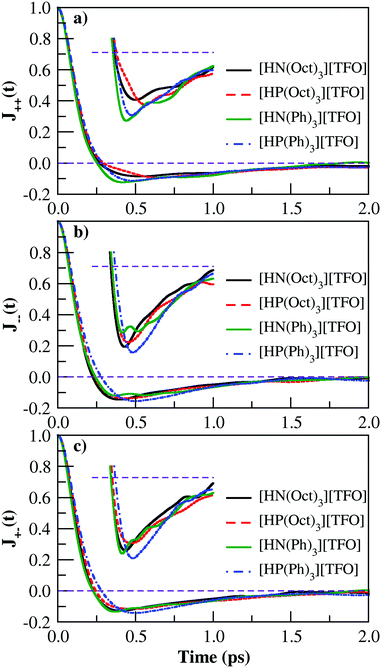
3.3.1 Electric current autocorrelation function. The electrical conductivity σ_GK is calculated using the electric current autocorrelation function which can be defined^62,63 aswhere, the j(t) is the electric-current function equal to ; q_i and v_i represent the charge and velocity of atom i at time t]. The electric current autocorrelation function is the sum of the cation–cation autocorrelation (j₊₊), anion–anion autocorrelation (j₋₋) and cation–anion cross correlation function (j₊₋).⁶⁴ These individual contributions are computed and shown in Fig. 5. The well depth seen in the decay of the electric-current function (see inset of Fig. 5) for all PILs indicates the caging of ion-pairs. The relative difference in the ion-pair cage strength is further examined by computing the center of mass velocity autocorrelation function.

Fig. 5 The electric current auto-correlation functions for PILs (a) cation–cation, (b) anion–anion and (c) cation–anion cross-correlation.

3.3.2 Velocity autocorrelation function. In order to characterize the dynamical processes in PILs, the normalized center of mass velocity autocorrelation function (VACF) for cations and anions is calculated (see Fig. 6). The first minimum is found to be deeper for the tri-aryl cations compared to tri-alkyl cations (see inset of Fig. 6a for [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO]). A significant decrease in well depth with an increase in the bulky nature of quaternary ammonium/phosphonium cation is also seen in our recent work.⁶⁰ The observation from cation VACF in the well depth variations suggests that the rattling motions seem more significant in [HN(Ph)₃][TFO] and [HP(Ph)₃][TFO]. A significant difference in well depth is seen for cations of aromatic PILs in inset of Fig. 6a. The exponential decay of the anion VACF is found to be different in tri-aryl cations than tri-alkyl cations (Fig. 6b).

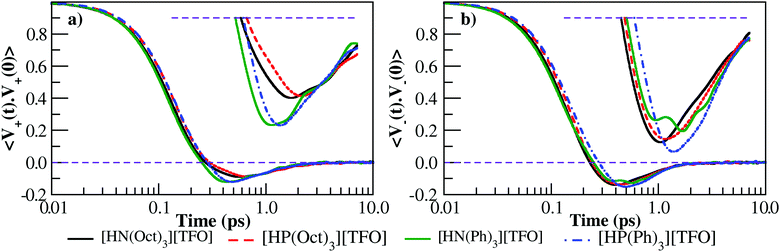Fig. 6 Velocity auto-correlation function of tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs for (a) cation–cation and (b) anion–anion respectively.

In order to quantitatively verify these observations, the diffusion coefficients of the ions (D_A in ×10⁻⁶ cm² s⁻¹) are calculated. The D_A calculated from MD simulations for tri-octyl/tri-phenyl ammonium triflate and for their phosphonium analogues is provided in Table S7 of the ESI.† For all PILs, the D_A of anions in the respective PIL is higher than compared to cations. For all temperatures, [TFO] anions diffuse faster than the cations which could be due to the bulkier nature of the cations compared with the anions. Moreover, the ionic conductivity within the approximation of independent ion motion can be calculated from diffusion coefficients using the Nernst–Einstein relation.⁶³ The σ_NE for all the ILs is given in Table S8 of the ESI.† We have calculated the electrical conductivity (σ_GK) using the Green–Kubo relation at various temperatures (see Table 3). The decreasing order of σ_GK at 393 K is as follows: [HP(Ph)₃][TFO] > [HP(Oct)₃][TFO] > [HN(Ph)₃][TFO] > [HN(Oct)₃][TFO]. This decreasing order of electrical conductivity in these PIL from simulations matches well with the ionic conductivity reported by Luo et al.³⁴ from experiment. The σ_GK is highest for [HP(Ph)₃][TFO] among all the PIL which shows the least intermolecular ion-pair interactions and a low ion-pair binding affinity. Moreover, an increase in temperature leads to an increase in σ_GK. From 393 K to 465 K, σ_GK increases by a factor of 7 for [HP(Ph)₃][TFO]. In the case of [HP(Oct)₃][TFO], [HN(Oct)₃][TFO], and [HN(Ph)₃][TFO], the σ_GK increases by a factor of 10, 11 and 14 respectively. Thus, an increase in temperature from 393 K to 465 K gives a tenfold or more than tenfold enhancement in σ_GK. Moreover, the ratio of σ_GK and σ_NE is calculated (see values in parenthesis of Table 3) which illustrates the ion-pair association. Except 393 K, the ratio of σ_GK and σ_NE suggests that ion-pair association in ammonium-based PILs is higher compared to their phosphonium analogues. It is due to more significant hydrogen-bonding interactions seen in ammonium-based PILs. These comparative trends seen in ion-pair association of ammonium salts and their phosphonium analogues are in excellent agreement with experiments³⁴ on these PILs.

Table 3 The electrical conductivity calculated using the Green–Kubo relation (σ_GK in S m⁻¹) from MD simulations of tri-octyl/tri-phenyl ammonium triflate and tri-octyl/tri-phenyl phosphonium triflate PILs (ratio of σ_GK with Nernst–Einstein conductivity (σ_NE) is given in parenthesis)

PIL	393 K	417 K	441 K	465 K
[HN(Oct)3][TFO]	0.022 (0.44)	0.053 (0.48)	0.13 (0.50)	0.23 (0.56)
[HP(Oct)3][TFO]	0.045 (0.56)	0.130 (0.68)	0.25 (0.71)	0.44 (0.73)
[HN(Ph)3][TFO]	0.025 (0.50)	0.092 (0.51)	0.20 (0.43)	0.36 (0.42)
[HP(Ph)3][TFO]	0.200 (0.42)	0.500 (0.52)	0.84 (0.54)	1.38 (0.59)

---

4 Conclusions

The quantum chemical calculations and MD simulations provide a molecular understanding of various properties of tri-alkyl/tri-aryl ammonium/phosphonium-based PILs. The difference in distances obtained from quantum chemical calculations for hydrogen bonding and C–H/π interactions clearly distinguishes the strength of ion-pair interactions for respective ammonium-based PILs versus their phosphonium analogues. The RDFs for N–H⋯O and P–H⋯O interactions reveal that hydrogen bonding interactions are weaker for phosphonium-based PILs. Similar observations are seen from the spatial distribution of anions (O/S atoms) over the acidic hydrogen of the cation. The distribution of anions around the acidic hydrogen of the cation is found to be the least for [HP(Ph)₃][TFO]. The bulky nature of the octyl chains in [HN(Oct)₃][TFO] and [HP(Oct)₃][TFO] limits the distribution of [TFO] anions around the N–H or P–H bond vector.

The dynamics of the ion-pairs are characterized by calculating the electric current autocorrelation function. The ion-pair association behavior is seen from the ratio of σ_GK and σ_NE which suggests that ion-pair association is higher in ammonium-based PILs compared to their phosphonium analogues. These results provide a molecular understanding of the superior electrochemical nature of phosphonium-based PILs over their ammonium analogues. This study can be further extended to investigate proton diffusion through ab initio MD methods and to explore the role of P-atom versus N-atom in proton diffusion.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Prof. Balasubramanian Sundaram, Jawaharlal Nehru Centre for Advanced Scientific Research (JNCASR), Bangalore (India) for his fruitful suggestions and valuable support. AM thanks Bhaskar Sen Gupta, MPI for Polymer Research for his valuable inputs. APS acknowledges DST for the INSPIRE Faculty Award (IFA'14 – MS-31) and C-DAC for the National PARAM Supercomputing Facility (NPSF). The authors acknowledge JNCASR's computing facilities for carrying out this work. Open Access funding provided by the Max Planck Society.

References

1. D. R. MacFarlane, J. Huang and M. Forsyth, Nature, 1999, 402, 792–794.
2. P.-J. Alarco, Y. Abu-Lebdeh, A. Abouimrane and M. Armand, Nat. Mater., 2004, 3, 476–481.
3. S. J. Pas, J. M. Pringle, M. Forsyth and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2004, 6, 3721–3725.
4. J. M. Pringle, P. C. Howlett, D. R. MacFarlane and M. Forsyth, J. Mater. Chem., 2010, 20, 2056–2062.
5. V. Armel, D. Velayutham, J. Sun, P. C. Howlett, M. Forsyth, D. R. MacFarlane and J. M. Pringle, J. Mater. Chem., 2011, 21, 7640–7650.
6. V. Armel, M. Forsyth, D. R. MacFarlane and J. M. Pringle, Energy Environ. Sci., 2011, 4, 2234–2239.
7. L. Jin, K. M. Nairn, C. M. Forsyth, A. J. Seeber, D. R. MacFarlane, P. C. Howlett, M. Forsyth and J. M. Pringle, J. Am. Chem. Soc., 2012, 134, 9688–9697.
8. Q. Li, X. Chen, J. Zhao, L. Qiu, Y. Zhang, B. Sun and F. Yan, J. Mater. Chem., 2012, 22, 6674–6679.
9. J. M. Pringle, Phys. Chem. Chem. Phys., 2013, 15, 1339–1351.
10. S. Li, L. Qiu, C. Shi, X. Chen and F. Yan, Adv. Mater., 2014, 26, 1266–1271.
11. Q. Li, J. Zhao, B. Sun, B. Lin, L. Qiu, Y. Zhang, X. Chen, J. Lu and F. Yan, Adv. Mater., 2012, 24, 945–950.
12. D. R. MacFarlane and M. Forsyth, Adv. Mater., 2001, 13, 957–966.
13. L. Jin, P. C. Howlett, J. M. Pringle, J. Janikowski, M. Armand, D. R. MacFarlane and M. Forsyth, Energy Environ. Sci., 2014, 7, 3352–3361.
14. P. Wang, Q. Dai, S. M. Zakeeruddin, M. Forsyth, D. R. MacFarlane and M. Grätzel, J. Am. Chem. Soc., 2004, 126, 13590–13591.
15. J. Golding, N. Hamid, D. R. MacFarlane, M. Forsyth, C. Forsyth, C. Collins and J. Huang, Chem. Mater., 2001, 13, 558–564.
16. M. Patel and A. J. Bhattacharyya, Energy Environ. Sci., 2011, 4, 429–432.
17. J. Luo, A. H. Jensen, N. R. Brooks, J. Sniekers, M. Knipper, D. Aili, Q. Li, B. Vanroy, M. Wubbenhorst, F. Yan, L. Van Meervelt, Z. Shao, J. Fang, Z.-H. Luo, D. E. De Vos, K. Binnemans and J. Fransaer, Energy Environ. Sci., 2015, 8, 1276–1291.
18. K. Dong, X. Liu, H. Dong, X. Zhang and S. Zhang, Chem. Rev., 2017, 117, 6636–6695.
19. E. I. Izgorodina, Z. L. Seeger, D. L. A. Scarborough and S. Y. S. Tan, Chem. Rev., 2017, 117, 6696–6754.
20. K. Fumino, E. Reichert, K. Wittler, R. Hempelmann and R. Ludwig, Angew. Chem., Int. Ed., 2012, 51, 6236–6240.
21. K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929.
22. S. S. Sarangi, W. Zhao, F. Müller-Plathe and S. Balasubramanian, ChemPhysChem, 2010, 11, 2001–2010.
23. A. Mondal and S. Balasubramanian, J. Phys. Chem. C, 2016, 120, 22903–22909.
24. A. Mondal, A. P. Sunda and S. Balasubramanian, Phys. Chem. Chem. Phys., 2016, 18, 2047–2053.
25. L. Jin, S. de Leeuw, M. V. Koudriachova, J. M. Pringle, P. C. Howlett, F. Chen and M. Forsyth, Phys. Chem. Chem. Phys., 2013, 15, 19570–19574.
26. M. Forsyth, T. Chimdi, A. Seeber, D. Gunzelmann and P. C. Howlett, J. Mater. Chem. A, 2014, 2, 3993–4003.
27. F. Chen, J. M. Pringle and M. Forsyth, Chem. Mater., 2015, 27, 2666–2672.
28. C. Shi, S. Li, W. Zhang, L. Qiu and F. Yan, J. Mater. Chem. A, 2013, 1, 13956–13962.
29. Q. Dai, D. R. MacFarlane, P. C. Howlett and M. Forsyth, Angew. Chem., Int. Ed., 2005, 44, 313–316.
30. K. Romanenko, J. M. Pringle, L. A. O'Dell and M. Forsyth, Phys. Chem. Chem. Phys., 2015, 17, 18991–19000.
31. X. Wang, H. Zhu, G. W. Greene, Y. Zhou, M. Yoshizawa-Fujita, Y. Miyachi, M. Armand, M. Forsyth, J. M. Pringle and P. C. Howlett, Adv. Mater. Technol., 2017, 2, 1700046.
32. U. A. Rana, R. Vijayaraghavan, M. Walther, J. Sun, A. A. J. Torriero, M. Forsyth and D. R. MacFarlane, Chem. Commun., 2011, 47, 11612–11614.
33. F. Philippi, D. Rauber, J. Zapp and R. Hempelmann, Phys. Chem. Chem. Phys., 2017, 19, 23015–23023.
34. J. Luo, O. Conrad and I. F. J. Vankelecom, J. Mater. Chem., 2012, 22, 20574–20579.
35. S. Seki, K. Hayamizu, S. Tsuzuki, K. Fujii, Y. Umebayashi, T. Mitsugi, T. Kobayashi, Y. Ohno, Y. Kobayashi, Y. Mita, H. Miyashiro and S.-i. Ishiguro, Phys. Chem. Chem. Phys., 2009, 11, 3509–3514.
36. N. Salem, S. Zavorine, D. Nucciarone, K. Whitbread, M. Moser and Y. Abu-Lebdeh, J. Electrochem. Soc., 2017, 164, H5202–H5209.
37. G. Zhou, X. Liu, S. Zhang, G. Yu and H. He, J. Phys. Chem. B, 2007, 111, 7078–7084.
38. X. Liu, G. Zhou, S. Zhang and G. Yu, Mol. Simul., 2010, 36, 79–86.
39. X. Liu, Y. Zhao, X. Zhang, G. Zhou and S. Zhang, J. Phys. Chem. B, 2012, 116, 4934–4942.
40. J. J. Hettige, J. C. Araque, H. K. Kashyap and C. J. Margulis, J. Chem. Phys., 2016, 144, 121102.
41. R. Dennington, T. Keith and J. Millam, GaussView Version 5, Semichem Inc., Shawnee Mission, KS, 2009.
42. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, et al., Gaussian 09 Revision D.01, Gaussian Inc., Wallingford CT, 2009.
43. J. Hutter, M. Iannuzzi, F. Schiffmann and J. VandeVondele, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2014, 4, 15–25.
44. S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703–1710.
45. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
46. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
47. S. Plimpton, J. Comput. Phys., 1995, 117, 1–19.
48. W. L. Jorgensen, D. S. Maxwell and J. Tirado-Rives, J. Am. Chem. Soc., 1996, 118, 11225–11236.
49. T. M. Chang, L. X. Dang, R. Devanathan and M. Dupuis, J. Phys. Chem. A, 2010, 114, 12764–12774.
50. Y.-L. Wang, F. U. Shah, S. Glavatskih, O. N. Antzutkin and A. Laaksonen, J. Phys. Chem. B, 2014, 118, 8711–8723.
51. M. Kohagen, M. Brehm, J. Thar, W. Zhao, F. Müller-Plathe and B. Kirchner, J. Phys. Chem. B, 2011, 115, 693–702.
52. C. Schröder, Phys. Chem. Chem. Phys., 2012, 14, 3089–3102.
53. V. Lesch, H. Montes-Campos, T. Méndez-Morales, L. J. Gallego, A. Heuer, C. Schröder and L. M. Varela, J. Chem. Phys., 2016, 145, 204507.
54. T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2010, 6, 2455–2468.
55. T. A. Manz and D. S. Sholl, J. Chem. Theory Comput., 2012, 8, 2844–2867.
56. L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164.
57. S. Nosé, J. Chem. Phys., 1984, 81, 511–519.
58. W. G. Hoover, Phys. Rev. A, 1985, 31, 1695–1697.
59. W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38.
60. A. P. Sunda, A. Mondal and S. Balasubramanian, Phys. Chem. Chem. Phys., 2015, 17, 4625–4633.
61. P. J. Daivis and D. J. Evans, J. Chem. Phys., 1994, 100, 541–547.
62. M. Harada, A. Yamanaka, M. Tanigaki and Y. Tada, J. Chem. Phys., 1982, 76, 1550–1556.
63. J.-P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, 3rd edn, 2006.
64. A. Mondal and S. Balasubramanian, J. Chem. Eng. Data, 2014, 59, 3061–3068.

---

Footnote

† Electronic supplementary information (ESI) available: Initial configurations of the[HN(Ph)₃][TFO] dimer, center of mass RDFs, partial charges on atoms and the complete set of force field parameters, the distances and angle obtained from quantum calculation for hydrogen bonding and C–H/π interactions, diffusion coefficients and Nernst–Einstein conductivity calculated from simulations are shown. See DOI: 10.1039/c8cp03004a

---