Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Morphology and ion diffusion in PEDOT:Tos. A coarse grained molecular dynamics simulation†
Mohsen
Modarresi
 ab,
Juan Felipe
Franco-Gonzalez
ab,
Juan Felipe
Franco-Gonzalez
 a and
Igor
Zozoulenko
a and
Igor
Zozoulenko
 *a
*a
aLaboratory of Organic Electronics, Department of Science and Technology, Linköping University, 60174 Norrköping, Sweden. E-mail: igor.zozoulenko@liu.se
bDepartment of Physics, Ferdowsi University of Mashhad, Mashhad, Iran
First published on 31st May 2018
Abstract
A Martini coarse-grained Molecular Dynamics (MD) model for the doped conducting polymer poly(3,4-ethylenedioxythiophene) (PEDOT) is developed. The morphology of PEDOT:Tos (i.e. PEDOT doped with molecular tosylate) and its crystallization in aqueous solution for different oxidation levels were calculated using the developed method and compared with corresponding all atomistic MD simulations. The diffusion coefficients of Na+ and Cl− ions in PEDOT:Tos are studied using the developed coarse-grained MD approach. It is shown that the diffusion coefficients decrease exponentially as the hydration level is reduced. It is also predicted that the diffusion coefficients decrease when the doping level of PEDOT is increased. The observed behavior is related to the evolution of water clusters and trapping of ions around the polymer matrix as the hydration level changes. The predicted behavior of the ionic diffusion coefficients can be tested experimentally, and we believe that molecular picture of ionic diffusion in PEDOT unraveled in the present study is instrumental for the design of polymeric materials and devices for better and enhanced performance.
1 Introduction
Conducting polymers provide an exciting possibility for cheap and easily processable printable and flexible electronic and bioelectronic devices. One of the most common conducting polymers is poly(3,4-ethylenedioxythiophene) (best known as PEDOT), which is typically polymerized in the presence of negative polystyrene sulfonate (PSS) counterions, or molecular counterions such as tosylate (Tos) that compensate oxidized PEDOT chains which are positively charged.1–9 The PEDOT oxidation level can be tuned by a chemical reducing agent10 or electrochemically.11Charge carriers in PEDOT are positive polaron or bipolaron quasi particles localized in chains due to a strong electron–lattice coupling.9,12–17 PEDOT films can reach an electrical conductivity exceeding 1000 S cm−1.1–5 The low work function (4.30 eV) and high conductivity make PEDOT an appropriate candidate for source and drain electrodes.18 The electrical conductivity, Seebeck coefficient and thermoelectric efficiency of PEDOT are dependent on its oxidation level.10 Because of the high ionic conductivity, PEDOT represents an excellent material for energy storage devices such as supercapacitors and fuel cells,19 as well as for biolectronic devices such as sensors, electrochemical transistors20 and ion pumps.21 Ionic conductivity enhancement with increased humidity level and the ionic Seebeck effect were recently reported for Na+ ions in PEDOT:PSS.5 Previously the effect of hydration level was mainly studied experimentally22,23 and theoretically24,25 in proton transport through hydrated Nafion for application in fuel cells.
The ionic and electronic transport properties of PEDOT:Tos are strongly related to and determined by its complex morphology.26 There are extensive experimental efforts to understand the morphology of PEDOT films.2–4,27 At the same time, theoretical work addressing the morphology of PEDOT:PSS is practically missing. In earlier theoretical work doped PEDOT with tosylate or other counterions was analyzed using density functional theory (DFT) assuming perfect infinite crystalline order.28–30 Recent All Atomistic (AA) Molecular Dynamics (MD) calculations for PEDOT doped with different molecular counterions (including Tos) reveal a complex morphology where small crystallites consisting of several π–π stacking PEDOT chains are embedded in a polymer matrix including PEDOT chains, Tos counterions and water molecules.16,31 Because of computational limitations, AA MD simulations do not always allow one to reach a length-scale needed to study the morphology of a realistic material. For example, a formation of PEDOT-rich and PSS-rich phases in PEDOT:PSS that happens on the scale of ∼20–30 nm32 is beyond the reach of AA MD. Theoretical investigation of the morphology of PEDOT on these scales requires coarse-grained (CG) approaches where the system is represented by reduced numbers of the degrees of freedom. In CG MD simulations the atoms are grouped in some specific beads to reduce complexity and computational cost for larger systems at longer time scales.
The Martini CG force field offers speed, accuracy, applicability, and versatility for MD simulations.33 So far, a Martini coarse-grained model for PEDOT is still missing, and therefore one of the aims of our study is to develop and validate the Martini coarse-grained model for doped PEDOT. A simplified CG model of PEDOT was used in ref. 34, where the entire EDOT monomer was treated as one bead. This model is however too crude and simplified and is not in a position to reproduce the most important morphological aspects of PEDOT on a sub-nanometer scale, such as its crystallization. On the contrary, our Martini CG model correctly reproduces the formation of π–π crystallites, as evidenced by the distributions of distance between chains. Our second aim is to apply the CG model to investigate and understand the ionic diffusion in PEDOT for different oxidation and water content. Such understanding is essential for improving device and material design because the diffusion of ions such as Na+ and Cl− determines the performance of PEDOT-based devices with mixed electron-ionic conductivity, including supercapacitors, organic electrochemical transistors, and ion pumps. At the same time, theoretical understanding of ionic diffusion in PEDOT, in particular the dependence of the ionic diffusion coefficients on the water content, is still absent.
In the present study, we develop and validate a Martini CG MD model for PEDOT, and use it to simulate the polymer morphology and calculate the diffusion coefficients of Na+ and Cl− ions in PEDOT:Tos. We find that the diffusion coefficient decreases exponentially as the hydration level is reduced. We also find that the diffusion coefficients decrease when the doping level of PEDOT is increased. The obtained behavior is analyzed based on the water cluster evolution and trapping of ions around the polymer matrix as the hydration level changes. The predicted behavior of the ionic diffusion coefficients can be tested experimentally, and we believe that the detailed molecular picture of ionic diffusion in PEDOT unraveled in the present study is instrumental for the design of polymeric materials and devices for better and enhanced performance.
2 The coarse-grained model for PEDOT
In this section we present the CG model for PEDOT and outline our CG MD simulations using the Martini CG force field. The latter was originally developed for biomolecular systems35,36 and later on extended for polymer systems.37–42 The Martini model categorizes the beads into polar (P), nonpolar (N), apolar (C), and charged (Q) ones. For each kind of bead, there are subgroups which give more freedom for choosing the appropriate bead type. For example, the N-type beads are categorized based on the H-bonding capabilities: none (N0), donor (Nd), acceptor (Na) and donor–acceptor (Nda).35 There are also S-type beads with a smaller radius and weaker van der Waals interactions for modeling of ring structures.35 Recently, the Martini model was successfully applied to polymers like poly(3-hexyl-thiophene) (P3HT),37–39,43 phenyl-C61-butyric acid methyl ester (PCBM),37 polystyrene40,41 and PSS.42 Also, a polarizable CG model for water is developed based on one neutral and two charged beads.44 The validity of the Martini polarizable water model for application to systems with charges is confirmed for the ionic conductivity of Na+ and Cl− ions in pure water.45 Based on the CG model for P3HT37–39,43 we use the SC2 and SC1 bead types for the thiophene ring in PEDOT, where the SC2 bead is used for the sulfur atom and two less polarized SC1 beads are used for the four carbons, see Fig. 1(a). The remaining dioxy group with hydrogen atoms is considered as a single SNda bead. The distance between nearest neighbor beads is constrained using the LINCS algorithm.46 A virtual site is placed in the center of mass of the sulfur and two neighboring carbon atoms to connect the thiophene rings and have more control of the PEDOT backbone.37,39,43 The connection between neighboring EDOT units is modeled by a harmonic force between virtual sites. The virtual site has a zero mass and it does not interact with other beads via van der Waals interactions. We consider doped PEDOT with different oxidation levels Cox, where positive charges in the polymer backbone are compensated for by negative counterions. Ab initio calculations show that for different values of Cox, the distribution of positive and negative charges is practically the same for different monomers (with some deviations for monomers at the ends of the chain).16 Therefore, in our CG model, we assume that for each oxidation level Cox, positive charges are equally distributed on virtual sites. For example, for Cox = 33.3% each virtual site gets a charge of +0.333e. Our CG model of the tosylate molecule is based on the model for PSS recently developed by Vögele et al.42 as shown in Fig. 1(b). The PSS model includes SCY and STY beads and considers the sulfonate group as a charged Qa bead.42 The water molecules are represented by the polarizable water model.44 The non-bonded parameters are described by Martini force field V2.2 alongside the required Martini beads and parameters for PSS and polarizable water.42,44,45,47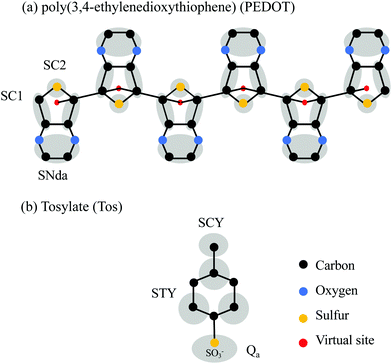 | ||
| Fig. 1 (a) The atomic structure and the CG model of (a) PEDOT and (b) TOS. The beads (SC1, SC2, and SNda for PEDOT and SCY, STY, and Qa for Tos) are indicated in grey; virtual sites are shown in red. | ||
The bonded parameters, which include equilibrium distances, angles, dihedrals and force constants between PEDOT beads, were extracted from the comparison of different distributions in the CG and AA models. For the AA MD simulation we use the general AMBER force field (GAFF),48 which was previously used to describe the morphology of PEDOT doped with various counterions including Tos16,31 and a related self-doped polymer ETE-S.49,50 A comparison between the bond lengths and angles calculated using the CG and AA approaches is given in section one of ESI,† SI1, see Fig. S1. The calculated parameters for the PEDOT CG model are listed in Table S1 (ESI†). Note that even though in the present study we focus on the morphology and ion diffusion for the case of molecular counterions such as Tos, our CG model for PEDOT can be used to study PEDOT crystallization in the presence of other polyanions such as PSS. For the Tos molecule, the CG model from ref. 42 is validated using the AA model of Tos reported in ref. 16, see Fig. S2 in Section SI2 (ESI†).
In our simulation we use a computational cubic box filled with randomly distributed PEDOT chains, tosylate and polarized water beads under 3D periodic boundary conditions. (Typically the computational box contains 400 PEDOT chains of length N = 12 monomer units, and 52![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 water molecules; the number of Tos molecules depends on the oxidation level and varies between 1600 for Cox = 33.3% and zero for Cox = 0%). The MD simulations start with water equilibration, where three equilibration steps are performed as follows. First, a canonical NVT ensemble is run with a 5 fs time step for 10 ns using the Berendsen thermostat.51 Then, the equilibration continues with another NVT ensemble for 100 ns with a 20 fs time step. Lastly, the system is equilibrated in an isothermal–isobaric NPT ensemble for 100 ns with a 20 fs time step by using the Berendsen barostat at 1 bar.51 During all water equilibration steps, we apply position restraints to both the PEDOT and tosylate molecules. Having equilibrated the water, we start the production run using the NPT ensemble and the Berendsen barostat for 200 ns and a 20 fs time step. The simulation temperature was T = 300 K during the equilibrations and the production run using the Berendsen thermostat. For all simulations, the long-range Coulomb electrostatic interactions are calculated using the Particle Mesh Ewald (PME) method.52 For the drying process, we remove the water beads in four steps and study the system with the hydration levels Hy = 80, 60, 40, 20 and 10 percent of water, where the hydration level (Hy) is defined as the water weight percent wt% with respect to the total solution weight. At each drying step, randomly chosen water molecules are removed from the box and the above MD equilibration routine is repeated. Our computation procedure for water evaporation is designed to mimic a corresponding experimental procedure performed by Palumbiny et al. for printed PEDOT:PSS.53
000 water molecules; the number of Tos molecules depends on the oxidation level and varies between 1600 for Cox = 33.3% and zero for Cox = 0%). The MD simulations start with water equilibration, where three equilibration steps are performed as follows. First, a canonical NVT ensemble is run with a 5 fs time step for 10 ns using the Berendsen thermostat.51 Then, the equilibration continues with another NVT ensemble for 100 ns with a 20 fs time step. Lastly, the system is equilibrated in an isothermal–isobaric NPT ensemble for 100 ns with a 20 fs time step by using the Berendsen barostat at 1 bar.51 During all water equilibration steps, we apply position restraints to both the PEDOT and tosylate molecules. Having equilibrated the water, we start the production run using the NPT ensemble and the Berendsen barostat for 200 ns and a 20 fs time step. The simulation temperature was T = 300 K during the equilibrations and the production run using the Berendsen thermostat. For all simulations, the long-range Coulomb electrostatic interactions are calculated using the Particle Mesh Ewald (PME) method.52 For the drying process, we remove the water beads in four steps and study the system with the hydration levels Hy = 80, 60, 40, 20 and 10 percent of water, where the hydration level (Hy) is defined as the water weight percent wt% with respect to the total solution weight. At each drying step, randomly chosen water molecules are removed from the box and the above MD equilibration routine is repeated. Our computation procedure for water evaporation is designed to mimic a corresponding experimental procedure performed by Palumbiny et al. for printed PEDOT:PSS.53
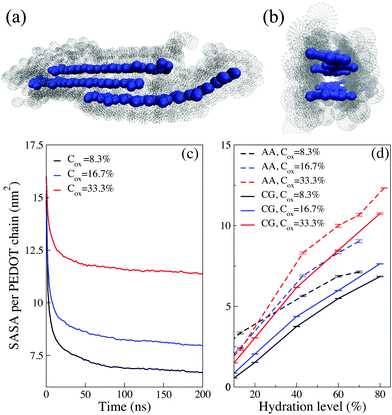
In the present study we also calculate and compare the solvent-accessible surface area (SASA) using the AA and CG models and in the present work, the SASA is calculated based on the double cubic lattice method54 as implemented in the Gromacs-v5 package.55–57 For CG simulations, the van der Waals radius for CG beads and probe radius are set to the potential energy minimum distance. For the 6–12 Lennard-Jones potential in the Martini force field, the minimum is at r = 21/6σ,58 where σ = 0.47 nm and σ = 0.43 nm for the ordinary and ring type beads, respectively. For the case of AA calculations, the probe radius is 0.14 nm, corresponding to the size of the water molecule, see ref. 16 for details.
We chose Na+ and Cl− as diffusive ions because they are used as an electrolyte in a typical electrochemical setup.32 Also, Na+ and Cl− represent biologically active ions providing the electrical activity needed to support muscle contractions and neuron activation and they are therefore utilized in various PEDOT-based bioelectronic devices.59 In CG calculations Na+ and Cl− are respectively described by single Qd and Qa Martini CG beads.35,44,45 The diffusion constant is calculated in a standard way by using the mean square displacement and the Einstein relation.45
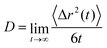 | (1) |
In earlier work, a validation of the Martini CG model was based on the calculation of the free energy and a comparison with AA MD simulations and available experimental results.35–37 In subsequent work, other physical and chemical quantities such as the mass density,37,40,45,65,66 the dielectric constant,42 the radius of gyration,40,42,65,67,68 film morphology37 and the diffusion coefficient40 were used to validate the CG model. In the present work for the validation of our CG model of PEDOT, we focus at the formation of π–π stacking between PEDOT chains, the number of chains in crystallites, the mass density and the SASA, and compare the CG results with corresponding AA simulations as well as with experimental values (where available).
3 Results and discussion
3.1 PEDOT:Tos morphology
The aim of this section is to investigate the morphology of PEDOT:Tos within the CG model and compare it with the corresponding AA MD previously reported results. The oxidation level of PEDOT:Tos per monomer unit is considered in the range 0 < Cox < 33.3%; in most simulations the length of PEDOT chains is chosen to be N = 12 monomer units. (Note that the oxidation level of pristine, i.e. as synthesized, PEDOT typically corresponds to Cox = 33.3%, and the experimental value for the PEDOT chain length is N = 5–15 monomer units8,69).Fig. 2(a)–(d) shows snapshots of PEDOT:Tos for the hydration levels Hy = 80 and 40% and the oxidation levels Cox = 16.7 and 33.3%. All molecular configuration snapshots are prepared using the VMD package.70 A formation of small PEDOT crystallites containing several chains in π–π stacking and surrounded by Tos molecules is clearly visible. For higher oxidation levels, the Coulomb repulsion between PEDOT chains and the attraction between PEDOT–Tos separates PEDOT chains and some Tos molecules intercalate into crystallites as shown in the red boxes of Fig. 2(c). This is consistent with the results of recent AA MD simulations predicting the same phenomenon at high oxidation levels.31 Our results shows that PEDOT crystallization in the presence of Tos molecules occurs at the initial evaporation stage. During water evaporation, a denser polymer structure with more curvature along the PEDOT chains is obtained. The average end-to-end distance of the PEDOT chains decreases from 4.177 ± 0.009 for the solution with Hy = 80% to 3.846 ± 0.003 nm in the dry phase. (The length of a completely straight PEDOT chain for N = 12 is 4.27 nm).
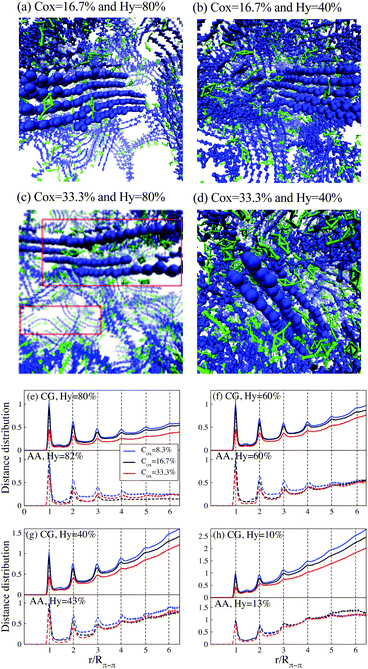 | ||
| Fig. 2 (a–d) Snapshots of PEDOT:Tos for different oxidation and hydration levels. PEDOT is shown in blue and Tos in green; water molecules are not displayed. Red boxes in (c) outline Tos molecules intercalated between PEDOT chains. (e–h) The distance distribution between virtual sites of PEDOT for different oxidation and hydration levels. The solid lines are CG results and dashed lines correspond to the AA simulations reported in ref. 16. | ||
To investigate PEDOT crystallization quantitatively, we calculate the distribution distance perpendicular to the PEDOT planes between virtual sites belonging to different chains with different oxidation levels and hydration levels and compare with present AA results.16 The distance distribution shows pronounced peaks at integer values of r/Rπ–π with Rπ–π = 4.6 Å being the π–π stacking distance between the adjacent chains, see Fig. 2(e)–(h). (Snapshots and the distance distribution chains of lengths N = 6, 12 and 18 are shown in ESI,† SI2). The value of Rπ–π = 4.6 Å obtained from CG simulations is somehow larger than the one obtained from both the AA MD simulations and experimental measurements, RAA MDπ–π ≈ Rexpπ–π = 3.5 Å.2,3,16 The discrepancy between the CG and the atomistic π–π stacking distances is related to the parametrization of the Martini force field mapping four atoms to one CG bead, making the size of the bead larger than the distance between the polymer chains. This discrepancy is known to be inherent to the Martini model and cannot be easily amended by adjusting the Martini force-field parametrization.37 However, it has been argued by Alessandri et al.37 that the discrepancy between CG and AA stacking distances does not impact the nanomorphology evolution. This conclusion is also supported by the agreement in the features of the calculated CG and AA morphologies as will be discussed below in the present section.
The number of peaks in g(r) apparently corresponds to the number of PEDOT chains in the crystallites. Experimentally the crystallite size is determined from the width of the π–π stacking peak in grazing incidence wide-angle X-ray scattering (GIWAXS) spectra using the Scherrer equation.71 The PEDOT experimental crystallite sizes vary in different studies, from 1.2 nm,8 to 3 nm,72 and 4.5 nm,2 which corresponds to 3–12 PEDOT chains. In our CG calculations the number of chains in the crystallites depends on the hydration and oxidation levels and varies between 3–9. For a given oxidation level the size of crystallites decreases when water is evaporated; at the same time, for a given water content, the larger the oxidation level, the smaller the crystallite size. This behavior is fully consistent with the corresponding results of AA MD calculations in Fig. 2.
For further validation of the CG results, we calculate the PEDOT:Tos mass density and compare it with our AA calculations, as well as with the available experimental data27 and density functional theory (DFT) calculations for an ideal crystal,73 see Table 1. The mass density of the AA model is very close to the experimental one.27 The difference between the CG and AA mass densities is lower than 10%. The lower mass density in CG is related to a larger bead size and a greater π–π stacking distance. A similar difference between the calculated CG and AA densities was found for other polymers, such as P3HT and PCBM.37 Note that for the ideal crystal in the DFT calculations73 and orthorhombic model with experimental lattice parameters,27 the densities, as expected, are higher than those obtained from the MD simulations.
Using the CG and AA models we calculate the solvent-accessible surface area (SASA) as described in the model and method section. The SASA corresponds to an area obtained by rolling a probe sphere with the radius of the CG water molecule around PEDOT chains, as illustrated in Fig. 3(a and b). Fig. 3(c) shows the evolution of the SASA during PEDOT crystallization for different oxidation levels at Hy = 80%. The SASA is apparently maximal at the starting time of the production run, t = 0, when all randomly distributed PEDOT chains are accessible by solvents. As PEDOT chains crystallize, the SASA decreases from the initial value by nearly 50, 45 and 30 percent for Cox = 8.3, 16.7, 33.3%, respectively, see Fig. 3(c). The decrease of the SASA is related to formation of π–π stacking between PEDOT chains where the inner surfaces are not included in the SASA, see Fig. 3(b). The decrease of the SASA is almost sudden during the first 20–30 ns initial time interval, which means that the crystallization mostly takes place during this time interval. The variation of the SASA with the hydration level is shown in Fig. 3(d) for the CG and AA models for different oxidation levels. There is a fair agreement between the calculated values of the SASA in the AA and CG models. Because of the difference between beads and atoms in CG and AA MD respectively, we do not expect the same values for the SASA, but we obtain the same trends for the two models. The CG model successfully reproduces the AA SASA behavior when the hydration and oxidation levels are varied. According to expectations, the SASA decreases as water evaporates because the evaporation results in a denser structure and thus a smaller SASA. At the same time, for a given hydration level, the crystallites are smaller for higher Cox, see Fig. 2. Thus, the available surface of PEDOT crystallites is larger, which results in the larger SASA for higher Cox, see Fig. 3(d).
3.2 Ion diffusion through PEDOT:Tos
We first start with the configuration of different components of the system (i.e. PEDOT chains, tosylate molecules, ions and water molecules) relative to each other. Fig. 4(a) shows the radial distribution function between positively charged PEDOT chains and negative Tos molecules, exhibiting peaks at the distances 0.53 nm, 0.74 nm, and 0.93 nm. The positions of the calculated peaks are in good agreement with the corresponding AA calculations.16 The radial distribution functions (RDF) for positive Na+ ions and negative Tos molecules, as well as for negative Cl− ions and positive PEDOT chains, are shown in Fig. 4(b). The RDF function for Na+–Tos− shows a strong peak at the distance 0.5 nm, indicating that the majority of positive Na+ ions are situated close to negative Tos− counterions. The RDF function for Cl−–PEDOT+ shows peaks at the same positions as those for the RDF function PEDOT+–Tos− in Fig. 4(a). The presence of several peaks in the RDF for Cl−–PEDOT+ (PEDOT+–Tos−) is apparently related to the fact that PEDOT is an extended molecule, such that the first peak corresponds to the distance from the ion (Cl− or Tos−) to the neighboring monomer, and the remaining peaks to more distant monomers.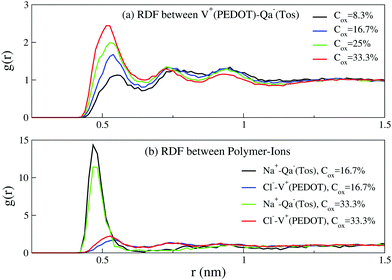 | ||
| Fig. 4 The radial distribution functions (RDF) between (a) PEDOT and tosylate, and (b) PEDOT and Na+ and Cl− ions for different oxidation levels Cox; Hy = 10%. | ||
Let us now study the diffusion of Na+ and Cl− ions in PEDOT:Tos for different hydration and oxidation levels. We first calculate the diffusion coefficients of Na+ and Cl− ions at a concentration of 100 mM using the developed Martini CG MD model in pure water and compare them the with corresponding AA MD simulations reported previously74 and experimental values in the infinitely diluted solution,75–77 see Table 2.
There is a fair agreement between the experimental, CG, and AA diffusion coefficients. Also, as in the case of the SASA (calculated in the previous section), we do not expect exact quantitative agreement between the AA and CG results. The previous AA simulations showed a system-size dependency80,81 and an effect of the truncation scheme of non-bonding interactions82 on the diffusion coefficient. In our calculations the system-size dependence is negligible because of a large size of the computational box, see Table S2 in Section SI3 (ESI†). For the truncation of the electrostatic interactions we use a standard PME method which is shown to be the most accurate one for the MD simulations with the polarizable Martini water model42,44,83 (for comparison of different truncation schemes see Table S3 in Section SI3, ESI†).
To calculate the diffusion coefficients DNa/Cl of Na+ and Cl− ions we add them to the system at each hydration level, keeping their concentration of 100 mM constant and use the Einstein relation for the last 10 ns of the ion's trajectory. In the calculation of the diffusion coefficients, the simulation time is chosen to be long enough to ensure that the diffusive regime is established (i.e. 〈Δr2(t)〉/t in the Einstein relation, eqn (1), saturates and becomes independent of time, see Fig. S4 in Section SI4, ESI†). Here we should mention that AA study of the diffusion process for our large simulation box and long time scale is computationally very expensive. Fig. 5 presents evolution of the diffusion coefficients as the hydration level Hy changes. It exhibits exponential dependence of the diffusion coefficients on the hydration level; the value of DNa/Cl decreases by three orders of magnitude when the hydration level is reduced from 80% to 10%. The exponential dependence of the ionic diffusion coefficients on the water content represents one of the main findings of the present study. We also find that the diffusion coefficient depends on the oxidation level. For example, for Hy = 10%, the diffusion coefficient of both the Na+ and Cl− ions decreases by a factor of ∼2.5 when the oxidation level increases from Cox = 0 to Cox = 33.3%. For a given oxidation level the calculated ion diffusion coefficients can be fitted to an exponential function,
| DNa/ClHy = DNa/Cl0e−λNa/Cl(1−Hy), | (2) |
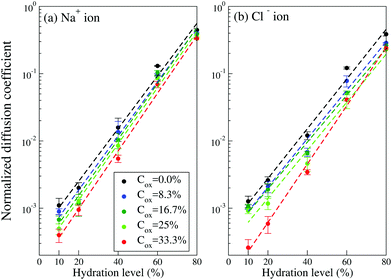 | ||
| Fig. 5 The diffusion coefficients of (a) Na+ and (b) Cl− ions in PEDOT:Tos with different hydration levels and oxidation levels. (The diffusion coefficients are normalized to the corresponding calculated CG Na+ and Cl− ionic diffusion coefficients in pure water as given in Table 2). Dashed lines are the exponential fit based on eqn (2). | ||
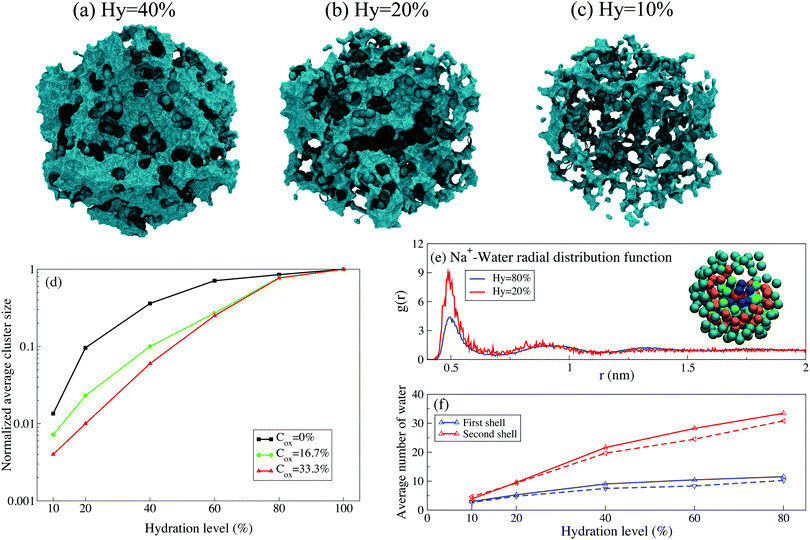
To understand the origin of the exponential behavior of the diffusion coefficient, let us focus on the evolution of the water clusters in the polymer matrix as the hydration level changes. We define the cluster as being composed of water molecules where for any molecule in the cluster one can find another molecule at the distance smaller than a critical distance; the critical distance is set to the diameter of the Martini CG water bead. (For pure water all water molecules apparently belong to a single cluster). As the hydration level decreases the clusters get fragmented into smaller clusters as illustrated in Fig. 6(a–c). The size of water clusters decreases as the hydration level is lowered, and for charged polymers (i.e. Cox ≠ 0) this decrease is exponential, see Fig. 6(d). At higher hydration level, there are wide diffusion paths of water molecules for ions to diffuse through the polymer matrix, Fig. 6(a). As water evaporates, the width and number of diffusion paths decrease and water clusters with weak connections are formed, and many clusters become disconnected, Fig. 6(b) and (c). Because ions primarily move in the water clusters, this leads to a decrease of the diffusion coefficient. The size of water clusters is also dependent on the PEDOT oxidation level. By adding more charges to PEDOT and Tos ions, the charged beads of polarizable water are attracted to the polymer matrix which decreases the water cluster size.
The radial distribution functions of water molecules around Na+ and Cl− ions show peaks corresponding to formation of the hydration shells around the ions, see Fig. 6(e). The first and second shells include water molecules situated respectively at the distances 0.45 < r < 0.65 nm and 0.65 < r < 1.2 nm from the ions. The number of water molecules in each shell decreases as the hydration level is reduced, see Fig. 6(f). The decrease of the number of water molecules in the hydration shells is connected to the thinning of the percolative paths as discussed above. Also, this decrease leads to the reduction of electrostatic screening of ions by water molecules, which, in turn, leads to the enhancement of the electrostatic interaction between ions and the polymer matrix (i.e. PEDOT+ chains and Tos− molecules).
Further insight into the behavior of the ionic diffusion coefficient can be obtained by investigating the relative position between the ions and polymer matrix (consisting of PEDOT+ chains and Tos− molecules). Fig. 7(a) and (b) show the distribution of the minimum distance d between Cl− (Na+) ions and the closest bead of PEDOT+(Tos−) molecules for different hydration levels (a definition of the minimum distance d is visualized in the inset of Fig. 7(b)). The minimum distance distribution has a sharp peak around 0.5 nm for all hydration levels, which shows that most positive (or negative) ions are localized close to the corresponding Tos− (or PEDOT+). There is however a strong qualitative difference in the tails of these distributions between the cases of high and low hydration levels Hy. For higher hydration levels (e.g. Hy = 80%) the calculated distribution shows a broad tail, indicating that many ions move quite far away from the polymer matrix. However, for Hy = 20% the distribution tends to zero already at the distance ≈0.5 nm, indicating that practically all ions are confined in the vicinity of PEDOT+ or Tos−, see Fig. 7(a) and (b). This is clearly seen in the animations presented in the ESI,† SI5 (see below for a more detailed discussion of the animations).
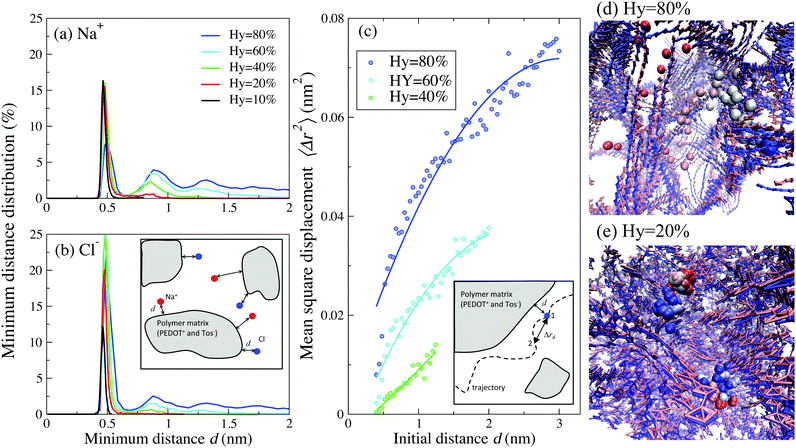 | ||
| Fig. 7 The distribution of a minimum distance d between (a) Na+–Tos and (b) Cl−-PEDOT for Cox = 16.7% and different hydration levels. (c) The mean square displacement 〈Δrd2〉 of Na+ and Cl− ions as a function of the initial distance d from the polymer matrix for Hy = 80, 60 and 40%. The inset in (c) visualizes the definition of 〈Δrd2〉: an ion starts at position 1 at the distance d from the polymer matrix, and arrives at position 2 after time τ; in the calculation τ is chosen as τ = 2 ns. The circles are data points and the solid lines are data regression. Trajectories during 200 ns of (d) one representative Cl− ion for Hy = 80% and (e) two representative Cl− ions for Hy = 20%; the oxidation level Cox = 16.7%. The PEDOT chains at initial and final time steps are in red and blue colors, respectively. The ions at t = 0 are shown in red and the color is changing continuously to reach blue for t = 200 ns. Animations of trajectories visualized in (d) and (e) can be found in the ESI,† SI5. | ||
To understand the importance of this difference, let us consider the average mean square displacement 〈Δrd2〉 for an ion that starts its motion at the distance d from the polymer matrix (a definition of 〈Δrd2〉 is visualized in the inset of Fig. 7(b)). Fig. 7(c) shows a dependence of 〈Δrd2〉 on d at Hy = 80, 60 and 40%. For Hy = 80% and at sufficiently high distances, d ≳ 3 nm, 〈Δrd2〉 is close to the value corresponding to pure water, i.e. ions do not feel the presence of a polymer matrix. The closer ions are situated to the polymer matrix, the smaller 〈Δrd2〉 is. This behavior of 〈Δrd2〉, combined with the distribution of the minimum distance d in Fig. 7(a) and (b), provides a molecular explanation of the pronounced decrease of the diffusion coefficient for lower water content presented in Fig. 5. Indeed, for small hydration levels, practically all ions are confined in the vicinity of the polymer matrix where the mean square displacement 〈Δrd2〉 is small. As a result, the corresponding diffusion coefficient, eqn (1), is also small. For high hydration levels, many ions move away from the polymer matrix where the mean square displacement 〈Δrd2〉 is large. This apparently results in the large diffusion coefficient. This molecular picture of the diffusion is illustrated in the trajectory snapshots for Hy = 80% (Fig. 7(d)) and Hy = 20% (Fig. 7(e)) and in two animations presented in the ESI.† Animation 1 correspond to the case of low water content (Hy = 20%). All ions in the system are confined close to the polymer matrix and execute a “trembling” motion with a very low displacement. In contrast, for high water content (Hy = 80%), an ion wanders around the whole system until it finally gets trapped in the vicinity of the polymer matrix, see Animation 2. (Note that after some time the ion will be “released” again and will continue its motion in the system).
The ionic conductivity σ is directly proportional to the diffusion coefficient of anions and cations in the solution through the Nernst–Einstein equation, 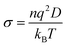 , where q is the ionic charge and n the ion concentration.45,84 Our results predicting the exponential enhancement of ionic conductivity in the polymer as the water content is increased can be tested in the laboratory. The conductivity enhancement with increasing water content is reported experimentally for Na+ ions in PEDOT:PSS,5,85–87 Na or Cs ions in PSS:poly(diallyldimethylammonium chloride)88 and nanofibrillated cellulose-PSSH.89 In the low molecular weight polymer LiCF3SO3PEG10 the anion and cation diffusion coefficients increase exponentially by two order of magnitude on adding water.90 The increase in ionic conductivity is even more intense for high molecular weight polymer Pb(CF3–SO3)2PEO16.91
, where q is the ionic charge and n the ion concentration.45,84 Our results predicting the exponential enhancement of ionic conductivity in the polymer as the water content is increased can be tested in the laboratory. The conductivity enhancement with increasing water content is reported experimentally for Na+ ions in PEDOT:PSS,5,85–87 Na or Cs ions in PSS:poly(diallyldimethylammonium chloride)88 and nanofibrillated cellulose-PSSH.89 In the low molecular weight polymer LiCF3SO3PEG10 the anion and cation diffusion coefficients increase exponentially by two order of magnitude on adding water.90 The increase in ionic conductivity is even more intense for high molecular weight polymer Pb(CF3–SO3)2PEO16.91
4 Conclusion
The ionic and electronic transport properties of highly doped conducting polymers, in particular of PEDOT, are strongly dependent on the material morphology. Massive experimental efforts are currently underway in order to investigate the complex morphology of PEDOT. At the same time, the corresponding theoretical modeling and simulations that experiments can rely upon are practically missing. Recently, all atomistic MD simulations of the morphology of doped PEDOT:Tos and its crystallization in aqueous solution have been reported.16 For many systems the utilization of all atomistic MD becomes computationally prohibitive, and the theoretical investigation of the morphology of conducting polymers on a scale exceeding tens of nanometers requires coarse-grained approaches where the system is represented by reduced numbers of the degrees of freedom. In the present study, we develop a Martini coarse-grained MD model for the doped conducting polymer PEDOT. The coarse-grained model is validated using a comparison with corresponding all atomistic MD simulations. In particular, we calculate the size of PEDOT crystallites; the radial distribution functions between PEDOT and Tos counterions, PEDOT and Na+ and Cl− ions, and Tos and Na+ and Cl− ions; the solvent-accessible surface area; and the PEDOT:Tos mass density.Using the developed coarse grained model we study diffusion of Na+ and Cl− ions in PEDOT:Tos. We find that the ionic diffusion coefficients are decreased exponentially when the hydration level is reduced, exhibiting a drop of almost three orders of magnitude when the hydration level Hy is decreased from 80% to 10% wt. We relate this behavior to the evolution of the water clusters in the polymer matrix. At higher hydration level, there are wide percolation paths of water molecules for ions to diffuse through the polymer matrix. As the hydration level decreases, the water clusters become fragmented into smaller and disconnected clusters and their sizes decrease exponentially. Another theoretical prediction is that the diffusion coefficients decrease when the doping level of PEDOT is increased. For example, for the hydration level Hy = 10%, the ionic diffusion coefficients in fully reduced PEDOT are by a factor of ∼2.5 larger than the diffusion coefficients in fully oxidized PEDOT at Cox = 33.3%.
A complementary insight into the observed exponential behavior of the diffusion coefficient is obtained from the analysis of the relative position of ions and the polymer matrix and the average mean square displacement 〈Δrd2〉 for an ion that starts its motion at the distance d from the polymer matrix. We demonstrate that at high hydration levels many ions move quite far away from the polymer matrix, and 〈Δrd2〉 is close to the value corresponding to pure water. However, for low hydration levels, most ions ions are confined in the vicinity of the polymer matrix where the mean square displacement 〈Δrd2〉 is negligible. As a result, the corresponding diffusion coefficient is decreased exponentially.
The predicted exponential dependence of the ionic diffusion coefficients on the hydration level and the predicted decrease of the diffusion coefficient with the increase of the oxidation level can be tested experimentally. We believe that our findings concerning the behavior of the ionic diffusion coefficients apply not only to PEDOT:Tos, but to a wider class of doped polymers with molecular counterions including polypyrrole, polyaniline, thiophene, etc., which exhibit similar character of disordered amorphous morphology with limited crystallinity. We also believe that the understanding of ionic diffusion on the molecular level provided in this study is important for designing devices with mixed electron–ion conductivity (such as supercapacitors, organic electrochemical transistors, and ion pumps) where the ionic diffusion determines the device performance.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the Troëdssons foundation (896/16), Knut and Alice Wallenberg Foundation through the project The Tail of the Sun, and the Swedish Research Council via “Research Environment grant” on “Disposable paper fuel cells” (201605990). IZ thanks the Advanced Functional Material center at Linköping University for financial support. Authors thank Eleni Stavrinidou for the discussions. The computations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at NSC and HPC2N.References
- B. Winther-Jensen and K. West, Macromolecules, 2004, 37, 4538–4543 CrossRef.
- Z. U. Khan, O. Bubnova, M. J. Jafari, R. Brooke, X. Liu, R. Gabrielsson, T. Ederth, D. R. Evans, J. W. Andreasen, M. Fahlman and X. Crispin, J. Mater. Chem. C, 2015, 3, 10616–10623 RSC.
- C. Yi, L. Zhang, R. Hu, S. S. C. Chuang, J. Zheng and X. Gong, J. Mater. Chem. A, 2016, 4, 12730–12738 Search PubMed.
- Y. H. Lee, J. Oh, S.-S. Lee, H. Kim and J. G. Son, ACS Macro Lett., 2017, 6, 386–392 CrossRef.
- H. Wang, U. Ail, R. Gabrielsson, M. Berggren and X. Crispin, Adv. Energy Mater., 2015, 5, 1500044 CrossRef.
- O. Bubnova, Z. U. Khan, H. Wang, S. Braun, D. R. Evans, M. Fabretto, P. Hojati-Talemi, D. Dagnelund, J.-B. Arlin, Y. H. Geerts, S. Desbief, D. W. Breiby, J. W. Andreasen, R. Lazzaroni, W. M. Chen, I. Zozoulenko, M. Fahlman, P. J. Murphy, M. Berggren and X. Crispin, Nat. Mater., 2014, 13, 190–194 CrossRef PubMed.
- J. Rivnay, S. Inal, B. A. Collins, M. Sessolo, E. Stavrinidou, X. Strakosas, C. Tassone, D. M. Delongchamp and G. G. Malliaras, Nat. Commun., 2016, 7, 11287 CrossRef PubMed.
- T. Takano, H. Masunaga, A. Fujiwara, H. Okuzaki and T. Sasaki, Macromolecules, 2012, 45, 3859–3865 CrossRef.
- R. Gangopadhyay, B. Das and M. R. Molla, RSC Adv., 2014, 4, 43912–43920 RSC.
- O. Bubnova, Z. U. Khan, A. Malti, S. Braun, M. Fahlman, M. Berggren and X. Crispin, Nat. Mater., 2011, 10, 429–433 CrossRef PubMed.
- T. Park, C. Park, B. Kim, H. Shin and E. Kim, Energy Environ. Sci., 2013, 6, 788–792 Search PubMed.
- M. P. Lima and G. M. e Silva, THEOCHEM, 2008, 852, 15–21 CrossRef.
- A. Dkhissi, D. Beljonne, R. Lazzaroni, F. Louwet and B. Groenendaal, Theor. Chem. Acc., 2008, 119, 305–312 CrossRef.
- J. A. van Haare, E. E. Havinga, J. L. van Dongen, R. A. Janssen, J. Cornil and J.-L. Brédas, Chem. – Eur. J., 1998, 4, 1509–1522 CrossRef.
- B.-w. Park, L. Yang, E. M. Johansson, N. Vlachopoulos, A. Chams, C. Perruchot, M. Jouini, G. Boschloo and A. Hagfeldt, J. Phys. Chem. C, 2013, 117, 22484–22491 Search PubMed.
- J. F. Franco-Gonzalez and I. V. Zozoulenko, J. Phys. Chem. B, 2017, 121, 4299–4307 CrossRef PubMed.
- W. A. Muñoz, S. K. Singh, J. F. Franco-Gonzalez, M. Linares, X. Crispin and I. V. Zozoulenko, Phys. Rev. B, 2016, 94, 205202 CrossRef.
- K. Hong, S. H. Kim, C. Yang, T. K. An, H. Cha, C. Park and C. E. Park, Org. Electron., 2011, 12, 516–519 CrossRef.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. WÅgberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed.
- J. Rivnay, P. Leleux, M. Ferro, M. Sessolo, A. Williamson, D. A. Koutsouras, D. Khodagholy, M. Ramuz, X. Strakosas, R. M. Owens, C. Benar, J.-M. Badier, C. Bernard and G. G. Malliaras, Sci. Adv., 2015, 1, 1400251 Search PubMed.
- A. Jonsson, Z. Song, D. Nilsson, B. A. Meyerson, D. T. Simon, B. Linderoth and M. Berggren, Sci. Adv., 2015, 1, 1500039 Search PubMed.
- C. Yin, L. Wang, J. Li, Y. Zhou, H. Zhang, P. Fang and C. He, Phys. Chem. Chem. Phys., 2017, 19, 15953–15961 RSC.
- X. He, G. He, A. Zhao, F. Wang, X. Mao, Y. Yin, L. Cao, B. Zhang, H. Wu and Z. Jiang, ACS Appl. Mater. Interfaces, 2017, 9, 27676–27687 Search PubMed.
- S. Feng and G. A. Voth, J. Phys. Chem. B, 2011, 115, 5903–5912 CrossRef PubMed.
- J. Karo, A. Aabloo, J. O. Thomas and D. Brandell, J. Phys. Chem. B, 2010, 114, 6056–6064 CrossRef PubMed.
- N. Rolland, J. F. Franco-Gonzalez, R. Volpi, M. Linares and I. V. Zozoulenko, Phys. Rev. Mater., 2018, 2, 045605 CrossRef.
- K. Aasmundtveit, E. Samuelsen, L. Pettersson, O. Inganäs, T. Johansson and R. Feidenhansl, Synth. Met., 1999, 101, 561–564 CrossRef.
- E.-G. Kim and J.-L. Brédas, J. Am. Chem. Soc., 2008, 130, 16880–16889 CrossRef PubMed.
- A. Lenz, H. Kariis, A. Pohl, P. Persson and L. Ojamäe, Chem. Phys., 2011, 384, 44–51 CrossRef.
- J. Casanovas, D. Zanuy and C. Aleman, Phys. Chem. Chem. Phys., 2017, 19, 9889–9899 RSC.
- S. Rudd, J. F. Franco-Gonzalez, S. Kumar Singh, Z. Ullah Khan, X. Crispin, J. W. Andreasen, I. Zozoulenko and D. Evans, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 97–104 CrossRef PubMed.
- A. V. Volkov, K. Wijeratne, E. Mitraka, U. Ail, D. Zhao, K. Tybrandt, J. W. Andreasen, M. Berggren, X. Crispin and I. V. Zozoulenko, Adv. Funct. Mater., 2017, 27, 1700329 CrossRef.
- S. J. Marrink, A. H. de Vries and A. E. Mark, J. Phys. Chem. B, 2004, 108, 750–760 CrossRef.
- C.-K. Lee, O. Wodo, B. Ganapathysubramanian and C.-W. Pao, ACS Appl. Mater. Interfaces, 2014, 6, 20612–20624 Search PubMed.
- S. J. Marrink, H. J. Risselada, S. Yefimov, D. P. Tieleman and A. H. de Vries, J. Phys. Chem. B, 2007, 111, 7812–7824 CrossRef PubMed.
- L. Monticelli, S. K. Kandasamy, X. Periole, R. G. Larson, D. P. Tieleman and S.-J. Marrink, J. Chem. Theory Comput., 2008, 4, 819–834 CrossRef PubMed.
- R. Alessandri, J. J. Uusitalo, A. H. de Vries, R. W. A. Havenith and S. J. Marrink, J. Am. Chem. Soc., 2017, 139, 3697–3705 CrossRef PubMed.
- M. Bockmann, T. Schemme, D. H. de Jong, C. Denz, A. Heuer and N. L. Doltsinis, Phys. Chem. Chem. Phys., 2015, 17, 28616–28625 RSC.
- T. Winands, M. Bockmann, T. Schemme, P.-M. T. Ly, D. H. de Jong, Z. Wang, C. Denz, A. Heuer and N. L. Doltsinis, Phys. Chem. Chem. Phys., 2016, 18, 6217–6227 RSC.
- G. Rossi, L. Monticelli, S. R. Puisto, I. Vattulainen and T. Ala-Nissila, Soft Matter, 2011, 7, 698–708 RSC.
- G. Rossi, I. G. Elliott, T. Ala-Nissila and R. Faller, Macromolecules, 2012, 45, 563–571 CrossRef.
- M. Vögele, C. Holm and J. Smiatek, J. Chem. Phys., 2015, 143, 243151 CrossRef PubMed.
- D. Janeliunas, PhD thesis, TU Delft, 2014.
- S. O. Yesylevskyy, L. V. Schäfer, D. Sengupta and S. J. Marrink, PLoS Comput. Biol., 2010, 6, e1000810 Search PubMed.
- M. Vögele, C. Holm and J. Smiatek, J. Mol. Liq., 2015, 212, 103–110 CrossRef.
- B. Hess, H. Bekker, H. J. C. Berendsen and J. G. E. M. Fraaije, J. Comput. Chem., 1997, 18, 1463–1472 CrossRef.
- D. H. de Jong, G. Singh, W. F. D. Bennett, C. Arnarez, T. A. Wassenaar, L. V. Schäfer, X. Periole, D. P. Tieleman and S. J. Marrink, J. Chem. Theory Comput., 2013, 9, 687–697 CrossRef PubMed.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174 CrossRef PubMed.
- J. F. Franco-Gonzalez, E. Pavlopoulou, E. Stavrinidou, R. Gabrielsson, D. T. Simon, M. Berggren and I. V. Zozoulenko, Nanoscale, 2017, 9, 13717–13724 RSC.
- E. Stavrinidou, R. Gabrielsson, K. P. R. Nilsson, S. K. Singh, J. F. Franco-Gonzalez, A. V. Volkov, M. P. Jonsson, A. Grimoldi, M. Elgland, I. V. Zozoulenko, D. T. Simon and M. Berggren, Proc. Natl. Acad. Sci. U. S. A., 2017, 114, 2807–2812 CrossRef PubMed.
- H. J. C. Berendsen, J. P. M. Postma, W. F. van Gunsteren, A. DiNola and J. R. Haak, J. Chem. Phys., 1984, 81, 3684–3690 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef.
- C. M. Palumbiny, F. Liu, T. P. Russell, A. Hexemer, C. Wang and P. Müller-Buschbaum, Adv. Mater., 2015, 27, 3391–3397 CrossRef PubMed.
- F. Eisenhaber, P. Lijnzaad, P. Argos, C. Sander and M. Scharf, J. Comput. Chem., 1995, 16, 273–284 CrossRef.
- D. Van Der Spoel, E. Lindahl, B. Hess, G. Groenhof, A. E. Mark and H. J. C. Berendsen, J. Comput. Chem., 2005, 26, 1701 CrossRef PubMed.
- M. J. Abraham, T. Murtola, R. Schulz, S. Páll, J. C. Smith, B. Hess and E. Lindahl, SoftwareX, 2015, 1–2, 19 CrossRef.
- H. Berendsen, D. van der Spoel and R. van Drunen, Comput. Phys. Commun., 1995, 91, 43 CrossRef.
- R. DeVane, W. Shinoda, P. B. Moore and M. L. Klein, J. Chem. Theory Comput., 2009, 5, 2115–2124 CrossRef PubMed.
- D. T. Simon, E. O. Gabrielsson, K. Tybrandt and M. Berggren, Chem. Rev., 2016, 116, 13009–13041 CrossRef PubMed.
- S. Markutsya and M. H. Lamm, J. Chem. Phys., 2014, 141, 174107 CrossRef PubMed.
- H. Mori, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef.
- R. Zwanzig, J. Stat. Phys., 1973, 9, 215–220 CrossRef.
- S. J. Marrink and D. P. Tieleman, Chem. Soc. Rev., 2013, 42, 6801–6822 RSC.
- D. H. de Jong, PhD thesis, Univ. of Groningen, 2013.
- C. A. Löpez, A. J. Rzepiela, A. H. de Vries, L. Dijkhuizen, P. H. Hünenberger and S. J. Marrink, J. Chem. Theory Comput., 2009, 5, 3195–3210 CrossRef PubMed.
- M. J. Hinner, S.-J. Marrink and A. H. de Vries, J. Phys. Chem. B, 2009, 113, 15807–15819 CrossRef PubMed.
- A. S. Raman, A. Vishnyakov and Y. Chiew, Mol. Simul., 2017, 43, 92–101 CrossRef.
- G. Rossi, P. F. J. Fuchs, J. Barnoud and L. Monticelli, J. Phys. Chem. B, 2012, 116, 14353–14362 CrossRef PubMed.
- J. Lu, N. J. Pinto and A. G. MacDiarmid, J. Appl. Phys., 2002, 92, 6033–6038 CrossRef.
- W. Humphrey, A. Dalke and K. Schulten, J. Mol. Graphics, 1996, 14, 33–38 CrossRef PubMed.
- D.-M. Smilgies, J. Appl. Crystallogr., 2009, 42, 1030–1034 CrossRef PubMed.
- A. Ugur, F. Katmis, M. Li, L. Wu, Y. Zhu, K. K. Varanasi and K. K. Gleason, Adv. Mater., 2015, 27, 4664 CrossRef.
- W. Shi, Z. Shuai and D. Wang, Adv. Funct. Mater., 2017, 27, 1702847 CrossRef.
- A. Ghaffari and A. Rahbar-Kelishami, J. Mol. Liq., 2013, 187, 238–245 CrossRef.
- E. Hawlicka, Z. Naturforsch., A: Phys. Sci., 1987, 42, 1014–1016 Search PubMed.
- E. Samson, J. Marchand and K. A. Snyder, Mater. Struct., 2003, 36, 156 CrossRef.
- L. Yuan-Hui and S. Gregory, Geochim. Cosmochim. Acta, 1974, 38, 703–714 CrossRef.
- J. P. Noworyta, S. Koneshan and J. C. Rasaiah, J. Am. Chem. Soc., 2000, 122, 11194–11202 CrossRef.
- S. Koneshan and J. C. Rasaiah, J. Chem. Phys., 2000, 113, 8125–8137 CrossRef.
- D. Spangberg and K. Hermansson, J. Chem. Phys., 2003, 119, 7263–7281 CrossRef.
- J. Torras and C. Alemán, J. Phys. Chem. B, 2013, 117, 10513–10522 CrossRef PubMed.
- P. Mark and L. Nilsson, J. Comput. Chem., 2002, 23, 1211–1219 CrossRef PubMed.
- G. Mustafa, P. P. Nandekar, X. Yu and R. C. Wade, J. Chem. Phys., 2015, 143, 243139 CrossRef PubMed.
- A. Annamareddy and J. Eapen, Sci. Rep., 2017, 7, 44149 CrossRef PubMed.
- H. Wang, D. Zhao, Z. U. Khan, S. Puzinas, M. P. Jonsson, M. Berggren and X. Crispin, Adv. Electron. Mater., 2017, 3, 1700013 CrossRef.
- O. Larsson, E. Said, M. Berggren and X. Crispin, Adv. Funct. Mater., 2009, 19, 3334–3341 CrossRef.
- U. Ail, M. J. Jafari, H. Wang, T. Ederth, M. Berggren and X. Crispin, Adv. Funct. Mater., 2016, 26, 6288–6296 CrossRef.
- S. De, C. Cramer and M. Schönhoff, Macromolecules, 2011, 44, 8936–8943 CrossRef.
- A. Malti, J. Edberg, H. Granberg, Z. U. Khan, J. W. Andreasen, X. Liu, D. Zhao, H. Zhang, Y. Yao, J. W. Brill, I. Engquist, M. Fahlman, L. Wågberg, X. Crispin and M. Berggren, Adv. Sci., 2016, 3, 1500305 CrossRef PubMed.
- A. Johansson, A. Lauenstein and J. Tegenfeldt, J. Chem. Phys., 1995, 99, 6163–6166 CrossRef.
- A. Lauenstein, A. Johansson and J. Tegenfeldt, J. Electrochem. Soc., 1994, 141, 1819–1823 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp02902d |
| This journal is © the Owner Societies 2018 |