Decoding the role of encapsulated ions in the electronic and magnetic properties of mixed-valence polyoxovanadate capsules {X@V₂₂O₅₄} (X = ClO₄⁻, SCN⁻, VO₂F₂⁻): a combined theoretical approach

Abstract

The electronic structure and magnetism of mixed-valence, host–guest polyoxovanadates {X@V^IV/V₂₂O₅₄} with diamagnetic (X =) ClO₄⁻ (T_d, 1) and SCN⁻ (C_∞v, 2) template anions are assessed by means of two theoretical methods: density functional theory and effective Hamiltonian calculations. The results are compared to those obtained for another member of this family with X = VO₂F₂⁻ (C_2v, 3) (see P. Kozłowski et al., Phys. Chem. Chem. Phys., 2017, 19, 29767–29771), for which complementary data are also acquired. It is demonstrated that the X guest anions strongly influence the electronic and magnetic properties of the system, leading to various valence states of vanadium and modifying V–O–V exchange interactions. Our findings are concordant with and elucidate the available experimental data (see K. Y. Monakhov et al., Chem. – Eur. J., 2015, 21, 2387–2397).

---

Introduction

Polyoxovanadates (POVs)—a subfamily of polyoxometalates (POMs)—are one of the most promising classes of molecular systems that, due to a large structural variety and the existence of many stable oxidation states of vanadium ions, find applications in various fields such as e.g. catalysis,^1–3 biochemistry, materials engineering and molecular magnetism,⁴ or are envisaged as components of technological applications including light-emitting diodes,⁵ redox flow batteries for large-scale energy storage,⁶ memory devices,⁷ quantum computing and magnetic spintronic devices.⁸ POVs can be functionalised by various organic and inorganic moieties^9,10 or by guest ions¹¹ encapsulated in the POV host-cages,¹² giving rise to a diversity of chemical and physical properties which can be tuned to obtain desired effects.

Because of possible applications in molecule-based quantum computing and spintronics,¹³ magnetic properties, which strongly depend on the oxidation states of vanadium ions, are of special importance. Due to the ease of reduction of vanadium V to IV, many mixed-valence POV species are synthetically accessible. Furthermore, in sufficiently symmetric mixed-valence POVs some of the valence electrons are not fully trapped at vanadium centres but rather have itinerant character, giving rise to magnetic effects induced by electron hopping.¹⁴ As a result, there are many POV molecules with nearly identical structure and completely different valence states.^15,16

Modelling of such molecules encounters various difficulties. It is often challenging to establish the correct valence state which is of crucial importance for modelling and design of molecular magnets with desired properties. The presence of itinerant electrons makes unavoidable the use of more complex and often computationally inaccessible effective Hamiltonians. Finally, the lack of clear-cut magneto-structural relations, such as for dimers,¹⁷ makes an a priori determination of microscopic parameters (e.g. exchange couplings) often impossible. Therefore, the use of advanced modelling methods verified by experiment is here indispensable.

Following the successful quantum-mechanical and magnetochemical modelling of {X@V₂₂O₅₄} with X = VO₂F₂⁻ (3),¹⁸ we herein present a systematic study of two other virtually isostructural members of the mixed-valence {X@V^IV/V₂₂O₅₄} family with X = ClO₄⁻ (1) and X = SCN⁻ (2), which feature localised and delocalised valence electrons. The properties of these three host–guest POVs (1–3) are compared in order to determine the dependence of their electronic and magnetic characteristics on the enclosed diamagnetic (X) template ions.

Herein we use and extend the computational procedure developed in ref. 18 which combines two complementary theoretical methods: density functional theory (DFT) and effective Hamiltonian calculations, and whose results are self-consistently harmonised with experiment including SQUID and electrochemical analyses.¹² Since the experimental determination of the number of valence electrons is sometimes intricate, e.g. due to possible protonation effects of the POV host-capsule (difficult to capture with standard X-ray diffraction techniques), the DFT calculations are carried out for a few potential valence states of the {X@V^IV/V₂₂O₅₄} system. The information on the distribution of valence electrons obtained in this way is used to ascertain particular forms of t–J effective Hamiltonians for each studied structure. Next, the experimental magnetic data (susceptibility vs. temperature and magnetisation vs. magnetic field) are fitted with the obtained effective Hamiltonians. The best fit, which has a distribution of the itinerant electrons in the ground state concordant with the results of DFT, indicates the optimal structure (valence state). Thus, a few potential valence states are compared to experiment‡ through the combination of DFT and effective Hamiltonian calculations and the best fitting one is chosen.

Due to a large number of parameters, the fitting procedure employed an evolutionary algorithm to optimise the search process. Despite the large size of the host–guest POVs, diagonalisation of the effective Hamiltonians was accomplished exactly by means of numerical methods exploiting fully the symmetry of 1, 2 and 3 and was performed on large scale parallel computers.

The paper is structured as follows. We first discuss the DFT results including in particular geometry optimisation and spin densities of 1 and 2 (as well as some additional findings for 3). Then, we build t–J models for 1 and 2 for two different point symmetry groups and different numbers of valence electrons, exploiting the data of DFT studies. With the help of these Hamiltonians the magnetic properties of 1 and 2 are determined by fitting the experimental data of the respective compounds. Additional details concerning the ground state of 3 are also provided. Finally, the concluding section summarises the obtained results from both computational approaches.

DFT studies

Computational details

DFT calculations were carried out using the ADF2016 package.^19–21 Structural minima were obtained with the BP86 functional²² and a Slater-type basis set of atomic orbitals of triple-ξ+polarisation²³ (TZP) quality with internal electron shells (1s for O, C and N; 1s–2p for S and Cl; and 1s–3p for V) treated by the frozen-core approximation.²⁴ We applied the symmetry constraints of the D_2d, C_2v, C_s, C₂ or C₁ point groups to the target POVs. Next to geometry optimisations, molecular properties were obtained from B3LYP single-point calculations with the TZ2P basis set and the conductor-like screening model (COSMO)^25,26 to mimic aqueous solutions (ε = 78.4). We applied the spin-unrestricted formalism in all calculations by virtue of the open-shell electronic nature of POVs. Both geometry optimisations and single point energy calculations were carried out with the maximal M_s = 7/2, 4 and 9/2 for 7, 8 and 9 unpaired electrons, respectively. All-parallel spins (or high-spin) solutions have two main advantages at the DFT level: they are correctly treated for their monodeterminantal nature and they facilitate tracing the distribution of unpaired electrons if the atomic spin densities (ASDs) are analysed. We also used D3 generation Grimme's dispersion corrections^27–33 and included scalar relativistic effects using the Zeroth Order Regular Approximation (ZORA).³⁴

Model systems

We analyse the possible differences induced in the electron distribution of the mixed-valence {X@V^IV/V₂₂O₅₄} host–guest structure by two anionic guest species, X = ClO₄⁻ (1n) and X = SCN⁻ (2n), represented in Fig. 1. Also, we look for possible differences arising in the {V₂₂O₅₄} cage depending on the encapsulated guest. We focus on the hydrogen-free [X@V^IV₇V^V₁₅O₅₄]⁶⁻ (Xb), [X@V^IV₈V^V₁₄O₅₄]⁷⁻ (Xa), and [X@V^IV₉V^V₁₃O₅₄]⁸⁻ (Xc) variants of POVs 1 and 2. The systems with different point group symmetry constraints are scrutinised. From now on, the label n = a, b, c stands for the structures with 8, 7 and 9 electrons, respectively.

Fig. 1 Ball-and-stick representation of POV capsules 1, 2 and 3. Black and grey spheres represent V and O atoms, respectively. Guest moieties (X) are shown in colour: Cl = dark green, O = red, N = blue, C = grey, S = yellow and F = light green. Different regions of the V₂₂ cage (apical, outer rings and the inner ring) are indicated on the left hand side.

Electronic structure. As for [VO₂F₂@V₂₂O₅₄]ⁿ⁻,¹⁸ we identified several large imaginary vibrational frequencies in the geometry optimisations applying symmetry constraints, revealing that the idealised maximal symmetry structures, D_2d for X = ClO₄⁻ (1) and C_2v for X = SCN⁻ (2), are not absolute minima. We therefore applied atomic displacements following the imaginary vibrational normal modes and re-optimised the molecular geometries with lower-symmetry constraints. The real minima found for structures 1n have C₂ symmetry due to a pseudo Jahn–Teller (PJT) effect.³⁵ The associated energy stabilisations caused by the symmetry descent are 0.13 eV (1a) and 0.09 eV (both 1b and 1c) with concomitant increments of SOMO–LUMO gaps, as shown in Fig. 2. For structures 2n we observed a similar trend, i.e. a symmetry decrease from C_2v to C₁ with somewhat smaller energy stabilisations of 0.08 eV (2a) and 0.06 eV (both 2b and 2c). The computed energy stabilisations thus range between 1.4 and 3.0 kcal mol⁻¹ in these systems. The evolution of the molecular orbitals from the high to the low symmetry situation is shown in Fig. 2a and b for each number of electrons. Low symmetry POVs feature a steady HOMO destabilisation as electrons (and negative charge) are added to the system (1b → 1a → 1c). Molecular reduction gives HOMO destabilisation energies of 0.22 eV and 0.16 for the first and second electrons added. For 2b → 2a → 2c reductions, the HOMO destabilisations are larger (0.26 eV and 0.25 eV, respectively). Fig. S2 (see ESI†) shows analogous information for compound 3.

Fig. 2 Electronic structure of POVs with different guests: (A) X = ClO₄⁻ and (B) X = SCN⁻. Computed SOMO–LUMO energy gaps (red) and orbital energies in high (black) and low (grey) symmetries are shown. Values are given in eV.

The number of metallic valence electrons on the POVs studied here is smaller than the number of V centres, hence the systems feature a mixture of V^IV/V centres. So, for the understanding of magnetic properties it is critical to know how these valence electrons are distributed among the metal atoms. The ground-state electronic structure of the herein discussed POVs has been estimated by DFT calculations. Not entering into the details of how electrons couple or which is the ground-state total S value, the location of metal electrons is reasonably well described by the high spin DFT solution of the system, which is straightforwardly computed and formally correct. In this regard, the unpaired electron distribution in the high spin configuration would be virtually the same as that in intermediate or low spin configurations.³⁶ Particularly, in POM systems, several studies showed that valence metallic electrons, if present, tend to spread out over as many metal sites as possible by virtue of the intersite hopping and Coulomb repulsion, with a concomitant tendency to multi-site delocalisation.³⁷ This evidence explains why only slight differences in the distribution of metal electrons (and in the electronic structure in general) are obtained when the real low-spin configuration is estimated from a high spin DFT calculation.

Following the above reasoning, we base the discussion of the distribution of unpaired electrons in the hypothetical empty cage and in structures 1 and 2 on atomic spin densities (ASDs) computed for the low symmetry absolute minima shown in Table 1. These values were obtained after geometry optimisation in one possible distortion displacement. As shown in Fig. 3, two equivalent low symmetry minima of each compound exist, resulting from distortions of the high symmetry structure in two different directions of the potential energy surface. The path connecting these minima via a transition state of higher symmetry defines the interconversion energy barrier. For 2, a transition state has a lower symmetry (C_s) than the highest symmetry structure (C_2v). From the relatively large energy barriers connecting the low symmetry minima for 1a–c (0.10 eV = 1160 K) it can be inferred that the interconversion between both minima of the same molecule can be of some importance only close to room temperature. However, since the two low symmetry isomers are magnetically equivalent, the interconversion does not influence magnetic modelling given the system does not spend much time in the high symmetry state. For 1 the probability of being in the high symmetry state P(D_2d) (assuming the canonical ensemble) is on average 109 times smaller (at T = 290 K) than the same probability for the low symmetry state P(C₂). Therefore, in the range of temperatures of interest, it can be safely assumed that each of these systems is confined into one of the low symmetry minima.

Table 1 Vanadium ASDs and region spin densities (RSD, in bold) computed for low symmetry minima (C₂ or C₁, see main text) for different numbers of unpaired electrons (a–c). In the case of structure 2, we denote the N- or the S-hemisphere, respectively. Values in italics correspond to formally V^V centres (ASD < 0.1)

Region	Empty cage						X = ClO4^− (1)						X = SCN^− (2)
	b (7 e^−)		a (8 e^−)		c (9 e^−)		b (7 e^−)		a (8 e^−)		c (9 e^−)		b (7 e^−)		a (8 e^−)		c (9 e^−)
Apical	0.64		0.40		0.79		0.81		0.45		0.86		0.80		0.77		0.54
	0.51		0.61		0.61		0.52		0.55		0.55		0.08		0.52		0.55
	0.03		0.04		0.04		0.03		0.04		0.04		0.20		0.04		0.04
Outer	0.53	2.10	0.57	3.06	0.51	2.59	0.55	1.43	0.62	2.98	0.56	2.52	0.08	0.59	0.57	2.55	0.63	2.96
Ring (V6)	0.40		0.67		0.26		0.21		0.64		0.19		0.03		0.29		0.57
	0.29		0.58		0.64		0.06		0.52		0.59		0.10		0.52		0.55		N
	0.34		0.60		0.54		0.06		0.62		0.59		0.10		0.62		0.62
	0.45		0.51		0.46		0.47		0.51		0.46		0.56		0.57		0.58
	0.33		0.07		0.63		0.56		0.08		0.63		0.53		0.66		0.07
	0.34		0.65		0.32		0.30		0.65		0.33		0.55		0.57		0.60
Inner	0.34	2.91	0.05	2.57	0.54	3.88	0.55	3.77	0.06	2.64	0.54	3.94	0.60	4.42	0.39	2.68	0.08	3.67
Ring (V8)	0.34		0.65		0.32		0.30		0.65		0.33		0.54		0.21		0.66
	0.34		0.05		0.54		0.55		0.06		0.54		0.53		0.06		0.67
	0.45		0.51		0.46		0.47		0.51		0.46		0.56		0.15		0.53
	0.33		0.07		0.63		0.56		0.08		0.63		0.56		0.08		0.49
	0.29		0.58		0.64		0.06		0.52		0.59		0.61		0.59		0.61
	0.03		0.04		0.04		0.03		0.04		0.04		0.26		0.03		0.22		S
Outer	0.34	2.10	0.60	3.06	0.54	2.59	0.06	1.43	0.62	2.98	0.59	2.52	0.57	1.60	0.58	2.96	0.57	2.63
Ring (V6)	0.40		0.67		0.26		0.21		0.64		0.19		0.03		0.58		0.04
	0.51		0.61		0.61		0.52		0.55		0.55		0.07		0.59		0.61
	0.53		0.57		0.51		0.55		0.62		0.56		0.06		0.58		0.59
Apical	0.64		0.40		0.79		0.81		0.45		0.86		0.77		0.50		0.83

---

Fig. 3 Schematic view of the energy stabilisation upon structural distortion for X = ClO₄⁻ (left) and X = SCN⁻ (right) in the {X@V₂₂O₅₄} system. The computed barriers of interconversion between low-symmetry minima are indicated.

For 2a–c, the barrier is much smaller (0.02 eV = 230 K) and interconversion can be important at much lower temperatures. The ratio P(C₁)/P(C_S) is on average equal to 4.5 at T = 290 K and to 20 at T = 100 K.

In Table 1 we also list the values of region spin densities (RSDs) in bold, as the sum of ASDs of the vanadium atoms located in each region. The following discussion is based on ASDs and RSDs listed in Table 1.

Empty {V₂₂O₅₄} cage

For this hypothetical structure, ASD values show that unpaired electrons tend to be regularly shared among metal atoms within a given region of the cage, especially in the V₈ inner ring. In structure b, the 7 unpaired electrons present a rather even distribution among the various regions, the apical centres having a somewhat accentuated V^IV character. When 8 electrons are present (a), it is remarkable that apical positions and the central ring are slightly electron depleted and the outer rings gain considerable electron density. Finally, in form c, an additional electron goes to the central ring, this RSD becoming close to 4, which causes some electron depletion in the outer rings by electrostatic repulsion, with two V^V sites appearing in each of these regions. Consequently, the apical sites gain V^IV character. All three structures present identical hemispheres by symmetry.

{X@V₂₂O₅₄} with X = ClO₄⁻

To a certain degree this structure is equivalent to the hypothetical empty cage, as both hemispheres are equivalent. For the least electron populated form (1b), ASDs suggest that apical sites have nearly one electron each (V^IV character), and each V₆ outer ring has roughly one electron (RSD = 1.43) with two V^V sites. The V₈ inner ring has between three and four electrons (RSD = 3.77). Recall that the unexpectedly large RSDs compared to the total unpaired electron count indicate that spin polarisation induces negative ASDs on the oxygen ligands that compensate for the total value.

This electron distribution concentrates more electrons in the apical and inner ring regions than the empty cage (b). As the empty cage, form 1a shows clear electron depletion in apical positions and in the central ring, whereas outer rings increase their RSDs from 1.4 to 3.0 compared to 1b. The 9-electron form (1c) has apical V^IV sites again and the inner rings recover a large fraction of the electron density by the same mechanism proposed for the empty cage. Remarkably, no V^IV sites appear in form 1a, which again is the one with the most regular electron distribution.

{X@V₂₂O₅₄} with X = SCN⁻

Because of the polar nature of the guest, the ASDs of 2 present a less regular electron distribution than 1. There are particularities related to the two hemispheres being non-equivalent in system 2. Despite that, for the least electron populated form, 2b, the unpaired electrons in the inner ring are as evenly distributed as in the other compounds but, interestingly, this is the most highly populated region of all the series (RSD = 4.42). The electronically depleted outer ring in the N-hemisphere (RSD = 0.59) is nearly electron-free and may be seen as a set of six V^V sites, whereas the S-hemisphere has RSD = 1.60. Apical sites have a notable V^IV character. The 8e⁻ form 2a presents important changes. First, the two outer rings are electron-rich (RSDs = 2.55 and 2.96) and the inner ring has between 1 and 2 electrons less than in form 2b. It is worth mentioning that the inner ring of 2a has unevenly distributed ASDs in the form of an alternating (V₂1e)(V₂)(V₂1e)(V₂) arrangement. This is present in no other form or compound so clearly. Fig. S3 in the ESI† depicts schematically this electron distribution. Such a pattern is obviously a consequence of the internal SCN⁻ dipole moment orientation, which polarises the unpaired electrons towards the less electron-populated N-hemisphere.

Finally, form 2c has one electron more in the inner ring than 2a. Minor changes occur in the other regions. When compared with the structures discussed above, structures 2 present, in general, less even ASD values due to the presence of the SCN⁻ guest. Nevertheless, the most electron populated form 2c features nearly the same ASDs as other 9-electron systems, suggesting that the guest anion has little effect in the distribution of unpaired electrons in this case. The two apical metal centres are V^IV and the inner ring electrons are evenly shared among the centres. Outer rings feature again two V^V centres each. D_2d and C_2v structures for compounds 1 and 2, respectively (not absolute minima), have ASDs that follow the high structural symmetry (see Table S2 in the ESI†). These ASDs evidence a marked (V^IV)_apical character at variance with low symmetry cases, which show mixed (V^V/IV)_apical character. Also, it can be observed that the inner region assembles more unpaired electrons, while the most electron depopulated regions are the outer rings. Structural distortion causes more even electron distributions.

Redox features. Species a–c of the same formula can be electrochemically interconverted. 1a can be oxidised to 1b or reduced to 1c. The same happens with homologous species 2. The computed energies associated with these processes are:

Oxidation: 1a → 1b + e⁻ E₁ = 5.21 eV

2a → 2b + e⁻ E₂ = 5.18 eV

Reduction: 1a + e⁻ → 1c E₃ = −4.86 eV

2a + e⁻ → 1c E₄ = −4.88 eV

These energies correspond to 0.73 (E₁), 0.70 (E₂), 0.38 (E₃) and 0.40 (E₄) V vs. Ag/AgCl (−4.48 eV). Another oxidation of 2b has been theoretically calculated with an associated value of 0.83 V. The oxidation energy of 1b has also been calculated (0.72 V) but for a species with residual imaginary frequencies of −33.78 and −25.93 cm⁻¹. If we consider the hypothetical empty cage [V₂₂O₅₄]⁶⁻, oxidation and reduction energies are 5.57 and −5.04 eV, respectively (1.09 V and 0.56 V vs. Ag/AgCl), showing that it is more difficult to take electrons from it and easier to give electrons to it than for the host–guest species. The lower negative charge of the cage explains these results. In general, the trends obtained from calculations reproduce well the experimental cyclic voltammograms (see Fig. S4 in the ESI†).

Basicity. The Molecular Electrostatic Potential (MEP) provides information about the electrostatic affinity that molecules have for other charged species, for instance H⁺. In our graphical representation of the MEP, the red colour corresponds to more negative potentials, so a priori it identifies nucleophilic regions of higher basicity. Fig. 4 depicts the MEPs for species 1a and 2a (with charge −7) identifying the selected bridging oxygen sites A to C (or D) in each case as the most nucleophilic ones by their electrostatic potential value.

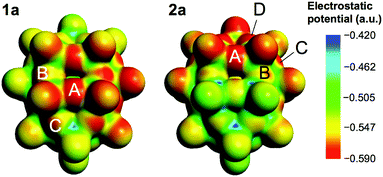Fig. 4 Nucleophilicity of 1a and 2a. The MEP is coloured as indicated in the scale and is plotted on an isodensity surface. The most nucleophilic oxygen sites in each case are labelled A–D.

After this qualitative view of the basicity, protonation of these bridging oxygens was computed and new structural minima were found. A quantitative estimate of the basicity is given by the protonation energies. For compound 1a, the values for each site are: A: −0.73/−0.81 eV, B: −0.82 eV, and C: −0.73 eV, showing that the most basic oxygen is B (triple bridging, OV₃), in clear competition with an A-type site (the closest to the guest). This result was also found for the {VO₂F₂@V₂₂O₅₄} system.¹⁸ For species 2a, protonation energies computed are: A: −0.79 eV, B: −0.84 eV, C: −0.97 eV, and D: −1.00 eV. The most basic sites are C and D, the latter being a OV₃ site with the most acute V–O–V angles, which is typically linked to a higher reactivity. All these basic oxygens are located in the N-hemisphere, the most electron rich as Table 1 and Table S2 in the ESI† show.

After completing the present results with those of the recently published host–guest system [VO₂F₂@V₂₂O₅₄]⁸⁻, i.e. with protonation energies between −0.86 and −1.07 eV, some general trends can be recognised. As for X = SCN⁻, one region of the external {V₂₂O₅₄} cage has increased basicity with respect to the rest of the structure. We suggest that for X = VO₂F₂⁻ and SCN⁻, the larger basicity present in some of their oxygen sites compared to {ClO₄@V₂₂O₅₄} is related to the electron density concentration/depletion in the cage produced by the polar guest, making one hemisphere more nucleophilic than the other (see Fig. 4, structure 2a). It is worth mentioning that we recently published results on the basicity of [VO₂F₂@V₂₂O₅₄]⁹⁻. Those values were obtained for the electron-rich form (charge −9), explaining the more negative protonation energies from −1.07 to −1.34 eV.

These results suggest that these species can be protonated. Upon protonation, occupied molecular orbitals of the system are stabilised and the POM can be further reduced. In addition, comparing both structures it is easy to observe that SCN@POV is slightly more basic than ClO₄@POV since the protonation energies are more negative.

Magnetism

The model and the method

In order to determine which of the three electron populations (a–c) agrees better with experiment and to explain the influence of the guest anions on the magnetism of 1, 2 and 3, the magnetic susceptibility and magnetisation of all these compounds are fitted to the experimental results. Since DFT gives fractional spin densities at many V ions the modelling of the magnetism has to take into account also non-localised valence electrons. For this purpose a semi-classical t–J effective Hamiltonian^14,18 is used: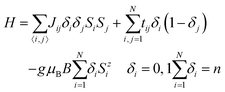Here δ_i are occupation numbers, n (equal to 8 for a, 7 for b and 9 for c) stands for the number of unpaired electrons and N is the number of vanadium sites that can host a valence electron. The particular values of N in (1) depend on the considered species and their symmetry (see Table 1 and Table S2 in the ESI†) and count all vanadium sites which are not formally V^V ions. At most, single occupancy (δ_i = 0, 1) is allowed because orbital effects are quenched due to the strongly distorted local octahedral symmetry of vanadium ions (square pyramid), which removes degeneration of the t_2g orbitals.³⁸ For a site i, which according to DFT is formally a V^IV vanadium site, δ_i = 1.

As mentioned above, the high spin DFT solution provides a good estimate for the ground state electron density despite the fact that the ground state of Hamiltonian (1) is not a high spin state.³⁹ Hamiltonian (1) depends not only on spin states {S_i}, but also on spin distribution {δ_i}. Its first term describes superexchange interactions between unpaired electrons/spins (S = 1/2). The second term accounts “classically” for electron hopping, and the last term describes the Zeeman energy in magnetic field B with gyromagnetic ratio g = 1.965 and Bohr magneton μ_B. The use of the fully quantum t–J model^40,41 is impossible because of the large size of Hamiltonian (1). It is however possible to add to (1) a term accounting explicitly for inter-site electron repulsion, which was shown to be important for some small molecules.⁴² However, a classical transfer term at least partially accounts also for inter-site repulsion. We checked (for 1 and 2) that explicit inclusion of inter-site repulsion does not improve the quality of the fits and some solutions obtained with this additional term give very similar values of couplings J and different values of t, which confirms the supposition that in the case of a semi-classical t–J model this term is at least partially superfluous. Similar effects may be expected for other position dependent terms in the Hamiltonian, like e.g. orbital energy.⁴² All these terms are however omitted because the classical in nature transfer term accounts at least partially for other position dependent effects and because inclusion of other terms in Hamiltonian (1) would lead to an increase in the number of fitting parameters, probably not balanced by an improved quality of the fits.

Following the approach described in ref. 18, it is assumed that couplings J_ij and t_ij are non-zero only for (topological) nearest neighbours and have only three different values corresponding to three different oxygen bridges connecting vanadium ions: single (J₁, t₁), single-shared (J₂, t₂) and double (J₃, t₃) (see Fig. S5 in the ESI†). It has been checked that more advanced coupling schemes lead to no essential change in the quality of fits. The parameters J and t in Hamiltonian (1) are determined by fitting the temperature dependence of susceptibility and the field dependence of magnetisation at T = 2 K.

To obtain reliable results in a realistic time a number of advanced techniques have been exploited. An evolutionary algorithm has been used to find optimal values of Hamiltonian parameters in ranges [−600 K, 1000 K] for J and [−8000 K, 8000 K] for t. The range for J includes extreme values for POVs found in the literature.^43,44 The values of magnetisation and susceptibility have been obtained by exact diagonalisation exploiting fully the symmetry of the Hamiltonian and the molecules, which has been performed on large scale parallel computers (for more details see ESI†).

Results of magnetochemical modelling

The fits to the experimental data have been done for all possible combinations of POVs (1 and 2), model structures (a, b, c) and symmetries (high and low). Only solutions with the ground state electron distribution concordant with the DFT results presented in Table 1 and Table S2 (see ESI†) have been considered.

{X@V₂₂O₅₄} with X = ClO₄⁻. For both high and low symmetries the best results have been obtained for structures a. For an odd number of valence electrons it was difficult to model properly a magnetisation profile (Fig. S6 in the ESI†). The solutions for C₂ symmetry are generally better than those for D_2d. Thus, the best fits have been obtained for 1a and correspond to two different parameter sets. One of them features only antiferromagnetic exchange interactions (I) and the other also ferromagnetic ones (II) (Table 2).

Table 2 Optimal Hamiltonian parameters (in K) for 1a in C₂ symmetry (models I and II) and 2a in C_2v symmetry. Results for 3c (in C_2v symmetry) are taken from ref. 18. Two values for J₁ and t₁ for 3c correspond to F and O hemispheres, respectively

	1a (I)	1a (II)	2a	3c (F, O)
J 1	297	247	431	581, 385
J 2	54	−413	6	−185
J 3	9	343	541	609
t 1	−3201	221	−173	1456, 2421
t 2	−3502	871	−70	3205
t 3	224	86	−78	1162

---

These two fits have very similar quality measured by the goodness of fit (6.24% for I and 5.36% for II). Yet at low temperatures fit I is better than II and at high temperatures fit II is superior (Fig. 5). Since we are concerned mainly with the low temperature behaviour (important for the comparison with the DFT results) we choose fit I as it gives a very good approximation to the magnetisation curve at T = 2 K and to the susceptibility up to almost 200 K. The existence of fit II may be due to overfitting/over-parametrisation (which is suggested by a seemingly too large value of the ferromagnetic coupling J₂) or may indicate that at high temperatures the parameters of the model should be changed. It is possible that due to some structural distortions caused by thermal energy the exchange and transfer couplings undergo some modifications.

Fig. 5 Molar susceptibility (B = 0.1 T) and magnetisation (T = 2 K) for 1a in C₂ symmetry. Circles stand for experimental data and solid lines for the best theoretical fits: I (red) and II (blue).

The ground state (at B = 0) is here 8-fold degenerate. 2-Fold degeneration comes from the geometry of the molecule and is due to two equivalent electron distributions (two different sets of δ_i – see Fig. 6 top). 4-Fold degeneration comes from two spin states with total spin S = 0 and S = 1. Such two different spin states with the same energy suggest the existence of two non-interacting doublets.⁴⁵ Indeed, each of the ground state electron distributions consists of two non-interacting clusters (Fig. 6, top) and is consistent with a DFT-computed set of ASDs. Thus, two doublets in each of the distributions can be attributed to two separate clusters. This supposition is elucidated by the profiles of local magnetisations m_i at T = 2 K (Fig. 7). m_i (i = 1,…,N) are magnetisations calculated at vanadium sites which add up to the total magnetisation M. For a high magnetic field, significant values of magnetisation can be observed only at four sites of the inner ring (non V^V sites) and add up to approximately 2, which corresponds to two electrons. Magnetisation at the remaining sites adds up approximately to zero. Yet, in both ground state electron distributions two electrons in the inner ring belong to two different non-interacting clusters (Fig. 6, top). This allows us to conclude that the magnetism of 1a at low temperature is determined mainly by two non-interacting electrons in the inner ring. Moreover, it can be found that taking into account two equivalent ground state electron distributions, the average number of electrons in the inner ring is equal to 2 and in each of the hemispheres (without the inner ring) is 3.

Fig. 6 Ground state electron distributions for the 8e⁻ containing compounds 1a (X = ClO₄⁻, top) and 2a (X = SCN⁻, bottom). For each compound, two electron distributions (green and blue) are shown, each composed of two non-interacting clusters with 5 and 3 electrons, (light- and dark-coloured vanadiums, respectively). Oxygen atoms and guest anions have been removed for clarity. Grey spheres are V^V.

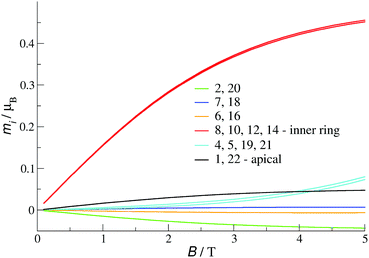Fig. 7 Local magnetisation profiles for 1a (parameter set 1) in C₂ symmetry at T = 2 K. Numbering of sites is shown in Fig. S7 (see ESI†).

These findings agree very well with the DFT results (Table 1), which after rescaling to the number of valence electrons give 2.9 electrons in each of the hemispheres and 2.2 electrons in the inner ring. The probability to find an electron at a given V^IV/V^V site according to DFT (rescaled to 8 valence electrons) changes from 0.38 at apical sites to 0.55 at other sites, which compares well to the uniform value 0.5 obtained for the ground state with the effective Hamiltonian (1). At finite temperatures this probability undergoes some minor changes (Fig. 8).

Fig. 8 Probability of finding a valence electron at V^IV/V^V sites in the cage of 1a and for parameter set I. The numbering of sites is shown in Fig. S7 (see ESI†).

{X@V₂₂O₅₄} with X = SCN⁻. As in the case of POV 1, the best fits have been obtained for structure a (Fig. S8 in the ESI†). Though the difference in goodness of fit between different structures is not very large (Table S3 in the ESI†) the curves obtained for 2a better reproduce the character of experimental results. e.g. an inflection point in the experimental magnetisation profile is properly modelled only in structure a, though it is a bit shifted towards higher fields (Fig. S9 in the ESI†). For structures b and c there is no inflection point.

There is no essential difference in the quality of the fits for high and low symmetry versions. For symmetry C₁ it was impossible to obtain ground state electron distributions concordant with the results of DFT. The same is expected for symmetry C_s and for the model taking into account interconversions between states of symmetry C₁ and C_s. This is due to the limitations of the employed semi-classical t–J Hamiltonian. Since for this low symmetry molecule there is only one electron distribution in the ground state there can be no fractional occupation numbers as suggested by DFT because δ_i is equal to zero or one. Fractional occupation numbers in this model can be obtained only if geometrical degeneration appears, which can only happen in higher symmetries. Therefore, for further analysis we take here a molecule with a higher C_2v symmetry. The best fit (goodness of fit = 4.81%) has been obtained with only antiferromagnetic exchange couplings (Table 2 and Fig. 9).

Fig. 9 Molar susceptibility (B = 0.1 T) and magnetisation (T = 2 K) for 2a in C_2v symmetry. Circles stand for experimental data and solid lines for the best theoretical fit.

The ground state is also 8-fold degenerate with 2-fold geometric degeneration and 4-fold magnetic degeneration corresponding to two spin states S = 0 and S = 1 with the same energy. Thus, again it can be considered as describing two non-interacting doublets corresponding to two non-interacting clusters in the ground state electron distributions. However, now the clusters are different (Fig. 6, bottom) and the local magnetisation profiles (Fig. 10) indicate also a different scenario than in the case of X = ClO₄⁻.

Fig. 10 Local magnetisation profiles for 2a in C_2v symmetry at T = 2 K. The numbering of sites is shown in Fig. S7 (see ESI†).

In a high magnetic field (around 5 T) significant values of magnetisation appear only at the upper (N) apical site (m₁ = 0.9) and in the lower (S) outer ring. The total magnetisation in the latter is equal to 1.3. Thus, the magnetism of 2a at low temperature is more complex and depends mainly on one localised electron at the upper (N) apical site and on three delocalised electrons in the lower (S) hemisphere. The average number of electrons in the inner ring is equal to 2 and there are 3 electrons in each of the hemispheres. This agrees very well with the prediction of DFT, which after rescaling to the number of valence electrons gives 2.3 electrons in the inner ring and 2.8 electrons in the upper (N) (2.9 in the lower (S)) hemisphere. The probability to find an electron at a given V^IV/V^V site according to DFT (rescaled to 8 valence electrons) changes from 0.47 to 0.51, Table 1, which compares well to the uniform value 0.5 obtained for the ground state of the effective Hamiltonian (1). At finite temperatures this probability undergoes no change. The apical sites are assumed to be of V^IV type (rescaled DFT gives a probability of occupation equal to 0.8).

{X@V₂₂O₅₄} with X = VO₂F₂⁻. Most of the results for this POV have already been published.¹⁸ Here for completeness we present some details concerning the ground state. The best fit (goodness of fit = 2.07%) has been obtained for nine valence electrons (structure 3c). Since the distribution of V^V ions in both low (C₁) and high (C_2v) symmetry structures has D_2d symmetry it was necessary to introduce some asymmetry in the coupling scheme in order to reproduce correctly the distribution of the delocalised electrons obtained by means of DFT. Therefore, in the best fit (Table 2), couplings J₁ and t₁ have different values in the F and O hemispheres. The ground state (at B = 0) is 16-fold degenerate with 4-fold geometric degeneration (4 equivalent electron distributions in the ground state) and 4-fold magnetic degeneration induced by the S = 3/2 spin state. Each equivalent ground state distribution forms one connected cluster (Fig. 11).

Fig. 11 Four ground state electron distributions for 3c. In each case, the coloured vanadium atoms (green, black, blue or orange, respectively) carry one unpaired electron each. Oxygen atoms and guest anions have been removed for clarity. Grey atoms are always electron depopulated (V^V ions).

The analysis of the exchange interactions and of the local magnetisations in a high magnetic field (Fig. 12) allows us to state that the magnetism of 3c at low temperature can be seen as coming mainly from three doublets interacting ferromagnetically.

Fig. 12 Local magnetisation profiles for 3c in C_2v symmetry at T = 2 K. The numbering of sites is shown in Fig. S7 (see ESI†).

Two doublets are related to localised electrons at apical sites and one comes from the remaining 7 itinerant electrons. The probability of finding a valence electron at a given V^IV/V^V site in the ground state (0.25 in the outer ring (O) and 0.5 at other V sites) agrees very well with the rescaled DFT prediction (0.29 in the outer ring (O) and 0.50–0.51 at other V sites). However, already at very low temperature, these probabilities change very rapidly to attain rather stable values for higher temperatures (Fig. 13).

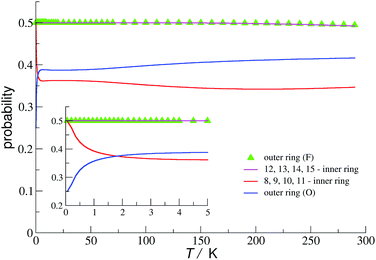Fig. 13 Probability of finding a valence electron at V^IV/V^V sites in the cage of 3c. In the inset the details at low temperature are shown. The numbering of sites is shown in Fig. S7 (see ESI†).

A slightly worse fit (in terms of a goodness of fit equal to 3.11) has been obtained for 7 valence electrons in C₁ symmetry.¹⁸ However, this fit has been rejected for the following reasons: the minimum of the susceptibility was not properly reproduced, the fit was obtained for large ferromagnetic couplings (J₁ and J₃) and the resulting probabilities of finding electrons at a given site in the ground state were completely different than those obtained from DFT. The last obstacle is at least partially due to the limitation of the model induced by the low symmetry of the molecule as discussed for SCN@V₂₂O₅₄. Nevertheless, the stability of 1b is unlikely also because its total energy (obtained by DFT) is higher than that obtained for 1c.

Critical discussion of the magnetochemical data

Hamiltonian parameters obtained by fitting experimental data should be considered with caution especially if a multidimensional fit is made. However in the case of our results the negative influence of over-parametrisation has been minimised by eliminating solutions which are not concordant with the DFT results (comparison of electron densities with the probabilities of occupation of a given V site in the ground state of the effective Hamiltonian). Besides, the search region for exchange couplings has been limited, but still contains extreme values found in the literature with some extra margin. The evolutionary algorithm is known to usually provide solutions which are very close to the optimal one, but not precisely the optimal one.⁴⁶ Thus, the results found in Table 2 cannot be considered as strictly unique, yet the intensive searches carried out with the help of the evolutionary algorithm ensure that other fits of the same high quality give only slightly different parameter sets. Of course particular values of these parameters depend on the details of the model. e.g. if more complicated coupling schemes are used the coupling sets will be different. It has been checked however that even then the general character (sign and strength) of the parameter sets is conserved. From the physical point of view further differentiation of the couplings is justified,¹⁸ but with a bigger number of parameters over-parametrisation effects (e.g. many different solutions) are unavoidable.

As expected for POV the prevailing exchange interactions are of antiferromagnetic character. Only for X = VO₂F₂⁻ no satisfactory fits consistent with the DFT results and containing only antiferromagnetic exchange couplings can be found. However, we managed to find one parameter set with no ferromagnetic exchange interactions which gave a very good fit to the experiment. Yet, the calculated distribution of valence electrons in the ground state did not agree with the results of DFT and some exchange couplings were apparently too large. Nevertheless, this corresponds well to the finding that for some parameter sets a fully quantum two-dimensional t–J model may exhibit effective ferromagnetic order which is induced only by antiferromagnetic exchange interactions and a transfer term.⁴⁷

The values of transfer couplings are rather difficult to comment on as they accumulate also other position dependent effects, and are seldom retrieved from experiment. They are usually estimated to be much larger than exchange couplings¹⁴ which is also the case here. Their different values can be interpreted as indicating that transfers between different neighbours have different priority.

The influence of the guest anions on the magnetism of {X@V₂₂O₅₄} seems to be due mostly to the modification of the electronic structure. Similar magnetic behaviour can be observed for two compounds (X = ClO₄⁻, SCN⁻) which contain only 8 valence electrons. They differ in this respect from the remaining one (X = VO₂F₂⁻) which features 9 valence electrons.¹⁸ The magnetism in these POVs originates from both localised and delocalised electrons (for X = ClO₄⁻, only delocalised). Localised electrons carry usually a large magnetic moment (apical sites in X = VO₂F₂⁻ and SCN⁻) whereas non-localised ones have usually a smaller magnetic moment. The reduced average magnetisations of delocalised electrons may be due to frustration effects^48,49 induced by the presence of competing interactions and the larger mobility of the electrons leading to a larger number of interactions.

The fact that the probabilities of finding an electron at a given vanadium site obtained with the effective Hamiltonian agree very well with spin densities obtained from high spin DFT can be considered as (post hoc) confirmation that high spin DFT indeed provides good estimates of electron densities even for broken symmetry states.

Due to the easiness of redox processes the existence of mixtures of structures a, b and c has also been considered. For 1 in symmetry C₂, calculations for 9 electrons (structure c) are very time consuming due to a large number of delocalised electrons which give rise to Hamiltonian matrices of size 1.6 × 10⁷ × 1.6 × 10⁷. Therefore, calculations for mixtures of POV 1 have been abandoned. For 3, fits obtained for mixtures (a, b, c) are only slightly better than the best fits for 3c. Thus, it can be safely assumed that the observed improvement is only due to a larger number of parameters and not to better physical modelling. In the case of 2 in C_2v symmetry, the fits obtained for mixtures are better than the best fits for single optimal structures. The improvement however is not large and the physical features like e.g. the inflection point in the magnetisation profile of 2 (Fig. S9 in the ESI†), are not better reproduced by mixtures. Thus, though it cannot be excluded that some mixtures of structures a, b and c exist, the fitting results do not allow us to prefer them over single components. Thus, the improved fitting for mixtures should be rather ascribed to a larger number of parameters. This finding is different to the results obtained for some V₁₆-type POVs whose magnetic properties could be properly reproduced only by a mixture of components with different valence states.⁵⁰

Given the total charge of the molecules and their predicted electronic states the following protonation can be expected: single for 1 {ClO₄@HV₂₂O₅₄} and 2 {SCN@HV₂₂O₅₄} and double for 3 {VO₂F₂@H₂V₂₂O₅₄}.

Conclusions

Using the method developed for {VO₂F₂@V₂₂O₅₄} (3)¹⁸ we elucidated electronic and magnetic properties of two other members of the same mixed-valence family (1 and 2). The theoretical results agree with each other and with experiment. It has been demonstrated that magnetic properties strongly depend on vanadium's valence states which are in turn dependent on the guest anions. POVs with X = ClO₄⁻ and SCN⁻ feature 8 valence electrons and an S = 1, S = 0 ground state, whereas the one with X = VO₂F₂⁻ has nine valence electrons and an S = 3/2 ground state. It is remarkable that if the symmetry of the distribution of V^V ions assumed in the effective Hamiltonians from DFT is the same as that of the molecule, we obtain electron densities in the ground state concordant with DFT without explicitly imposing this condition. If the symmetry of the V^V distribution is higher than that of the POV molecule (which is the case with X = VO₂F₂⁻) it is enough to introduce a proper asymmetry of the couplings to attain a good agreement with DFT. For POVs with very low symmetry, agreement with electron densities obtained by means of DFT could not be reached due to the limitation of the effective Hamiltonian model stemming from the classical nature of the transfer term. Despite this obstacle finite temperature fits to susceptibility and magnetisation are still very good.

An investigation of mixtures of POVs with different valence states leads to the conclusion that generally better fits for the mixtures do not explain better various physical features, which allows us to assume that the improvement of the fits’ quality is due only to a bigger number of parameters, and thus pure components should be preferred.

Our approach limits typical shortcomings of effective Hamiltonian fits to experimental data by exploiting the results of DFT calculations in a two-step procedure: (1) some details of the effective Hamiltonians are fixed by using the positions of formally V^V and V^IV ions obtained by DFT, (2) the optimal fit is chosen by rejecting those fits that lead to a distribution of the valence electrons in the ground state non-concordant with DFT predictions.

This method can also be applied to other large mixed-valent POMs for which a fully quantum approach is impossible. Of special interest, due to possible application in single molecule electronics, is the influence of electric field on the magnetism of such molecules, which has been already demonstrated for smaller compounds.^45,51 Our preliminary calculations indicate that similar effects can also be expected in larger molecules.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

K. Y. M. thanks the Deutsche Forschungsgemeinschaft (DFG) for an Emmy Noether fellowship. This work was supported by the Spanish government (Project No. CTQ2017-83566-P), the Generalitat de Catalunya (2017-SGR629 and XRQTC), and the COST Action CM1203 “Polyoxometalate Chemistry for Molecular Nanoscience” (PoCheMoN). Model Hamiltonian calculations were carried out at the Academic Computer Centre in Gdańsk and in Poznań Supercomputing and Networking Centre, both in Poland.

Notes and references

1. M. I. Khan, S. Tabussum, C. L. Marshall and M. K. Neylon, Catal. Lett., 2006, 112, 1–12.
2. S. Chakrabarty and R. Banerjee, Catal. Sci. Technol., 2012, 2, 2224–2226.
3. M.-P. Santoni, G. La Ganga, V. M. Nardo, M. Natali, F. Puntoriero, F. Scandola and S. Campagna, J. Am. Chem. Soc., 2014, 136, 8189–8192.
4. A. Müller, F. Peters, M. T. Pope and D. Gatteschi, Chem. Rev., 1998, 98, 239–271.
5. C. Kong, Z. Xu, S. Zhao, F. Zhang, G. Yan, W. Gong, R. Liu and Q. Sun, J. Nanosci. Nanotechnol., 2011, 11, 9451–9455.
6. L. Li, S. Kim, W. Wang, M. Vijayakumar, Z. Nie, B. Chen, J. Zhang, G. Xia, J. Hu, G. Graff, J. Liu and Z. Yang, Adv. Energy Mater., 2011, 1, 394–400.
7. C. Busche, L. Vilà-Nadal, J. Yan, H. N. Miras, D.-L. Long, V. P. Georgiev, A. Asenov, R. H. Pedersen, N. Gadegaard, M. M. Mirza, D. J. Paul, J. M. Poblet and L. Cronin, Nature, 2014, 515, 545–549.
8. J. M. Clemente-Juan, E. Coronado and A. Gaita-Ariño, Chem. Soc. Rev., 2012, 41, 7464.
9. K. Y. Monakhov, W. Bensch and P. Kögerler, Chem. Soc. Rev., 2015, 44, 8443–8483.
10. M. Stuckart and K. Yu. Monakhov, Vanadium: Polyoxometalate chemistry, in Encyclopedia of Inorganic and Bioinorganic Chemistry, John Wiley & Sons, 2018,  DOI:10.1002/9781119951438.eibc2615.
11. A. Müller, H. Reuter and S. Dillinger, Angew. Chem., Int. Ed. Engl., 1995, 34, 2328–2361.
12. K. Y. Monakhov, O. Linnenberg, P. Kozłowski, J. van Leusen, C. Besson, T. Secker, A. Ellern, X. López, J. M. Poblet and P. Kögerler, Chem. – Eur. J., 2015, 21, 2387–2397.
13. K. Y. Monakhov, M. Moors and P. Kögerler, Adv. Inorg. Chem., 2017, 69, 251–286.
14. C. J. Calzado, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño and N. Suaud, Inorg. Chem., 2008, 47, 5889–5901.
15. A. Müller, R. Sessoli, E. Krickemeyer, H. Bögge, J. Meyer, D. Gatteschi, L. Pardi, J. Westphal, K. Hovemeier, R. Rohlfing, J. Döring, F. Hellweg, C. Beugholt and M. Schmidtmann, Inorg. Chem., 1997, 36, 5239–5250.
16. T. D. Keene, D. M. Dalessandro, K. W. Krämer, J. R. Price, D. J. Price, S. Decurtins and C. J. Kepert, Inorg. Chem., 2012, 51, 9192–9199.
17. W. Plass, Angew. Chem., Int. Ed. Engl., 1996, 35, 627–631.
18. P. Kozłowski, A. Notario-Estévez, C. de Graaf, X. López and K. Y. Monakhov, Phys. Chem. Chem. Phys., 2017, 19, 29767–29771.
19. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen and J. G. Snijders, J. Comput. Chem., 2001, 22, 931–967.
20. H. scm. co. ADF2016, SCM, Theoretical Chemistry, Vrije Universiteit, Amsterdam, The Netherlands.
21. C. Fonseca Guerra, J. G. Snijders, G. te Velde and E. J. Baerends, Theor. Chem. Acc., 1998, 99, 391–403.
22. M. Swart and J. G. Snijders, Theor. Chem. Acc., 2003, 110, 34–41.
23. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
24. E. J. Baerends, D. E. Ellis and P. Ros, Chem. Phys., 1973, 2, 41–51.
25. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
26. A. Klamt, V. Jonas, T. Bürger and J. C. W. Lohrenz, J. Phys. Chem. A, 1998, 102, 5074–5085.
27. S. Grimme, J. Comput. Chem., 2004, 25, 1463–1473.
28. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
29. S. Grimme, J. Antony, T. Schwabe and C. Mück-Lichtenfeld, Org. Biomol. Chem., 2007, 5, 741–758.
30. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
31. S. Grimme, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2011, 1, 211–228.
32. S. Grimme, R. Huenerbein and S. Ehrlich, ChemPhysChem, 2011, 12, 1258–1261.
33. S. Grimme, Chem. – Eur. J., 2012, 18, 9955–9964.
34. W. Klopper, J. H. Van Lenthe and A. C. Hennum, J. Chem. Phys., 2000, 113, 9957–9965.
35. L. Yan, X. López, J. J. Carbó, R. Sniatynsky, D. C. Duncan and J. M. Poblet, J. Am. Chem. Soc., 2008, 130, 8223–8233.
36. R. Caballol, O. Castell, F. Illas, I. de P. R. Moreira and J. P. Malrieu, J. Phys. Chem. A, 1997, 101, 7860–7866.
37. N. Suaud, A. Gaita-Ariño, J. M. Clemente-Juan and E. Coronado, Chem. – Eur. J., 2004, 10, 4041–4053.
38. E. E. Kaul, PhD thesis, Technical University Dresden, 2005.
39. K. Yu Monakhov, X. López, M. Speldrich, J. van Leusen, P. Kögerler, P. Braunstein and J. M. Poblet, Chem. – Eur. J., 2014, 20, 3769–3781.
40. J. M. Clemente-Juan, J. J. Borrás-Almenar, E. Coronado, A. V. Palii and B. S. Tsukerblat, Inorg. Chem., 2009, 48, 4557–4568.
41. J. J. Borrás-Almenar, S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. V. Palii and B. S. Tsukerblat, J. Comput. Chem., 2010, 31, 1321–1332.
42. N. Suaud, X. López, N. Ben Amor, N. A. G. Bandeira, C. de Graaf and J. M. Poblet, J. Chem. Theory Comput., 2015, 11, 550–559.
43. E. M. Zueva, S. A. Borshch, M. M. Petrova, H. Chermette and A. M. Kuznetsov, Eur. J. Inorg. Chem., 2007, 4317–4325.
44. Y. Nishisaka, Y. Furukawa, Y. Fujiyoshi, K. Kumagai and P. Kögerler, AIP Conf. Proc., 2006, 850, 1145–1146.
45. S. Cardona-Serra, J. M. Clemente-Juan, E. Coronado, A. Gaita-Ariño, N. Suaud, O. Svoboda, R. Bastardis, N. Guihéry and J. J. Palacios, Chem. – Eur. J., 2015, 21, 763–769.
46. Z. Michalewicz, Genetic Algorithms + Data Structures = Evolution Programs, Springer-Verlag, Berlin Heidelberg, 1996.
47. E. Eisenberg, R. Berkovits, D. Huse and B. Altshuler, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 134437.
48. P. Kögerler, B. Tsukerblat and A. Müller, Dalton Trans., 2010, 39, 21–36.
49. J. Schnack, Dalton Trans., 2010, 39, 4677.
50. O. Linnenberg, P. Kozłowski, C. Besson, J. van Leusen, U. Englert and K. Y. Monakhov, Cryst. Growth Des., 2017, 17, 2342–2350.
51. S. Cardona-Serra, J. M. Clemente-Juan, A. Gaita-Ariño, N. Suaud, O. Svoboda and E. Coronado, Chem. Commun., 2013, 49, 9621–9623.

---

Footnotes

† Electronic supplementary information (ESI) available: Details of DFT calculations and magnetochemical modelling. See DOI: 10.1039/c8cp02669f

‡ X-ray photoelectron spectroscopy (XPS) analysis of {X@V₂₂O₅₄} where X = VO₂F₂⁻ (3) was additionally performed in order to assess the possibilities of this method in the determination of very tiny differences in the redox structure of POVs. The XPS measurements reveal (see Fig. S1 and Table S1 in the ESI†) that it is impossible to differentiate between the two analysed V^IV : V^V electron populations 8 : 15 and 9 : 14 of compound 3, corresponding to the [V^VO₂F₂@HV^IV₈V^V₁₄O₅₄]⁶⁻ and [V^VO₂F₂@H₂V^IV₉V^V₁₃O₅₄]⁶⁻ models, respectively. This shows that in such intricate electron distribution situations herein described we can rely only on the combined results of DFT and model Hamiltonian calculations.

---