Estimation of diffusive states from single-particle trajectory in heterogeneous medium using machine-learning methods
Received
23rd April 2018
, Accepted 24th August 2018
First published on 11th September 2018
Abstract
We propose a novel approach to analyze random walks in heterogeneous medium using a hybrid machine-learning method based on a gamma mixture and a hidden Markov model. A gamma mixture and a hidden Markov model respectively provide the number and the most probable sequence of diffusive states from the time series position data of particles/molecules obtained by single-particle/molecule tracking (SPT/SMT) method. We evaluate the performance of our proposed method for numerically generated trajectories. It is shown that our proposed method can correctly extract the number of diffusive states when each trajectory is long enough to be frame averaged. We also indicate that our method can provide an indicator whether the assumption of a medium consisting of discrete diffusive states is appropriate or not based on the available amount of trajectory data. Then, we demonstrate an application of our method to the analysis of experimentally obtained SPT data.
1. Introduction
Single-particle/molecule tracking (SPT/SMT) techniques are widely used to investigate intercellular kinetics and biophysical processes at cell membranes1–9 and extract non-bulk information on soft-materials.10–12 As a quantity of interest for SPT/SMT trajectory data, mean-squared displacement (MSD) is widely used. The shape of an MSD indicates the modes of the particle/molecule motion: normal, anomalous, directed, and confined diffusion.1,7,13 For example, an MSD for a trajectory of a particle/molecule in a homogeneous medium is a linear function of time, and the slope of the MSD indicates the diffusion coefficient. Though the transient behavior of MSD contains further information about particle/molecule motion, the MSD analysis is not convenient for practical use due to scattering of MSD plot induced by the limitation of available trajectory data. Thus, MSD is usually adopted to extract the diffusion coefficient of particles/molecule moving in a homogeneous medium. To analyze SPT/SMT trajectories containing adsorption/desorption motion and diffusion anisotropy, several analysis methods have been developed.14–20
In the past few years, new approaches based on Bayesian and machine-learning methods have been developed. Metzner et al.21 developed a Bayesian inference method based on a time-discrete Ornstein–Uhlenbeck process. Their method is specialized for analyzing a Brownian motion with drift and can extract time-dependent statistical parameters. Ott et al.22 applied a hidden Markov model (HMM) to an analysis of two different modes of diffusion: a fast and a slow diffusive state in heterogeneous medium. The drawback of their method is that the number of diffusive states has to be fixed a priori in their maximum likelihood approach to an HMM analysis. Persson et al.23 proposed an analysis method, the variational Bayes SPT (vbSPT), based on a variational Bayesian treatment of an HMM.24–26 Their vbSPT can estimate the number of diffusive states and state transition rates from trajectories in a heterogeneous medium. Their vbSPT is a powerful analysis method when a sufficient amount of trajectory data is available. However, it is often pointed out that a proper choice of a prior distribution is difficult and a large amount of data is required for a reliable estimation of parameters in a variational Bayesian treatment. For example, more than 3000 trajectories (one trajectory consists of steps less than 20) were analyzed for the reliable estimation of the number of diffusive states in the vbSPT.23 Unfortunately, there remains many situations that limited number of samples is available27–30 due to photobleaching of the dyes, limited imaging area, and so on. Moreover, since these studies22,23 provided the discussion in the dimensional form, the users have to adjust parameters to their problem.
In this study, we extend these HMM approaches by introducing a gamma mixture model (GMM).31 In other word, we propose a hybrid machine learning method based on a GMM and an HMM. Our method is simple and can be easily implemented in a postprocessing program for SPT/SMT. The number of diffusive states is estimated by the GMM with the expectation–maximization (EM) algorithm32 because the GMM is a more suitable classification algorithm than an HMM. An HMM originally estimate the most probable path of hidden states, where the number of the states are given as a prior knowledge.32 By combining GMM and HMM, we can estimate most probable sequence of diffusive states from the trajectory data by HMM based on the number of the states estimated by the GMM in our method. We apply our proposed method to a numerically generated Brownian motion to investigate the performance. Since the previous studies such as ref. 20, 22 and 23 and our present method assumed that a medium consists of discrete diffusive states, we also discuss the statistical validity of the assumption from the given number of data points of trajectories. Then, the experimentally obtained SPT data is analyzed as a demonstration.
2. Numerical model of Brownian motion
We assume that a particle is a single point; that is, the position of a maker and the center of diffusion are indistinguishable. Since the positions of the maker and the diffusion center cannot be distinguished in an ordinary optical microscope due to the diffraction limit,1,3,4 this assumption is reasonable in most SPT/SMT experiments. We consider the trajectory of a particle in a medium consisting of K media of the diffusion coefficients ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) m (m = 1, 2, 3,…,K), where
m (m = 1, 2, 3,…,K), where ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) m may be expressed as a function of position or time. The diffusion coefficients as functions of position and time correspond to a spatially heterogeneous medium such as a surface having adsorption sites22,33–35 and to a temporally heterogeneous medium whose property is temporally controlled,36,37 respectively. We also assume that the particle isotropically diffuses in each medium and the effect of interfaces between the media on the particle motion is negligible. The trajectory is generated by the Wiener process described by the overdamped Langevin equation as follows
m may be expressed as a function of position or time. The diffusion coefficients as functions of position and time correspond to a spatially heterogeneous medium such as a surface having adsorption sites22,33–35 and to a temporally heterogeneous medium whose property is temporally controlled,36,37 respectively. We also assume that the particle isotropically diffuses in each medium and the effect of interfaces between the media on the particle motion is negligible. The trajectory is generated by the Wiener process described by the overdamped Langevin equation as follows| |  | (1) |
where ![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) is the position vector of the particle at time
) is the position vector of the particle at time ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) . The variables ξ(
. The variables ξ(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) is Gaussian random with
) is Gaussian random with ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [ξi(
[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )] = 0, var[ξi(
)] = 0, var[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )] = 1, and
)] = 1, and ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [ξi(
[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )ξi(
)ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ′)] = δ(
′)] = δ(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) −
− ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ′), where
′), where ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [⋯] and var[⋯] indicate expectation and variance, respectively. The subscripts, i = 1, 2, 3, corresponding to components of axes x, y, z, respectively. We introduce the characteristic time τ and length
[⋯] and var[⋯] indicate expectation and variance, respectively. The subscripts, i = 1, 2, 3, corresponding to components of axes x, y, z, respectively. We introduce the characteristic time τ and length  . Then, eqn (1) is nondimensionalized as
. Then, eqn (1) is nondimensionalized as| |  | (2) |
where the r and t are nondimensionalized quantities, and DR,m is the ratio of Dm to D1 (the subscript R indicates ratio). Eqn (2) is numerically solved by the finite difference method expressed by| | 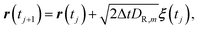 | (3) |
where tj is the time of j-th time step, and Δt is the discretized time (i.e., tj = jΔt). The dimensional time step τΔt corresponds to the time interval between each frame of SPT/SMT experiment. In this study, τ = 1 to simplify the discussion. To obtain particle trajectories having a few diffusive states, DR,m is varied in the calculation of eqn (3). We treat DR,m as a function of time varying with given state transition probability, because it is difficult to obtain the trajectories under the controlled condition with treating DR,m as a function of position. Since the squared displacement is the only feature and does not contain the position information of the particle, this treatment of DR,m is reasonable in our method.
Fig. 1 shows the sample trajectory under the conditions of t = 1.0 × 10−2, DR,1 = 1.0, and DR,2 = 5.0. The total number of time steps is 50. The locations of a particle are classified by color according to the diffusive states.
 |
| | Fig. 1 Sample trajectory of Brownian motion with two diffusive states (state 1 and 2) under the conditions of Δt = 1.0 × 10−2, DR,1 = 1.0, and DR,2 = 5.0. The total number of time steps is 50. | |
3. Machine-learning methods of SMT/SPT data
3.1 Gamma mixture model
After experimentally/numerically obtaining trajectory data, a squared displacement d(tj) at the time of j-th time step is calculated as| | | d(tj) = |r(tj) − r(tj−1)|2. | (4) |
Considering ensemble average of the squared displacement, one can obtain mean squared displacement (MSD). We use only the squared displacement d(tj) as the feature in our proposed method; thus, our method can be applied to multi-dimensional trajectories without any modification. Since the probability distribution of r(tj) − r(tj−1) follows a Gaussian distribution (see eqn (3)), the probability distribution of d(tj) follows a gamma distribution. Then, the number of diffusive states and its diffusion coefficients are estimated from the squared displacement d(tj) using a univariate GMM.31
We apply the EM algorithm to find maximum likelihood solutions for models having unobserved latent variables. Here, we introduce a GMM following the introduction procedure of a well-known mixture distribution, a Gaussian mixture model.32 The univariate gamma distribution with a shape parameter α and an inverse scale parameter β is written as
| |  | (5) |
where
Γ(
x) is the gamma function. In the gamma mixture distribution, the probability distribution
p(
x) is expressed as a linear superposition of gamma distributions as follows:
| |  | (6) |
where
πk are the mixing coefficients with 0 ≤
πk ≤ 1 and

. The number of gamma distributions having different parameters is represented as
K, which also corresponds to the number of diffusive states in our method. Here, we introduce latent variables of a
K-dimensional binary (0 or 1) random variable
z = {
z1,
z2,…,
zK} with

. This means that the probability of an observation
x comes from
zk is represented by
p(
zk = 1) =
πk. Since
z is a binary random variable, the distribution
p(
zk = 1) can be written in the form
| |  | (7) |
The conditional distribution of
x at given
z is also expressed as
| | 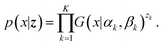 | (8) |
When we consider a data set
X = (
x1,
x2,…,
xN)
T consisting of
N observations, the corresponding latent variables can be written by an
N ×
K matrix of
Z in which with
n-th row is given by
zTn, where the superscript T means transpose. Using
eqn (7) and (8), the likelihood for the data set {
X,
Z} is expressed as
| |  | (9) |
where
α = (
α1,
α2,…,
αK)
T,
β = (
β1,
β2,…,
βK)
T,
π = (
π1,
π2,…,
πK)
T, and
znk is
n,
k element of
Z. By maximizing the likelihood, we can find the best model to fit the data set. The log likelihood is written as
| | 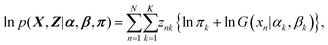 | (10) |
The direct maximization of
eqn (10) is difficult, because the
Z is unobserved variables. Therefore, we consider the maximization problem of the expectation of
eqn (10) with respect to the posterior distribution of the latent variables
Z. The posterior distribution
p(
Z|
X,
α,
β,
π) is obtained from
eqn (7) and (8) with Bayes’ theorem as
| |  | (11) |
Then the expectation of
znk with respect to the posterior distribution is calculated as
| |  | (12) |
Using
eqn (12), the expectation of the log likelihood is expressed as
| | 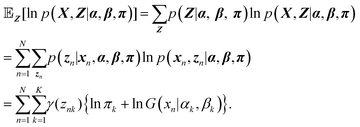 | (13) |
As shown in
eqn (13), the expectation of the log likelihood consists of the two terms,
γ(
znk)ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πk
πk and
γ(
znk){ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G
G(
x|
αk,
βk)}. First, we maximize the expectation of the log likelihood with respect to the mixing coefficients
πk. Since there is the constraint condition

, we introduce a Lagrange multiplier
λ and consider the following Lagrange function
Λ(
π,
λ):
| |  | (14) |
Then, taking the derivative of
Λ(
π,
λ) with respect to
πk equal to 0, we can obtain
| |  | (15) |
Multiplying
eqn (15) by
πk and summing over
k with the condition of

, the equation,
N = −
λ, is obtained. Then,
eqn (15) can be written as
| | 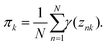 | (16) |
To maximize the term
γ(
znk){ln
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G
G(
x|
αk,
βk)} in
eqn (13), the partial derivatives of it with respect to
αk and
βk are set to be 0 as follows,
| |  | (17) |
| |  | (18) |
Eqn (18) can be easily solved as
| |  | (19) |
Using
eqn (19),
αk is expressed as
| | 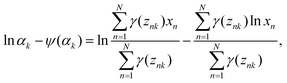 | (20) |
where
ψ is the digamma function. Since
eqn (20) cannot be analytically solved,
αk is numerically calculated. Now we can calculate the parameters for GMM using the EM algorithm: first, the initial values for parameters
αold,
βold,
πold are chosen. Second, as the expectation (E) step,
γ(
znk) is calculated from
eqn (12) based on
αold,
βold,
πold. Third, as the maximization (M) step,
αnew,
βnew,
πnew are calculated from
eqn (20), (19) and (16), respectively. The maximum likelihood parameters can be obtained by the iterative calculation of the E and M steps.
The number of gamma distributions having different parameters or the number of diffusive states K is extracted based on the Bayesian information criterion (BIC) represented as
| | BIC(K) = −2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(X|α,β,π,K) + m p(X|α,β,π,K) + m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N, N, | (21) |
where
m is the number of estimated parameters. We adopt
K to minimize BIC in
eqn (21) as the number of diffusive states to avoid the over-fitting of GMM to the data. The ratios of diffusion coefficients,
DR,
m, can be calculated as the mean values of each gamma distribution. When the EM algorithm converge to a local solution or some of the mixing coefficients are degenerate (
πk ≪ 1), we seek the maximum likelihood solution by randomly resetting initial conditions of the parameters.
3.2 Hidden Markov model
After extracting the number of diffusion states, an HMM is applied to the sequential data of the squared displacements d(t) to extract the most probable path of the diffusive sates. In this study, we use an HMM based on the maximum likelihood approach. Latent variables are also considered in the HMM. An observation d(tj) is generated through an emission probability (conditional distribution of the observation from a specific state)32 from the corresponding latent variable as in the case of the GMM. The latent variable transfers from one state to another following the transition probability. The transition and emission probabilities are estimated by the Baum–Welch algorithm.32 Then, using the estimated transition and emission probabilities, the most likely path is calculated by the Viterbi algorithm.32 The detail of these algorithm is described in text books such as ref. 32. Since libraries of HMMs are widely distributed (ex. Statistics and Machine Learning Toolbox of Matlab38 and hmmlearn for Python39), one can easily implement an HMM in their code. In the following calculation, we use the Statistics and Machine Learning Toolbox Ver. 11.2 of Matlab R2017a. We compare the results by Matlab with those by Python 3.5.2, showing good agreement between both results.
4. Results and discussions
We validate our proposed method using numerically generated trajectories (see eqn (3)) in which the number and sequence of diffusive states are given and known in advance. Then, we apply our method to experimentally obtained SPT data as a demonstration.
4.1 Classification performance of GMM for trajectories with localization error
We first compare our method with the existing methods.20,23 In ref. 20 they compare their method with vbSPT23 under several conditions. They numerically generated trajectories of 1000 tracks of 1000 frames. The conditions are given in dimensional form as ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 1 = 0.015 μm2 s−1,
1 = 0.015 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 2 = 0.06 μm2 s−1, and Δ
2 = 0.06 μm2 s−1, and Δ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 4.0 × 10−2 s in ref. 20. The lifetimes of each state are equal, and hence the fractions of each state are equal. The localization error of the particle is set at 20 nm. On this condition, the correctness of the estimation for the number of diffusive states are estimated and reported as 0.78 in ref. 20 and 0.8 by vbSPT.23
= 4.0 × 10−2 s in ref. 20. The lifetimes of each state are equal, and hence the fractions of each state are equal. The localization error of the particle is set at 20 nm. On this condition, the correctness of the estimation for the number of diffusive states are estimated and reported as 0.78 in ref. 20 and 0.8 by vbSPT.23
Following the numerical condition used in ref. 20, we numerically generate the trajectories of 1000 tracks of 1000 frames under the conditions of DR,1 = 1.0, DR,2 = 4.0, Δt = 4.0 × 10−2, and the localization error of 0.16, where the characteristic time and length are τ = 1 s and 0.122 μm. A frame average is used to reduce the scattering of data in ref. 20. We also consider a frame average for the squared displacements at the time of j-th time step as follows
| | 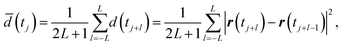 | (22) |
where 2
L + 1 is the number of averaged frames and 2
L + 1 of the squared displacements are averaged. After calculating and averaging the squared displacement for each trajectory, we estimate the number of diffusive states using all trajectories. It is assumed that the trajectories are independent and identically distributed. In this study, we calculate the correctness of estimation for the number of diffusive states calculated from 50 independent trials. The correctness is 1.0 for
L = 1 and
L = 2. These
L are equivalent to the value adopted in
ref. 20. However, the correctness is lower (<0.1) for
L = 0 (without a frame average). These results indicate that our method shows better performance when each trajectory is long enough to be frame averaged. This can be achieved under the conditions of relatively small Δ
t or long diffusion-state lifetime.
11,14 On the other hand, vbSPT
23 shows better performance for short trajectories as explained in
ref. 20 and 23.
4.2 Performance for trajectories having two diffusive states without localization error
4.2.1 Typical example of estimation.
We investigate the detailed performance of our method based on the analysis of the trajectories consisting of two diffusive states. Hereafter, we consider the trajectories without the localization error of the particles. Since the localization error will increase the apparent diffusion coefficient of the particles and obscure the true value, we compare the estimated diffusion coefficient with the exact one without considering the localization error. The trajectories are generated under the conditions of DR,1 = 1.0, DR,2 = 4.0, and Δt = 4.0 × 10−2. The particles transfer between the two diffusive states with the transition probability of 0.05 or stay in the same states with the probability of 0.95 during the time interval of Δt. We prepare 1000 trajectories with consecutive 30 frames (time steps). These conditions are similar to those discussed in the previous section and the literature20,22,23 in which the conditions were determined as a model of membrane or protein kinetics. We extract the number of the diffusive states, their most probable sequence, and the transition probability from the trajectories using our method. The squared displacements, d(t), defined by eqn (4) are calculated from the generated trajectory data. Then, the number of diffusive states and each diffusion coefficient are estimated from the probability distribution of the squared displacement using the GMM. We consider a frame average of the squared displacements defined as eqn (22) to reduce the scattering of the squared displacements and improve the estimation by the GMM. The choice of a certain value of L means that the probability of the state transition is sufficiently small in the frames of 2L + 1, and L should be less than 10 in the experimental conditions reported in the literature.20,22,23 By substituting ![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (tj) for xj, γ(znk) is calculated by eqn (12) as the E step. Then, as the M step, αnew, βnew, and πnew are calculated from eqn (20), (19) and (16), respectively. In the GMM, the maximum likelihood parameters are obtained by the iterative calculation of the E and M steps. Fig. 2a shows the typical result of the GMM for the trajectories, where consecutive 5 (L = 2) steps of the squared displacements are averaged. The histogram of the squared displacement is also shown in the figure for the comparison. Note that the histogram is not used in the GMM calculation and the bin width does not affect the GMM result. Two peaks corresponding to the two diffusive states have been detected using the GMM. The ratios of diffusion coefficients are estimated as DR,1 = 1.03 and DR,2 = 3.68 in this example. In the HMM calculation, the initial estimation of transfer probability between each state is determined based on the number of frames for averaging (5 in this example). The most likely path for each trajectory is calculated by the Viterbi algorithm. Fig. 2b shows a typical example of an estimation for the most likely path. The correctness of the estimation is defined as
(tj) for xj, γ(znk) is calculated by eqn (12) as the E step. Then, as the M step, αnew, βnew, and πnew are calculated from eqn (20), (19) and (16), respectively. In the GMM, the maximum likelihood parameters are obtained by the iterative calculation of the E and M steps. Fig. 2a shows the typical result of the GMM for the trajectories, where consecutive 5 (L = 2) steps of the squared displacements are averaged. The histogram of the squared displacement is also shown in the figure for the comparison. Note that the histogram is not used in the GMM calculation and the bin width does not affect the GMM result. Two peaks corresponding to the two diffusive states have been detected using the GMM. The ratios of diffusion coefficients are estimated as DR,1 = 1.03 and DR,2 = 3.68 in this example. In the HMM calculation, the initial estimation of transfer probability between each state is determined based on the number of frames for averaging (5 in this example). The most likely path for each trajectory is calculated by the Viterbi algorithm. Fig. 2b shows a typical example of an estimation for the most likely path. The correctness of the estimation is defined as| |  | (23) |
In this example, CHMM = 0.966, and the reliability of the estimation is reduced near the transition from state 1 to state 2 (time step of 14 in Fig. 2b). The transition probability is estimated as 0.033 from state 1 to 2, where the exact probability is 0.05. This example shows that our proposed method is effective to extract the diffusive states and estimate the transfer between the states.
 |
| | Fig. 2 Typical results of the estimation using our proposed method. The trajectory was generated under the conditions of Δt = 4.0 × 10−2, DR,1 = 1.0, and DR,2 = 4.0. The number of trajectories is 1000, and each trajectory consists of consecutive 30 time steps. (a) Estimation for the number of diffusive states using the GMM. (b) Most likely sequential path estimated by the Viterbi algorithm is shown as circles and the actual state path given in the trajectory generation is shown as triangles (left y axis). The squared displacements are also shown in squares (right y axis). | |
4.2.2 Effect of number of averaging frames and trajectories.
We investigate the dependence of the classifying performance on the number of averaging frames (2L + 1). One thousand trajectories are prepared under the condition of DR,1 = 1.0, DR,2 = 4.0, Δt = 4.0 × 10−2, and each trajectory consists of 15 to 60 time steps. Fig. 3a shows the correctness of the estimated the number of diffusive states using the GMM, where the correctness of estimation by the GMM, CGMM, is defined as following equation,| |  | (24) |
In this study, we calculate CGMM from 50 independent trials. The tested numbers of averaging frames are from 3, 5, and 7 (L = 1, 2, 3). The correctness, CGMM, drastically increases with increasing number of averaging frames or time steps as shown in Fig. 3a. The correctness, CGMM, is 0 for L = 0, when the time steps of each trajectory is from 15 to 100. This result shows that our method works well when each trajectory is long enough to calculate a frame average (>15). Fig. 3b shows the estimated DR,1 and DR,2 calculated from the correct estimations of the number of diffusion states for L = 2. The estimated value of DesR,2 approaches the assigned value for large numbers of time steps. Though DesR,1 is larger than the assigned value, the deviation of DesR,1 from the assigned value is small (∼3%).
 |
| | Fig. 3 Performance of the proposed method. Trajectories are generated under the conditions of Δt = 4.0 × 10−2, DR,1 = 1.0, and DR,2 = 4.0. (a) Correctness of estimation for number of diffusive states using the GMM. The number of averaging frames are L = 1, 2, 3. (b) Ratio of the estimated diffusion coefficients (superscript “es”) to the input (superscript “in”) coefficients for L = 2. | |
In the above discussion, the number of trajectories is fixed at 1000. In the following, we fix the time steps of each trajectory of 30 and vary the number of trajectories. The other conditions remain the same (i.e., DR,1 = 1.0, DR,2 = 4.0, Δt = 4.0 × 10−2, L = 2). Fig. 4a shows the correctness of estimation by the GMM, CGMM. The correctness CGMM monotonically increases and is larger than 0.9 when the number of trajectories is larger than 50. The estimated DR,1 and DR,2 shown in Fig. 4b indicate that reliable estimation is achieved by our method even when the number of trajectories is small. For example, the DR,1 and DR,2 can be estimated with 10% when the number of trajectories larger than 25.
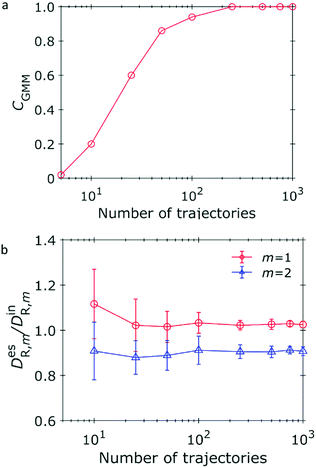 |
| | Fig. 4 Dependence of estimation on the number of trajectories. Trajectories of 30 time steps are generated under the conditions of Δt = 4.0 × 10−2, DR,1 = 1.0, and DR,2 = 4.0. (a) Correctness of estimation for number of diffusive states using the GMM. The number of averaging frames is L = 2. (b) Ratio of the estimated diffusion coefficients (superscript “es”) to the input (superscript “in”) coefficients for L = 2. | |
4.2.3 Effect of ratio of diffusion coefficient.
The classifying performance would depend on the ratio of diffusion coefficient, DR,2. We prepare 1000 trajectories consisting of 30 time steps under the conditions of DR,1 = 1.0, 1.8 ≤ DR,2 ≤ 4.0, Δt = 4.0 × 10−2. Fig. 5 shows the correctness CGMM, where L = 1, 2, 3. It is considered that the correct estimation will be difficult for small DR,2. The correctness also drastically increases with increasing DR,2 for L = 2, and the reliable estimation is achieved for L = 3 even when DR,2 is small (CGMM = 0.74 for DR,2 = 2.0). The correctness for L = 1 is low even when DR,2 ≥ 4. Thus, a larger number of trajectories or time steps of each trajectory is required for reliable estimation when L = 1 (see also Fig. 3).
 |
| | Fig. 5 Correctness of estimation for number of diffusive states using the GMM, CGMM. The number of averaging frames are L = 1, 2, 3. The trajectory was generated under the conditions of Δt = 4.0 × 10−2 and DR,1 = 1.0 (fixed). The number of trajectories is 1000, and each trajectory consists of consecutive 30 time steps. | |
We also investigate the effect of the time step Δt for L = 2 and confirm that Δt does not affect the result because the mean ratio of the squared displacements does not change in different Δt.
4.2.4 Performance of HMM.
The most probable path of diffusive sates is estimated for each trajectory. The correctness CHMM and transfer probability depend on the number of time steps. Note that the frame average is not used in the HMM calculation. The trajectories are generated under the conditions of DR,1 = 1.0, DR,2 = 4.0, Δt = 4.0 × 10−2, and the transition probabilities from state 1 to 2 and vice versa are set at 0.05. These conditions are the same as those of Section 4.2.1. We prepare 1000 trajectories varying the time steps of each trajectory and calculate the most probable path for each trajectory by the HMM. Fig. 6 shows the correctness, CHMM, and the estimated transfer probability from state 1 to 2. The correctness, CHMM, gradually increases with increasing the time steps of each trajectory. However, CHMM is smaller than CGMM. Though there are a lot of trajectories without state transitions in the given time steps due to small transition probability and number of time steps, the HMM always classifies the data into two states; thus, CHMM is small and the transition probability is over estimated for the small numbers of time steps.
 |
| | Fig. 6 Correctness of estimated state path and transition probability using the HMM, CHMM. Trajectories are generated under the conditions of Δt = 4.0 × 10−2, DR,1 = 1.0, and DR,2 = 4.0. The transition probabilities from state 1 to 2 and vice versa are set at 0.05. The number of trajectories is 1000 and the time steps of each trajectory is shown as horizontal axis. | |
4.3 Three diffusive states
We discuss the application of our method to the analysis of the trajectories for particles traveling in a medium having three diffusive states. We generate the trajectories under the following conditions: three diffusive states with DR,1 = 1.0 (state 1), DR,2 = 4.0 (state 2), and DR,3 = 12.0 (state 3) and the discretized time Δt = 3.0 × 10−3. The characteristic time and length are τ = 1 s and 0.5 μm, respectively. The particles transfer each state during the time interval of Δt under the following probabilities: the transition probability from state 1 to state 2 is 0.031 and to state 3 is 0.1. The transition probability from state 2 to state 1 is 0.017 and to state 3 is 0.01. The transition probability from state 3 to state 1 is 0.055 and to state 3 is 0.055. These conditions correspond to those discussed in Persson et al.,23 where the parameters were given in dimensional quantities: ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 1 = 0.25 μm2 s−1,
1 = 0.25 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 2 = 1.0 μm2 s−1,
2 = 1.0 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 3 = 3.0 μm2 s−1, and Δ
3 = 3.0 μm2 s−1, and Δ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 3.0 × 10−3 s.
= 3.0 × 10−3 s.
We estimate the number of diffusive states, where the time steps of each trajectory are fixed at 30. The correctness for the estimation of number of diffusive states is calculated from 50 independent trials as shown in Fig. 7a. The correctness rapidly increases in 100 trajectories and reaches to unity over 750 trajectories. The correctness for this 3 states estimation is smaller than that for 2 states estimation shown in Fig. 4a because the number of data in each state is smaller by construction. Fig. 7b shows the estimated ratio of diffusion coefficients. The estimated DR,1 converges to the input value with 1000 trajectories. On the other hand, the estimated DR,2 and DR,3 are 10% or 20% lager than the input values because the variances of squared displacement generated from DR,2 and DR,3 are larger than that from DR,1. Our method works well in the 3-states problem.
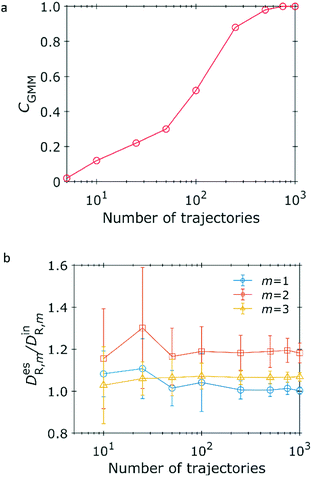 |
| | Fig. 7 Dependence of estimation on number of trajectories. Trajectories of 30 time steps are generated under the conditions of Δt = 3.0 × 10−3, DR,1 = 1.0, DR,2 = 4.0, and DR,3 = 12.0. (a) Correctness of estimation for number of diffusive states using the GMM. The number of averaging frames are L = 2. (b) Ratio of the estimated diffusion coefficients (superscript “es”) to the input (superscript “in”) coefficients for L = 2. | |
4.4 Distinction of discrete diffusive states
In the above discussions, we have considered the particle trajectories in a medium having discrete diffusive states. The medium is assumed as consisting of several discrete diffusive states because HMM can treat only discrete hidden states.32 This is one of the limitation of the HMM. It is sometimes convenient to regard a medium consisting of multiple discrete diffusive states or particle motion is approximately expressed as such, when the underlying process is unclear before the analysis.28,40–42 Therefore, it is worth clarifying how much amount of data is necessary for treating a medium consisting of discrete diffusive states. Fig. 3a, 4a, 5 and 7a can be understood as showing the required amount of data to determine whether a medium consists of discrete diffusive states or not by the GMM based on BIC.
As a comparison to a medium having several discrete diffusive states, we consider a case where a particle travels in a medium having a continuously varying diffusion coefficient. One thousand trajectories are generated by eqn (3), where DR,m is replaced by the time varying diffusion coefficient DR(tj). The diffusion coefficient linearly varies from 1 to Dmax as DR(tj) = (Dmax − 1)(j − 1)/(N − 1) + 1, where Dmax = 4.0 and the time steps N = 30. This condition corresponds to that discussed in Section 4.2.2 except for a continuously varying diffusion coefficient, and the correctness is unity when the number of frame averaging is over 5 (L ≥ 2) in Fig. 3a. Fig. 8 shows the probability densities for the squared displacements of the trajectories with the continuously varying diffusion coefficient DR(tj) and the discrete diffusion states (DR,1 = 1.0, and DR,2 = 4.0) for comparison, where the number of frame averaging is 5 (L = 2). The solid and dashed curves are obtained by the GMM in which the number of the mixing distribution is determined by BIC. The GMM returns a single state with the diffusion coefficient of 2.45 corresponding to the time average of DR(tj) for the trajectory with the continuously varying diffusion coefficient (solid line). For the trajectory traveling in the discrete states, the discrete diffusive states are successfully classified by the GMM (dashed line). As shown in figures from 3 to 7, the GMM can classify the discrete diffusive states when the sufficient number of time steps is available and/or the number of averaging frames is sufficiently large for the trajectories with the discrete diffusive states. By contrast, for the trajectory in the continuously varying diffusion coefficient, the estimated number of diffusive states is determined as one by our method even when the large number of times steps and/or averaging frames are used. Our method provides a statistical validity of the assumption that a medium can be treated as consisting of discrete diffusive states for the given number of data points of trajectory.
 |
| | Fig. 8 Typical results of probability densities for trajectories in a medium with continuously varying diffusion coefficient and that consisting of two discrete diffusive states. The solid and dashed curves show the result of the GMM for each condition. | |
4.5 Analysis of experimentally obtained SPT data
Now, we apply our proposed method to the analysis of experimentally obtained SPT data. The SPT data was obtained by an optical microscope in the same manner as that of our previous study.43 We used ZnS–AgInS2 nanoparticles44–46 as probe particles, and mixed it into a polydimethylsiloxane (PDMS) layer. An oil immersion objective lens with 100 times magnification with N.A. of 1.4 was used. The time step (frame interval) was Δt = 0.2 s. The SPT images were captured after 20 h adding a curing agent in the PDMS layer at a room temperature of 20 °C. The SPT images were analyzed using IDL-code.47 For the completely cured PDMS layer, the diffusion coefficient was calculated as O(10−4) μm2 s−1. This indicates that the localization error is considered as O(102) nm. Under this condition, there were some diffusive states in the PDMS layer.43Fig. 9a shows the estimation result of the number of diffusive states using the GMM. Fig. 9b shows the single particle trajectory having 185 location data points with the most probable diffusive states. In the GMM analysis, it was found that there were three diffusive states of diffusion coefficients of 4 × 10−3, 8 × 10−3, and 12 × 10−3 μm2 s−1. These values reasonably agreed with those obtained by MSD analysis.43 The particle motions having relatively large displacement can be captured as the fast state (large diffusion coefficient). Though there is the place around x = 0.25, y = 0.12 containing two diffusive states due to the estimation error induced from the small amount of the data, each diffusive state occupies different place in the layer as shown in Fig. 9b. It is considered that the PDMS layer consists of several portions having different viscosity, when we assume discrete diffusive states. We conclude that our proposed method is applicable to the analysis of experimental SPT/SMT data.
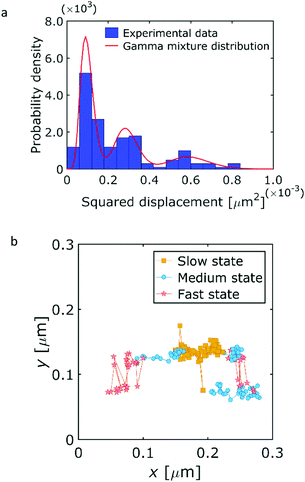 |
| | Fig. 9 Analysis results for the experimentally obtained SPT trajectory. (a) The estimation for number of diffusive states using GMM. (b) The classified result using HMM. | |
5. Conclusions
In this article, we have proposed a hybrid method of a gamma mixture model (GMM) and a hidden Markov model (HMM) to classify particle trajectory for a particle moving in a heterogeneous medium. We introduce a GMM as an extension of a Gaussian mixture model based on the expectation–maximization (EM) algorithm. The number of diffusive states is estimated by the GMM, and then the HMM is used to extract the most likely path of the diffusive states. The correct estimation of the number of diffusive states can be achieved from small amount of trajectory data by considering frame average of squared displacements. The transition path of diffusive states is estimated by the Viterbi algorithm based on the estimated number of diffusive states. We compare our method with existing methods by calculating trajectory for a particle moving in a medium having two diffusive states. It is shown that our proposed method can extract the number of diffusive states more reliably than existing methods when the number of averaging frames is large. Thus, our method is a powerful tool for the trajectories obtained with relatively large frame rate or having long diffusion-state lifetime. Furthermore, we also indicate that our method can provide an indicator whether the assumption of a medium consisting of discrete diffusive states is appropriate or not based on the amount of the given data. Our hybrid method of the GMM and HMM is promising method for analyzing single-particle/molecule tracking data when limited number of data is available.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
We thank K. Tomita for his assistance with the simulations by Python. This work was partly supported by a JSPS Grant-in-Aid for Scientific Research (B), No. 16H04277 and a research encouragement grants from the Asahi Glass Foundation.
References
- M. J. Saxton and K. Jacobson, Annu. Rev. Biophys. Biomol. Struct., 1997, 26, 373–399 CrossRef PubMed.
- M. J. Saxton, Biophys. J., 1997, 72 Search PubMed.
- W. E. Moerner and D. P. Fromm, Rev. Sci. Instrum., 2003, 74, 3597 CrossRef.
-
J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer, 3rd edn, 2006 Search PubMed.
- N. Ruthardt, D. C. Lamb and C. Brauchle, Mol. Ther., 2011, 19, 1199–1211 CrossRef PubMed.
- A. Kusumi, T. A. Tsunoyama, K. M. Hirosawa, R. S. Kasai and T. K. Fujiwara, Nat. Chem. Biol., 2014, 10, 524–532 CrossRef PubMed.
- C. Manzo and M. F. Garcia-Parajo, Rep. Prog. Phys., 2015, 78, 124601 CrossRef PubMed.
- T. Chen and B. M. Reinhard, Small, 2013, 9, 876–884 CrossRef PubMed.
- J. A. Varela, C. Aberg, J. C. Simpson and K. A. Dawson, Small, 2015, 11, 2026–2031 CrossRef PubMed.
- D. Woll, H. Uji-i, T. Schnitzler, J. Hotta, P. Dedecker, A. Herrmann, F. C. De Schryver, K. Mullen and J. Hofkens, Angew. Chem., Int. Ed. Engl., 2008, 47, 783–787 CrossRef PubMed.
- S. Ito, K. Itoh, S. Pramanik, T. Kusumi, S. Takei and H. Miyasaka, Appl. Phys. Express, 2009, 2, 075004 CrossRef.
- K. Paeng and L. J. Kaufman, Macromolecules, 2016, 49, 2876–2885 CrossRef.
- H. Qian, M. P. Sheetz and E. L. Elson, Biophys. J., 1991, 60, 910–921 CrossRef PubMed.
- L. C. Elliott, M. Barhoum, J. M. Harris and P. W. Bohn, Phys. Chem. Chem. Phys., 2011, 13, 4326–4334 RSC.
- C. Ribrault, A. Triller and K. Sekimoto, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021112 CrossRef PubMed.
- S. Burov, S. M. Tabei, T. Huynh, M. P. Murrell, L. H. Philipson, S. A. Rice, M. L. Gardel, N. F. Scherer and A. R. Dinner, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 19689–19694 CrossRef PubMed.
- I. Hanasaki and Y. Isono, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 85, 051134 CrossRef PubMed.
- I. Hanasaki, S. Uehara, Y. Arai, T. Nagai and S. Kawano, Jpn. J. Appl. Phys., 2015, 54, 125601 CrossRef.
- Y. Matsuda, I. Hanasaki, R. Iwao, H. Yamaguchi and T. Niimi, Anal. Chem., 2016, 88, 4502–4507 CrossRef PubMed.
- P. J. Bosch, J. S. Kanger and V. Subramaniam, Biophys. J., 2014, 107, 588–598 CrossRef PubMed.
- C. Metzner, C. Mark, J. Steinwachs, L. Lautscham, F. Stadler and B. Fabry, Nat. Commun., 2015, 6, 7516 CrossRef PubMed.
- M. Ott, Y. Shai and G. Haran, J. Phys. Chem. B, 2013, 117, 13308–13321 CrossRef PubMed.
- F. Persson, M. Linden, C. Unoson and J. Elf, Nat. Methods, 2013, 10, 265–269 CrossRef PubMed.
- Z. Ghahramani, Int. J. Pattern Recognit. Artif. Intell., 2001, 15, 9–42 CrossRef.
- J. E. Bronson, J. Fei, J. M. Hofman, R. L. Gonzalez, Jr. and C. H. Wiggins, Biophys. J., 2009, 97, 3196–3205 CrossRef PubMed.
- K. Okamoto and Y. Sako, Biophys. J., 2012, 103, 1315–1324 CrossRef PubMed.
- Y. Gu, X. Di, W. Sun, G. Wang and N. Fang, Anal. Chem., 2012, 84, 4111–4117 CrossRef PubMed.
- S. Habuchi, S. Fujiwara, T. Yamamoto, M. Vacha and Y. Tezuka, Anal. Chem., 2013, 85, 7369–7376 CrossRef PubMed.
- L. O. Mair and R. Superfine, Soft Matter, 2014, 10, 4118–4125 RSC.
- M. Kanke, E. Tahara, P. J. Huis In't Veld and T. Nishiyama, EMBO J., 2016, 35, 2686–2698 CrossRef PubMed.
- A. R. Webb, Pattern Recogn., 2000, 33, 2045–2054 CrossRef.
-
C. M. Bishop, Pattern Recognition and Machine Learning (Information Science and Statistics), Springer-Verlag Inc., New York, 2006 Search PubMed.
- H. Shen, L. J. Tauzin, W. Wang, B. Hoener, B. Shuang, L. Kisley, A. Hoggard and C. F. Landes, Anal. Chem., 2016, 88, 9926–9933 CrossRef PubMed.
- M. J. Skaug, J. N. Mabry and D. K. Schwartz, J. Am. Chem. Soc., 2014, 136, 1327–1332 CrossRef PubMed.
- C. Yu, J. Guan, K. Chen, S. C. Bae and S. Granick, ACS Nano, 2013, 7, 9735–9742 CrossRef PubMed.
- S. Juodkazis, N. Mukai, R. Wakaki, A. Yamaguchi, S. Matsuo and H. Misawa, Nature, 2000, 408, 178–181 CrossRef PubMed.
- A. M. Kloxin, A. M. Kasko, C. N. Salinas and K. S. Anseth, Science, 2009, 324, 59–63 CrossRef PubMed.
- MathWorks, Statistics and Machine Learning Toolbox, https://jp.mathworks.com/products/statistics.html.
- R. Weiss, S. Du, J. Grobler, D. Cournapeau, F. Pedregosa, G. Varoquaux, A. Mueller, B. Thirion, D. Nouri, G. Louppe, J. Vanderplas, J. Benediktsson, L. Buitinck, M. Korobov, R. McGibbon, S. Lattarini, V. Niculae, csytracy, A. Gramfort, S. Lebedev, D. Huppenkothen, C. Farrow and A. Yanenko, hmmlearn: Hidden Markov Models in Python, with scikit-learn like API, http://hmmlearn.readthedocs.io/en/latest/.
- J. Kirstein, B. Platschek, C. Jung, R. Brown, T. Bein and C. Brauchle, Nat. Mater., 2007, 6, 303–310 CrossRef PubMed.
- C. Hellriegel, J. Kirstein and C. Bräuchle, New J. Phys., 2005, 7, 23 CrossRef.
- S. Habuchi, N. Satoh, T. Yamamoto, Y. Tezuka and M. Vacha, Angew. Chem., Int. Ed. Engl., 2010, 49, 1418–1421 CrossRef PubMed.
-
R. Iwao, Y. Matsuda, H. Yamaguchi and T. Niimi, MHS, 2015, DOI:10.1109/MHS.2015.7438256.
- T. Torimoto, T. Adachi, K. Okazaki, M. Sakuraoka, T. Shibayama, B. Ohtani, A. Kudo and S. Kuwabata, J. Am. Chem. Soc., 2007, 129, 12388–12389 CrossRef PubMed.
- T. Torimoto, S. Ogawa, T. Adachi, T. Kameyama, K. Okazaki, T. Shibayama, A. Kudo and S. Kuwabata, Chem. Commun., 2010, 46, 2082–2084 RSC.
- Y. Matsuda, T. Torimoto, T. Kameya, T. Kameyama, S. Kuwabata, H. Yamaguchi and T. Niimi, Sens. Actuators, B, 2013, 176, 505–508 CrossRef.
- J. C. Crocker and D. G. Grier, J. Colloid Interface Sci., 1996, 179, 298 CrossRef.
|
| This journal is © the Owner Societies 2018 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a,
Itsuo
Hanasaki
*a,
Itsuo
Hanasaki
 b,
Ryo
Iwao
c,
Hiroki
Yamaguchi
b,
Ryo
Iwao
c,
Hiroki
Yamaguchi
 c and
Tomohide
Niimi
c
c and
Tomohide
Niimi
c
![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) m (m = 1, 2, 3,…,K), where
m (m = 1, 2, 3,…,K), where ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) m may be expressed as a function of position or time. The diffusion coefficients as functions of position and time correspond to a spatially heterogeneous medium such as a surface having adsorption sites22,33–35 and to a temporally heterogeneous medium whose property is temporally controlled,36,37 respectively. We also assume that the particle isotropically diffuses in each medium and the effect of interfaces between the media on the particle motion is negligible. The trajectory is generated by the Wiener process described by the overdamped Langevin equation as follows
m may be expressed as a function of position or time. The diffusion coefficients as functions of position and time correspond to a spatially heterogeneous medium such as a surface having adsorption sites22,33–35 and to a temporally heterogeneous medium whose property is temporally controlled,36,37 respectively. We also assume that the particle isotropically diffuses in each medium and the effect of interfaces between the media on the particle motion is negligible. The trajectory is generated by the Wiener process described by the overdamped Langevin equation as follows
![[r with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0072_0302.gif) (
(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) is the position vector of the particle at time
) is the position vector of the particle at time ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) . The variables ξ(
. The variables ξ(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ) is Gaussian random with
) is Gaussian random with ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [ξi(
[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )] = 0, var[ξi(
)] = 0, var[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )] = 1, and
)] = 1, and ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [ξi(
[ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) )ξi(
)ξi(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ′)] = δ(
′)] = δ(![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) −
− ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) ′), where
′), where ![[Doublestruck E]](https://www.rsc.org/images/entities/char_e168.gif) [⋯] and var[⋯] indicate expectation and variance, respectively. The subscripts, i = 1, 2, 3, corresponding to components of axes x, y, z, respectively. We introduce the characteristic time τ and length
[⋯] and var[⋯] indicate expectation and variance, respectively. The subscripts, i = 1, 2, 3, corresponding to components of axes x, y, z, respectively. We introduce the characteristic time τ and length  . Then, eqn (1) is nondimensionalized as
. Then, eqn (1) is nondimensionalized as
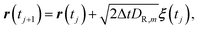



 . The number of gamma distributions having different parameters is represented as K, which also corresponds to the number of diffusive states in our method. Here, we introduce latent variables of a K-dimensional binary (0 or 1) random variable z = {z1, z2,…,zK} with
. The number of gamma distributions having different parameters is represented as K, which also corresponds to the number of diffusive states in our method. Here, we introduce latent variables of a K-dimensional binary (0 or 1) random variable z = {z1, z2,…,zK} with  . This means that the probability of an observation x comes from zk is represented by p(zk = 1) = πk. Since z is a binary random variable, the distribution p(zk = 1) can be written in the form
. This means that the probability of an observation x comes from zk is represented by p(zk = 1) = πk. Since z is a binary random variable, the distribution p(zk = 1) can be written in the form
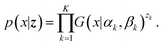

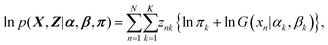


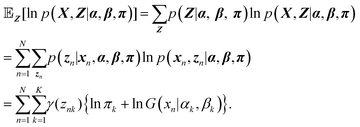
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) πk and γ(znk){ln
πk and γ(znk){ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(x|αk,βk)}. First, we maximize the expectation of the log likelihood with respect to the mixing coefficients πk. Since there is the constraint condition
G(x|αk,βk)}. First, we maximize the expectation of the log likelihood with respect to the mixing coefficients πk. Since there is the constraint condition  , we introduce a Lagrange multiplier λ and consider the following Lagrange function Λ(π,λ):
, we introduce a Lagrange multiplier λ and consider the following Lagrange function Λ(π,λ):

 , the equation, N = −λ, is obtained. Then, eqn (15) can be written as
, the equation, N = −λ, is obtained. Then, eqn (15) can be written as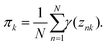
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) G(x|αk,βk)} in eqn (13), the partial derivatives of it with respect to αk and βk are set to be 0 as follows,
G(x|αk,βk)} in eqn (13), the partial derivatives of it with respect to αk and βk are set to be 0 as follows,


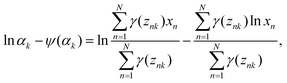
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) p(X|α,β,π,K) + m
p(X|α,β,π,K) + m![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N,
N,![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 1 = 0.015 μm2 s−1,
1 = 0.015 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 2 = 0.06 μm2 s−1, and Δ
2 = 0.06 μm2 s−1, and Δ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 4.0 × 10−2 s in ref. 20. The lifetimes of each state are equal, and hence the fractions of each state are equal. The localization error of the particle is set at 20 nm. On this condition, the correctness of the estimation for the number of diffusive states are estimated and reported as 0.78 in ref. 20 and 0.8 by vbSPT.23
= 4.0 × 10−2 s in ref. 20. The lifetimes of each state are equal, and hence the fractions of each state are equal. The localization error of the particle is set at 20 nm. On this condition, the correctness of the estimation for the number of diffusive states are estimated and reported as 0.78 in ref. 20 and 0.8 by vbSPT.23
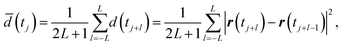
![[d with combining macron]](https://www.rsc.org/images/entities/i_char_0064_0304.gif) (tj) for xj, γ(znk) is calculated by eqn (12) as the E step. Then, as the M step, αnew, βnew, and πnew are calculated from eqn (20), (19) and (16), respectively. In the GMM, the maximum likelihood parameters are obtained by the iterative calculation of the E and M steps. Fig. 2a shows the typical result of the GMM for the trajectories, where consecutive 5 (L = 2) steps of the squared displacements are averaged. The histogram of the squared displacement is also shown in the figure for the comparison. Note that the histogram is not used in the GMM calculation and the bin width does not affect the GMM result. Two peaks corresponding to the two diffusive states have been detected using the GMM. The ratios of diffusion coefficients are estimated as DR,1 = 1.03 and DR,2 = 3.68 in this example. In the HMM calculation, the initial estimation of transfer probability between each state is determined based on the number of frames for averaging (5 in this example). The most likely path for each trajectory is calculated by the Viterbi algorithm. Fig. 2b shows a typical example of an estimation for the most likely path. The correctness of the estimation is defined as
(tj) for xj, γ(znk) is calculated by eqn (12) as the E step. Then, as the M step, αnew, βnew, and πnew are calculated from eqn (20), (19) and (16), respectively. In the GMM, the maximum likelihood parameters are obtained by the iterative calculation of the E and M steps. Fig. 2a shows the typical result of the GMM for the trajectories, where consecutive 5 (L = 2) steps of the squared displacements are averaged. The histogram of the squared displacement is also shown in the figure for the comparison. Note that the histogram is not used in the GMM calculation and the bin width does not affect the GMM result. Two peaks corresponding to the two diffusive states have been detected using the GMM. The ratios of diffusion coefficients are estimated as DR,1 = 1.03 and DR,2 = 3.68 in this example. In the HMM calculation, the initial estimation of transfer probability between each state is determined based on the number of frames for averaging (5 in this example). The most likely path for each trajectory is calculated by the Viterbi algorithm. Fig. 2b shows a typical example of an estimation for the most likely path. The correctness of the estimation is defined as

![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 1 = 0.25 μm2 s−1,
1 = 0.25 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 2 = 1.0 μm2 s−1,
2 = 1.0 μm2 s−1, ![[D with combining circumflex]](https://www.rsc.org/images/entities/i_char_0044_0302.gif) 3 = 3.0 μm2 s−1, and Δ
3 = 3.0 μm2 s−1, and Δ![[t with combining circumflex]](https://www.rsc.org/images/entities/i_char_0074_0302.gif) = 3.0 × 10−3 s.
= 3.0 × 10−3 s.








