Photoelectron shake-ups as a probe of molecular symmetry: 4d XPS analysis of I₃⁻ in solution

Abstract

A combination of multi-configurational restricted active space calculations with a Dyson orbital formalism has been applied for accurate simulations of 4d photo-electron spectra of the I₃⁻ molecular ion. The analysis based on the occupation numbers of natural orbitals allowed to predict and rationalize the spectral fingerprints of solvent-induced nuclear asymmetry. In particular, it demonstrates how the nuclear asymmetry directly causes an increase of shake-up intensity. The relative intensity of shake-up and main features of the I 4d XPS spectrum could therefore serve as a simplified experimental observable of structural asymmetry, complementary to changes in the shape of the main spectral features.

---

1 Introduction

Photoelectron spectroscopy is one of the most powerful and widely applied experimental methods for studies of electronic structure of matter, which in the X-ray regime (XPS), by targeting of core-levels, constitutes an element-specific local probe around distinct atomic sites in molecules and complex materials.¹ With the development of new delivering systems such as liquid jets combined with improved X-ray sources, XPS studies in the liquid phase have become increasingly viable to investigate the effects of solute–solvent interactions in e.g. electrolyte solutions^2,3 and at liquid interfaces.⁴ Robust and detailed analysis of such experiments, however, often demands comparison to accurate theoretical simulations of spectra. Here, a crucial point is to predict and identify spectral signatures that are characteristic and yet readily detected in measurements, in addition to assigning and rationalizing the spectral features to facilitate an understanding of the underlying chemical and spectroscopic mechanisms.

As an important component in dye-sensitized solar cells, the electronic, structural and dynamic properties of I₃⁻ in solution have been studied in great detail both with experimental^5–7 and theoretical methods.^8–12 These studies all demonstrate how the structure of the molecular ion and, in particular, its degree of nuclear asymmetry can be directly correlated with the varied strength of solvent–solute interaction in different solutions. In aqueous solution, the strong hydrogen bonding drives large amplitude asymmetrical stretches and charge localization, leading to an electronic structure more akin to an I₂⋯I⁻ configuration. The influence of hydrogen bonding is less pronounced in, e.g., ethanol and acetonitrile where the charge stays fairly delocalized over the whole moiety, [I–I–I]⁻, and structural symmetry is comparatively preserved. In previous work^11,12 it has been demonstrated how the solvent-induced nuclear asymmetry may be evidenced from altered features of the main signal in 4d XPS measurements. Thus, I₃⁻ constitutes an ideal model system to explore not only the possible effects of nuclear asymmetry on electrochemical functionality, but also its interplay with XPS intensities.

Due to a recent implementation by Grell et al.¹³ both main and shake-up XPS intensities can now be simulated within a Dyson orbital formalism with orbitals derived from the multi-configurational second order perturbation theory restricted active space method (RASPT2)^14,15 that can account for the multitude of effects that may influence spectral intensities such as: various types of chemical bonding, multi-configurational character of states, dynamic correlation, scalar relativistic effects, and spin–orbit coupling. The development thereby directly enables extension of previous I₃⁻ studies, with simulations of XPS spectra at an accuracy level that motivates theoretical predictions for possible future approval by experimental measurements. Complementarily, we also demonstrate in the current work how a framework for assignment and analysis, based on the multi-configurational Dyson orbital, may be conveniently formulated in terms of occupation numbers of the natural orbitals, to rationalize the predicted spectral trends.

2 Computational details

2.1 Molecular geometries

To study the principal influence of nuclear asymmetry on I₃⁻ 4d XPS, spectral simulations were performed and compared for a symmetric and an asymmetrically stretched geometry. The symmetric geometry (representing [I–I–I]⁻ as in e.g. EtOH solution) with 2.91 Å I–I bond lengths corresponds to a CASPT2(16,9) I₃⁻(g) optimization.⁷ The linear asymmetric geometry (representing I₂⋯I⁻) with I–I bonds of 3.37 Å and 2.82 Å was chosen to have the largest asymmetric stretch among structures found in a number of previous molecular dynamic simulations of aqueous LiI₃ solution.¹¹

2.2 Electronic structure calculations

The electronic wave functions of the initial electronic state of I₃⁻ and the final core-ionized states of the neutral I₃ were calculated on the RASSCF¹⁴ and RASPT2¹⁵ levels, as implemented in the Molcas 8.0 program package.¹⁶ A RAS(15, 3; 34 e⁻, 1 h⁺) active space was employed as illustrated in Fig. 1, i.e. 15 orbitals in the RAS1 space (one hole is allowed) and 3 orbitals in the RAS2 space (full CI) with a total of 34 active electrons (33 for the final states). The calculations were performed without explicit use of symmetry, a separate orbital constraint was, however, applied to the 15 4d orbitals to exclude orbital rotation with other occupied valence orbitals. Thereby, we ensure core-rather than valence-excitations in the final state calculation. Solvent effects, beyond their impact on the nuclear geometry, were not included in the calculations; previous work has, however, demonstrated the effects of explicit water solvation to mainly result in additional broadening and altered absolute shift of the XPS spectrum.¹¹

Fig. 1 Active space of the RAS(15, 3; 34 e⁻, 1 h⁺) calculations and representative multi-state RASPT2 natural orbitals as obtained for the I₃⁻ singlet species. One electron hole (h⁺) in RAS1 allows for core-ionization (core-excitation in the neutral I₃ species) out of the 15 × 4d core orbitals; the RAS2 space allows for simultaneous valence-excitations and correlation within the 3 × 5p_z orbitals. The orbitals obtained for the symmetric geometry can be naturally grouped as 10 × terminal (t) and 5 × central (c) 4d core orbitals, in addition to 3 × 5p_z valence orbitals of bonding (σ), non-bonding (n) and anti-bonding (σ*) character. The 5p_z orbitals are further characterized by their inversion symmetry parity: gerade (g) and ungerade (u). The orbitals obtained for the asymmetric geometry are instead naturally grouped as 5 × ionic (i), 5 × terminal (t) and 5 × central (c) 4d core orbitals, in addition to 3 × 5p_z valence orbitals that are bonding (σ) and anti-bonding (σ*) on the I₂ moiety and of non-bonding (n) character on the I⁻ ion (i).

For the molecular ion I₃⁻ (i.e. the initial states of the XPS process), both the singlet ground state and the first triplet spin-free (pure multiplicity) states were calculated. For the neutral molecule I₃ (i.e. the final states of the XPS process), all possible spin-free states were calculated within the state averaging formalism, namely 143 doublets (135 core-ionized) and 46 quartets (45 core-ionized). Subsequent multi-state RASPT2 calculations were carried out with an imaginary shift of 0.2 Hartree to accelerate convergence. For the doublet I₃⁻ calculations of the asymmetric geometry, the 10 states with highest energy were excluded from the multi-state RASPT2 due to the intruder states problems; this does not significantly affect the results as these states anyway fall outside the XPS energy range analyzed in the current work. Scalar relativistic effects were included via a Douglas–Kroll (DK) Hamiltonian^17,18 and the relativistically contracted ANO-RCC-VTZP¹⁹ basis set. Spin–orbit coupling was included through the restricted active space state interaction (RASSI) method,^20,21via atomic mean field integrals²² with the electron repulsion integrals approximated through a density-fitting procedure.^23–25

2.3 XPS intensities

XPS intensities were obtained within a Dyson orbital (DO) formalism, as described in detail in previous work.¹³ In short, for the initial state i and final bound state of the ionized system f with the respective N and N − 1-electron wave functions Ψ^N_i and Ψ^N−1_f, the photo-electron matrix element can be written as

D_fi = 〈Ψ^N−1_fψ^el(k)|d̂|Ψ^N_i〉 = 〈ψ^el(k)|d̂|ϕ^DO_fi〉. (1)

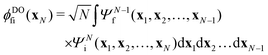Here, ψ^el(k) is the photo-electron wave function (k its momentum), d̂ the electronic dipole operator, and ϕ^DO_fi stands for the one-electron DOthat (after normalization) formally corresponds to the wave function of the photo-electron prior to the ionization. With ϕ^DO_fi obtained from the quantum chemical calculation the spectral intensity of the transition i → f is proportional to |D_fi|².

The results of the current work are all obtained within the sudden approximation (SA) where the energy (and thus k) dependence of ψ^el(k) is neglected to obtain

|D_fi|² = |〈ψ^el(k)|d̂|ϕ^DO_fi〉|² ∝ ‖ϕ^DO_fi‖² (3)

where the proportionality constant is taken to be the same for all transitions.

The SA is well justified for our present comparison to experiments performed with 600 eV photon energies as shown in ESI,† Section S1. This fact allowed us to avoid the most demanding step of computing transition matrix elements with continuum functions. We emphasize, however, that the approximation cannot be trivially assumed to hold equally well for other systems and binding energy ranges. Therefore, we advocate a case by case validation also in future studies.

All XPS transitions were shifted by 2.9 eV (1.5 eV at RASSCF level) and rescaled to align the main feature of the spectrum for the symmetric geometry to the experiment. The discrete XPS intensities from the calculations were convoluted with a Gaussian function with full-width-half-maximum of 1.1 eV, previously shown to yield good agreement with experiments.¹¹

2.4 Assignment and analysis

The DO formalism constitutes a convenient framework for assigning XPS transitions within a molecular orbital picture. The multi-configurational DO carries information both about the photo-electron and shake-up excitations in the molecular system, as may be expressed in terms of occupation numbers of the natural orbitals. For a multi-configurational state Ψ_j, an occupation vector

n_j = (occ_j(φ₁),occ_j(φ₂),…,occ_j(φ_M)) (4)

may be defined from the occupation numbers of the M active molecular orbitals {φ_l}, where the components sum to the total number of active electrons. Similarly, an occupation-like vector

n^DO_fi = (|〈ϕ^DO_fi|φ₁〉|, |〈ϕ^DO_fi|φ₂〉|,…,|〈ϕ^DO_fi|φ_M〉|) (5)

may be defined for the normalized DO, which carries information about the contributions of different active orbitals {φ_l} to the photo-electron prior to the ionization, where the components instead sum to one. In other words, in a description accounting for electron correlation, the normalized DO corresponds to a quasiparticle, with a wave function being a superposition of initial state active molecular orbitals. Due to electron correlation (i.e. multi-configurational character of the initial and/or final states), ionization may additionally be accompanied by electronic shake-up (and shake-down) excitations in the molecular system as expressed in the residual occupation vector

n^res_fi = n^N−1_f + n^DO_fi − n^N_i. (6)

In a frozen-orbital approximation, the residual occupation is the zero vector for main lines (single-electron ionization). In contrast, for shake-up transitions it contains the occupation change due to the electronic excitations accompanying one-electron ionization. In the present case, with a multi-configurational self-consistent field method, both the DO and residual occupations are additionally affected by the orbital relaxation upon photo-ionization, i.e. the basis of orbitals {φ_l} may differ for the initial and final states. Consequently, occupation number analysis is complicated by the possible differences in orbital bases for the I₃⁻ and I₃ species. As shown below, this effect is mainly seen for the asymmetric geometry.

3 Results and discussion

3.1 Comparison to experimental spectra

In Fig. 2(a), the spectra of the symmetric and asymmetric geometries simulated at the RASPT2 level are compared to the reported experimental I₃⁻ 4d signal in EtOH solution.¹¹ Firstly, comparison of the symmetric geometry and the experiment shows that the simulation protocol accurately reproduces both the main and shake-up features. Secondly, comparison of the XPS for symmetric and asymmetric geometries indicates the influence of solvent-induced nuclear asymmetry: while the peak positions are quite similar for both geometries, the asymmetry manifests itself in the changes in shape of the main features and the increased shake-up intensity. The spectral features are assigned and the observed trends are rationalized through occupation number analysis in Section 3.2.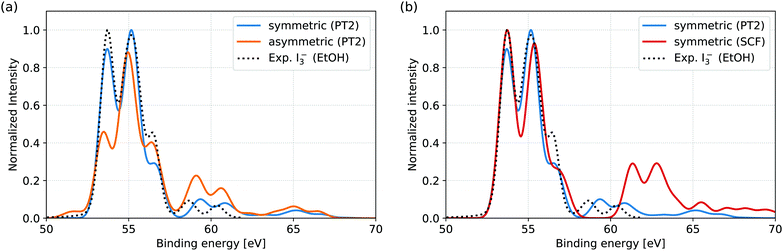

Fig. 2 Comparison of simulated XPS spectra to experimental reference of I₃⁻ in EtOH solution. The experimental spectrum represents the isolated I₃⁻ 4d signal, obtained after subtraction of the Li⁺ 1s counter ion signal from the total measured spectrum.¹¹ (a) RASPT2 level simulations for the symmetric and asymmetric geometries. The experimental spectrum is well reproduced from the symmetric geometry, both for main lines (from 50 eV to 57.5 eV) and shake-up features (above 57.5 eV). In comparison, the asymmetric geometry results in both altered main line spectral shape and appreciably increased shake-up intensities. Note that the smaller energy range of the measurement (49.1 eV to 61.8 eV) excludes some of the features (near 65 eV) found in the simulations. (b) Comparison of RASPT2 and RASSCF level simulations for the symmetric geometry. While the main line features are very similar for the two computational levels, the intensity of the shake-up features and their energy splitting from the main features are both clearly overestimated at RASSCF level.

In the available experimental studies for EtOH and aqueous solutions aiming at the analysis of the main signal,¹¹ Li⁺ was used as a counter ion. As the Li 1s direct ionization spectrally overlaps with the I₃⁻ 4d shake-up features, the Li⁺ 1s signal had to be subtracted from the total measured spectrum to obtain the I 4d signal, as presented for EtOH in Fig. 2. In aqueous solution, further subtraction of I⁻ and I₂(g) signal components was also necessary. This leaves too large uncertainties for a quantitative comparison, as indicated by the highly differing spectra obtained through different subtraction schemes.¹¹ We therefore refrain from direct comparison of our simulations to aqueous solution and hope that potential future experiments, aimed also at shake-up analysis, may be performed under more stable circumstances enabled by, e.g., a different choice of counter ion and I₂/I⁻ ratio.

For comparison to the RASPT2 results, XPS spectra were also simulated directly from the RASSCF electronic states; the results for the symmetric geometry are shown in Fig. 2(a). While the main features of the spectra are nearly identical at the two levels of theory, the shake-up features are highly overestimated both in terms of intensity and energetic distance from the main features. The effect can therefore be ascribed to the limited account for electron correlation provided by the active space. However, the current RASSCF calculations cannot be straightforwardly improved through inclusion of further valence orbitals, due to the already high computational cost of the setup with 15 × 4d core-orbitals that is necessary to describe the XPS process. The accurate simulation and analysis of shake-up features is thereby directly enabled by the multi-configurational second order perturbation theory and would not be possible at reduced computational level.

3.2 XPS assignment and occupation number analysis

The XPS features obtained at RASPT2 level for the symmetric and asymmetric geometry are assigned and rationalized through occupation number analysis, as visualized in Fig. 3. The DO (n^DO_fi) and residual occupations (n^res_fi) (see eqn (6)) are shown in the panels in the left (a and c) and right (b and d) columns, respectively. Upper row of panels (a and b) corresponds to the symmetric and lower row (c and d) to the asymmetric geometries. In each panel, the respective occupation vector for a particular transition energy (x-axis) represents a vertical slice. Different segments of these slices (y-axis) correspond to the active molecular orbitals.

Fig. 3 Occupation number analysis of the multi-state RASTP2 natural orbitals for main ionization and shake-up transitions in the I₃⁻ 4d XPS spectra. DO (n^DO_fi) and residual (n^res_fi) occupation numbers (see eqn (6)) are given in the left (a and c) and right (b and d) columns of panels, respectively. Rows of panels correspond to the symmetric (upper, a and b) and asymmetric (lower, c and d) geometries. In each panel, the respective occupation vector for a particular transition energy (x-axis) represents a vertical slice. Different segments of these slices (y-axis) correspond to the active molecular orbitals. Occupation numbers are only shown for transitions with intensities larger than 0.05 of the most intense transition to filter out a large number of spectroscopically irrelevant transitions. The occupation numbers have been convoluted along the binding energy axis in the same way as the spectral intensities to facilitate visual comparison. For each panel the occupation numbers were subsequently renormalized to a range of −1 to 1. The lower part of each panel shows the occupation numbers averaged over the different orbital types as compared to the normalized XPS spectrum (dashed lines), thereby indicating the contributions from the different orbital types.

Important for the analysis of spectral changes is to distinguish between different types of orbitals. The 15 × 4d orbitals can be grouped together based on their atomic site localization, with representative examples shown in Fig. 1. We denote them as 10 × central 4d(c) and 5 × terminal 4d(t) for the symmetric geometry. For the asymmetric geometry there are instead 5 × ionic orbitals 4d(i) localized on I⁻, and 5 × central 4d(c) and 5 × terminal 4d(t) orbitals of I₂. Crucial for the current work is also an understanding of shake-up effects due to 5p → 5p valence excitations. Three combinations of symmetrized 5p orbitals are present for the symmetric geometry, which we denote as bonding 5σp_z(u), non-bonding 5np_z(g), and anti-bonding 5σ*p_z(u). Note that the inversion symmetry parity labels ‘g’ and ‘u’ are only applicable for the symmetric geometry. For the asymmetric geometry, the 5p_z orbitals instead form a non-bonding orbital 5np_z(i) on the I⁻ ion, and the bonding 5σp_z and anti-bonding 5σ*p_z combinations for the I₂ moiety.

For the symmetric geometry, the main features of the 4d spectrum can be assigned to ionization from orbitals localized mainly on either the terminal 4d(t) or central 4d(c) sites in accordance with previous calculations.^11,12 Each type of orbital gives rise to two features separated by spin–orbit splitting of 1.6 eV between the 4d_3/2 and 4d_5/2 levels, seen as two parallel vertical lines in the occupations (Fig. 3a) near −53.6 eV and −55.2 eV (terminal) and, respectively, near −55.1 eV and −56.7 eV (central). The overlap of transitions near −55 eV gives effectively rise to three main features in the spectrum. Further, two distinct shake-up features are found near −59.3 eV and −60.8 eV. As can be seen from the DO occupations (Fig. 3a), only ionization from the terminal sites is involved in these transitions; their intrinsic energy splitting is the same spin–orbit splitting as for the main features, while their distance from the main peaks is the result of the 5np_z(g) (HOMO) to 5σ*p_z(u) (LUMO) shake-up excitation that can be confidently assigned from the clear transfer of occupation between these two orbitals in the associated residual occupations (Fig. 3b). The assignment can be rationalized through an inversion-symmetry argument previously given for the I 3d XPS spectrum of triiodide by Arbman et al.²⁶ that emphasizes the crucial impact of nuclear and electronic symmetry on shake-up features: shake-up excitation from gerade to ungerade orbitals is symmetry forbidden to occur together with ionization from central site orbitals, due to their gerade symmetry. The shake-up excitation is, however, allowed in combination with core-ionization at the terminal sites, as localization of the core-hole to either terminal site breaks the electronic symmetry in the final state. Shake-up features associated with central site ionization are instead seen at much lower intensity near −65.1 eV and −66.7 eV, i.e. at energies associated with the 5σp_z(u) (HOMO−4) to 5σ*p_z(u) (LUMO) excitation of parity-conserving ungerade to ungerade character.

Main feature assignments at the asymmetric geometry are also well described by the previous grouping of 4d orbitals. Assignment from the DO occupations (Fig. 3c) evidences dominant photo-ionization from the ionic site 4d(i) at 1.3 eV to 2.0 eV higher (−53.4 eV and −55.0 eV) rather than from the terminal 4d(t) (−54.8 eV and −56.3 eV) and central site 4d(c) (−55.4 eV and 56.9 eV), as explained by localization of surplus negative charge on the I⁻ site.^11,12 The single exception is a weak feature (less than 0.05 of maximal intensity) near −51.6 eV, ascribed to ionization from the central site 4d(c), rationalized in ESI,† Section S2.3. We note that while the characters and the order of the 5p_z orbitals are essentially preserved upon ionization in the symmetric geometry, this is not the case for the asymmetric geometry. Hence, we conclude that the frozen orbital approximation (initially assumed for occupation number analysis) is clearly violated. This is a crucial aspect for the assignment of the shake-up excitations. As can be seen from the full set of orbitals for both the I₃⁻ and I₃ species shown in the ESI,† Section S1 and Fig. S3, the ionic 5np_z(i) (HOMO) and bonding 5σp_z (HOMO−7) orbitals permute their order, and the ionic orbital relaxes from an anti-bonding to bonding character towards the I₂ part, upon photo-ionization. This type of difference in orbital bases invalidates a straightforward comparison of initial and final states, and thereby makes simple characterization of shake-ups transitions in terms of e.g. HOMO, LUMO, etc impossible. The effect is clearly seen in the residual occupations (Fig. 3d), with strong contributions present even within the nominal main peaks of the spectrum. Nevertheless, the intense shake-up features near −59.0 eV and −60.6 eV can be clearly associated with ionization from all three sites, based on their DO occupations (Fig. 3c), which are expressed exclusively in the initial state orbital basis. Thus, the symmetry limitations introduced for these features in the symmetric geometry are lifted, which directly explains their increased absolute intensity.

Based on comparison and rationalization of the symmetric and asymmetric spectra, it is clear that the degree of nuclear asymmetry is directly reflected in the relative intensity of main and shake-up features: integrating the XPS intensities between −50 eV to −57.5 eV (main features) and, respectively, −57.5 eV to −62 eV (shake-up features) one obtains the two highly different ratios of 9.6% for shake-up-to-main intensity ratio in the symmetric spectrum and 24.2% in the asymmetric spectrum. This theoretical prediction thus suggests a single scalar observable evidencing solvent-induced nuclear asymmetry in the I₃⁻ ion. It could be conveniently extracted from experimentally measured 4d XPS spectra given an appropriate choice of counter ion. This simplifies the analysis otherwise often based on a complete comparison of spectral features.

4 Conclusion

In summary, our RASPT2 calculations combined with a DO formalism can accurately reproduce I₃⁻ 4d XPS spectra, which allows us to predict the influence of nuclear asymmetry on XPS intensities and, in particular, shake-up features. Based on an analysis of natural orbital occupation numbers, we assign an increased shake-up intensity upon asymmetric stretching to result from the break-down of inversion-symmetry dependent selection rules for XPS transitions. The ratio of shake-up-to-main feature intensities could thereby serve as a simple scalar quantity to measure nuclear asymmetry in I₃⁻ with 4d XPS. This example demonstrates how the high accuracy of RASPT2 calculations can be utilized for theoretical predictions of XPS spectra, and motivates future experimental measurements of I₃⁻ in solution to further elucidate the influence of solvent-induced symmetry breaking.

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

JN and MO acknowledge financial support from the Helmholtz Virtual Institute VI419 “Dynamic Pathways in Multidimensional Landscapes”. MO also acknowledges financial support from the Swedish Research Council (Contract 2015-03956) and the Swedish Energy Agency (Contract 2017-006797). SIB acknowledges financial support from Deutsche Forschungsgemeinschaft (Grant No. BO 4915/1-1). We thank Ida Josefsson for stimulating and productive discussions.

References

1. K. Siegbahn, C. Nordling and A. Fahlman, ESCA, atomic, molecular and solid state structure studied by means of electron spectroscopy, Almqvist and wiksell technical report, 1967.
2. B. Winter and M. Faubel, Chem. Rev., 2006, 106, 1176–1211.
3. R. Golnak, S. I. Bokarev, R. Seidel, J. Xiao, G. Grell, K. Atak, I. Unger, S. Thürmer, S. G. Aziz, O. Kühn, B. Winter and E. F. Aziz, Sci. Rep., 2016, 6, 24659.
4. O. Björneholm, M. H. Hansen, A. Hodgson, L.-M. Liu, D. T. Limmer, A. Michaelides, P. Pedevilla, J. Rossmeisl, H. Shen, G. Tocci, E. Tyrode, M.-M. Walz, J. Werner and H. Bluhm, Chem. Rev., 2016, 116, 7698–7726.
5. A. E. Johnson and A. B. Myers, J. Phys. Chem., 1996, 100, 7778–7788.
6. K. H. Kim, J. H. Lee, J. Kim, S. Nozawa, T. Sato, A. Tomita, K. Ichiyanagi, H. Ki, J. Kim, S.-i. Adachi and H. Ihee, Phys. Rev. Lett., 2013, 110, 165505.
7. S. K. Eriksson, I. Josefsson, N. Ottosson, G. Öhrwall, O. Björneholm, H. Siegbahn, A. Hagfeldt, M. Odelius and H. Rensmo, J. Phys. Chem. B, 2014, 118, 3164–3174.
8. C. Margulis, D. Coker and R. Lynden-Bell, Chem. Phys. Lett., 2001, 341, 557–560.
9. F. S. Zhang and R. M. Lynden-Bell, Phys. Rev. Lett., 2003, 90, 185505.
10. C. Margulis, D. Coker and R. Lynden-Bell, J. Chem. Phys., 2001, 114, 367–376.
11. I. Josefsson, S. K. Eriksson, N. Ottosson, G. Öhrwall, H. Siegbahn, A. Hagfeldt, H. Rensmo, O. Björneholm and M. Odelius, Phys. Chem. Chem. Phys., 2013, 15, 20189–20196.
12. N. K. Jena, I. Josefsson, S. K. Eriksson, A. Hagfeldt, H. Siegbahn, O. Björneholm, H. Rensmo and M. Odelius, Chem. – Eur. J., 2015, 21, 4049–4055.
13. G. Grell, S. I. Bokarev, B. Winter, R. Seidel, E. F. Aziz, S. G. Aziz and O. Kühn, J. Chem. Phys., 2015, 143, 074104.
14. P. A. Malmqvist, A. Rendell and B. O. Roos, J. Phys. Chem., 1990, 94, 5477–5482.
15. P. A. Malmqvist, K. Pierloot, A. R. M. Shahi, C. J. Cramer and L. Gagliardi, J. Chem. Phys., 2008, 128, 204109.
16. F. Aquilante, J. Autschbach, R. K. Carlson, L. F. Chibotaru, M. G. Delcey, L. De Vico, I. Fdez Galván, N. Ferré, L. M. Frutos, L. Gagliardi, M. Garavelli, A. Giussani, C. E. Hoyer, G. Li Manni, H. Lischka, D. Ma, P. Å. Malmqvist, T. Müller, A. Nenov, M. Olivucci, T. B. Pedersen, D. Peng, F. Plasser, B. Pritchard, M. Reiher, I. Rivalta, I. Schapiro, J. Segarra-Martí, M. Stenrup, D. G. Truhlar, L. Ungur, A. Valentini, S. Vancoillie, V. Veryazov, V. P. Vysotskiy, O. Weingart, F. Zapata and R. Lindh, J. Comput. Chem., 2016, 37, 506–541.
17. M. Douglas and N. M. Kroll, Ann. Phys., 1974, 82, 89–155.
18. B. A. Hess, Phys. Rev. A: At., Mol., Opt. Phys., 1986, 33, 3742–3748.
19. B. O. Roos, R. Lindh, P. Å. Malmqvist, V. Veryazov and P. O. Widmark, J. Phys. Chem. A, 2004, 108, 2851–2858.
20. P.-Å. Malmqvist and B. O. Roos, Chem. Phys. Lett., 1989, 155, 189–194.
21. P. Å. Malmqvist, B. O. Roos and B. Schimmelpfennig, Chem. Phys. Lett., 2002, 357, 230–240.
22. B. A. Hess, C. M. Marian, U. Wahlgren and O. Gropen, Chem. Phys. Lett., 1996, 251, 365–371.
23. F. Aquilante, T. B. Pedersen and R. Lindh, J. Chem. Phys., 2007, 126, 194106.
24. F. Aquilante, P.-Å. Malmqvist, T. B. Pedersen, A. Ghosh and B. O. Roos, J. Chem. Theory Comput., 2008, 4, 694–702.
25. J. Boström, M. G. Delcey, F. Aquilante, L. Serrano-Andrés, T. B. Pedersen and R. Lindh, J. Chem. Theory Comput., 2010, 6, 747–754.
26. M. Arbman, S. Holmberg, M. Lundholm, H. Siegbahn, O. Gropen and U. Wahlgren, Chem. Phys., 1983, 81, 113–119.

---

Footnote

† Electronic supplementary information (ESI) available: Motivation of sudden approximation via ezDyson 3.0 integration, extended definition of occupation numbers, multiplicity-decomposed spectrum, and the full set of relevant molecular orbitals. See DOI: 10.1039/c8cp02530d

---