Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Chemical kinetics in an atmospheric pressure helium plasma containing humidity†
Sandra
Schröter
 *a,
Apiwat
Wijaikhum‡
*a,
Apiwat
Wijaikhum‡
 a,
Andrew R.
Gibson
a,
Andrew R.
Gibson
 ab,
Andrew
West§
ab,
Andrew
West§
 a,
Helen L.
Davies
a,
Helen L.
Davies
 ac,
Nicolas
Minesi¶
a,
James
Dedrick
ac,
Nicolas
Minesi¶
a,
James
Dedrick
 a,
Erik
Wagenaars
a,
Erik
Wagenaars
 a,
Nelson
de Oliveira
d,
Laurent
Nahon
d,
Mark J.
Kushner
a,
Nelson
de Oliveira
d,
Laurent
Nahon
d,
Mark J.
Kushner
 e,
Jean-Paul
Booth
e,
Jean-Paul
Booth
 b,
Kari
Niemi
b,
Kari
Niemi
 a,
Timo
Gans
a,
Timo
Gans
 a and
Deborah
O'Connell
a and
Deborah
O'Connell
 a
a
aYork Plasma Institute, Department of Physics, University of York, Heslington, York YO10 5DD, UK. E-mail: sandra.schroeter@york.ac.uk
bLPP, CNRS, Ecole Polytechnique, UPMC Univ. Paris-Sud, Observatoire de Paris, Université Paris-Saclay, Sorbonne Universités, PSL Research University, 91128 Palaiseau, France
cCentre of Immunology and Infection, Department of Biology and Hull York Medical School, University of York, Heslington, York YO10 5DD, UK
dSynchrotron Soleil, l'Orme des Merisiers, St. Aubin BP 48, 91192 Gif sur Yvette Cedex, France
eDepartment of Electrical Engineering and Computer Science, University of Michigan, 1301 Beal Ave., Ann Arbor, Michigan 48109-2122, USA
First published on 13th September 2018
Abstract
Atmospheric pressure plasmas are sources of biologically active oxygen and nitrogen species, which makes them potentially suitable for the use as biomedical devices. Here, experiments and simulations are combined to investigate the formation of the key reactive oxygen species, atomic oxygen (O) and hydroxyl radicals (OH), in a radio-frequency driven atmospheric pressure plasma jet operated in humidified helium. Vacuum ultra-violet high-resolution Fourier-transform absorption spectroscopy and ultra-violet broad-band absorption spectroscopy are used to measure absolute densities of O and OH. These densities increase with increasing H2O content in the feed gas, and approach saturation values at higher admixtures on the order of 3 × 1014 cm−3 for OH and 3 × 1013 cm−3 for O. Experimental results are used to benchmark densities obtained from zero-dimensional plasma chemical kinetics simulations, which reveal the dominant formation pathways. At low humidity content, O is formed from OH+ by proton transfer to H2O, which also initiates the formation of large cluster ions. At higher humidity content, O is created by reactions between OH radicals, and lost by recombination with OH. OH is produced mainly from H2O+ by proton transfer to H2O and by electron impact dissociation of H2O. It is lost by reactions with other OH molecules to form either H2O + O or H2O2. Formation pathways change as a function of humidity content and position in the plasma channel. The understanding of the chemical kinetics of O and OH gained in this work will help in the development of plasma tailoring strategies to optimise their densities in applications.
1 Introduction
The interaction of non-thermal atmospheric pressure plasmas (APPs) with biological matter and their potential applications as biomedical devices1–4 are currently a topic of significant interest. APPs have been shown to be effective in many different areas of biomedicine, such as sterilization,5–7 cancer treatment,8–12 and wound healing,13–15 and have recently been identified as potential triggers of beneficial immune responses.16 First trials on patients confirm the effectiveness of APPs.13,17,18 APPs may offer advantages compared to conventional therapeutics due to their typically small dimensions, offering the possibility of locally confined treatment, low production cost, and the potential to tailor sources for specific applications.A key question in plasma interactions with biological matter is the role played by plasma produced reactive species (RS). RS are known to interact with cells and their membranes, and often serve as signaling agents in cell metabolism.19,20 They can also cause severe damage to cells at high concentrations.19,21
For APPs to fulfil their potential in any biomedical application, a full characterization of the sources used to produce them is necessary, including the quantification of RS produced. Reactive oxygen and nitrogen species (RONS), such as atomic oxygen and nitrogen (O and N), ozone (O3), excited states of molecular oxygen (e.g. O2(a 1Δ)), or nitric oxides, have previously been quantified both experimentally and numerically in O2 and N2 containing plasmas.22–28 Here, the production of RS in an enclosed APP operating in helium with small contents of humidity is investigated. Water is typically present in the direct vicinity of biological material, and can easily enter the gas phase via evaporation. Therefore, RS produced from water vapor can be created during the treatment of the material when plasmas are applied. Water is also usually present as a feed gas impurity.29 Therefore, the investigation of RS directly produced from water vapor, such as O and the hydroxyl radical OH, is of interest for biomedical applications. These species can act as precursors for longer-lived species such as hydrogen peroxide (H2O2), an important signaling agent in cells,19,30 and O3. In high concentrations both of these species can have toxic effects on biological material.
The quantification of RS in APPs represents a challenge for diagnostics based on optical emission from excited states, since the plasma emission is strongly quenched by the ambient gas due to the high pressure. Laser Induced Fluorescence (LIF) and Two-photon Absorption LIF (TALIF) have been previously used to detect species such as O and OH produced from water vapor.31–34 However, in order to accurately predict the effect of quenching using these techniques at atmospheric pressure, the densities of all potential quenching particles are needed. This is increasingly challenging in complex gas mixtures and in regions with gradual gas mixing, like the plasma effluent. These techniques also rely on quenching rate coefficients for investigated species with all possible quenchers, which for some cases, particularly quenching involving water molecules, are only poorly known. The implementation of faster laser systems such as picosecond or femtosecond lasers35–37 can help to quantify the effect of these quenching processes. In addition to accounting for the effects of quenching to obtain absolute density measurements using TALIF, an additional calibration measurement involving a gas with a known quantity is typically needed. An alternative diagnostic technique, which is independent of collisional quenching, is mass spectrometry. This technique has recently been used to detect RS such as OH and H2O2 produced from water vapor in the plasma effluent.38 Similar to LIF and TALIF, this technique requires a calibration measurement to obtain absolute species densities. Mass spectrometry has also been used to detect high order protonated water clusters39,40 produced in APPs. Species deposited in a liquid by plasma treatment are sometimes investigated by means of absorption spectroscopy in the liquid phase, and electron paramagnetic resonance spectroscopy.41,42 However, to calculate gas-phase densities from liquid-phase densities, usually a calibration is required.
An established optical diagnostic technique for the quantification of OH in the gas-phase is ultra-violet (UV) Absorption Spectroscopy (AS),34,43–45 which is independent of collisional quenching and does not require an additional calibration measurement. However, measuring ground state densities of atomic species produced in water-containing plasmas, such as O, is challenging using AS since the energy gaps between the ground and excited states of the atoms are large. Therefore, the required excitation wavelengths typically lie in the vacuum ultra-violet (VUV) spectral range, which is strongly absorbed by air. However, atomic species, in particular O and N, have previously been quantified in an APP using synchrotron radiation and a spectrometer with an ultra-high spectral resolution, so-called VUV high-resolution Fourier-Transform Absorption Spectroscopy (VUV-FTAS).22,23
In this work, we combine VUV-FTAS and UV broad-band AS (UV-BBAS) to determine absolute densities of gas-phase O and OH in a radio-frequency APP jet operated in helium (He) for different values of humidity up to 1.3%. We combine the experimental investigations with zero-dimensional, plug-flow plasma simulations to model the chemical kinetics in the source. These models are commonly used to study properties of atmospheric pressure plasmas.46–51 The role of humidity on the plasma chemistry in APPs has been subject of numerical investigations in the past,48,52–54 that have established the baseline understanding of these systems. We build upon these prior works by comparison of modeling results to experiments performed for the same conditions. Species densities are measured and simulated mainly in the plasma bulk, to validate the reaction mechanism. The resulting reaction mechanism can then be used to investigate important formation pathways for different RS, and to predict additional species densities that are difficult to measure. In many applications, reactive species exit the plasma source into ambient air where the chemical kinetics will differ from the active plasma region. This transition is not investigated here, but the validated reaction mechanism constructed in this work will act as a base to be built upon for future studies in this area.
2 Experimental setup
2.1 Atmospheric pressure plasma jet
The production of atomic oxygen (O), and hydroxyl radicals (OH), in an atmospheric pressure plasma jet (APPJ) operating in 5 slm helium (either grade 4.6 with 25 ppm N2 and 7 ppm O2 impurities, or grade 5 with 3 ppm H2O and 2 ppm O2 impurities) with water vapor (H2O) admixtures is investigated. The plasma jet used in this work is shown in Fig. 1 and is the same as described by Dedrick et al.23 The jet has a plane-parallel electrode configuration. One electrode with an area of 2.4 × 0.86 cm2 is powered by a sinusoidal voltage at a frequency of 13.56 MHz while the other electrode, which is the housing of the source, is grounded. Powered and grounded electrodes are separated by 0.1 cm, keeping the critical dimensions and operating parameters close to the ‘COST Reference Microplasma Jet’,55 but with a smaller surface-to-volume ratio (22 cm−1 here instead of 40 cm−1 for the ‘COST Reference Microplasma Jet’). An impedance matching network unit (L-configuration) is used to optimise the power coupled into the plasma. The applied voltage across the gap is monitored using a high-voltage probe. A list with the equipment for the power coupling and voltage monitoring can be found in Appendix B.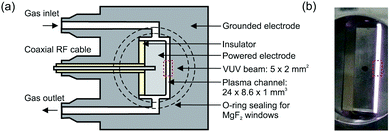 | ||
| Fig. 1 (a) Schematic cross-section and (b) photograph of the plasma source. The perpendicular orientation of the synchrotron vacuum ultraviolet (VUV) beam with respect to the plasma channel is indicated by the dashed rectangle. Images taken from Dedrick et al.,23 under a Creative Commons Attribution 3.0 licence (https://creativecommons.org/licenses/by/3.0/). | ||
We generally conduct experiments at a fixed generator power. For measurements of OH, we set the generator power close to the arcing point of the plasma in pure helium, which is independent of the generator power when using different generators and which typically occurs around 520 ± 10 Vpp. Starting at this point also maximises the measurement range with respect to water content. The water content is varied while keeping the settings on the generator constant. The implications of this on the coupled power to the plasma will be further discussed in Section 2.4. At higher voltages, the plasma tends to extend around the powered electrode when operated in pure He, and transitions from a homogeneous glow-like discharge into a constricted “arc” mode at the electrode edges, which can damage the source.
For the O measurements, the source is operated in a vacuum vessel, with limited options for visually identifying the plasma mode through a transparent vacuum flange. In this case measurements are carried out at a lower voltage of 470 Vpp to avoid the ‘constricted mode’ and related damage of the electrodes.
For the spatially resolved measurement of OH (presented in Section 4.1), a different plasma source, as described elsewhere,22 has been used. It utilises the same design concept, i.e. the same gap size of 1 mm, but a slightly larger electrode area of (1.1 × 3) cm2, compared to the source described earlier. Since the surface-to-volume ratios for both designs are very similar, we assume the RS production to be comparable under similar operating conditions (gas flow, power density).
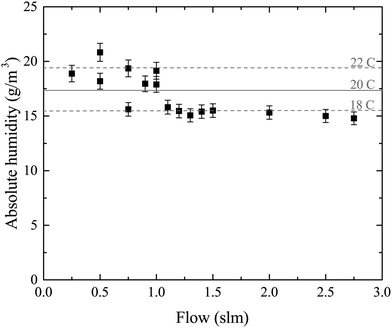
Water vapor is admixed into the He flow using two mass flow controllers and a homemade bubbler, which consists of a domed glass adapter (Biallec GmbH) clamped to a KF40 flange. Two stainless steel pipes welded to the flange provide gas in- and out-lets. Both mass flow controllers are fed with dry He, while the outlet flow of one controller passes through the bubbler before being mixed with the other. By changing the ratio of the humidified to the dry He flow, the water vapor content of the total gas flow can be regulated.34,43,45 With the humidity level in the He flow leaving the bubbler being saturated (see below), the vapor pressure 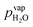 can be calculated using the semi-empirical expression given below.56 The total amount of water in the vapor phase can then be calculated using the vapor pressure of H2O (in bar) and the flow rate of the He through the bubbler FbubblerHe, as described in ref. 34:
can be calculated using the semi-empirical expression given below.56 The total amount of water in the vapor phase can then be calculated using the vapor pressure of H2O (in bar) and the flow rate of the He through the bubbler FbubblerHe, as described in ref. 34:
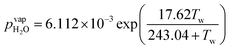 | (1) |
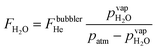 | (2) |
2.2 VUV high-resolution Fourier-transform absorption spectroscopy
Absolute line-averaged O atom ground state densities are measured at the DESIRS beamline at the synchrotron SOLEIL,57 with its unique ultra-high resolution VUV Fourier-Transform spectrometer58 able to cover the complete VUV spectral range down to 40 nm with a resolving power (λ/Δλ) of up to 106. The atomic oxygen transition O(2p4 3PJ=2 → 3s 3S1) is investigated in this work.The measurement and analysis procedure is described in detail elsewhere.22 The spectrometer yields a transmission spectrum ST, which includes the convolution of the plasma transmission T (accounting for Doppler and pressure broadening of the corresponding spectral line profile) with the sinc-shaped instrumental function 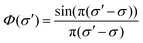 of the FT spectrometer
of the FT spectrometer
| ST(σ′) = S0(σ′)[Φ(σ′ − σ) × T(σ)]. | (3) |
| T(σ) = exp(−A(σ)) = exp(−k(σ)·l), | (4) |
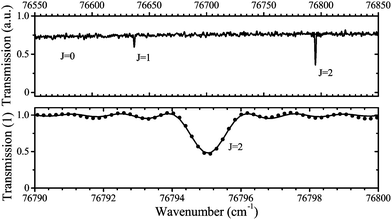
A typical transmission spectrum is presented in Fig. 3. We only evaluate the strongest J = 2 transition of the O(2p4 3PJ=2) triplet from the fine structure split ground state to the first electronically excited state because of the low signal-to-noise ratio of the weaker J = 0, 1 transitions. In order to estimate the total ground state density 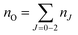 , the Boltzmann factor
, the Boltzmann factor
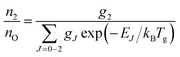 | (5) |
The main uncertainties in this technique lie in the estimated absorption length (uncertainty of 5%), and the accuracy of the transition probability Aik (≤3%60), which are included in the expression for the absorption coefficient in eqn (4). A change of the gas temperature within 10 K influences the Boltzmann factor calculated using eqn (5) by less than 2%. We therefore estimate the systematic error in all VUV-FTAS measurements presented here to be within 10%.
2.3 UV broad-band absorption spectroscopy
Absolute OH densities are measured in the same plasma source using UV-BBAS using two different experimental setups to ensure reproducibility. The experimental setup UV-BBAS I is presented in Fig. 4(a). Light from an ultra-stable broad-band plasma lamp (Energetiq EQ-99) is guided through the middle of the plasma channel and focused on the entrance slit of a 320 mm spectrograph (Isoplane SCT320) with a 2400 grooves per mm grating. Spectra are recorded using a photodiode array detector (Hamamatsu S-3904). The setup is described in detail elsewhere.61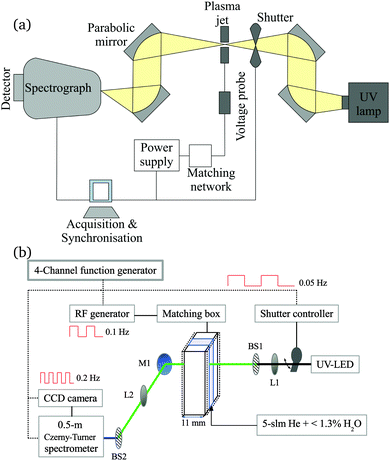 | ||
| Fig. 4 Schematics of the experimental setups used for the UV-BBAS measurements of OH. UV-BBAS I (a) and UV-BBAS II (b). Figure (b) was adapted from Wijaikhum et al.,24 under a Creative Commons Attribution 3.0 licence (https://creativecommons.org/licenses/by/3.0/). | ||
The second setup (UV-BBAS II), which is shown in Fig. 4(b), comprises several different components, mainly a UV LED (UVTOP-305-FW-TO18, Roithner Lasertechnik GmbH) as light source and a CCD camera (Andor Newton 940) in combination with a spectrometer (Andor SR-500i) as detector. For the UV-BBAS II setup, the plasma is mounted on an automated x–z stage, allowing for spatially resolved measurements in the plasma channel. The experimental setup is described in detail elsewhere.24
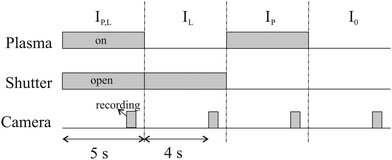
To calculate the absorbance in eqn (4), four signals are required: plasma on and light source on (IP,L), plasma on only (IP), light source on only (IL) and a background with both plasma and light source off (I0). Each signal is integrated over a time period of 50 ms, with a plasma stabilisation time of 4 s beforehand. A schematic showing this sequence is shown in Fig. 5. The plasma transmission T in eqn (4) is calculated as
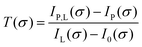 | (6) |
An example spectrum of the OH absorbance A is shown in Fig. 6. Using two setups, an admixture range of 200–13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ppm humidity content is investigated.
000 ppm humidity content is investigated.
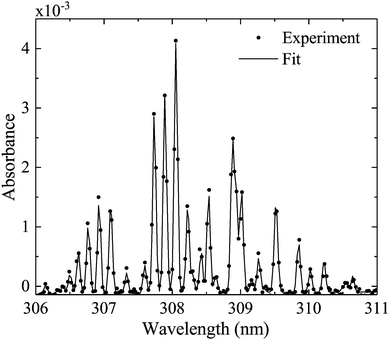
Measured OH rotational absorbance spectra of the transition OH(X 2Πi, υ′ = 0) → OH(A 2Σ+, υ′′ = 0) are fitted using a spectral simulation in order to obtain absolute OH(X 2Πi, υ′ = 0) densities. The fitting programme is based on a calculation of the Einstein coefficients and wavelengths for the individual transitions within the investigated rotation band, as described by Dieke and Crosswhite.62 Based on the selection rules for the total angular momentum J = L ± S and the angular momentum L (without electron spin S = 1/2 for the OH radical), relative intensities are calculated for 12 possible branches, using expressions derived by Earls.63 An experimental value for the radiative lifetime for a rotationless upper state F1(J′′ = 0.5) has been determined as 0.688 μs64 (here, F1 donates the doublet component of the upper state with J = L + 1/2, in accordance with Diecke and Crosswhite62). Therefore, all calculated relative Einstein coefficients can be normalised to this value. Our calculated values are in good agreement with those from Goldman and Gillis.65 As in Dilecce et al.,45 the spectral fitting includes an instrumental function, whose width represents the spectral resolution of the spectrometer, which depends on the pixel size of the detector array, the optical grating and the width of the spectrograph's entrance slit. We assume the instrumental function to be Gaussian. Examples of measured and simulated absorbance spectra are shown in Fig. 6. Here, the instrumental width is 56 pm (UV-BBAS I) or 34 pm (UV-BBAS II), which is much larger than the Doppler (ΔλD (304 K) = 0.098 cm−1 = 0.93 pm) and pressure broadening (estimated as ΔλP (1 atm) = 0.07 cm−1 = 0.66 pm, as in ref. 66). The fitting programme is also used to calculate OH rotational temperatures.
The main systematic uncertainties of UV-BBAS lie in the estimation of the absorption length (5%), and the accuracy of the calculated Einstein coefficients, which we estimate here to be within 10%. For the absorbance measured with the UV-BBAS II setup (featuring the LED), the standard deviation of the noise is in the order of 3 × 10−4, which places a lower limit on the measurable OH density at 3.6 × 1013 cm−3. For the UV-BBAS I setup (featuring the ultra-stable light source), the noise level of the measured absorbance is typically an order of magnitude lower, and therefore disregarded in the uncertainty estimation. The combination of the systematic error and a statistical error of 7% is shown as error bars in the results that follow.
2.4 Determination of plasma power
For accurate comparison between simulation and experiment the rf power dissipated in the plasma is a particularly important. Experimentally, this so-called plasma power is measured by determining current, voltage and phase shift using current (Ion Physics Corp. CM-100-L 1 V/A) and voltage probes (PMK-14KVAC). The probes are installed between the impedance matching unit and the plasma source. The time averaged power P is given by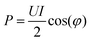 | (7) |
| Pd(I2) = Pon(I2) − Poff(I2) | (8) |
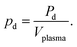 | (9) |
The instrumental phase shift of the measurement system (probes, BNC signaling cables, and digital oscilloscope) is determined using a variable air capacitor with known phase shift (MFJ 282-2018-1). For the calibration measurement, the plasma source with its rf cable to the matching box is replaced by this capacitor.
Current and voltage waveforms are recorded by a fast oscilloscope (LeCroy WaveSurfer10, 10 GS per s sample rate). The voltage and current amplitude as well as the corresponding phase shift are determined by a Fourier analysis of this data. Pd was found to be approximately constant (within 15%) as a function of feed gas water content at a constant generator power and matching settings. The average of Pd over several different water contents is used as an input for the simulations over the whole range of water content. The average value of Pd was determined as 2.8 W (≈14 W cm−3) for the UV-BBAS measurements of OH (at approximately 510 Vpp), and 2.1 W (≈10 W cm−3) for the measurement of O using VUV-FTAS (at approximately 470 Vpp). These values are used as the input for the simulations, unless otherwise stated.
Power measurements are carried out separately from the density measurements using two power generators: coaxial RFG-150-13 (150 W maximum output power, same model as used for the OH measurements using the UV-BBAS II setup), and coaxial RFG-50-13 (50 W maximum output power, smaller range of powers for a better stability). We find a similar average power using these two setups, and that the power stays constant as a function of water content within one measurement set with a standard deviation of all points below 5%. We estimate a total uncertainty of 15% from repetitive measurements. These variations are small enough to not significantly influence measured species densities, particularly for OH, which we found to be only weakly dependent on applied voltage, and therefore power (increase of about 40% when the voltage is increased from 490 to 850 Vpp, not shown here).
3 Plasma simulations
3.1 Model description and reaction mechanism
To better understand the dynamics of reactive species in cold atmospheric pressure plasmas, zero-dimensional plasma chemical kinetics simulations (global models) are often used.51 In this work, experimental results are compared to those obtained using the GlobalKin code as described elsewhere.50 GlobalKin solves the continuity equation for mass conservation for both charged and neutral species, taking into account particle production and loss through gas phase reactions and interactions with surfaces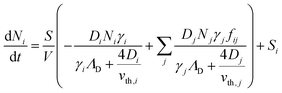 | (10) |
 the surface to volume ratio, ΛD the diffusion length, D the diffusion coefficient, γ the surface sticking coefficient, f the return fraction of species from walls, and Si the source term, which accounts for gas phase production and losses. In addition, the electron energy conservation equation is solved to calculate the electron temperature in the plasma by taking into account the balance of power input and loss of electron energy due to elastic and inelastic collisions with heavy particles
the surface to volume ratio, ΛD the diffusion length, D the diffusion coefficient, γ the surface sticking coefficient, f the return fraction of species from walls, and Si the source term, which accounts for gas phase production and losses. In addition, the electron energy conservation equation is solved to calculate the electron temperature in the plasma by taking into account the balance of power input and loss of electron energy due to elastic and inelastic collisions with heavy particles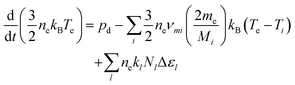 | (11) |
In this work we apply a temporally constant power deposition corresponding to the time averaged power measured in the experiment. For rf APPs the electron heating is strongly modulated in time, leading to a power and electron impact rate coefficients, that vary during the rf cycle.69,70 This effect is not captured in our model. However, Lazzaroni et al.,70 investigated the differences between a conventional global model, using a time averaged power deposition, and one that takes into account time-varying power deposition within the rf period. For their case, using a He/O2 reaction mechanism, the densities of neutral species calculated by the modified model (O, O3, O*, O2*) were typically within a factor of 2 of those from the conventional model. The trends in the results of the two models were similar. Therefore, we expect that neglecting the time-varying power deposition in our model will only lead to a quantitative difference in the results, while the trends should remain valid.
Gas temperatures are self-consistently calculated using the GlobalKin code using50
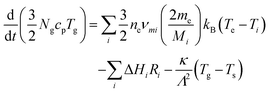 | (12) |
The model incorporates 43 species and 390 reactions. Table 1 contains the species in the mechanism. The plasma reaction mechanism is in Appendix A (Tables 5–8). At the surfaces, it is assumed that most neutral and negatively charged species (except electrons) do not react, while positive ions are neutralised with a probability of 1. The species assumed to react differently are listed in Table 4 in the Appendix A. A detailed discussion of the role of surface interactions in a similar simulation system is given elsewhere.71
| Neutral | Positive | Negative | |
|---|---|---|---|
| He | He, He*, He2* | He+, He2+ | |
| O | O, O(1D), O(1S), O2, O2(a 1Δ), O2(b 1Σ), O3 | O+, O2+, O4+ | O−, O2− |
| H | H, H2 | H− | |
| OH | OH, HO2, H2O, H2O2 | OH+, H2O+(H2O)n=0,1 | OH−, H2O2−, OH−(H2O)n=1–3 |
| H+(H2O)n=1–9 | |||
| O2+(H2O) | |||
| Others | e |
In this work, the model is solved for a channel length of 2.4 cm, with a gas flow rate of 5 slm, which corresponds to a gas velocity of about 11 m s−1. Using a pseudo-1D plug flow, temporally computed densities are converted into spatially dependent quantities. Where species densities are presented as a function of humidity content, densities are extracted from the simulation at the axial centre of the source (at 1.2 cm), which is the position where measurements were made.
From the plasma dimensions, the diffusion length ΛD, a necessary parameter for determining diffusion losses of particles, is calculated as72
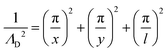 | (13) |
3.2 Pathway analysis
The PumpKin software73 is used to identify the production and destruction pathways for the selected neutral species. The reaction pathway of a species of interest results from (a) analysing the elementary reactions that contribute directly or in subsequence to the formation of this species and selecting the significant ones only, (b) algebraically summing up the formal notations of these reactions, and (c) eliminating shorter-lived species, here the electrons and some ions, to end up with a simplified net reaction. The short-lived species are defined as those with a lifetime shorter than a lifetime set by the user, which we denote as τp. Note, that this so-called net reaction should not be mistaken as an elementary reaction, since it is specific to the choice of eliminated species. This approach is particularly useful for understanding the production and destruction of species which are formed via complex reaction pathways involving a chain of elementary reactions, as opposed to simply one or two.Among the neutral species considered in this work He* and He2* metastables have the shortest effective lifetime. For the pathway analysis, we therefore choose τp to be slightly shorter than the lifetime of these species, which is in accordance with previous work.52Table 2 shows the strong dependence of the simulated lifetime on the humidity admixture for specific plasma conditions. These findings support the conclusion of Niemi et al.,46 that the metastable character of these helium species at high pressure is significantly reduced in the presence of small admixtures or even impurity levels of molecular gases through Penning ionization under atmospheric pressure conditions.
| H2O content (ppm) | He* lifetime (μs) | He2* lifetime (μs) |
|---|---|---|
| 10 | 2.539 | 1.931 |
| 100 | 0.350 | 0.188 |
| 1000 | 0.036 | 0.021 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
0.004 | 0.013 |
4 Results
4.1 OH densities along plasma channel
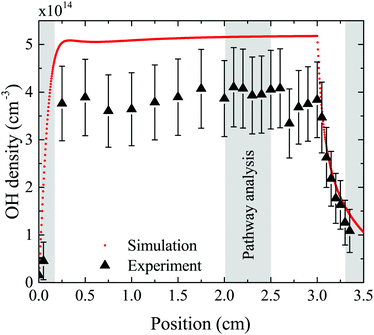
The density of OH along the plasma channel for an intermediate humidity content of 5400 ppm and a plasma power density of 18 W cm−3 is shown in Fig. 7. Experimental results show a rapid increase of the OH density over the first 2 mm of the channel. With increasing distance from the gas inlet the density stays approximately constant between 3.5 × 1014 cm3 and 4.0 × 1014 cm3 up to the end of the channel. A similar trend is also observed in the simulation. Absolute simulated and experimental densities agree well within around 25%, which is likely within the combined uncertainties of experimental data (as shown as error bars in Fig. 7) and simulations. Uncertainties in the simulation results would most likely occur due to uncertainties in used reaction rate coefficients, and considered reaction pathways, and were shown to be within a factor 10 for a He/O2 reaction mechanism under similar plasma conditions.74To gain insight into the dynamics of OH formation, a pathway analysis is performed for the three regions highlighted in Fig. 7, which correspond to the fast build-up of OH at the entrance of the plasma channel (0–0.2 cm), a steady-state region (2–2.5 cm) and the decay of OH in the plasma effluent (3.3–3.5 cm). The dominant production and consumption pathways for OH, averaged over each region, are shown in Fig. 8.
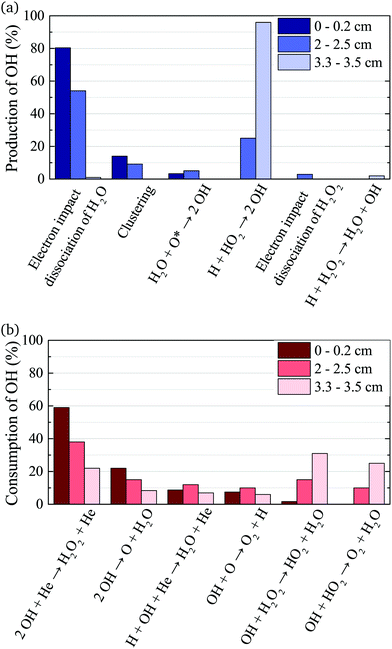 | ||
| Fig. 8 Production (a) and consumption (b) pathways of OH at different positions in the plasma source, as indicated in Fig. 7. | ||
At the entrance of the discharge channel (0–0.2 cm), the gas consists mainly of the initial feed gas mixture plus some rapidly forming species such as ions and electrons. Therefore, the main production reaction for OH is through electron impact with water vapor, either via dissociation or dissociative attachment
| e + H2O → OH + H + e (60%) | (14) |
| e + H2O → OH + H + e (9%) | (15) |
| e + H2O → OH + H− (11%) | (16) |
Another production mechanism for OH is through the formation, and subsequent destruction, of charged water clusters, as was previously identified by Ding and Lieberman.52 The formation of these clusters is typically a multi-step process. For positive clusters, this process usually begins through ionisation of H2O, either through electron impact or Penning ionisation with He*. These water ions then collide with water molecules to form the cluster ion H+(H2O), which accumulates additional water molecules through a series of reactions:
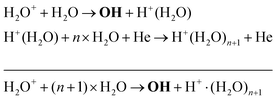 | (17) |
The main consumption pathway for OH in the first 0.2 cm of the jet is the formation of H2O2, and recombination to water through
| 2OH + He → H2O2 + He (59%) | (18) |
| 2OH → H2O + O (22%) | (19) |
| H + OH + He → H2O + He (9%) | (20) |
In the quasi steady state region (2–2.5 cm), the previous pathways still dominate. However, additional species with intermediate lifetimes build up along the channel and begin to play a role in the formation of OH. For example, hydroperoxy radicals (HO2) promote production of OH through reactions with H
| H + HO2 → 2OH (25%) | (21) |
| OH + H2O2 → HO2 + H2O (15%) | (22) |
| OH + HO2 → O2 + H2O (10%) | (23) |
In the afterglow region (3.3–3.5 cm), a rapid decay of OH occurs both in experiment and simulation, as shown in Fig. 7. Short lived species such as ions and electrons recombine rapidly, while metastable species like He* and He2* are consumed through Penning ionization with water before reaching this region. Therefore, the chemistry in the plasma effluent is dominated by intermediate and long lived neutral species, where OH is produced mainly through reactions between H and longer-lived neutral species:
| H + HO2 → 2OH (96%) | (24) |
| H + H2O2 → OH + H2O (2%) | (25) |
4.2 OH densities under varying humidity content
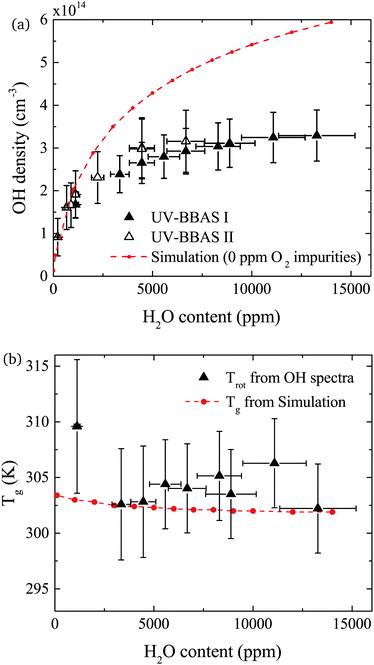
The density of OH measured by UV-BBAS in the centre of the plasma channel (at position 1.2 cm) as a function of the H2O content in the feed gas is shown in Fig. 9(a). The OH density increases sub-linearly with increasing H2O content, as previously observed.34,43 Absolute densities obtained in this work also agree well with results obtained by others.34,43 Absolute OH densities measured with the two different experimental setups agree well within the uncertainties in each measurement.The simulated OH densities at different feed gas humidity contents are shown in Fig. 9(a). In general, good agreement in the trends of experimental and simulation results is observed. Absolute OH densities agree particularly well at low H2O contents <2000 ppm. Towards higher H2O contents, simulated densities are higher than those measured experimentally. The largest difference is a factor 1.8 at the highest H2O content, which is reasonable agreement given the previously mentioned uncertainties.
OH(X) rotational temperatures and gas temperatures calculated using GlobalKin are shown in Fig. 9(b), and found to be in good quantitative agreement with each other. In both experiment and simulations, temperatures stay fairly constant with increasing water content. While in the simulation, a very small decrease of the gas temperature is observed, the experimental data is more scattered, and a clear trend cannot be observed taking into account the uncertainties of the measurement.
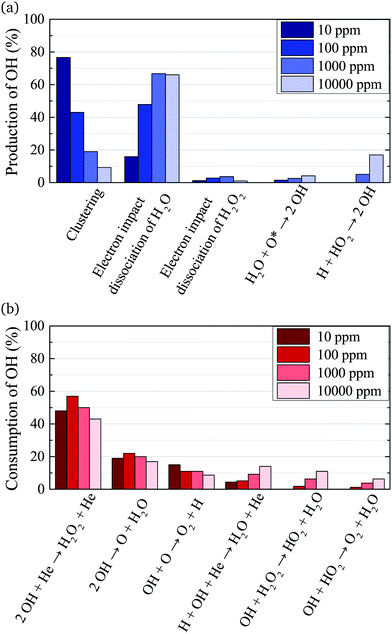
The main production and consumption pathways for OH at different H2O admixtures are shown in Fig. 10. Two production pathways dominate for all H2O admixtures. The dominant pathway for OH production at lower H2O contents is via Penning ionisation of H2O, and subsequent cluster association reactions (eqn (17)). At any stage of the clustering process, the clusters can be destroyed by dissociative recombination with electrons
| e + H+(H2O)n → H + n × H2O | (26) |
OH is mainly consumed by reactions with other OH radicals (eqn (18) and (19)) and O
| OH + O → O2 + H | (27) |
Towards higher water admixtures, the contributions of these reactions to the consumption of OH decrease slightly, and reactions of OH with H, and more slowly forming species such as H2O2 and HO2 become more important.
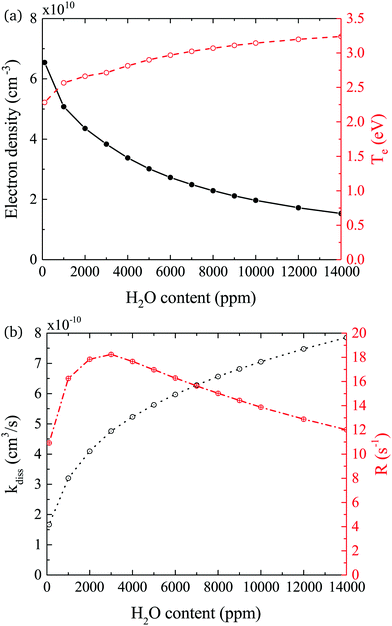
In both experiment and simulation, OH densities increase rapidly with increasing H2O at low H2O content, and less rapidly at high H2O content. The transition between these two regimes occurs at lower H2O content (around 2000 ppm) in the experiment compared to the simulation (around 3000 ppm). This leads to the increasing discrepancy between simulation and experiment at higher H2O contents where the experimental OH densities saturate and the simulated OH densities continue to slowly increase. The reason for this transition is investigated by looking at the most important formation pathways for OH, which are production by electron impact dissociation and dissociative attachment of H2O (eqn (14)–(16)), and consumption via reactions with OH to form H2O2 and H2O (eqn (18) and (19)). As the gas temperature remains relatively constant with changing water content, rate coefficients for consumption of OH also stay approximately constant. The reaction rate coefficient for production of OH is dependent on the electron temperature Te, and the electron density ne. Fig. 11(a) shows the two quantities as a function of humidity content. Te and ne show opposite trends with increasing H2O admixture. Te, which is calculated from balancing the electron energy sources and losses (see eqn (11)), increases with increasing H2O content due to increasing electron energy losses in inelastic collisions with water molecules. For constant power input, the increased electron energy losses and Te are balanced by a decrease in ne with increasing H2O content.
The effect of these changes on the total rate coefficient for dissociation kdiss = k14 + k15 + k16 and the dissociation frequency R = kdissne is shown in Fig. 11(b). Due to the variation in Te, kdiss increases with increasing humidity content, exhibiting a similar trend to the OH densities shown in Fig. 9. Here, the transition from a fast to a slow increase also occurs around 3000 ppm. The dissociation frequency R exhibits a peak at this humidity content, which represents the optimum between the increasing Te and decreasing ne. Thus, the origin of the transition between fast and slow increase in OH density with increasing humidity content is a result of the transition between an increasing dissociation frequency below 3000 ppm H2O to a decreasing dissociation frequency above 3000 ppm H2O. Overall, the dissociation rate R × nH2O, and therefore the OH density, increases over the whole range due to the increasing value of nH2O. Based on this discussion, the differing H2O contents at which the transition occurs in the experiment and simulation may indicate that the rate of electron energy loss with increasing H2O content is misrepresented in the simulation. Another reason for the discrepancy between the simulated and measured trend in OH densities at higher water contents might be due to an additional consumption mechanism for OH, which is not taken into account in this work, such as the population of vibrationally excited states, which would also scale with Te.
4.3 O densities as a function of humidity content
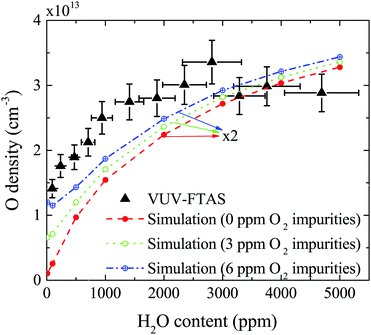
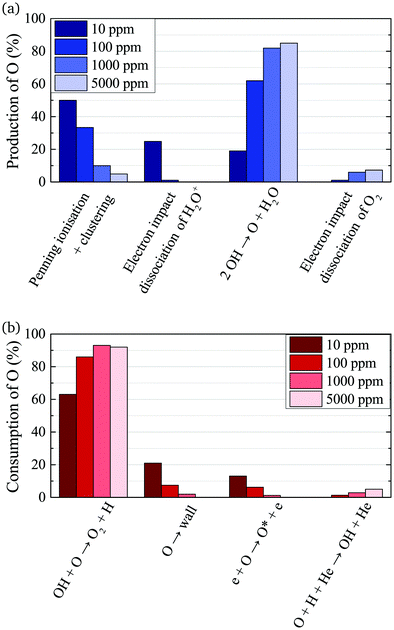
The absolute O density measured by VUV-FTAS in the centre of the discharge (at x = 1.2 cm, triangles) as a function of H2O content in the feed gas is shown in Fig. 12. The O density increases with increasing H2O content and approaches a steady-state value of around 3 × 1013 cm−3. The simulated O density also shows an increase towards higher H2O admixtures, however, the O densities continue to increase more significantly at higher H2O content than the experimental results. This is similar to the case of the OH density discussed earlier. Simulated O densities are around a factor 2 lower than those obtained experimentally. The measured densities agree well with previous measurements in a similar source using two-photon absorption laser induced fluorescence.34A possible explanation for the difference in absolute O densities and trends between the experiment and simulation may be limitations in the global model, particularly the accuracy of the rate coefficients used, as discussed earlier. O is not directly produced from H2O due to electron or heavy particle impact dissociation in significant amounts at the electron temperature of interest. As a result, O must be formed in a process taking at least two steps, meaning that the uncertainties in multiple rate coefficients will play a role in determining the uncertainty in the simulated O density. As a result, the simulated O density is likely to have a larger uncertainty than the simulated OH density, whose dominant formation occurs directly from electron collisions with H2O. As shown in Fig. 13, the dominant production mechanism of O is via recombination of two OH molecules to form H2O and O. At lower H2O contents, O is also formed through processes involving positive ion water clusters:
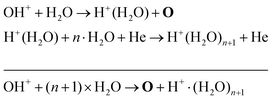 | (28) |
With increasing H2O admixture the formation of O2 is also increased. As a result, electron impact dissociation of O2 becomes a more important production pathway for O:
| e + O2 → 2O + e (6 eV) | (29) |
| e + O2 → O + O(1D) + e (8.4 eV) | (30) |
Where the numbers in brackets represent the electron energy thresholds for these reactions. O is mainly consumed by reactions involving OH forming O2 and H (eqn (27)).
The measured and simulated O densities show an increased discrepancy towards smaller H2O admixtures <1000 ppm. A possible explanation for this might lie in the presence of unintentional air impurities in the experiment, which have been found previously to be able to influence the chemical kinetics in atmospheric pressure plasmas.75–77 For the measurement of O, we use helium with a purity level of 99.999%, whereas the main impurities are H2O (3 ppm) and O2 (2 ppm). Additional small impurities could arise from residual gases in the feed gas line. Simulations for two different non-zero O2 impurity concentrations in the order of typical O2 impurities originating from the feed gas supply are shown in Fig. 12. Particularly at low H2O content, these impurities lead to an increase of O compared to the simulation without O2 added as an impurity. Since the density of O produced from H2O is low, typically a few ppm, even small O2 containing impurities can significantly influence the O density produced in the plasma. At high H2O content, the influence of O2 impurities on the O density is smaller, and the plasma chemistry is dominated by hydrogen containing species.
4.4 Numerical investigation of the production of longer-lived species
The OH density reaches a steady-state value in the simulation well before the end of the plasma channel in both simulation and experiment. Particularly at higher H2O content, this is a result of OH being primarily produced by direct electron impact dissociation of H2O in a one step process (eqn (14)) and is consumed in interactions with other OH molecules. Atomic hydrogen behaves similarly, being produced mainly by electron impact dissociation and consumed via interactions with surfaces,71 both of which occur relatively quickly. However, other species do not reach a steady state within the length of the plasma channel, and instead continuously increase in density up to the outlet of the plasma source. This is particularly true for slowly forming, long-lived species such as O2, H2O2 and H2, as shown in Fig. 14. This finding suggests that the length of the plasma source, or the gas flow rate, and therefore the residence time of the gas, can be used to control the ratio of different species densities by taking advantage of the different timescales required for them to reach steady-state.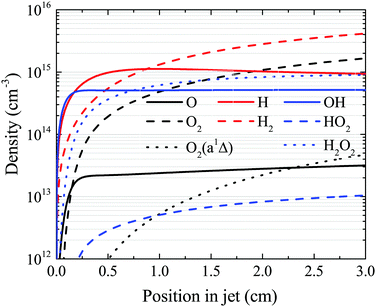 | ||
| Fig. 14 Spatial development for several species of interest as a function of position in the plasma channel, under the same conditions shown in Fig. 7 (18 W cm−3 plasma power, 5400 ppm humidity). | ||
First, we will discuss the formation of O in more detail. The density of O does not reach a steady-state value in the simulation within the plasma channel for most investigated conditions using a He–H2O gas mixture. Long timescales for simulations of atmospheric pressure He–H2O plasmas to reach steady-state have also been found by others.78 This is in contrast to the case where similar sources are operated in He–O2 mixtures.79 In the work described in ref. 79, O densities approach steady-state towards the end of the plasma channel of the AAPPJ. In Fig. 14, O densities are increasing sharply within the first few millimetres of the channel, and then at a lower rate up to the end of the channel. Therefore, O densities follow a similar dependence as the OH densities also shown in Fig. 14. This is not surprising when considering that both the dominant production and consumption pathways are related to OH, i.e. production by reactions of two OH molecules to form H2O and O (eqn (19)), and consumption via collisions with OH to form O2 and H (eqn (27)). The fact that O is still building up within the channel, while OH approaches a steady-state value, is due to the continuous build-up of O2 in the channel, also shown in Fig. 14. Electron impact dissociation of O2 (eqn (29) and (30)) provides an additional formation mechanism for O further into the channel, although eqn (19) and (27) are still the dominant production and consumption pathways for O. Overall, this leads to a slow increase of the O density while the O2 density continues to increase.
The formation of species that reach steady-state on timescales longer than the residence time in the discharge channel are usually comprised of a complex multi-step processes. As an example, we demonstrate the dominant pathways for formation of O2, which is an important precursor for the formation of excited states of O2, such as O2(a 1Δ). Since O2 is a slowly forming species, we look at dominant production and consumption pathways for a longer timescale τp than those previously given in Table 2. The time scale of interest in the simulation is chosen so that only He, H2O, O2, O2(a 1Δ), H2, and H2O2 are treated as long-lived species, in accordance with previous studies.52 The computational lifetimes of the shortest-lived species of these six are listed in Table 3 for different H2O contents.
| H2O content (ppm) | O2(a 1Δ) lifetime (ms) | H2O2 lifetime (ms) |
|---|---|---|
| 100 | 2.78 | 4.38 |
| 1000 | 2.74 | 2.74 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
4.55 | 1.35 |
The two main net production reactions for the formation of molecular oxygen are found to be
| 2H2O → 2H2 + O2 | (31) |
| H2O2 → H2 + O2 | (32) |
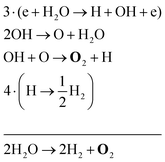 | (33) |
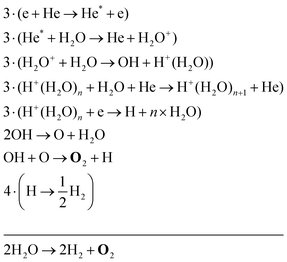 | (34) |
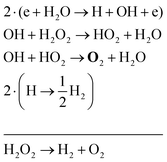 | (35) |
Note that eqn (33) and (34) have the same net production reaction, although the intermediate steps towards the formation of O2 (i.e. the pathway) are different. Eqn (33) starts with the electron impact dissociation of H2O molecules. The reaction of OH with OH and O leads to the formation of O2. The H atoms formed recombine at surfaces to form H2.
Eqn (34) is the same net reaction, however, the step-by-step analysis reveals a different pathway. In this case, H2O molecules are first ionised via Penning ionisation with He*. H2O+ ions then start accumulating more H2O molecules in a clustering process, where OH is produced. Similar to the previous pathways, the reaction of OH with OH and O lead to the formation of O2. The cluster ions produced are consumed by dissociative recombination with electrons, and H, which is formed in that process, is lost by surface recombination. Other pathways exists that involve the formation of clusters, but are not explicitly discussed here.
Eqn (35) has a different net production reaction than the others. In this case, OH produced from electron impact dissociation reacts with H2O2 to form reactive HO2, which then forms O2 during reactions with OH.
5 Conclusions
In this work, the chemical kinetics in an rf atmospheric pressure plasma with humidity are investigated using experimental and numerical techniques. By using this combination, computed species densities are benchmarked against experimental densities. The simulations are then used to reveal the dominant formation pathways of species of interest, here OH and O, and longer lived species such as O2, which is an important precursor for the formation of its excited states, such as O2(a 1Δ). This work provides a detailed understanding of chemical kinetics in the active plasma. In many applications, reactive species will exit the plasma source and transit into an effluent region where they will mix with ambient air, where their chemical kinetics will differ. While this is not considered in this work, the results presented here provide a basis to be built on in future work to understand reactive species kinetics in this transition region.Absolute number densities of O and OH are determined experimentally using VUV high-resolution Fourier-transform absorption spectroscopy, UV broad-band absorption spectroscopy, and numerically by using the 0-D plasma chemical kinetics code GlobalKin.
Absolute OH densities and formation pathways are investigated as a function of position in the discharge. Three different regions can be identified i.e. (a) a strong increase of OH density in the first few millimeters of the plasma channel, (b) a quasi steady-state region, and (c) a rapid drop of OH density in the plasma effluent region. During the fast increase and steady-state regions, OH is mainly produced via fast processes such as electron impact dissociation of H2O, and consumed predominantly via reactions with other OH molecules to form H2O2 or H2O. These relatively simple chemical kinetics make it possible for OH to reach an equilibrium value within the plasma channel.
Other species, whose densities have not been measured, are investigated numerically as a function of position in the plasma channel. Simulation results show that the H density approaches a steady-state value within the plasma channel, similarly to OH as discussed previously, as it is mostly formed directly via electron impact dissociation of water, and consumed at surfaces to form stable H2. However, most other species generated in the He–H2O plasma studied in this work do not reach a steady-state value within the length of the plasma channel due to more complex formation mechanisms. This has been shown using O2 as an example. Therefore, the length of the plasma source could be used as a control parameter to tune the chemical composition of the gas at the end of the plasma jet for applications.
Both OH and O densities are also investigated as a function of the humidity content in the He feed gas. It is found, both in experiments and simulations, that O and OH densities increase non-linearly with increasing feed gas humidity, offering the possibility of tailoring reactive species densities by changing the feed gas composition.
The maximum OH density is on the order of 3–4 × 1014 cm−3 (13–17 ppm). It is found that at very low water content, OH is mainly produced via reactions between H2O+ and water molecules to form OH and protonated water clusters of the form H+·(H2O)n, while electron impact dissociation of H2O becomes an increasingly important production pathway with increasing water content. The main loss channel for OH at all H2O contents is recombination to form H2O2.
The maximum O density on the other hand is found to be in the order of 3 × 1013 cm−3 (1.3 ppm). Recombination of two OH molecules is the most important production process for O at all H2O contents, while at very low water content, OH is also strongly produced via reactions between OH+ and water molecules to form O and protonated water clusters. Since the dominant destruction pathway of O is recombination with OH to form O2 and H, the formation of O is strongly coupled to the OH density in the gas flow. At higher H2O concentrations, electron impact dissociation of accumulated O2 can also contribute to the production of O. It is also found that towards low H2O content, production of O from air impurities in the ppm range originating from the feed gas can increase the O density via direct electron impact dissociation of O2. Towards higher H2O admixtures, this effect becomes less significant due to increased production via collisions involving OH. Therefore, larger amounts of purposely admixed molecules lead to a better control of the plasma properties and reactive species than operating the source with small or no intentional admixtures.
Conflicts of interest
There are no conflicts to declare.Appendix
A. Reaction mechanism
Table 4 shows wall recombination coefficients and return species for the simulations used in this work.Table 5 shows electron impact reactions used in this work. Reaction rate coefficients are either taken from the literature, or calculated by the GlobalKin two-term Boltzmann equation solver. For the latter, reaction rate coefficients are indicated as f(E), and collisional cross sections are taken from the indicated literature. Electron impact cross-sections are taken from several databases, for example He,82,83 or H2O.84 Although not all of the reactions from these databases are included in the plasma-chemical reaction mechanism shown here, they are still accounted for in the Boltzmann solver calculation for the electron energy distribution function and electron transport coefficients. Any other approach to obtain reaction rate coefficients is denoted by footnotes.
| No. | E Thr (eV) | Reaction (rxn) | Ratea,b | Ref. |
|---|---|---|---|---|
| a In m3 s−1 and m6 s−1 for two- and three-body processes, respectively. b f(E) denotes rate coefficients are calculated by the internal GlobalKin two-term Boltzmann equation solver using cross sections obtained from the indicated literature. c Cross sections are calculated from an expression in cited reference. d Calculated assuming a Maxwell distribution function and cross sections from the given reference. e Vibrational excitation cross section included in cross section set for two-term Boltzmann solver. Vibrational states not simulated self-consistently in reaction kinetics. f Rotational excitation cross section included in cross section set for two-term Boltzmann solver. Rotations states not simulated self-consistently in reaction kinetics. g Electronic excitation cross section included in cross section set for two-term Boltzmann solver. This electronic state is not simulated self-consistently in reaction kinetics. h Cross section estimated by shifting and scaling the corresponding cross section for the ground state by the excitation threshold of the excited state. i Born–Bethe fit to data in the cited reference. j Obtained from reverse process by detailed balance. k In the reference reaction rates were calculated using Bolsig+121 and cross sections obtained from the Morgan database122 for a He/H2O plasma. l Cross section assumed to be the same as that for CO. m Value is approximated in reference based on cross section for electron impact dissociation of O2. n Value is estimated in reference. | ||||
| Elastic scattering and momentum transfer | ||||
| 1 | 0.00 | e + He → He + e | f(E) | 82 and 83 |
| 2 | 0.00 | e + H2O → H2O + e | f(E) | 84 and 89 |
| 3 | 0.00 | e + O2 → O2 + e | f(E) | 90 |
| Electron impact excitation and ionisation | ||||
| 4 | 19.80 | e + He → He* + e | f(E) | 82 and 83 |
| 5 | 20.62 | e + He → He* + e | f(E) | 82 and 83 |
| 6 | 24.58 | e + He → He+ + e | f(E) | 82 and 83 |
| 7 | 4.77 | e + He* → He+ + 2e | f(E) | 91 |
| 8 | 3.90 | e + He2* → He2+ + 2e | 2.06 × 10−13e−4.28/Te | 92 |
| 9 | 0.20 | e + H2O → H2O + e | f(E) | 84 |
| 10 | 0.45 | e + H2O → H2O + e | f(E) | 84 |
| 11 | 0.47 | e + H2O → H2O + e | f(E) | 84 |
| 12 | 13.50 | e + H2O → H2O+ + 2e | f(E) | 84 |
| 13 | 13.50 | e + OH → OH+ + 2e | f(E) | 93 |
| 14 | 1.97 | e + O → O(1D) + e | f(E) | 94 |
| 15 | 4.19 | e + O → O(1S) + e | f(E) | 94 |
| 16 | 13.62 | e + O → O+ + 2e | f(E) | 94 |
| 17 | 11.65 | e + O(1D) → O+ + 2e | f(E) | 91 |
| 18 | 9.43 | e + O(1S) → O+ + 2e | f(E) | 95 |
| 19 | 0.02 | e + O2 → O2 + e | f(E) | 90 |
| 20 | 0.19 | e + O2 → O2 + e | f(E) | 90 |
| 21 | 0.19 | e + O2 → O2 + e | f(E) | 90 |
| 22 | 0.38 | e + O2 → O2 + e | f(E) | 90 |
| 23 | 0.38 | e + O2 → O2 + e | f(E) | 90 |
| 24 | 0.57 | e + O2 → O2 + e | f(E) | 90 |
| 25 | 0.75 | e + O2 → O2 + e | f(E) | 90 |
| 26 | 0.98 | e + O2 → O2(a 1Δ) + e | f(E) | 90 |
| 27 | 1.63 | e + O2 → O2(b 1Σ) + e | f(E) | 90 |
| 28 | 4.50 | e + O2 → O2 + e | f(E) | 90 |
| 29 | 12.06 | e + O2 → O2+ + e | f(E) | 90 |
| 30 | 0.02 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 19h |
| 31 | 0.19 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 20h |
| 32 | 0.19 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 21h |
| 33 | 0.38 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 22h |
| 34 | 0.38 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 23h |
| 35 | 0.57 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 24h |
| 36 | 0.75 | e + O2(a 1Δ) → O2(a 1Δ) + e | f(E) | As rxn 25h |
| 37 | 0.65 | e + O2(a 1Δ) → O2(b 1Σ) + e | f(E) | 96 |
| 38 | 3.52 | e + O2(a 1Δ) → O2 + 2e | f(E) | As rxn 28h |
| 39 | 11.08 | e + O2(a 1Δ) → O2+ + e | f(E) | As rxn 29h |
| 40 | 0.02 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 19h |
| 41 | 0.19 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 20h |
| 42 | 0.19 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 21h |
| 43 | 0.38 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 22h |
| 44 | 0.38 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 23h |
| 45 | 0.57 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 24h |
| 46 | 0.75 | e + O2(b 1Σ) → O2(b 1Σ) + e | f(E) | As rxn 25h |
| 47 | 2.87 | e + O2(b 1Σ) → O2 + e | f(E) | As rxn 28h |
| 48 | 10.43 | e + O2(b 1Σ) → O2+ + 2e | f(E) | As rxn 29h |
| Super-elastic collisions | ||||
| 49 | −19.80 | e + He* → He + e | f(E) | 82 and 83 |
| 50 | −1.97 | e + O(1D) → O + e | f(E) | 94 |
| 51 | −4.19 | e + O(1S) → O + e | f(E) | 94 |
| 52 | −0.98 | e + O2(a 1Δ) → O2 + e | f(E) | 90 |
| 53 | −1.63 | e + O2(b 1Σ) → O2 + e | f(E) | 90 |
| 54 | −0.65 | e + O2(b 1Σ) → O2(a 1Δ) + e | f(E) | As rxn 37j |
| Electron impact dissociation | ||||
| 55 | 0.00 | e + He2* → 2He + e | 3.8 × 10−15 | 97 |
| 56 | 13.50 | e + H2O → O(1S) + 2H + e | f(E) | 84 and 98 |
| 57 | 7.62 | e + H2O → H + OH + e | f(E) | 84 and 99 |
| 58 | 9.00 | e + H2O → H + OH + e | f(E) | 84 |
| 59 | 13.00 | e + H2O → H2 + O(1D) + e | 2.42 × 10−14Te−0.062e−22.42/Te | 78 |
| 60 | 8.80 | e + H2 → 2H + e | f(E) | 100 |
| 61 | 11.37 | e + H2 → 2H + e | f(E) | 101 |
| 62 | 12.96 | e + OH → O + H + e | f(E) | 102 |
| 63 | e + H2O2 → 2OH + e | 2.36 × 10−15 | 103 | |
| 64 | 6.00 | e + O2 → O + O + e | f(E) | 90 |
| 65 | 8.40 | e + O2 → O(1D) + O + e | f(E) | 90 |
| 66 | 10.00 | e + O2 → O(1D) + O + e | f(E) | 90 |
| 67 | 5.02 | e + O2(a 1Δ) → O + O + e | f(E) | As rxn 64h |
| 68 | 7.42 | e + O2(a 1Δ) → O(1D) + O + e | f(E) | As rxn 65h |
| 69 | 9.02 | e + O2(a 1Δ) → O(1D) + O + e | f(E) | As rxn 66h |
| 70 | 4.37 | e + O2(b 1Σ) → O + O + e | f(E) | As rxn 64h |
| 71 | 6.77 | e + O2(b 1Σ) → O(1D) + O + e | f(E) | As rxn 65h |
| 72 | 8.37 | e + O2(b 1Σ) → O(1D) + O + e | f(E) | As rxn 66h |
| 73 | 2.60 | e + O3 → O + O2 + e | 1.7 × 10−14Te−0.57e−2.48/Te | 74 and 104 |
| 74 | 5.72 | e + O3 → O(1D) + O2(a 1Δ) + e | 3.22 × 10−13Te−1.18e−9.17/Te | 74 and 104 |
| Dissociative ionisation | ||||
| 75 | 17.50 | e + H2O → OH+ + H + 2e | f(E) | 84 |
| 76 | 25.00 | e + H2O → O+ + 2H + 2e | f(E) | 84 |
| (Dissociative) electron attachment | ||||
| 77 | 5.30 | e + H2O → OH + H− | f(E) | 84 and 105 |
| 78 | 4.43 | e + H2O → H2 + O− | f(E) | 84 and 105 |
| 79 | 4.30 | e + H2O → H + OH− | f(E) | 84 and 105 |
| 80 | 0.00 | e + H2O2 → H2O + O− | f(E) | 106 |
| 81 | 0.00 | e + H2O2 → OH + OH− | f(E) | 106 |
| 82 | 5.38 | e + O2 → O + O− | f(E) | 90 |
| 83 | 3.50 | e + O2(a 1Δ) → O + O− | f(E) | 107 |
| 84 | 2.85 | e + O2(b 1Σ) → O + O− | f(E) | As rxn 83h |
| 85 | 0.00 | e + O3 → O2 + O− | f(E) | 108 |
| 86 | 0.25 | e + O3 → O2− + O | f(E) | 108 |
| Electron detachment | ||||
| 87 | 1.55 | e + H− → H + e + e | f(E) | 109 |
| 88 | 3.37 | e + OH− → OH + e + e | f(E) | 110 |
| 89 | 2.70 | e + O− → O + e + e | f(E) | 111 |
| 90 | 4.00 | e + O2− → O2 + e + e | f(E) | 174 |
| Recombination | ||||
| 91 | 0.00 | e + H2O+ → H + OH | 8.6 × 10−14Te−0.5 | 112 and 113 |
| 92 | 0.00 | e + H2O+ → 2H + O | 3.05 × 10−13Te−0.5 | 112 and 113 |
| 93 | 0.00 | e + H2O+ → H2 + O | 3.87 × 10−14Te−0.5 | 112 and 113 |
| 94 | 0.00 | e + H+·(H2O) → H + H2O | 7.09 × 10−14Te−0.5 | 112, 114 and 115 |
| 95 | 0.00 | e + H+·(H2O) → OH + H2 | 5.37 × 10−14Te−0.5 | 112, 114 and 115 |
| 96 | 0.00 | e + H+·(H2O) → OH + 2H | 3.05 × 10−13Te−0.5 | 112, 114 and 115 |
| 97 | 0.00 | e + H+·(H2O)2 → H + 2H2O | 1.84 × 10−12Te−0.08 | 116 |
| 98 | 0.00 | e + H+·(H2O)3 → 3H2O + H | 2.24 × 10−12Te−0.08 | 116 |
| 99 | 0.00 | e + H+·(H2O)4 → 4H2O + H | 3.6 × 10−12 | 116 |
| 100 | 0.00 | e + H+·(H2O)5 → 5H2O + H | 4.1 × 10−12 | 117 |
| 101 | 0.00 | e + H+·(H2O)6 → 6H2O + H | 5.13 × 10−12 | 117 |
| 102 | 0.00 | e + H+·(H2O)7 → 7H2O + H | 1.0 × 10−12 | 117 |
| 103 | 0.00 | e + H+·(H2O)8 → 8H2O + H | 4.1 × 10−12 | As rxn 100 |
| 104 | 0.00 | e + H+·(H2O)9 → 9H2O + H | 4.1 × 10−12 | As rxn 100 |
| 105 | 0.00 | e + H2O+·(H2O) → H + OH + H2O | 9.63 × 10−13Te−0.2 | 118 |
| 106 | 0.00 | e + O2+ → 2O | 3.72 × 10−15Te−0.7 | 119 |
| 107 | 0.00 | e + O2+ → O + O(1D) | 7.44 × 10−15Te−0.7 | 119 and 120 |
| 108 | 0.00 | e + O2+ → 2O(1D) | 7.44 × 10−15Te−0.7 | 119 and 120 |
| 109 | 0.00 | e + O2+·(H2O) → O2 + H2O | 7.22 × 10−13Te−0.2 | 118 |
| 110 | 0.00 | e + O4+ → 2O + O2 | 5.17 × 10−14Te−1.0 | 118 |
| 111 | 0.00 | e + O4+ → 2O2 | 2.76 × 10−13Te−0.5 | 86 |
Table 6 shows reaction rate coefficients for ion–ion recombination processes. It is generally known that ion–ion recombination processes can occur both as two- or three-body processes, depending on the gas pressure. Two-body reaction rate coefficients for several different gases have been obtained in ref. 85 at low pressure, and found to be in the order of 10−13 m3 s−1 or lower. Taking into account the He density at atmospheric pressure and at 315 K, and the rate coefficient for three-body ion–ion recombination proposed by Kossyi,86 the effective two-body reaction rate amounts to a value in the order of 10−12 m3 s−1. Due to this higher effective rate coefficient under our conditions, we only include three-body ion–ion recombination rate coefficients in this work. These reactions are found to be particularly important for the destruction of the higher-mass water clusters, which are abundant at higher H2O admixtures. Similar observations have been made by Liu et al.,48 who, after an analysis of the robustness of their chemistry model, only included a few ion–ion recombination reactions in their simplified models, a large fraction of which were three-body recombination processes for the collisions of higher mass cluster ions. We also found that under our conditions, ion–ion recombination between positive He ions and negative ions are negligible due to the rapidly decreasing He ion density with increasing water content, which again is in accordance with the findings of Liu et al.,48 and the fact that He ions undergo charge exchange reactions with most neutral species due to their high ionisation potential.
| No. | Reaction (rxn) | Ratea | Ref. |
|---|---|---|---|
| a In m6 s−1. b Value estimated in reference. c For A = O, O2, OH, H2O and B = O, O2, H, OH, H2O2. d For A = O and B = O, O2, H, OH, H2O2. e For A = O, O2, OH, H2O and n = 1–3. f For A = O and n = 1–3. g For m = 1–9 and B = O, H, OH. h For m = 1–9 and n = 1–3. i For m = 1–9. j For B = O, O2, H, OH, H2O2. k For n = 1–3. | |||
| Three-body collisions | |||
| 112–131 | A+ + B− + He → A + B + He | 2.0 × 10−37T0−2.5 | 86 , |
| 132–136 | A4+ + B− + He → 2A2 + B + He | 2.0 × 10−37T0−2.5 | 86 , |
| 137–148 | A+ + OH−·(H2O)n + He → A + OH + n × H2O + He | 2.0 × 10−37T0−2.5 | 86 , |
| 149–151 | A4+ + OH−·(H2O)n + He → 2A2 + OH + n × H2O + He | 2.0 × 10−37T0−2.5 | 86 , |
| 152–187 | H+·(H2O)m + B− + He → m × H2O + H·B | 2.0 × 10−37T0−2.5 | 86 , |
| 188–214 | H+·(H2O)m + OH−·(H2O)n + He → (m + n + 1) × H2O + He | 2.0 × 10−37T0−2.5 | 86 , |
| 215–223 | H+·(H2O)m + H2O2− + He → (m + 1) × H2O + OH | 2.0 × 10−37T0−2.5 | 86 , |
| 224–228 | H2O+·H2O + B− + He → 2H2O + B + He | 2.0 × 10−37T0−2.5 | 86 , |
| 229–231 | H2O+·H2O + OH−·(H2O)n + He → (n + 2) × H2O + OH + He | 2.0 × 10−37T0−2.5 | 86 , |
| 232–236 | O2+·(H2O) + B− + He → H2O + O2 + B | 2.0 × 10−37T0−2.5 | 86 , |
| 237–239 | O2+·(H2O) + OH−·(H2O)n + He → (n + 1) × H2O + O2 + OH | 2.0 × 10−37T0−2.5 | 86 , |
Table 7 shows reaction rate coefficients for collisions between ions and neutrals. In this table a number of three-body processes are included. Three-body processes are typically characterised by a pressure dependence. The nature of these reactions mean that this pressure dependence normally takes the form of a curve exhibiting low- and high-pressure limits. In the low-pressure limit the effective rate coefficient (i.e. the three-body rate coefficient multiplied by the third body density) is linear with the third body density. In the high pressure limit the effective rate coefficient is independent of the density of the third body. In the region between the two limits the effective rate coefficient is non-linear with the third body density. For a number of reactions, this transition region occurs around atmospheric pressure, therefore effective rate coefficients must be calculated using available knowledge of the high and low pressure limits. The coefficients which have been explicitly calculated for atmospheric pressure are marked as “effective” in Tables 7 and 8. Among these reactions is the formation and destruction of protonated water clusters H+·(H2O)n, where the rate coefficients are given by Sieck et al.87 Here, the expressions given in ref. 87 are used to calculate the effective rate coefficients for these reactions under our plasma operating conditions (atmospheric pressure, Tg = 280–350 K). Results are fitted with an Arrhenius expression, where possible, in order to keep the temperature dependence for these reactions, since the formation of cluster ions is highly temperature dependent.87 The rate coefficients for the formation of the two highest order clusters taken into account in this work are estimated by extrapolating the coefficients k3000 and A given by Sieck et al. using an exponential fit, and using constant values n = 16, B = 5000, and kL = 10−24 (see Sieck et al.87 for further description of these coefficients).
| No. | Reaction (rxn) | Ratea | Ref. |
|---|---|---|---|
| a In s−1, m3 s−1 and m6 s−1 for one-, two- and three-body reactions, respectively. b Value is estimated in reference. c Effective rate coefficients calculated from pressure dependent rates as described by Sieck87 for 1 atm and a temperature range 280–350 K. d Background gas is (humid) air in given reference. Gas efficiency factors for He background gas are not known for these reactions, but could potentially change calculated reaction rate coefficients if taken into account. e Rate coefficients are estimated by extrapolating the coefficients k3000 and A given by Sieck et al.87 using an exponential fit, and using constant values n = 16, B = 5000, and kL = 10−24. f Value is listed as a lower limit in reference. g Estimated branching ratio. h Third body is H2O in reference. | |||
| Two-body collisions – positive ions | |||
| 240 | He+ + OH → O+ + H + He | 1.1 × 10−15T0−0.5 | 112 and 123 |
| 241 | He+ + H2O → H2O+ + He | 6.05 × 10−17T0−0.5 | 112 and 124 |
| 242 | He+ + H2O → OH+ + H + He | 2.86 × 10−16T0−0.5 | 112 and 124 |
| 243 | He+ + O → O+ + He | 5.00 × 10−17 | 125 |
| 244 | He+ + O2 → O+ + O + He | 1.1 × 10−15 | 112 and 126 |
| 245 | He+ + O2 → O2+ + He | 3.3 × 10−17 | 112 and 126 |
| 246 | He2+ + OH → O+ + H + 2He | 1.1 × 10−15 | As rxn 240 |
| 247 | He2+ + H2O → H2O+ + 2He | 6.05 × 10−17T0−0.5 | As rxn 241 |
| 248 | He2+ + H2O → H+·(H2O) + 2He | 2.86 × 10−16T0−0.5 | As rxn 242 |
| 249 | He2+ + O2 → O+ + O + 2He | 1.1 × 10−15 | As rxn 244 |
| 250 | He2+ + O2 → O2+ + 2He | 3.3 × 10−17 | As rxn 245 |
| 251 | H+·(H2O)2 (+ He) → H+·(H2O) + H2O (+ He) | Effective | 87 , |
| 252 | H+·(H2O)3 (+ He) → H+·(H2O)2 + H2O (+ He) | Effective | 87 , |
| 253 | H+·(H2O)4 (+ He) → H+·(H2O)3 + H2O (+ He) | Effective | 87 , |
| 254 | H+·(H2O)5 (+ He) → H+·(H2O)4 + H2O (+ He) | Effective | 87 , |
| 255 | H+·(H2O)6 (+ He) → H+·(H2O)5 + H2O (+ He) | Effective | 87 , |
| 256 | H+·(H2O)7 (+ He) → H+·(H2O)6 + H2O (+ He) | Effective | 87 , |
| 257 | H+·(H2O)8 (+ He) → H+·(H2O)7 + H2O (+ He) | Effective | est.e |
| 258 | H+·(H2O)9 (+ He) → H+·(H2O)8 + H2O (+ He) | Effective | est.e |
| 259 | OH+ + H2 → H2O+ + H | 1.01 × 10−15 | 112 and 127 |
| 260 | OH+ + OH → H2O+ + O | 7.0 × 10−16T0−0.5 | 112 and 123 |
| 261 | OH+ + H2O → H2O+ + OH | 1.56 × 10−15 | 128 |
| 262 | OH+ + H2O → H+·(H2O) + O | 1.27 × 10−15 | 128 |
| 263 | OH+ + O → O2+ + H | 7.1 × 10−16 | 112 and 123 |
| 264 | OH+ + O2 → O2+ + OH | 5.9 × 10−16 | 112 and 127 |
| 265 | H2O+ + H2 → H+·(H2O) + H | 6.4 × 10−16 | 112 and 129 |
| 266 | H2O+ + OH → H+·(H2O) + O | 6.9 × 10−16T0−0.5 | 112 and 123 |
| 267 | H2O+ + H2O → H+·(H2O) + OH | 2.05 × 10−15 | 128 |
| 268 | H2O+ + O → O2+ + H2 | 4.0 × 10−17 | 112 and 130 |
| 269 | H2O+ + O2 → O2+ + H2O | 3.3 × 10−16 | 131 |
| 270 | H2O+·H2O + H2O → H+·(H2O)2 + OH | 1.4 × 10−15 | 118 |
| 271 | O+ + H2 → OH+ + H | 1.7 × 10−15 | 112 and 132 |
| 272 | O+ + OH → OH+ + O | 3.6 × 10−15T0−0.5 | 112 and 123 |
| 273 | O+ + OH → O2+ + H | 3.6 × 10−15T0−0.5 | 112 and 123 |
| 274 | O+ + H2O → H2O+ + O | 3.2 × 10−15 | 132 |
| 275 | O+ + O2 → O2+ + O | 2.0 × 10−17T0−0.4 | 133 |
| 276 | O2+·H2O (+ He) → O2+ + H2O (+ He) | Effective | 87 , |
| 277 | O2+·H2O + H2O → H2O+·H2O + O2 | 1.0 × 10−15 | 118 |
| 278 | O4+ + He → O2+ + O2 + He | 3.4 × 10−20 | 74 and 134 |
| 279 | O4+ + H2O → O2+·H2O + O2 | 1.7 × 10−15 | 135 |
| 280 | O4+ + O → O2+ + O3 | 3.0 × 10−16 | 118 |
| 281 | O4+ + O2 → O2+ + 2O2 | 1.0 × 10−11T0−4.2e−5400/Tg | 74 and 134 |
| 282 | O4+ + O2(a 1Δ) → O2+ + 2O2 | 1.0 × 10−16 | 118 |
| 283 | O4+ + O2(b 1Σ) → O2+ + 2O2 | 1.0 × 10−16 | As rxn 282 |
| Two-body collisions – negative ions | |||
| 284 | H− + He → H + He + e | 4.43 × 10−17e−5829/Tg | 136 |
| 285 | H− + H2O → OH− + H2 | 4.8 × 10−15 | 112 and 137 |
| 286 | OH− + H → H2O + e | 1.4 × 10−15 | 112 and 138 |
| 287 | H2O2− + H2O → OH−·(H2O) + OH | 1.0 × 10−17 | 139 |
| 288 | O− + H2O → OH− + OH | 1.4 × 10−15 | 105 |
| 289 | O− + O2 → O2− + O | 1.0 × 10−18 | 74 and 134 |
| 290 | O− + O2(a 1Δ) → O2− + O | 7.9 × 10−16e−890/Tg | 74 and 140 |
| 291 | O− + O2(a 1Δ) → O3 + e | 6.1 × 10−16 | 74 and 140 |
| 292 | O− + O2(b 1Σ) → O2− + O | 7.9 × 10−16e−890/Tg | As rxn 290 |
| 293 | O− + O2(b 1Σ) → O3 + e | 6.1 × 10−16 | 74 and 140 |
| 294 | O− + O3 → O2− + O2 | 1.0 × 10−17 | 74 and 134 |
| 295 | O2− + O → O− + O2 | 8.5 × 10−17T0−1.7 | 141 |
| 296 | O2− + O → O3 + e | 8.5 × 10−17T0−1.7 | 141 |
| Three-body collisions – positive ions | |||
| 297 | He+ + 2He → He2+ + He | 1.4 × 10−43T0−0.6 | 142 |
| 298 | H+·(H2O) + H2O (+ He) → H+·(H2O)2 (+ He) | Effective | 87 and 143 , |
| 299 | H+·(H2O)2 + H2O (+ He) → H+·(H2O)3 (+ He) | Effective | 87 and 143 , |
| 300 | H+·(H2O)3 + H2O (+ He) → H+·(H2O)4 (+ He) | Effective | 87 and 143 , |
| 301 | H+·(H2O)4 + H2O (+ He) → H+·(H2O)5 (+ He) | Effective | 87 and 143 , |
| 302 | H+·(H2O)5 + H2O (+ He) → H+·(H2O)6 (+ He) | Effective | 87 and 143 , |
| 303 | H+·(H2O)6 + H2O (+ He) → H+·(H2O)7 (+ He) | Effective | 87 and 143 , , |
| 304 | H+·(H2O)7 + H2O (+ He) → H+·(H2O)8 (+ He) | Effective | est.e |
| 305 | H+·(H2O)8 + H2O (+ He) →H+·(H2O)9 (+ He) | Effective | est.e |
| 306 | O2+ + H2O (+ He) → O2+·H2O (+ He) | Effective | 87 , |
| 307 | O2+ + O2 (+ He) → O4+ (+ He) | Effective | 87 , |
| Three-body collisions – negative ions | |||
| 308 | OH− + H2O + He → OH−·(H2O) + He | 8.0 × 10−42 | 144 |
| 309 | OH−·(H2O) + H2O + He → OH−·(H2O)2 + He | 2.5 × 10−43 | 144 |
| 310 | OH−·(H2O)2 + H2O + He → OH−·(H2O)3 + He | 1.5 × 10−43 | 144 |
| 311 | O− + H2O + He → H2O2− + He | 1.3 × 10−40 | 139 |
| No. | Reaction (rxn) | Ratea | Ref. |
|---|---|---|---|
| a In m3 s−1 and m6 s−1 for two- and three-body collisions, respectively. b Value in an upper limit in reference. c Estimated value in reference. d Estimated branching ratio. e Branching ratios taken from Sanders.168 f Third body is Ar instead of He in reference. The gas efficiency factor is assumed to be 1. g Third body is Ar instead of He in reference. The gas efficiency factor is assumed to be 0.65. This factor is calculated by dividing reaction rate coefficients for He and Ar as background gases for the same reaction measured by Zellner et al.169 h Effective rate coefficients calculated from pressure dependent rates for 1 atm and fitted by an Arrhenius expression in the temperature range 280–350 K. i Third body is N2 instead of He in reference. The gas efficiency factor is assumed to be 0.43. This factor is calculated by dividing reaction rate coefficients for He and N2 as background gases for the same reaction measured by Hsu et al.170 j Recommended rate coefficient in reference is for N2 background gas instead of He. We apply a gas efficiency factor of 0.41 to the low-pressure limit reaction rate coefficient to account for this. This factor is calculated by dividing the room temperature rate coefficient from the given reference for He background gas (measured by Forster et al.171) by the recommended value (measured by Fulle et al.172). k Third body is Ar instead of He in reference. The gas efficiency factor is assumed to be 0.77. This factor is calculated by dividing reaction rate coefficients for He and Ar as background gases for the same reaction measured by Campbell and Thrush.169 l Third body is N2 instead of He in reference. The gas efficiency factor is assumed to be 0.61. This factor is calculated by dividing reaction rate coefficients for He and N2 as background gases for the same reaction measured by Lin and Leu.173 | |||
| Two-body collisions | |||
| 312 | He + O(1D) → O + He | 7.0 × 10−22 | 145 |
| 313 | He + O(1S) → O + He | 7.0 × 10−22 | As rxn 312 |
| 314 | He + O2(a 1Δ) → O2 + He | 8.0 × 10−27 | 146 |
| 315 | He + O2(b 1Σ) → O2(a 1Δ) + He | 1.0 × 10−23T00.5 | 125 |
| 316 | 2He* → He + He+ + e | 4.5 × 10−16 | 46 and 97 |
| 317 | 2He* → He2+ + e | 1.05 × 10−15 | 46 and 97 |
| 318 | He* + He2* → 2He + He+ + e | 5.0 × 10−16 | 97 |
| 319 | He* + He2* → He + He2+ + e | 2.0 × 10−15 | 97 |
| 320 | He* + OH → OH+ + He + e | 6.08 × 10−16 | As rxn 321 |
| 321 | He* + H2O → He + H2O+ + e | 6.08 × 10−16 | 147 |
| 322 | He* + H2O → He + OH+ + H + e | 1.39 × 10−16 | 147 |
| 323 | He* + H2O2 → He + OH+ + OH + e | 6.08 × 10−16 | As rxn 321 |
| 324 | He* + O → O+ + He + e | 2.54 × 10−16 | As rxn 327 |
| 325 | He* + O(1D) → O+ + He + e | 2.54 × 10−16 | As rxn 327 |
| 326 | He* + O(1S) → O+ + He + e | 2.54 × 10−16 | As rxn 327 |
| 327 | He* + O2 → O2+ + He + e | 2.54 × 10−16 | 148 |
| 328 | He* + O2(a 1Δ) → O2+ + He + e | 2.54 × 10−16 | As rxn 327 |
| 329 | He* + O2(b 1Σ) → O2+ + He + e | 2.54 × 10−16 | As rxn 327 |
| 330 | He* + O3 → O2+ + O + He + e | 2.6 × 10−16 | 74 |
| 331 | He2* + H2O → 2He + H2O+ + e | 2.2 × 10−15 | 149 |
| 332 | He2* + O → O+ + 2He + e | 3.6 × 10−16 | As rxn 335 |
| 333 | He2* + O(1D) → O+ + 2He + e | 3.6 × 10−16 | As rxn 335 |
| 334 | He2* + O(1S) → O+ + 2He + e | 3.6 × 10−16 | As rxn 335 |
| 335 | He2* + O2 → O2+ + 2He + e | 3.6 × 10−16 | 149 |
| 336 | He2* + O2(a 1Δ) → O2+ + 2He + e | 3.6 × 10−16 | As rxn 335 |
| 337 | He2* + O2(b 1Σ) → O2+ + 2He + e | 3.6 × 10−16 | As rxn 335 |
| 338 | He2* + O3 → O2+ + O + 2He + e | 3.6 × 10−16 | 74 |
| 339 | H + HO2 → H2 + O2 | 5.6 × 10−18 | 88 |
| 340 | H + HO2 → 2OH | 7.2 × 10−17 | 88 |
| 341 | H + HO2 → H2O + O | 2.4 × 10−18 | 88 |
| 342 | H + H2O2 → H2O + OH | 1.7 × 10−17e−1800/Tg | 150 |
| 343 | H + H2O2 → H2 + HO2 | 2.8 × 10−18e−1890/Tg | 150 |
| 344 | H + O3 → OH + O2 | 1.4 × 10−16e−470/Tg | 151 and 152 |
| 345 | H2 + OH → H2O + H | 4.27 × 10−19T02.41e−1240/Tg | 153 |
| 346 | H2 + O(1D) → OH + H | 1.2 × 10−16 | 88 |
| 347 | H2 + O(1S) → OH + H | 1.2 × 10−16 | As rxn 346 |
| 348 | 2OH → H2O + O | 6.2 × 10−20T02.6e945/Tg | 88 |
| 349 | OH + HO2 → O2 + H2O | 4.8 × 10−17e250/Tg | 88, 154 and 155 |
| 350 | OH + H2O2 → HO2 + H2O | 2.9 × 10−18e−160/Tg | 88 |
| 351 | OH + O → H + O2 | 2.4 × 10−17e110/Tg | 88, 156 and 157 |
| 352 | OH + O(1D) → O2 + H | 2.4 × 10−17e110/Tg | As rxn 351 |
| 353 | OH + O(1S) → O2 + H | 2.4 × 10−17e110/Tg | As rxn 351 |
| 354 | OH + O3 → O2 + HO2 | 1.7 × 10−18e−940/Tg | 88 |
| 355 | H2O + O(1D) → 2OH | 1.63 × 10−16e60/Tg | 151 |
| 356 | H2O + O(1S) → O + H2O | 4.5 × 10−17 | 158 |
| 357 | H2O + O(1S) → O(1D) + H2O | 1.5 × 10−16 | 158 |
| 358 | H2O + O(1S) → 2OH | 3.05 × 10−16 | 158 |
| 359 | H2O + O2(a 1Δ) → O2 + H2O | 4.8 × 10−24 | 151 |
| 360 | H2O + O2(b 1Σ) → O2 + H2O | 3.9 × 10−18e125/Tg | 151 |
| 361 | HO2 + O → OH + O2 | 2.7 × 10−17e224/Tg | 88 and 155 |
| 362 | HO2 + O(1D) → OH + O2 | 5.2 × 10−16 | As rxn 364 |
| 363 | HO2 + O(1S) → OH + O2 | 5.2 × 10−16 | As rxn 364 |
| 364 | H2O2 + O(1D) → H2O + O2 | 5.2 × 10−16 | 159 |
| 365 | H2O2 + O(1S) → H2O + O2 | 5.2 × 10−16 | As rxn 364 |
| 366 | O + O(1D) → 2O | 8.0 × 10−18 | 160 |
| 367 | O + O(1S) → 2O | 3.33 × 10−17e−300/Tg | 125 and 161 |
| 368 | O + O(1S) → O(1D) + O | 1.67 × 10−17e−300/Tg | 125 and 161 |
| 369 | O(1D) + O2 → O + O2 | 6.4 × 10−18 | 88 |
| 370 | O(1D) + O2 → O + O2(b 1Σ) | 2.56 × 10−17 | 88 |
| 371 | O(1D) + O3 → 2O2 | 1.2 × 10−16 | 88 |
| 372 | O(1D) + O3 → O2 + 2O | 1.2 × 10−16 | 88 |
| 373 | O(1S) + O3 → 2O2 | 1.2 × 10−16 | As rxn 371 |
| 374 | O(1S) + O3 → O2 + 2O | 1.2 × 10−16 | As rxn 372 |
| 375 | O2 + O2(a 1Δ) → 2O2 | 3.0 × 10−24e−200/Tg | 88 |
| 376 | O2 + O2(b 1Σ) → O2 + O2(a 1Δ) | 3.6 × 10−23T00.5 | 125 |
| 377 | 2O2(a 1Δ) → O2(b 1Σ) + O2 | 1.8 × 10−24T03.8e700/Tg | 162 and 163 |
| 378 | O2(a 1Δ) + O3 → O + 2O2 | 5.2 × 10−17e−2840/Tg | 151 |
| 379 | O2(b 1Σ) + O3 → O + 2O2 | 3.5 × 10−17e−135/Tg | 151 |
| Three-body collisions | |||
| 380 | 2He + He* → He + He2* | 2.0 × 10−46 | 164 |
| 381 | He + He* + H2O → H2O+ + 2He + e | 1.48 × 10−41 | 147 |
| 382 | He + He* + O → O+ + 2He + e | 8.2 × 10−42 | As rxn 385 |
| 383 | He + He* + O2 → O2+ + 2He + e | 8.2 × 10−42 | 165 |
| 384 | He + H + H → H2 + He | 6.04 × 10−45T0−1.0 | 150 and 152 |
| 385 | He + H + OH → H2O + He | 9.23 × 10−44T0−1.527e−185/Tg | 166 |
| 386 | He + H + O → OH + He | 4.36 × 10−44T0−1.0 | 167 |
| 387 | (He+) H + O2 → HO2 (+He) | Effective | 88 , |
| 388 | (He+) 2OH → H2O2 (+He) | Effective | 88 , |
| 389 | He + 2O → O2 + He | 3.99 × 10−47e900/Tg | 167 |
| 390 | He + O + O2 → O3 + He | 3.66 × 10−46T0−2.6 | 88 |
Table 8 shows reaction rate coefficients for collisions between ions and neutrals. Similar to the description of ion-neutral reactions in Table 7, a number reactions rates in Table 8, including neutral reactions of several O and H containing species, are specified as “effective”. Data to calculate rate coefficients for these reactions has generally been taken from the IUPAC chemical kinetics database.88
For the calculation of “effective” decay rates, and generally for three-body processes, we have multiplied the three-body rate coefficient from the respective sources by a background gas dependent efficiency factor, if available, where the collider gas is different from He in the reference. This accounts for the fact that He is a less effective quencher compared to other background gases. More details for specific reactions are denoted in footnotes.
In addition to the He–H2O chemistry, we also include oxygen neutrals and ions. This makes it possible to investigate the influence of O2 impurities at low H2O contents on the plasma chemistry. In contrast to Liu et al., we do not include the ions HeH+, H+, and H2+ due to their generally low densities compared to the more abundant protonated water clusters under all investigated conditions, and the fact that in this work, the focus lies on the investigation of the neutral particle dynamics.
B. List of equipment
The equipment used for the investigations in this work is listed in Table 9.| Equipment | O FTAS | OH UV-BBAS I | OH UV-BBAS II |
|---|---|---|---|
| Power supply | Tabor WS8352 | Advanced Energy RFX-600 | TTi TGA 121104 |
| IFI SCCX100 | Coaxial Power Systems RFG150 | ||
| Matching box | Coaxial Power Systems MMN150 | Coaxial Power Systems MMN150 | Coaxial Power Systems MMN150 |
| Voltage probe | PMK-14KVAC | Tektronix P5100A | PMK-14KVAC |
| Oscilloscope | Lecroy Wavejet 354A | Teledyne LeCroy HDO4104 | Agilent DSO-X-2004-A |
| Light source | DESIRS beamline57 (Soleil) | Energetiq LDLS | UVTOP-305-FW-TO18 (Roithner Lasertechnik GmbH) |
| Spectrometer | DESIRS beamline57 (Soleil) | Princeton Instruments IsoPlane SCT320 | Andor SR-500i |
| Detector | DESIRS beamline57 (Soleil) | Hamamatsu S-3904 | Andor Newton 940 |
Acknowledgements
The authors would like to thank Dr Daniel Schröder, Dr Mickaël Foucher and Richard Armitage for helping with experimental setups and taking measurements. We are grateful to Denis Joyeux for the development of the FTS and for his help during the synchrotron campaign. This work was financially supported by the UK EPSRC (EP/K018388/1 & EP/H003797/2), and the York-Paris Low Temperature Plasma Collaborative Research Centre. Additionally, this work was performed within the LABEX Plas@par project and received financial state aid, managed by the Agence National de la Recherche as part of the programme “Investissements d'avenir” (ANR-11-IDEX-0004-02). Apiwat Wijaikhum acknowledges financial support from the Development and Promotion of Science and Technology Talents Project (DPST), Royal Government of Thailand scholarship, and ThEP Center through project ‘Cold atmospheric pressure plasma against drug resistant microorganisms for wound healing’ (ThEP-60-PHM-CMU1). Andrew R. Gibson acknowledges funding from the Wellcome Trust [ref. 204829] through the Centre for Future Health (CFH) at the University of York. Helen Davies acknowledges financial support from the Wellcome Trust 4 year PhD programme [WT095024MA]: “Combating Infectious Disease: Computation Approaches in Translational Science”. James Dedrick acknowledges financial support from an Australian Government Endeavour Research Fellowship. The participation of Mark J. Kushner was supported by the US Department of Energy (DE-SC0001319 and DE-SC0014132) and US National Science Foundation (PHY-1519117).Notes and references
- G. Fridman, G. Friedman, A. Gutsol, A. B. Shekhter, V. N. Vasilets and A. Fridman, Plasma Processes Polym., 2008, 5, 503–533 CrossRef
.
- M. G. Kong, G. Kroesen, G. Morfill, T. Nosenko, T. Shimizu, J. van Dijk and J. L. Zimmermann, New J. Phys., 2009, 11, 115012 CrossRef
.
- T. von Woedtke, S. Reuter, K. Masur and K.-D. Weltmann, Phys. Rep., 2013, 530, 291–320 CrossRef
.
- X. Lu, G. V. Naidis, M. Laroussi, S. Reuter, D. B. Graves and K. Ostrikov, Phys. Rep., 2016, 630, 1–84 CrossRef
.
- M. Laroussi, IEEE Trans. Plasma Sci., 2002, 30, 1409–1415 CrossRef
.
- M. Laroussi, Plasma Processes Polym., 2005, 2, 391–400 CrossRef
.
- R. E. J. Sladek and E. Stoffels, J. Phys. D: Appl. Phys., 2005, 38, 1716–1721 CrossRef
.
- A. M. Hirst, M. S. Simms, V. M. Mann, N. J. Maitland, D. O'Connell and F. M. Frame, Br. J. Cancer, 2015, 112, 1536–1545 CrossRef PubMed
.
- E. A. Ratovitski, X. Cheng, D. Yan, J. H. Sherman, J. Canady, B. Trink and M. Keidar, Plasma Processes Polym., 2014, 11, 1128–1137 CrossRef
.
- M. Vandamme, E. Robert, S. Lerondel, V. Sarron, D. Ries, S. Dozias, J. Sobilo, D. Gosset, C. Kieda, B. Legrain, J. M. Pouvesle and A. Le Pape, Int. J. Cancer, 2011, 130, 2185–2194 CrossRef PubMed
.
- A. R. Gibson, H. O. McCarthy, A. A. Ali, D. O'Connell and W. G. Graham, Plasma Processes Polym., 2014, 11, 1142–1149 CrossRef
.
- D. O'Connell, L. J. Cox, W. B. Hyland, S. J. McMahon, S. Reuter, W. G. Graham, T. Gans and F. J. Currell, Appl. Phys. Lett., 2011, 98, 043701 CrossRef
.
- G. Isbary, J. Heinlin, T. Shimizu, J. L. Zimmermann, G. Morfill, H.-U. Schmidt, R. Monetti, B. Steffes, W. Bunk, Y. Li, T. Klaempfl, S. Karrer, M. Landthaler and W. Stolz, Br. J. Dermatol., 2012, 167, 404–410 CrossRef PubMed
.
- A. V. Nastuta, I. Topala, C. Grigoras, V. Pohoata and G. Popa, J. Phys. D: Appl. Phys., 2011, 44, 105204 CrossRef
.
- R. S. Tipa and G. M. W. Kroesen, IEEE Trans. Plasma Sci., 2011, 39, 2978–2979 Search PubMed
.
- K. Mizuno, K. Yonetamari, Y. Shirakawa, T. Akiyama and R. Ono, J. Phys. D: Appl. Phys., 2017, 50, 12LT01 CrossRef
.
- G. Isbary, G. Morfill, H. U. Schmidt, M. Georgi, K. Ramrath, J. Heinlin, S. Karrer, M. Landthaler, T. Shimizu, B. Steffes, W. Bunk, R. Monetti, J. L. Zimmermann, R. Pompl and W. Stolz, Br. J. Dermatol., 2010, 163, 78–82 Search PubMed
.
- M. Schuster, C. Seebauer, R. Rutkowski, A. Hauschild, F. Podmelle, C. Metelmann, B. Metelmann, T. von Woedtke, S. Hasse, K.-D. Weltmann and H.-R. Metelmann, J. Craniomaxillofac. Surg., 2016, 44, 1445–1452 CrossRef PubMed
.
- D. B. Graves, J. Phys. D: Appl. Phys., 2012, 45, 263001 CrossRef
.
-
B. Halliwell and J. M. C. Gutteridge. Free radicals in biology & medicine. Oxford University Press, 4th edn, 2007 Search PubMed
.
- H. Sies, Exp. Physiol., 1997, 82, 291–295 CrossRef PubMed
.
- K. Niemi, D. O'Connell, N. de Oliveira, D. Joyeux, L. Nahon, J. P. Booth and T. Gans, Appl. Phys. Lett., 2013, 103, 034102 CrossRef
.
- J. Dedrick, S. Schröter, K. Niemi, A. Wijaikhum, E. Wagenaars, N. de Oliveira, L. Nahon, J. P. Booth, D. O'Connell and T. Gans, J. Phys. D: Appl. Phys., 2017, 50, 455204 CrossRef
.
- A. Wijaikhum, D. Schroeder, S. Schröter, A. R. Gibson, K. Niemi, J. Friderich, A. Greb, V. Schulz-vonder Gathen, D. O'Connell and T. Gans, Plasma Sources Sci. Technol., 2017, 26, 115004 CrossRef
.
- C. Douat, S. Hübner, R. Engeln and J. Benedikt, Plasma Sources Sci. Technol., 2016, 25, 025027 CrossRef
.
- W. Van Gaens, S. Iseni, A. Schmidt-Bleker, K. D. Weltmann, S. Reuter and A. Bogaerts, New J. Phys., 2015, 17, 033003 CrossRef
.
- J. S. Sousa, K. Niemi, L. J. Cox, Q. Th. Algwari, T. Gans and D. O'Connell, J. Appl. Phys., 2011, 109, 123302 CrossRef
.
- J. Waskoenig, K. Niemi, N. Knake, L. M. Graham, S. Reuter, V. Schulz-vonder Gathen and T. Gans, Plasma Sources Sci. Technol., 2010, 19, 045018 CrossRef
.
- S. Große-Kreul, S. Hübner, S. Schneider, A. von Keudell and J. Benedikt, EPJ Techn. Instrum., 2016, 3, 1–16 CrossRef
.
- H. J. Forman, J. M. Fukuto, T. Miller, H. Zhang, A. Rinna and S. Levy, Arch. Biochem. Biophys., 2008, 477, 183–195 CrossRef PubMed
.
- T. Verreycken, N. Sadeghi and P. J. Bruggeman, Plasma Sources Sci. Technol., 2014, 23, 045005 CrossRef
.
- A. Nikiforov, L. Li, N. Britun, R. Snyders, P. Vanraes and C. Leys, Plasma Sources Sci. Technol., 2014, 23, 015015 CrossRef
.
- I. Yagi, R. Ono, T. Oda and K. Takaki, Plasma Sources Sci. Technol., 2014, 24, 015002 CrossRef
.
- J. Benedikt, D. Schröder, S. Schneider, G. Willems, A. Pajdarová, J. Vlček and V. Schulz-vonder Gathen, Plasma Sources Sci. Technol., 2016, 25, 045013 CrossRef
.
- W. D. Kulatilaka, J. R. Gord, V. R. Katta and S. Roy, Opt. Lett., 2012, 37, 3051 CrossRef PubMed
.
- J. B. Schmidt, B. L. Sands, W. D. Kulatilaka, S. Roy, J. Scofield and J. R. Gord, Plasma Sources Sci. Technol., 2015, 24, 032004 CrossRef
.
- J. B. Schmidt, B. Sands, J. Scofield, J. R. Gord and S. Roy, Plasma Sources Sci. Technol., 2017, 26, 055004 CrossRef
.
- G. Willems, J. Benedikt and A. von Keudell, J. Phys. D: Appl. Phys., 2017, 50, 335204 CrossRef
.
- Z. Abd-Allah, D. A. G. Sawtell, K. McKay, G. T. West, P. J. Kelly and J. W. Bradley, J. Phys. D: Appl. Phys., 2015, 48, 085202 CrossRef
.
- P. Bruggeman, F. Iza, D. Lauwers and Y. A. Gonzalvo, J. Phys. D: Appl. Phys., 2009, 43, 012003 CrossRef
.
- Y. Gorbanev, C. C. W. Verlackt, S. Tinck, E. Tuenter, K. Foubert, P. Cos and A. Bogaerts, Phys. Chem. Chem. Phys., 2018, 20, 2797–2808 RSC
.
- J. Winter, H. Tresp, M. U. Hammer, S. Iseni, S. Kupsch, A. Schmidt-Bleker, K. Wende, M. Dünnbier, K. Masur and K.-D. Weltmann,
et al.
, J. Phys. D: Appl. Phys., 2014, 47, 285401 CrossRef
.
- P. Bruggeman, G. Cunge and N. Sadeghi, Plasma Sources Sci. Technol., 2012, 21, 035019 CrossRef
.
- C. Hibert, I. Gaurand, O. Motret and J. M. Pouvesle, J. Appl. Phys., 1999, 85, 7070–7075 CrossRef
.
- G. Dilecce, P. F. Ambrico, M. Simek and S. De Benedictis, J. Phys. D: Appl. Phys., 2012, 45, 125203 CrossRef
.
- K. Niemi, J. Waskoenig, N. Sadeghi, T. Gans and D. O'Connell, Plasma Sources Sci. Technol., 2011, 20, 055005 CrossRef
.
- C. Lazzaroni, P. Chabert, M. A. Lieberman, A. J. Lichtenberg and A. Leblanc, Plasma Sources Sci. Technol., 2012, 21, 035013 CrossRef
.
- D. X. Liu, P. Bruggeman, F. Iza, M. Z. Rong and M. G. Kong, Plasma Sources Sci. Technol., 2010, 19, 025018 CrossRef
.
- W. Van Gaens and A. Bogaerts, J. Phys. D: Appl. Phys., 2014, 47, 079502 CrossRef
.
- A. M. Lietz and M. J. Kushner, J. Phys. D: Appl. Phys., 2016, 49, 425204 CrossRef
.
- A. Hurlbatt, A. R. Gibson, S. Schröter, J. Bredin, A. P. S. Foote, P. Grondein, D. O'Connell and T. Gans, Plasma Processes Polym., 2016, 14, 1600138 CrossRef
.
- K. Ding and M. A. Lieberman, J. Phys. D: Appl. Phys., 2014, 48, 035401 CrossRef
.
- K. McKay, D. X. Liu, M. Z. Rong, F. Iza and M. G. Kong, J. Phys. D: Appl. Phys., 2012, 45, 172001 CrossRef
.
- D. X. Liu, F. Iza, X. H. Wang, M. G. Kong and M. Z. Rong, Appl. Phys. Lett., 2011, 98, 221501 CrossRef
.
- J. Golda, J. Held, B. Redeker, M. Konkowski, P. Beijer, A. Sobota, G. Kroesen, N. St. J. Braithwaite, S. Reuter, M. M. Turner, T. Gans, D. O'Connell and V. Schulz-von der Gathen, J. Phys. D: Appl. Phys., 2016, 49, 084003 CrossRef
.
- O. A. Alduchov and R. E. Eskridge, J. Appl. Meteorol., 1996, 35, 601–609 CrossRef
.
- L. Nahon, N. de Oliveira, G. A. Garcia, J.-F. Gil, B. Pilette, O. Marcouillé, B. Lagarde and F. Polack, J. Synchrotron Radiat., 2012, 19, 508–520 CrossRef PubMed
.
- N. de Oliveira, M. Roudjane, D. Joyeux, D. Phalippou, J.-C. Rodier and L. Nahon, Nat. Photonics, 2011, 5, 149–153 CrossRef
.
- D. Marinov, C. Drag, C. Blondel, O. Guaitella, J. Golda, B. Klarenaar, R. Engeln, V. Schulz-vonder Gathen and J.-P. Booth, Plasma Sources Sci. Technol., 2016, 25, 06LT03 CrossRef
.
- A. Kramida, Yu. Ralchenko and J. Reader, Available: http://physics.nist.gov/asd, 2016, December 15, [Online], National Institute of Standards and NIST ASD Team, NIST Atomic Spectra Database (ver. 5.3), and MD. Technology, Gaithersburg.
- M. Foucher, D. Marinov, E. Carbone, P. Chabert and J.-P. Booth, Plasma Sources Sci. Technol., 2015, 24, 042001 CrossRef
.
- G. H. Dieke and H. M. Crosswhite, J. Quant. Spectrosc. Radiat. Transfer, 1962, 2, 97–199 CrossRef
.
- L. Earls, Phys. Rev., 1935, 48, 423–424 CrossRef
.
- K. R. German, J. Chem. Phys., 1975, 62, 2584–2587 CrossRef
.
- A. Goldman and J. R. Gillis, J. Quant. Spectrosc. Radiat. Transfer, 1981, 25, 111–135 CrossRef
.
- V. L. Kasyutich, Eur. Phys. J. D, 2005, 33, 29–33 CrossRef
.
- S. Hofmann, A. F. H. van Gessel, T. Verreycken and P. Bruggeman, Plasma Sources Sci. Technol., 2011, 20, 065010 CrossRef
.
- D. Marinov and N. St. J. Braithwaite, Plasma Sources Sci. Technol., 2014, 23, 062005 CrossRef
.
- K. Niemi, T. Gans and D. O'Connell, Plasma Sources Sci. Technol., 2013, 22, 032001 CrossRef
.
- C. Lazzaroni, M. A. Lieberman, A. J. Lichtenberg and P. Chabert, J. Phys. D: Appl. Phys., 2012, 45, 495204 CrossRef
.
- S. Schröter, A. R. Gibson, M. J. Kushner, T. Gans and D. O'Connell, Plasma Phys. Controlled Fusion, 2018, 60, 014035 CrossRef
.
-
J. R. Roth. Industrial Plasma Processing. IOP Publishing, Bristol and Philadelphia, 1995 Search PubMed
.
- A. H. Markosyan, A. Luque, F. J. Gordillo-Vázquez and U. Ebert, Comput. Phys. Commun., 2014, 185, 2697–2702 CrossRef
.
- M. M. Turner, Plasma Sources Sci. Technol., 2015, 24, 035027 CrossRef
.
- T. Murakami, K. Niemi, T. Gans, D. O'Connell and W. G. Graham, Plasma Sources Sci. Technol., 2013, 22, 015003 CrossRef
.
- T. Murakami, K. Niemi, T. Gans, D. O'Connell and W. G. Graham, Plasma Sources Sci. Technol., 2013, 22, 045010 CrossRef
.
- T. Murakami, K. Niemi, T. Gans, D. O'Connell and W. G. Graham, Plasma Sources Sci. Technol., 2014, 23, 025005 CrossRef
.
- K. Ding, M. A. Lieberman and A. J. Lichtenberg, J. Phys. D: Appl. Phys., 2014, 47, 305203 CrossRef
.
- N. Knake and V. Schulz-vonder Gathen, Eur. Phys. J. D, 2010, 60, 645–652 CrossRef
.
- B. F. Gordiets, C. M. Ferreira, V. L. Guerra, J. M. A. H. Loureiro, J. Nahorny, D. Pagnon, M. Touzeau and M. Vialle, IEEE Trans. Plasma Sci., 1995, 23, 750–768 CrossRef
.
- I. Méndez, F. J. Gordillo-Vazquez, V. J. Herrero and I. Tanarro, J. Phys. Chem. A, 2006, 110, 6060–6066 CrossRef PubMed
.
- Biagi v8.9 database, http://www.lxcat.net, retrieved July 2012.
- S. F. Biagi, Fortran program, MAGBOLTZ, versions 8.9 and after.
- Y. Itikawa and N. Mason, J. Phys. Chem. Ref. Data, 2005, 34, 1–22 CrossRef
.
- T. M. Miller, N. S. Shuman and A. A. Viggiano, J. Chem. Phys., 2012, 136, 204306 CrossRef PubMed
.
- I. A. Kossyi, A. Y. Kostinsky, A. A. Matveyev and V. P. Silakov, Plasma Sources Sci. Technol., 1992, 1, 207–220 CrossRef
.
- L. Wayne Sieck, J. T. Heron and D. S. Green, Plasma Chem. Plasma Process, 2000, 20, 235–258 CrossRef
.
- R. Atkinson, D. L. Baulch, R. A. Cox, J. N. Crowley, R. F. Hampson, R. G. Hynes, M. E. Jenkin, M. J. Rossi and J. Troe, Atmos. Chem. Phys., 2004, 4, 1461–1738 CrossRef
.
- M. Yousfi and M. D. Benabdessadok, J. Appl. Phys., 1996, 80, 6619–6630 CrossRef
.
- S. A. Lawton and A. V. Phelps, J. Chem. Phys., 1978, 69, 1055–1068 CrossRef
.
- L. Vriens, Phys. Lett., 1964, 5, 260–261 CrossRef
.
- M. R. Flannery, K. J. McCann and N. W. Winter, J. Phys. B: At. Mol. Phys., 1981, 14, 3789–3796 CrossRef
.
- R. Riahi, P. Teulet, Z. Ben Lakhdar and A. Gleizes, Eur. Phys. J. D, 2006, 40, 223–230 CrossRef
.
- R. R. Laher and F. R. Gilmore, J. Phys. Chem. Ref. Data, 1990, 19, 277–305 CrossRef
.
- M. Gryziński, Phys. Rev., 1965, 138, A336–A358 CrossRef
.
- R. I. Hall and S. Trajmar, J. Phys. B: At. Mol. Phys., 1975, 8, L293–L296 CrossRef
.
- R. Deloche, P. Monchicourt, M. Cheret and F. Lambert, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 1140–1176 CrossRef
.
- W. Kedzierski, J. Derbyshire, C. Malone and J. W. McConkey, J. Phys. B: At., Mol. Opt. Phys., 1998, 31, 5361–5368 CrossRef
.
- T. Harb, W. Kedzierski and J. W. McConkey, J. Chem. Phys., 2001, 115, 5507–5512 CrossRef
.
- S. J. B. Corrigan, J. Chem. Phys., 1965, 43, 4381–4386 CrossRef
.
- M. Hayashi, J. Phys., Colloq., 1979, 40, C7/45–C7/46 Search PubMed
.
- W. Liu and G. A. Victor, Astrophys. J., 1994, 435, 909–919 CrossRef
.
- I. A. Soloshenko, V. V. Tsiolko, S. S. Pogulay, A. G. Terent'yeva, V. Y. Bazhenov, A. I. Shchedrin, A. V. Ryabtsev and A. I. Kuzmichev, Plasma Sources Sci. Technol., 2007, 16, 56–66 CrossRef
.
- M. Gupta and K. L. Baluja, J. Phys. B: At., Mol. Opt. Phys., 2005, 38, 4057–4073 CrossRef
.
- C. E. Melton and G. A. Neece, J. Am. Chem. Soc., 1971, 93, 6757–6759 CrossRef
.
- D. Nandi, E. Krishnakumar, A. Rosa, W.-F. Schmidt and E. Illenberger, Chem. Phys. Lett., 2003, 373, 454–459 CrossRef
.
- P. D. Burrow., J. Chem. Phys., 1973, 59, 4922–4931 CrossRef
.
- S. Matejcik, A. Kiendler, P. Cicman, J. Skalny, P. Stampfli, E. Illenberger, Y. Chu, A. Stamatovic and T. D. Märk, Plasma Sources Sci. Technol., 1997, 6, 140–146 CrossRef
.
-
R. K. Janev, W. D. Langer, K. Evans Jr. and D. E. Post Jr., Elementary Processes in Hydrogen-Helium Plasmas: Cross Sections and Reaction Rate Coefficients, Springer-Verlag, Berlin, 1987, ch. 7 Search PubMed
.
- H. B. Pedersen, N. Djurić, M. J. Jensen, D. Kella, C. P. Safvan, H. T. Schmidt, L. Vejby-Christensen and L. H. Andersen, Phys. Rev. A: At., Mol., Opt. Phys., 1999, 60, 2882–2899 CrossRef
.
- H. Deutsch, P. Scheier, K. Becker and T. D. Märk, Chem. Phys. Lett., 2003, 382, 26–31 CrossRef
.
- D. McElroy, C. Walsh, A. J. Markwick, M. A. Cordiner, K. Smith and T. J. Millar, Astron. Astrophys., 2013, 550, A36 CrossRef
.
- S. Rosén, A. Derkatch, J. Semaniak, A. Neau, A. Al-Khalili, A. Le Padellec, L. Vikor, R. Thomas, H. Danared, M. af Ugglas and M. Larsson, Faraday Discuss., 2000, 115, 295–302 RSC
.
- M. J. Jensen, R. C. Bilodeau, C. P. Safvan, K. Seiersen, L. H. Andersen, H. B. Pedersen and O. Heber, Astrophys. J., 2000, 543, 764–774 CrossRef
.
- O. Novotný, H. Buhr, J. Stuützel, M. B. Mendes, M. H. Berg, D. Bing, M. Froese, M. Grieser, O. Heber, B. Jordon-Thaden, C. Krantz, M. Lange, M. Lestinsky, S. Novotny, S. Menk, D. A. Orlov, A. Petrignani, M. L. Rappaport, A. Shornikov, D. Schwalm, D. Zajfman and A. Wolf, J. Phys. Chem. A, 2010, 114, 4870–4874 CrossRef PubMed
.
- C.-M. Huang, M. Whitaker, M. A. Biondi and R. Johnsen, Phys. Rev. A: At., Mol., Opt. Phys., 1978, 18, 64–67 CrossRef
.
- M. T. Leu, M. A. Biondi and R. Johnsen, Phys. Rev. A: At., Mol., Opt. Phys., 1973, 7, 292–298 CrossRef
.
-
M. H. Bortner and T. Baurer. Defense Nuclear Agency reaction rate handbook, revision no. 7, DaD Nuclear Information and Analysis Center, 7th edn, 1979 Search PubMed
.
- R. Peverall, S. Rosén, J. R. Peterson, M. Larsson, A. Al-Khalili, L. Vikor, J. Semaniak, R. Bobbenkamp, A. Le Padellec and A. N. Maurellis,
et al.
, J. Chem. Phys., 2001, 114, 6679–6689 CrossRef
.
- A. I. Florescu Mitchell and J. B. A. Mitchell, Phys. Rep., 2006, 430, 277–374 CrossRef
.
- G. J. M. Hagelaar and L. C. Pitchford, Plasma Sources Sci. Technol., 2005, 14, 722–733 CrossRef
.
- Morgan (Kinema Research & Software) database, http://www.lxcat.net, retrieved on.
- S. S. Prasad and W. T. Huntress Jr., Astrophys. J., Suppl. Ser., 1980, 43, 1–35 CrossRef
.
- G. Mauclaire, R. Derai and R. Marx, Int. J. Mass Spectrom. Ion Phys., 1978, 26, 289–301 CrossRef
.
- D. S. Stafford and M. J. Kushner, J. Appl. Phys., 2004, 96, 2451–2465 CrossRef
.
- N. G. Adams and D. Smith, J. Phys. B: At. Mol. Phys., 1976, 9, 1439–1451 CrossRef
.
- J. D. C. Jones, K. Birkinshaw and N. D. Twiddy, Chem. Phys. Lett., 1981, 77, 484–488 CrossRef
.
- W. T. Huntress, J. Chem. Phys., 1973, 59, 4742–4756 CrossRef
.
- A. B. Rakshit and P. Warneck, J. Chem. Soc., Faraday Trans. 2, 1980, 76, 1084–1094 RSC
.
- A. A. Viggiano, D. L. Albritton, F. C. Fehsenfeld, N. G. Adams, D. Smith and F. Howorka, Astrophys. J., 1980, 236, 492–497 CrossRef
.
- V. G. Anicich, J. Phys. Chem. Ref. Data, 1993, 22, 1469–1569 CrossRef
.
- D. Smith, N. G. Adams and T. M. Miller, J. Chem. Phys., 1978, 69, 308–318 CrossRef
.
- M. McFarland, J. Chem. Phys., 1973, 59, 6620–6628 CrossRef
.
-
Y. Ikezoe, S. Matsuoka, M. Takebe and A. Viggiano, Gas Phase Ion–Molecule Reaction Rate Constants Through 1986, Maruzen Company Ltd., 1987 Search PubMed
.
- A. B. Rakshit and P. Warneck, J. Chem. Phys., 1980, 73, 5074–5080 CrossRef
.
- R. L. Champion, L. D. Doverspike and S. K. Lam, Phys. Rev. A: At., Mol., Opt. Phys., 1976, 13, 617–621 CrossRef
.
- O. Martinez, Z. Yang, N. J. Demarais, T. P. Snow and V. M. Bierbaum, Astrophys. J., 2010, 720, 173–177 CrossRef
.
- E. E. Ferguson, At. Data Nucl. Data Tables, 1973, 12, 159–178 CrossRef
.
- F. C. Fehsenfeld and E. E. Ferguson, J. Chem. Phys., 1974, 61, 3181–3191 CrossRef
.
- A. Midey, I. Dotan and A. A. Viggiano, J. Phys. Chem. A, 2008, 112, 3040–3045 CrossRef PubMed
.
- S. G. Ard, J. J. Melko, B. Jiang, Y. Li, N. S. Shuman, H. Guo and A. A. Viggiano, J. Chem. Phys., 2013, 139, 144302 CrossRef PubMed
.
- H. Böhringer, W. Glebe and F. Arnold, J. Phys. B: At. Mol. Phys., 1983, 16, 2619–2626 CrossRef
.
- Y. K. Lau, S. Ikuta and P. Kebarle, J. Am. Chem. Soc., 1982, 104, 1462–1469 CrossRef
.
- J. de Urquijo, A. Bekstein, G. Ruiz-Vargas and F. J. Gordillo-Váquez, J. Phys. D: Appl. Phys., 2012, 46, 035201 CrossRef
.
- R. F. Heidner III and D. Husain, Int. J. Chem. Kinet., 1974, 6, 77–87 CrossRef
.
- F. D. Findlay, J. Chem. Phys., 1971, 55, 545–551 CrossRef
.
- C. B. Collins and F. W. Lee, J. Chem. Phys., 1979, 70, 1275–1285 CrossRef
.
- J. M. Pouvesle, A. Khacef, J. Stevefelt, H. Jahani, V. V. Gylys and C. B. Collins, J. Chem. Phys., 1988, 88, 3061–3071 CrossRef
.
- J. M. Pouvesle, J. Stevefelt., W. Lee, H. R. Jahani, V. T. Gylys and C. B. Collins, J. Chem. Phys., 1985, 83, 2836–2839 CrossRef
.
- D. L. Baulch, C. J. Cobos, R. A. Cox, C. Esser, P. Frank, Th. Just, J. A. Kerr, M. J. Pilling, J. Troe and R. W. Walker,
et al.
, J. Phys. Chem. Ref. Data, 1992, 21, 411–734 CrossRef
.
- J. B. Burkholder, S. P. Sander, J. Abbatt, J. R. Barker, R. E. Huie, C. E. Kolb, M. J. Kurylo, V. L. Orkin, D. M. Wilmouth and P. H. Wine. JPL Publication 15-10, Jet Propulsion Laboratory, Pasadena, 2015, http://jpldataeval.jpl.nasa.gov/.
- J. A. Manion, R. E. Huie, R. D. Levin, D. R. Burgess Jr., V. L. Orkin, W. Tsang, W. S. McGivern, J. W. Hudgens, V. D. Knyazev, D. B. Atkinson, E. Chai, A. M. Tereza, C.-Y. Lin, T. C. Allison, W. G. Mallard, F. Westley, J. T. Herron, R. F. Hampson and D. H. Frizzell, NIST Chemical KineticsDatabase, NIST Standard ReferenceDatabase 17, Version 7.0 (Web Version), Release 1.6.8, Data version2015.12. National Institute of Standards and Technology, Gaithersburg, Maryland, 20899-8320. Web address: http://kinetics.nist.gov/.
- V. L. Orkin, S. N. Kozlov, G. A. Poskrebyshev and M. J. Kurylo, J. Phys. Chem. A, 2006, 110, 6978–6985 CrossRef PubMed
.
- L. F. Keyser, J. Phys. Chem., 1988, 92, 1193–1200 CrossRef
.
- D. L. Baulch, C. T. Bowman, C. J. Cobos, R. A. Cox, Th. Just, J. A. Kerr, M. J. Pilling, D. Stocker, J. Troe, W. Tsang and R. W. Walker, J. Phys. Chem. Ref. Data, 2005, 34, 757–1397 CrossRef
.
- R. S. Lewis and R. T. Watson, J. Phys. Chem., 1980, 84, 3495–3503 CrossRef
.
- M. J. Howard and I. W. M. Smith, J. Chem. Soc., Faraday Trans. 2, 1981, 77, 997–1008 RSC
.
- T. G. Slanger and G. Black, J. Chem. Phys., 1978, 68, 989–997 CrossRef
.
- I. S. Fletcher and D. Husain, Rev. Can. Chim., 1976, 54, 1765–1770 CrossRef
.
- V. J. Abreu, J. H. Yee, S. C. Solomon and A. Dalgarno, Planet. Space Sci., 1986, 34, 1143–1145 CrossRef
.
- K. Schofield, J. Photochem., 1978, 9, 55–68 CrossRef
.
- R. G. Derwent and B. A. Thrush, Trans. Faraday Soc., 1971, 67, 2036–2043 RSC
.
- R. F. Heidner III, C. E. Gardner, T. M. El-Sayed, G. I. Segal and J. V. V. Kasper, J. Chem. Phys., 1981, 74, 5618–5626 CrossRef
.
- G. Myers and A. J. Cunningham, J. Chem. Phys., 1977, 67, 247–253 CrossRef
.
- G. Myers and A. J. Cunningham, J. Chem. Phys., 1977, 67, 3352–3359 CrossRef
.
- S. R. Sellevåg, Y. Georgievskii and J. A. Miller, J. Phys. Chem. A, 2008, 112, 5085–5095 CrossRef PubMed
.
- W. Tsang and R. F. Hampson, J. Phys. Chem. Ref. Data, 1986, 15, 1087–1222 CrossRef
.
- R. A. Sanders and E. E. Muschlitz, Int. J. Mass Spectrom. Ion Phys., 1977, 23, 99–108 CrossRef
.
- R. Zellner, K. Erler and D. Field, Symp. (Int.) Combust., [Proc.], 1977, 16, 939–948 CrossRef
.
- K. J. Hsu, J. L. Durant and F. Kaufman, J. Phys. Chem., 1987, 91, 1895–1899 CrossRef
.
- R. Forster, M. Frost, D. Fulle, H. F. Hamann, H. Hippler, A. Schlepegrell and J. Troe, J. Chem. Phys., 1995, 103, 2949–2958 CrossRef
.
- D. Fulle, H. F. Hamann, H. Hippler and J. Troe, J. Chem. Phys., 1996, 105, 1001–1006 CrossRef
.
- C. L. Lin and M. T. Leu, Int. J. Chem. Kinet., 1982, 14, 417–434 CrossRef
.
- H. Deutsch, K. Becker, M. Probst, W. Zhu and T. D. Märk, Int. J. Mass. Spectrom., 2008, 277, 151–154 CrossRef
.
Footnotes |
| † Data underpinning the figures in this manuscript can be found at DOI: http://10.15124/1a186859-ad12-4e33-bf17-ccfcbad48ba0. |
| ‡ Current address: Plasma and Beam Physics Research Facility, Faculty of Science, Chiang Mai University, Chiang Mai 50200, Thailand. |
| § Current address: School of Electrical and Electronic Engineering, The University of Manchester, Manchester M13 9PL, UK. |
| ¶ Current address: Laboratoire EM2C, CNRS, CentraleSupélec, Université Paris-Saclay, 3, rue Joliot Curie, 91192 Gif-sur-Yvette Cedex, France. |
| This journal is © the Owner Societies 2018 |