Open Access Article
Open Access ArticleEffects of probe energy and competing pathways on time-resolved photoelectron spectroscopy: the ring-opening of 1,3-cyclohexadiene
Maria
Tudorovskaya
a,
Russell S.
Minns
b and
Adam
Kirrander
 *a
*a
aEaStCHEM, School of Chemistry, University of Edinburgh, David Brewster Road, EH9 3FJ, Edinburgh, UK. E-mail: Adam.Kirrander@ed.ac.uk; Tel: +44 (0)131 6504716
bChemistry, University of Southampton, Highfield, SO17 1BJ, Southampton, UK
First published on 30th May 2018
Abstract
The ring-opening dynamics of 1,3-cyclohexadiene (CHD) following UV excitation is studied using a model based on quantum molecular dynamics simulations with the ab initio multiconfigurational Ehrenfest (AI-MCE) method coupled to the Dyson orbital approach for photoionisation cross sections. Time-dependent photoelectron spectra are calculated for probe photon energies in the range 2–15 eV. The calculations demonstrate the value of universal high-energy probes, capable of tracking the dynamics in full, but also the utility of more selective lower-energy probes with a more restricted ionisation range. The predicted signal, especially with the universal probes, becomes highly convoluted due to the contributions from multiple reaction paths, rendering interpretation challenging unless complementary measurements and theoretical comparisons are available.
1 Introduction
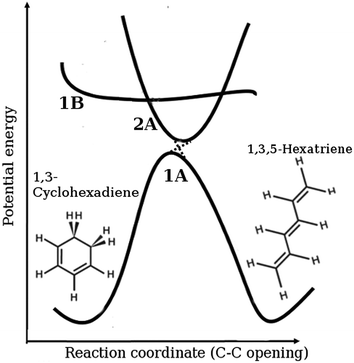
The molecule 1,3-cyclohexadiene (CHD) is a six-membered carbon ring that undergoes an ultrafast ring-opening reaction following excitation by UV light. The reaction forms an essential part of the biosynthesis of Previtamin D3, the thermal precursor to the human nutrient Vitamin D3,1–3 and is involved in a number of interesting applications including photochromic dyes4,5 and devices,6 optical switching,7 and nanomechanical motors.8 In broad terms, the reaction is understood by the mechanism schematically outlined in Fig. 1.9–11 Absorption of UV light at approximately 266 nm places the wavepacket on the steeply repulsive potential energy surface of the optically bright 1B 1ππ* state, with the wavepacket accelerated ballistically towards the diabatic 2A spectroscopically dark state on a <50 fs timescale. It returns to the 1A electronic ground state through a conical intersection, leading to either the ring-open 1,3,5-hexatriene (HT) photoproduct or the ring-closed CHD molecule. The main steps in the reaction are concluded within 200 fs, providing a spectacular example of fast internal conversion. The molecule carries a large excess of vibrational energy, once it has relaxed back to the electronic ground state. In solution, this energy is dissipated to the bath, cooling the internal temperature from an estimated 2200 K to the ambient temperature of the surroundings.12Interest in this reaction is driven by its role as a model system for modern mechanistic photochemistry.9–11 The CHD ring-opening is a prototypical pericyclic reaction and has contributed to the development and corroboration of the Woodward–Hoffman rules,13 which predict the stereochemical outcome for pericyclic reactions by correlating the first excited state of the reactant with the first excited state of the product and the ground state of the reactant with a doubly excited state of the product, and vice versa. This yields a pericyclic minimum in the first excited state, which acts as photochemical funnel that provides an efficient path for internal conversion.14–16
The reaction has been studied extensively using a wide array of time-resolved techniques in solution and gas phase, including resonance Raman spectroscopy,17–19 transient absorption,12,20,21 photoelectron spectroscopy,22–24 and dissociative intense-field ionisation.25–27 Computational studies include electronic structure calculations16,28–33 and dynamics,34–42 as well as joint theoretical and experimental work.23,43–45 It is notable that despite such extensive study, the understanding of the reaction is not complete. Apparent discrepancies include the branching ratio between ring-open and ring-closed products, possibly related to whether the experiment is performed in solution or gas phase. There is also an ongoing discussion regarding what dynamics occurs when the molecule is pumped at 200 nm rather than 267 nm.46,47
Finally, and perhaps most importantly, CHD has been used extensively to demonstrate new techniques and concepts. This includes coherent control, both experiment43,48,49 and theory,7,50,51 and a range of new ultrafast imaging techniques52 such as electron diffraction,53–56 X-ray scattering,44,45 Coulomb explosion,57 and near-edge X-ray absorption fine structure (NEXAFS).58 The variety of complementary observations generated by these techniques holds great promise for tying down a complete understanding of this important and complex reaction, for instance by combining X-ray scattering and photoelectron data such as in ref. 59.
In the present article, we explore the potential of tunable UV and XUV ultrafast lasers to probe photochemical dynamics in detail. Specifically, using a compact model of the dynamics excited by a 266 nm pump pulse, we examine the effect of changing the energy of the ionising probe pulse. The theoretical model is based on a reduced version of detailed quantum molecular dynamics simulations using the ab initio multiconfigurational Ehrenfest (AI-MCE) method,60 with a subset of representative trajectories extracted by comparison to X-ray scattering45 and photoelectron59 experimental data. Time-dependent photoionisation cross-sections are calculated using the Dyson orbital approach.61 The resulting model allow us to predict the time-resolved photoelectron spectra for the ring-opening reaction and test the effectiveness of a variety of probe energies and the importance of including a sufficient number of ionisation channels in the theoretical description.
2 Theory
2.1 Dynamics
The nonadiabatic dynamics of photoexcited CHD molecules are simulated using the AI-MCE method.62,63 In this approach, the molecular wavefunction |Ψ(t)〉 is expanded as a sum of trajectory-guided Ehrenfest wavepackets, |ψk(t)〉, also referred to as trajectories, | (1) |
 | (2) |
 is a product of three-dimensional Gaussian coherent states for each atom where Nat is the number of atoms. The labels Qmα(t) and Pmα(t) are the coordinates and the momenta of a trajectory-guided three-dimensional Gaussian coherent state with width γα. The component for the atom with index α in coordinate representation is then,
is a product of three-dimensional Gaussian coherent states for each atom where Nat is the number of atoms. The labels Qmα(t) and Pmα(t) are the coordinates and the momenta of a trajectory-guided three-dimensional Gaussian coherent state with width γα. The component for the atom with index α in coordinate representation is then, | (3) |
Each individual trajectory, |ψm(t)〉, is propagated semiclassically along phase-space coordinates {![[Q with combining macron]](https://www.rsc.org/images/entities/b_char_0051_0304.gif) mα(t),
mα(t),![[P with combining macron]](https://www.rsc.org/images/entities/b_char_0050_0304.gif) mα(t)}along with the Ehrenfest coefficients aim(t) and the expansion coefficients Bm(t). The time-dependent variation in the amplitudes Bm(t) is due to coupling between trajectories. The propagation uses electronic potential energies and nonadiabatic couplings obtained from ab initio electronic structure calculations. Readers interested in further details are directed to ref. 62 and 63. In this article, a reduced model based on a subset of Ehrenfest trajectories is used in the subsequent analysis of the photoelectron spectra (see Section 3.2 for details).
mα(t)}along with the Ehrenfest coefficients aim(t) and the expansion coefficients Bm(t). The time-dependent variation in the amplitudes Bm(t) is due to coupling between trajectories. The propagation uses electronic potential energies and nonadiabatic couplings obtained from ab initio electronic structure calculations. Readers interested in further details are directed to ref. 62 and 63. In this article, a reduced model based on a subset of Ehrenfest trajectories is used in the subsequent analysis of the photoelectron spectra (see Section 3.2 for details).
2.2 Photoionisation
The quantum molecular dynamics simulations are coupled to calculations of the photoionisation cross-sections and photoelectron spectra in the perturbative regime, corresponding to a Keldysh parameter γK ≫ 1, with , where ω is the angular frequency of the probe, Ip the ionisation potential, and I the laser intensity. Assuming that lowest-order perturbation theory is valid,64,65 the n-photon ionisation rate is given by Γn = σnIn, with n the number of photons and σn the generalized photoionisation cross section. Presently we consider single photon n = 1 processes for which the photoelectron energy is,
, where ω is the angular frequency of the probe, Ip the ionisation potential, and I the laser intensity. Assuming that lowest-order perturbation theory is valid,64,65 the n-photon ionisation rate is given by Γn = σnIn, with n the number of photons and σn the generalized photoionisation cross section. Presently we consider single photon n = 1 processes for which the photoelectron energy is,| Ek = ħω − Ip = ħ2k2/2me, | (4) |
 | (5) |
![[small epsilon, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e107.gif) the unit polarisation vector of the probe field, and 〈Φf(Ek)|r|ϕi〉 the dipole transition moment with r the dipole moment operator, assuming the wavelength of the probe is sufficient for the dipole approximation, |ϕi〉 the initial state, and |Φf(Ek)〉 the final energy-normalised continuum state which would normally satisfy incoming wave boundary conditions (see e.g.ref. 67–69). Any required integration over orientation quantum numbers is implicit.
the unit polarisation vector of the probe field, and 〈Φf(Ek)|r|ϕi〉 the dipole transition moment with r the dipole moment operator, assuming the wavelength of the probe is sufficient for the dipole approximation, |ϕi〉 the initial state, and |Φf(Ek)〉 the final energy-normalised continuum state which would normally satisfy incoming wave boundary conditions (see e.g.ref. 67–69). Any required integration over orientation quantum numbers is implicit.
We proceed by assuming that ionisation occurs between specific electronic states of the neutral molecule and the ion, and disregard coupling between ionisation channels or the vibrational states of the ion. Under these circumstances each contributing channel is identified by the initial electronic state ϕi and that of the molecular ion ϕj. Upon ionisation, the electron is considered to be a free particle in the Coulomb field of the ion, and does not interact with the remaining core electrons. Following these approximations, one may use the Dyson orbital approach,61,70,71 which gives the dipole transition moment as,
| Dij(Eijk) = 〈Ψkel|r|ϕDij〉, | (6) |
 | (7) |
 | (8) |
 | (9) |
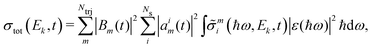 | (10) |
 | ||
| Fig. 2 Schematic depiction of the ionisation channels, Dij, with ithe electronic state of the neutral CHD molecule (S0, S1, S2, i = 0, 1, 2) and j of the CHD+ ion (D0, D1, D2, j = 0, 1, 2). Each combination of i and j corresponds to a different Dyson orbital as shown in Fig. 4. Channels corresponding to ionisation from the ground state S0 are shown in blue, from the first excited state S1 in red, and from the second excited state S2 in green. The ionisation potentials for each of the channels are Iijp = Ej − Ei, with i and j as above. | ||
3 Computational details
3.1 Dynamics
The AI-MCE72 dynamics are calculated using the adiabatic electronic energies, gradients, and nonadiabatic couplings calculated on-the-fly at the SA3-CAS(6,4)-SCF/cc-pVDZ level of theory using the ab initio electronic structure package MOLPRO.73 The choice of the SA3-CAS(6,4) active space is guided by previous investigations74 that demonstrate that it provides reasonable energy and gradient information on the relevant electronic states for the dynamics. The simulations assume that the vertical excitation is instantaneous, with the initial phase-space coordinates on the excited state generated using the vibrational Wigner distribution75 for the ν = 0 vibrational state on the electronic ground state, | (11) |
3.2 Compact model
The calculations of photoionisation cross sections along each of the Ehrenfest trajectories is computationally expensive, and importantly, the purpose of our analysis is to evaluate the link between dynamics, reaction paths, and the energy of the probe pulse on the signals, rather than the best-possible accuracy of the predicted total signal. We therefore define a compact model of the dynamics based on the full set of trajectories, but which consists of a small subset of these. The subset is determined by minimising the discrepancy between the signal predicted by the full set of trajectories and experimental data from ultrafast X-ray scattering, with the (in this case time-independent) expansion coefficients Bm used as variables in the optimisation as described in ref. 45. It is found that only four trajectories are sufficient to account for >70% of the scattering signal. The model obtained was independently validated against resonant photoionisation time-dependent experimental data, again finding good agreement.59 Further insight into the effectiveness of the model is obtained from a cluster analysis of the full set of trajectories, which shows that the actual dynamics can be represented by a much smaller set of trajectories corresponding to a small number of self-similar sets.76 In effect, the four trajectories in the model represent effective reaction coordinates. The main benefit of this approach is that it dramatically reduces the cost of otherwise expensive calculations and enables a detailed analysis of the correlation between the features of each trajectory and the resulting time-resolved photoelectron spectra. The four trajectories used hereon are labeled a, b, c and d. They are described in detail in Section 4.2, but broadly, the two trajectories labeled as a and c correspond to ring-opening dynamics, while the two trajectories labeled as b and d correspond to ring-closed dynamics.3.3 Photoionisation
For the calculations of the ionisation cross section and the photoelectron spectra we take into account the ground and two excited states of the neutral molecule and the target ion, providing nine independent ionisation channels. These channels are shown in Fig. 2 and are labeled as Dij, where i and j identify the initial and final states. In all figures hereon, we show the channels associated with states S0, S1 and S2, in blue, red and green, respectively. Note that all photoionisation cross sections are evaluated at the center of each Gaussian wavepacket (see discussion of BAT approximation e.g. in ref. 60).The Dyson orbitals are calculated using Q-Chem,77 with initial and final state electronic wavefunctions calculated at the EOM-CC/6-311G* level of theory. At each point, the output files generated with Q-Chem are used to extract the ionisation energies. The cross sections for each channel are then calculated using the ezDyson code.70 The free electron wavefunction is expanded in a series of partial waves with angular momentum l = 0–5 using a spatial grid with 251 grid points extending to a radius of 25 Bohr. Cross sections are calculated at 41 values of the kinetic energy in the range 0.3–15 eV. All calculations are performed in the laboratory frame assuming rotational averaging. The computations of the photoionisation cross sections are automated using a script, which reads the molecular geometry and electronic state populations from the simulations, calculates the Dyson orbitals using Q-Chem, and then runs ezDyson to obtain the cross sections. The ionisation cross sections are calculated every 10 fs for the dynamics. The signal is convoluted by the intensity profile of the probe laser |ε(ħω)|2, which is assumed to be Gaussian with FWHM 0.3 eV and centered at the probe energy ħω0.
4 Results
4.1 Photoionisation validation
To validate the calculated photoionisation cross sections, we compare the calculations for the neutral ground-state CHD molecule at the equilibrium (t < 0) geometry with experimental data from photoionisation mass spectrometry.78 In the experiments, the photon-energy dependent yield of the C6H8+ (so-called channel 1) and C6H7+ (channel 2) ionisation products are measured, which are taken to be proportional to the ionisation cross sections. The experimental yields are compared to energy-integrated calculated cross sections for the channels D00, D01, and D02 (i.e. the channels that correspond to ionisation of the neutral ground state molecule in Fig. 2). The lowest ionisation potential is 8.3 eV, corresponding to the channel D00. After the initial increase in cross section around the first ionisation potential, both experiment and computations show a plateau up to 11 eV. At 11 eV, the D01 and D02 channels become open and a large increase in ionisation cross section is observed. The two channels D01 and D02 have similar ionisation potentials and their cross sections are also similar as can be seen in Fig. 3a. In the experimental data, the signal in the so-called channel 2 corresponding to detection of C6H7+, also appears at approximately 11 eV, which strongly suggests that the experimental channel 2 correlates with the ionisation channels D01 and D02. This indicates that ionisation into excited electronic states of the CHD+ cation eventually leads to dissociative decay and fragmentation of the cation. | ||
| Fig. 3 Validation of calculated photoionisation cross sections by comparison to experimental data. (a) Total interpolated photoionisation cross section from the ground state (shown in red) compared to experimental data from Wang et al.78 (in green). The black lines show the calculated partial cross sections. (b) Calculated photoelectron spectrum (in black) compared to experimental data (blue dashed line) from Adachi et al.22 | ||
A second validation undertaken is to compare the calculated photoelectron spectrum of the ground state CHD to previous experimental spectra.22,79Fig. 3b, where the calculated data has been scaled by a single number for comparison, shows good agreement between experiment and theory both in terms of the positions of the two peaks and their relative intensity. The difference in the broadness of the peak at higher energy is due to the presence of higher excited states of the ion that are not included in the calculation. In summary, the two comparisons used to validate the Dyson-orbital calculations indicate that the approach provides a reasonably accurate description of the photoionisation cross sections over the energy range considered, at least for the ground state of CHD.
Fig. 4 shows the calculated Dyson orbitals as the molecule progresses along trajectory a. The top row shows the Dyson orbitals corresponding to each of the ionisation channels in the ground state geometry (t < 0), while the bottom row shows the same Dyson orbitals at time t = 180 fs in the ring-opening trajectory a. The shape of the orbitals clearly indicates that there might be significant anisotropy in the photoionisation signal, however, this is currently not accounted for as the signal is integrated over all orientations.
4.2 Dynamics
In the following, we discuss the four trajectories used to represent the overall dynamics of the photoexcited CHD. As discussed in Section 3.1, these should be seen to represent effective reaction coordinates. The trajectories are labelled a–d. Trajectories (a, c) relate to the main ring-opening pathways, while trajectories (b, d) to ring-closing pathways. The changes in molecular geometry for each trajectory can be characterized by the C1–C6 bond distance, corresponding to the bond that is broken during ring-opening, and shown in red in Fig. 5 for each of the trajectories. The black curves in the same figure show how three of the other C–C bonds change with time (these curves have been shifted by +3 Å for clarity). The ring-closed trajectories (b, d) exhibit strong oscillatory behavior in the C1–C6 distance that decreases over time as the energy disperses to other internal degrees of freedom. The ring-opening trajectories (a, c) demonstrate rapid lengthening of the C1–C6 bond with little variation in the other C–C bonds. The rapid C1–C6 extension in trajectory c quickly leads to large C1–C6 distances of ≈6 Å. The slower ring-opening in trajectory a, while still leading to bond breaking, maintains much closer proximity of C1 and C6 over the course of the simulation.The time-dependent electronic state populations plotted in Fig. 6 provide an explanation for some of these differences. In trajectory a the majority of the dynamics occurs on the S1 surface. There is a nonadiabatic transient transfer of population to the S2 and S0 states between 20 fs and 60 fs, but a large fraction of the population remains on the S1 surface while the C1–C6 bond breaks, such that this trajectory can be considered an excited-state ring-opening. At a comparatively late stage in the dynamics (≈150 fs) approximately half of the S1 population decays to the ground state. As for the other three trajectories (b, c and d), these follow a more typical pattern with a rapid transfer of population into the ground S0 state. In each case the ground state is reached within 50 fs following excitation. All four trajectories demonstrate limited transfer of population to the S2 state at early times, occurring when the wavepacket propagating on the S1 state reaches the region of the S2/S1 conical intersection. In this region, the S1 state changes from predominantly 1B to predominantly 2A character. For trajectory c, which leads to ring-opening, exchange of population between the electronic states occurs along the entire pathway, while for trajectories b and d the main transfer occurs at around t = 150 fs. In particular for trajectories (b, c and d) the rapid electronic state relaxation leads to excess vibrational energy that in trajectory c is transferred into motion of molecule that drives C1 and C6 rapidly away from each other. For the trajectories that remain closed the excess energy disperses into multiple vibrations around the ring leading to rapid and large amplitude changes in the C–C distances. The weighted average of the populations from all four trajectories combined, shown as a function of time in Fig. 7, agrees with the accepted view of the CHD ring-opening reaction described in Section 1. Comparison of Fig. 6 and 7 also highlights that the total populations mask the underlying mechanisms at play and that examination of the individual trajectories contributes to a more detailed picture of the dynamics.
 | ||
| Fig. 6 Populations |aik(t)|2 in the electronic states i = S0, S1, and S2 as a function of time for the four trajectories (a, b, c and d) shown in panels a–d (labels correspond to Fig. 5). | ||
 | ||
| Fig. 7 The effective electronic state population as a function of time for all four trajectories combined. The population of the S2 state remains low throughout. | ||
4.3 Time-resolved photoelectron spectra
In order to analyse photoionisation signals it is important to comprehend the changes in ionisation potential over the course of the reaction. The changes in ionisation potential control the measured photoelectron energy for any given probe-photon energy, and are critical for the assignment of features within the spectrum. The calculated ionisation potentials for all nine ionisation channels considered here are shown in Fig. 8 for each of the four trajectories. Generally, the ionisation potentials associated with the excited states, S1 and S2, show more variation than those associated with S0. At early times the rapid changes in the C1–C6 distance lead to pronounced shifts in ionisation potential. For trajectories (b and d) changes in the ionisation potential at longer times, t > 100 fs, correlate with the rapid oscillations in the remaining C–C bonds as seen in Fig. 5. | ||
| Fig. 8 Ionisation potentials Iijp = Ej − Ei as a function of time for each of the trajectories (a, b, c and d) shown in the corresponding panels a–d (labels as in Fig. 5). Ei is the potential energy of CHD in states i = 0, 1, 2 (S0, S1 and S2) and Ej that of CHD+ in states j = 0, 1, 2 (D0, D1 and D2), resulting in nine channels overall. The channels that originate in S0, S1 and S2, are shown in blue, red and green, respectively, and channels that correspond to excited states of CHD+ (j > 0) are shown as dashed lines. | ||
We proceed to examine the time-dependent photoionisation cross sections as a function of photon energy. The total cross sections are calculated by integrating expression eqn (9) over Ek, and are shown as a function of the photon energy ħω and the time t in Fig. 9. The ionisation cross section for probe energies below 8 eV decreases once the molecule relaxes to the ground state via the conical intersection at around t = 30–50 fs. This highlights one of the key drawbacks associated with UV photoelectron spectroscopy, in that the lifetimes measured often relate to the time the wavepacket remains in an ionisable region of the excited state potential and not necessarily the fundamental lifetimes of the molecule. In contrast, the increase of population on the ground state for t > 50 fs leads to a large effective cross sections for high energy (>10 eV) probe photons.
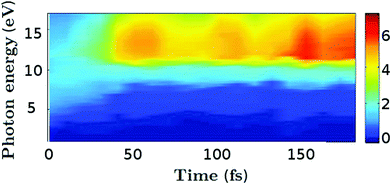 | ||
| Fig. 9 Total photoionisation cross section in atomic units for all four trajectories as a function of time (fs) and probe photon energy (eV). | ||
The time-dependent photoelectron spectrum at probe energies 2 eV, 6 eV, 9.2 eV and 15 eV as calculated by eqn (10) is shown in Fig. 10. The 2 eV probe is chosen to demonstrate the utility of a highly selective probe, the 6 eV probe represents to the maximum energy attainable from conventional non-linear optics, while 9.2 eV and 15 eV probes are within the range covered by femtosecond filamentation sources, high-harmonic generation, or seeded free-electron laser sources80–83 and approach energies sufficiently high to be considered universal photoionisation probes.
The spectra shown in Fig. 10 show increasing complexity and structure, the greater the probe energy. The signal from the 2 eV probe shown in Fig. 10a is rather weak, nearly two orders of magnitude lower in intensity and less complex than the higher energy probes, but is selective in its sensitivity to the transient population in the S2 state. The 6 eV probe in Fig. 10b provides a measure of the dynamics in the S1 and S2 excited states, in turn. The spectrum shifts to higher binding energies during the first 50 fs as the C1–C6 bond extends and the wavepacket moves down towards the conical intersection that funnels the wavepacket onto the ground state. Once the wavepacket is on the S0 state, the 6 eV probe can no longer ionise the wavepacket and the signal decreases in intensity. The 6 eV probe thus provides no information on the dynamics in the ground state or the formation of the final reaction products.
Increasing the probe energy beyond 6 eV provides a more universal measure of the dynamics. The 9.2 eV and 15 eV probes, shown in Fig. 10c and d, give rise to more complex spectra which include contributions from the S0 ground state. The redistribution of population at the conical intersection is seen in Fig. 10c and d at around 40 fs as a splitting of the main photoelectron feature, with the remaining S1 population contributing to a feature at around 5 eV, while the signal related to the ground state continues to shift to higher binding energies. Notably, ionisation from S0 contributes the most to the signal. Importantly, the highest energy 15 eV probe is capable of distinguishing the CHD and HT forms on the S0 potential energy surface.79,81 The CHD and HT photoionisation spectra are almost identical for the HOMO peak, but starting with HOMO−1 the spectra are clearly distinguishable.81
Fig. 11 presents the decomposition of the time-resolved photoelectron signal obtained with the 15 eV probe in Fig. 10d in terms of the contributions from each of the four trajectories a–d (shown in corresponding panels a–d). The partial spectra for the two ring-closed trajectories (b and d) are more intense for t > 50 fs, which relates to the more complete transfer of population to the electronic ground state S0 for the ring-closed trajectories on the time-scale of the simulations and that the cross section for photoionisation is large in the S0 state. The overall slower decay of the excited state population in the ring-opening (a, c) trajectories also implies that spectroscopic assessment of the branching ratio between CHD and HT should be done at asymptotically long times rather than at short times. All four trajectories exhibit a rapid increase in the photoelectron binding energy Eb at early times, corresponding to the wavepacket sliding down the potential-energy funnel towards the conical intersection and the subsequent internal conversion at the conical intersection. The intense higher-energy bands for the ring-closed trajectories (b, d) exhibit distinct beats. Out of the two ring-opening trajectories (a, c), the electronic state population dynamics for trajectory c is more similar to the ring-closed trajectories (b, d), and correspondingly it also exhibits features at low- and mid-energy that are qualitatively similar to those of the spectra for the ring-closed trajectories. Finally, the distinct character of all four time-resolved spectra emphasises the challenge in deconvoluting and interpreting the total spectrum shown in Fig. 10d previously.
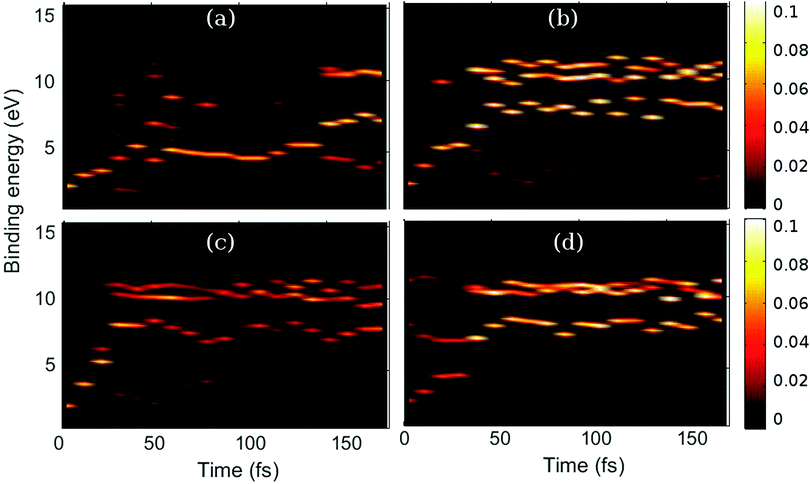 | ||
| Fig. 11 Photoelectron spectra for each of the trajectories (a, b, c and d) shown in corresponding panels a–d. The signal intensity is shown as a function of time and photoelectron binding energy Eb = ħω0 − Ek. The spectra in all four panels are calculated with the 15 eV probe (the corresponding total signal is shown in Fig. 10d). Panels (a and c) correspond to ring-opening, and panels (b and d) to ring-closed trajectories as before, matching the labels in Fig. 5. | ||
To quantify the importance of including ionisation channels corresponding to excited electronic states of the cation when predicting photoelectron spectra obtained with high-energy probes, we evaluate separately the contribution to the total signal from ionisation channels corresponding to the ground and excited states of the cation, as shown in Fig. 12, at 9.2 and 15 eV probe energies. At 9.2 eV the fraction of the signal due to excited cation states remains comparatively small, with a rather stable 30% fraction at all times. For the 15 eV probe, the excited states of the cation become important, and constitute >50% of the signal at times t > 50 fs. Although the importance of the excited-state channels is indisputable for high-energy probes, it is interesting to note that at t < 50 fs, the excited cation fraction for the 15 eV probe is as low as 15%, which is a consequence of the ionisation potentials and photoionisation cross sections for molecular geometries close to the ring-closed equilibrium geometry.
Finally, it is worth pointing out that the most direct comparison to experiment lies with the work of Adachi et al.22 who used a HHG probe of 13.6 eV. Those measurements show an early shift in the peak position associated with the excited state population which is taken as the transfer of population from the S1 to the S2 electronically excited state. The energy of the excited state bands at a binding energy around 5 eV which matches our calculated values associated the excited state driven dynamics on trajectory a. The measurements show a delayed increase in the ground state population of the ground state CHD and HT, although the measurements are hindered by an experimental artifact as discussed in ref. 22 that obscures the early-time dynamics at <200 fs, precluding direct comparison.
5 Conclusions
Using a compact model based on AI-MCE quantum molecular dynamics45 and a Dyson orbital approach for calculating ionisation cross sections,61 we have simulated time-resolved photoelectron spectra for the ring-opening reaction that transforms 1,3-cyclohexadiene (CHD) to hexatriene (HT). The calculations of photoelectron cross sections are validated against experimental CHD spectra, which provides an opportunity to assign the so-called channel two observed by mass spectrometry78 to excited-state fragmentation of the CHD+ cation. In the time-resolved spectra, the energy shift in the photoelectron spectrum at early times provides a direct reflection of the photochemical funnel which guides the initially excited wavepacket towards the conical intersection region in this archetypal Woodward–Hoffman molecule, and reflects the importance of the ionisation potentials in the analysis of photoelectron spectra. Ultimately, however, quantitative analysis requires knowledge of the photoionisation cross sections.We proceed to investigate the utility of a range of probe photon energies in time-resolved photoelectron spectroscopy using our model, from selective low-energy 2 eV probes to universal high-energy 15 eV probes. In CHD, the 2 eV photons are tuned to probe the transient S2 population, providing detailed insight into the dynamics. In contrast, the high-energy 9.2 and 15 eV probes are capable of following the wavepacket all the way down to the electronic S0 ground state, providing a complete view of internal conversion and the reaction path. Interestingly, differentiation of the two products, CHD and HT, requires the highest energy 15 eV probe since the molecules only appear different in the spectra once the excited states of the ion are considered, in agreement with previous findings.79,81
The calculations demonstrate that with a sufficiently high-energy probe, a complete picture of the photochemical processes can be obtained. This is particularly evident in dynamically simple systems fully described by a single pathway. However, as soon as several pathways are present, the signal becomes convoluted, making analysis complicated. If anything, including more trajectories in our model and compensating for the tendency towards overcoherence in Ehrenfest dynamics63 should strengthen this conclusion. This will be common for all universal probes where their global nature implies that selectivity is reduced. CHD is a particularly challenging example as the structural similarity of the products and starting molecule combined with similar timescales for all associated reaction paths increases the spectral congestion and hides many of the features when the data is energy-resolved only. It is clear from our analysis that it is difficult to disentangle the individual contributions to the total signal, a similar conclusion to the one drawn in a recent paper by Ruckenbauer et al.84 This strengthens the argument in favour of combining data from complementary experimental techniques,59 which can constrain calculations and inform reduced dimensionality models.
The issues associated with overlapping features and spectral congestion are also evident in other examples of global probes such as those based on diffraction45 or NEXAFS,58 with both studies using theoretically calculated dynamics to deconvolute and interpret the data. These examples, and the results in this article, support the case for accurate simulations of dynamics, but also demonstrate the need for accurate predictions of how the dynamics projects onto the measurement. With photoelectron spectroscopy specifically, there are additional experimental routes to deconvolute the contributions from the various reaction paths. This includes multiplexing the data through the collection of photoelectron angular distributions, or coincidence measurements where different products, for instance in dissociation, are produced. To extend the applicability of these situation, key steps will include extending the simulations to provide angular distributions and a more accurate description of the ionisation process such that channel interactions and the vibrational states of cation are taken into account. Measurement of ionisation via intermediate resonances may also carry extra information, but at the cost of increased complexity of the analysis.85,86 The final conclusion is that without extra information beyond the photoelectron spectrum, be that theory or angular distributions or something else, extracting information on complex and competing dynamic processes is quite challenging.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
Kenichiro Saita (Hokkaido University) is thanked for his work on the quantum molecular dynamics simulations and Samer Gozem (Georgia State University) is thanked for his help with the ezDyson calculations. RSM, AK, and MT thank the Leverhulme Trust for research funding (RPG-2013-365). AK acknowledges funding from the European Union (FP7-PEOPLE-2013-CIG-NEWLIGHT) and the Carnegie Trust via a Collaborative Research Grant held with Martin Paterson (HW). RSM acknowledges a Royal Society University Research Fellowship (UF150655). Part of the computational work reported used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk) and the Edinburgh Computer and Data Facility (ECDF) (http://www.ecdf.ed.ac.uk).References
- E. Havinga, R. J. D. Kock and M. P. Rappoldt, Tetrahedron, 1960, 11, 276–284 CrossRef.
- E. Havinga and J. L. M. A. Schlatmann, Tetrahedron, 1961, 16, 146–152 CrossRef.
- N. A. Anderson, J. J. Shiang and R. J. Sension, J. Phys. Chem. A, 1999, 103, 10730–10736 CrossRef.
- Photochromism: Molecules and Systems, ed. H. Dürr and H. Bouas-Laurent, Elsevier Science, 1st edn, 2003 Search PubMed.
- M. Irie, Chem. Rev., 2000, 100, 1685–1716 CrossRef PubMed.
- M. Irie, S. Kobatake and M. Horichi, Science, 2001, 291, 1769–1772 CrossRef PubMed.
- D. Geppert, L. Seyfarth and R. de Vivie-Riedle, Appl. Phys. B: Lasers Opt., 2004, 79, 987–992 CrossRef.
- S. Kobatake, S. Takami, H. Muto, T. Ishikawa and M. Irie, Nature, 2007, 446, 778–781 CrossRef PubMed.
- S. Deb and P. M. Weber, Annu. Rev. Phys. Chem., 2011, 62, 19 CrossRef PubMed.
- B. C. Arruda and R. J. Sension, Phys. Chem. Chem. Phys., 2014, 16, 4439–4455 RSC.
- M. N. R. Ashfold, M. Bain, C. S. Hansen, R. A. Ingle, T. N. V. Karsili, B. Marchetti and D. Murdock, J. Phys. Chem. Lett., 2017, 8, 3440–3451 CrossRef PubMed.
- N. A. Anderson, S. H. Pullen, L. A. Walker II, J. J. Shiang and R. J. Sension, J. Phys. Chem. A, 1998, 102, 10588–10598 CrossRef.
- R. B. Woodward and R. Hoffmann, Angew. Chem., Int. Ed., 1969, 8, 781–853 CrossRef.
- W. T. A. M. V. der Lugt and L. J. Oosterhoff, J. Am. Chem. Soc., 1969, 91, 6042–6049 CrossRef.
- M. Klessinger and J. Michl, Excited States and Photochemistry of Organic Molecules, Wiley-VCH, 1st edn, 1995 Search PubMed.
- M. Garavelli, C. S. Page, P. Celani, M. Olivucci, W. E. Schmid, S. A. Trushin and W. Fuss, J. Phys. Chem. A, 2001, 105, 4458–4469 CrossRef.
- P. J. Reid, S. J. Doig, S. D. Wickham and R. A. Mathies, J. Am. Chem. Soc., 1993, 115, 4754–4763 CrossRef.
- P. J. Reid, M. K. Lawless, S. D. Wickham and R. A. Mathies, J. Phys. Chem., 1994, 98, 5597–5606 CrossRef.
- M. K. Lawless, S. D. Wickham and R. A. Mathies, Acc. Chem. Res., 1995, 28, 493–502 CrossRef.
- S. H. Pullen, N. A. Anderson, L. A. Walker II and R. J. Sension, J. Chem. Phys., 1998, 108, 556–563 CrossRef.
- S. Lochbrunner, W. Fuss, W. E. Schmid and K.-L. Kompa, J. Phys. Chem. A, 1998, 102, 9334–9344 CrossRef.
- S. Adachi, M. Sato and T. Suzuki, J. Phys. Chem. Lett., 2015, 6, 343–346 CrossRef PubMed.
- O. Schalk, T. Geng, T. Thompson, N. Baluyot, R. D. Thomas, E. Tapavicza and T. Hansson, J. Phys. Chem. A, 2016, 120, 2320–2329 CrossRef PubMed.
- N. Kuthirummal, F. M. Rudakov, C. L. Evans and P. M. Weber, J. Chem. Phys., 2006, 125, 133307 CrossRef PubMed.
- S. A. Trushin, W. Fuß, T. Schikarski, W. E. Schmid and K. L. Kompa, J. Chem. Phys., 1997, 106, 9386–9389 CrossRef.
- W. Fuß, W. E. Schmid and S. A. Trushin, J. Chem. Phys., 2000, 112, 8347–8362 CrossRef.
- K. Kosma, S. A. Trushin, W. Fuß and W. E. Schmid, Phys. Chem. Chem. Phys., 2009, 11, 172–181 RSC.
- P. Celani, S. Ottani, M. Olivucci, F. Bernardi and M. A. Robb, J. Am. Chem. Soc., 1994, 116, 10141–10151 CrossRef.
- M. Merchán, L. Serrano-András, L. S. Slater, B. O. Roos, R. McDiarmid and X. Xing, J. Phys. Chem. A, 1999, 103, 5468–5476 CrossRef.
- S. Sakai and S. Takane, J. Phys. Chem. A, 1999, 103, 2878–2882 CrossRef.
- H. Tamura, S. Nanbu, H. Nakamura and T. Ishida, Chem. Phys. Lett., 2005, 401, 487–491 CrossRef.
- T. Mori and S. Kato, Chem. Phys. Lett., 2009, 476, 97–100 CrossRef.
- A. Nenov, P. Kölle, M. A. Robb and R. de Vivie-Riedle, J. Org. Chem., 2010, 75, 123–129 CrossRef PubMed.
- M. Garavelli, P. Celani, M. Fato, M. J. Bearpark, B. R. Smith, M. Olivucci and M. A. Robb, J. Phys. Chem. A, 1997, 101, 2023–2032 CrossRef.
- A. Hofmann and R. de Vivie-Riedle, J. Chem. Phys., 2000, 112, 5054–5059 CrossRef.
- C. Nonnenberg, S. Grimm and I. Frank, J. Chem. Phys., 2003, 119, 11585–11590 CrossRef.
- H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 124, 084313 CrossRef PubMed.
- A. Li, S. Yuan, Y. Dou, Y. Wang and Z. Wen, Chem. Phys. Lett., 2009, 478, 28–32 CrossRef.
- J. B. Schönborn, J. Sielk and B. Hartke, J. Phys. Chem. A, 2010, 114, 4036 CrossRef PubMed.
- A. Ohta, O. Kobayashi, S. O. Danielache and S. Nanbu, Chem. Phys., 2015, 459, 45–53 CrossRef.
- J. Kim, H. Tao, T. J. Martinez and P. Bucksbaum, J. Phys. B: At., Mol. Opt. Phys., 2015, 48, 164003 CrossRef.
- Y. Lei, H. Wu, X. Zheng, G. Zhai and C. Zhu, J. Photochem. Photobiol., A, 2016, 317, 39–49 CrossRef.
- J. Kim, H. Tao, J. L. White, V. S. Petrovič, T. J. Martinez and P. H. Bucksbaum, J. Phys. Chem. A, 2012, 116, 2758–2763 CrossRef PubMed.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. Robinson, T. J. Lane, D. Ratner, K. Saita, T. Northey, B. Stankus, V. Cofer-Shabica, J. Hastings and P. M. Weber, Faraday Discuss., 2014, 171, 81 RSC.
- M. P. Minitti, J. M. Budarz, A. Kirrander, J. S. Robinson, D. Ratner, T. J. Lane, D. Zhu, J. M. Glownia, M. Kozina, H. T. Lemke, M. Sikorski, Y. Feng, S. Nelson, K. Saita, B. Stankus, T. Northey, J. B. Hastings and P. M. Weber, Phys. Rev. Lett., 2015, 114, 255501 CrossRef PubMed.
- R. Iikubo, T. Sekikawa, Y. Harabuchi and T. Taketsugu, Faraday Discuss., 2016, 194, 147–160 RSC.
- A. J. Orr-Ewing, J. R. R. Verlet, T. J. Penfold, R. S. Minns, M. P. Minitti, T. I. Solling, O. Schalk, M. Kowalewski, J. P. Marangos, M. A. Robb, A. S. Johnson, H. J. Wörner, D. V. Shalashilin, R. J. D. Miller, W. Domcke, K. Ueda, P. M. Weber, R. Cireasa, M. Vacher, G. M. Roberts, P. Decleva, F. Bencivenga, D. M. Neumark, O. Gessner, A. Stolow, P. K. Mishra, I. Polyak, K. K. Baeck, A. Kirrander, D. Dowek, Á. Jiménez-Galán, F. Martín, S. Mukamel, T. Sekikawa, M. F. Gelin, D. Townsend, D. V. Makhov and S. P. Neville, Faraday Discuss., 2016, 194, 209–257 RSC.
- E. C. Carroll, B. J. Pearson, A. C. Florean, P. H. Bucksbaum and R. J. Sension, J. Chem. Phys., 2006, 124, 114506 CrossRef PubMed.
- E. C. Carroll, J. L. White, A. C. Florean, P. H. Bucksbaum and R. J. Sension, J. Phys. Chem. A, 2008, 112, 6811–6822 CrossRef PubMed.
- D. Geppert and R. de Vivie-Riedle, Chem. Phys. Lett., 2005, 404, 289–295 CrossRef.
- H. Tamura, S. Nanbu, T. Ishida and H. Nakamura, J. Chem. Phys., 2006, 125, 034307 CrossRef PubMed.
- R. S. Minns and A. Kirrander, Faraday Discuss., 2016, 194, 11–13 RSC.
- R. C. Dudek and P. M. Weber, J. Phys. Chem. A, 2001, 105, 4167–4171 CrossRef.
- C.-Y. Ruan, V. A. Lobastov, R. Srinivasan, B. M. Goodson, H. Ihee and A. H. Zewail, Proc. Natl. Acad. Sci. U. S. A., 2001, 98, 7117 CrossRef PubMed.
- H. Ihee, V. A. Lobastov, U. M. Gomez, B. M. Goodson, R. Srinivasan, C.-Y. Ruan and A. H. Zewail, Science, 2001, 291, 458 CrossRef PubMed.
- J. D. Cardoza, R. C. Dudek, R. J. Mawhorter and P. M. Weber, Chem. Phys., 2004, 299, 307–312 CrossRef.
- V. S. Petrovič, M. Siano, J. L. White, N. Berrah, C. Bostedt, J. D. Bozek, D. Broege, M. Chalfin, R. N. Coffee, J. Cryan, L. Fang, J. P. Farrell, L. J. Frasinski, J. M. Glownia, M. Gühr, M. Hoener, D. M. P. Holland, J. Kim, J. P. Marangos, T. Martinez, B. K. McFarland, R. S. Minns, S. Miyabe, S. Schorb, R. J. Sension, L. S. Spector, R. Squibb, H. Tao, J. G. Underwood and P. H. Bucksbaum, Phys. Rev. Lett., 2012, 108, 253006 CrossRef PubMed.
- A. R. Attar, A. Bhattacherjee, C. D. Pemmaraju, K. Schnorr, K. D. Closser, D. Prendergast and S. R. Leone, Science, 2017, 356, 54–59 CrossRef PubMed.
- C. C. Pemberton, Y. Zhang, K. Saita, A. Kirrander and P. M. Weber, J. Phys. Chem. A, 2015, 119, 8832 CrossRef PubMed.
- A. Kirrander, K. Saita and D. V. Shalashilin, J. Chem. Theory Comput., 2016, 12, 957–967 CrossRef PubMed.
- S. Gozem, A. O. Gunina, T. Ichino, D. L. Osborn, J. F. Stanton and A. I. Krylov, J. Phys. Chem. Lett., 2015, 6, 4532–4540 CrossRef PubMed.
- D. V. Shalashilin, Faraday Discuss., 2011, 153, 105 RSC.
- D. V. Makhov, W. J. Glover, T. J. Martinez and D. V. Shalashilin, J. Chem. Phys., 2014, 141, 054110 CrossRef PubMed.
- F. Fabre, G. Petite, P. Agostini and M. Clement, J. Phys. B: At. Mol. Phys., 1982, 15, 1353–1369 CrossRef.
- G. Petite, F. Fabre, P. Agostini, M. Crance and M. Aymar, Phys. Rev. A: At., Mol., Opt. Phys., 1984, 29, 2677–2689 CrossRef.
- U. Fano and A. R. P. Rau, Atomic collisions and spectra, Academic Press, 1st edn, 1986 Search PubMed.
- A. Kirrander, H. H. Fielding and C. Jungen, J. Chem. Phys., 2007, 127, 164301 CrossRef PubMed.
- A. Kirrander, H. H. Fielding and C. Jungen, J. Chem. Phys., 2010, 132, 024313 CrossRef PubMed.
- A. Kirrander, Ch. Jungen and H. H. Fielding, Phys. Chem. Chem. Phys., 2010, 12, 8948 RSC.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2007, 127, 234106 CrossRef PubMed.
- C. M. Oana and A. I. Krylov, J. Chem. Phys., 2009, 131, 124114 CrossRef PubMed.
- K. Saita and D. V. Shalashilin, J. Chem. Phys., 2012, 137, 22A506 CrossRef PubMed.
- H.-J. Werner, P. J. Knowles, G. Knizia, F. R. Manby and M. Schütz, et al., MOLPRO, version 2012.1, a package of ab initio programs.
- H. Tao, PhD thesis, Stanford University, California, 2011.
- R. C. Brown and E. J. Heller, J. Chem. Phys., 1981, 75, 186 CrossRef.
- N. Zotev and A. Kirrander, Manuscript in preparation.
- Y. Shao, L. F. Molnar, Y. Jung, J. Kussmann, C. Ochsenfeld, S. T. Brown, A. T. Gilbert, L. V. Slipchenko, S. V. Levchenko, D. P. O'Neill, R. A. DiStasio Jr, R. C. Lochan, T. Wang, G. J. Beran, N. A. Besley, J. M. Herbert, C. Yeh Lin, T. Van Voorhis, S. Hung Chien, A. Sodt, R. P. Steele, V. A. Rassolov, P. E. Maslen, P. P. Korambath, R. D. Adamson, B. Austin, J. Baker, E. F. C. Byrd, H. Dachsel, R. J. Doerksen, A. Dreuw, B. D. Dunietz, A. D. Dutoi, T. R. Furlani, S. R. Gwaltney, A. Heyden, S. Hirata, C.-P. Hsu, G. Kedziora, R. Z. Khalliulin, P. Klunzinger, A. M. Lee, M. S. Lee, W. Liang, I. Lotan, N. Nair, B. Peters, E. I. Proynov, P. A. Pieniazek, Y. Min Rhee, J. Ritchie, E. Rosta, C. David Sherrill, A. C. Simmonett, J. E. Subotnik, H. Lee Woodcock III, W. Zhang, A. T. Bell, A. K. Chakraborty, D. M. Chipman, F. J. Keil, A. Warshel, W. J. Hehre, H. F. Schaefer III, J. Kong, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Phys. Chem. Chem. Phys., 2006, 8, 3172–3191 RSC.
- J. Wang, B. Yang, T. A. Cool, N. Hansen and T. Kasper, Int. J. Mass Spectrom., 2008, 269, 210–220 CrossRef.
- K. Kimura, Handbook of HeI Photoelectron Spectra of Fundamental Organic Molecules, Japan Scientific Societies Press, Tokyo, Japan, 1981 Search PubMed.
- T. Horio, R. Spesyvtsev, Y. Furumido and T. Suzuki, J. Chem. Phys., 2017, 147, 013932 CrossRef PubMed.
- J. Nishitani, C. W. West, C. Higashimura and T. Suzuki, Chem. Phys. Lett., 2017, 684, 397–401 CrossRef.
- R. J. Squibb, M. Sapunar, A. Ponzi, R. Richter, A. Kivimäki, O. Plekan, P. Finetti, N. Sisourat, V. Zhaunerchyk, T. Marchenko, L. Journel, R. Guillemin, R. Cucini, M. Coreno, C. Grazioli, M. D. Fraia, C. Callegari, K. C. Prince, P. Decleva, M. Simon, J. H. D. Eland, N. Doslič, R. Feifel and M. N. Piancastelli, Nat. Commun., 2018, 9, 63 CrossRef PubMed.
- A. D. Smith, E. M. Warne, D. Bellshaw, D. A. Horke, M. Tudorovskya, E. Springate, A. J. H. Jones, C. Cacho, R. T. Chapman, A. Kirrander and R. S. Minns, Phys. Rev. Lett., 2018, 120, 183003 CrossRef PubMed.
- M. Ruckenbauer, S. Mai, P. Marquetand and L. González, Sci. Rep., 2016, 6, 35522 CrossRef PubMed.
- B. Stankus, J. M. Budarz, A. Kirrander, D. Rogers, J. Robinson, T. J. Lane, D. Ratner, J. Hastings, M. P. Minitti and P. M. Weber, Faraday Discuss., 2016, 194, 525–536 RSC.
- B. Stankus, N. Zotev, D. M. Rogers, Y. Gao, A. Odate, A. Kirrander and P. M. Weber, J. Chem. Phys., 2018, 148, 194306 CrossRef.
| This journal is © the Owner Societies 2018 |