How to treat C–F stretching vibrations? A vibrational CD study on chiral fluorinated molecules†
Abstract
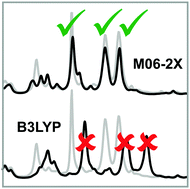
The analysis of vibrational circular dichroism and infrared spectra typically requires the prediction of spectra on the density functional theory level. In particular for absolute configuration determinations, for which the comparison between experiment and theory is often supported by similarity analysis algorithms, it is important that frequencies, relative band intensities and VCD signs are predicted correctly. Due to the poor prediction of harmonic frequencies, carbon–fluorine stretching vibrations are often strongly misplaced by common hybrid functionals such as B3LYP. Herein we show that the M06-2X functional provides harmonic C–F stretching frequencies with an accuracy sufficient for a reliable spectra analysis. We briefly discuss the origin of this exceptional performance and show that it is likely to be related to a cancellation of errors.
- This article is part of the themed collection: Challenges in spectroscopy: accuracy vs interpretation from isolated molecules to condensed phases


 Please wait while we load your content...
Please wait while we load your content...