Distinguishing different classes of secondary relaxations from vapour deposited ultrastable glasses

Abstract

Secondary relaxations persistent in the glassy state after structural arrest are especially relevant for the properties of the glass. A major thrust in research in dynamics of glass-forming liquids is to identify what secondary relaxations exhibit a connection to the structural relaxation and are hence more relevant. Via the Coupling Model, secondary relaxations having such connection have been identified by properties similar to the primitive relaxation of the Coupling Model and are called the Johari–Goldstein (JG) β-relaxations. They involve the motion of the entire molecule and act as the precursor of the structural α-relaxation. The change in dynamics of the secondary relaxation by aging an ordinary glass is one way to understand the connection between the two relaxations, but the results are often equivocal. Ultrastable glasses, formed by physical vapour deposition, exhibit density and enthalpy levels comparable to ordinary glasses aged for thousands of years, as well as some particular molecular arrangement. Thus, ultrastable glasses enable the monitoring of the evolution of secondary processes in case aging does not provide any definitive information. Here, we study the secondary relaxation of several ultrastable glasses to identify different types of secondary relaxations from their different relationship with the structural relaxation. We show the existence of two clearly differentiated groups of relaxations: those becoming slower in the ultrastable state and those becoming faster, with respect to the ordinary unaged glass. We propose ultrastability as a way to distinguish between secondary processes arising from the particular microstructure of the system and those connected in properties to and acting as the precursor of the structural relaxation in the sense of the Coupling Model.

---

Introduction

When a liquid is supercooled, its viscosity and structural α-relaxation time increase dramatically until the structural dynamics fall out of equilibrium and the ergodicity is broken at the glass transition temperature, T_g. Conventionally, when the structural α-relaxation time of the system exceeds 10²–10³ seconds the liquid is considered to become a glass.¹ However, in the glassy state, other relaxations remain active, originating from some structural degrees of freedom. These secondary relaxations are associated with local and non-correlated molecular reorientations.² There is no general agreement concerning the origin of the secondary relaxations or their characteristics. The simplest classification is based on the molecular origin,²i.e., whether the whole molecular unit is involved in the process (Johari–Goldstein (JG) relaxation) or only a part of it (non-JG relaxation). However, it is still debated whether all molecules in the system contribute to the secondary relaxation, or only part of them, located in some “islands of mobility” due to density heterogeneities,³i.e., local regions in the rigid glassy structure where density is lower.^4,5 On the other hand, according to the Coupling Model (CM), one of the characteristics of the secondary relaxations that makes them important is their link in properties to the structural relaxation, in analogy to the primitive relaxation of the model.² With this criterion in mind, Ngai and Paluch distinguish secondary relaxations based on their sensitivity to pressure, thermal history, and other properties mimicking the corresponding properties of the structural α-relaxation,⁶ and the nomenclature, Johari–Goldstein (JG) β-relaxation, was adopted.²

The lack of agreement of the observed behaviour of the secondary relaxation is manifested in a number of reported works on aging of ordinary glasses. For example, in dipropylene glycol dibenzonate, the secondary relaxation slows down on aging.⁷ The same was observed during aging of the secondary process of etoricoxib with properties similar to the JG β-relaxation⁸ and in sucrose.⁹ On the contrary, various works have shown a speeding up of the secondary relaxation in several materials undergoing aging.^5,10–12 A recent paper reported that the change in the JG β-relaxation time and dielectric strength during physical aging of two PMMA glasses formed at 188 MPa and at 0.1 MPa are the same.¹³ Thus, the change of the secondary relaxation with aging is found to be independent of the density, since the glass formed at high pressure of 188 MPa is denser than that formed at 0.1 MPa. To rationalize this observation, the authors of ref. 13 suggested that the average density does not govern the dynamics of the glass, but rather the local structure and barriers for thermal fluctuations of density are the main control parameters. All these complicated and uneven observed changes of the secondary relaxation on aging make them inappropriate to distinguish secondary relaxation having connection to the α-relaxation or not.

Aging of glasses has been considered as a useful tool to study secondary relaxations, but as aforementioned, the effects are varied and complicated. Moreover, aging is a slow and inefficient process for densification and impractically long times are required to observe a significant change. Recently, vapour deposition emerged as a unique tool to prepare glasses with an unprecedented thermodynamic and kinetic stability,^14–16 comparable to glasses aged for thousands or millions of years^17,18 such as ambers.^19,20 Choosing the appropriate deposition conditions, it is possible to obtain over short times the so-called ultrastable glass (USG), with a density around 1.5% higher than that of ordinary glasses (OG) prepared by cooling from the liquid.^21–23 This remarkable increase in density and equivalent age of the glass implies a significant alteration of the properties of the secondary relaxation,^8,18 accompanying the dramatic slowing down of the structural α-relaxation,^16,24,25 and the immense shift of the α-relaxation to lower frequencies. Here, we have chosen six different materials and analysed some of their secondary relaxations in the USG state produced by vapour deposition, as well as in the OG state of the same samples obtained by cooling below the nominal T_g. The purpose of the work is to understand how the secondary relaxations in these materials respond to the remarkable change in thermodynamic and dynamic properties in the USG compared to the OG.

Methods

Preparation of samples

Etoricoxib was purchased from Aopharm with purity higher than 99%. Telmisartan was supplied from Dr Reddy's Laboratories Limited, with purity higher than 98%. β-D-Maltose octa-acetate was purchased from Alpha Aesar, with purity level of 98%. Carvedilol was synthetized in the laboratories of Polpharma. Celecoxib was obtained from Haihang Industry Co. with purity level higher than 98%. All materials were used in crystalline form and without further purification. USG films with thickness of around 25 μm were grown by thermal evaporation within a UHV setup with base pressure of 5 × 10⁻⁸ mbar. A liquid nitrogen cold trap was used to improve the vacuum quality. The growth rate was fixed to 0.25 ± 0.02 nm s⁻¹ and measured with a quartz crystal from Inficon. The deposition temperature was set at ∼0.85T_g for each material (etoricoxib, T_dep = 280 K, telmisartan, T_dep = 340 K, β-D-maltose octaacetate, T_dep = 282 K, carvedilol, T_dep = 285 K and celecoxib, T_dep = 278 K) and controlled using a PID controlled thermal socket. The films were grown onto steel electrodes used for BDS and in aluminum foil for DSC measurements (see corresponding subsections). The OG was prepared either by annealing of the USG above T_on or, alternatively, by melting crystalline powder directly onto a steel electrode on a hot plate at the corresponding melting temperature, covered by another electrode (separated by Teflon spacers with 0.1 mm of thickness) and then cooled down in a refrigerated cooper plate.

Differential scanning calorimetry (DSC)

Calorimetric measurements were carried out using a Mettler-Toledo DSC 1. Temperature and enthalpy calibrations were performed using indium and zinc standards. Aluminum crucibles of 40 μL were filled with the USG sample grown on top of aluminum foil and closed using the crucible sealing press. The examined material was heated at 10 K min⁻¹ until devitrification, cooled down at the same rate to produce the OG and measured again.

Broadband dielectric spectroscopy (BDS)

Isobaric dielectric measurements at atmospheric pressure were performed using a Novocontrol GMBH Alfa-A analyzer with maximum frequency range from 10⁻² Hz to 10⁶ Hz. The measurement temperature was controlled by a Quatro temperature controller using a nitrogen gas cryostat with accuracy better than 0.1 K. During the measurements, the samples were placed between the steel electrodes of the capacitor (15 mm diameter).

Dielectric data was fitted by the Havriliak–Negami (HN) equation,

where ε_∞ is the limiting high-frequency permittivity, τ_HN denotes the characteristic relaxation time, the exponents α and β characterize symmetric and asymmetric broadenings of the dielectric loss curve respectively, Δε is the relaxation strength and ω is the angular frequency. Values of relaxation time were calculated from the maximum of the dielectric permittivity peaks using the expression τ = (2πf_max)⁻¹.

Results and discussion

In all the investigated cases, the observed secondary process is well separated from the structural relaxation, which facilitates accurate determination of the relaxation times and strength. The difference in calorimetric T_on between USG and OG for each material, shown in Table 1 (calorimetric curves shown in Fig. S1–S4, ESI†), is a signature of the enhancement in kinetic stability of the former. In Fig. 1 we show, in an Arrhenius plot, the relaxation times of the measured secondary processes in the USG and OG of different materials (the complete set of dielectric spectra can be found in Fig. S5–S9, ESI†). From these plots, we distinguish two groups of secondary relaxations, based on the differences in the characteristics between USG and OG. The first group (Fig. 1A–C) exhibits slower relaxation time in the USG than in the OG. The second group (Fig. 1D–F) reveals the opposite behaviour, which seems striking since there is enhancement in kinetic stability and density of the all USG compared to the OG. In all cases, the strength of the process decreases in the USG (see ESI†). In Fig. 2, we show the dielectric loss at particular temperatures for the USG and OG of etoricoxib and β-D-maltose octa-acetate, as representatives of the two groups. We note that this classification is completely independent from the well-known classification by A. Kudlik et al., who distinguish two types of glass-forming materials, types A and B, by the fact of whether they exhibit a resolved or discernible β-process or not.²⁶

Table 1 Change in onset temperature of devitrification, T_on, and secondary relaxation time, τ, between USG and OG. Changes in T_on are measured from DSC scans (see ESI). τ values correspond to the calorimetric T_g, i.e. at the same temperature for USG and OG

	T on,USG − Ton,OG (K)	log(τUSG(Tg)) − log(τOG(Tg))
Toluene	7	0.74
Telmisartan	26	0.75
Etoricoxib	33	0.66
β-D-Maltose octa-acetate	21	−0.33
Carvedilol	15	−0.24
Celecoxib	18	−0.7

---

Fig. 1 Map of relaxation time of the analysed secondary relaxations. Black and red closed symbols correspond to the USG and the OG obtained after transformation of the USG and subsequent cooling down, respectively. The red open points and the orange VFT fit to the structural α-relaxation are obtained from the literature (etoricoxib,^32,33 telmisartan,^34,35 maltose octa-acetate,³⁶ carvedilol³⁷ and celecoxib³⁸). All data for toluene and etoricoxib are extracted from H. B. Yu et al.¹⁸ and Rodriguez-Tinoco et al.,⁸ respectively. The black and red circles indicate the value of secondary relaxation time at T_on. The horizontal blue lines in (a–c) graphs remark the invariance of the secondary relaxation time at T_on. The sketch of each molecule is also depicted.

Fig. 2 Dielectric loss of USG and OG of etoricoxib and β-D-maltose octa-acetate, measured at three different temperatures in the glassy state, showing the analyzed secondary relaxation process and its difference in the USG and OG states.

The main and most interesting feature extracted from the reported relaxations in the first group of Fig. 1(A–C) is their link in properties with the structural α-relaxation. As a consequence of the increase of density in the USG, they become slower, in parallel with the α-relaxation. The secondary relaxation time of these materials at T_on, defined as the temperature at which the glass relaxes back to equilibrium upon heating (τ_α ≈ 100 s), is the same in the USG and in the OG, as elucidated by the horizontal blue lines in Fig. 1(A–C). As a consequence, when we plot the data in Fig. 1 as a function of T_on/T, the secondary relaxation of USG and OG collapse into a single curve (Fig. 3, blue regions). This invariance is equivalent to the one observed in glasses under elevated pressure, p, at T_g(p), i.e., the secondary relaxation slows down in a way that at T_g(p), the value of τ_β(p) is invariant,^2,27–30 and moreover log τ_α(p) and log τ_β(p) collapse each into a single curve when represented as a function of T_g(p)/T (Fig. S10–S12, ESI†). From calorimetric data, Rodríguez-Tinoco and co-workers inferred the structural relaxation times of vapour deposited glasses of indomethacin and toluene embedded with different thermodynamic stability.¹⁶ When represented as a function of T_on/T, all data corresponding to the structural relaxation of the different glasses of each material collapse into a single curve (Fig. S13, ESI†), in the same way as the secondary relaxation, as seen for toluene in the inset of Fig. 3. Furthermore, it was also shown for etoricoxib and toluene that the secondary relaxation defines an equilibrium state which is consistent with the one defined by the structural relaxation. In other words, one can use a single fictive temperature to connect the characteristics of the secondary relaxation to those of the α-relaxation.^8,18 All these observations indicate a strong connection between this type of secondary relaxation and the structural process, and this connection is manifested either by elevating pressure or by ultrastability. This observation is related to the property invoked by Ngai and co-workers to explain the nearly invariance of surface diffusion in different types of glasses (USG, aged or thin film), and was attributed to the approximate agreement between the secondary relaxation time and the primitive relaxation time.³¹ By contrast, the behaviour of the secondary relaxations pertaining to the second group in Fig. 1D–F is the opposite to the previous case. In these Arrhenius plots, the secondary relaxation time in USG and OG becomes more separated when represented as a function of T_on/T in Fig. 3 (red region). This contrasting behaviour can be also appreciated from the data in Table 1, where we compare the difference between the calorimetric T_on of USG and OG with the difference in secondary relaxation time at T_g. It is also noticeable that, in all cases, the change in relaxation time is considerably small (around one order of magnitude), which contrasts with the remarkable enhancement of structural stability in USG, as indicated by the large increase in T_on with respect to the OG, and by the increase in transformation time of USG with respect to OG by 4–5 orders of magnitude found in other studies.^16,24,25

Fig. 3 Secondary relaxations of different materials as a function of T_on/T. Two groups are distinguished: those relaxations which are slower in the USG with respect to the OG (blue area) and those which are faster in the USG with respect to the OG (red area). The relaxations in the blue area are strongly linked to the structural relaxation and, as a consequence, USG and OG relaxations collapse one into the other when normalized by T_on, which is related to the structural relaxation. In the inset, together with the secondary relaxation data of toluene shown in the main figure, we plot structural relaxation data inferred from reported calorimetric data.¹⁶ Together with the data from the USG (closed squares) and the OG (open stars), data corresponding to an intermediate stability is included (open circles). Secondary relaxation data corresponding to toluene and etoricoxib have been taken from the literature.^8,18

The different directions of change of secondary relaxation time in OG to USG shown in Fig. 3 indicate the existence of two types of secondary relaxations. Importantly, the analysed secondary relaxations in toluene¹⁸ and telmisartan^34,35 have been previously identified to belong to the class of the Johari–Goldstein (JG) β-relaxation, and the one observed in etoricoxib has been considered as pseudo-JG or JG-γ, as a consequence of its properties mimicking those of the structural relaxation.^8,33 From the structural point of view, JG relaxations correspond to movements of the whole molecular unit. All these JG related relaxations correspond to the blue region in Fig. 3. On the other hand, the secondary relaxation of celecoxib considered in Fig. 1–3 was reported to be a delta relaxation,³⁸ being the much slower JG β-relaxation not well resolved at ambient pressure. From the analysis of the relaxation processes in β-D-maltose octa-acetate and carvedilol and its comparison to the primitive relaxation time of the CM we can conclude that these relaxations are also not the JG β-relaxation (Fig. S14–S16, ESI†), and, hence, they correspond to movements of only part of the molecule, probably a rotation of a side group. Thus, all three relaxations belonging to the red group in Fig. 3 are not JG β-relaxation, while those three in the blue group are either JG β-relaxation or JG γ-relaxation. This match conveys that USG is no different from OG in asserting the fundamental importance of the JG β-relaxation as the indispensable originator of the α-relaxation. We have to be cautious with this statement though, since there are reported measurements of JG relaxations which speed up upon aging.^5,10–12 However, those reported relaxations are extremely close to the structural relaxation, which complicates the data analysis, or in polymers, which may behave differently than molecular glasses. Notwithstanding, the classification indicated in Fig. 3 clearly establishes a distinction between two kinds of process, independently of the assigned nomenclature or molecular origin. The invariance or not of the secondary relaxation time at T_on of USG and OG provides a key element in the classification of secondary relaxations.

It is important to remark that the existence of relaxations from one group does not exclude the presence of relaxations from the other for the same molecule. For example, telmisartan and etoricoxib exhibit, apart from the JG relaxation analysed in this work, a faster relaxation which has not been analysed here.^32,35 Also, as commented above, celecoxib exhibits a hidden and low intensity JG relaxation close to the structural relaxation.³⁸ The further remarkable decrease of the intensity of the secondary process in the USG precludes its analysis in this work. If measurable, we would expect the JG process in celecoxib to pertain to the blue group in Fig. 3, together with the relaxation exhibited in etoricoxib, very similar to celecoxib from the structural point of view, but faster and easily measurable in the USG. With these remarks we want to stress that the elucidated distinction between types of secondary relaxations is not related to the material itself or to its molecular structure but to the particular analysed secondary relaxation, to their connection with the α relaxation or whether they are originated from inter or intramolecular motions.

The suitability of using USG to classify secondary relaxations into the two mentioned groups is remarkable and relevant, especially when analysing the evolution of the secondary relaxation time during the aging shown in Fig. 4. In general, the characteristics of the secondary relaxation in USG is mirrored in the evolution of the process during aging, as expected since vapour deposition yields glasses which are, in many aspects, equivalent to OG aged for much longer times. The variations observed after several hours of aging are, though, dramatically smaller than those observed in USG (as seen in the inset of Fig. 3), and, in some cases, changes in relaxation time induced by aging are subtle and difficult to detect, as seen in the ESI† (Fig. S17–S20). Changes observed in USG compared to OG are much clearer, as seen in the inset of Fig. 4 (as well as in Fig. S6–S9, ESI†). Especially relevant is the case of β-D-maltose octa-acetate, whose secondary relaxation does not show any significant tendency during aging, while a clear speeding up is observed in the USG.

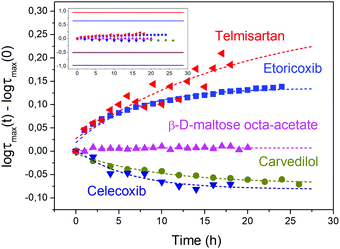Fig. 4 Evolution of the secondary relaxation time during aging at 0.9T_g for different materials. The measurement temperatures for each material are reported in the ESI.† In the inset, the same data is reproduced together with the difference between the secondary relaxation time in the USG and OG at the same measuring temperature for all molecules, remarking the suitability of USG to monitor those differences.

The clear distinction between the two types of relaxations becomes more evident when considering the effects of elevated pressure. In fact, pressure is used as a variable to classify secondary relaxation processes.⁶ In the case of etoricoxib, from the first group of relaxations (blue region of Fig. 3), the increase of secondary relaxation time as a result of ultrastability, aging or pressurization is positive in all cases.⁸ Furthermore, the secondary relaxation time at T_on does not depend on the particular method followed to increase T_on (in the case of the glass at elevated pressure T_on= T_gP),⁸ meaning that an increase of pressure or ultrastability affect its secondary relaxation in the same manner as they affect its structural relaxation. On the other hand, when a β-D-maltose octa-acetate glass is subjected to elevated pressure, its secondary relaxation time increases (Fig. S21, ESI†), while an increase of density due to ultrastability does not induce an increase of the secondary relaxation time but a decrease (Fig. 1 and 2). In all cases, an increase of density is associated with a slowing down in the structural relaxation of the system, which translates in an increase in the T_on. In particular, dT_g/dp in β-D-maltose octa-acetate is 0.281 K MPa⁻¹,³⁹ meaning that an OG at 75 MPa exhibits the same T_g = T_on than the USG at ambient pressure. As a result of this, we would have two glasses of the same material, with the same T_on, but with different secondary relaxation times. It was also reported for polyvinyl-ethylene (PVE) that the glass produced by aging exhibits a faster secondary process than the original unaged glass, while the glass prepared at high pressure, considered to have higher density, exhibits slower relaxation time.¹¹ These observations go in the direction of and are compatible with the thermodynamic scaling of different kinds of relaxation processes. Ngai and Paluch have shown that the thermodynamic scaling of the structural relaxation satisfied in many glass-forming liquids originates from the scaling of the primitive relaxation process (identified as the JG β-relaxation),⁴⁰ meaning that both structural and JG β-relaxations are governed by the same thermodynamic variables. Romanini et al. show for ternidazole, which exhibits three secondary relaxations processes, that only the structural and the slowest of the secondary relaxation processes (identified as a JG β-relaxation) satisfy the thermodynamic scaling.⁴¹ These reports, together with the results reported in this work, indicate that some kind of relaxations are linked with the structural relaxation, while the other is influenced by other factors. The same is also reflected in the aging behaviour of dipropylene glycol dibenzonate, with two secondary relaxation processes, the slowest of which slows down with time, in correlation with the structural relaxation, while the faster one remains unchanged.⁷ Ultrastability emerges as a useful tool to distinguish between distinct types of secondary relaxations.

The slowing down of the secondary process in USG or by aging can be rationalized in terms of the increase of density, and the link between structural and secondary relaxation processes are the basis of the CM.² However the reported speeding up of some other relaxations on aging in several materials is an intriguing and controversial phenomenon.^3,42 As deduced from the red region in Fig. 3, an increase of the average macroscopic density induced by ultrastability results in a decrease of the associated secondary relaxation time, i.e. average density and secondary relaxation time anticorrelate. We propose here two plausible scenarios to explain the observed phenomena. One explanation is based on the observation that the relaxations in the blue region of Fig. 3 are JG while those in the red regions are non-JG, and can be traced to two factors. Firstly, the non-JG secondary relaxation time is usually much shorter and involves motion of a small part of the molecule with intramolecular degree of freedom. Secondly, the micro structure of USG is different from OG as inferred from the birefringence of USG, whether it is due to molecular orientations,^43–46 or other causes.⁴⁷ The change in packing accompanying molecular ordering may enhance the mobility of the very local non-JG secondary relaxation in USG to a larger extend compared to the OG, despite the increase in density. On the other hand, the JG relaxation is known to involve the entire molecule in order to perform as the precursor of the α-relaxation. Its larger length-scale implies a higher sensitivity to the increase in macroscopic density than the non-JG relaxation. Furthermore, its relaxation time has to increase in concert with the increase of the α-relaxation time in USG because of the fundamental connection between these two relaxations.

The second plausible scenario is based on the concept of islands of mobility. According to this idea, secondary relaxations are originated in looser regions in the otherwise rigid structure of the glass.³ Some works refer to it as a kind of glue or connective tissue between clusters.⁴⁸ This idea emerges from the analogy to well-known theories based on the structural heterogeneity of glasses, such as Stillinger's model,⁴⁹ the modified continuous random network model by Greaves,⁵⁰ the entropy and density fluctuation model by Ediger,⁵¹ and the concept of cooperatively rearranging region (CRR) and its correlation length by Donth.⁵² A similar model was also considered to explain the properties of fragile metallic glass formers.⁵³ The anticorrelation between density and relaxation time observed in some systems has been often attributed to this inherent heterogeneity of the molecular structure in the glass.^4,5,10–12 We suggest a combination of this interpretation with the fundamental point of the Coupling Model, which considers the secondary JG relaxations as precursor of the structural relaxation. Hence, in this scenario, the relaxations in the blue or red regions of Fig. 3 originate from inside clusters or in the connective tissue around them, respectively. When the glass ages or is produced by vapour deposition in USG conditions, groups of molecules forming clusters stick together and become denser, resulting in a higher overall density. The secondary relaxations originated in those clusters are slower in the USG as a consequence of the higher overall density. At the same time, the connective tissue around clusters become looser as a consequence of the shrinking of the later, and the associated secondary relaxation process becomes faster in the USG. When applying elevated pressures, a homogeneous increase in density always slows down the process, regardless of its origin, as commented before. It is important to remark that the secondary relaxation process originated in low density areas are not necessary independent of the structural relaxation. Indeed, Roland and Casalini indicated that the evolution of the secondary relaxation in polyvinylethylene¹¹ or in polymethylmethacrylate,¹³ both speeding up with age, can be used to determine the structural relaxation of the system. K. Kaminski et al. also suggested that the structural relaxation of the system could be measured from the evolution of different types of secondary relaxation, including intramolecular ones, a priori without connection to the structural process.⁹ This interpretation is compatible with both visions: while the secondary processes originated from the clusters are the precursor of the structural relaxation in the sense of the CM, those from the connective tissue are influenced by the structural relaxation and can be still used to trace back the dynamics of the structural process, as discussed in the literature, even though other factors may have influence on its dynamics.

Notwithstanding, in both scenarios one type of secondary relaxation is directly related with and unambiguously determined by the structural relaxation (as manifested through the invariance of τ_sec at T_on or the overlap of the secondary relaxation plots when normalized by T_on) and the other is, additionally, influenced by the microstructure of the glass. Therefore, the difference in the response to the ultrastability of secondary relaxations is a useful and practical criterion to distinguish between two major classes of secondary relaxations, rather than the molecular origin underneath.

It would be ideal if one can tell which class the observed secondary relaxation belongs to, directly from the molecular structure of the glass-former. This is clearly not possible for the six glass-formers from their molecular structures shown in Fig. 1. Although this is possible if an additional criterion related to molecular structure is utilized, which is whether the entire molecule, or part of it, is involved in the secondary relaxation.^2,6 Obviously the secondary relaxation of the totally rigid molecule of toluene involves the motion of entire molecule, and accounts for it in the blue group. Two secondary relaxations β and γ were found in telmisartan, and in this work we study the slower β-relaxation for its response to ultrastability. Since it is the slowest secondary relaxation, it can involve the motion of the entire telmisartan molecule, and hence telmisartan belongs to the blue group based on the criterion related to molecular structure. If one needs further affirmation of this identification, the β-relaxation time was shown approximately the same as the primitive relaxation time of the CM in toluene^2,6 and telmisartan.^34,35 In the case of etoricoxib, its molecular structure by itself is not helpful to rationalize why the observed secondary relaxation belongs to the blue group, because the molecular structure of celecoxib is similar and yet the secondary relaxation observed belongs to the red group. This conundrum is resolved by the contrasting response to applied pressure. While the secondary relaxation in etoricoxib⁸ is sensitive to pressure, it is not found in celecoxib.³⁸ Previous studies have shown that the relaxation of celecoxib in Fig. 1, 3 and 4 is not the slowest secondary relaxation.³⁸ The latter has very weak dielectric strength and barely resolved in the glassy state, and its relaxation time at T_g is in agreement with the primitive relaxation time. Thus, without the help of other facts in the cases of etoricoxib and celecoxib, molecular structures alone cannot be used to characterize the secondary relaxation. On the other hand, the molecular structures of maltose octa-acetate, and carvedilol are instructive to infer that the secondary relaxation observed in Fig. 1, 3 and 4 involve the motion of part of the molecule and is intramolecular in origin. The flexible glycosidic bond and the C–O–OCH₃ groups in maltose octa-acetate, and the long flexible side chains in carvedilol are likely the source of the intramolecular secondary relaxations, making them to belong to the red group from its response to ultrastability. Additional evidence comes from the very short relaxation time at T_g, as well as the small activation energy of the secondary relaxation.

Conclusions

In summary, we have presented a new classification of secondary relaxations based on their behaviour in ultrastable glasses. On one hand, some secondary relaxations are strongly linked to the structural relaxation, manifested by the invariance of the secondary relaxation time at T_on, i.e. the temperature at which the system relaxes back to equilibrium, as well as through the superposition of USG and OG secondary relaxation times when represented as a function of T_on/T. This is a generalization extending to USG the strong connection between the α-relaxation and the secondary relaxation established before in other systems in the OG or liquid state using pressure as a measuring variable, such as DGEBA,⁸ PPGE²⁸ or others.²⁹ Observed is the approximate invariance of the ratio, τ_α(p,T)/τ_β(p,T), to variations of p and T while either τ_α(p,T) or τ_β(p,T) is kept the same. On the other hand, some other secondary relaxations appear to be faster in the USG state than in the OG at all temperatures and in particular at T_on. These novel findings in USG provide another criterion to classify secondary relaxations into two types. This criterion derived from the response of secondary relaxations to ultrastability is novel, but it is also consistent with the conventional criterion of whether the secondary relaxation is strongly connected with the structural relaxation or not.^2,6,27,30,40 It is beneficial to continue using this new criterion to distinguish secondary relaxations, particularly in those cases where the molecular origin of the secondary relaxation is unclear.

It is remarkable that the differences observed in the secondary relaxations in USG, whether in the blue or red group of Fig. 3, are much more intense than the differences yielded by aging, which in some cases is not sufficient to observe any significant trend in the evolution of secondary relaxations. In this sense, vapour deposition offers a new benchmark, since it permits to obtain glasses that, from a thermodynamic point of view, are equivalent to glasses aged for thousands or millions of years, time scales inaccessible in laboratories. Furthermore, vapour deposition permits to tune the molecular orientation of molecular glasses and, therefore, it offers the opportunity to explore the effect of orientation in the characteristics of secondary relaxation and provide relevant information concerning the microstructure of the system, especially if different preparation methods (vapour deposition, aging, densification by pressurization, or others) are compared.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. R.-T., M. R.-B. and M. P. acknowledge the support from the National Science Centre through the Polonez scheme (Grant No. DEC-2015/19/P/ST3/03540/2). This project has received funding from the European Union's Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 665778. C. R.-T. also thanks Joan Ràfols-Ribé and Ana Vila-Costa for support during the preparations of the samples.

References

1. P. G. Debenedetti and F. H. Stillinger, Supercooled liquids and the glass transition, Nature, 2001, 410, 259–267.
2. K. L. Ngai, Relaxation and Diffusion in Complex Systems, Springer New York, New York, NY, 2011.
3. G. Johari, Localized molecular motions of β-relaxation and its energy landscape, J. Non-Cryst. Solids, 2002, 307–310, 317–325.
4. N. B. Olsen, T. Christensen and J. C. Dyre, β relaxation of nonpolymeric liquids close to the glass transition, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 4435–4438.
5. J. K. Vij and G. Power, Physical ageing and the Johari–Goldstein relaxation in molecular glasses, J. Non-Cryst. Solids, 2011, 357, 783–792.
6. K. L. Ngai and M. Paluch, Classification of secondary relaxation in glass-formers based on dynamic properties, J. Chem. Phys., 2004, 120, 857–873.
7. D. Prevosto, S. Capaccioli, M. Lucchesi, P. A. Rolla and K. L. Ngai, Dynamics of supercooled and glassy dipropyleneglycol dibenzoate as functions of temperature and aging: Interpretation within the coupling model framework, J. Chem. Phys., 2004, 120, 4808–4815.
8. C. Rodríguez-Tinoco, M. Rams-Baron, K. L. Ngai, K. Jurkiewicz, J. Rodríguez-Viejo and M. Paluch, Secondary relaxation in ultrastable etoricoxib: evidence of correlation with structural relaxation, Phys. Chem. Chem. Phys., 2018, 20, 3939–3945.
9. K. Kaminski, K. Adrjanowicz, E. Kaminska and M. Paluch, Probing of structural relaxation times in the glassy state of sucrose and trehalose based on dynamical properties of two secondary relaxation processes, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 83, 61502.
10. H. Yardimci and R. L. Leheny, Aging of the Johari–Goldstein relaxation in the glass-forming liquids sorbitol and xylitol, J. Chem. Phys., 2006, 124, 214503.
11. R. Casalini and C. M. Roland, Anomalous properties of the local dynamics in polymer glasses, J. Chem. Phys., 2009, 131, 114501.
12. G. Power, J. K. Vij and G. P. Johari, Kinetics of spontaneous change in the localized motions of D-sorbitol glass, J. Chem. Phys., 2006, 124, 74509.
13. R. Casalini and C. M. Roland, Communication: Effect of density on the physical aging of pressure-densified polymethylmethacrylate, J. Chem. Phys., 2017, 147, 91104.
14. S. F. Swallen, K. L. Kearns, M. K. Mapes, Y. S. Kim, R. J. McMahon, M. D. Ediger, T. Wu, L. Yu and S. Satija, Organic Glasses with Exceptional Thermodynamic and Kinetic Stability, Science, 2007, 315, 353–356.
15. E. A. A. Pogna, C. Rodríguez-Tinoco, G. Cerullo, C. Ferrante, J. Rodríguez-Viejo and T. Scopigno, Probing equilibrium glass flow up to exapoise viscosities, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 2331–2336.
16. C. Rodríguez-Tinoco, J. Ràfols-Ribé, M. González-Silveira and J. Rodríguez-Viejo, Relaxation dynamics of glasses along a wide stability and temperature range, Sci. Rep., 2016, 6, 35607.
17. K. L. Kearns, S. F. Swallen, M. D. Ediger, T. Wu, Y. Sun and L. Yu, Hiking down the Energy Landscape: Progress Toward the Kauzmann Temperature via Vapor Deposition, J. Phys. Chem. B, 2008, 112, 4934–4942.
18. H. B. Yu, M. Tylinski, A. Guiseppi-Elie, M. D. Ediger and R. Richert, Suppression of β Relaxation in Vapor-Deposited Ultrastable Glasses, Phys. Rev. Lett., 2015, 115, 185501.
19. T. Pérez-Castañeda, R. J. Jiménez-Riobóo and M. A. Ramos, Two-Level Systems and Boson Peak Remain Stable in 110-Million-Year-Old Amber Glass, Phys. Rev. Lett., 2014, 112, 165901.
20. J. Zhao, S. L. Simon and G. B. McKenna, Using 20-million-year-old amber to test the super-Arrhenius behaviour of glass-forming systems, Nat. Commun., 2013, 4, 1783.
21. S. S. Dalal, Z. Fakhraai and M. D. Ediger, High-throughput ellipsometric characterization of vapor-deposited indomethacin glasses, J. Phys. Chem. B, 2013, 117, 15415–15425.
22. A. Laventure, A. Gujral, O. Lebel, C. Pellerin and M. D. Ediger, Influence of Hydrogen Bonding on the Kinetic Stability of Vapor-Deposited Glasses of Triazine Derivatives, J. Phys. Chem. B, 2017, 121, 2350–2358.
23. D. M. Walters, R. Richert and M. D. Ediger, Thermal stability of vapor-deposited stable glasses of an organic semiconductor, J. Chem. Phys., 2015, 142, 134504.
24. Z. Chen, A. Sepúlveda, M. D. Ediger and R. Richert, Dynamics of glass-forming liquids. XVI. Observation of ultrastable glass transformation via dielectric spectroscopy, J. Chem. Phys., 2013, 138, 12A519.
25. C. J. Fullerton and L. Berthier, Density controls the kinetic stability of ultrastable glasses, EPL, 2017, 119, 36003.
26. A. Kudlik, S. Benkhof, T. Blochowicz, C. Tschirwitz and E. Rössler, The dielectric response of simple organic glass formers, J. Mol. Struct., 1999, 479, 201–218.
27. K. L. Ngai, J. Habasaki, D. Prevosto, S. Capaccioli and M. Paluch, Thermodynamic scaling of α-relaxation time and viscosity stems from the Johari–Goldstein β-relaxation or the primitive relaxation of the coupling model, J. Chem. Phys., 2012, 137, 34511.
28. D. Prevosto, S. Capaccioli, S. Sharifi, K. Kessairi, M. Lucchesi and P. A. Rolla, Secondary dynamics in glass formers: Relation with the structural dynamics and the glass transition, J. Non-Cryst. Solids, 2007, 353, 4278–4282.
29. D. Prevosto, S. Capaccioli, M. Lucchesi, P. A. Rolla and K. L. Ngai, Does the entropy and volume dependence of the structural α-relaxation originate from the Johari–Goldstein β-relaxation?, J. Non-Cryst. Solids, 2009, 355, 705–711.
30. M. Mierzwa, S. Pawlus, M. Paluch, E. Kaminska and K. L. Ngai, Correlation between primary and secondary Johari–Goldstein relaxations in supercooled liquids: invariance to changes in thermodynamic conditions, J. Chem. Phys., 2008, 128, 44512.
31. K. L. Ngai, M. Paluch and C. Rodríguez-Tinoco, Why is surface diffusion the same in ultrastable, ordinary, aged, and ultrathin molecular glasses?, Phys. Chem. Chem. Phys., 2017, 19, 29905–29912.
32. M. Rams-Baron, Z. Wojnarowska, K. Grzybowska, M. Dulski, J. Knapik, K. Jurkiewicz, W. Smolka, W. Sawicki, A. Ratuszna and M. Paluch, Toward a Better Understanding of the Physical Stability of Amorphous Anti-Inflammatory Agents: The Roles of Molecular Mobility and Molecular Interaction Patterns, Mol. Pharmacol., 2015, 12, 3628–3638.
33. M. Rams-Baron, Z. Wojnarowska, J. Knapik-Kowalczuk, K. Jurkiewicz, A. Burian, M. Wojtyniak, J. Pionteck, M. Jaworska, C. Rodríguez-Tinoco and M. Paluch, The dielectric signature of glass density, Appl. Phys. Lett., 2017, 111, 121902.
34. K. Adrjanowicz, M. Paluch and K. L. Ngai, Determining the structural relaxation times deep in the glassy state of the pharmaceutical Telmisartan, J. Phys.: Condens. Matter, 2010, 22, 125902.
35. K. Adrjanowicz, Z. Wojnarowska, P. Wlodarczyk, K. Kaminski, M. Paluch and J. Mazgalski, Molecular mobility in liquid and glassy states of Telmisartan (TEL) studied by Broadband Dielectric Spectroscopy, Eur. J. Pharm. Sci., 2009, 38, 395–404.
36. K. Grzybowska, M. Paluch, P. Wlodarczyk, A. Grzybowski, K. Kaminski, L. Hawelek, D. Zakowiecki, A. Kasprzycka and I. Jankowska-Sumara, Enhancement of amorphous celecoxib stability by mixing it with octaacetylmaltose: the molecular dynamics study, Mol. Pharmacol., 2012, 9, 894–904.
37. Z. Wojnarowska, Y. Wang, J. Pionteck, K. Grzybowska, A. P. Sokolov and M. Paluch, High Pressure as a Key Factor to Identify the Conductivity Mechanism in Protic Ionic Liquids, Phys. Rev. Lett., 2013, 111, 225703.
38. K. Grzybowska, M. Paluch, A. Grzybowski, Z. Wojnarowska, L. Hawelek, K. Kolodziejczyk and K. L. Ngai, Molecular Dynamics and Physical Stability of Amorphous Anti-Inflammatory Drug: Celecoxib, J. Phys. Chem. B, 2010, 114, 12792–12801.
39. K. Kaminski, S. Pawlus, K. Adrjanowicz, Z. Wojnarowska, P. Wlodarczyk and M. Paluch, The importance of the activation volume for the description of the molecular dynamics of glass-forming liquids, J. Phys.: Condens. Matter, 2012, 24, 65105.
40. K. L. Ngai and M. Paluch, Corroborative evidences of TV^γ-scaling of the α-relaxation originating from the primitive relaxation/JG β relaxation, J. Non-Cryst. Solids, 2017, 478, 1–11.
41. M. Romanini, M. Barrio, R. Macovez, M. D. Ruiz-Martin, S. Capaccioli and J. L. Tamarit, Thermodynamic Scaling of the Dynamics of a Strongly Hydrogen-Bonded Glass-Former, Sci. Rep., 2017, 7, 1346.
42. G. Power, G. P. Johari and J. K. Vij, Relaxation strength of localized motions in D-sorbitol and mimicry of glass-softening thermodynamics, J. Chem. Phys., 2003, 119, 435–442.
43. S. S. Dalal and M. D. Ediger, Molecular Orientation in Stable Glasses of Indomethacin, J. Phys. Chem. Lett., 2012, 3, 1229–1233.
44. S. S. Dalal, A. Sepúlveda, G. K. Pribil, Z. Fakhraai and M. D. Ediger, Density and birefringence of a highly stable α,α,β-trisnaphthylbenzene glass, J. Chem. Phys., 2012, 136, 204501.
45. T. Liu, K. Cheng, E. Salami-Ranjbaran, F. Gao, C. Li, X. Tong, Y.-C. Lin, Y. Zhang, W. Zhang, L. Klinge, P. J. Walsh and Z. Fakhraai, The effect of chemical structure on the stability of physical vapor deposited glasses of 1,3,5-triarylbenzene, J. Chem. Phys., 2015, 143, 84506.
46. T. Perez-Castaneda, C. Rodriguez-Tinoco, J. Rodriguez-Viejo and M. A. Ramos, Suppression of tunneling two-level systems in ultrastable glasses of indomethacin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 11275–11280.
47. T. Liu, A. L. Exarhos, E. C. Alguire, F. Gao, E. Salami-Ranjbaran, K. Cheng, T. Jia, J. E. Subotnik, P. J. Walsh, J. M. Kikkawa and Z. Fakhraai, Birefringent Stable Glass with Predominantly Isotropic Molecular Orientation, Phys. Rev. Lett., 2017, 119, 95502.
48. J. Köplinger, G. Kasper and S. Hunklinger, Glass transition in chlorobenzene-decalin under pressure, J. Chem. Phys., 2000, 113, 4701–4706.
49. F. H. Stillinger, Relaxation and flow mechanisms in ‘“fragile”’ glass-forming liquids, J. Chem. Phys., 1988, 89, 6461–6469.
50. G. N. Greaves, EXAFS and the structure of glass, J. Non-Cryst. Solids, 1985, 71, 203–217.
51. M. D. Ediger, Can density or entropy fluctuations explain enhanced translational diffusion in glass-forming liquids?, J. Non-Cryst. Solids, 1998, 235–237, 10–18.
52. E. Donth, The size of cooperatively rearranging regions at the glass transition, J. Non-Cryst. Solids, 1982, 53, 325–330.
53. T. Ichitsubo, E. Matsubara, T. Yamamoto, H. S. Chen, N. Nishiyama, J. Saida and K. Anazawa, Microstructure of Fragile Metallic Glasses Inferred from Ultrasound-Accelerated Crystallization in Pd-Based Metallic Glasses, Phys. Rev. Lett., 2005, 95, 245501.

---

Footnote

† Electronic supplementary information (ESI) available: Complete set of dielectric and calorimetric data corresponding to the results shown in Fig. 1–3. Detail of aging processes reported in Fig. 4. Additional scaling analysis of relaxation data from the literature. See DOI: 10.1039/c8cp02341g

---