Water adsorption on the Fe₃O₄(111) surface: dissociation and network formation

Abstract

We monitored adsorption of water on a well-defined Fe₃O₄(111) film surface at different temperatures as a function of coverage using infrared reflection–absorption spectroscopy, temperature programmed desorption, and single crystal adsorption calorimetry. Additionally, density functional theory was employed using a Fe₃O₄(111)-(2 × 2) slab model to generate 15 energy minimum structures for various coverages. Corresponding vibrational properties of the adsorbed water species were also computed. The results show that water molecules readily dissociate on regular surface Fe_tet1–O ion pairs to form “monomers”, i.e., terminal Fe–OH and surface OH groups. Further water molecules adsorb on the hydroxyl covered surface non-dissociatively and form “dimers” and larger oligomers, which ultimately assemble into an ordered (2 × 2) hydrogen-bonded network structure with increasing coverage prior to the formation of a solid water film.

---

1. Introduction

Water interaction with iron oxides plays an important role in geology, electrochemistry, corrosion, and catalysis, etc.^1,2 Among the various iron oxides, magnetite (Fe₃O₄) surfaces seem to be the most explored using a “surface science” approach.^3–5 While recent experimental and theoretical work on Fe₃O₄(001) single crystal surfaces suggested that this surface is well-understood, a controversy remains for the (111) surface. Low energy electron diffraction (LEED) studies of Fe₃O₄(111) thin films in combination with scanning tunneling microscopy (STM) characterization suggested a termination with a 1/4 monolayer of tetrahedrally coordinated Fe³⁺ ions over the close-packed oxygen layer,^6–8 which can be obtained by cutting the magnetite structure along the Fe_tet1 layer. Also density functional theory (DFT) calculations predict the Fe_tet1-terminated surface as the most stable one under typical pressure and temperature conditions applied in UHV based experiments.^9–14 On the other hand, a double metal (Fe_oct2–Fe_tet1) termination was favored on the basis of infrared reflection–absorption spectroscopy (IRAS) studies of CO and water adsorption.^13,15,16 Our recent study¹⁷ has eliminated such a discrepancy by providing DFT analysis of CO vibrational bands, which ruled out the presence of octahedrally coordinated iron ions (Fe_oct2) on the regular surface except for defect sites such as step edges.

It is instructive here to summarize the key findings of previous experimental studies on water adsorption on Fe₃O₄(111) surfaces prepared either as thin films or single crystals. We only address water coverages below the formation of a “multilayer” amorphous solid water (ASW) film.

– Ultraviolet and X-ray photoelectron spectroscopy studies revealed electronic states, which were assigned to OH species^18–21 thus suggesting water dissociation. This was found both at room and low temperatures depending on the partial pressure of water.

– Temperature programmed desorption (TPD) studies revealed water desorption in a wide temperature range, between 200 and 400 K.^20,22,23 In particular, desorption signals above 300 K were attributed to the recombinative desorption of dissociated water.

– The heat of adsorption measured by single crystal adsorption calorimetry (SCAC),¹⁶ falls in the range of 100 kJ mol⁻¹ at the limit of low water coverage and decreases down to 55 kJ mol⁻¹ with increasing coverage.

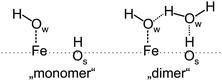
– The first appearing bands (at 2712 and 2691 cm⁻¹) in the IRA spectra²³ were originally assigned to stretching vibrations of two hydroxyls, Fe–O_wD and O_sD species, respectively, which were formed upon water dissociation. (O_w and O_s label oxygen atoms in water and in the oxide, respectively). This assignment was doubted in another IRAS study,¹⁶ suggesting the formation of a half-dissociated dimer from the onset.

– STM studies of adsorbed water are scarce. STM images of the pristine Fe₃O₄(111) films even showed a variety of adsorbate-like species,²⁴ which were attributed to the reaction with traces of water in the UHV background. STM studies of water adsorption on a Fe₃O₄(111) single crystal¹⁹ suggested that water dissociation only occurs on the Fe_tet1-terminated surface. In essence, the same behavior was observed on the Fe₃O₄(111) selvedge surface of a Fe₂O₃(0001) single crystal.²⁵

As for theoretical studies, DFT calculations were primarily applied to the Fe_tet1-terminated surface using a (1 × 1) slab model which implies, at least, one monolayer (ML) water coverage. For the case of dissociative water adsorption, Grillo et al.¹⁴ found an adsorption energy of −95 kJ mol⁻¹. With respect to calculations using a (2 × 2) cell corresponding to the 1/4 ML water coverage, Rim et al.²⁵ reported an adsorption energy of −126 kJ mol⁻¹ for the dissociative pathway, which is by 47 kJ mol⁻¹ more stable than molecular adsorption. Also, these calculations found a small activation barrier for dissociation (∼10 kJ mol⁻¹). Recently, a virtually identical result for dissociative adsorption (−123 kJ mol⁻¹) was obtained in our own study on the (2 × 2) cell.²⁶ Calculations for 1 ML coverage, using a single dissociated molecule in the (1 × 1) surface unit cell involving symmetry-related constraints, resulted in the reduced adsorption energy, i.e., of −75 kJ mol⁻¹.¹³ At increasing coverage up to two water molecules per unit cell, all theoretical studies converge to similar structures, i.e. a dimer composed of a dissociated and a non-dissociated water molecule (a “half-dissociated” water dimer). Regarding the role of surface termination, Yang et al.²⁷ reached the conclusion that the Fe_tet1-terminated surface is more favorable for water adsorption than the Fe_oct2-terminated one. However, Zhou et al.,²⁸ who addressed the dissociation mechanisms solely on the Fe_oct2-terminated surface, found it more active than the Fe_tet1-terminated surface. Although the latter calculations do not include a Hubbard-type U parameter for correlation effects, these results suggested direct dissociation to be unfavorable. However, water dissociation can be facilitated by adjacent water molecules (i.e., via dimer formation). The higher reactivity of the Fe_oct2-termination towards H₂O and CO adsorption was confirmed by recent DFT+U studies.^13,17

Thus, the adsorption of water on the Fe₃O₄(111) surface is controversially discussed in the literature. For all planar systems, surface preparation and even vacuum conditions play an important role. Also from a theoretical point of view, iron oxide systems need careful consideration as far as electronic and magnetic properties are concerned.¹³

In a recent communication,²⁶ we provided experimental results obtained by IRAS and TPD, corroborated by DFT calculations showing that water readily dissociates on Fe_tet1 sites to form two hydroxyl species. These act as an anchor for water molecules to form a dimer complex which self-assembles into an ordered (2 × 2) structure. The ordering in the water ad-layer is rationalized in terms of a cooperative effect induced by a hydrogen bonding network. In an attempt to provide a more detailed picture of the interaction of water with the Fe₃O₄(111) surface that goes beyond the evidence from our previous study,²⁶ here we provide results obtained by different experimental techniques (IRAS, TPD, and SCAC), and DFT calculations.

2. Methods and materials

2.1. Experimental section

The experiments were performed in several UHV chambers with a background pressure below 2 × 10⁻¹⁰ mbar. All setups were equipped with standard facilities necessary to grow well-ordered F₃O₄(111) films on a Pt(111) substrate. The quality of the films was checked by LEED showing sharp diffraction spots with low background intensity, and no other elements beyond Fe and O were observed by Auger electron spectroscopy. TPD spectra were recorded using a quadrupole mass spectrometer (QMS) having a gold-plated cone shield in order to minimize signals from the heating stage. IRA spectra were measured with a spectrometer (Bruker 66 ivs) at grazing angle 8° with the resolution of 4 cm⁻¹. In the TPD/IRAS setup, water (D₂O, Sigma-Aldrich) was dosed with a calibrated molecular beam. In a second (“TPD”) chamber, water was dosed using a directional doser.

Calorimetric results and sticking probabilities were measured with SCAC in a separate UHV chamber that is described in detail elsewhere.²⁹ Briefly, an effusive, doubly differentially pumped multi-channel array was used to produce a molecular beam of D₂O water. A chopper cut this beam into pulses 266 ms in length. The heat of adsorption was measured with a heat detector consisting of a 9 μm-thick pyroelectric ribbon (β-polyvinylidene fluoride) coated with Au on both sides and calibrated with pulses of HeNe laser light (λ = 632.8 nm, 5 mW). Simultaneously, the fraction of molecules that adsorb in a single pulse (i.e., the sticking probability) was measured by the modified King–Wells method³⁰ with a non-line-of-sight QMS.

The Fe₃O₄(111) films, with a thickness of about 5 nm, were grown on a Pt(111) substrate as described elsewhere.^6–8,15 The first step includes formation of the FeO(111) monolayer film on the clean Pt(111) surface.³ This step is also used for calibration of the Fe deposition flux. The next step involves several (3–5) cycles of Fe deposition in amounts equivalent to 5–10 monolayers of FeO(111) onto a substrate (kept either at 100 or 300 K), followed by oxidation in 10⁻⁶ mbar of O₂ at ∼930 K for 5–10 minutes. Oxygen was pumped out at sample temperature around 500 K. In the final step, the films were oxidized at 930–940 K for ca. 5 min. The samples were always flashed in UHV to 900 K prior to the water adsorption measurements. Although the precise preparation parameters (Fe flux, oxidation temperature, time and oxygen pressure) may slightly deviate in the UHV setups used, all oxide films under study showed sharp LEED patterns with low background intensity.

2.2. Computational details

Electronic and ionic structure calculations were performed using the projector-augmented-wave (PAW) method^31,32 as implemented in the Vienna ab initio simulation package (VASP).^33,34 Plane waves up to a kinetic energy of 800 eV were employed as a basis set. Onsite Coulomb correlation effects of Fe 3d orbitals were taken care of via the spin-polarized DFT+U approach^35,36 following Dudarev et al.^37,38 An effective U parameter of 3.8 eV was employed following previous DFT studies on Fe₃O₄ surfaces.^11,39–41 Regarding the exchange–correlation functional, we used the generalized-gradient approximation after Perdew, Burke, and Ernzerhof (PBE).⁴²

We use PAW pseudopotentials to describe the electron–ion interaction as released with VASP 5.2. The potential for Fe uses 14 valence electrons (Fe_pv:⁴³ 3p⁶ 3d⁷ 4s¹ as the atomic reference configuration) and the pseudopotential for O uses six valence electrons (O: [He] 2s² 2p⁴). Electronic optimizations were performed using a break criterion of 10⁻⁵ eV and Gaussian-type of a smearing with a width of 0.1 eV. Structures have been optimized to better than 0.02 eV Å⁻¹, which is the modulus of the maximum force acting on the atoms as employed in ref. 13.

With respect to structural surface models, we employ asymmetric stoichiometric slabs comprising twelve atomic layers and a (2 × 2)-periodicity, i.e., the clean Fe_tet1-terminated Fe₃O₄(111) surface has a cell content equivalent to Fe₄₈O₆₄. To avoid image interactions in the direction normal to the surface unit cell, a vacuum distance of approximately 10 Å was employed. Extensive tests showed that this vacuum distance is sufficient to obtain converged results. Coordinates of the atoms in the bottommost four atomic layers were kept frozen, i.e., during structure optimization their positions remain as in the bulk phase. For the Brillouin zone integration Γ-centered Monkhorst–Pack grids⁴⁴ with a (3 × 3 × 1) grid density were employed. Spurious dipole–dipole interactions between periodic images of slabs (in direction of the surface normal) were compensated by the approach after Makov and Payne⁴⁵ as implemented in the VASP code. Calculations of wavenumbers corresponding to the normal modes of adsorbed water uses all water related ad-atoms, as well as the coordinated Fe ions and protonated surface oxygen ions in the partial Hessian. Wavenumbers of deuterated ad-water were calculated by diagonalization of the mass-weighted partial Hessian using a mass of 2.014. Harmonic wavenumbers obtained using central finite differences (step size of 0.015 Å) based on the analytic Hellmann–Feynman gradient at atomic coordinates were scaled with a factor of 0.9935 (see ref. 16 and 26). This scaling was employed to effectively account for systematic errors in harmonic force constants and neglected anharmonicities. The water molecule was simulated in a box identical to the slab together with the identical plane wave cutoff used in surface calculations. Corrections for dispersive interactions^46,47 have been calculated at the PBE+U minimum energy structures, and a single water molecule contributes about −14 kJ mol⁻¹, on average (see below). Thus, results and conclusions of the present work are not affected qualitatively by adding an estimate for dispersion effects.

3. Results and discussion

3.1. Temperature programmed desorption (TPD)

Fig. 1a shows a series of TPD spectra obtained upon water exposure (in Langmuirs (L), 1 L = 10⁻⁶ Torr s) at 140 K to minimize the signal from an amorphous solid water (ASW) which is manifested by the peak at around 160 K. Desorption peaks at ∼200, 225, and 255 K are sequentially populated with increasing exposure following first order desorption kinetics. In contrast, the broad signal above ∼275 K shows characteristics of second order desorption due to the recombinative desorption of dissociated water. The small feature at ∼375 K can be assigned to the adsorption on defects sites. These spectra differ substantially from those reported previously which revealed, in essence, featureless desorption traces in the 200–300 K region.^20,21,23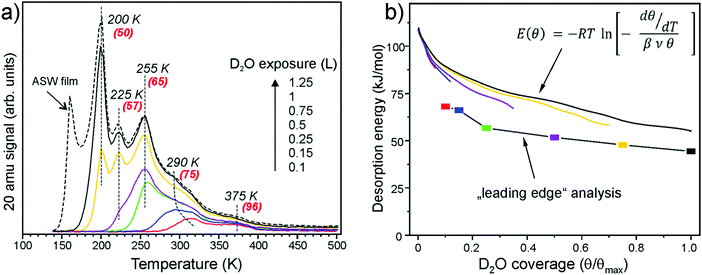

Fig. 1 (a) TPD spectra of D₂O (20 amu) adsorbed at 140 K at increasing exposures as indicated. The heating rate was 3 K s⁻¹. At the highest exposure, the formation of an ASW film sets in. The numbers in parenthesis show desorption energies obtained by the Redhead formalism⁴⁸ using a pre-factor ν = 10¹³ s⁻¹. (b) Desorption energy as a function of water coverage obtained by a “leading edge” analysis⁴⁹ and by inversion analysis of the Polanyi–Wigner equation with a pre-factor ν = 10¹³ s⁻¹. Water coverage is normalized to the maximum obtained before the ASW related peak sets in.

Using the conventional Redhead analysis⁴⁸ and a typical pre-factor of 10¹³ s⁻¹, one obtains a range of desorption energies from 50 kJ mol⁻¹ for the peak at ∼200 K up to 95 kJ mol⁻¹ for the peak at ∼375 K. Changing the pre-factor by one order of magnitude up or down changes the desorption energies by approximately ±5 kJ mol⁻¹. We refer to ref. 50 for a general discussion. Another approach to determine water adsorption energies from TPD spectra is a “leading edge” analysis,^49,51 which, in principle, does not include an assumption about the pre-exponential factor. In this method, the desorption leading edge (the onset of desorption) is approximated by the Arrhenius-type behavior, and the changes in the initial coverage are neglected. When applied to the spectra shown in Fig. 1a, the analysis resulted in an energy of 68 kJ mol⁻¹ at low coverage that gradually decreases with the increasing coverage as shown in Fig. 1b. Basically, these results are very similar to those obtained by the Redhead analysis suggesting the pre-factor of 10¹³ s⁻¹ as a good approximation. Finally, we employed inversion analysis of the Polanyi–Wigner equation for the 1-st order desorption kinetics,⁵² which results in a desorption energy (E): 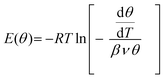where β is a heating rate, ν is a pre-factor, and θ(T) is a temperature (or time) dependent coverage, which is determined by integration of the desorption curve. In this analysis, each spectrum can be transformed into a coverage dependent energy curve, all plotted in Fig. 1b, for ν = 10¹³ s⁻¹. Some deviation between the curves may be indicative of kinetic effects. These results show again, that the desorption energy decreases with increasing coverage, most markedly in the low coverage regime (θ/θ_max < 0.1). All applied methods give a similar picture.

Water coverage has been calibrated using D₂O adsorption on the clean Pt(111) surface. It is well-documented in the literature that water forms a hexagonal ice film in one of two structures ((√3 × √3)R30° or (√39 × √39)R16.1°) depending on exposure conditions.⁵³ The formation of ordered ice films manifests in TPD as desorption at a slightly higher temperature as compared to the ASW film. In our experiments, a (√3 × √3)R30° ice film has been formed on Pt(111) as determined by LEED. Since the TPD measurements were performed with the same setup and on the same Pt crystal as used for the iron oxide film, all possible apparatus effects cancel. Therefore, the total amount of water adsorbed on Fe₃O₄(111) prior to the ASW film formation (θ_max) corresponds to 2.3 ± 0.2 ML (where 1 ML is defined as one H₂O molecule per Fe₃O₄(111) unit cell exposing one Fe ion, i.e. 3.2 × 10¹⁴ cm⁻²).

Well-resolved desorption peaks observed in our spectra (Fig. 1a) suggest desorption of species having discrete adsorption energies. In addition, sharp peaks imply that the corresponding water molecules desorb almost simultaneously in time, thus suggesting a certain degree of ordering at the surface, which was monitored by LEED.²⁶ LEED patterns of the ASW film, formed by 1.5 L of D₂O exposure at 140 K and confirmed by TPD, only showed (1 × 1) diffraction spots of a Fe₃O₄(111) substrate. Also, in the low coverage regime, i.e. by adsorption at 300 K, LEED showed no new diffraction features. However, additional spots identified as Fe₃O₄(111)-(2 × 2) structure appeared if the sample is exposed to saturated amounts of water at temperatures between 200 and 255 K, that is in the range where thermal desorption peaks are observed. In addition, its formation was independent of the adsorption temperature, i.e. 140 K vs. 250 K. It only depends on the water coverage, suggesting that the ordering of water is thermodynamically driven.

3.2. Single-crystal adsorption calorimetry (SCAC)

Fig. 2a shows the average sticking probability measured as a function of water coverage at different surface temperatures between 120 and 300 K. Here we define the sticking probability as the probability that a gas water molecule strikes the surface, sticks, and remains on the surface until the next gas pulse starts (with the period of 5 s). Even if dissociation is occurring, the coverages reported here refer to the total amount of D₂O that has adsorbed on the Fe₃O₄(111) surface, irrespective of the products formed. The initial sticking probabilities start off high, i.e. 0.71 to 0.93 (±0.05), at all temperatures. At 300, 240, and 180 K, the sticking probability approaches zero as D₂O saturates the surface at an approximate coverage of 0.4, 1.0, and 2.2 ML, respectively, which are in nice agreement with coverages estimated by TPD (see above). At 120 K, the sticking probability remains high (∼0.6) at high coverages, indicating growth of an ASW film.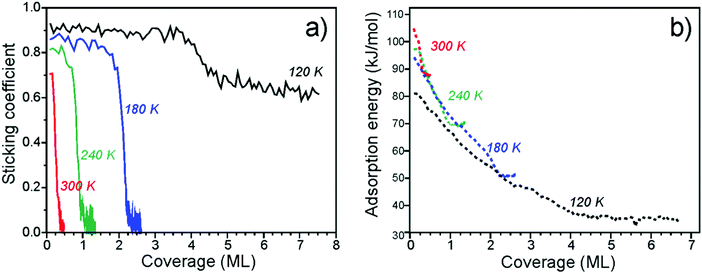

Fig. 2 Sticking coefficient (a) and differential heats of adsorption (b) of D₂O on Fe₃O₄(111) as a function of coverage obtained at several different temperatures.

The differential heats of adsorption of D₂O on Fe₃O₄(111) at four different temperatures are shown in Fig. 2b. At 120 K, the heat of adsorption is 82 kJ mol⁻¹ at the limit of low coverage and decreases with increasing coverage until multilayers of water are formed. The heats measured at 120 K are approximately 10 kJ mol⁻¹ lower than the heats measured at higher temperatures. This difference is likely related to kinetic effects of water dissociation, i.e. an activation barrier is required to overcome for dissociation. At higher temperatures (180–300 K), water initially adsorbs with a heat of 95–105 kJ mol⁻¹. All three of these heat of adsorption curves decrease with increasing coverage and largely overlap until each individual curve saturates.

The adsorption energies found here are consistent with what has been reported before for other oxide surfaces. For example, tetragonal zirconia (ZrO₂) values of 94 ± 19 and 70 ± 14 kJ mol⁻¹ have been obtained from adsorption experiments⁵⁴ and assigned to dissociative and molecular adsorption on the basis of DFT calculations performed for the (101) surface. The calculated average values were 123 and 95 kJ mol⁻¹ for water loadings of 0.5 and 1.0 molecules per Zr⁴⁺ surface site.⁵⁵

The measured adsorption energies and their coverage dependence are fully consistent with the TPD analysis above. Our calorimetric results give similar adsorption curves as determined by both inversion analysis of the Polanyi–Wigner equation and leading edge analysis. This suggests that the adsorption and dissociation of water is reversible under these conditions.

3.3. Infrared reflection–absorption spectroscopy (IRAS)

IRAS measurements were carried out in another UHV chamber on the films prepared using the same recipe and flashed to 900 K prior to the water exposure. TPD spectra revealed desorption profiles like those shown in Fig. 1, albeit with a lower resolution of the QMS available in the chamber (see Fig. S1 in the ESI†). This allows one to link the TPD and the IRAS results obtained in two different setups.

We first address water adsorption at room temperature. The four top spectra shown in Fig. 3 are recorded after sequential water pulses of 6 × 10¹³ cm⁻² each. Two sharp bands at 2723 and 2680 cm⁻¹ appear immediately at almost saturated intensities. However, the spectra measured at 320 and 350 K depicted in the same panel suggest that these two bands behave independently. Indeed, the signal at 2680 cm⁻¹ shows up at temperatures as high as 350 K and slightly gains intensity upon dosing at 320 and 300 K. In contrast, the 2723 cm⁻¹ band only appears at 320 K and then doubles intensity at 300 K. Tentatively, the 2680 cm⁻¹ band can be assigned to adsorption on defects, whereas the 2723 cm⁻¹ band reflects the initial stages of adsorption on the regular sites.

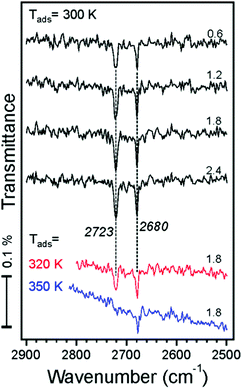Fig. 3 IRA spectra recorded after dosing the Fe₃O₄(111) film to D₂O molecular beam pulses (accumulative dosage (×10¹⁴ cm⁻²) is indicated). The spectra are offset for clarity.

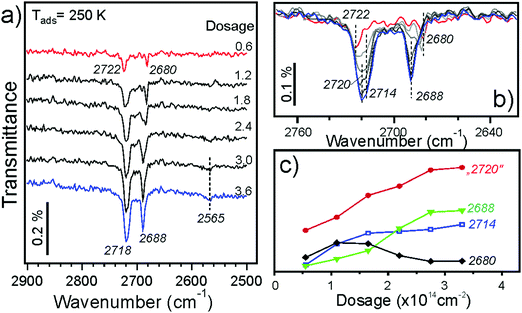
Fig. 4a displays IRA spectra measured at 250 K. After the first pulse, the two bands (2722 and 2680 cm⁻¹) appear in the same manner as observed at 300 K (Fig. 3). At increasing dosage, both signals grow in intensity, but one shifts to a lower frequency (2718 cm⁻¹) while another to a higher (2688 cm⁻¹) frequency. In addition, a weak band at ∼2565 cm⁻¹ is detected at high dosages. Spectral evolution, shown in more detail in Fig. 4b, indicates the presence of a new band at 2714 cm⁻¹ as a shoulder to the main band at 2722 cm⁻¹ which, in turn, gains intensity and shifts to 2120 cm⁻¹ at increasing coverage. This shift is quite small and is close to the spectral resolution (4 cm⁻¹). The changes in the low frequency band are more pronounced: the 2680 cm⁻¹ band attenuates, although may remain as a shoulder to the 2688 cm⁻¹ band, which definitely grows and starts to dominate in this region. The intensities of deconvoluted bands are plotted in Fig. 4c as a function of water dosage, although precise deconvolution may suffer from a relatively low signal-to-noise ratio. Apparently, both bands at 2720 and 2714 cm⁻¹ correlate with the one at 2688 cm⁻¹, and as such they all have likely the same origin. The band at 2680 cm⁻¹ practically vanishes at high exposures and inversely correlates with the one at ∼2565 cm⁻¹. The latter falls in the range of hydrogen bonded species, and, therefore, may originate from further water interaction with OD on defect sites associated with the 2680 cm⁻¹ band.

Fig. 4 (a) IRA spectra of D₂O adsorption on Fe₃O₄(111) at 250 K at increasing dosage (×10¹⁴ cm⁻²). (b) The same spectra are superimposed to highlight spectral changes. The first and the last spectra are marked in red and in blue, respectively. (c) Integral intensity (in arb. units) of the deconvoluted bands as a function of D₂O dosage.

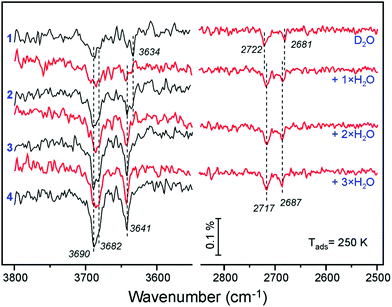
To shed more light on the origin of spectral evolution we studied H₂O adsorption onto the D₂O pre-covered surface and vice versa. Fig. 5 compares IRA spectra obtained upon sequential pulses of H₂O on the clean Fe₃O₄(111) surface and on the surface first exposed to one pulse of D₂O. The spectra for H₂O adsorption on the clean surface exhibits essentially the same coverage-dependent behavior as for the case of D₂O (see Fig. 4a). At increasing H₂O dosage, the band at 3682 cm⁻¹ develops as a shoulder to the main band at 3690 cm⁻¹. In the low frequency region, the initial band at 3634 cm⁻¹ attenuates while the 3641 cm⁻¹ band gains in intensity. The first pulse of D₂O onto the clean surface results in the same two bands (2722 and 2681 cm⁻¹) as discussed above (see Fig. 4a). When this surface is exposed to one pulse of H₂O, the 3682 and 3641 cm⁻¹ bands, which normally appear only at higher exposures, appear immediately, since the species associated with the 3690 and 3634 cm⁻¹ bands were already formed from pre-exposed D₂O as OD equivalent. It is interesting, however, that the ν(OD) bands shift (to 2717 and 2687 cm⁻¹, respectively) in the same manner as observed for the case of pure D₂O adsorption at increasing coverage (see Fig. 4b). Since the formation of new OD species upon H₂O exposure is impossible, the observed shifts must be due to coverage-induced effects.

Fig. 5 ν(OH) and ν(OD) regions in the spectra obtained by n pulses of H₂O (as indicated) on the clean Fe₃O₄(111) surface (in black) and on the surface first exposed to one pulse of D₂O (in red), all at 250 K. Each pulse contains 6 × 10¹³ molecules cm⁻².

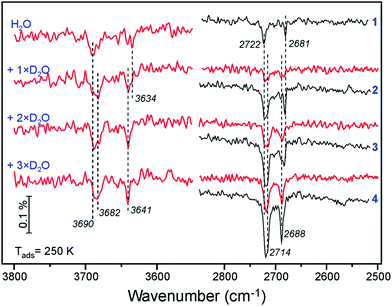
A similar picture evolves upon D₂O adsorption onto the surface pre-covered with H₂O (Fig. 6). Again, the first pulse of D₂O causes the ν(OH) bands shift, i.e. from 3690 to 3682 cm⁻¹, and from 3634 to 3641 cm⁻¹. Accordingly, the 2722 and 2681 cm⁻¹ bands in the ν(OD) region are suppressed since the respective hydoxyl species are partially formed from pre-adsorbed H₂O. Therefore, the results of H₂O and D₂O co-adsorption experiments suggest that the spectral evolution in this low coverage regime is caused by progressive formation of hydroxyl species leading to coverage-induced frequency shifts. In principle, the shift may originate from interaction of neighboring oscillators or from the changes in electronic properties of the iron oxide surface as the coverage increases.

Fig. 6 ν(OH) and ν(OD) regions in the IRA spectra obtained by n pulses of D₂O (as indicated) on the clean Fe₃O₄(111) surface (in black) and on the surface first exposed to one pulse of H₂O (in red), all at 250 K. Each pulse contains 6 × 10¹³ molecules cm⁻².

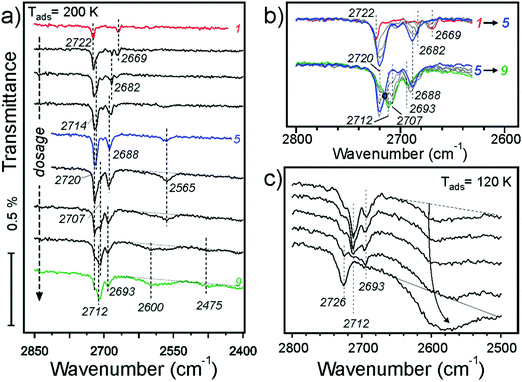
Now we address adsorption at higher coverages caused by adsorption at lower temperatures. Fig. 7a shows IRA spectra obtained at 200 K. The first pulse results in the 2722 cm⁻¹ band, as in the case for adsorption at 250 and 300 K. However, in the low frequency region a new band at 2669 cm⁻¹ appears, which was not previously observed. The band disappears after a few more pulses while the 2682 cm⁻¹ band increases in intensity, indicating that surface diffusion affects its formation. In principle, this finding is consistent with its tentative assignment of water reacting with defects.

Fig. 7 (a) IRA spectra of D₂O adsorption on Fe₃O₄(111) at 200 K at increasing dosage (from top to bottom). The spectra are offset for clarity. To highlight spectral changes, the same spectra are superimposed in two groups in panel (b) in the same color code as in panel (a). The isosbestic point is marked with a small circle. (c) Selected IRA spectra of D₂O adsorption at 120 K, where the first spectrum corresponds to the coverage of the last (green) spectrum in panels (a) and (b). At high coverages, the ASW film starts to grow.

At higher dosage the spectra follow the same evolution as for adsorption at 250 K (see Fig. 4b). The changes observed at further increasing coverage are highlighted in the second group of spectra (5–9) in Fig. 7b. The bands with an envelope peaked at 2720 cm⁻¹ attenuate while the bands at 2712 and 2707 cm⁻¹ grow up, resulting in an isosbestic point (marked with a circle). The picture is less obvious in the low frequency region. Apparently, the 2688 cm⁻¹ band shifts to 2693 cm⁻¹ and loses intensity. Finally, broad bands centered at 2600 and 2475 cm⁻¹ develop at highest exposures (see Fig. 7a), which are characteristic for systems with an extended network of hydrogen bonds.

Finally, water adsorption was examined at lower temperatures (120–180 K). As the spectral evolution at low coverages follows those studied at 200–300 K, Fig. 7c only displays the spectra obtained at high coverages, ultimately resulting in the ASW film. The latter shows an isolated band at 2726 cm⁻¹ and a broad band centered at ∼2580 cm⁻¹ which are assigned to stretching vibrations of dangling OH species at the surface and H-bonded OH species in water clusters, respectively. In this high coverage regime, the band at ∼2712 cm⁻¹ starts to attenuate before the band at 2693 cm⁻¹ does, both disappearing as the ASW film formation sets in.

To elucidate the adsorption mechanism, we employed isotopic labeling of oxygen in oxide and water with ¹⁸O. Our previously reported measurements at 250 K showed that the band at 2720 cm⁻¹ (see Fig. 4) involves oxygen in water (O_w) whereas the band at 2688 cm⁻¹ involves oxygen in the oxide (O_s). These results provided compelling evidence that water dissociates on anion–cation (O²⁻–Fe³⁺) pairs resulting in a terminal O_wD hydroxyl on top of the Fe_tet1 ion with second D adsorbing on the surface O ion.

Further experiments with D₂¹⁶O adsorption on the ¹⁸O-labeled film showed isotopic shift also for the 2681 and 2669 cm⁻¹ bands (see Fig. S2 in ESI†) which are only observed at very low coverages and thus attributed to adsorption at defects. As the 2681 cm⁻¹ band may even appear before the terminal Fe–O_wD band sets in (see Fig. 3), it implies adsorption on such defects which may result in O_wD species similar in nature to O_sD species. This, for example, could be the case for water adsorption on oxygen vacancies resulting in O_wD filling the vacancy and hence resembling O_sD species.

Fig. 8 compares selected IRA spectra of D₂¹⁶O at moderate coverages obtained on the Fe₃¹⁶O₄(111) and Fe₃¹⁸O₄(111) films at 200 K. Again, the 2688 cm⁻¹ band experiences an isotopic shift (∼16 cm⁻¹). Since the band at 2672 cm⁻¹ on the ¹⁸O-labelled film is now well-separated from the high-frequency region (compare to Fig. 7a), it becomes clear that the band slightly blue-shifts and considerably attenuates at increasing coverages at which isosbestic behavior for the high-frequency region is observed (Fig. 7b). This implies that O_sD species are involved in further water coordination via H-bonding which usually causes a strong red-shift (about 250 cm⁻¹) and band broadening. Interestingly, the weak band at 2565 cm⁻¹ does not shift upon ¹⁸O labeling, indicating that this vibrational band solely involves O_wD species which experience hydrogen bonding, based on a strongly red-shifted frequency as compared to a terminal OD. Overall, the results of isotopic experiments showed that only the IRA bands in the 2690–2670 cm⁻¹ region include oxygen in the film, and as such their spectral changes are associated with coverage-dependent evolution of O_sD hydroxyls that result from water dissociation.

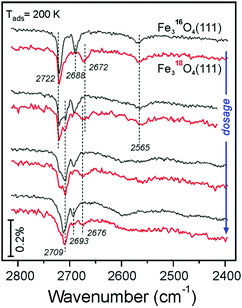Fig. 8 Selected IRA spectra recorded upon D₂¹⁶O adsorption at 200 K onto Fe₃¹⁶O₄(111) (in black) and Fe₃¹⁸O₄(111) (in red) films. The spectra are offset and grouped in pairs for direct comparison.

3.4. Density functional theory (DFT) results

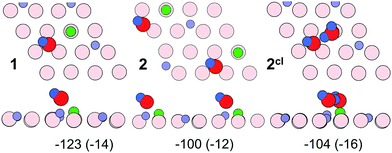
To rationalize the coverage-dependent IR spectra, we performed DFT calculations of harmonic wavenumbers for the water species in relevant energy minimum structures. For a direct comparison with observed fundamentals, we report scaled wavenumbers that effectively account for both systematic errors in the harmonic force constants and neglected anharmonicities. We use the scaling factor 0.9935 obtained from the ratio of observed and calculated wavenumbers for the symmetric and antisymmetric OH (OD) stretches of the gas phase water molecule as described in ref. 16 and 26.

Starting with a single water molecule per (2 × 2) unit cell, the computational results show that dissociative adsorption is thermodynamically most favorable. The energy minimum structure 1 shown in Fig. 9 involves two hydoxyl species O_wD as well as O_sD on the surface, which are schematically shown in Fig. 10. As outlined in ref. 13, dissociative adsorption of a single water molecule is more favorable (by ∼14 kJ mol⁻¹) than molecular (non-dissociative) adsorption. Note also that the previous theoretical calculations²⁵ revealed a low barrier, about 0.1 eV, for the dissociative reaction pathway of a single water molecule. Therefore, thermodynamically driven water dissociation is expected not to be kinetically hindered.

Fig. 9 Top and side views of a single dissociated water molecule (structure 1), two dissociated molecules (2), and a “half-dissociated” dimer complex (2^cl) on the Fe₃O₄(111)-(2 × 2) cell obtained using PBE+U. Adsorption energies per molecule (in kJ mol⁻¹) are given below individual structures. The dispersion contribution per molecule is given in parenthesis. Surface Fe_tet1 ions are violet, surface O_s ions are pink, oxygen in water (O_w) is red, proton atop O_s is green, hydrogen in water or hydroxyl is blue.

Fig. 10 Schemes for the dissociatively adsorbed water monomer (left) and water dimer (right).

The O_wD and O_sD groups are clearly discernable via their stretching wavenumbers of 2736 cm⁻¹ for O_wD and 2699 cm⁻¹ for O_sD. These values, separated by Δν = 37 cm⁻¹, compare well with the bands at 2720 and 2688 cm⁻¹ (Δν = 32 cm⁻¹) observed in experiments at low coverage (see Fig. 4). This assignment assumes that the first appearing band at 2681 cm⁻¹ relates to adsorption on defects.

For two water molecules per (2 × 2) cell, one must consider the formation of a second dissociated “monomer” (structure 2) as well as a half-dissociated “dimer” complex (structure 2^cl, see Fig. 10, right panel). Henceforth, we use the superscript cl to highlight water clustering. The calculated adsorption energies per water molecule in the cell (−100 (−112) and −104 (−120) kJ mol⁻¹ for the structures 2 and 2^cl, respectively) suggest that both structures are equally stable. The values given in parenthesis include the Grimme D2 dispersion correction (see Table S3 in the ESI†). The computed wavenumbers for O_wD and O_sD stretching vibrations of structure 2 (2729 and 2697 cm⁻¹) suggest a small red-shift for the O_wD band when compared to a single monomer in the cell (structure 1), i.e., in agreement with the experimental finding at low coverage (Fig. 4). As far as the dimer structure 2^cl is concerned, the computed wavenumbers for the stretching modes, 2735 cm⁻¹ for O_wD coordinated to Fe, and 2732 cm⁻¹ for terminal OD in the non-dissociated water molecule, are close and the corresponding bands may overlap. Therefore, the spontaneous formation of a dimer from the onset will manifest itself in a single, presumably broad band at a frequency close to that of “monomeric” Fe–O_wD. However, the dimer lacks an O_sD-related band in this region, since all hydrogen-bonded OD species in this structure experience a strong red-shift of about 300–350 cm⁻¹.

Fig. 11 shows energy minimum structures for two, three, and four water molecules per (2 × 2) surface unit cell that correspond to the respective coverages of 0.5, 0.75 and 1 ML. Comparison of the adsorption energies per water molecule (displayed below each structure) suggests that the formation of dimers may have a stabilizing effect on a water ad-layer. For example, two dimers in the cell (4^cl) are more stable than four monomers (4).

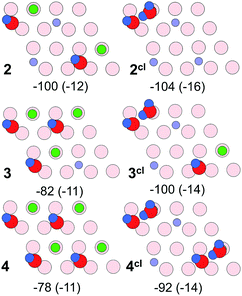Fig. 11 Top views of energy minimum structures involving two, three and four water molecules per the Fe₃O₄(111)-(2 × 2) cell. The adsorption energies (in kJ mol⁻¹) are indicated below individual structures. The dispersion contribution per molecule is given in parenthesis. (Color code as in Fig. 9).

Scaled harmonic wavenumbers obtained for these structures (see Table S1 in the ESI†) shows that high-frequency bands associated with Fe–O_wD species in monomeric structures 2, 3, and 4 exhibit an envelope centered at a wavenumber close to the one observed for a single monomer (1). A similar effect is observed for the O_sD region. These results agree with experimental spectra (Fig. 4) showing that both bands gain intensity at increasing dosage and only slightly shift, most likely due to crowding effects (see Fig. 5 and 6). For comparison, structure 4^cl not only lacks the experimentally observed O_sD band in this region, but also features the O_wD band at ∼2715 cm⁻¹, that is strongly (by ca. 15–20 cm⁻¹) red-shifted with respect to the monomeric Fe–O_wD bands. Also, structure 3^cl involving a coexisting dimer and a monomer reveals a considerably shifted O_sD band (2710 cm⁻¹), i.e. not observed in experiment. This suggests that water first dissociates creating monomeric species, although adventitious dimer formation cannot be excluded at coverages approaching 1 ML.

Fig. 12 displays water adlayer structures obtained at higher coverage of five to eight water molecules per (2 × 2) cell, i.e. 1.25–2.0 ML. At these high coverages, all structures feature at least one dimer. In addition, we considered structures with dimers forming a hydrogen bonded network, henceforth labelled with the superscript n. Fig. 13 compares the calculated wavenumbers for selected structures. For other structures not shown here, we refer to Fig. S4 and Table S1 in the ESI.† Among the possible candidates, the calculated wavenumbers of 5^cl(2) and 6ⁿ agree best with the experimental results obtained at 200 K (Fig. 7a) up to saturation corresponding to approximately 1.5 ML. The calculations revealed the red-shift of about 16 cm⁻¹ for O_wD stretching mode (blue sticks in Fig. 13) and the blue-shift of about 5 cm⁻¹ for the O_sD stretching (green sticks) taking the averaged wavenumbers for structures 1–4 as reference. Certainly, the formation of water aggregates occurs at the expense of monomeric species, ultimately resulting in the isosbestic point observed in IRAS (Fig. 7b). At further increasing coverage of 1.75 and 2 ML, all computed OD bands start to overlap and coalesce into one band, which (taking the systematic deviation into account) can be associated with a band at 2712 cm⁻¹ (Fig. 7c) dominating the spectra at 120 K prior to formation of the ASW film.

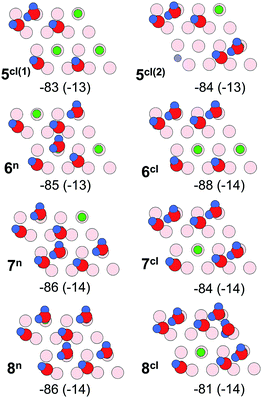Fig. 12 Top views of energy minimum structures involving five to eight water molecules per Fe₃O₄(111)-(2 × 2) cell. The adsorption energies (in kJ mol⁻¹) are indicated below individual structures. The dispersion contribution per molecule is given in parenthesis. (Color code as in Fig. 9).

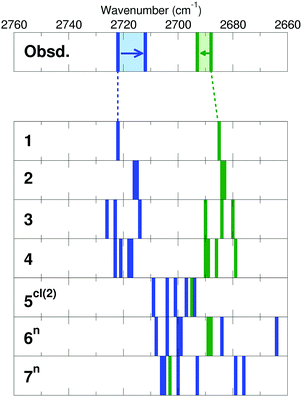Fig. 13 Stick representation of O_wD (blue) and O_sD (green) stretching modes (cm⁻¹) calculated for structures shown in Fig. 9, 11 and 12 (see also Fig. S4 in the ESI†). Note that all calculated wavenumbers are red-shifted by 14 cm⁻¹ in order to facilitate the comparison with the experimental results shown on top panel. Original numbers are presented in Table S1 in the ESI.†

With respect to a comparison of TPD desorption energies discussed in Section 3.1. with calculated values, we refer to ref. 50 and 56. The experimental values are Arrhenius activation energies of desorption and differ from the enthalpy of desorption by RT. Table 1 summarizes (electronic or DFT) adsorption energies, ΔE^ads, the zero-point-vibrational-energy correction (ZPVE), and the enthalpy in kJ mol⁻¹ per H₂O molecule. The calculated value for ΔH^ads of −102 kJ mol⁻¹ for structure 1 agrees well with the differential heats of adsorption obtained by microcalorimetry (−95 to −105 kJ mol⁻¹, see Section 3.2) and the TPD desorption energies of ∼110 kJ mol⁻¹ at low coverage. This value is lowered by −14 kJ mol⁻¹ per water molecule upon inclusion of dispersion effects (see Table S3 in the ESI†). The calculated adsorption energies per water molecule revealed all structures shown in Fig. 12 to be thermodynamically stable, with network structures becoming more favorable at increasing coverage (see ref. 26 for a more detailed analysis).

Table 1 Coverage, adsorption energies, zero-point-vibrational-energy correction (ZPVE), and heat of adsorption including RT for T = 200 K (kJ mol⁻¹). Results are given per H₂O molecule

	θ	ΔE^ads	ΔZPVE^a	ΔH^ads	ΔH^ads + RT
a The ZPVE for the H2O molecule is 54.8 kJ mol^−1.
1	0.25	−123.6	19.6	−104.0	−102.3
2	0.5	−100.0	20.3	−79.7	−77.9
2^cl	0.5	−103.7	15.0	−88.7	−87.1
3	0.75	−82.1	19.4	−62.7	−61.1
3^cl	0.75	−100.0	16.8	−83.2	−81.6
4	1	−78.0	19.6	−58.4	−56.7
4^cl	1	−92.2	15.7	−76.5	−74.9
5^cl(1)	1.25	−83.5	18.0	−65.5	−63.8
5^cl(2)	1.25	−83.9	16.5	−67.4	−65.8
6^n	1.5	−85.1	17.3	−67.8	−66.2
6^cl	1.5	−88.3	16.9	−71.4	−69.7
7^n	1.75	−86.3	15.8	−70.5	−68.8
7^cl	1.75	−83.7	16.3	−67.4	−65.8
8^n	2	−85.8	15.9	−69.9	−68.3
8^cl	2	−80.5	15.7	−64.8	−63.2

---

4. Conclusions

A combined thermal desorption, microcalorimetry, and IR spectroscopy study was carried out for water adsorption on the well-defined Fe₃O₄(111) surfaces as a function of temperature and dosage. The results were corroborated by DFT (PBE+U) calculations using a Fe₃O₄(111)-(2 × 2) slab model to address energy minimum structures and vibrational properties of adsorbed water species in a wide range of coverages (0.25–2 ML).

Water adsorption on defects dominates at high temperatures, e.g. above ∼320 K. At increasing water coverage, dissociative adsorption takes place on the regular Fe_tet1-terminated surface thus resulting in a terminal Fe–O_wD hydroxyl showing an IRA band at 2720 cm⁻¹ and an O_sD hydroxyl band at 2688 cm⁻¹. Our DFT calculations are compatible with this observation. Specifically, the computed adsorption enthalpy of the monomer is −102 kJ mol⁻¹ and the aforementioned OD bands are 2736 and 2699 cm⁻¹, respectively. At increasing coverages up to 1 ML, both bands slightly shift as suggested by D₂O and H₂O co-adsorption experiments. At further increasing coverage, water molecules start to form dimer complexes with pre-existing hydroxyls which is reflected via an isosbestic point in the IRA spectra. At high coverages, dimers and oligomers ultimately assemble into an ordered (2 × 2) hydrogen-bonded network structure prior to the formation of a multilayer solid water film. Again, our DFT results are compatible with the observed shifts at higher coverage and adsorption energies predict thermodynamically favorable H-bonded 2D network structures. These results highlight a delicate balance that exists in water adlayers on oxide surfaces where hydrogen bonding may play an important role in stabilizing particular structures.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the Deutsche Forschungsgemeinschaft through SFB 1109, by the Fonds der Chemischen Industrie as well as by generous grants for computing time at the North-German Supercomputing Alliance in Berlin and Hannover. JP gratefully acknowledges the Stiftung Industrieforschung, Humboldt-Universität zu Berlin for financial support. FM thanks the International Max-Planck Research School “Functional Interfaces in Physics and Chemistry” for a fellowship. Open Access funding provided by the Max Planck Society.

References

1. M. A. Henderson, Surf. Sci. Rep., 2002, 46, 1–308.
2. P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385.
3. W. Weiss and W. Ranke, Prog. Surf. Sci., 2002, 70, 1–151.
4. G. S. Parkinson, Surf. Sci. Rep., 2016, 71, 272–365.
5. H. Kuhlenbeck, S. Shaikhutdinov and H.-J. Freund, Chem. Rev., 2013, 113, 3986–4034.
6. M. Ritter and W. Weiss, Surf. Sci., 1999, 432, 81–94.
7. S. K. Shaikhutdinov, M. Ritter, X. G. Wang, H. Over and W. Weiss, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 11062–11069.
8. A. Sala, H. Marchetto, Z. H. Qin, S. Shaikhutdinov, T. Schmidt and H. J. Freund, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 155430.
9. A. Kiejna, T. Ossowski and T. Pabisiak, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 125414.
10. J. Noh, O. I. Osman, S. G. Aziz, P. Winget and J.-L. Brédas, Chem. Mater., 2015, 27, 5856–5867.
11. X. Yu, C.-F. Huo, Y.-W. Li, J. Wang and H. Jiao, Surf. Sci., 2012, 606, 872–879.
12. D. Santos-Carballal, A. Roldan, R. Grau-Crespo and N. H. de Leeuw, Phys. Chem. Chem. Phys., 2014, 16, 21082–21097.
13. X. Li and J. Paier, J. Phys. Chem. C, 2016, 120, 1056–1065.
14. M. E. Grillo, M. W. Finnis and W. Ranke, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 075407.
15. C. Lemire, R. Meyer, V. E. Henrich, S. Shaikhutdinov and H. J. Freund, Surf. Sci., 2004, 572, 103–114.
16. P. Dementyev, K.-H. Dostert, F. Ivars-Barceló, C. P. O'Brien, F. Mirabella, S. Schauermann, X. Li, J. Paier, J. Sauer and H.-J. Freund, Angew. Chem., Int. Ed., 2015, 54, 13942–13946.
17. X. Li, J. Paier, J. Sauer, F. Mirabella, E. Zaki, F. Ivars-Barceló, S. Shaikhutdinov and H. J. Freund, J. Phys. Chem. B, 2018, 122, 527–533.
18. T. Kendelewicz, P. Liu, C. S. Doyle, G. E. Brown Jr, E. J. Nelson and S. A. Chambers, Surf. Sci., 2000, 453, 32–46.
19. R. S. Cutting, C. A. Muryn, D. J. Vaughan and G. Thornton, Surf. Sci., 2008, 602, 1155–1165.
20. Y. Joseph, C. Kuhrs, W. Ranke, M. Ritter and W. Weiss, Chem. Phys. Lett., 1999, 314, 195–202.
21. Y. Joseph, W. Ranke and W. Weiss, J. Phys. Chem. B, 2000, 104, 3224–3236.
22. K. Adib, G. G. Totir, J. P. Fitts, K. T. Rim, T. Mueller, G. W. Flynn, S. A. Joyce and R. M. Osgood Jr, Surf. Sci., 2003, 537, 191–204.
23. U. Leist, W. Ranke and K. Al-Shamery, Phys. Chem. Chem. Phys., 2003, 5, 2435–2441.
24. S. Shaikhutdinov and W. Weiss, J. Mol. Catal. A: Chem., 2000, 158, 129–133.
25. K. T. Rim, D. Eom, S.-W. Chan, M. Flytzani-Stephanopoulos, G. W. Flynn, X.-D. Wen and E. R. Batista, J. Am. Chem. Soc., 2012, 134, 18979–18985.
26. F. Mirabella, E. Zaki, F. Ivars-Barcelo, X. Li, J. Paier, J. Sauer, S. Shaikhutdinov and H.-J. Freund, Angew. Chem., Int. Ed., 2017, 57, 1409–1413.
27. T. Yang, X.-d. Wen, D.-b. Cao, Y.-w. Li, J.-g. Wang and C.-f. Huo, J. Fuel Chem. Technol., 2009, 37, 506–512.
28. C. Zhou, Q. Zhang, L. Chen, B. Han, G. Ni, J. Wu, D. Garg and H. Cheng, J. Phys. Chem. C, 2010, 114, 21405–21410.
29. J.-H. Fischer-Wolfarth, J. Hartmann, J. A. Farmer, J. M. Flores-Camacho, C. T. Campbell, S. Schauermann and H.-J. Freund, Rev. Sci. Instrum., 2011, 82, 024102.
30. D. A. King and M. G. Wells, Surf. Sci., 1972, 29, 454–482.
31. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
32. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
33. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
34. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
35. V. I. Anisimov, J. Zaanen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 943–954.
36. A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, R5467–R5470.
37. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509.
38. O. Bengone, M. Alouani, P. Blöchl and J. Hugel, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 16392–16401.
39. I. Leonov, A. N. Yaresko, V. N. Antonov, M. A. Korotin and V. I. Anisimov, Phys. Rev. Lett., 2004, 93, 146404.
40. H. T. Jeng, G. Y. Guo and D. J. Huang, Phys. Rev. Lett., 2004, 93, 156403.
41. X. Yu, Y. Li, Y.-W. Li, J. Wang and H. Jiao, J. Phys. Chem. C, 2013, 117, 7648–7655.
42. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
43. A. Önsten, D. Stoltz, P. Palmgren, S. Yu, M. Göthelid and U. O. Karlsson, J. Phys. Chem. C, 2010, 114, 11157–11161.
44. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192.
45. G. Makov and M. C. Payne, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
46. S. Grimme, J. Comput. Chem., 2006, 27, 1787–1799.
47. T. Kerber, M. Sierka and J. Sauer, J. Comput. Chem., 2008, 29, 2088–2097.
48. P. A. Redhead, Vacuum, 1962, 12, 203–211.
49. A. M. de Jong and J. W. Niemantsverdriet, Surf. Sci., 1990, 233, 355–365.
50. A. D. Boese and J. Sauer, Phys. Chem. Chem. Phys., 2013, 15, 16481–16493.
51. E. Habenschaden and J. Küppers, Surf. Sci., 1984, 138, L147–L150.
52. S. L. Tait, Z. Dohnálek, C. T. Campbell and B. D. Kay, J. Chem. Phys., 2005, 122, 164707.
53. S. Haq, J. Harnett and A. Hodgson, Surf. Sci., 2002, 505, 171–182.
54. S. Raz, K. Sasaki, J. Maier and I. Riess, Solid State Ionics, 2001, 143, 181–204.
55. A. Hofmann and J. Sauer, J. Phys. Chem. B, 2004, 108, 14652–14662.
56. S. Tosoni and J. Sauer, Phys. Chem. Chem. Phys., 2010, 12, 14330–14340.

---

Footnotes

† Electronic supplementary information (ESI) available: TPD spectra obtained in IRAS setup; selected IRA spectra for D₂O adsorbed on an O¹⁶ and O¹⁸ labelled Fe₃O₄ films; top views on structures for higher coverage; table with computed frequencies for all structures; comparison of observed shifts and computed wavenumbers for other structures not shown in main text; total energies; structure coordinates. See DOI: 10.1039/c8cp02333f

‡ These authors contributed equally to the work.

---