On the relationship between the structural and volumetric properties of solvated metal ions in O-donor solvents using new structural data in amide solvents

Abstract

The structures of the N,N-dimethylformamide (dmf), N,N-dimethylacetamide (dma), and N,N-dimethylpropionamide (dmp) solvated strontium and barium ions have been determined in solution using large angle X-ray scattering and EXAFS spectroscopy. The strontium ion has a mean coordination number (CN) between 6.2 and 6.8, and the barium ion has a mean CN between 7.1 and 7.8 in these amide solvents. The non-integer numbers indicates that equilibria between different coordination numbers and geometries exist in these systems. Structural information of the alkali, alkaline earth, and selected transition metal and lanthanoid(III) ions, and the halide ions in water, methanol, ethanol, dimethylsulfoxide, formamide, dmf and dma has been combined with previously reported standard partial molar volumes, V⁰. The ionic radii and charge densities (charge/ionic volume), and corresponding V⁰ values have been used to gain information on the relationship between structural and volumetric properties. For the structure-breaking ions, i.e. the alkali metal and halide ions, there is an almost linear relationship between the ionic radius and V⁰. On the other hand, for the structure-making ions, here the alkaline earth, transition metal and lanthanoid(III) ions, a linear relationship is observed between the charge density and V⁰. Solvents with a well-defined bulk structure through hydrogen bonding, specifically, water, methanol and ethanol, will be more contracted through solvation than aprotic solvents, as the space between the solvent molecules is lost as a result of the hydrogen bonding. In this respect, methanol stands out as the most compressed solvent participating in solvation compared to its bulk structure.

---

Introduction

The concept of structure-making and structure-breaking ions refers to their contractibility of the surrounding solvent molecules through solvation.¹ Generally, large ions with low charge density have to break up the solvent structure to obtain solvent molecules for their own solvation but also to make room for themselves, and their solvation is generally weak. Thereby, the solvated ion ends up requiring more space than the corresponding number of solvent molecules in the neat solvent; such ions are regarded as structure-breakers. On the other hand, small ions with high charge density are strongly solvated and they contract the solvent molecules upon solvation to such a degree that the solvate complex requires less space than the corresponding number of solvent molecules in the neat solvent; such ions are regarded as structure-makers. In general, monovalent cations and anions are, with the exception of the lithium and fluoride ions, regarded as structure-breaking ions, whereas di- and especially trivalent ions are regarded as structure-making ones.^1,2 The networks of hydrogen bonds in e.g. liquid water and short-chain alcohols are mainly responsible for the volume properties of the solvent, while for aprotic solvents the much weaker dipole–dipole or van der Waals interactions determine how close the solvent molecules can be packed in the solvent bulk.

The apparent molar volume, V_ϕ is defined as the difference between the volume of the solution and the volume of the pure solvent per mole of solute. This value depends on both concentration and temperature but also, by definition, its limiting value as the concentration approaches zero i.e. the standard partial molar volume, V⁰, is dependent on temperature. Standard partial molar volumes provide useful information on ion–solvent interactions. In solutions of solvents with high relative dielectric constants it is assumed that salts are completely dissociated, without any form of ion-pairing, at infinite dilution.³ Taking this into account, an extra-thermodynamic assumption based on the additivity rule must be applied to split the standard partial molar volumes into two contributions, one for the cationic part and another for the anionic one.⁴ By applying this reasoning for different salts in different solvents, the ionic contribution can be compared within and between different types of solvents, thereby providing information on the structure-making and structure-breaking properties of the individual ions. This subject has been reviewed for aqueous solutions by Marcus.¹ Structure-making ions organize the solvent molecules more tightly in proximity to the ion than in bulk, which is reflected in negative values of the standard partial molar volume. The opposite is found for structure-breaking ions which have positive V⁰ values. To better understand this phenomenon, it is convenient to present V⁰ as a sum of two contributions i.e. the intrinsic volume which is proportional to the cube of the ionic radius, r, and the electrostriction volume which depends on the square of ionic charge, z, and is also inversely proportional to the ionic radius. This simple, semi-empirical approach was proposed by Hepler in 1957:

V⁰ = Ar³ − Bz²/r, (1)

where A is proportional to the size of the ion and depends on the packing effects of the ions in the solution, while B is a solvent-dependent value.^5,6 Since then, more sophisticated equations have been proposed in an attempt to explain the contributions to the partial molar volumes of ions in both aqueous and non-aqueous solutions, as reviewed by Marcus.⁶ However, the Hepler equation (eqn (1)) with clearly defined contributions is sufficient for our further discussion.

Solvents with similar fundamental physico-chemical properties but different molecular size and steric congestion form good model systems to study whether a possible change in the coordination chemistry affects derived thermodynamic properties, such as the partial standard molar volume of individual ions. The aprotic solvents N,N-dimethylformamide (dmf), N,N-dimethylacetamide (dma) and N,N-dimethylpropionamide (dmp), Fig. 1, are all dipolar amide solvents with similar physico-chemical properties as summarized in Table S1 (ESI†). The main difference lies in the amide carbon sidechain. Furthermore, the dmp molecule exists in bulk as two conformers, a planar cis and a non-planar staggered one, and some studies have indicated that the latter is more favorable upon coordination.^7–9

Fig. 1 Structural models of the three studied amides (from left to right): N,N-dimethylformamide (dmf), N,N-dimethylacetamide (dma), and N,N-dimethylpropionamide (dmp).

When it comes to selecting ion systems, one can notice that the smaller divalent alkaline earth metal ions, magnesium and calcium, are sufficiently strongly solvated to crystallize with a full first solvation shell, and a lot of information of their solvate structures in the solid state is therefore available in the literature.^10,11 On the other hand, the larger ones, strontium and barium, are more weakly solvated and mixed complexes with the solvent and counter ions as ligands are common, with significantly fewer examples reported. For instance, the magnesium ion binds six dmf^12–17 or dma¹⁸ molecules in an octahedral fashion with a mean Mg–O bond distance of 2.058 Å, and the Mg–O–C bond angle varies a lot in the studied compounds, 127–158°. The calcium ion binds six dmf,^19–24 dma²⁵ or N,N-diethylacetamide (dea)²⁶ molecules octahedrally with a mean Ca–O bond distance of 2.305 Å, and the Ca–O–C bond angles are usually close to 145°. Three compounds with an amide-solvated strontium ion are reported where strontium binds six dma molecules octahedrally with a mean Sr–O bond distance of 2.451 Å.²⁷ The dmf-solvated strontium ion in solution is reported to be seven-coordinated with a mean Sr–O bond distance of 2.555 Å.²⁸ In the dmf-solvated strontium trifluoromethanesulfonate salt, [Sr(dmf)₂(CF₃SO₃)₂]_n, strontium is eight-coordinated in a square antiprismatic fashion where oxygens from four dmf molecules and four trifluoromethanesulfonate ions bridge strontium ions forming one-dimensional chains;²⁸ the mean Sr–O bond distance is 2.589 Å. Only one dmf-solvated barium compound with crystal coordinates is reported, where barium binds six dmf molecules and two oxygens from bridging dodecamolybdate ions giving a total coordination number (CN) of eight in a square antiprismatic fashion.²⁹ The mean Ba–O bond distance to the dmf molecules is 2.704 Å. Also, one dinuclear, eight-coordinated dma-solvated barium compound crystallizes with two μ-bridging dma molecules, three additional dma molecules, two perchlorate ions, and a water molecule for each barium.³⁰ The mean Ba–O bond distance to the dma molecules is 2.679 Å, and 2.725 Å for all ligands. Additionally, in a cross-solvent comparison, the coordination numbers of the hydrated magnesium, calcium, strontium and barium ions are six, eight, eight and eight, respectively,³¹ and in the aprotic solvent dimethylsulfoxide, dmso, the coordination numbers are six, six, seven and close to eight, respectively.^28,32

All alkaline earth metal ions are regarded as hard electron-pair acceptors forming mainly electrostatic bonds, and the coordination number is largely dependent on the number of ligands which can physically be clustered around the metal ion. The largest coordination numbers are therefore observed for small solvent molecules with limited steric requirements, such as water and dmf. For the amide solvents in the present study, the steric requirements on coordination increase in the order dmf < dma < dmp, Fig. 1. Furthermore, the coordination number in the solid state is also affected by the lattice energies which favor complexes with high symmetry over those with low. This is nicely demonstrated for the N,N′-dimethylpropyleneurea solvated lanthanoid(III) ions which are octahedrally six-coordinated in the solid state, though predominantly seven-coordinated in solution.³³ It is therefore important to stress that structural information in the solid state cannot be transferred to the situation in solution without experimental evidence.

The aim of this study is to determine the structures of the dmf-, dma- and dmp-solvated strontium and barium ions in solution using the large angle X-ray scattering and EXAFS techniques as such data are lacking, and to study the relationship between standard partial molar volume and structure using the alkali, alkaline earth, selected transition metal, selected lanthanoid(III), and halide ions in the protic solvents water, methanol and ethanol, and the aprotic solvents dmso, dmf and dma. The metal–solvent ligand bonds in the solvates of the studied metal ions have mainly electrostatic character, which means that these metal ions in solution have the highest number of solvent molecules bound that is sterically allowed. The aprotic solvents in this study have different spatial requirements upon coordination, and as such may have different coordination numbers. The alkaline earth metal ions have only been the subject of a limited number of coordination chemistry studies and the coordination numbers of the heavier alkaline earth metal ions in solution have not been studied systematically. Lastly, Shannon's proposed ionic radii for different coordination numbers of the alkaline earth metal ions³⁴ will be compared to those obtained experimentally and through structure database surveys in this study.

Experimental

Chemicals

Anhydrous strontium and barium trifluoromethanesulfonate were prepared by neutralization of aqueous solutions of octaaquastrontium and barium hydroxide (Sigma Aldrich, 99.9% metal basis) with a slight excess of trifluoromethanesulfonic acid (Fluka, AR grade, ≥99%). The excess water and acid was boiled off, and the formed solid salts were mortared and dried repeatedly, and finally stored in an oven at 470 K.

Solvents

N,N-Dimethylformamide, dmf, (Sigma-Aldrich, AR, 99.8%) and N,N-dimethylacetamide, dma, (Sigma-Aldrich, ReagentPlus®, ≥99%) were used without further purification. N,N-Dimethylpropionamide, dmp, (Sigma-Aldrich, AR, 98%) was distilled under reduced pressure using calcium hydride (Merck) as a drying agent prior to use.

Solutions

The dmf, dma and dmp solutions of strontium and barium trifluoromethanesulfonate were prepared by weighing appropriate amounts of the respective anhydrous trifluoromethanesulfonate salt, which was dissolved in the respective solvent. The compositions together with solution densities and absorption coefficients of the solutions studied by LAXS are given in Table 1. In the EXAFS studies the same dmf and dma solutions as in the LAXS studies were used, and the dmp solutions were saturated with strontium and barium trifluoromethanesulfonate. The solubilities of strontium and barium trifluoromethanesulfonate are too low to allow LAXS studies. After several years in a refrigerator, crystals formed in the dma solution of barium trifluoromethanesulfonate. The structure mimics the previously reported structure of dma-solvated barium perchlorate³⁰ and will be reported elsewhere.

Table 1 Concentrations, densities (ρ), and linear absorption coefficients (μ) of the dmf and dma solutions of M(CF₃SO₃)₂ (M = Sr or Ba) used in the described LAXS measurements

Salt	Solvent	[M^2+]	[CF3SO3^−]	[Solvent]	ρ/g cm^−3	μ/cm^−1
Sr(CF3SO3)2	dmf	0.5845	1.1690	11.4975	1.0959	8.864
	dma	0.6457	1.2914	9.4197	1.1018	9.676
Ba(CF3SO3)2	dmf	0.7339	1.4677	11.4908	1.1595	5.765
	dma	0.7074	1.4148	9.5978	1.1442	5.549

---

Large angle X-ray scattering measurements. The scattering of Mo-Kα radiation (λ = 0.7107 Å) on the free surface of dmf and dma solutions of strontium and barium trifluoromethanesulfonate was measured with a large-angle θ–θ diffractometer as described elsewhere.³⁵ A Teflon cup with the solution was placed inside the radiation shield with beryllium windows. The intensity of the scattered radiation, after monochromatization with a focusing LiF crystal, was measured at 450 discrete points in the range 1 < θ < 65° (the scattering angle is 2θ). A total of 100 000 X-ray quanta within a region of interest were collected at each angle and the whole angular range was scanned twice, corresponding to a statistical uncertainty of about 0.3%. The divergence of the primary X-ray beam was limited by ¼ and 1° slits for different θ regions with some parts of the data sets overlapping for scaling purposes.

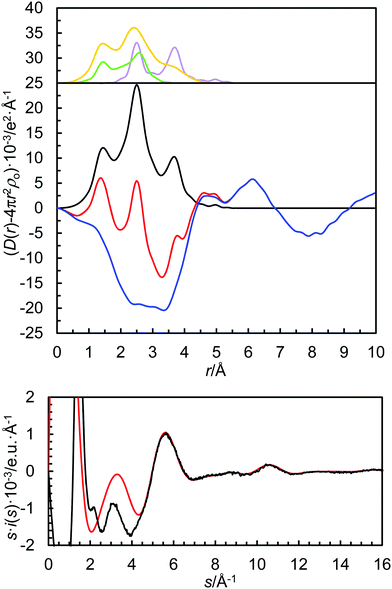
All data treatment was carried out by using the KURVLR program³⁶ as described in detail elsewhere.³⁵ The experimental intensities were normalized to a stoichiometric unit of volume containing one metal atom, using the scattering factors ƒ for neutral atoms, including corrections for anomalous dispersion, Δƒ′ and Δƒ′′,³⁷ and values for Compton scattering.³⁸ To receive a better alignment of the intensity function, a Fourier back-transformation was applied to eliminate spurious peaks not related to any interatomic distances below 1.2 Å in the radial distribution function.³⁹ Least-squares refinements of the model parameters were performed by means of the STEPLR program⁴⁰ to minimize the error square sum U, .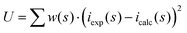

EXAFS – data collection. The EXAFS measurements at the strontium K and barium L₃ absorption edges were performed at the Stanford Synchrotron Radiation Lightsource (SSRL), Stanford, USA, beam-line 4–1, and beam-line I811 at MAX-lab, Lund University. The data collection was performed simultaneously in transmission and fluorescence mode using ion chambers with a gentle flow of nitrogen and a 13-element germanium array detector at SSRL, and ion chambers with stationary gas mixtures and a Passivated Implanted Planar Silicon (PIPS) detector (http://www.canberra.com/products/438239.asp; accessed April 9, 2018) for the fluorescence measurements. The EXAFS stations were equipped with a Si[220] (SSRL) or Si[111] (MAX-lab) double crystal monochromator. SSRL operated at 3.0 GeV and a maximum current of 100 mA in top-up mode, and MAX-lab operated at 1.5 GeV and a maximum current of 200 mA.

In order to remove higher order harmonics, the beam intensity was detuned to 60% (Sr K edge) or 30% (Ba L₃ edge) of the maximum intensity at the end of the scans. The energy scales of the X-ray absorption spectra were calibrated by assigning the first inflection point of the metallic strontium K-edge and barium L₃ edge at 16 105 and 5247 eV, respectively.⁴¹ For each sample 3–4 scans were averaged, giving a satisfactory signal-to-noise ratio. The studied solutions were contained in cells made of a Teflon spacer of appropriate thickness and 6 μm polypropylene X-ray film windows held together with titanium frames.

EXAFS – data analysis. The EXAFSPAK⁴² and GNXAS⁴³ program packages were used for the data treatment. When using the EXAFSPAK program, the theoretical phases and amplitudes used in the refinements were calculated by the use of the FEFF7 program.⁴⁴ The standard deviations given for the refined parameters are obtained from k³-weighted least-squares refinement of the EXAFS function χ(k), and do not include systematic errors of the measurements. These statistical error estimates provide a measure of the precision of the results and allow reasonable comparisons e.g. of the significance of relative shifts in the distances. However, the variations in the refined parameters, including the shift of the E₀ value (for which k = 0), using different models and data ranges, indicate that the absolute accuracy of the distances given for the separate complexes is within ±0.005 to 0.02 Å for well-defined interactions. The “standard deviations” given in the text have been increased accordingly to include the estimated additional effects of systematic errors.

The GNXAS code is based on the calculation of the EXAFS signal and a subsequent refinement of the structural parameters.⁴³ The GNXAS method accounts for multiple scattering (MS) paths by including the configurational average of all the MS signals to allow the fitting of correlated distances and bond distance variances described by Debye–Waller factors. A detailed description of the distribution of the ion–solvent distances in a coordination shell should in principle take asymmetry into account.^45,46 Therefore the M–O two-body signals associated with the first coordination shells were modeled with Γ-like distribution functions, which depend on four parameters, the (coordination) number of degeneracy N, the centroid distance R (the first moment of the function ), the mean-square variation in the mean distance σ, and the skewness parameter β.

Results

Ionic radii of the strontium and barium ions in CNs 6 to 9

A database survey of reported crystal structures of hydrated and solvated alkaline earth ions and complexes and compounds with neutral, monodentate ligands in the solid state is given in Table S2 (ESI†). The ionic radii for the coordination numbers 6, 7, 8 and 9 are obtained by subtracting the radius of the oxygen atom in coordinated water molecules, 1.34 Å, which has been found to be the same value for oxygen in most oxygen donor ligands⁴⁷ from observed M–O mean bond distances; ethers are an exception, and amide oxygens have been reported to have a slightly smaller radius.⁴⁸ The obtained ionic radii are summarized in Table 2 with estimated values for nine-coordinate calcium and seven-coordinate barium ions. Most of the ionic radii of the alkaline earth metal ions obtained from this survey are in fairly good agreement, ±0.015 Å, with those listed by Shannon.³⁴ However, the ionic radii for the strontium and barium ions in six-coordination from this new survey are significantly shorter, whereas the ionic radii of the higher coordination numbers of strontium and barium are somewhat larger than those proposed by Shannon,³⁴Table 2.

Table 2 Calculated ionic radii for the alkaline earth metal ions^a using the mean bond distances in the structure surveys, Table S2 (ESI), using r₀ = 1.34 Å, ref. 47, as the radius of coordinated oxygen; the number of crystal structures used to obtain these ionic radii are listed within subscript square brackets with the radii proposed by Shannon, ref. 34, given in italics

Ionic radius/Å
Ion	CN = 6		CN = 7		CN = 8		CN = 9
a The radius of the four-coordinated beryllium(II) ion is rBe(II),CN4 = 0.273[13] and 0.27 Å; the radii of the four- and five-coordinated magnesium ions are rMg(II),CN4 = 0.567[3] and 0.57 Å, rMg(II),CN5 = 0.664[2] and 0.66 Å; the radius of the ten-coordinated barium(II) ion is rBa(II),CN10 = 1.511[1] and 1.52 Å; no hydrate or solvate data is available for the radium(II) ion, but Shannon lists rRa(II),CN8 = 1.48 Å. b Estimated radius derived from a second-degree polynomial with a slope (rCa(II),CN9(est) = −0.0125 CN^2 + 0.2535 CN − 0.098) comparable to that of the strontium (6 ≤ CN ≤ 9) and barium ions (CN = 6, 8, 9). c Estimated radius derived from a second-degree polynomial with a slope (rBa(II),CN7(est) = −0.0097 CN^2 + 0.2043 CN + 0.414) comparable to that of the calcium (6 ≤ CN ≤ 8) and strontium (6 ≤ CN ≤ 9) ions.
Mg^2+	0.724[368]	0.720			n/a	0.89
Ca^2+	0.973[41]	1.00	1.064[22]	1.06	1.130[13]	1.12	1.17[0]^b	1.18
Sr^2+	1.128[7]	1.18	1.224[2]	1.21	1.274[13]	1.26	1.332[2]	1.31
Ba^2+	1.292[4]	1.35	1.38[0]^c	1.38	1.430[3]	1.42	1.489[7]	1.47

---

Structure of solvated alkaline earth metal ions in dmf, dma and dmp solution

Large angle X-ray scattering (LAXS). The RDFs from the LAXS experiments on dmf and dma solutions of strontium and barium trifluoromethanesulfonate reveal three peaks at around 1.5, 2.5–2.7 and 3.7 Å, Fig. 2 and Fig. S1–S3 (ESI†). The peak at 1.5 Å corresponds to intramolecular distances in the trifluoromethanesulfonate ion and the solvent. The peaks at 2.5 or 2.7 Å correspond to the Sr–O and Ba–O bond distances in the dmf and dma solvated strontium and barium ions, respectively, but they also include contributions from interatomic distances from the solvent and the trifluoromethanesulfonate ion, respectively, Fig. 2 and Fig. S1–S3 (ESI†). The peak or shoulder at ca. 3.7 Å corresponds to the M⋯C distance. The respective angles were calculated from the obtained M–O and M⋯C distances using the average C–O bond length for coordinated dmf and dma molecules in solvates of alkaline earth metal ions in the solid state; the mean C–O value for dmf is 1.244 Å, for dma it equals 1.250 Å,^12–25,27 a value also used for dmp. The applied coordination numbers have been obtained by linear regression calculations using the refined M–O bond distance and the correlation of mean M–O bond distances of metal complexes with neutral, monodentate ligands for the coordination numbers 6, 7, 8 and 9, where applicable, Fig. 3. The results show clearly that the obtained M–O bond distances are inbetween the expected ones for a well-defined bond distance with a given coordination number. Furthermore, the temperature factor coefficients, b, are much larger than expected for solvates with one well-defined coordination figure. It seems therefore very likely that there are equilibria between at least two coordination numbers resulting in non-integer mean numbers, Table 3. The large b values are due to an average of two or more structures with different bond distances.

Fig. 2 LAXS radial distribution function of Sr(CF₃SO₃)₂ solution in dmf. Top, upper panel: separate model contributions (offset: 25) of the strontium ion solvated by N,N-dimethylformamide (purple line), the trifluoromethanesulfonate ion (green line) and dmf molecule (yellow line). Top, lower panel: experimental RDF (red line); sum of model contributions (black line); the difference (blue line). Bottom: Reduced intensity function (experimental results – black line; model – red line).

Fig. 3 The relationship of the ionic radius-coordination number (CN), re-calculated to the expected M–O bond distance by adding 1.32 Å (the oxygen radius in amide solvents, ref. 48), from solid state structures for the strontium and barium ions (blue and orange filled circles and the calculated trend line as a dashed line). The solid lines represents Sr²⁺/dmf (green), Sr²⁺/dma (purple), Sr²⁺/dmp (brown), Ba²⁺/dmf (dark red), Ba²⁺/dma (yellow), and Ba²⁺/dmp (grey).

Table 3 Interaction pathway, degeneracy number of distances, N, mean bond distances, d/Å, and temperature coefficients, b/Ų, in the LAXS studies of the solvated strontium(II) and barium(II) ions in dmf and dma solutions at room temperature. The M–O–C angle, calculated from the given bond distances, is listed for each species

Species	Path	N	d	b
Strontium(II) trifluoromethanesulfonate in dmf, 0.5845 mol dm^−3
[Sr(OCHN(CH3)2)N]^2+	Sr–O	6.8	2.513(6)	0.0104(2)
	Sr⋯C	6.8	3.730(8)	0.0156(10)
	∠(Sr–O–C): 165(5)°
Strontium(II) trifluoromethanesulfonate in dma, 0.6457 mol dm^−3
[Sr(OC(CH3)N(CH3)2)N]^2+	Sr–O	6.7	2.506(4)	0.0109(2)
	Sr⋯C	6.7	3.725(4)	0.0134(4)
	∠(Sr–O–C): 164(3)°
Barium(II) trifluoromethanesulfonate in dmf, 0.7339 mol dm^−3
[Ba(OCHN(CH3)2)N]^2+	Ba–O	7.8	2.736(4)	0.0096(5)
	Ba⋯C	7.8	3.769(4)	0.0175(5)
	∠(Ba–O–C): 139.4(10)°
Barium(II) trifluoromethanesulfonate in dma, 0.7074 mol dm^−3
[Ba(OC(CH3)N(CH3)2)N]^2+	Ba–O	7.3	2.707(3)	0.0145(3)
	Ba⋯C	7.3	3.787(7)	0.0233(11)
	∠(Ba–O–C): 143.7(12)°

---

The mean Sr–O bond distances in the dmf- and dma-solvated strontium ions in solution are within the limits of error the same, 2.51(1) Å, and the Sr–O–C bond angle is ca. 165°. The mean Sr–O bond distance in the three reported octahedral dma-solvated strontium ions is 2.45 Å, and the mean Sr–O–C bond angle is 153°.^25,27 The mean Sr–O bond distances are significantly longer in solution than in the solid state showing that the coordination number in solution is larger than six.^25,27 The corresponding mean Ba–O bond distances are 2.74(1) and 2.71(1) Å, and the Ba–O–C bond angles are 139 and 144°, respectively. The mean Ba–O bond distance in the only reported solid state structure containing a dmf-solvated barium ion is 2.80 Å,²⁹ showing that the mean coordination numbers in dmf and dma solutions are smaller than eight.

In order to extrapolate the mean coordination number from the refined M–O bond distance, the relationship between ionic radius (recalculated to the expected M–O bond distance by adding 1.32 Å, the oxygen radius in amide solvents⁴⁸) and coordination number is plotted in Fig. 3. The refined structure parameters and the extrapolated coordination numbers as determined by LAXS are given in Table 3. The fit of the experimental data, the RDFs and the individual contributions from the solvated metal ion, the trifluoromethanesulfonate ion and the solvent are shown in Fig. 2 and Fig. S1–S3 (ESI†).

Extended X-ray absorption fine structure (EXAFS). The structure parameters obtained by EXAFS are in excellent agreement with those obtained by LAXS for the dmf- and dma-solvated strontium and barium ions, Tables 3 and 4; the mean coordination numbers are derived using Fig. 3. The dmp solvates of both strontium and barium display shorter M–O bond distances and thereby lower mean coordination numbers than the corresponding dmf and dma solvates, Table 4, due to the more space-demanding properties on coordination of dmp. The refined structure parameters are summarized in Table 4. The fit of the raw EXAFS and the Fourier transforms are shown in Fig. 4 and Fig. S4 (ESI†), respectively.

Table 4 Number of distances, N, mean bond distances, R/Å, and Debye–Waller factor coefficients, σ²/Ų from the refinements using EXAFSPAK; and N, R/Å, maximum of the bond distance distribution, R_max/Å, σ²/Ų and the third cumulant, C₃ = β·σ³/ų, describing the asymmetry in the bond distance distribution, from refinement with the GNXAS program package (in italics) from the EXAFS studies of the solvated strontium and barium ions in dmf, dma and dmp solutions at room temperature

	N	R	σ ^2	R/R max	σ ^2
Strontium(II) trifluoromethanesulfonate in dmf, 0.5845 mol dm^−3
Sr–O	6.8	2.508(2)	0.0172(2)	2.510/2.500	0.0104
				β = 0.0239	C 3 = 2.5 × 10^−5
Sr⋯C	6.8	3.730(8)	0.0106(11)	3.735	0.0158
Sr–O–C	13.6	3.786(5)	0.0134(18)	1.244	0.0025
MS (SrO6)	3 × 2.4	5.016(8)	0.0183(14)
	∠Sr–O–C: 167(4)°			161.3°
Strontium(II) trifluoromethanesulfonate in dma, 0.6457 mol dm^−3
Sr–O	6.7	2.505(2)	0.0123(2)	2.507/2.497	0.0098
				β = 0.0237	C 3 = 2.3 × 10^−5
Sr⋯C	6.7	3.724(9)	0.0125(13)	3.732	0.0234
Sr–O–C	13.4	3.709(5)	0.0171(12)	1.250	0.0025
MS (SrO6)	3 × 2.6	4.979(8)	0.013(2)
	∠Sr–O–C: 164(4)°			167.7°
Strontium(II) trifluoromethanesulfonate in dmp, saturated solution
Sr–O	6.2	2.465(2)	0.0093(2)	2.471/2.451	0.0116
				β = 0.2012	C 3 = 2.5 × 10^−4
Sr⋯C	6.2	3.601(12)	0.017(3)	3.605	0.0209
Sr–O–C	12.4	3.676(5)	0.0132(9)	1.250	0.0025
MS (SrO6)	3 × 4.8	4.95(2)	0.016(2)
	∠Sr–O–C: 150(2)°			149.6°
Barium(II) trifluoromethanesulfonate in dmf, 0.7339 mol dm^−3
Ba–O	7.8	2.727(2)	0.0152(6)	2.730	0.0160
Ba⋯C	7.8	3.758(9)	0.0166(10)	3.76	0.0254
Ba–O–C	15.6	3.846(7)	0.0186(9)	1.244	0.0019
	∠Ba–O–C: 139.2(13)°			139.1°
Barium(II) trifluoromethanesulfonate in dma, 0.7074 mol dm^−3
Ba–O	7.3	2.706(3)	0.0141(5)	2.705	0.0137
Ba⋯C	7.3	3.783(3)	0.018(3)	3.788	0.0203
Ba–O–C	14.6	3.879(2)	0.023(3)	1.250	0.0025
	∠Ba–O–C: 143.3(14)°			144.0°
Barium(II) trifluoromethanesulfonate in dmp, saturated solution
Ba–O	7.1	2.689(2)	0.0132(1)	2.686	0.0127
Ba⋯C	7.1	3.772(4)	0.0145(6)	3.765	0.0153
Ba–O–C	14.2	3.860(7)	0.021(2)	1.250	0.0025
	∠Ba–O–C: 143.9(9)°			143.5°

---

Fig. 4 Experimental EXAFS data (solid black lines) fitted with a model formed by ab initio-calculated scattering paths (red solid lines), listed in Table 4.

Discussion

Structures of amide solvated alkaline earth metal ions in solid state and solution

The EXAFS and LAXS data of the structures of the solvated strontium and barium ions in dmf, dma and dmp show M–O bond distances different from those expected for a well-defined coordination number. By using the correlation between M–O bond distance and coordination number, Table 2 and Fig. 3, the coordination number has been extrapolated from the obtained M–O bond distance, Tables 3 and 4. The obtained non-integer coordination numbers indicate an equilibrium between at least two configurations (coordination numbers), which is supported by large temperature factors (LAXS) and Debye–Waller factor coefficients (EXAFS), Tables 3 and 4.

The mean Sr–O and Ba–O bond distances and the corresponding mean coordination numbers decrease with the increasing steric demand of the solvent molecule on coordination, thus dmf > dma > dmp, Tables 3 and 4. The derived coordination numbers of the dmf, dma and dmp solvated strontium ions, 6.8, 6.7 and 6.2, are slightly smaller, ca. 0.8, than for the corresponding barium solvates, 7.8, 7.3 and 7.1, respectively, Tables 3 and 4, due to the larger ionic radius of the barium(II) ion, Table 2. The Sr–O and Ba–O bond distances in the dimethylsulfoxide (dmso) solvates, 2.54⁴⁷ and 2.540 Å,²⁸ and 2.76 Å,⁴⁹ respectively, are quite different from the coordination numbers given in one of the original papers. Using the same type of correlation as in Fig. 3, but with an assumed atomic radius of oxygen of 1.34 Å, the mean coordination numbers of the dmso solvates in solutions of strontium and barium should be revised to 6.9 and 7.8, respectively, Fig. S5 (ESI†), which for strontium is in very good agreement with ref. 28.

The mean Sr–O–C bond angle in the dmf-, dma-, and dmp- solvated strontium ions is in the range 150–165°, while the mean Ba–O–C bond angle in the corresponding barium solvates is smaller, in the range 140–145°, Tables 3 and 4. The M–O–C bond angles for the amide solvated alkaline earth metal ions deviate largely but with a weak trend in the order Mg²⁺ < Ca²⁺ ≈ Sr²⁺ > Ba²⁺, Table S2b (ESI†), showing that more space becomes available with increasing ionic radius. The bond angles observed in solution are slightly larger than in the solid state most likely due to a higher mean coordination number and larger crowding.

Standard partial molar volumes

To provide information about the relationship between structural and volumetric properties, structural data have been summarized for the alkali metal, alkaline earth metal, selected transition metal, lanthanum(III), gadolinium(III), and lutetium(III), halide, perchlorate and trifluoromethanesulfonate ions in dmf, dma, dmso, water, methanol and ethanol using, if possible, data from studies in solution. These data are compiled to extract the relationship between these structural and thermodynamic properties. The standard partial molar volumes of the ions studied in dmf, dma, water, dmso, methanol and ethanol are given in Table 5.

Table 5 Standard partial molar volumes at 298 K for the alkali metal, alkaline earth metal, selected transition metal(II), selected lanthanoid(III), aluminium(III), chromium(III), iron(III), halide, perchlorate and trifluoromethanesulfonate ions in dmf, dma, dmso, water, methanol, and ethanol

	V ^0/cm^3 mol^−1
	dmf	dma	dmso	H2O	Methanol	Ethanol
a Ref. 2. b Ref. 50. c Ref. 51. d Ref. 52. e Ref. 53. f Ref. 54. g Ref. 55. h Ref. 56. i Ref. 57. j Ref. 58. k Ref. 59. l Ref. 60. m Ref. 61. n Ref. 62.
Na^+	−2^a		3^a	−6.7^b	−19^a	−6^a
K^+	6^a		11^a	3.5^b	−8^a	3^a
Rb^+	10^a		17^a	8.6^b	−4^a	9^a
Cs^+	17^a		23^a	15.8^b	3^a	17^a
Mg^2+	−31.2^c	−52.6^c	−18^d	−32.2^b	−83^d
Ca^2+	−22.1^c	−29.7^c	−8^d	−28.9^b	−69^d
Sr^2+	−11.3^c	−19.3^c	−5^d	−29.2^b	−63^d	−27^a
Ba^2+	−10.9^c	−18.4^c	0.5^d	−23.5^b	−55^d
Mn^2+	−29.8^e	−44.6^f	−21^g	−28.7^b	−74^g
Co^2+	−34.5^e	−52.1^f	−25^g	−35^b	−82^g
Ni^2+	−37.6^e	−54.4^f	−27^g	−35^b	−89^g
Cu^2+	−33.3^e	−44.6^f	−26^g	−38.8^b	−76^g	−40^h
Zn^2+	−33.8^e	−40.3^f	−24^g	−32.6^b	−85^g
La^3+	−49.1^h	−63.0^h	−31.8^i	−55.6^b	−93.8^i
Gd^3+	−49.9^h	−63.8^h	−38.7^i	−56.4^b	−102.7^i
Lu^3+	−55.0^h	−63.8^h	−34.8^i	−64.5^b	−105.5^i
Al^3+			−51.8^j	−58.7^b
Cr^3+				−56^b
Fe^3+			−45.6^j	−60.2^b
F^−	−15.1^k		−2^a	+4.3^b	−1^a
Cl^−	+4^a	+24^a	+10^a	+23.3^b	+15^a
Br^−	+9^a	+33^a	+17^a	+30.2^b	+23^a
I^−	+24^a	+39^a	+31^a	+41.7^b	+31^a
ClO4^−	+35.1^l	+37.4^l	+41.7^m	+49.6^b	+37.4^n
CF3SO3^−	+70.8^h	+72.1^h	+77^d	+81.7^b	+77.5^d

---

The standard partial molar volumes of individual ions should be strongly related to the corresponding structure of the hydrated or solvated ion. For a given M–O bond distance, the coordination number of the metal ion solvate increases with an increasing charge of the metal ion. The hydrated sodium, calcium, europium(III) and thorium(IV) ions all have a M–O bond distance of ca. 2.45 Å, but the coordination numbers are 6, 8, 9 and 9, respectively,^63–66 and for the dmso-solvated sodium, calcium and europium(III) and thorium(IV) ions with bond distances of 2.43, 2.36, 2.40 and 2.47 Å, the coordination numbers are 6, 7, 8 and 9, respectively.^31,63,67,68

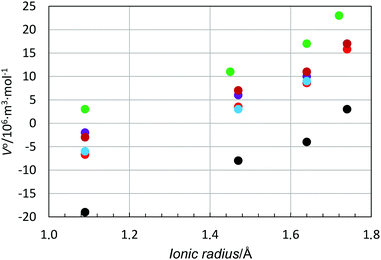
In order to study the relationship between the solvate structure and the standard partial molar volume in more detail, the standard partial molar volume has been plotted as function of the ionic radius and charge density of the ion, i.e. charge/volume of the ion based on its ionic radius for a given coordination number. The ionic radii of the metal ions used in Table 6 are based on solvate structures in solution, if available, otherwise solid state structures have also been included, Table 6 and Fig. S5 (ESI†). The standard partial molar volume vs. ionic radius plot becomes a scatter plot with an increasing standard partial molar volume with increasing ionic radius, Fig. S6 (ESI†). However, for the alkali metal ions, which are regarded as structure-breakers, a regular pattern is seen with an almost parallel relationship for all solvents studied, with positive standard partial molar volumes for dmso and negative ones for methanol, Fig. 5.

Table 6 Structural information about the hydrated and dmf, dma, dmso, methanol and ethanol solvated alkali metal, alkaline earth metal, lanthanum(III), gadolinium(III) and lutetium(III) ions in solution given as coordination number/M–O bond distance (Å), ionic radius (Å), and charge density (charge per ionic volume in ų, based on ionic radius). Data in italics are estimated structure parameters based on the size of the solvent molecule

	Na^+	K^+	Rb^+	Cs^+	Ref.
Water	6/2.43/1.09/0.184	7/2.81/1.47/0.075	8/2.98/1.64/0.054	8/3.08/1.74/0.045	63 and 69
dmf	6/2.42/1.09/0.184	7/2.80/1.47/0.075	8/2.97/1.64/0.054	8/3.07/1.74/0.045
dma	6/2.42/1.09/0.184	7/2.80/1.47/0.075	8/2.97/1.64/0.054	8/3.07/1.74/0.045
dmso	6/2.43/1.09/0.184	7/2.79/1.45/0.078	8/2.98/1.64/0.054	8/3.06/1.72/0.047	63 and 69
Methanol	6/2.43/1.09/0.184	7/2.81/1.47/0.075	8/2.98/1.64/0.054	8/3.08/1.74/0.045
Ethanol	6/2.43/1.09/0.184	7/2.81/1.47/0.075	8/2.98/1.64/0.054	8/3.08/1.74/0.045

---

	Mg^2+	Ca^2+	Sr^2+	Ba^2+	Ref.
Water	6/2.07/0.73/1.227	8/2.48/1.14/0.322	8/2.62/1.28/0.228	8/2.79/1.45/0.157	49, 64, 70 and 71 & Table S1 (ESI)
dmf	6/2.057/0.725/1.253	6/2.31/0.97/0.523	6.5/2.51/1.12/0.298	7.4/2.73/1.39/0.178	Tables 4, 5 & Table S2 (ESI)
dma	6/2.06/0.73/1.227	7/2.31/0.97/0.523	6.4/2.49/1.17/0.314	7/32.71/1.37/0.186	Tables 4, 5 & Table S2 (ESI)
dmso	6/2.07/0.73/1.227	7/2.36/1.02/0.450	6.9/2.54/1.20/0.276	7.7/2.76/1.42/0.167	31,49 & Table S3 (ESI)
Methanol	6/2.07/0.73/1.227	8/2.48/1.14/0.322	8/2.62/1.28/0.228	8/2.79/1.45/0.157	Table S3 (ESI)
Ethanol	6/2.07/0.73/1.227	8/2.48/1.14/0.322	8/2.62/1.28/0.228	8/2.79/1.45/0.157	Table S3 (ESI)

---

	Mn^2+	Co^2+	Ni^2+	Zn^2+	Ref.
Water	6/2.175/0.835/0.820	6/2.09/0.75/1.132	6/2.055/0.715/1.306	6/2.089/0.75/1.123	72–75 & Table S1 (ESI)
dmf	6/2.17/0.84/0.806	6/2.085/0.755/1.109	6/2.045/0.715/1.306	6/2.104/0.765/1.066	Table S3 (ESI)
dma	6/2.20/0.86/0.751	6/2.08/0.74/1.178	6/2.066/0.725/1.253	6/2.08/0.74/1.178	Table S3 (ESI)
dmso	6/2.17/0.83/0.835	6/2.096/0.755/1.109	6/2.068/0.73/1.227	6/2.11/0.77/1.046	73, 76 and 77 & Table S3 (ESI)
Methanol	6/2.164/0.825/0.850	6/2.09/0.75/1.132	6/2.061/0.72/1.279	6/2.086/0.745/1.253	78 & Table S3 (ESI)
Ethanol	6/2.20/0.86/0.751	6/2.09/0.75/1.132	6/2.055/0.715/1.306	6/2.079/0.74/1.178	Table S3 (ESI)

---

	La^3+	Gd^3+	Lu^3+	Ref.
Water	9/2.56/1.22/0.394	9/2.41/1.07/0.585	8.2/2.31/0.97/0.785	65 & Table 1
dmf	9/2.55/1.22/0.394	8/2.38/1.05/0.619	8/2.30/0.97/0.785	48 & Table S3 (ESI)
dma	8/2.50/1.16/0.459	8/2.39/1.05/0.619	8/2.23/0.89/1.016	48 & Table S3 (ESI)
dmso	8/2.49/1.15/0.471	8/2.38/1.04/0.637	8/2.30/0.96/0.601	67 & Table S3 (ESI)
Methanol	9/2.56/1.22/0.394	8/2.39/1.05/0.619	8/2.29/0.95/0.835	Table S3 (ESI)
Ethanol	9/2.56/1.22/0.394	8/2.39/1.05/0.619	8/2.29/0.95/0.835	Table S3 (ESI)

---

	Al^3+	Cr^3+	Fe^3+	Ref.
Water	6/1.90/0.56/4.08	6/1.96/0.62/3.01	6/2.00/0.66/2.49	79–81 & Table S3 (ESI)
dmso	6/1.90/0.56/4.08		6/2.00/0.66/2.49	82 and Table S3 (ESI)

---

Fig. 5 Scatter plot of standard partial molar volumes versus ionic radii of the alkali metal ions in water (red), methanol (black), ethanol (light blue), dmso (green), dmf (purple), and formamide (dark red).

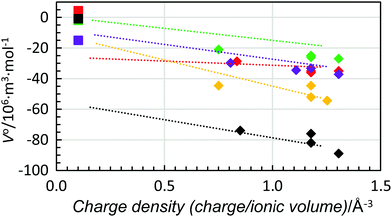
When the standard partial molar volume is plotted as a function of charge density, almost linear relationships with very similar low slopes are observed for the structure-making di- and trivalent metal ions with a decreasing standard partial molar volume with increasing charge density, Fig. 6. Also in this case the least negative standard partial molar volumes are observed for dmso and the most negative ones for methanol. Corresponding data for four transition metal ions, manganese(II), cobalt(II), nickel(II) and zinc(II), were compared with the ions with noble gas electron configuration, and all were regarded as structure-making ions, Fig. 7. For the solvents water, methanol and dma, the data for the transition metal ions are on the line obtained for the alkaline earth metal ions, while they are slightly below for dmf and dmso, at 5 and 10 × 10⁻⁶ m³ mol⁻¹, respectively, but the slopes are the same as for the alkaline earth metal ions. This shows that for structure-making ions the relationship of charge contractibility vs. density is very strict for every solvent and the standard partial molar volume can be predicted with good accuracy from the charge density even though the standard partial molar volumes differ a lot between different solvents.

Fig. 6 Scatter plot of standard partial molar volumes versus charge density of the alkali metal ions (filled circles), alkaline earth metal ions (squares) and lanthanum(III), gadolinium(III) and lutetium(III) ions (triangles) in water (red), methanol (black), dmso (green), dmf (purple) and dma (orange).

Fig. 7 Scatter plot of standard partial molar volumes versus charge density of the manganese(II), cobalt(II), nickel and zinc ions (diamonds) and fluoride ions (squares) in water (red), methanol (black), dmso (green), dmf (purple) and dma (orange). The dashed lines are the trend-lines of the divalent alkaline earth metal ions from Fig. 6.

The data for the halide ions, regarded as structure-breaking ions, except the fluoride ion, have been plotted together with those for the alkali metal ions in Fig. 8. The relationship of standard partial molar volume vs. ionic radius follows the very same pattern for all ions, including the fluoride ion, Fig. 8, even though it is regarded as a moderate structure-making ion.¹ For the solvents water, methanol and dma the standard partial molar volumes are slightly more positive for the halide ion in comparison to the alkali metal ions, while the opposite is found for dmf and dmso. However, the differences are very small and for a certain ionic radius, independent of positively or negatively charged ions, the difference in standard partial molar volume is less than 20 × 10⁻⁶ m³ mol⁻¹, Fig. 8. If one regards the standard partial molar volume as a measure of structure-breaking ability, it increases with increasing radius of the ion.

Fig. 8 Scatter plot of standard partial molar volumes versus ionic radii of the alkali metal ions (filled circles) and the halide ions (filled diamonds) in water (red), methanol (black), ethanol (light blue), dmso (green), dmf (purple), and formamide (dark red).

The aprotic organic solvents dmso, dmf and dma seem to be less compressed by structure-making ions than the protic ones, and at the same time they are broken up to a larger extent by structure-breaking ions. This is most likely because these solvents have only weak intermolecular interactions and they cannot come that much closer to each other through strong solvation by metal ions with high charge density than in the solvent bulk. For the structure-breaking ions, they have to make room for themselves and thereby the solvent molecules move far from each other. The crystal structure of dmf shows very weak intermolecular hydrogen bonding between the amide oxygen and proton,⁸³ while such intermolecular interactions are not possible in dma. However, these weak hydrogen bonds do not seem to affect the volumetric properties as the V⁰ values are systematically more negative for dma than for dmf, Fig. 7.

There is a large difference between water and methanol with methanol being very much more compressed by both structure-making and breaking ions, Fig. 5–8. The reason is most likely that methanol molecules forming one-dimensional hydrogen bonds are more easily broken up and the presence of ions, both structure-making and breaking ones, causes a breakdown of the hydrogen bonds compressing the solvent bulk. Water, on the other hand, forms a very stable three-dimensional hydrogen-bond network in the aqueous bulk, which alters the local hydrogen bonds close to the ions, whereas the water molecules not involved in the hydration of the ion maintain the aqueous bulk hydrogen bond network structure.

Fig. 9 shows the standard partial molar volumes of the trivalent lanthanoid(III) ions in the solvents studied plotted together with respective values for the aluminium(III), chromium(III) and iron(III) ions in water and dmso. As seen, the trend-lines for all trivalent ions are almost identical. Moreover, for dmso the strong correlation between charge density and standard partial molar volumes is observed, while in water, it seems that the standard partial molar volumes are independent of charge density (as also found for the divalent metal ions). It is worth adding that for hydrated ions the independency of the partial molar volumes of charge density was postulated by Hepler 60 years ago,⁵ but not proven until now.

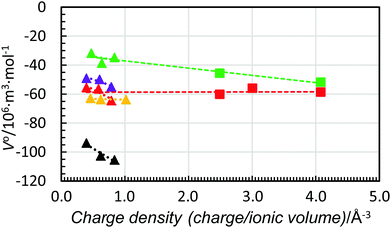Fig. 9 Scatter plot of standard partial molar volumes versus charge density of the aluminium(III), chromium(III) and iron(III) ions (squares) and the lanthanum(III), gadolinium(III) and lutetium(III) ions (triangles) in water (red), methanol (black), dmso (green), dmf (purple) and dma (orange). The dashed lines are the trend-lines of the trivalent lanthanoid(III) ions from Fig. 6. The values of the standard partial molar volumes of the aluminium(III), chromium(III) and iron(III) in water and dmso are given in Table 6.

Conclusions

The structures of dmf- and dma-solvated strontium and barium ions show larger mean coordination numbers in solution than in solid state. An equilibrium between at least two coordination numbers seems to exist in solution. The mean coordination number decreases with increasing spatial demands on coordination, thus, CN(dmf) > CN(dma) > CN(dmp) of the studied amide solvents. The relationship between the structural and volumetric properties shows that for structure-breaking ions there is an almost linear relationship between the ionic radius and the standard partial molar volume, Fig. 8, with decreasing contractibility with increasing ionic radius. For structure-making ions a linear relationship between the charge density and the standard partial molar volume is observed, Fig. 6, with only a very minor influence of the charge density on the contractibility. Instead, the mean intermolecular volume caused by intermolecular interactions such as hydrogen bonds seems to be an important factor for the contractibility. Of the studied solvents, methanol has the highest ability to contract, followed by water. On the other hand, the contractibility of the aprotic solvents is much weaker as the intermolecular interactions in the bulk solvent are weak allowing close packing of the solvent molecules in the neat solvents. The standard partial molar volumes are independent of charge density as postulated by Hepler.⁵ The contractibility of solvent molecules around an ion is very much dependent on the charge density seen in the in the coordination numbers of e.g. hydrated sodium, calcium, europium(III) and thorium(IV) ions, which are six-, eight-, nine-, and nine-coordinated in aqueous solution, respectively, but the metal ion-oxygen bond distance is the same, ca. 2.45 Å. Lastly, the ionic radii for all alkaline earth metals have been revised with respect to those listed by Shannon,³⁴ some by as much as 0.05 Å. This was made possible with a statistically much larger dataset covering CNs 4–9 from the small beryllium ion to the significantly larger barium ion. This leaves radium with the only uninvestigated ionic radius, due to its radioactive nature and the fact that the alkaline earth metal ions do not behave as predictably as the actinoid(III) ions.⁸⁴

Conflicts of interest

There are no conflicts of interest to declare.

Acknowledgements

The Swedish Institute is acknowledged for supporting AF through the Visby Program during her stay in Sweden. The support for the solution chemistry research from the Swedish Research Council is gratefully acknowledged. Portions of this research were carried out at beamline I811, MAX-lab synchrotron radiation source, Lund University, Sweden. Funding for the beamline I811 project was provided by the Swedish Research Council and The Knut and Alice Wallenbergs Foundation. The use of the Stanford Synchrotron Radiation Lightsource, SLAC National Accelerator Laboratory, is supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences under Contract No. DE-AC02-76SF00515. The SSRL Structural Molecular Biology Program is supported by the DOE Office of Biological and Environmental Research, and by the National Institutes of Health, National Institute of General Medical Sciences (including P41GM103393). The contents of this publication are solely the responsibility of the authors and do not necessarily represent the official views of NIGMS or NIH.

References

1. Y. Marcus, Chem. Rev., 2009, 109, 1346–1370 , and references therein.
2. Y. Marcus and G. Hefter, Chem. Rev., 2004, 104, 3405–3452 , and references therein.
3. Y. Marcus and G. Hefter, Chem. Rev., 2006, 106, 4585–4621 , and references therein.
4. G. Hefter and Y. Marcus, J. Solution Chem., 1997, 26, 249–266.
5. L. G. Hepler, J. Phys. Chem., 1957, 61, 1426–1429.
6. Y. Marcus, J. Mol. Liq., 2005, 118, 3–8.
7. M. Asada, T. Mitsugi, K. Fujii, R. Kanzaki, Y. Umebayashi and S.-i. Ishiguro, J. Mol. Liq., 2007, 136, 138–146.
8. R. Murugan and S. Mohan, Spectrochim. Acta, Part A, 1995, 51, 735.
9. Y. Umebayashi, K. Matsumoto, Y. Mune, Y. Zhang and S.-i. Ishiguro, Phys. Chem. Chem. Phys., 2003, 5, 2552–2556.
10. F. H. Allen, Acta Crystallogr., Sect. B: Struct. Sci., 2002, 58, 380–388 , CSD ConQuest build 1.19.
11. Inorganic Crystal Structure Database 1.4.6 (release: 2017-1); FIZ/NIST.
12. C. P. Rao, A. M. Rao and C. N. R. Rao, Inorg. Chem., 1984, 23, 2080–2085.
13. H. Krautscheid and F. Vielsack, Z. Anorg. Allg. Chem., 1999, 625, 562–566.
14. M. Ruben, D. Walther, R. Knake, H. Gorls and R. Beckert, Eur. J. Inorg. Chem., 2000, 1055–1064.
15. B. L. Barker, D. Aubry, F. R. Fronczek, S. F. Watkins and G. G. Stanley, Acta Crystallogr., Sect. E: Struct. Rep. Online, 2006, 62, m942–m944.
16. C. Nitschke, M. Kockerling, E. Bernhardt, T. Kuppers and H. Willner, Dalton Trans., 2014, 43, 7128–7138.
17. J. Landmann, J. A. P. Sprenger, M. Hailmann, V. Bernhardt-Pitchougina, H. Willner, N. Ignat'ev, E. Bernhardt and M. Finze, Angew. Chem., Int. Ed., 2015, 54, 11259.
18. L. Pavanello, P. Visona, S. Bresadola and G. Bandoli, Z. Kristallogr., 1994, 209, 946–949.
19. X. Liu, L.-Z. Cai, G.-C. Guo, Q. Li and J.-S. Huang, Jiegou Huaxue, 2006, 25, 90–94.
20. D. Fenske, G. Baum, H. Wolkers, B. Schreiner, F. Weller and K. Dehnicke, Z. Anorg. Allg. Chem., 1993, 619, 489–499.
21. Y.-M. Li, S.-Q. Xia, J.-J. Zhang, X.-T. Wu, L.-S. Wang, W.-X. Du and S.-M. Hu, Jiegou Huaxue, 2005, 24, 716–722.
22. S. Perruchas, F. Simon, S. Uriel, N. Avarvari, K. Boubekeur and P. Batail, J. Organomet. Chem., 2002, 643–644, 301–306.
23. X.-J. Tan, S.-X. Sun, J.-P. Ma, L.-D. Liu, Y.-B. Dong, W.-T. Yu and D.-X. Xing, Acta Crystallogr., Sect. C: Cryst. Struct. Commun., 2004, 60, m476–m478.
24. H. Yu, W. Zhang, X. Wu, T. Sheng, Q. Wang and P. Lin, Angew. Chem., Int. Ed., 1998, 37, 2520–2524.
25. Y. H. Kim, J. Calabrese and C. McEwen, J. Am. Chem. Soc., 1996, 118, 1545–1546.
26. L. Chen, H. Yu, L. Wu, W. Du, X. Gao, P. Lin, W. Zhang, C. Cui and X. Wu, J. Solid State Chem., 2000, 151, 286–293.
27. J. Zhang, S. Meng, Y. Song, H. Zhao, J. Li, G. Qu, L. Sun, M. G. Humphrey and C. Z. Zhang, Chem. – Eur. J., 2010, 16, 13946–13950.
28. G. Moreau, R. Scopelliti, L. Helm, J. Purans and A. Merbach, J. Phys. Chem. A, 2002, 106, 9612–9622.
29. J. Wang, J. Li and J. Niu, J. Coord. Chem., 2005, 58, 1639–1651.
30. P. Lemoine and P. Herpin, Acta Crystallogr., Sect. B: Struct. Crystallogr. Cryst. Chem., 1980, 36, 2608–2612.
31. I. Persson, Pure Appl. Chem., 2010, 82, 1901–1917 , and references therein.
32. A.-S. Ullström, D. Warminska and I. Persson, J. Coord. Chem., 2005, 58, 611–622.
33. D. Lundberg, I. Persson, L. Eriksson, P. D’Angelo and S. De Panfilis, Inorg. Chem., 2010, 49, 4420–4432.
34. R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32, 751–767.
35. C. M. V. Stålhandske, I. Persson, M. Sandström and E. Kamieńska-Piotrowicz, Inorg. Chem., 1997, 36, 3174–3182.
36. G. Johansson and M. Sandström, Chem. Scr., 1973, 4, 195–198.
37. International Tables for X-ray Crystallography, Kynoch Press, Birmingham, UK, 1974, vol. 4.
38. D. T. Cromer, J. Chem. Phys., 1969, 50, 4857–4859.
39. H. A. Levy, M. D. Danford and A. H. Narten, Data Collection and Evaluation with an X-ray Diffractometer Designed for the Study of Liquid Structure, Technical Report-3960, Oak Ridge National Laboratory, 1966.
40. M. Molund and I. Persson, Chem. Scr., 1985, 25, 197.
41. J. W. Robinson, Handbook of Spectroscopy, CRC Press, Boca Raton, FL, 1991.
42. G. N. George and I. J. Pickering, EXAFSPAK – A Suite of Computer Programs for Analysis of X-ray Absorption Spectra, SSRL, Stanford, CA, 1993.
43. (a) A. Filipponi, A. Di Cicco and C. R. Natoli, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15122–15134; (b) A. Filipponi and A. Di Cicco, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 15135–15149; (c) A. Filipponi and A. Di Cicco, Task Quarterly, 2000, 4, 575–669.
44. S. I. Zabinsky, J. J. Rehr, A. Ankudinov, R. C. Albers and M. Eller, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 2995–3009.
45. A. Filipponi, J. Phys.: Condens. Matter, 1994, 6, 8415–8427.
46. L. Hedin and B. I. Lundqvist, J. Phys. C: Solid State Phys., 1971, 4, 2064–2083.
47. J. K. Beattie, S. P. Best, B. W. Skelton and A. H. White, J. Chem. Soc., Dalton Trans., 1981, 2105–2111.
48. A. Fuchs, D. Lundberg, D. Warmińska and I. Persson, J. Phys. Chem. B, 2013, 117, 8502–8511.
49. I. Persson, M. Sandström, H. Yokoyama and M. Chaudhry, Z. Naturforsch., A: Phys. Sci., 1995, 50, 21–37.
50. Y. Marcus, Ion Properties, Marcel Dekker, New York, 1997.
51. D. Warmińska and D. Lundberg, J. Chem. Thermodyn., 2016, 92, 108–117.
52. D. Warmińska, J. Wawer and W. Grzybkowski, J. Chem. Thermodyn., 2010, 42, 1116–1125.
53. D. Warmińska, J. Krakowiak and W. Grzybkowski, J. Chem. Eng. Data, 2005, 50, 221–225.
54. J. Krakowiak, H. Koziel and W. Grzybkowski, J. Mol. Liq., 2005, 118, 57–65.
55. D. Warmińska, J. Wawer and W. Grzybkowski, J. Chem. Eng. Data, 2010, 55, 2116–2122.
56. D. Warmińska, A. Fuchs and D. Lundberg, J. Chem. Thermodyn., 2013, 58, 46–54.
57. D. Warmińska and J. Wawer, J. Chem. Thermodyn., 2012, 55, 79–84.
58. D. Bobicz and W. Grzybkowski, J. Solution Chem., 2002, 31, 223–234.
59. Y. Marcus, G. Hefter and T. Pang, J. Chem. Soc., Faraday Trans., 1994, 90, 1899–1903.
60. A. Płaczek, H. Koziel and W. Grzybkowski, J. Chem. Eng. Data, 2007, 52, 699–706.
61. D. Warmińska and W. Grzybkowski, J. Chem. Thermodyn., 2010, 42, 1451–1457.
62. J. Wawer, J. Krakowiak and W. Grzybkowski, J. Chem. Thermodyn., 2008, 40, 1193–1199.
63. J. Mähler and I. Persson, Inorg. Chem., 2012, 51, 425–438.
64. (a) F. Jalilehvand, D. Spångberg, P. Lindqvist-Reis, K. Hermansson, I. Persson and M. Sandström, J. Am. Chem. Soc., 2001, 123, 431–441; (b) D. Spångberg, K. Hermansson, P. Lindqvist-Reis, F. Jalilehvand, M. Sandström and I. Persson, J. Phys. Chem. B, 2000, 104, 10467–10472.
65. (a) I. Persson, P. D’Angelo, S. De Panfilis, M. Sandström and L. Eriksson, Chem. – Eur. J., 2008, 14, 3056–3066; (b) P. D'Angelo, S. De Panfilis, A. Filipponi and I. Persson, Chem. – Eur. J., 2008, 14, 3045–3055; (c) P. D’Angelo, A. Zitolo, V. Migliorati, G. Mancini, I. Persson and G. Chillemi, Inorg. Chem., 2009, 48, 10239–10248; (d) P. D’Angelo, A. Zitolo, V. Migliorati and I. Persson, Chem. – Eur. J., 2010, 16, 684–692.
66. N. Torapava, I. Persson, L. Eriksson and D. Lundberg, Inorg. Chem., 2009, 48, 11712–11723.
67. (a) I. Persson, E. Damian-Risberg, P. D’Angelo, S. De Panfilis, M. Sandström and A. Abbasi, Inorg. Chem., 2007, 46, 7742–7748; (b) P. D’Angelo, V. Migliorati, R. Spezia, S. De Panfilis, I. Persson and A. Zitolo, Phys. Chem. Chem. Phys., 2013, 15, 8684–8691.
68. N. Torapava, D. Lundberg and I. Persson, Eur. J. Inorg. Chem., 2011, 5273–5278.
69. P. D’Angelo and I. Persson, Inorg. Chem., 2004, 43, 3543–3549.
70. R. Caminiti, A. Musinu, G. Paschina and G. Pinna, J. Appl. Crystallogr., 1982, 15, 482–487.
71. J. N. Albright, J. Chem. Phys., 1972, 56, 3783–3786.
72. (a) T. K. Sham, J. B. Hastings and M. L. Perlman, Chem. Phys. Lett., 1981, 83, 391–396; (b) H. Ohtaki, T. Yamaguchi and M. Maeda, Bull. Chem. Soc. Jpn., 1976, 49, 701–708; (c) I. M. Schapolalov and I. V. Radchenko, J. Struct. Chem., 1971, 12, 705–708.
73. (a) R. Spezia, M. Duvail, P. Vitorge, T. Cartailler, J. Tortajada, G. Chillemi, P. D‘Angelo and M.-P. Gaigeot, J. Phys. Chem. A, 2006, 110, 13081–13088; (b) P. D’Angelo, V. Barone, G. Chillemi, N. Sanna, W. Meyer-Klaucke and N. V. Pavel, J. Am. Chem. Soc., 2002, 124, 1958–1967; (c) P. D’Angelo, M. Benfatto, S. Della Longa and N. V. Pavel, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 66, 064209; (d) M. Ichihashi, H. Wakita and I. Masuda, J. Solution Chem., 1984, 13, 505–516; (e) M. Magini and G. Giubileo, Gazz. Chim. Ital., 1981, 111, 449–454; (f) W. Bol, G. J. A. Gerrits and C. L. van Panthaleon van Eck, J. Appl. Crystallogr., 1970, 3, 486–492.
74. O. Kristiansson, I. Persson, D. Bobicz and D. Xu, Inorg. Chim. Acta, 2003, 344, 15–27.
75. (a) V. Migliorati, G. Mancini, S. Tatoli, A. Zitolo, A. Filipponi, S. De Panfilis, A. Di Cicco and P. D’Angelo, Inorg. Chem., 2013, 52, 1141–1150; (b) V. Migliorati, A. Zitolo, G. Chillemi and P. D’Angelo, ChemPlusChem, 2012, 77, 234–239; (c) D. H. Powell, P. M. N. Gullidge, G. W. Neilson and M. C. Bellissent-Funel, Mol. Phys., 1990, 71, 1107–1116; (d) T. Radnai, K. Inoue and H. Ohtaki, Bull. Chem. Soc. Jpn., 1990, 63, 3420–3425; (e) A. Musinu, G. Pachina, G. Piccalugam and M. Magini, J. Appl. Crystallogr., 1982, 15, 621–625.
76. I. Persson, Acta Chem. Scand., Ser. A, 1982, 36, 7–13.
77. Y. Inada, H. Hayashi, K.-i. Sugimoto and S. Funahashi, J. Phys. Chem. A, 1999, 103, 1401–1406.
78. V. Migliorati, G. Chillemi and P. D'Angelo, Inorg. Chem., 2011, 50, 8509–8515.
79. (a) R. Caminiti, G. Licheri, G. Piccaluga, G. Pinna and T. Radnai, J. Chem. Phys., 1979, 71, 2473–2476; (b) R. Caminiti and T. Radnai, Z. Naturforsch., A: Phys., Phys. Chem., Kosmophys., 1980, 35, 1368–1372; (c) W. Bol and T. Welzen, Chem. Phys. Lett., 1977, 49, 189–192.
80. (a) N. Torapava, A. Radkevich, D. Davydov, A. Titov and I. Persson, Inorg. Chem., 2009, 48, 10383–10388; (b) P. Lindqvist-Reis, S. Díaz-Moreno, A. Munoz-Páez, S. Pattanaik, I. Persson and M. Sandström, Inorg. Chem., 1998, 37, 6675–6683.
81. D. Lundberg, A.-S. Ullström, P. D’Angelo and I. Persson, Inorg. Chim. Acta, 2007, 360, 1809–1818 , and references therein.
82. A. Molla-Abbassi, M. Skripkin, M. Kritikos, I. Persson, J. Mink and M. Sandström, J. Chem. Soc., Dalton Trans., 2003, 1746–1753.
83. H. Borrmann, I. Persson, M. Sandström and C. M. V. Stålhandske, J. Chem. Soc., Perkin Trans. 2, 2000, 393–402.
84. D. Lundberg and I. Persson, Coord. Chem. Rev., 2016, 318, 131–134.

---

Footnotes

† Electronic supplementary information (ESI) available: Physico-chemical properties of the studied solvents, summary of the solvates and related structures of the alkaline earth metal ions in the solid state, rdf functions and Fourier transforms of the dmf and dma solvated strontium and barium ion solutions studied by LAXS and EXAFS, respectively. See DOI: 10.1039/c8cp02244e

‡ Present address: Biomontan, Regensburger Straße 5, AT-4470 Enns, Austria.

---