 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermodynamics and defect chemistry of substitutional and interstitial cation doping in layered α-V2O5†
Kit
McColl
 ,
Ian
Johnson
and
Furio
Corà
*
,
Ian
Johnson
and
Furio
Corà
*
Department of Chemistry, Christopher Ingold Building, University College London, 20 Gordon Street, London WC1H 0AJ, UK. E-mail: f.cora@ucl.ac.uk
First published on 11th May 2018
Abstract
A systematic study of the location and energetics of cation dopants in α-V2O5 has been conducted using pair-potential methods, supplemented by first-principles calculations. The consequences of doping on intrinsic defect equilibria have been discussed and the effects of selected dopants on Li+ and Mg2+ diffusion energy barriers have been investigated.
The use of a metallic multivalent (MV) anode (i.e. Mg2+, Ca2+ or Al3+) represents a strategy to improve charge and energy density beyond present Li-ion battery technology.1 MV ions introduce a charge multiplicity factor, and can also result in saving on space by avoiding the anode intercalation processes necessary for Li. For example, Mg anodes do not exhibit the same dendritic growth issues upon cycling that plague Li-metal anodes,2 and thus metallic Mg can provide a far higher volumetric (Mg = 3833 mA h cm−3vs. LiC6 = 800 mA h cm−3) and gravimetric (Mg = 2205 mA h g−1vs. LiC6 = 372 mA h g−1) capacity than intercalation anodes for Li.3 A major challenge in the development of MV battery technologies is optimisation of cathode materials, many of which are currently limited by poor ion mobility, and show limited electrochemical performance.4 V2O5 was first investigated in the 1970's as a Li-ion intercalation cathode, but commercialization was never achieved, due to issues with cycling stability, electronic conductivity and Li-ion mobility.5 However interest has re-emerged as recent work has identified V2O5 as one of only a few materials which can reversibly intercalate Mg2+ ions,6 following discovery of the prototype MV cathode MgxMo3S4.7 Ion mobility and other issues have been partially overcome in V2O5 cathodes for Li-ion batteries through the introduction of dopants, many of which have offered improved electrochemical performance,8–15 and a summary of the figures of merit for doped V2O5 cathode materials can be found ref. 15. Such doping strategies may also be effective for MV V2O5 cathodes. However a systematic evaluation of the likely location of dopants and the effects they have on V2O5 electrochemistry is thus far missing from the literature. Empirically-fitted pair potential methods have been demonstrated to provide insight into defect chemistry and ionic diffusion properties of battery materials.16 In this study we employ these methods, supplemented by first-principles calculations, to investigate the thermodynamics of cation doping in α-V2O5, and the effect of these dopants on the mobility of Li+ and Mg2+ ions.
The stable polymorph of V2O5 at ambient conditions is the orthorhombic α-phase with space group Pmmn (no. 59) and lattice constants a = 3.564, b = 11.512, c = 4.368 Å.17 The layered structure is formed of distorted VO5 square pyramids, arranged sharing three corners and two edges with neighbouring pyramids (Fig. 1), with corner-sharing and edge sharing pairs oriented in opposite directions along the [001] axis. There are two V2O5 formula units in the crystallographic unit cell, which contains four symmetry unique atoms: one vanadium and three oxygen atoms, conventionally denoted O1, O2 and O3,18 with O1 corresponding to the oxygen at the end of the short (1.585 Å) V–O1vanadyl bond. Two-fold coordinate O2 atoms link between corner sharing VO5 pyramids in the [010] direction and three-fold coordinate O3 atoms link corner-sharing pyramids in the [100] direction. The interatomic V–O1interlayer distance of 2.785 Å is considered too long to be a conventional ionic or covalent interaction19 and the interlayer forces are therefore predominantly of a weak van der Waals (vdW) type.
V2O5 exhibiting conventional interlayer spacing (i.e. not of the aerogel or xerogel type)20 can incorporate dopant cations into two possible sites: interstitial, residing between the V2O5 layers, or substitutional, replacing V5+ ions (Fig. 1). Steric effects can be expected to influence dopant location for ions of the same valence, however the predominant thermodynamic driving force determining the location of dopants of different valence is expected to be the energy of the associated defects that form to maintain overall charge neutrality in the lattice. Substitutional replacement of V5+ with cations of a lower charge will produce a net negative charge, which can be compensated by oxygen-ion vacancies, which have a net positive charge. Interstitial incorporation of dopants introduces a net positive charge to the lattice, which can be compensated either by interstitial oxygen-ions or vanadium-ion vacancies, both of which bring a net negative charge to the lattice.
Initial investigations, considering a range of dopants with charge between +1 and +4 and all reasonable combinations of clustered and isolated cation and oxygen-ion defects, were conducted to determine the most stable charge compensation schemes for each dopant when incorporated into substitutional or interstitial sites. A full description of the calculations undertaken can be found in the ESI.† The results indicate that when a substitutional cation with a lower charge than V5+ is accompanied by the formation of an oxygen-ion vacancy, the most stable arrangement is always as a clustered defect with the oxygen-ion vacancy at the short-bond O1 of the substitutional site. In other words, the (VO)3+ vanadyl-like group behaves as a single unit and undergoes replacement as a whole. In the following, we consider this to be the predominant defect mechanism for substitutional Mn+ dopants. Calculations (ESI†) also determined that the prevalent charge balance for interstitial cations was by the formation of interstitial oxide ions, rather than the reduction of V to V4+ oxidation state, i.e. the localization of an electron on a V site to form a polaron, indicated as 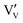 in Kröger–Vink (K–V) notation. V5+ or (VO)3+ vacancies were never found to be stable relative to interstitial oxygen-ions as charge balance for interstitial Mn+ dopants. Hereafter we present a series of defect formation equations in K–V notation that represent the most stable schemes for incorporation of substitutional and interstitial Mn+ ions (n = 1, 2, 3, 4) into α-V2O5.
in Kröger–Vink (K–V) notation. V5+ or (VO)3+ vacancies were never found to be stable relative to interstitial oxygen-ions as charge balance for interstitial Mn+ dopants. Hereafter we present a series of defect formation equations in K–V notation that represent the most stable schemes for incorporation of substitutional and interstitial Mn+ ions (n = 1, 2, 3, 4) into α-V2O5.
M+ ions:
 | (i) |
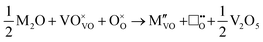 | (ii) |
M2+ ions:
 | (iii) |
 | (iv) |
M3+ ions:
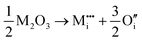 | (v) |
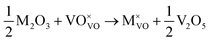 | (vi) |
M4+ ions:
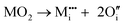 | (vii) |
 | (viii) |
The calculated reaction energies for the schemes detailed above, conducted for a range of 28 Mn+ ions listed in the ESI,† are reported in Fig. 2, plotted as a function of ionic radii. The results indicate that the interstitial sites for all M+ (red) and M2+ ions (gold) are more stable than substitutional incorporation, the difference being ∼6 eV for M+ and ∼4 eV for M2+ ions. Our calculations therefore suggest that M+ and M2+ ions will only be incorporated interstitially, regardless of their ionic radius. The M+ and M2+ interstitial sites are most stable at an ionic radius of ∼1 Å, which indicates that the V2O5 structure is suited to accommodate ion of this size within the interlayer space.
 | ||
| Fig. 2 Reaction energy energies for Mn+ cations (ESI†) as a function of dopant ionic radius. Circles indicate substitutional defects, and crosses indicate interstitial defects. Different dopant cation valences are indicated by the differently colored markers. Approximate trends in cation series of the same valence are indicated by the solid and dotted coloured lines, which are intended as guides for the eye only. A dashed vertical line at 0.54 Å indicates the ionic radius of V5+. The dashed vertical line at 1.0 Å indicates the approximate minimum reaction energy for substitutional ions, and is an estimate for the effective ionic radius of the vanadyl ion. | ||
The M3+ interstitial defects become more stable as the ionic radius of the dopant increases. The larger variation in energy as a function of ionic radius for the M3+ ions compared to the M+ and M2+ ions indicates that the higher charge of the M3+ ions creates a greater distortion of the lattice around the dopant, and this distortion is more pronounced when the ions are smaller. The reaction energy of the substitutional M3+ defects are close in energy to the M3+ interstitial defects. The reaction energy increases less quickly as a function of decreasing M3+ ionic radius for substitutional rather than for the interstitial defects, and thus the most stable site for M3+ defects swaps from substitutional to interstitial as ionic radius increases. The calculations suggest that for M3+ ions whose ionic radius is greater than ∼0.7 Å, interstitial sites are more stable, whereas ions smaller than this are more stable in substitutional sites. Consequently, both substitutional and interstitial defects may be possible for M3+ ions, and the location of the dopant may be tailored by the use of kinetic or thermodynamic control during synthesis and post-processing. For M4+ ions, substitutional sites are more stable than interstitial sites for all ionic radii, with a much greater difference in energy for smaller ions, which will only occupy substitutional sites. There is a narrowing of the energy difference between substitutional and interstitial sites for larger M4+ ions. The calculations therefore suggest that large interstitial M4+ doped V2O5 may be a metastable product accessible under some kinetically controlled synthesis conditions. A correlation between substitutional dopant ionic radius and reaction energy has been observed for several solids, including perovskites, and it usually yields lowest energy when the ionic radius of the dopant and the host crystal ion it replaces are similar.21 This is not the case here, since we find that Mn+ dopants (n < 5) replace (VO3+) ions as a whole, rather than V5+ ions. The position of the minimum reaction energy, which is found at an ionic radius of ∼1.0 Å for substitutional dopants of all net charges, suggests this is an estimate for the effective radius of the vanadyl ion.
Whilst these atomistic simulation methods have been applied successfully to investigate dopants in battery materials previously,16,22 their empirical nature and the challenges of representing a complex layered structure like V2O5 using fitted potentials mean that the values of reaction energies will be subject to some error, the magnitude of which is challenging to evaluate accurately. Any errors present will be particularly important for the predictions of thermodynamic stability of M3+ ions, and large M4+ where the substitutional and interstitial sites are similar in energy. As a test of their reliability, we have compared the pair-potential results with calculations performed using density functional theory (DFT), investigating substitutional Al3+ and Fe3+ incorporation (ESI†). The results show good agreement between the techniques, and reproduction of the pair-potential results using quantum-mechanics supports their validity.
The location of dopants in V2O5 and the defects that form to compensate the dopant charge, influence the concentration of V4+ and oxygen vacancies in the material, which in turn are expected to affect the electrochemical performance.23,24 As with many early transition metal oxides, V2O5 is typically an oxygen-deficient intrinsic n-type semiconductor25 (and may therefore more accurately denoted as V2O5−δ), often due to a combination of incomplete oxidation of the vanadium ions in the precursor and facile oxygen vacancy formation in the bulk material. Intrinsic oxygen deficiency is charge compensated in the structure of V2O5 by the presence of a measurable concentration of V4+ ions, whose d1 electrons (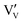 ) are associated with increased electronic conductivity.26 The formation of oxygen vacancies and V4+ in V2O5 can be represented, in Kröger–Vink notation as:
) are associated with increased electronic conductivity.26 The formation of oxygen vacancies and V4+ in V2O5 can be represented, in Kröger–Vink notation as:
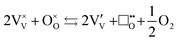 | (ix) |
 | (x) |
 | (xi) |
 | (xii) |
 | (xiii) |
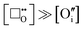 | (xiv) |
Calculations discussed earlier indicate that M+, M2+ and large M3+ ions are expected to be incorporated interstitially, along with interstitial oxygen-ions. The tendency for oxygen deficiency and the accessible redox of V5+/V4+ in the lattice means that rather than residing in the structure, extrinsic interstitial oxygen-ions will anneal out some of the intrinsic oxygen vacancies:
 | (xv) |
Due to the limitations of the available potential models, no atomistic defect formation calculations were performed for M5+ or M6+ ions. We can however infer from the trends in the M+ to M4+ series, that both M5+ and M6+ ions will prefer to be incorporated substitutionally rather than interstitially regardless of their size. M5+ ions will not require charge balancing upon incorporation, and are therefore not expected to significantly modify the concentration of V4+ and oxygen vacancies relative to pristine V2O5. M6+ ions are likely to substitute and either anneal out oxygen-ion vacancies, or introduce interstitial oxygen ions:
 | (xvi) |
 | (xvii) |
The location of dopants in V2O5 will have an influence on the mobility of ions through the structure. Possible effects include modifying the interlayer separation,13 blocking diffusion channels,29 introducing additional Coulombic interactions between intercalants and dopants ions and providing sites for nucleation and growth of different phases during cycling.30 Dopants may also be expected to alter the extent and effect of local polaronic distortions, which have been demonstrated to produce lithiation gradients and inhibit Li+ mobility in V2O5 nanowires.31 Here we consider the effects of interstitial Na+ and Ba2+, and substitutional Al3+ dopants on the energy barriers for Li+ and Mg2+ diffusion in the [100] direction of α-V2O5. The diffusion pathways relative to the dopants are indicated on Fig. 3a and b, and the energy barriers in Fig. 3c and d.
For the Al doped phase, formation of a Al×VO defect removes one O1 from the interlayer space, below Al (Fig. 3b). Pathway 1 indicates Li+/Mg2+ migration through the O-vacancy, whilst pathway 2 relates to migration through the layer above Al, where the O1 ion is more tightly bound to the two adjacent layers. In undoped V2O, the barrier for Li+ diffusion (0.23 eV) is significantly lower than for Mg2+ (1.51 eV), consistent with first-principles calculations.3,32 For Li+ diffusion, all the selected dopants cause an increase in energy barrier, indicating that any distortion along the diffusion pathway induced by a dopant can hinder ion mobility. Electrostatic interactions between the dopants and diffusing ions also contribute to the increased energy barriers. For Mg2+ diffusion, the Al3+ substituted system displays an increased energy barrier for path 2 (2.23 eV), but a reduced barrier for path 1 (1.4 eV). Despite the barrier reduction, an energy of 1.4 eV effectively renders diffusion unachievable at room temperature. The interstitially doped structures have energy barriers of 1.02 eV (Naint+) and 1.20 eV (Baint2+), a substantial reduction from 1.61 eV for the undoped system. The lower energy barriers can be explained by an expansion of the interlayer space upon introduction of the dopant, which shifts the relative energy of the 8-coordinated stable insertion site and 3-coordinated barrier site closer together.33 Ba2+ is larger than Na+ and causes a greater interlayer expansion, yet Ba2+ doping results in a higher energy barrier than Na+ doping for Mg2+ diffusion, suggesting that there is an optimal expansion to the interlayer space that will minimize the diffusion energy barrier, and that this may be achieved by tailoring the dopant concentration and size. The results of these diffusion barrier calculations can be used as a guide for future, more detailed investigation of dopant effects on ion diffusion, using quantum-mechanical techniques.
The authors acknowledge funding from the EPSRC through grant EP/R023662/1 and the use of the UCL Grace and Legion High Performance Computing Facilities (Grace@UCL, Legion@UCL), and associated support services. Via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by the EPSRC (EP/L000202), this work used the ARCHER UK National Supercomputing Service (http://www.archer.ac.uk).
Conflicts of interest
There are no conflicts to declare.References
- P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341 CrossRef PubMed.
- W. Xu, J. Wang, F. Ding, X. Chen, E. Nasybulin, Y. Zhang and J.-G. Zhang, Energy Environ. Sci., 2014, 7, 513–537 Search PubMed.
- G. S. Gautam, P. Canepa, R. Malik, M. Liu, K. Persson and G. Ceder, Chem. Commun., 2015, 51, 13619–13622 RSC.
- H. D. Yoo, I. Shterenberg, Y. Gofer, G. Gershinsky, N. Pour and D. Aurbach, Energy Environ. Sci., 2013, 6, 2265–2279 Search PubMed.
- M. S. Whittingham, Chem. Rev., 2004, 104, 4271–4301 CrossRef PubMed.
- G. G. Amatucci, F. Badway, A. Singhal, B. Beaudoin, G. Skandan, T. Bowmer, I. Plitz, N. Pereira, T. Chapman and R. Jaworski, J. Electrochem. Soc., 2001, 148, A940–A950 CrossRef.
- D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727 CrossRef PubMed.
- Y.-Z. Zheng, H. Ding, E. Uchaker, X. Tao, J.-F. Chen, Q. Zhang and G. Cao, J. Mater. Chem. A, 2015, 3, 1979–1985 Search PubMed.
- F. Coustier, J. Hill, B. B. Owens, S. Passerini and W. H. Smyrl, J. Electrochem. Soc., 1999, 146, 1355–1360 CrossRef.
- H. Zeng, D. Liu, Y. Zhang, K. A. See, Y. S. Jun, G. Wu, J. A. Gerbec, X. Ji and G. D. Stucky, Chem. Mater., 2015, 27, 7331–7336 CrossRef.
- X. Li, C. Liu, C. Zhang, H. Fu, X. Nan, W. Ma, Z. Li, K. Wang, H. Wu and G. Cao, ACS Appl. Mater. Interfaces, 2016, 8, 24629–24637 Search PubMed.
- Y. Wei, C. W. Ryu and K. B. Kim, J. Alloys Compd., 2008, 459, 13–17 CrossRef.
- Z. Li, C. Zhang, C. Liu, H. Fu, X. Nan, K. Wang, X. Li, W. Ma, X. Lu and G. Cao, Electrochim. Acta, 2016, 222, 1831–1838 CrossRef.
- Y. Li, J. Yao, E. Uchaker, M. Zhang, J. Tian, X. Liu and G. Cao, J. Phys. Chem. C, 2013, 117, 23507–23514 Search PubMed.
- X. Liu, J. Zeng, H. Yang, K. Zhou and D. Pan, RSC Adv., 2018, 8, 4014–4031 RSC.
- M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204 RSC.
- R. Enjalbert and J. Galy, Acta Crystallogr., 1986, C42, 1467–1469 Search PubMed.
- D. O. Scanlon, A. Walsh, B. J. Morgan and G. W. Watson, J. Phys. Chem. C, 2008, 112, 9903–9911 Search PubMed.
- V. Riffet, J. Contreras-Garclá, J. Carrasco and M. Calatayud, J. Phys. Chem. C, 2016, 120, 4259–4265 Search PubMed.
- M. Giorgetti, M. Berrettoni and W. H. Smyrl, Chem. Mater., 2007, 19, 5991–6000 CrossRef.
- M. S. Islam, J. Mater. Chem., 2000, 10, 1027–1038 RSC.
- J. S. Braithwaite, C. R. A. Catlow, J. D. Gale and J. H. Harding, Chem. Mater., 1999, 11, 1990–1998 CrossRef.
- Y. L. Cheah, V. Aravindan and S. Madhavi, ACS Appl. Mater. Interfaces, 2012, 4, 3270–3277 Search PubMed.
- X. Liang, G. Gao, Y. Liu, T. Zhang and G. Wu, J. Alloys Compd., 2017, 715, 374–383 CrossRef.
- T. Allersma, R. Hakim, T. N. Kennedy and J. D. Mackenzie, J. Chem. Phys., 1967, 46, 154–160 CrossRef.
- I. B. Ioffe and V. A. Patrina, Phys. Status Solidi, 1970, 389, 389–395 CrossRef.
- M. B. Sahana, C. Sudakar, C. Thapa, V. M. Naik, G. W. Auner, R. Naik and K. R. Padmanabhan, Thin Solid Films, 2009, 517, 6642–6651 CrossRef.
- C. F. Armer, M. Lübke, M. V. Reddy, J. A. Darr, X. Li and A. Lowe, J. Power Sources, 2017, 353, 40–50 CrossRef.
- M. Panagopoulou, D. Vernardou, E. Koudoumas, N. Katsarakis, D. Tsoukalas and Y. S. Raptis, J. Phys. Chem. C, 2017, 121, 70–79 Search PubMed.
- D. M. Yu, S. T. Zhang, D. W. Liu, X. Y. Zhou, S. H. Xie, Q. F. Zhang, Y. Y. Liu and G. Z. Cao, J. Mater. Chem., 2010, 20, 10841–10846 RSC.
- L. R. De Jesus, G. A. Horrocks, Y. Liang, A. Parija, C. Jaye, L. Wangoh, J. Wang, D. A. Fischer, L. F. J. Piper, D. Prendergast and S. Banerjee, Nat. Commun., 2016, 7, 12022 CrossRef PubMed.
- A. Parija, Y. Liang, J. L. Andrews, L. R. De Jesus, D. Prendergast and S. Banerjee, Chem. Mater., 2016, 28, 5611–5620 CrossRef.
- Z. Rong, R. Malik, P. Canepa, G. Sai Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Chem. Mater., 2015, 27, 6016–6021 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp02187b |
| This journal is © the Owner Societies 2018 |


