Open Access Article
Open Access ArticleShifted equilibria of organic acids and bases in the aqueous surface region†
Josephina
Werner
 *ab,
Ingmar
Persson
*ab,
Ingmar
Persson
 b,
Olle
Björneholm
a,
Delphine
Kawecki‡
a,
Clara-Magdalena
Saak
b,
Olle
Björneholm
a,
Delphine
Kawecki‡
a,
Clara-Magdalena
Saak
 a,
Marie-Madeleine
Walz§
a,
Marie-Madeleine
Walz§
 a,
Victor
Ekholm
a,
Victor
Ekholm
 a,
Isaak
Unger
a,
Corina
Valtl
a,
Carl
Caleman
a,
Isaak
Unger
a,
Corina
Valtl
a,
Carl
Caleman
 ac,
Gunnar
Öhrwall
ac,
Gunnar
Öhrwall
 d and
Nønne L.
Prisle
d and
Nønne L.
Prisle
 ef
ef
aDepartment of Physics and Astronomy, Uppsala University, Box 516, SE-751 20 Uppsala, Sweden. E-mail: josephina.werner@gmail.com
bDepartment of Molecular Sciences, Swedish University of Agricultural Sciences, Box 7015, SE-750 07 Uppsala, Sweden
cCenter for Free-Electron Laser Science, Deutsches Elektronen-Synchrotron, Notkestraße 85, DE-22607 Hamburg, Germany
dMAX IV Laboratory, Lund University, Box 118, SE-22100 Lund, Sweden
eFaculty of Science, Nano and Molecular Systems Research Unit, University of Oulu, Box 3000, FI-90014, Finland
fDepartment of Physics, Division of Atmospheric Science, University of Helsinki, Box 64, FI-00014, Finland
First published on 31st August 2018
Abstract
Acid–base equilibria of carboxylic acids and alkyl amines in the aqueous surface region were studied using surface-sensitive X-ray photoelectron spectroscopy and molecular dynamics simulations. Solutions of these organic compounds were examined as a function of pH, concentration and chain length to investigate the distribution of acid and base form in the surface region as compared to the aqueous bulk. Results from these experiments show that the neutral forms of the studied acid–base pairs are strongly enriched in the aqueous surface region. Moreover, we show that for species with at least four carbon atoms in their alkyl-chain, their charged forms are also found to be abundant in the surface region. Using a combination of XPS and MD results, a model is proposed that effectively describes the surface composition. Resulting absolute surface concentration estimations show clearly that the total organic mole fractions in the surface region change drastically as a function of solution pH. The origin of the observed surface phenomena, hydronium/hydroxide concentrations in the aqueous surface region and why standard chemical equations, used to describe equilibria in dilute bulk solution are not valid in the aqueous surface region, are discussed in detail. The reported results are of considerable importance especially for the detailed understanding of properties of small aqueous droplets that can be found in the atmosphere.
Introduction
Acid–base chemistry at the aqueous interface is of great importance for many processes e.g. in atmospheric chemistry and biochemistry. The different physico-chemical properties of the aqueous surface region in comparison to the bulk have been investigated throughout the last decades. For inorganic salts, the classic electrostatic model with an ion-free surface region,1 has been replaced by a model in which ions may be present, and even enriched, at the surface.2,3 Also the possibly changed protolytic properties of the aqueous surface region and its underlying mechanisms have been subject to intensive discussions. These protolytic surface properties have been investigated using different experimental and theoretical approaches, with rather contradictory outcomes.4–14Discrepancies among experimental results and modeled systems regarding the spatial distribution of hydronium and hydroxide ions at the air–water interface have been debated intensively.4,6–8,10,15 These ions are rather small species with relatively high charge densities. They are strongly hydrated as can be seen from their large hydration enthalpies, 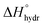 , of −1091 (H+) and −460 (OH−) kJ mol−1, respectively.16 The effect of the hydration behavior of these chemical species on their residence in the aqueous surface region, their general role in surface chemistry and the influence of the bulk equilibria on the chemical speciation in the surface region are often discussed aspects in this context.
, of −1091 (H+) and −460 (OH−) kJ mol−1, respectively.16 The effect of the hydration behavior of these chemical species on their residence in the aqueous surface region, their general role in surface chemistry and the influence of the bulk equilibria on the chemical speciation in the surface region are often discussed aspects in this context.
Numerous studies draw conclusions about the pH, i.e. the local hydronium and hydroxide concentrations, in the aqueous surface region upon investigation of indicator species and their ability for protonation/deprotonation at the aqueous surface region.6,8,10,11,13,17 Although acid–base equilibria in the aqueous surface region have been investigated for several chemical compounds by various experimental and theoretical techniques, no study has been conducted investigating proton acceptors and donors using the same approach. Results of separate studies on individual compounds show that neutral forms of carboxylic acids7 and amines10 are more abundant at the surface region in comparison to their respective charged forms, i.e. carboxylate and ammonium ions. It was found that some ionic species are depleted from the interfacial region, due to the reduced possibility to be fully hydrated.10,17 In another study, a thermodynamic approach was used to explain the different degree of protonation in the aqueous surface region to be caused by the different hydration enthalpies of protonated and deprotonated species.12 Whether these studies allow general conclusions on changed abundances of hydronium/hydroxide ions in the interfacial region as compared with the bulk water is a major concern and should be carefully validated.
In this paper we show that the pH-dependent speciation and distribution of the acid and base forms are quite different in the surface region as compared to the bulk and that it is not possible to draw conclusions on the interfacial hydronium or hydroxide concentration by only examining a neutral species and its respective conjugated charged form. We refer to the surface region as the air–water interface and the number of water molecule layers below (surface-near-bulk region), required to reach bulk solution properties, throughout this work. The depth of this region is difficult to specify, and it is likely dependent on temperature, ionic strength of the aqueous bulk and the specific dissolved solutes. The surface region is thus characterized by distinctly different physico-chemical properties, i.e. solute concentrations, structure, dynamics etc., in comparison with the bulk solution.
Previous XPS studies have shown that the concentration of neutral compounds is significantly higher in the aqueous surface region as compared to the bulk, also in cases where the compound is miscible with water.7,18,19 It can be assumed that the physico-chemical properties of water at the air–water interface and some water molecule layers below the interface are significantly different from bulk water. One example for the deviating properties of water in the bulk and in the surface region is its relative permittivity. In bulk water it amounts to εr = 78.520 and promotes dissociation of salts and hydration of inorganic ions, and polar or charged functional groups. As discussed above, neutral molecules are more abundant in the surface region than their charged conjugates. This suggests that the relative permittivity of water in the surface region is significantly lower than in aqueous bulk. An equilibrium between species X in the aqueous bulk and the surface region is established, Xbulk ⇌ Xsurface. For neutral chemical species, especially those with a hydrophobic group, this equilibrium is strongly shifted to the right. On the other hand, this equilibrium is most likely shifted to the left for charged species and even more so with increasing charge density and need for hydration. Furthermore, a minimum relative permittivity is required for salts to dissociate, which is increasing with the charge density of the ions. It has not been possible to experimentally determine the relative permittivity of water in the surface region, but the observed distribution between neutral and charged species strongly indicates that it is lower in this region than in the bulk, possibly sufficiently low to hinder dissociation of salts. A consequence of this is that it is difficult for single ions, which are dissolved in the aqueous bulk solution, to reach the surface region and even more so with increasing charge density of the ion. However, ion-pair formation offers one possibility for charged species to reach to the surface region, or at least to be close to it. One such documented example is the two-dimensional guanidinium ion, (C(NH2)3)+, which can reside very close to the air–water interface, when it is accompanied by chloride ions.21 Guanidinium ions were shown to reach significantly closer to the water surface than in systems without a counter-ion that is able to reside in the surface region.22 In another study it was shown that ammonium ions, which are usually depleted from the surface region, are strongly attracted to the aqueous surface region by co-dissolved carboxylate ions.23
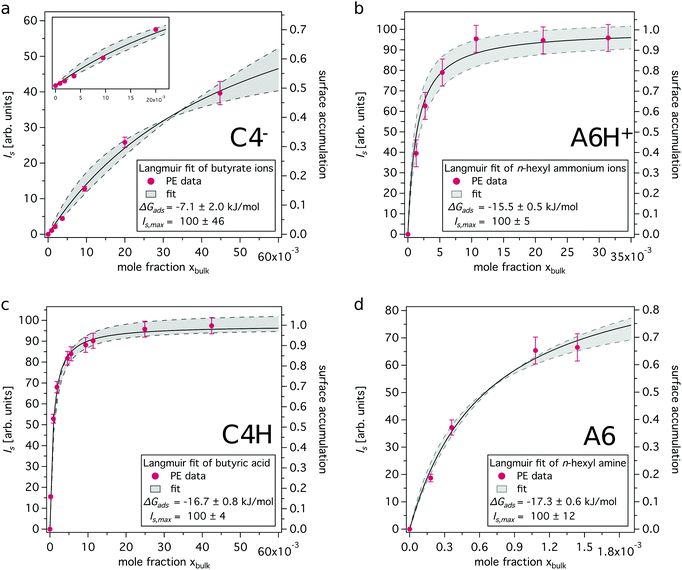
The dissociation of an acid (HA) in aqueous solution is quantified by a dissociation constant Ka (or its negative logarithm: pKa), defined as the ratio of the activities of the reaction's products (H+ and A−) and the reactant (HA). For weak acids and their conjugated bases and for dilute solutions, concentrations (denoted as [species]) can be used instead of activities (a) by assuming the activity coefficients to be unity.
| HA + H2O ⇆ H3O+ + A− | (1) |
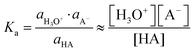 | (2) |
The effect of the pH on the actual concentrations of acid and base form of a conjugated acid–base pair in the bulk is given by the so-called Henderson–Hasselbalch equation:24
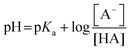 | (3) |
Rearranging eqn (3), we find that the ratio R of the acid and base concentration in the bulk of the solution can be expressed as
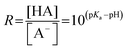 | (4) |
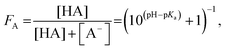 | (5) |
Eqn (1)–(5) can be written in a similar way for the protonation of an organic base B using the dissociation constant Kb (and its negative logarithm: pKb).
| B + H2O ⇄ BH+ + OH− | (6) |
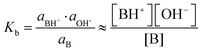 | (7) |
| Kw = [H3O+][OH−] = Ka·Kb | (8) |
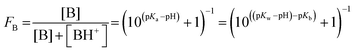 | (9) |
Experimental
XPS experiments
XPS experiments were performed at the synchrotron facility MAX-lab, Lund University, using beamline I411, where X-ray radiation was intersected with a liquid micro-jet containing sample solutions of different organic solutes, pH and concentrations. Our experimental setup is operated in the present study in the same way as described elsewhere.19,25 Photon energies were chosen to create C 1s or N 1s photoelectrons with roughly 70 eV kinetic energy, making the experiments surface sensitive with an electron attenuation length in the order of 10 Å.26–28 This means that species residing close to the air–water interface contribute strongly to the overall recorded photoemission (PE) intensities. Using a simple two-layer model,19 the solution is divided into a bulk and surface region (see definition in the Introduction). This yields a contribution of the surface region to the recorded PE signal of about 33–50%, see ESI† for details, which is in accordance with previously reported values.29 Hence, the recorded PE intensities yield information of both, the bulk and the surface region. During the analysis, relative PE intensities are used to identify qualitative differences between the surface region and the aqueous bulk region. Furthermore, we consider different approximations to determine actual surface concentrations from recorded PE signals. Total PE intensities of surface enriched species are compared with intensities recorded from surface depleted species, which are used to model bulk contributions to the recorded PE intensities. For the use of these bulk reference intensities, a set of assumptions need to be accepted.19,25,30Sample solutions with concentrations given in mol dm−3 (M) were prepared freshly with deionized water (Millipore Direct-Q, resistivity >18.2 MΩ cm) and commercially available chemicals from Sigma Aldrich: butyric acid, pentanoic acid, sodium hydroxide, hydrochloric acid, n-butyl amine, n-hexyl amine. The purities were >99%. All sample solutions were made from dilution of stock solutions and the solution pH was adjusted using sodium hydroxide or hydrochloric acid. Series of pH-dependent XPS experiments were conducted of all named organic compounds in dilute solutions (at less than half the solubility limit in water). Series of concentration-dependent XPS experiments were conducted for butyric acid, sodium butyrate, n-hexyl amine and n-hexyl ammonium chloride. To gain more insight in the acid–base behavior of the studied systems at the actual ionic strength in bulk solutions, additional acid–base titrations were conducted for each compound (except for C5H which is taken from ref. 31) at both 25 °C and 10 °C, as the latter is close to the expected temperature of the XPS experiment. The obtained pKa values are used in the analysis of the XPS results.
Evaluation of PE spectra
Carboxylic acids and their respective conjugated bases (C4H/C4−, C5H/C5−) were monitored via their C 1s PE intensities, i.e. the intensity of the alkyl chain (C 1s(CH2)), the carboxylic acid group (C 1s(COOH)) and its deprotonated form (C 1s(COO−)) (see Fig. 1). Alkyl amines and their respective conjugated acids (A4/A4H+, A6/A6H+) were observed via both N 1s and C 1s intensities, i.e. the intensity of the alkyl chain (C 1s(CH2)), the ammonium group (N 1s(NH2)) and its protonated form (N 1s(NH3+)). Recorded intensities can be compared between different samples when measured during unchanged conditions, i.e. if sample injection and synchrotron radiation operated stably throughout the acquisition time. To monitor the stability of the measurements, the intensity of the water 1b1 level of a 50 mM NaCl aqueous solution was monitored between all sample solutions and intensity variations were ≤5%. Details on the fitting procedure are described in the ESI.†To study differences in the degree of protonation of the investigated compounds in the probed part of the aqueous solution, acid fractions FA = C 1s(COOH)/(C 1s(COOH) + C 1s(COO−)) (eqn (5)) and base fractions FB = N 1s(NH2)/(N 1s(NH2) + N 1s(NH3+)) (eqn (9)) were calculated from the PE intensities, respectively, and plotted as a function of solution pH. The same results were used to estimate surface concentrations of the studied solutions as a function of pH with aid of the simple two-layer model (see ESI†). Furthermore, concentration dependent studies were analyzed by means of the Langmuir adsorption model. Results are discussed in detail taking into account molecular-scale driving forces and chemical equilibria.
Results & discussion
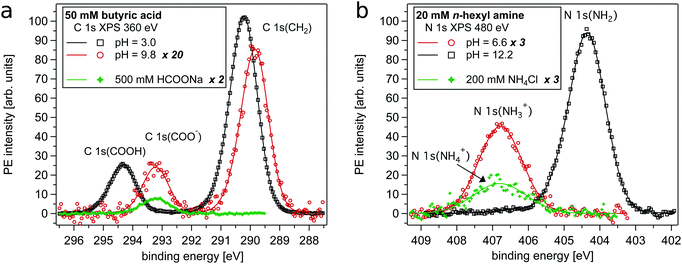
In Fig. 1a example spectra of a carboxylic acid, here C 1s spectra of butyric acid, in different protonation states are shown together with a spectrum of formate ions (HCOO−). The latter is used as bulk reference signal as formate ions can be assumed to be depleted from the aqueous surface region due to their strong hydration and lack of a hydrophobic group.30,32 Please note, as annotated in the figures' legends, the intensities of the distinct spectra are scaled differently. Two PE lines characterize the C 1s spectra, where the peak at lower binding energy (<291 eV) is assigned to the carbon atoms of the alkyl chain (C 1s(CH2)). The peaks at higher binding energies originate from the carbon atom in the carboxylic acid group, where the neutral form is found at 294.3 eV (C 1s(COOH)) and the deprotonated form at 293.2 eV (C 1s(COO−)). Fig. 1b shows example spectra of an amine, here N 1s of n-hexyl amine, in different protonation states together with a spectrum of ammonium ions (NH4+), which is used as bulk reference signal for the N 1s region for the same reason as mentioned above for formate for the C 1s region. The N 1s PE line of the neutral form can be found at 404.4 eV (N 1s(NH2)), while the protonated (charged) form is found at 406.7 eV (N 1s(NH3+)). The neutral forms of the studied compounds are slightly volatile leading to weak gas phase contributions in the recorded spectra, which can be observed as a small shoulder towards higher binding energy. It can be seen that the sensitivity of XPS to the local binding environments enables the spectroscopic distinction of the protonation states of alkyl-amines and carboxylic acids.The XPS spectra show that the overall C 1s PE intensity of butyric acid (pH = 3.0) is much larger than the recorded intensity of butyrate (pH = 9.8) and formate ions. We observe that the PE intensity of alkyl carbons as compared to carboxylic carbons of butyric acid is larger than the corresponding relative intensities of butyrate ions. This shows that butyric acid is significantly enriched in the surface region, probably with its alkyl chain on average oriented perpendicular to the air–water interface. As seen from the relative N 1s PE intensity displayed in Fig. 1b, the n-hexyl amine/n-hexyl ammonium ion system displays a somewhat different behavior with both the neutral and the charged form being strongly enriched in the surface region. PE intensity ratios of the organic solutes with formate or ammonium ions enable a more quantitative analysis of their surface behavior. This will be presented and discussed after discussing the pH dependent measurement series.
Acid and base fractions as a function of solution pH
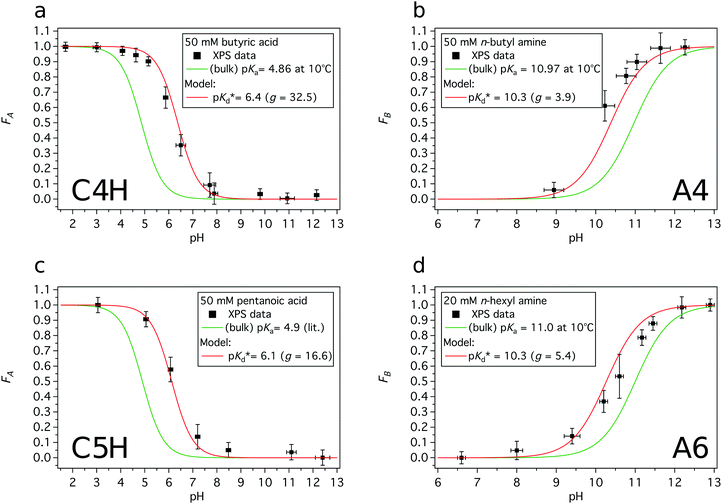
Acid or base fractions, resulting from pH-dependent XPS studies of C4H, C5H, A4 and A6 solutions were computed and are plotted as a function of solution pH, see Fig. 2. These fractions were fitted using versions of eqn (5) for an acid and eqn (9) for a base, where the maximum fraction (additional factor) and the apparent pKd* value (instead of pKa) were introduced as free fit parameters. The abundances of acid and base in the bulk of the solutions, given via the dissociation constant of the acid (pKa), are added to each plot.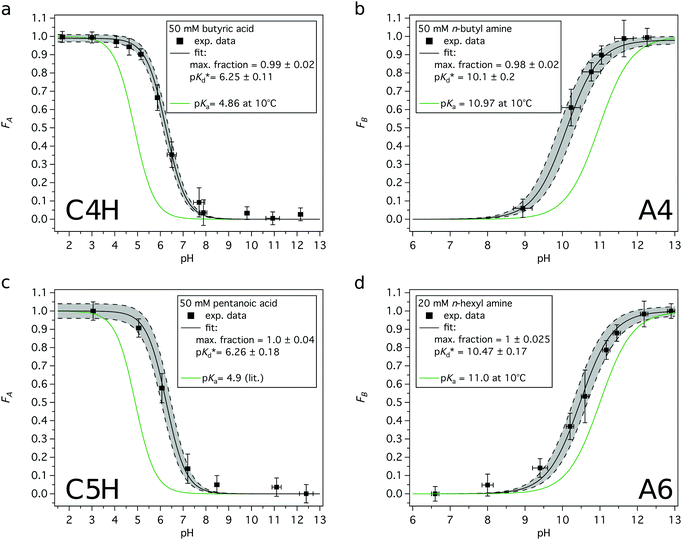 | ||
| Fig. 2 Experimentally obtained acid or base fractions of organic compounds in the aqueous surface region as a function of the solution pH. The bulk acid/base fractions given by the bulk dissociation constants pKa and the fit parameters (max. fraction and pKd*) were added to each plot. The pKa values were experimentally determined except for C5H, which was from literature.31 (a) Acid fraction of a 50 mM butyric acid solution, (b) base fraction of a 50 mM n-butyl amine solution, (c) acid fraction of a 50 mM pentanoic acid solution, and (d) base fraction of a 20 mM n-hexyl amine solution. | ||
In general, the pH corresponding to the midpoint of a weak acid or base fraction curve (FA = 0.5; FB = 0.5) is defined to be numerically equal to the pKa value of the acid form. At that point the concentration of the protonated and deprotonated forms of the species in the probed volume is equal. The fractions obtained from XPS experiments, however, reveal to a large extent the composition of the solution's surface region, while the pH-axis gives a bulk-related property. Hence, the pH corresponding to the midpoint of these XPS-derived fraction curves is referred to as apparent pKd*, which is introduced here to effectively describe the acid/base fraction curves obtained from XPS results.
It can be clearly seen that the acid and base fraction curves for the region probed with XPS and the aqueous bulk solution have similar shapes but are shifted with respect to each other along the solution pH axis. The curves are shifted towards higher pH values for carboxylic acids and towards lower pH values for n-alkyl amines. Hence, for a given solution pH, the region probed by XPS contains more neutral carboxylic acid or alkyl amine molecules than their corresponding charged forms. As this region yields information of both the surface and the bulk region, it can be inferred also from these data sets that the neutral forms are enriched in the surface region as compared to the aqueous bulk. The observed shifts of the fraction curves were interpreted as a different pH4–6,9 or pKa10–12 in the surface region by others, but we will show here that other effects are more important.
To understand the origin of the observed relative abundances and the role of the pH variation in the bulk of the solution, surface propensities and abundances of the studied organic compounds were investigated in separate experiments. Results are presented and discussed in the following paragraphs, where, with the aid of different model approaches, also absolute surface concentrations are estimated.
Compound specific surface enrichment
The neutral forms of the studied compounds yield much stronger PE intensities, see Fig. 1. Hence, we can infer that their effective density is higher closer to the air–water interface as compared to their corresponding charged forms. Applying the simple two-layer model (see ESI† for details), enables the estimation of enrichment factors (g) for a certain compound at a specific concentration.19,30 These enrichment factors are defined as the ratio of the surface and bulk concentration of a compound. A so-called sensitivity factor (nb/ns) is introduced that quantifies the sensitivity of XPS to the aqueous surface region. Assuming the surface region contributes with 33–49% to the recorded PE signal, a range of possible enrichment factors are derived and presented in Table 1 (second column). It can be seen that the neutral forms have higher enrichment factors, while the ones for the charged conjugates are lower. The derived values for alkyl amines are overall higher than the ones derived for carboxylic acids. Furthermore, another trend is visible for the studied amines and the carboxylic acids: the longer the alkyl-chain is, the higher the enrichment factors are. Details on Table 1, column 3 and 4 follow later in the text.| Aq. solution | Enrichment based on the simple two-layer model nb/ns = 1 to 1.5 | Enrichment based on Fig. 3 Langmuir model | Relative enrichment grelative = gneutral/gcharged; nb/ns =1 |
|---|---|---|---|
| 50 mM A4H+ | 7–11 | — | 3.9 |
| 50 mM A4 | 27–40 | — | |
| 20 mM A6H+ | 23–35 | 71 | 5.4 |
| 20 mM A6 | 124–186 | 133 | |
| 50 mM C4− | 2–3 | 4 | 32.5 |
| 50 mM C4H | 65–98 | 113 | |
| 50 mM C5− | 5–7 | — | 16.6 |
| 50 mM C5H | 83–125 | — | |
Results of concentration-dependent XPS studies enable a more detailed quantification of the surface propensity and accumulation capability as well as enrichment factors for different bulk concentrations of a given compound, employing Langmuir's adsorption theory. It was shown before, that, despite all simplifications this theory is based on, the obtained results offer new insights and an intuitive way to advance the analysis.33–35
The surface contributions of the recorded XPS data (Is, referred to as ‘surface signal’) are plotted as a function of bulk mole fraction xbulk (see ESI† for details) and fitted to the standard Langmuir equation. This yields compound specific adsorption free energies (ΔGads), which are a measure of the accumulation capability of a compound in the surface region, and surface coverage p = Is/Is,max. Is,max corresponds to the maximum surface signal recorded from a pure compound (xbulk = 1). The surface coverage is a term, which is historically connected to Langmuir analysis of monolayers. We use it here to describe and quantify the accumulation capability of solutes in the surface region and thus refer to it as surface accumulation in the followings.
In Fig. 3 experimentally obtained XPS intensities are shown together with the resulting Langmuir fits. The model matches the data well, especially for the neutral species, i.e. butyric acid and n-hexyl amine. ΔGads was found to be roughly −7 kJ mol−1 for butyrate ions, −15.5 kJ mol−1 for n-hexyl ammonium ions and approximately −17 kJ mol−1 for both butyric acid and n-hexyl amine molecules. The Langmuir fits of the neutral species yield more negative ΔGads values, indicating a stronger propensity to reside in the surface region than their charged conjugates. The difference between the charged and the neutral form is more pronounced for the studied carboxylic acids as compared to the studied amine systems.
 | ||
| Fig. 3 Surface C 1s PE signal versus bulk mole fraction together with Langmuir adsorption fits. Details on the Langmuir fitting procedure can be found in the ESI.† (a) Butyrate ions, (b) n-hexyl ammonium ions, (c) butyric acid and (d) n-hexyl amine. Note the difference in x-axis for amine/ammonium pair. | ||
The absolute values given for the maximum surface PE signal Is,max cannot be compared between the different data sets shown in Fig. 3. However, surface accumulation values can be compared, see Fig. 3, right axis. For the concentrations discussed above, i.e. 50 mM and 20 mM for C4H and A6, respectively, the surface accumulation is determined to be 0.52 and 0.35, respectively. For their respective charged forms the surface accumulation is found to be 0.02 and 0.19, respectively, which is considerably lower as compared to the neutral forms. These values enable the estimation of surface concentrations cs, assuming that the maximum surface concentration cs,max is equal to the concentration that corresponds to the pure compounds35 (C4−, C4H ≈ 10.9 M; A6H+, A6 ≈ 7.6 M), see ESI† for details.
Surface enrichment factors derived from the concentration-dependent studies are listed in Table 1 (column 3). They are overall similar to the ones derived using the simple two-layer model (column 2), showing a stronger enrichment of the neutral species as compared to the charged forms. Values derived from Langmuir fits for C4−, C4H and A6H+ are found on the upper limit of the range estimated using the simple two-layer model approach or higher, while the value for A6 is found closer to the lower limit.
Hydration motifs and driving forces
To discuss the origin of the observed different surface enrichments, which are strongly connected to a species' solubility in the surface and bulk region, molecular-scale water–solute interactions are considered.12,36 There are energetically more or less favorable interactions between the constituents of a solution that compete with one another. Hydrophilic groups, such as charged functional or polar groups, interact strongly with water, followed by water–water interactions and the weakest, hydrophobic–water interactions. The solution as a system seeks to minimize its energy, and to do so, strong interactions are favored while weak ones are reduced. Due to the presence of hydrophobic alkyl chains the hydrogen bonding of bulk water is considerably rearranged, as water molecules are forced to form voids around them.37 Unbranched alkyl-chains situated at the air–water interface, may point towards the aerial side. Thereby the weak interactions between hydrophobic groups and water are significantly reduced.18,35 With an increasing number of organic molecules residing in the surface region fewer water molecules are required to occupy the energetically less favorable surface sites directly. The water molecules close to the solutions' surface can form hydrogen bonds (H-bonds) with the polar head groups or other water molecules close by, which is energetically more favorable for the system. Species that require a high number of H-bonds in three dimensions for hydration, e.g. charged or highly polar groups, are either favored in the surface-near-bulk region or avoid the surface region completely, to have sufficient hydrating water molecules around them. In this way, the energetically favorable hydrophilic–water interactions are maximized, whereas the energetically unfavorable hydrophobic–water interactions are minimized.To obtain a deeper understanding of the underlying processes, we complement our experimental results with MD simulations. Computational details can be found in the ESI,† where also snapshots of the simulated species in the aqueous surface region are presented. The modeled results show that the carboxylic acid group of butyric acid forms on average 3.1 ± 0.9 H-bonds with the surrounding water, while its deprotonated conjugate (for the case of butyrate ions) forms 6.7 ± 0.9. Similar values have been reported by ref. 38 using a related computational technique. The number of H-bonds formed by water and an amine/ammonium group (here for the case of n-hexyl amine/ammonium) are more similar to one another with 2.4 ± 0.9 or 2.8 ± 0.5, respectively (see ESI†). Hence, the number of H-bonds is more than doubled when a carboxylic acid group is deprotonated, while the number of H-bonds only increases slightly when the amine group is protonated. This explains the smaller relative enrichments of the neutral and the charged form of the studied amines in comparison with the carboxylic acids (see Table 1, column 4) and also reflects their relative ability to accumulate in the surface region (see Fig. 3).
Furthermore, the lengths of the hydrophobic alkyl chains are decisive for the hydration behavior and surface propensity of the studied species. Organic molecules with long alkyl chains will reside more readily in the surface region, despite attached ionic functional groups.7,39 The longer the alkyl chain, the more important hydrophobic interactions become that outweigh the hydrophilic–water interactions, resulting in a more similar surface enrichment of the charged and non-charged species, as seen for A6/A6H+, A4/A4H+ and C5−/C5H in Table 1. For up to three carbon atoms in an alkyl chain, the hydrophilic interactions dominate the overall hydration behavior, yielding relatively large differences in the surface enrichment factors of a carboxylic acid and its conjugated carboxylate ion, see results on C4−/C4H in Table 1.
In the classic electrostatic model of ions close to the aqueous surface,1 ions are repelled from the surface by image charge repulsion, leading to a depletion of ions in the surface region. By describing the solution as a classic continuum, our findings can also be qualitatively described by means of a declining relative permittivity in the surface region of an aqueous solution. A low dielectric constant in the aqueous surface region may explain the observed strong surface propensity of neutral molecules. Highly polar or charged species instead require a higher relative permittivity to remain dissociated, which explains their depletion from the air–water interface (as well as in vacuum). If the relative permittivity of the surface region is sufficiently low, the dissociation of salts of monovalent ions is hindered. Nevertheless, through the formation of ion-pairs21,23,40 charged species can reduce their local charge and thereby get closer to the air–water interface.41 Their effective surface propensity is a result of the sensitive balance between the hydrophobicity of the alkyl chain(s), the hydration of the charged groups and the co-dissolved counter-ions in solution. The latter two points are crucial for the ionic species' ability to form ion-pairs. The closer two ions can come towards each other, the stronger the complex and the larger the effective local charge-screening is. It is therefore reasonable to assume that strong hydration hampers the possibility of ion-pair formation. Hence, a strongly hydrated carboxylate group cannot come as close to its counter-ion as the more weakly hydrated ammonium group. This affects in turn how close these species can reside with respect to the air–water interface. This interpretation also explains why the difference in PE signal intensity between neutral and charged species is much larger for the carboxylic acid–carboxylate systems than the ammonium–amine systems, see Table 1, column 4.
From this analysis and discussion it is clear that for the studied acid–base pairs the surface region stabilizes the neutral forms particularly well, while the charged conjugates are less abundant in the aqueous surface region. Furthermore, the surface orientation and structure is a direct result of the relative solubility in the bulk and the surface region, respectively. With the determined enrichment factors from the previous paragraph, the discussion of the pH-dependent measurement series is resumed and extended in the following.
Composition of the surface region as a function of solution pH
By changing the solution pH, the distribution of the neutral and charged form of the investigated organic species is regulated in the bulk of the solution. Their relative surface abundances are different, as shown in Fig. 2. Using the resulting enrichment factors from the simple two-layer model (Table 1) the absolute amounts of each species in the surface region as a function of solution pH can now be estimated. For further analysis, a sensitivity factor of nb/ns = 1 is chosen, yielding the lower surface enrichment factors (see ESI† for details). In Fig. 4, the surface concentrations of each organic compound is plotted as a function of solution pH.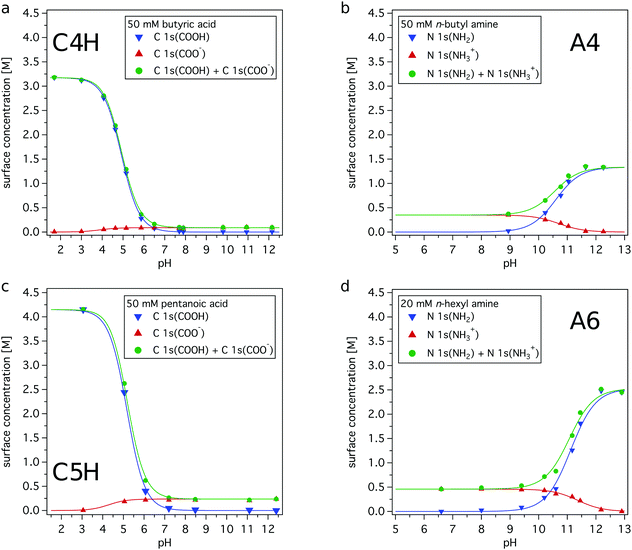 | ||
| Fig. 4 Concentration of organic compounds in the surface region as a function of pH. The surface concentrations are estimated using the simple two-layer model with a sensitivity factor nb/ns = 1, see Table 1. (a) 50 mM butyric acid; (b) 50 mM n-butyl amine; (c) 50 mM pentanoic acid; (d) 20 mM n-hexyl amine. | ||
It is clearly seen that the total amount of organic species in the surface region changes dramatically as a function of pH. The charged carboxylates yield rather low surface concentrations, while the carboxylic acid molecules are strongly surface enriched. In comparison to the carboxylates, the studied alkyl ammonium ions have a higher concentration in the surface region. The alkyl amines yield a higher surface concentration than their charged conjugates, but overall lower than the maximum surface concentrations estimated for the studied carboxylic acids. Thus, the relative enrichments of the amines, i.e. the A4/A4H+ and A6/A6H+ pairs, are smaller than the ones of carboxylic acids, i.e. the C4H/C4− and C5H/C5− pairs.
Considering these results, it becomes clear that eqn (1)–(9) cannot be used to derive a pH value or other properties for the surface region. The reason is that the large amount of organic solutes and the mismatch between organic molecule and charged conjugate in the surface region, leads to properties very different from an ideal, dilute solution for the discussed organic species.
Chemical equilibria
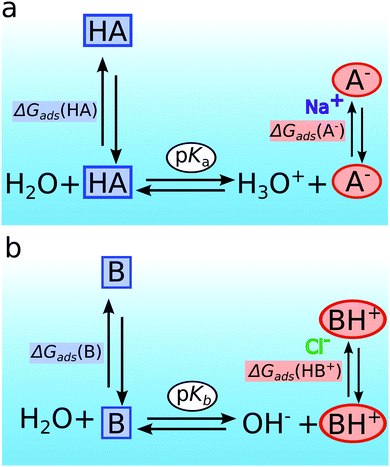
Let us consider an organic acid or base in a solution that consists of two idealized regions, a surface and a bulk region. The prevailing equilibria, i.e. bulk speciation and surface enrichment, for an organic acid (HA) and its ionic form (A−) are sketched in Fig. 5a. The corresponding ones for an organic base (B) and its ionic form (BH+) are shown in Fig. 5b. The introduced apparent pKd* value, which was introduced to effectively describe the relative acid/base abundances found from results of XPS experiments, does not describe the actual dynamic equilibrium between a neutral acid or base in the surface region with its conjugated charged base and acid, respectively. Instead three coupled equilibria describe the observed relative acid/base abundances in the surface region. These are (i) the acid–base equilibrium in the bulk of the solution (horizontal equilibria in Fig. 5), which is specified by the pH and the pKa (or pKb) value of the organic solutes, respectively;(ii) the distribution equilibrium (left vertical equilibria in Fig. 5) of the neutral acid or base species between the bulk solution and the aqueous surface region, and,
(iii) the distribution equilibrium of the charged forms between the surface region and the bulk of the solution (right vertical equilibria in Fig. 5), which in turn is linked to their ability to attract their co-dissolved counter-ions to the surface region and their attached hydrophobic group, see discussion above.
All these equilibria are expected to establish fast without kinetic restrictions. The difference between the pKa value in the aqueous bulk and the observed apparent pKd* is thus a result of the difference between the two vertical surface–bulk equilibria, where the neutral forms are more strongly surface enriched than the charged species. This shifts the fraction curves to higher solution pH values for the studied organic acids and to lower pH values for the studied organic bases, as observed by the XPS experiments, see Fig. 2. Hence, the relative surface propensities of the acid–base pairs and the concentration in the aqueous bulk determine the resulting amount of species and its charged conjugate in the surface region. To further prove our interpretations in a quantitative manner, we propose modifications to eqn (5) and (9), implementing the effective relative surface enrichments of the solutes, which is presented in the following paragraph.
Modeling the relative acid/base abundances in the surface region
As the apparent shift of the curves are mostly governed by the relative surface propensities and abundances of the organic species, eqn (5) and (9) were modified to take their relative surface enrichments into account. This enables the description of the surface acid–base abundances of the different studied compounds as a function of solution pH. For this purpose, the concentrations in the surface region ([species]S) are given as the bulk concentrations ([species]) multiplied with a surface enrichment factor gHA, gA− for the acid or gB, gBH+ for the base system.| [HA]S = gHA[HA], [A−]S = gA−[A−] and [B]S = gB[B], [BH+]S = gBH+[BH+] |
Together with eqn (5) and (9), the interfacial acid and base fractions are then expressed as
| FA = (1 + [A−]/(g[HA]))−1 = (1 + 10pH–pKa–log(g))−1 | (10) |
| FB = (1 + 10pKa–log(g)–pH)−1 | (11) |
The apparent pKd* is defined as pKd* := pKa + log(g) resulting in pKd* − pKa = log(g) for an acid and pKd* − pKa = log(1/g) for a base. Note, pKd* is not a real equilibrium constant but the result of three coupled equilibria as described above. In Fig. 6 the original acid and base fractions obtained from results of XPS experiments are shown together with the modeled fractions using eqn (10) and (11) and the relative enrichments factors given in Table 1, column 4.
The modeled fraction curves mimic the experimental data well. This indicates that the difference of the observed apparent pKd* in the surface region and the dissociation equilibrium in the bulk of the solution, given by pKa, are directly related to the relative enrichment of the acid and its conjugated base (or base and its conjugated acid). In Fig. 7 the model behavior is shown together with experimentally obtained values for butyric acid, n-butyl amine, n-hexyl amine and pentanoic acid. The difference between the apparent pKd* and pKa is plotted as a function of relative enrichment. It can be seen that the greater the relative enrichment of the neutral species over its charged conjugate, the larger the difference between pKd* and pKa. Moreover, as the relative enrichments of surface-active compounds decrease with increasing bulk concentration cbulk, due to surface saturation, see Fig. 3 and ref. 19, 35, we can anticipate smaller shifts of the observed pKd* for higher bulk concentrations, as indicated by the arrows in Fig. 7.
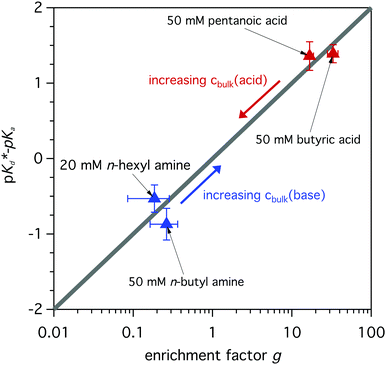 | ||
| Fig. 7 Difference between the apparent pKd* and the dissociation equilibrium pKa of the bulk of the solution as a function of relative enrichment. The model describes the generally linear behavior, which is in good agreement with the experimentally determined values. For increasing bulk concentration a decreased shift is expected, compare with Langmuir behavior in Fig. 3. | ||
It can be concluded that the resulting acid–base abundance in the surface region is described effectively by taking into account the relative enrichments of the surface-active organic species only. Other possible effects, such as a changed surface pH or different dissociation behavior of a solute in the surface region may still add to the observed abundances, but their contributions can only be of minor extent.
Systems in nature often contain both organic acids and bases. The present results enable us to speculate about the distribution of organic species between bulk and surface region in such mixed aqueous systems, which can, in the case of atmospheric aerosols, have rather diverse pH values.42Fig. 8 schematically shows the surface behavior of a carboxylic acid (HA) and an alkyl amine (B), with sufficiently different pKa and pKb values, at different pH values. The combined amount of organic acids and bases in the surface region will be higher for both low and high pH values than for intermediate pH values (between 6 and 9). In addition to this, the dominating organic constituents at the surface change with pH. At low pH, neutral organic acids dominate the surface region, while the neutral organic bases dominate this region at high pH. At intermediate pH values, the much smaller amount of organic compounds present in the surface region will be composed of charged species, carboxylate and alkyl ammonium ions.
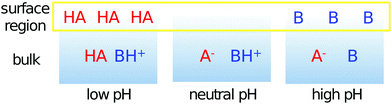 | ||
| Fig. 8 Schematic illustration of the pH-dependent composition of the surface and bulk regions of a mixed solution containing a carboxylic acid (HA) and an alkyl amine (B). | ||
Conclusions
The surface characteristics of carboxylic acids and alkyl amines with different alkyl-chain lengths in aqueous solution were investigated using surface-sensitive XPS. Results of pH-dependent studies show an apparent shift of the derived acid/base fraction curves with respect to the equilibria describing the acid–base distribution in the aqueous bulk. Using absolute PE intensities from concentration-dependent studies, the absolute surface abundances of the studied acid–base pairs were quantified using different model approaches. It was found that the neutral species are strongly enriched in the surface region. The charged conjugates with more than three carbon atoms in their alkyl-chain were also found to be surface enriched, but less strongly than their respective neutral forms, and are most likely present as ion-pairs in the surface region. The origin of the relative surface propensities of the studied compounds is found to be solely dependent on the differences in the hydration of the species in the bulk and in the surface region. For the charged species, their ability to attract their co-dissolved counter ions towards the surface region in combination with the hydrophobicity of their attached organic group determine their hydration in the aqueous surface region and thereby the ability to reach it.With aid of the derived surface enrichment factors, surface concentrations of the organic compounds were calculated as a function of solution pH. These estimates illustrate that, depending on the solution pH, the surface region can have a much higher organic mole fraction than the bulk solution, also in cases where the solute is fully miscible with water.
Furthermore, it is concluded that the Henderson–Hasselbalch equation is not applicable for the aqueous surface region, especially when surface-active compounds are examined. The implicit assumption of mass conservation does not apply in the surface region, due to locally inhomogeneous species distributions and steep concentration gradients. This is also the reason for why eqn (1)–(9) cannot be used for indirect conclusions on the hydronium nor hydroxide concentrations in the surface region (to compare with ref. 6, 13 and 14).
Instead a combination of bulk acid/base and surface adsorption equilibria describe the observed acid/base abundances in the aqueous surface region. This becomes apparent from Fig. 2, which shows parallel shifted XPS acid–base fraction curves with respect to the bulk abundances specified by pKa, comprising the equilibrium constants of both the vertical and the horizontal equilibria (Fig. 5). The relative enrichments of the studied species explain the observed shifts of the acid or base fraction curves in the surface region relative to the bulk solution. A model is proposed which enables the prediction of surface dissociation curves from relative enrichments of a neutral species and its charged conjugate. As the relative enrichments are sufficient to account for the observed shifted speciation in the surface region, we can infer that there are no significant effects expected of any surface specific dissociation equilibrium or changed pH, even though such effects are not excluded. Instead the species' respective surface and bulk hydration mechanisms combined with the bulk acid–base equilibrium explain the observed shifted acid–base abundances in the surface region as compared to the bulk.
The presented results are especially relevant for small systems, e.g. submicron aqueous aerosols and droplets, as the importance of surface phenomena generally increases with decreasing droplet size.30,43 Many chemical processes in the atmosphere are strongly pH dependent, e.g. secondary organic particle formation and gas-particle partitioning.44–46 Thermodynamic equilibrium models based on classic chemical equilibria are often used to estimate aerosol properties, such as composition and acidity, for climate modeling.47 The reason for this is that it is extremely challenging to measure the composition and pH of atmospheric droplets. Parameterizations based on either empirical evidence or empirically validated relations from a firm understanding of the underlying physics are often used for modeling of atmospheric particle properties. In this study, we propose parameterizations based on the organic compounds surface behavior, which may help to generalize models and thereby further reduce major uncertainties48,49 in climate modeling in the future.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Swedish Research Council (2013-3940) and the Helmholtz Association through the Center for Free-Electron Laser Science at DESY. MAX IV Laboratory, Lund University, Sweden, is acknowledged for the allocation of beamtime and laboratory facilities. This project has received funding from the European Research Council (ERC) under the European Union's Horizon 2020 research and innovation programme (Project SURFACE, Grant Agreement No. 717022). N. L. Prisle also gratefully acknowledges funding from the Academy of Finland (Grants 257411 and 308238).References
- L. Onsager and N. N. T. Samaras, J. Chem. Phys., 1934, 2, 528–536 CrossRef.
- P. B. Petersen and R. J. Saykally, Annu. Rev. Phys. Chem., 2006, 57, 333–364 CrossRef PubMed.
- R. R. Netz and D. Horinek, Annu. Rev. Phys. Chem., 2012, 63, 401–418 CrossRef PubMed.
- J. S. Hub, M. G. Wolf, C. Caleman, P. J. van Maaren, G. Groenhof and D. van der Spoel, Chem. Sci., 2014, 5, 1745–1749 RSC.
- R. J. Saykally, Nat. Chem., 2013, 5, 82–84 CrossRef PubMed.
- H. Mishra, S. Enami, R. J. Nielsen, L. A. Stewart, M. R. Hoffmann, W. A. Goddard and A. J. Colussi, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 18679–18683 CrossRef PubMed.
- N. Ottosson, E. Wernersson, J. Söderström, W. Pokapanich, S. Kaufmann, S. Svensson, I. Persson, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2011, 13, 12261–12267 RSC.
- N. Ottosson, L. Cwiklik, J. Söderström, O. Björneholm, G. Öhrwall and P. Jungwirth, J. Phys. Chem. Lett., 2011, 2, 972–976 CrossRef.
- P. B. Petersen and R. J. Saykally, Chem. Phys. Lett., 2008, 458, 255–261 CrossRef.
- X. Zhao, S. Subrahmanyan and K. B. Eisenthal, Chem. Phys. Lett., 1990, 171, 558–562 CrossRef.
- M. Sato, T. Kaieda, K. Ohmukai, H. Kawazumi, A. Harata and T. Ogawa, J. Phys. Chem. B, 2000, 104, 9873–9877 CrossRef.
- Y. Tabe, N. Kikkawa, H. Takahashi and A. Morita, J. Phys. Chem. C, 2014, 118, 977–988 CrossRef.
- S. Enami, M. R. Hoffmann and A. J. Colussi, J. Phys. Chem. Lett., 2010, 1, 1599–1604 CrossRef.
- S. Yamaguchi, A. Kundu, P. Sen and T. Tahara, J. Chem. Phys., 2012, 137, 151101 CrossRef PubMed.
- N. Agmon, H. J. Bakker, R. K. Campen, R. H. Henchman, P. Pohl, S. Roke, M. Thämer and A. Hassanali, Chem. Rev., 2016, 116, 7642–7672 CrossRef PubMed.
- D. W. Smith, J. Chem. Educ., 1977, 54, 540–542 CrossRef.
- T. Lewis, B. Winter, A. C. Stern, M. D. Baer, C. J. Mundy, D. J. Tobias and J. C. Hemminger, J. Phys. Chem. C, 2011, 115, 21183–21190 CrossRef.
- M.-T. Lee, F. Orlando, L. Artiglia, S. Chen and M. Ammann, J. Phys. Chem. A, 2016, 120, 9749–9758 CrossRef PubMed.
- J. Werner, J. Julin, M. Dalirian, N. L. Prisle, G. Ohrwall, I. Persson, O. Björneholm, I. Riipinen, G. Öhrwall, I. Persson, O. Björneholm and I. Riipinen, Phys. Chem. Chem. Phys., 2014, 16, 21486–21495 RSC.
- C. G. Malmberg and A. A. Maryott, J. Res. Natl. Bur. Stand., 1956, 56, 2641–2648 Search PubMed.
- J. Werner, E. Wernersson, V. Ekholm, N. Ottosson, G. Öhrwall, J. Heyda, I. Persson, J. Söderström, P. Jungwirth, O. Björneholm and G. Ohrwall, J. Phys. Chem. B, 2014, 118, 7119–7127 CrossRef PubMed.
- V. Ekholm, M. Vazdar, P. E. Mason, E. Bialik, M.-M. Walz, G. Öhrwall, J. Werner, J.-E. Rubensson, P. Jungwirth and O. Björneholm, J. Chem. Phys., 2018, 148, 144508 CrossRef PubMed.
- G. Öhrwall, N. L. Prisle, N. Ottosson, J. Werner, V. Ekholm, M.-M. Walz and O. Björneholm, J. Phys. Chem. B, 2015, 119, 4033–4040 CrossRef PubMed.
- P. Muller, Pure Appl. Chem., 1994, 66, 1077–1184 Search PubMed.
- M.-M. Walz, C. Caleman, J. Werner, V. Ekholm, D. Lundberg, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2015, 17, 14036–14044 RSC.
- N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth, B. Winter, A. Nilsson, J. Guo, N. Ottosson, M. Faubel, S. E. Bradforth, P. Jungwirth and B. Winter, J. Electron Spectrosc. Relat. Phenom., 2010, 177, 60–70 CrossRef.
- H. Nikjoo, S. Uehara, D. Emfietzoglou and A. Brahme, New J. Phys., 2008, 10, 1–28 CrossRef.
- S. Hüfner, Photoelectron Spectroscopy: Principles and Applications, Springer Verlag, Berlin, Heidelberg, 2003 Search PubMed.
- G. Olivieri, K. M. Parry, C. J. Powell, D. J. Tobias and M. A. Brown, J. Chem. Phys., 2016, 144, 154704 CrossRef PubMed.
- N. L. Prisle, N. Ottosson, G. Öhrwall, J. Söderström, M. Dal Maso and O. Björneholm, Atmos. Chem. Phys., 2012, 12, 12227–12242 CrossRef.
- Handbook of Chemistry and Physics, ed. D. R. Lide, CRC Press, Boca Ranton, FL, 90th edn, 2010 Search PubMed.
- B. Minofar, P. Jungwirth, M. R. Das, W. Kunz and S. Mahiuddin, J. Phys. Chem. C, 2007, 111, 8242–8247 CrossRef.
- R. M. Onorato, D. E. Otten and R. J. Saykally, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 15176–15180 CrossRef PubMed.
- K. A. Perrine, M. H. C. Van Spyk, A. M. Margarella, B. Winter, M. Faubel, H. Bluhm and J. C. Hemminger, J. Phys. Chem. C, 2014, 118, 29378–29388 CrossRef.
- M.-M. Walz, J. Werner, V. Ekholm, N. L. Prisle, G. Öhrwall and O. Björneholm, Phys. Chem. Chem. Phys., 2016, 18, 6648–6656 RSC.
- J. S. Hub, C. Caleman and D. van der Spoel, Phys. Chem. Chem. Phys., 2012, 14, 9537–9545 RSC.
- Y. Marcus, J. Solution Chem., 2008, 37, 1071–1098 CrossRef.
- M. V. Fedotova and S. E. Kruchinin, J. Mol. Liq., 2011, 164, 201–206 CrossRef.
- C. Houriez, M. Meot-Ner Mautner and M. Masella, J. Phys. Chem. B, 2015, 119, 12094–12107 CrossRef PubMed.
- E. M. Adams, B. A. Wellen, R. Thiraux, S. K. Reddy, A. S. Vidalis, F. Paesani, H. C. Allen, J. A. Zasadzinski, G. S. Smith, C. D. Cappa, T. H. Bertram, K. A. Prather, V. H. Grassian, E. A. Stone, M. V. Santander, T. H. Bertram, C. D. Cappa, F. Azam, P. J. Demott, V. H. Grassian and K. A. Prather, Phys. Chem. Chem. Phys., 2017, 19, 10481–10490 RSC.
- V. Venkateshwaran, S. Vembanur and S. Garde, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 8729–8734 CrossRef PubMed.
- W. C. Keene, R. Sander, A. A. Pszenny, R. Vogt, P. J. Crutzen and J. N. Galloway, J. Aerosol Sci., 1998, 29, 339–356 CrossRef.
- B. Noziere, Science, 2016, 351, 1396–1397 CrossRef PubMed.
- M. Jang, N. M. Czoschke, S. Lee and R. M. Kamens, Science, 2002, 298, 814–817 CrossRef PubMed.
- J. D. Rindelaub, R. L. Craig, L. Nandy, A. L. Bondy, C. S. Dutcher, P. B. Shepson and A. P. Ault, J. Phys. Chem. A, 2016, 120, 911–917 CrossRef PubMed.
- D. J. Losey, R. G. Parker and M. A. Freedman, J. Phys. Chem. Lett., 2016, 7, 3861–3865 CrossRef PubMed.
- C. J. Hennigan, J. Izumi, A. P. Sullivan, R. J. Weber and A. Nenes, Atmos. Chem. Phys., 2015, 15, 2775–2790 CrossRef.
- T. Stocker, D. Qin, G. Plattner and M. Tignor, Climate change 2013: the physical science basis, Cambridge University Press, 2013 Search PubMed.
- J. B. Burkholder, J. P. D. Abbatt, I. Barnes, J. M. Roberts, M. L. Melamed, M. Ammann, A. K. Bertram, C. D. Cappa, A. G. Carlton, L. J. Carpenter, J. N. Crowley, Y. Dubowski, C. George, D. E. Heard, H. Herrmann, F. N. Keutsch, J. H. Kroll, V. F. McNeill, N. L. Ng, S. A. Nizkorodov, J. J. Orlando, C. J. Percival, B. Picquet-Varrault, Y. Rudich, P. W. Seakins, J. D. Surratt, H. Tanimoto, J. A. Thornton, Z. Tong, G. S. Tyndall, A. Wahner, C. J. Weschler, K. R. Wilson and P. J. Ziemann, Environ. Sci. Technol., 2017, 51, 2519–2528 CrossRef PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: 10.1039/c8cp01898g |
| ‡ Present address: Technology and Society Laboratory, Empa – Swiss Federal Laboratories for Materials Science and Technology, St. Gallen, Switzerland. |
| § Present address: Department of Cell and Molecular Biology, Uppsala University, Box 596, SE-75124 Uppsala, Sweden. |
| This journal is © the Owner Societies 2018 |