Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Macroscale precipitation kinetics: towards complex precipitate structure design
Nirmali Prabha
Das
a,
Brigitta
Müller
a,
Ágota
Tóth
 a,
Dezső
Horváth
a,
Dezső
Horváth
 b and
Gábor
Schuszter
b and
Gábor
Schuszter
 *a
*a
aDepartment of Physical Chemistry and Materials Science, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary. E-mail: schuszti@chem.u-szeged.hu; Fax: +36-62-546-482; Tel: +36-62-544-212
bDepartment of Applied and Environmental Chemistry, University of Szeged, Rerrich Béla tér 1., Szeged, H-6720, Hungary
First published on 17th May 2018
Abstract
Producing self-assembled inorganic precipitate micro- and macro-structures with tailored properties may pave the way for new possibilities in, e.g., materials science and the pharmaceutical industry. One set of important parameters to maintain appropriate control over the yield falls in the frame of reaction kinetics, which affects the possible coupling between hydrodynamics and chemical reactions under flow conditions. In this study, we present a spectrophotometric method to experimentally determine the characteristic timescales of precipitation reactions. It is also shown that the nickel–oxalate model system – despite the fast chemical complexation equilibria taking place – can be kinetically described by either Classical Nucleation Theory or the classical homogeneous kinetics approach. The applicability of our results is illustrated via injection experiments intrinsically exhibiting coupling between chemistry and hydrodynamics. Therefore, we suggest that easy-to-handle power law functions may be applied to characterize the precipitation kinetics in flow systems.
1 Introduction
The formation of precipitates from two liquid precursors is gaining more and more importance in the field of materials science due to its relevance in synthesizing and engineering bottom-up made solid materials with appropriate properties.1–6 Precipitation may occur via the intermixing of two separate homogeneous solutions of the ionic ingredients of a sparingly soluble salt in concentrations exceeding the solubility product of the given salt.Depending on how such mixing is accomplished, different product properties may be achieved. The simplest possibility consists of mixing the two reactants in a well-stirred container, usually resulting in the thermodynamically most stable product.7,8 Another method – widely termed as flow-driven precipitation – involves the radial injection of one reactant into the other one either being confined between two plates9,10 or forming a thin solution layer open to the air.8,11 Such a technique providing spatial gradients (concentration, density, pH, etc.) opens the door to producing thermodynamically unstable polymorphs and differently shaped crystals showing a well-defined spatial distribution. This kind of promising possibility has attracted the attention of the pharmaceutical industry as well, where the role of polymorphism is obvious.12,13 In addition, the interplay between chemical reactions and hydrodynamics gives rise to complex spatial patterns, which may be important for CO2 sequestration by means of calcite precipitation taking place in confined domains.14,15 Self-assembled 3D precipitate structures can be achieved as well via flow-injection techniques providing good control of the evolving tube-like membranes usually referred to as chemical gardens. Those inorganic living-like structures are also found in nature in hydrothermal vents6 and have been a subject of interest due to their wide applicability in designing materials and devices.16–20
Although it can be seen that precipitation performed under appropriate conditions may pave the way for various scientific advances, it is definitely a challenge to choose the right chemicals yielding a product with tunable properties (e.g. chemical composition, crystal morphology and size distribution, micro- and macro-structures of composite systems, etc.). There have been studies focusing on either 1D, 2D, or 3D precipitation patterns as the macroscopic descriptors of the microscale behaviour. Research was undertaken on how the chemical character of the reactants influences the resulting patterns,10,17,21 how the mobility of different ions determines the precipitate wall evolution,22,23 and how the chemical character of the products corresponds to the physical properties of precipitate membranes.24–26
To enhance the capabilities of precipitation systems applying flow-injection techniques, one may also consider the coupling between kinetics and in situ hydrodynamics. The flow field being affected by different transport processes and spatial effects (diffusion, osmosis, gravity currents, and permeability changes) has been thoroughly investigated.8,23,24,26,27 However, to the best of our knowledge, no kinetic characterization has been performed for macroscopic precipitation systems. As a starting point, one may probe this in two different ways. First, the classical homogeneous reaction kinetics approach could be tested for such a reactive heterogeneous system to see whether any rate law based on the initial reactant concentrations could be found with meaningful orders with respect to individual components.28,29 When applying this method, it is not obvious that the appearance of a solid/liquid interface in the bulk will not significantly change the system behavior. The other reasonable way of investigation could be based on Classical Nucleation Theory (CNT) directly elaborated for the nucleation and crystal growth steps of supersaturated non-reactive systems.30,31 Although this approach must be definitely applicable independent of the solid/liquid interface, the reactive character of the nickel–oxalate system (also involving numerous chemical equilibria) may render the theory set up for one component, supersaturated systems invalid. In addition, compared to standard crystallization studies, relatively large supersaturation levels must be maintained to produce a sufficient amount of precipitate for the formation of well-defined, macroscopic, and self-supporting solid structures. Also, applying CNT for macroscopic systems is circuitous since the required parameters are on the molecular level and hard to access for many relevant reactants. Therefore, in this study, presenting experimental kinetics results for the nickel–oxalate precipitation in the macroscale, we focus on comparing the applicability of both the classical homogeneous reaction kinetics and the CNT approaches. Furthermore, we show that easy-to-use power law functions obtained in well-stirred batch systems may be successfully used to estimate the precipitation timescale in flows.
2 Experimental
When two precipitants are mixed together in such concentrations that the solubility product of the appropriate sparingly soluble salt is exceeded, precipitation will take place sooner or later. If precipitation is not too fast (i.e. the mixture is stable for at least tens of seconds), its temporal evolution can be followed via turbidity (T), since the solid particles scatter light. Throughout this study, systematic spectrophotometric measurements of nickel–oxalate precipitation were carried out using a UV-Visible spectrophotometer (VWR UV-3100PC). We highlight here that the transmittance of the dissolved molecules does not contribute to the decrease of the light intensity at the wavelength provided (340 nm).For the experiments, stock solutions of NiCl2 and Na2(COO)2 were prepared from analytical grade chemicals. All solutions were prepared by using ion-exchanged water (Purite RO100 instrument, 2.1 μS cm−1 conductance at 25 °C). Measurements were performed for concentrations ranging from 0.005 to 0.140 M in such a way that both reactants had equal concentrations in the mixture. The pH of the stock oxalate solution was always maintained at 4 by adding droplets of HCl. Since the reactant mixture is greenish, the wavelength was fixed at 340 nm for all measurements to avoid the absorbance of Niaq2+ ions. To measure the turbidity over time, a commercial quartz cuvette (1 × 1 × 4 cm3) was used to hold the reaction mixture. To begin the experiment, the cuvette was first filled with 2 mL of an aqueous solution of Na2(COO)2 to set as the background (T = 0). Then, 1 mL of oxalate was pipetted out and another 1 mL of NiCl2 solution was added to prepare a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 concentration ratio solution. The cuvette was then sealed and the system was kept under vigorous stirring (mimicking the mixing present with flow-injection techniques) throughout the reaction. The turbidity was scanned with a time interval of 2 s in every case with the total scan time depending on the reactant concentrations. To check the reproducibility, for each concentration, the experiments were repeated at least three times. For the measurements described above, the stirring rate was fixed to ≈700 rpm. However, to test the robustness of our system against stochastic effects, we also performed experiments by changing the speed of the stirrer to higher (≈1000 rpm) and lower (≈380 rpm) rates. It was observed that once the solution is sufficiently stirred to be homogeneous, which is in fact the case for all those rates, there is no significant effect of the stirring rate on the turbidity and thus on the precipitate formation. It was also checked via doubling the volume of the reactant mixture that the characteristic reaction time is independent of the volume of the reactants, if the mixing is efficient.
1 concentration ratio solution. The cuvette was then sealed and the system was kept under vigorous stirring (mimicking the mixing present with flow-injection techniques) throughout the reaction. The turbidity was scanned with a time interval of 2 s in every case with the total scan time depending on the reactant concentrations. To check the reproducibility, for each concentration, the experiments were repeated at least three times. For the measurements described above, the stirring rate was fixed to ≈700 rpm. However, to test the robustness of our system against stochastic effects, we also performed experiments by changing the speed of the stirrer to higher (≈1000 rpm) and lower (≈380 rpm) rates. It was observed that once the solution is sufficiently stirred to be homogeneous, which is in fact the case for all those rates, there is no significant effect of the stirring rate on the turbidity and thus on the precipitate formation. It was also checked via doubling the volume of the reactant mixture that the characteristic reaction time is independent of the volume of the reactants, if the mixing is efficient.
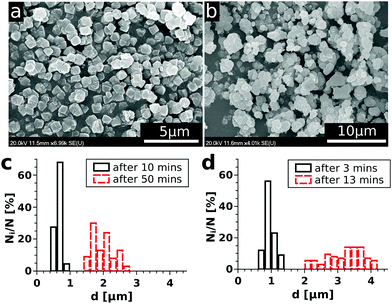
To perform a time-elapsed characterization of the precipitate size distribution, scanning electron microscopy was applied (Hitachi S-4700). Samples were prepared by mixing the two reactants in equal amounts as previously, thus resulting in a reactant mixture with a total volume of 30 mL. The mixture was kept under continuous stirring. When precipitation started, 5 mL was pipetted out from the mixture into a beaker containing 100 mL to slow down the reaction. At regular intervals, 5 more samples were taken in the same way in separate beakers. Those measurements were performed for higher (a mixture of 0.14 M NiCl2 and 0.14 M Na2(COO)2 solutions) and lower (0.05 M NiCl2 and 0.05 M Na2(COO)2 solutions) reactant concentrations as well. The time step for sampling was 2 min for the higher reactant concentration and 10 min for the lower reactant concentration. The suspensions were first filtered (Pall GN-6 Metricel Membrane Filter, 0.45 μm) and then the solid samples were thoroughly rinsed and collected for analysis.
3 Results and discussion
3.1 Particle size distribution
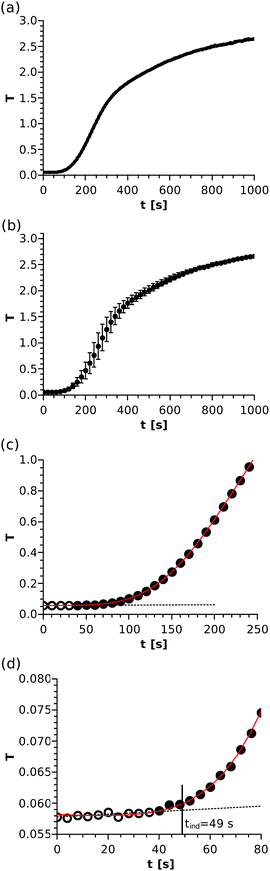
In the spectrophotometric measurements, the T–t graph depicts an S-shaped curve, as shown in Fig. 1(a), for one such experiment. The reactants are mixed (and thus supersaturation is reached) at t = 0 s. It is seen in the initial stage that turbidity is technically zero. Later on, after a certain period of time, T starts to increase, which manifests as an inclination in the curve. From that point, the turbidity grows more or less linearly with a slope depending on the reactant concentration. Finally, the curve slowly reaches saturation. Although the entire T–t graph is reproducible (see Fig. 1(b)) and reveals the kinetic description of the reaction, some characteristics of the system must be taken into consideration. When precipitation starts, not only the number of nuclei but also their size may change with time. Therefore, those two parallel effects could simultaneously contribute to the turbidity growth, making the data processing difficult at later stages.One of the main goals of the present study is to provide an easy-to-use method for gathering experimental data relevant for the precipitation kinetics and also for their convenient evaluation. Therefore, we investigated the time evolution of the precipitate microstructure to see whether the entire turbidity evolution could be easily applied. To do so, scanning electron microscopic images were taken at regular time periods for the reactions carried out with different initial reactant concentrations. As an example, some selected SEM images are shown in Fig. 2(a) and (b) for a solution composition of 0.070 M with respect to both NiCl2 and Na2(COO)2. From this figure, it can be seen that the Ni–oxalate precipitate is characterized by a cubic shape. Also, the particles are well separated and closely monodisperse in size for the samples taken shortly after the beginning of precipitation (Fig. 2(a)). After a longer time, however, coagulation of the precipitate occurs and aggregates form (Fig. 2(b)). The time required for the turbidity to reach saturation depends on the reactant concentration. Therefore, the size distribution of the particles was investigated more often (2 min intervals) for the higher concentration than for the lower one (10 min). A selection of such size distributions allowing the comparison of particles present shortly after reaching supersaturation and also close to the end of the reaction is shown in Fig. 2(c and d) for two different initial concentrations. We see that the size of the particles (0.65 ± 0.08 μm for the lower concentration and 0.95 ± 0.12 μm for the higher concentration) is similar for both concentrations in the beginning of the measurements. Later on, however, both the particle size for one particular case and also the size difference between the two cases are significantly increased and the distributions become broader. To determine the size distribution, overall, more than a thousand particles were taken into account.
In conclusion, we can say that – in our reactive system – the measured turbidity change mostly corresponds to the increasing number of particles at the beginning of precipitation since the size distribution is narrow. However, as time passes, both the increasing particle number and the size distribution shift contribute simultaneously to the turbidity change. Therefore, to validly apply the experimental results for investigating the kinetics of precipitation, not the entire T–t curve but only its initial portion could be easily used. It is also important to point out that the size of the particles at the beginning of precipitation barely depends on the reactant concentration, therefore, we expect no additional uncertainty of the detection arising from this source.
3.2 Determination of the induction period
By mixing the two reactants in appropriate concentrations, supersaturation and thus a thermodynamically unstable situation is obtained, which will lead, sooner or later, to precipitate formation. The time elapsed after maintaining supersaturation until solid particles form in an observable amount is usually referred to as the induction period, tind.32–34In our experiments, the light scattering of the solid particles is used for detection. Turbidity technically does not change until precipitation starts, thus a line (f(t)) can be fitted throughout the data points recorded in the time period considered as the background (black dotted line in Fig. 1(c)). The standard deviation for such turbidity values where no trend is seen (i.e. the error of the measurement, σ) is found to be in the range of (1–10) × 10−4. Once precipitation starts, T is going to increase steeply and monotonically. The trend of the data set (i.e. the time evolution of T) can be nicely recovered by fitting a high-order polynomial (g(t)) through an appropriately chosen time interval (solid red line in Fig. 1(c)), which partially overlaps with the linearly fitted part. To determine the induction period of precipitation, we apply a standard approach taken from analytical chemistry, namely that a measured value can be considered significantly different from the background if it deviates by at least three times the standard deviation of the background (σ). Therefore, the time where g(t) − f(t) = 3σ is sought; this procedure is depicted in detail in Fig. 1(d). For this example case, the tind = 49 s induction period is determined. Although the size of the symbols does not correspond to the error of the measured points, the typical uncertainty of the determination can be estimated from the deviation of the fitted line and the polynomial taking the corresponding turbidity values into account.
3.3 Equilibrium composition
The rate of a reaction in most cases depends on the concentration of the reactants with the exception of zero-order reactions (e.g. heterogeneous catalysis). As discussed above, the part of the T–t curve where the reactants are mostly present in the mixture and the product only starts to appear will be used for analysis. It is, therefore, essential to know the initial composition of the reactant mixture for each concentration used throughout the experiments. In the present system, when NiCl2 and Na2(COO)2 solutions are mixed, complexation reactions being much faster than the precipitation itself take place first. For this reason, in the example case shown in Fig. 1, T is not absolutely zero for the reactant mixture since, due to technical reasons, only the oxalate solution was taken as the background (T = 0). The color of the reactant mixture is determined by the complexes for which the complexation equilibria (eqn (1)–(5)) are listed below:| Ni2+ + (COO)22− ⇌ Ni(COO)2(aq) | (1) |
| Ni2+ + OH− ⇌ Ni(OH)+ | (2) |
| Ni2+ + 2OH− ⇌ Ni(OH)2(aq) | (3) |
| Ni2+ + 3OH− ⇌ Ni(OH)3− | (4) |
| Ni2+ + 4OH− ⇌ Ni(OH)42− | (5) |
In eqn (1)–(5), the stability constants of the complexes (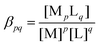 for the complexation reaction of pM + qL ⇌ MpLq) are lg
for the complexation reaction of pM + qL ⇌ MpLq) are lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 5.16, lg
β = 5.16, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) βOH1 = 3.58, lg
βOH1 = 3.58, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH2 = 8.1, lg
βOH2 = 8.1, lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH3 = 11.2, and lg
βOH3 = 11.2, and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) βOH4 = 11.9, respectively.35 To calculate the equilibrium composition of the reactant mixture, all those equilibria are taken into account together with the first and second protonation steps of the oxalate ions (eqn (6) and (7), lg
βOH4 = 11.9, respectively.35 To calculate the equilibrium composition of the reactant mixture, all those equilibria are taken into account together with the first and second protonation steps of the oxalate ions (eqn (6) and (7), lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) KH1 = 4.27 and lg
KH1 = 4.27 and lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) KH2 = 1.2535):
KH2 = 1.2535):
| (COO)22− + H+ ⇌ HOOC–COO− | (6) |
| HOOC–COO− + H+ ⇌ (COOH)2 | (7) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β = 4.5 and 5.5 values. It was found that the 1
β = 4.5 and 5.5 values. It was found that the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio complex is still dominant even if its percentage slightly decreases for a lower lg
1 ratio complex is still dominant even if its percentage slightly decreases for a lower lg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β. We highlight here that according to ref. 35, the Ni2+ ion has only one type of complex with the oxalate ion. Due to the stability of such a complex, precipitation does not take place immediately after mixing the reactants despite the relatively large concentrations. However, after the induction period, where no significant increase of the turbidity is seen, precipitation begins due to the consecutive equilibria of
β. We highlight here that according to ref. 35, the Ni2+ ion has only one type of complex with the oxalate ion. Due to the stability of such a complex, precipitation does not take place immediately after mixing the reactants despite the relatively large concentrations. However, after the induction period, where no significant increase of the turbidity is seen, precipitation begins due to the consecutive equilibria of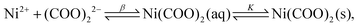 | (8) |
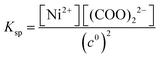 ). Therefore, from here on, all the presented results are based on the concentration of the Ni(COO)2(aq) complex (as a precipitate precursor) instead of showing the concentration of the precipitants in the mixture.
). Therefore, from here on, all the presented results are based on the concentration of the Ni(COO)2(aq) complex (as a precipitate precursor) instead of showing the concentration of the precipitants in the mixture.
3.4 Approach I: classical homogeneous kinetics
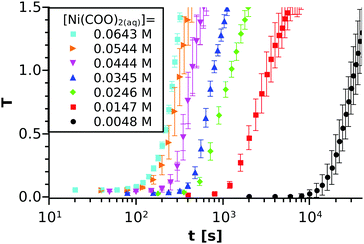
The spectrophotometric experiments have been performed for 15 different initial compositions of the reactant mixture in order to investigate how tind depends on the Ni(COO)2(aq) concentration. For comparison, some selected T–t curves are shown in Fig. 3 using the logarithmic timescale. Although several studies have proved the stochastic character of crystallisation processes,33,34 it can be seen from the graph that our macroscopic precipitation experiment (i.e. reactive crystallisation) is reproducible in the concentration and time ranges applied because fluctuations are small. We also observe that tind strongly decreases (orders of magnitude) with increasing concentration.For each experiment carried out, tind was separately determined by the method described above and then the averaged values were plotted as a function of the Ni(COO)2(aq) concentration (denoted as c further on), as shown in Fig. 4. At this point, we recall eqn (8) where a fast complexation equilibrium is assumed before precipitation takes place. Therefore, as a first step, the two reactant ions (Ni2+ and (COO)22−) form an uncharged complex (Ni(COO)2(aq)). Upon collision, two of those complex molecules may form a nucleus, which will either dissociate or grow in size and initiate crystallisation. In this context, one may assume that the rate of the reaction – and thus the reciprocal of the characteristic induction period – is proportional to the Ni(COO)2(aq) concentration. Therefore, a non-linear fitting through the tind–c data points is performed using the formula tind = ac−α, which is also drawn as the red dashed line in Fig. 4. The parameters a and α are found to be 0.28 ± 0.07 and 1.88 ± 0.07, respectively, from which the reaction can be considered as second order for the Ni(COO)2(aq) concentration. We emphasize here that those results are obtained by simply applying the classical homogeneous kinetics method for which the appearance of a solid phase could be a limiting factor. However, we see that if there is one dominant complex in the mixture and the characteristic time is defined in such a way that not much solid is present, the initial rate of precipitation can be expressed as a function of the complex concentration according to the classical homogeneous kinetics.
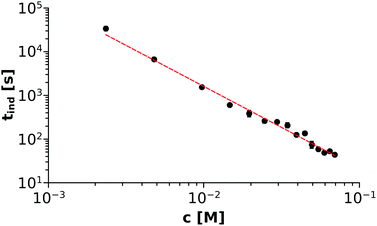 | ||
| Fig. 4 log–log plot showing the Ni(COO)2(aq) concentration dependency of the induction period (tind). Error bars are presented as well but smaller than the symbols. | ||
3.5 Approach II: classical nucleation theory
As was already mentioned in the Introduction section, crystallization processes may be characterized according to Classical Nucleation Theory (CNT) as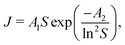 | (9) |
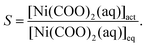 | (10) |
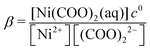 is taken from the literature,35 the solubility product
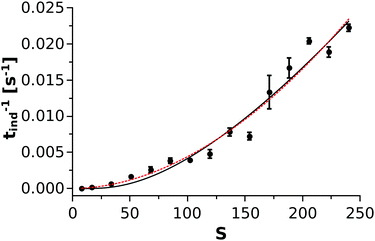
is taken from the literature,35 the solubility product 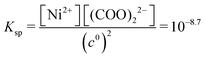 is determined via standard conductometric measurements, and c0 = 1 mol dm−3. To investigate whether eqn (9) could be validly applied for the kinetics of the nickel–oxalate precipitation reaction, the reciprocal of the measured induction periods (corresponding to J) is plotted as a function of S in Fig. 5. It can be seen from the solid black line that CNT describes well the trend observed in the experiments with parameters A1 = (7.3 ± 3.0) × 10−4 s−1 and A2 = 60.6 ± 10.4. In addition, a power law according to the classical homogeneous kinetics approach (tind−1 = bSβ) is also fitted through the data set (dashed red line) where parameters b and β are found to be (6.72 ± 5.87) × 10−7 s−1 and 1.91 ± 0.17, respectively. Hence, it is found that both curves can be used for the characterization of the precipitation kinetics. Furthermore, since the exponents α and β obtained from the power law fittings seen in Fig. 4 and 5 are equal within error, we can conclude that tind is closely proportional to the square of either the Ni(COO)2(aq) concentration or its supersaturation level.
is determined via standard conductometric measurements, and c0 = 1 mol dm−3. To investigate whether eqn (9) could be validly applied for the kinetics of the nickel–oxalate precipitation reaction, the reciprocal of the measured induction periods (corresponding to J) is plotted as a function of S in Fig. 5. It can be seen from the solid black line that CNT describes well the trend observed in the experiments with parameters A1 = (7.3 ± 3.0) × 10−4 s−1 and A2 = 60.6 ± 10.4. In addition, a power law according to the classical homogeneous kinetics approach (tind−1 = bSβ) is also fitted through the data set (dashed red line) where parameters b and β are found to be (6.72 ± 5.87) × 10−7 s−1 and 1.91 ± 0.17, respectively. Hence, it is found that both curves can be used for the characterization of the precipitation kinetics. Furthermore, since the exponents α and β obtained from the power law fittings seen in Fig. 4 and 5 are equal within error, we can conclude that tind is closely proportional to the square of either the Ni(COO)2(aq) concentration or its supersaturation level.
4 Probe of applicability
The purpose of the present kinetic investigation is to provide easy-to-use rate laws for the design of macroscopic precipitation experiments coupled with flow to form tailored precipitate structures. To see whether our results corresponding to a well-stirred system could be used under flow conditions, flow-injection precipitation experiments were performed in a radial geometry introduced elsewhere.8,11,36,37 In the present case, 1 M NiCl2 solution was injected from below into a large pool of Na2(COO)2 solution with different concentrations (0.100, 0.125, 0.150, and 0.200 M). The injection was carried out by a peristaltic pump at 20 mL h−1 flow rate. The NiCl2 solution being significantly denser (1.1104 g cm−3) than the oxalate (1.008, 1.010, 1.012, and 1.018 g cm−3, respectively) spreads on the bottom of the reaction vessel and mixes with the upper lying oxalate open to the air. After some time, depending on the oxalate concentration, the precipitate formed and settled down, forming a radial structure (Fig. 6). Although such a pattern evolving due to buoyancy-driven instability emerging at the miscible interface of the displaced and invading solutions has been known in the literature for a long time,38,39 the exact relation between the radius of the precipitate-less inner circle and the reaction rate has not yet been found. In the present case, a relatively large inner circle (ID ≈ 5 cm) evolves because of the coupling of slow precipitation and radial flow. We highlight here that applying such a low injection rate ensures a negligible particle drift. For comparison, no precipitate-less inner circle was found in the case of Ca(COO)2(s),8 and it was significantly smaller for Co(COO)2(s)11 than for Ni(COO)2(s), which already suggests a difference in the rate of the reactions.The injection experiments were reproduced three times for each concentration and the top view images were recorded with 3 s intervals. In every case, the time elapsed from the start of injection until the precipitate appeared was sought. Just as in the well-stirred system, the precipitate appeared earlier (i.e., inner circle formed with a smaller diameter) with increasing reactant concentration (see Table 1). During the injection, the concentration distribution of the species changed with time and space, which makes it difficult to estimate the in situ concentration of the nickel–oxalate complex used for the classical homogeneous kinetics approach (Fig. 4). Therefore, Fig. 7 shows the induction time as a function of the total concentration of the oxalate ions as the only varying parameter of the injection experiments. A power function of tind = (2.61 ± 0.24)coxalate−(1.84±0.04) is found where the exponent agrees well with that determined by applying the classical nucleation theory approach. To understand how the induction period could be proportional to the square of either the nickel–oxalate complex concentration or to the total concentration of oxalate ions, one may consider the following. Taking the results of the well-stirred system into account, one can estimate the in situ concentration of the nickel–oxalate complex ([Ni(COO)2(aq)]act) based on the equation tind = 0.28ccomplex−2. Thus calculated values together with the experimentally determined induction periods are listed in Table 1. When the denser NiCl2 solution advances on the bottom of the vessel, it mixes with the less dense Na2(COO)2 solution. The properties of the evolving convective region depend on the density distribution, which is in fact quite similar for the different concentrations since the density of the oxalate solution varies by less than 1%. Therefore, we can assume that the dilution of the solutions caused by the mixing is technically the same in every case as it is supported by the ratio of the total concentration of the oxalate ions to that of the nickel–oxalate complex (the last column of Table 1). At the tip of the invading solution, nickel ions are in stoichiometric excess and thus the concentration of the complex is limited by the concentration of the oxalate ions intermixed, which explains how equations tind ≈ coxalate−2 and tind ≈ ccomplex−2 can both be valid. Therefore, we see that the result obtained in a well-stirred system (tind ≈ ccomplex−2) could be usefully applied to estimate the timescale of precipitation under flow conditions even if the exact coefficient depends on the hydrodynamics (e.g. what dilution and stoichiometric ratio are maintained in the mixing zone).
| [Na2(COO)2]/M | t/s | [Ni(COO)2(aq)]act /M | [Na2(COO)2]/[Ni(COO)2(aq)]act |
|---|---|---|---|
| 0.100 | 182 ± 2 | 0.039 | 2.56 |
| 0.125 | 118 ± 2 | 0.049 | 2.55 |
| 0.150 | 86 ± 5 | 0.057 | 2.63 |
| 0.200 | 52 ± 3 | 0.075 | 2.67 |
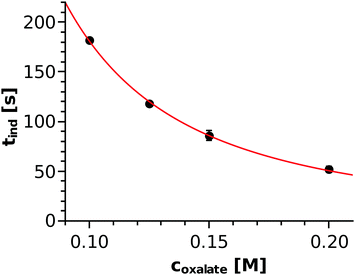 | ||
| Fig. 7 Induction period determined in injection experiments as a function of the total oxalate concentration and the power function fitted through the points. | ||
5 Conclusion
Precipitation experiments bear relevance to many different applications. To maintain good control over the precipitate micro- and macro-structures, appropriate experimental conditions should be applied among which the kinetic characteristics play an important role. It can be seen that the induction period – being a characteristic time of the reaction – can be reproducibly determined following turbidity as a function of time in a well-stirred batch reactor. We described how such an induction period decreases strongly with increasing precipitant concentration. It was found in the nickel–oxalate model system exhibiting fast complexation and slow precipitation equilibria that both the Classical Nucleation Theory based on the supersaturation level and the classical homogeneous kinetics approach based on reactant concentrations may be validly used to describe the precipitation kinetics and estimate induction periods. The applicability of the easy-to-use power law function determined in the well-stirred batch is proved by investigating the same reaction under flow conditions. Therefore, in the future, we will apply the presented spectrophotometric method to systematically investigate the precipitation kinetics of several reactions that are relevant for the production of complex and promising small-scale precipitate structures.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research, Development and Innovation Office (K119795 and PD121010) and GINOP-2.3.2-15-2016-00013 projects.References
- C. N. Kaplan, W. L. Noorduin, L. Li, R. Sadza, L. Folkertsma, J. Aizenberg and L. Mahadevan, Controlled Growth and Form of Precipitating Microsculptures, Science, 2017, 355, 1395–1399 CrossRef PubMed.
- I. Polishchuk, A. A. Bracha, L. Bloch, D. Levy, S. Kozachkevich, Y. Etinger-Geller, Y. Kauffmann, M. Burghammer, C. Giacobbe, J. Villanova, G. Hendler, C. Y. Sun, A. J. Giuffre, M. A. Marcus, L. Kundanati, P. Zaslansky, N. M. Pugno, P. U. P. A. Gilbert, A. Katsman and B. Pokroy, Coherently Aligned Nanoparticles within a Biogenic Single Crystal: A Biological Presterssing Strategy, Science, 2017, 3358, 1294–1298 CrossRef PubMed.
- J. R. Shimpi, D. S. Sidhaye and B. L. V. Prasad, Digestive Ripening: A Fine Chemical Machining Process on the Nanoscale, Langmuir, 2017, 33, 9491–9507 CrossRef.
- J. Schlomach, K. Quarch and M. Kind, Investigation of Precipitation of Calcium Carbonate at High Supersaturations, Chem. Eng. Technol., 2006, 29, 215–220 CrossRef.
- D. Wang, Q. Wang and T. Wing, Morphology-controllable Synthesis of Cobalt Oxalates and their Conversion to Mesoporous Co3O4 Nanostructures for Application in Supercapacitors, Inorg. Chem., 2011, 50(14), 6482–6492 CrossRef PubMed.
- E. Nakouzi and O. Steinbock, Self-organization in Precipitation Reactions Far From the Equilibrium, Sci. Adv., 2016, 2, 1–13 Search PubMed.
- L. Zhu, L. Y. Wang, Z. L. Sha, Y. F. Wang, L. B. Yang, X. Y. Zhao and W. Du, Interplay between Thermodynamics and Kinetics on Polymorphic Appearance in the Solution Crystallization of an Enantiotropic System, Gestodene, Cryst. Growth Des., 2017, 17, 4582 Search PubMed.
- B. Bohner, G. Schuszter, O. Berkesi, D. Horváth and Á. Tóth, Self-organization of Calcium Oxalate by Flow-driven Precipitation, Chem. Commun., 2014, 50, 4289 RSC.
- F. Haudin, J. H. E. Cartwright and F. Brau, and A. De Wit, Spiral Precipitation Patterns in Confined Chemical Gardens, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 17363 CrossRef PubMed.
- F. Haudin, V. Brasiliense, J. H. E. Cartwright and F. Brau, and A. De Wit, Genericity of Confined Chemical Garden Patterns with Regard to Changes in the Reactants, Phys. Chem. Chem. Phys., 2015, 17, 12804 RSC.
- E. Tóth-Szeles, G. Schuszter, Á. Tóth, Z. Kónya and D. Horváth, Flow-driven Morphology Control in the Cobalt – Oxalate System, CrystEngComm, 2016, 18, 2057 RSC.
- A. D. Bond, R. Boese and G. R. Desiraju, On the Polymorphism of Aspirin: Crystalline Aspirin as Intergrowths of Two “Polymorphic” Domains, Angew. Chem., Int. Ed., 2007, 46, 618–662 CrossRef PubMed.
- J. Sibik, M. J. Sargent, M. Franklin and J. A. Zeitler, Crystallization and Phase Changes in Paracetamol from the Amorphous Solid to the Liquid Phase, Mol. Pharmaceutics, 2014, 11, 1326–1334 CrossRef PubMed.
- J. M. Matter, M. Stute, S. O. Snaebjornsdottir, E. H. Oelkers, S. R. Gislason, E. S. Aradottir, B. Sigfusson, I. Gunnarsson, H. Sigurdardottir, E. Gunnlaugsson, G. Axelsson, H. A. Alfredsson, D. Wolff Boenisch, K. Mesfin, D. F. de la R. Taya, J. Hall, K. Dideriksen and W. S. Broecker, Rapid Carbon Mineralization for Permanent Disposal of Anthropogenic Carbon Dioxide Emissions, Science, 2016, 352, 1312 CrossRef PubMed.
- G. Schuszter, F. Brau and A. De Wit, Calcium Carbonate Mineralization in a Confined Geometry, Environ. Sci. Technol. Lett., 2016, 3, 156 CrossRef.
- L. M. Barge, S. S. S. Cardoso, J. H. E. Cartwright, G. J. T. Cooper, L. Cronin, A. De Wit, I. J. Doloboff, B. Escribano, R. E. Goldstein, F. Haudin, D. E. H. Jones, A. L. Mackay, J. Maselko, J. J. Pagano, J. Pantaleone, M. J. Russell, C. I. Sainz-Díaz, O. Steinbock, D. A. Stone, Y. Tanimoto and N. L. Thomas, From Chemical Gardens to Chemobrionics, Chem. Rev., 2015, 115, 8652 CrossRef PubMed.
- J. H. E. Cartwright, B. Escribano, S. Khokhlov and C. I. Sainz-Díaz, Chemical Gardens from Silicates and Cations of Group 2: A Comparative Study of Composition, Morphology and Microstructure, Phys. Chem. Chem. Phys., 2011, 13, 1030 RSC.
- S. S. S. Cardoso, J. H. E. Cartwright, O. Steinbock, D. A. Stone and N. L. Thomas, Cement Nanotubes: On Chemical Gardens and Cement, Struct. Chem., 2017, 28, 33 CrossRef.
- F. Brau, F. Haudin, S. Thouvenel-Romans, A. De Wit, O. Steinbock, S. S. S. Cardoso and J. H. E. Cartwright, Filament Dynamics in Confined Chemical Gardens and in Filiform Corrosion, Phys. Chem. Chem. Phys., 2018, 20, 784–793 RSC.
- F. Glaab, M. Kellermeier, W. Kunz, E. Morallon and J. M. García-Ruiz, Formation and Evolution of Chemical Gradients and Potential Differences Across Self-assembling Inorganic Membranes, Angew. Chem., 2012, 124, 4393–4397 CrossRef.
- G. Schuszter and A. De Wit, Comparison of Flow-controlled Calcium and Barium Carbonate Precipitation Patterns, J. Chem. Phys., 2016, 145, 224201 CrossRef PubMed.
- B. C. Batista and O. Steinbock, Growing Inorganic Membranes in Microfluidic Devices: Chemical Gardens Reduced to Linear Walls, J. Phys. Chem. C, 2015, 119(48), 27045–27052 Search PubMed.
- Q. Wang, M. R. Bentley and O. Steinbock, Self-Organization of Layered Inorganic Membranes in Microfluidic Devices, J. Phys. Chem. C, 2017, 121(26), 14120–14127 Search PubMed.
- F. Glaab, J. Rieder, J. M. García-Ruiz, W. Kunz and M. Kellermeier, Diffusion and Precipitation Processes in Iron-based Silica Gardens, Phys. Chem. Chem. Phys., 2016, 18, 24850–24858 RSC.
- J. Pantaleone, Á. Tóth, D. Horváth, L. RoseFigura and J. Maselko, Pressure Oscillations in a Chemical Garden, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2009, 79(5), 056221 CrossRef PubMed.
- E. Rauscher, G. Schuszter, B. Bohner, Á. Tóth and D. Horváth, Osmotic Contribution to the Flow-driven Tube Formation of Copper – Phosphate and Copper – Silicate Chemical Gardens, Phys. Chem. Chem. Phys., 2018, 20, 5766 RSC.
- Y. Nagatsu, Y. Ishii, Y. Tada and A. De Wit, Hydrodynamic Fingering Instability Induced by a Precipitation Reaction, Phys. Rev. Lett., 2014, 113, 024502 CrossRef PubMed.
- P. Atkins and J. de Paula, Physical Chemistry, Oxford University Press, 9th edn, 2010 Search PubMed.
- G. Lente, Deterministic Kinetics in Chemistry and Systems Biology, The Dynamics of Complex Reaction Networks, Springer, 2015, ISBN: 978-3-319-15481-7 Search PubMed.
- R. P. Sear, Nucleation: Theory and Applications to Protein Solutions and Colloidal Suspensions, J. Phys.: Condens. Matter, 2007, 19, 033101 CrossRef.
- Y. Xiao, S. K. Tang, H. Hao, R. J. Davey and T. Vetter, Quantifying the Inherent Uncertainty Associated with Nucleation Rates Estimated from Induction Time Data Measured in Small Volumes, Cryst. Growth Des., 2017, 17, 2852–2863 Search PubMed.
- A. G. Xyla, E. K. Giannimaras and P. Koutsoukos, The Precipitation of Calcium Carbonate in Aqueous Solutions, Colloids Surf., 1991, 53, 241–255 CrossRef.
- S. Jiang and J. H. ter Horst, Crystal Nucleation Rates from Probability Distributions of Induction Times, Cryst. Growth Des., 2011, 11, 256 Search PubMed.
- C. Brandel and J. H. ter Horst, Measuring Induction Times and Crystal Nucleation Rates, Faraday Discuss., 2015, 179, 199 RSC.
- S. Kotrlý and L. Šucha, Handbook of Chemical Equilibria in Analytical Chemistry, Ellis Horwood Limited, England, 1985 Search PubMed.
- B. Bohner, G. Schuszter, D. Horváth and Á. Tóth, Morphology Control by Flow-driven Self-organizing Precipitation, Chem. Phys. Lett., 2015, 631–632, 114–117 CrossRef.
- B. Bohner, B. Endrödi, D. Horváth and Á. Tóth, Flow-driven Pattern Formation in the Calcium-oxalate System, J. Chem. Phys., 2016, textit144, 164504 CrossRef PubMed.
- A. Baker, Á. Tóth, D. Horváth, J. Walkush, A. S. Ali, W. Morgan, Á. Kukovecz, J. J. Pantaleone and J. Maselko, Precipitation Pattern Formation in the Copper(II) Oxalate System with Gravity Flow and Axial Symmetry, J. Phys. Chem. A, 2009, 113, 8243–8248 CrossRef PubMed.
- F. Haudin, L. A. Riolfo, B. Knaepen, G. M. Homsy and A. De Wit, Experimental Study of a Buoyancy-driven Instability of a Miscible Horizontal Displacement in a Hele-Shaw Cell, Phys. Fluids, 2014, 26, 044102 CrossRef.
| This journal is © the Owner Societies 2018 |