 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solubility prediction from first principles: a density of states approach
Simon
Boothroyd
a,
Andy
Kerridge
 a,
Anders
Broo
b,
David
Buttar
c and
Jamshed
Anwar
a,
Anders
Broo
b,
David
Buttar
c and
Jamshed
Anwar
 *a
*a
aChemical Theory and Computation, Department of Chemistry, Lancaster University, Lancaster LA1 4YB, UK. E-mail: j.anwar@lancaster.ac.uk
bPharmaceutical Science IMED Biotech unit, AstraZeneca, Pepparedsleden 1, Mölndal, 431 83, Sweden
cPharmaceutical Science IMED Biotech unit, AstraZeneca, Silk Road Business Park, Macclesfield, SK10 2NA, UK
First published on 19th July 2018
Abstract
Solubility is a fundamental property of widespread significance. Despite its importance, its efficient and accurate prediction from first principles remains a major challenge. Here we propose a novel method to predict the solubility of molecules using a density of states (DOS) approach from classical molecular simulation. The method offers a potential route to solubility prediction for large (including drug-like) molecules over a range of temperatures and pressures, all from a modest number of simulations. The method was employed to predict the solubility of sodium chloride in water at ambient conditions, yielding a value of 3.77(5) mol kg−1. This is in close agreement with other approaches based on molecular simulation, the consensus literature value being 3.71(25) mol kg−1. The predicted solubility is about half of the experimental value, the disparity being attributed to the known limitation of the Joung–Cheatham force field model employed for NaCl. The proposed method also accurately predicted the NaCl model's solubility over the temperature range 298–373 K directly from the density of states data used to predict the ambient solubility.
1. Introduction
When dissolving a substance in solution, there comes a point when no more will dissolve. The concentration at which this occurs is the solubility limit (the solubility) and depends on the properties of both the solute and solvent. Being a fundamental property, the solubility is of interest across a spectrum of application domains that include chemical toxicity, formulation of foods and development of chemical and pharmaceutical products,1 weathering of the terrestrial and built environments, and formation and dynamics of ecological environments such as soil including fate of pollutants. The solubility is also an important factor in many disease states which include cholesterol deposition in atherosclerosis, formation of gall and kidney stones, and formation of amyloid plaques in disease such as Alzheimer's.2 Another notable example is the interest in the solubility of carbon in the Earth's upper mantle, the latter represents the largest reservoir of carbon on Earth.3 For each of these, considerations of solubility are important for devising relevant interventions. For some of these e.g. pharmaceuticals, being able to accurately predict the solubility from the molecular structure would be a ‘game-changer’.4,5There are three main approaches to solubility prediction: empirical, correlation-based methods,6 quantum mechanical (QM) continuum solvation models such as COSMO-RS,7 and molecular simulation.8 Correlation methods include quantitative structure property relationships (QSPR) based on molecular descriptors, with the parameters being optimised against a dataset of molecular structures with known solubilities. Such models are limited in their usage, breaking down when predicting solubility for molecules that are distinct from the training set. Furthermore, the solubility can only be predicted at the conditions (e.g. temperature and pressure) at which the training set data were collected. The continuum solvation approaches neglect sampling of the solvent degrees of freedom and involve parameterisation, in particular requiring a fitted value for the free energy of fusion for the prediction of solubility of solids.
Molecular simulation offers potentially the more powerful approach to solubility prediction, with the solubility being accessed via statistical mechanics. There are two distinct approaches: via calculation of the chemical potentials9 (summarised below), or direct (brute force) simulation of the dissolution of the solid in a solvent towards equilibrium.10 The latter requires large system sizes to minimise finite-size effects and very long simulations to attain the essential near equilibrium conditions.
At the solubility limit xs, the (undissolved) solid phase coexists with its solution. As the two are in equilibrium, the chemical potential of the solute in the solid phase (μsolid) and that in solution (μsoln) are identical at the given temperature T and pressure p, μsolid(T,p) = μsoln(T,p). Prediction of the solubility therefore requires in general the calculation of the chemical potential of the solute in solution for a series of concentrations, and then interpolation to find where it intersects the chemical potential of the solid (which is calculated separately). Both of these chemical potentials are accessible by molecular simulation. The chemical potential of the solid phase can be calculated via thermodynamic integration of an Einstein crystal11,12 or by quasi-harmonic lattice dynamics. Calculation of the chemical potential of the solute in solution is more demanding, though the methods are well established and include thermodynamic integration,13,14 the so-called perturbation approach,15–17 expanded ensembles,18,19 and variations on these.20 These methods involve ‘growing’ the solute molecule from its reference state reversibly in the solvent. While both thermodynamic integration (TI) and perturbation techniques are robust and effective (particularly when coupled with soft-core21 and dampening potentials22), large drug-like molecules are still challenging, and these methods are computationally very demanding. Each chemical potential determination requires at least a dozen or so separate simulations, which need to be repeated for any other temperature and pressure conditions of interest. To date there are only a few studies that have attempted to predict solubilities from molecular simulation via chemical potential calculations.19,23–28 Much of the focus of these studies has been on the alkali halides with NaCl becoming a model test case.
Here we present a novel method to calculate the solubility directly from the density of states of a system. Density of states (DOS) calculations are well established, being particularly effective and efficient for determining phase co-existence.29–31 The application of DOS methods however has been largely restricted to single, pure component systems. We utilise the DOS framework for multicomponent systems to access phase coexistence of a solid in equilibrium with its solution, and hence the solubility. The method in principle is able to predict solubility for a range of temperatures, pressures and solid forms using a single, density of states. It is more efficient than thermodynamic integration and the perturbation approach. We have successfully applied the methodology to predict the aqueous solubility of sodium chloride.
2. Solubility from density of states
We start by considering a pure system to illustrate how phase coexistence can be determined via a density of states approach, before considering its application to more complicated multicomponent systems.The isothermal–isobaric (NpT) partition function is given by
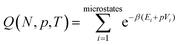 | (1) |
 | (2) |
 | (3) |
If the density of states is known, the phase coexistence condition can be determined by exploring the probability distribution at a given pressure whilst scanning in temperature, or vice versa. The probability distribution of a single component at coexistence exhibits two peaks of equal area, indicating that both phases are equally likely under these conditions. A key feature of the DOS approach is that the density of states Ω(V,E) is independent of T and p. This means that, in principle, coexistence conditions can be determined for a range of temperatures and pressures all from a single density of states.29
We now consider a multicomponent system composed of a number of different molecular species i, j, k,…. Within this system, we allow the number of molecules of one component Ni to fluctuate, while the populations of the other components Nj,Nk,…, are kept fixed.
For such a system, the partition function is given by
 | (4) |
 | (5) |
As before, if Ω(Ni,V,E)Nj,Nk,… is known, exploration of the above probability distribution would enable coexistence conditions to be identified – including the sought-after coexistence point at which the solid phase of component i would be in equilibrium with its solution phase i.e. the solubility. Thus for a given temperature and pressure, tweaking the chemical potential for component i would yield a bimodal probability distribution as a function of number of particles Ni in the Nj,Nk,… mixture system at the solubility limit, from which the solubility concentration can be ascertained. The two coexistence states would be the 100% solute (solid) phase, and its saturated solution (Fig. 1).
We do not, however, need to determine the density of states for the whole spectrum of mole fraction values from xi = 0 (pure solvent) to xi = 1 (pure solute) as implied, though we could. Given that at the solubility limit, μsolid(T,p) = μsoln(T,p), one could substitute the chemical potential of the solid, if it were known, into the probability distribution (eqn (5)). This would guarantee that a peak is observed at xi = 1. A second peak would then be expected at some lower mole fraction, which would correspond to the solubility (Fig. 1). Thus, we can calculate the chemical potential of the solid phase separately, and therefore focus on a limited mole fraction range where the solute remains in solution; the solubility condition will reveal itself as a single peak in the probability distribution located at the corresponding concentration.
The primary challenge therefore is to access the density of states Ω(Ni,V,E)Nj,Nk,…, techniques for which are now well established.33 Here we employ a 3-dimensional variant of the efficient Monte Carlo scheme originally developed by Wang and Landau.32 Configurations are generated according to probability
 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(Ni,V,E)Nj,Nk,…new = ln
Ω(Ni,V,E)Nj,Nk,…new = ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f + ln
f + ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(Ni,V,E)Nj,Nk,…old, where ln
Ω(Ni,V,E)Nj,Nk,…old, where ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f is an arbitrary modification factor. When Ω(Ni,V,E)Nj,Nk,… has converged to its true value, all possible states in the system would be visited with an equal probability. This convergence is tracked by means of a separate histogram of visits to particular states h(Ni,V,E). The density of states is said to have converged when the histogram becomes ‘sufficiently’ flat.
f is an arbitrary modification factor. When Ω(Ni,V,E)Nj,Nk,… has converged to its true value, all possible states in the system would be visited with an equal probability. This convergence is tracked by means of a separate histogram of visits to particular states h(Ni,V,E). The density of states is said to have converged when the histogram becomes ‘sufficiently’ flat.
The density of states is evolved over a number of iterations, beginning with a (gross) value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f = 1. When the histrogram of visits h(Ni,V,E) is sufficiently flat (in our case, when the minimum value is greater than 80% of the average), the value of ln
f = 1. When the histrogram of visits h(Ni,V,E) is sufficiently flat (in our case, when the minimum value is greater than 80% of the average), the value of ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) f is reduced to
f is reduced to  , and the histogram of visits is reset to zero for the next iteration.
, and the histogram of visits is reset to zero for the next iteration.
To explore the (Ni,V,E) space associated with Ω(Ni,V,E)Nj,Nk,…, we employed Monte Carlo simulations involving particle translation, volume scaling, and solute insertion/deletion moves. The respective moves were accepted or rejected in accordance with the following criteria,27 which are valid provided that the volume is sampled logarithmically:
 | (7) |
As is well known, insertion/deletion moves present a particular challenge for dense systems and large solute molecules. Insertions of such molecules in dense systems are invariably rejected due to overlaps, while deletion of species with a high affinity for each other e.g. ion pairs, will often be unfavourable. Here we have devised a creative solution wherein we extend the sampled volume space for the liquid (solution) state to the gas phase for each of the Ni systems, and then proceed to carry out the particle insertion/deletion there (see Fig. 2).
The procedure to predict the solubility, therefore, comprises two distinct stages:
(i) Determination of the 2-d density of states Ω(Ni,V,E)Nj,Nk,… for each solution concentration (…, Ni − 1, Ni, Ni + 1,…), calculated (independently) in the NpT ensemble. The energy and volume ranges are chosen so that both the liquid and gas states are sampled at each particular Ni.
(ii) Determination of the density of states in the gas phase of the full assembly of multiple concentration systems (…, Ni − 1, Ni, Ni + 1,…) in an μVT ensemble (involving particle insertions and deletions) over the entire chosen concentration range, where the volume is chosen such that the number density of the system is sufficiently low that insertion/deletion moves become feasible.
As the density of states for each window is calculated to within a multiplicative constant, the individual density of states windows must be combined using a fitting procedure. This requires finding a set of offsets Cm using least squares, which minimises the error function
 | (8) |
This approach has significant advantages. Firstly, the insertion/deletion moves are favourable even for large solute molecules – the minimum, system number-density (maximum volume) sampled can be increased arbitrarily to accommodate this. Secondly, exploring the volume and concentration dimensions independently greatly reduces the space that must be explored. Instead of having to sample the entire, combined 3-dimensional energy, volume and concentration space (E–V–Ni), one essentially samples the 2-dimensional E–V and E–Ni spaces. Finally, to study broader temperature and pressure ranges, only the solution (liquid) portion of the windows need to be expanded (so as to cover the energies and volumes accessible to the system over the range of conditions to be studied), the rest remains constant. This significantly reduces the number of simulations that must be run when exploring temperature and pressure.
3. Technical details
The above methodology was applied to predict the solubility of NaCl in water. The molecular system contained 200 water molecules and between 6 and 18 sodium chloride pairs, covering a concentration range of ∼1.67–5.00 mol kg−1. The SPC/E model was used to represent the water molecules, while the sodium chloride ion pair were modelled by the Joung–Cheatham (JC/SPC/E) force field.34 A short MC simulation in the NpT ensemble was run for each of the concentrations at T = 298 K and p = 1 atm and T = 373 K and p = 1 atm to determine the accessible energy and volume ranges for the liquid portions of each concentration window. The simulations were repeated in the NVT ensemble at the elevated temperature of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K to determine the maximum and minimum energies accessible for each concentration in the gas phase. The high temperature was necessary to ensure that NaCl ions did not cluster together into a single nucleus, the formation of which would hinder the particle removal moves. The volume for the gas phase was fixed at 28.38 nm3 which, by trial and error, was found to be large enough to easily accommodate the solute insertion moves.
000 K to determine the maximum and minimum energies accessible for each concentration in the gas phase. The high temperature was necessary to ensure that NaCl ions did not cluster together into a single nucleus, the formation of which would hinder the particle removal moves. The volume for the gas phase was fixed at 28.38 nm3 which, by trial and error, was found to be large enough to easily accommodate the solute insertion moves.
We explored two approaches for choosing the accessible volume and energy ranges for states between the liquid and gas regions, shown in Fig. 3. The first approach was to simply interpolate the accessible energies and volumes between the liquid and gas values. For the second approach, at low volumes (those accessible to the liquid) we allowed the system to explore energies ranging from the liquid values all the way to close to the gas values, essentially allowing the liquid to pass into a supercritical regime. At higher volumes, moving towards the gas volume, the system was restricted to exploring only the high energy states. This second pathway was found to give a much faster convergence of the density of states (possibly because the system navigates around the first-order gas to liquid transition), and hence was used in this study.
The energy range (for the whole system i.e. un-normalised by the number of molecules in the system) was discretised into bins of width 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 kJ mol−1 while the logged volume range was discretised into bins of width 0.008. These values where chosen so that the curvature of the peaks in the probability distributions was sufficiently captured, which is also a good indicator that the curvature of the density of states has been sufficiently captured.
000 kJ mol−1 while the logged volume range was discretised into bins of width 0.008. These values where chosen so that the curvature of the peaks in the probability distributions was sufficiently captured, which is also a good indicator that the curvature of the density of states has been sufficiently captured.
The initial value of the Wang–Landau convergence factor was set to 1.0 and was allowed to decrease to 2.384 × 10−7. By this point the relative change in the logged density of states between the current and previous iterations was sufficiently low, indicating that the density of states was converged. Further, both the chemical potentials and the probability distributions had also reached convergence by this point. It is crucial for this method that the density of states has indeed converged as small errors in the density of states can lead to large errors in the probability distribution.
The Monte Carlo code was parallelised using the scheme proposed by Vogel et al.35 to expedite convergence and precision. The (Ni,E,V) space was partitioned into small overlapping chunks with multiple walkers being assigned to each chunk. Three walkers were found to be optimal for each liquid–gas window chunk and four walkers for each gas window chunk.
4. Results and discussion
The probability distribution for the JC/SPC/E model of sodium chloride at 298 K and 1 atm, calculated directly from the density of states by reweighting according to eqn (5), is shown in Fig. 4. The NaCl solid chemical potential was taken as μi = −770.92 kJ mol−1 as reported by Benavides et al.8 Their choice of a de Broglie wavelength of 1.0 Å was adopted in this study. This choice does not affect the phase coexistence as the same value is used for the solution and solid phase calculations.36 | ||
| Fig. 4 The probability distribution for the aqueous sodium chloride system at T = 298 K and p = 1 atm, averaged over five independent runs. | ||
The probability distribution reveals a dominant peak at about 13 NaCl pairs. Taking an ensemble average
 | (9) |
This value is actually roughly half of the experimental solubility of 6.14 mol kg−1. The disparity between the calculated and experimental solubility is due to the model itself (which is currently the best available).8 In relative terms the solubility prediction is decent given that aqueous solubilities predicted by continuum solvation methods are at best within 4-fold of experimental data and often worse. The handful of solubility predictions from molecular simulation that have been reported (including the current study) reveal the critical nature of the force field parameters. Coexistence points are known to challenge force fields but for the same reason serve as essential data points for developing and optimising force field parameter sets.
We then used the determined density of states to ascertain how the chemical potential of NaCl solutions varies as function of concentration, using two distinct approaches. Firstly, we calculated the chemical potential from the density of states for a series of NaCl concentrations by calculating the free energy as a function of concentration, to which a polynomial was fitted and then differentiated with respect to Ni. In the second approach we switched the independent–dependent variables and estimated the NaCl concentrations from probability distributions (as for NaCl solubility) corresponding to a series of chosen chemical potential values between −770.5 and −773.5 kJ mol−1. While both approaches were in good agreement, the latter approach yielded values closer to those calculated by others – the data for which are presented in Fig. 5 along with values presented in the literature for this model.8,26 As can be seen, the predicted values are in excellent agreement with the literature values, confirming that the presented DOS methodology not only offers a robust route to solubility prediction, but also enables the calculation of chemical potentials. In principle, these chemical potentials could be used to obtain the mean ionic activity coefficient of NaCl37 as a function of temperature, provided the chemical potential of NaCl at infinite dilution is also estimated.
 | ||
| Fig. 5 The chemical potential of the JC/SPC/E NaCl model as a function of concentration as calculated by this work (crosses), Vega et al.8 (triangles), Panagiotopoulos et al.26 (squares). | ||
As a further validation of the method, the solubility of the JC/SPC/E NaCl model was calculated for a range of temperatures between 298 K and 374 K, from the same density of states surface as used for the calculation at 298 K. The predicted solubility as a function of temperature is presented in Fig. 6. For each of these calculations, the chemical potential of the NaCl crystal is required at the respective temperature, which was calculated following the procedure outlined by Argones et al.38 and is presented in Table 1.
| T/K | μ solid/kJ mol−1 |
|---|---|
| 313.00 | −770.288(2) |
| 333.00 | −769.359(2) |
| 353.00 | −768.473(2) |
| 373.15 | −767.610(4) |
These chemical potential values of the NaCl solid, along with the density of states, were inserted into eqn (5) in order to generate probability distributions for each temperature, from which the NaCl solubility was determined as before. Counter-intuitively, the solubility of the NaCl model actually decreases as the temperature increases. This result has also been observed by Mester and Panagiotopouls,26 who calculated the solubility of the Joung–Cheatham model of NaCl at 373.15 K to be 3.01(5) mol kg−1 – in close agreement with our value of 2.99(4) mol kg−1. This unexpected behaviour is again attributed as a limitation of the model itself.26
A possible issue with the density of states approach for determining coexistence points is the potential for inadequate sampling of the coexistence states. The required nucleation step characterising first-order transitions (particularly the solid–liquid transition) is often suppressed as the creation of a surface involves an energy penalty. This is not an issue for the solubility prediction approach developed here. We are not sampling the dissolution of the solid nor its crystallisation but rather determining the density of states for the most part of the solution state, albeit around saturation.
There are three main sources of error within the methodology: errors associated with insufficient sampling, detailed balance not being satisfied, and the saturation of error caused by the modification factor reduction scheme. The errors due to saturation and detailed balance have been discussed at depth in the literature,29,39 and are expected to be small relative to the sampling error. Notably, the overall estimated errors in the solubility and chemical potential calculations as determined from five independent sets of simulation were relatively small.
The efficiency gain of the DOS approach with respect to total computing requirement is probably not that marked for a single point solubility calculation relative to existing methods, such as TI or perturbation. The key gain arises from the DOS approach's inherent ability to predict solubilities over a range of temperature and pressure conditions from a single density of states. The calculation of the solid chemical potential is the same regardless whether the DOS approach or an existing methodology is employed, and so no efficiency is gained here. For the solution phase, a chemical potential calculation for a single concentration at a single fixed temperature by TI would involve around 21 simulations, one per lambda state.8 Calculating the chemical potential of, say 10 concentrations, would then require 210 simulations. Should these then be repeated for the four additional temperatures considered by us, would result in a total of 1050 simulations. In contrast, for the DOS approach, we will probably need to investigate between 10–20 different concentrations to locate and fully capture the probability distribution that corresponds to the solution at saturation. For each of these concentrations we require three simulations – one to calculate the DOS of the solution phase, one to connect the solution and supercritical states, and one to connect the supercritical and gas states. For say 20 concentrations, this would amount to 60 simulations, plus one additional DOS calculation in the gas phase that connects the individual concentrations. Comparing the 61 DOS simulations with 1050 TI simulations yields a speed-up of about 17×.
While the DOS method has been applied only to a simple ionic system, we do not expect any significant challenges in extending the approach to larger solute molecules (including drug-like) in both aqueous and non-aqueous solvents. The switching from ions to molecules only requires a change in the density of the gas phase, avoiding the problematic creation and annihilation of particles in a condensed phase, which is a key benefit of the proposed method. Further, as the method samples only according to the density of states (i.e. entropy space), thermal barriers, such as those limiting dihedral rotations are expected to be less of an issue here than perhaps in other methods. For more challenging flexible molecules, the method could be coupled with established configurational-bias Monte Carlo moves to facilitate more efficient sampling of their molecular degrees of freedom.
In summary, we have developed and demonstrated a density of states approach to predicting solubility from molecular simulation. The method entails calculation of the density of states for a multicomponent solution, followed by exploration of the probability distribution as a function of number of solute particles in the system and the chemical potential of the solid, to identify coexistence conditions corresponding to the solubility. The density of states calculation is made possible by a unique pathway that avoids the problematic annihilation and/or creation of particles which is common to established methods. Consequently, the method is expected to perform well even for large, drug-like molecules. Further, it is able to yield, relatively efficiently, solubilities over a range of temperatures and pressures. The predicted solubility of the NaCl model at 298 K was found to be in close agreement with the literature.
Author contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
S. B. would like to thank the EPSRC, Lancaster University, and AstraZeneca for his PhD CASE Studentship (EP/L504804/1). We acknowledge the use of Lancaster University's high-performance computing (HPC) facility (HEC) and the N8 (consortium of the U.K.'s northern universities) HPC facility (Polaris).References
- S. P. Pinho and E. A. Macedo, Dev. Appl. Solubility, Royal Society of Chemistry, Cambridge, 2007, pp. 305–322 Search PubMed.
- J. D. Harper and P. T. Lansbury, Annu. Rev. Biochem., 1997, 66, 385 CrossRef PubMed.
- R. Dasgupta and D. Walker, Geochim. Cosmochim. Acta, 2008, 72, 4627 CrossRef.
- C. R. Gardner, C. T. Walsh and Ö. Almarsson, Nat. Rev. Drug Discovery, 2004, 3, 926 CrossRef PubMed.
- B. Faller and P. Ertl, Adv. Drug Delivery Rev., 2007, 59, 533 CrossRef PubMed.
- W. L. Jorgensen and E. M. Duffy, Adv. Drug Delivery Rev., 2002, 54, 355 CrossRef PubMed.
- A. Klamt, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1338 Search PubMed.
- A. L. Benavides, J. L. Aragones and C. Vega, J. Chem. Phys., 2016, 144, 124504 CrossRef PubMed.
- M. Ferrario, G. Ciccotti, E. Spohr, T. Cartailler and P. Turq, J. Chem. Phys., 2002, 117, 4947 CrossRef.
- J. R. Espinosa, J. M. Young, H. Jiang, D. Gupta, C. Vega, E. Sanz, P. G. Debenedetti and A. Z. Panagiotopoulos, J. Chem. Phys., 2016, 145, 154111 CrossRef PubMed.
- D. Frenkel and A. J. C. Ladd, J. Chem. Phys., 1984, 81, 3188 CrossRef.
- C. Vega and E. G. Noya, J. Chem. Phys., 2007, 127, 154113 CrossRef PubMed.
- T. P. Straatsma and H. J. C. Berendsen, J. Chem. Phys., 1988, 89, 5876 CrossRef.
- T. P. Straatsma and J. A. McCammon, Annu. Rev. Phys. Chem., 1992, 43, 407 CrossRef.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300 CrossRef.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420 CrossRef.
- Free Energy Calculations Theory and Applications in Chemistry and Biology, ed. C. Chipot and A. Pohorille, Springer, Berlin, Heidelberg, 2007, pp. 33–75 Search PubMed.
- A. P. Lyubartsev, A. A. Martsinovski, S. V. Shevkunov and P. N. Vorontsov-Velyaminov, J. Chem. Phys., 1992, 96, 1776 CrossRef.
- A. S. Paluch, D. D. Cryan and E. J. Maginn, J. Chem. Eng. Data, 2011, 56, 1587 CrossRef.
- F. Moučka, I. Nezbeda and W. R. Smith, J. Chem. Phys., 2013, 138, 154102 CrossRef PubMed.
- T. C. Beutler, A. E. Mark, R. C. van Schaik, P. R. Gerber and W. F. van Gunsteren, Chem. Phys. Lett., 1994, 222, 529 CrossRef.
- J. Anwar and D. M. Heyes, J. Chem. Phys., 2005, 122, 224117 CrossRef PubMed.
- M. A. Barroso and A. L. Ferreira, J. Chem. Phys., 2002, 116, 7145 CrossRef.
- J. L. Aragones, E. Sanz and C. Vega, J. Chem. Phys., 2012, 136, 244508 CrossRef PubMed.
- M. Lísal, W. R. Smith and J. J. Kolafa, J. Phys. Chem. B, 2005, 109, 12956 CrossRef PubMed.
- Z. Mester and A. Z. Panagiotopoulos, J. Chem. Phys., 2015, 143, 44505 CrossRef PubMed.
- C. Herdes, T. S. Totton and E. A. Müller, Fluid Phase Equilib., 2015, 406, 91 CrossRef.
- L. Li, T. Totton and D. Frenkel, J. Chem. Phys., 2017, 146, 214110 CrossRef PubMed.
- M. S. Shell, P. G. Debenedetti and A. Z. Panagiotopoulos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 56703 CrossRef PubMed.
- E. A. Mastny and J. J. de Pablo, J. Chem. Phys., 2005, 122, 124109 CrossRef PubMed.
- Q. Yan, R. Faller and J. J. de Pablo, J. Chem. Phys., 2002, 116, 8745 CrossRef.
- F. Wang and D. P. Landau, Phys. Rev. Lett., 2001, 86, 2050 CrossRef PubMed.
- S. Singh, M. Chopra and J. J. de Pablo, Annu. Rev. Chem. Biomol. Eng., 2012, 3, 369 CrossRef PubMed.
- I. S. Joung and T. E. Cheatham, J. Phys. Chem. B, 2008, 112, 9020 CrossRef PubMed.
- T. Vogel, Y. W. Li, T. Wüst and D. P. Landau, Phys. Rev. Lett., 2013, 110, 210603 CrossRef PubMed.
- C. Vega, E. Sanz, J. L. F. Abascal and E. G. Noya, J. Phys.: Condens. Matter, 2008, 20, 153101 CrossRef.
- Z. Mester and A. Z. Panagiotopoulos, J. Chem. Phys., 2015, 142, 44507 CrossRef PubMed.
- J. L. Aragones, C. Valeriani and C. Vega, J. Chem. Phys., 2012, 137, 146101 CrossRef PubMed.
- S. Schneider, M. Mueller and W. Janke, Comput. Phys. Commun., 2017, 216, 1 CrossRef.
| This journal is © the Owner Societies 2018 |







